平行线模型经典例题
平行线四种常见模型解题技巧(解析版)--2024年新八年级数学

平行线四种常见模型解题技巧题型聚焦题型一:“猪蹄”模型题型二:“铅笔”模型题型三:“鸡翅”模型题型四:“骨折”模型难题突破模型一:“猪蹄”模型如图,若AB⎳CD,你能确定∠B、∠D与∠BED的大小关系吗?解:∠B+∠D=∠DEB.理由如下:过点E 作 EF⎳AB又 ∵AB⎳CD.∴EF⎳CD.∴∠D=∠DEF.∠B=∠BEF.∴∠B+∠D=∠BEF+∠DEF=∠DEB即∠B+∠D=∠DEB.猪蹄模型的基本特征:一组平行线,中间有一个点,分别与平行线上的点构成“猪蹄”。
如图,已知AB∥CD,求∠E、∠B、∠D之间的数量关系.思路1:过拐点作平行线过点E作EF∥AB,∴∠B=∠BEF,又∵AB∥CD,∴EF∥CD,∴∠D=∠DEF,∴∠E=∠BEF+∠DEF=∠B+∠D.∴∠E=∠B+∠D.思路2:延长BE交CD于点F∵AB∥CD,∴∠B=∠BFD,∴∠D+∠BFD=∠BED,∴∠B+∠D=∠E.小结证明的方法还有很多,同学们可以多多尝试。
重点在于构造平行线的三线八角,就可以得到经典结论:猪蹄模型顶点在同一侧的角之和等于顶点在另一侧的角之和。
猪蹄模型(又名燕尾模型、M字模型)结论:∠B+∠D=∠E步骤总结步骤一:过猪蹄(拐点)作平行线步骤二:借助平行线的性质找相等或互补的角步骤三:推导出角的数量关系模型二、“铅笔”模型如图,AB⎳CD,探索∠B、∠D与∠DEB的大小关系?解:∠B+∠D+∠DEB=360°.理由如下:过点E 作 EF⎳AB.又 ∵AB⎳CD.∴EF⎳CD.∴∠B+∠BEF=180°.∠D+∠DEF=180°.∴∠B+∠D+∠DEB=∠B+∠D+∠BEF+∠DEF=360°.即∠B+∠D+∠DEB=360°.从猪蹄模型可以看出,点E是凹进去了,如果点E是凸出来,如下图:那么,像这样的模型,我们就称为铅笔头模型。
模型结论:∠B+∠E+∠D=360°二、模型证明如图,若AB⎳CD,求证:∠B+∠E+∠D=360°证明一:如图,过点E作FG⎳AB∵ AB⎳FG,AB⎳CD∴ FG⎳CD∵ AB⎳FG∴∠BEF+∠B=180°(两直线平行,同旁内角互补)∵FG⎳CD∴ ∠D+∠DEF=180°(两直线平行,同旁内角互补)∴ ∠BEF+∠B+∠D+∠DEF=360°∴∠B+∠D+∠BED=360°证明二:如图,连接BD,∵AB⎳CD∴∠ABD+∠BDC=180°在△BDE中,∠DBE+∠E+∠EDB=180°∴ ∠DBE+∠E+∠EDB+∠ABD+∠BDC=360°∴ ∠ABD+∠DBE+∠E+∠EDB+∠BDC=360°∴∠ABE+∠E+∠CDE=360°证明该模型结论的还有其他方法,这里就没有全部写出来,可以自行证明。
平行线常见模型专题练习(基础)(解析版)

平行线常见模型(基础)专题练习模型一:结论:∠E =∠B +∠C1、如图,已知直线a ∥b ,∠1=40°,∠2=60°.则∠3等于( )A. 100°B. 60°C. 40°D. 20°答案:A解答:过点C 作CD ∥a ,∵a ∥b ,∴CD ∥a ∥b ,∴∠ACD =∠1=40°,∠BCD =∠2=60°,∴∠3=∠ACD +∠BCD =100°.选A.2、如图,∠BCD =70°,AB ∥DE ,则∠α与∠β满足( )A. ∠α+∠β=110°B. ∠α+∠β=70°C. ∠β-∠α=70°D. ∠α+∠β=90°答案:B解答:如图,过点C 作CF ∥AB , DAbD∵AB ∥DE ,∴AB ∥CF ∥DE ,∴∠BCF =∠α,∠DCF =∠β,∵∠BCD =70°,∴∠BCD =∠BCF +∠DCF =∠α+∠β=70°,∴∠α+∠β=70°.选B.3、如图,已知AB //CD ,∠A =40°,∠C =60°,试求∠AEC 为( ).A. 90°B. 100°C. 110°D. 120°答案:B解答:如图,过点E 作EF //AB ,∵AB //CD ,EF //AB ,∴EF //CD.∴∠A =∠AEF =40°,∠C =∠CEF =60°故∠AEC =∠AEF +∠CEF =∠A +∠C =100°.4、如图,已知//130235AB DE ∠︒∠︒,=,=,则∠BCE 的度数为( )A. 70°B. 65°C. 35°D. 55°答案:B解答:过点C 作CF//AB ,//130235AB DE ∠︒∠︒,=,=∴CF//AB//DE∴130,235FCE ∠∠︒∠=∠=︒=BCF=∴1265BCE BCF ECF ∠=∠+=∠+∠=︒.选B.5、如图,已知//a b ,将直角三角形如图放置,若∠2=40°,则∠1为( )A. 120°B. 130°C. 140°D. 150°答案:B解答:标注字母,如图所示,过A 作AB ∥a ,∵a ∥b ,∴a ∥b ∥AB ,∴∠2=∠3=40°,∠4=∠5,又∵∠CAD =90°,∴∠4=50°,∴∠5=50°,∴∠1=180°-50°=130°,选B.6、如图,AB ∥EF ,CD ⊥EF ,∠BAC =50°,则∠ACD =( )A. 120°B. 130°C. 140°D. 150°答案:C解答:如图,延长AC交EF于点G;∵AB∥EF,∴∠DGC=∠BAC=50°;∵CD⊥EF,∴∠CDG=90°,∴∠ACD=90°+50°=140°,选C.7、如图,AB//EF,CD⊥EF于点D,若∠ABC=40°,则∠BCD=().A. 140°B. 130°C. 120°D. 110°答案:B解答:过点C作CG//AB,由题意可得:AB//EF//CG,故∠B=∠BCG,∠GCD=90°,则∠BCD=40°+90°=130°.8、如图,AB//CD,ME⊥MF,∠EAB=36°,则∠FCD=().A. 36°B. 54°C. 72°D. 25°答案:B解答:过点M 作MN //AB ,∵AB //CD ,∴AB //CD //MN ,∴∠AMN =∠EAB =36°,∵ME ⊥MF ,∴∠AMC =90°,∴∠NMC =90°-36°=54°,∴∠FCD =54°.故答案为54°.9、如图,AB //CD ,15,25A C ︒︒∠=∠=则M ∠=______答案:40°解答:过点M 作//MN AB ,//AB CD ,////MN AB CD ∴,115A ∴∠=∠=︒,225C ∠=∠=︒,12152540AMC ∴∠=∠+∠=︒+︒=︒.故答案为:40︒.10、如图,直线a //b ,则∠ACB =______.答案:78°解答:如图,延长BC 与a 相交,∵a //b ,∴∠1=∠50°,∴∠ACB =∠1+28°=50°+28°=78°,故应填78°.11、如图,AFf //CD ,ABf //EF ,BCf //ED ,则x =______°.答案:100解答:∵AB //EF∴∠AFE =180°-∠BAF =60°∵BC //ED∴∠EDC =∠BCF =40°根据猪蹄模型,∠FED =∠AFE +∠CDE ,即x =60°+40°=100°.12、如图,//,,3527'EE MN CA CB EAC ⊥∠=︒,则MBC ∠=______.答案:5433'解答:过C 点做EF 的平行线,GH//,EF MN////,EF GH MN ∴3527'EAC ACH ∴∠=∠=,又,CA CB ⊥90,ACB ∴∠=︒5433',HCB ACB ACH ∴∠=∠-∠=︒又//,GH MN5433'HCB CBM ∴∠=∠=.故答案为:5433'.13、如图所示,AB //CD ,∠1=50°,∠2=110°,则∠3=______.答案:60°解答:如图所示,过点P 作l //AB ,又AB //CD ,则l //CD ,∴∠4=∠1=50°,∠5=180°-∠2=180°-110°=70°,∠3=180°-∠4-∠5=180°-50°-70°=60°.14、如图,AB //CD ,且∠BAP =60°-α,∠APC =45°+α,∠PCD =30°-α,则α=______°.答案:15解答:过P 点作直线l ,使得l //AB //CD ,∵l //AB //CD ,∴∠BAP =∠1,∠DCP =∠2,∵∠APC =∠1+∠2,∴∠APC =∠BAP +∠DCP ,∴45°+α=60°-α+30°-α=90°-2α,解得:α=15°.15、在数学课本中,有这样一道题:已知:如图1,B C BEC ∠+∠=∠.求证://AB CD 请补充下面证明过程:证明:过点E ,作//EF AB ,如图2∴B ∠=∠______(________________________)∵B C BEC ∠+∠=∠,BEF ∠+∠______=BEC ∠(已知)∴B C BEF FEC ∠+∠=∠+∠(________________________)∴∠______=∠______∴//EF ______(________________________)∵//EF AB∴//AB CD答案:BEF ;两直线平行内错角相等;FEC ;等量代换;C ;FEC ;DC ;内错角相等两直线平行解答:证明:过点E ,作//EF AB ,如图2,B BEF ∴∠=∠(两直线平行内错角相等), B C BEC ∠+∠=∠,BEF FEC BEC ∠+∠=∠(已知),B C BEF FEC ∴∠+∠=∠+∠(等量代换),C FEC ∴∠=∠,//EF DC ∴(内错角相等两直线平行), //EF AB ,//AB CD ∴.故答案为:BEF ,两直线平行内错角相等,FEC ,等量代换,C ,FEC ,DC ,内错角相等两直线平行.16、如图,已知AB //CD ,试写出、、∠AEC 、∠A 、∠C 的数量关系并证明.答案:解答:证明:过点E 作ME //AB∵AB //CD (已知),ME //AB (已作)∴ME //CD (平行于同一直线的两直线平行)∴∠A =∠AEM ,∠C =∠CEM (两直线平行,内错角相等)∵∠AEC =∠AEM +∠CEM (已知)∴∠AEC =∠A +∠C (等量代换).17、如图,已知:∠A +∠D =180°,∠B =55°,∠C =35°.求证:BE ⊥CE .答案:证明见解答.解答:过E 作EF //AB ,∵∠A +∠D =180°,∴AB //DC ,∴EF //DC.∵EF //AB ,∠B =55°,∴∠BEF =∠B =55°.∵EF //DC ,∠C =35°,∴∠CEF =∠C =35°,∴∠BEC =∠BEF +CEF =90°,∴BE ⊥CE .模型二:结论:∠B +∠C +∠E =360°18、如图,已知//AB DE ,则123∠+∠+∠的度数是( )A. 180︒B. 270︒C. 360︒D. 540︒ 答案:C解答:过点C 作CF //AB ,∵CF //AB ,//AB DE ,∴CF //ED ,∴∠1+∠ACF =180°,∠FCD +∠3=180°,∵∠2=∠FCD +∠ACF ,∴123∠+∠+∠=∠1+∠ACF +∠FCD +∠3=180°+180°=360°. 选C.19、如图,已知AB //CD ,则α∠,β∠,γ∠之间的等量关系为( )DAEA. 180αβγ∠+∠-∠=︒B. 180βγα︒∠+∠-∠=C.360αβγ︒∠+∠+∠= D. 180αβγ∠+∠+∠=︒答案:C解答:过点E 作EF ∥AB ,则EF ∥CD ,如图,∵AB ∥EF ∥CD ,∴∠γ+∠FED =180°,∵∠ABE +∠FEB =180°,∠ABE =∠α,∠FED +∠FEB =∠β,∴∠γ+∠FED +∠ABE +∠FEB =360°,∴∠α+∠β+∠γ=360°,选C.20、如图所示,AB //ED ,∠α=∠A +∠E ,∠β=∠B +∠C +∠D ,则β和α的数量关系是().A. 2β=3αB. β=2αC. 2β=5αD. β=3α 答案:B解答:∵AB //ED ,∴∠α=∠A +∠E =180°,∵五边形内角和为180°×5-2=540°,∴∠β=∠B +∠C +∠D =540°-∠A -∠E =540°-180°=360°,∴β和α的数量关系是β=2α.选B.21、如图,已知AB//CD//EF,EH⊥CD于H,则∠BAC+∠ACE+∠CEH等于______°.答案:270解答:∵AB//CD,∴∠BAC+∠ACD=180°,同理∠DCE+∠CEF=180°,∴∠BAC+∠ACE+∠CEF=360°;又∵EH⊥CD于H,∴∠HEF=90°,∴∠BAC+∠ACE+∠CEH=∠BAC+∠ACE+∠CEF-∠HEF=360°-90°=270°.22、如图,a//b,M、N分别为a、b上,P为两平行线间一点,则∠1+∠2+∠3=______.答案:360°解答:过点P作P A//a,∵a//b,P A//a,∴a//b(//P A,∴∠1+∠MP A=180°,∠3+∠APN=180°,∴∠1+∠MP A+∠3+∠APN=180°+180°=360°,∴∠1+∠2+∠3=360°.故答案为:360°.模型三: 结论:∠C =∠B +∠E23、如图,已知AB //CD ,若∠A =15°,∠E =25°,则∠C 的值为( ).A. 15°B. 25°C. 35°D. 40°答案:D解答:有图形知∠E =∠C -∠A =25°.所以∠C =40°.24、如图,直线AB //CD ,∠A =100°,∠C =75°,则∠E 等于______.答案:25°解答:设DC 、AE 交于点F ,∵直线AB //CD ,∠A =100°,∴∠EFD =∠A =100°,∵∠EFD 是△CEF 的外角,∴∠E =∠EFD -∠C =100°-75°=25°.25、如图,已知AB //CD ,试写出∠BPD 、∠B 、∠D 的数量关系并证明.DA答案:解答:证明:过P 点做AB 的平行线MN∵AB //CD (已知),MN //AB (已作)∴MN //CD (平行于同一直线的两直线平行)∴∠MPD =∠D ,∠MPB =∠B (两直线平行,内错角相等)∵∠BPD =∠MPD -∠MPB (已知)∴∠BPD =∠D -∠B (等量代换)模型四:结论:∠B =∠C +∠E26、如图,CD //BE ,则∠2+∠3-∠1的度数等于( ).A. 90°B. 120°C. 150°D. 180°答案:D解答:过A 点作AK //BE∴∠3=∠BAK .AD //CD∴∠KAC +∠2=180°∠KAC =∠BAK -∠1D CA∴∠KAC =∠3-∠1.∴∠3-∠1+∠2=180°.27、已知如图所示,DE //CB ,求证:∠AED =∠A +∠B.答案:证明见解答.解答:过A 作AF //CB ,如图所示,则有∠F AB =∠B ,因为DE //CB ,故AF //DE ,∠AED =∠EAF =∠EAB +∠F AB ,即∠AED =∠A +∠B.28、如图所示,//AD BC ,1CFE D ∠=∠+∠,30B CFE ∠-∠=︒,求2∠的度数.答案:230∠=︒.解答:因为//AD BC ,结合题意,由靴子图ABEFC 知,1B CFE ∠=∠+∠,130B CFE ∠=∠-∠=︒,由靴子图ABEDC 知,12B BED D D ∠=∠+∠=∠+∠+∠,1B CFE ∠=∠+∠,121D CFE ∴∠+∠+∠=∠+∠即2D CFE ∠+∠=∠,1CFE D ∠=∠+∠,2130∴∠=∠=︒29、“平行线”是转化角的重要“桥梁”,运用平行线的判定和性质解决下面的问题: 在下列三个图形中,已知AB //CD ,P 是平面内一点.(1)填空:在图1中,∠P 与∠A 、∠C 的关系是______;在图2中,∠P与∠A、∠C的关系是______;在图3中,∠P与∠A、∠C的关系是______.(2)选择图2证明你的结论(不用注明理由).答案:(1)∠P=∠A+∠C;∠P=∠C-∠A;∠P=∠A-∠C (2)证明见解答.解答:(1)图1:∠P=∠A+∠C.图2:∠P=∠C-∠A.图3:∠P=∠A-∠C.(2)图2证明过程:过点P作EF//AB,∴∠A=∠EP A,∵AB//CD,∴EF//CD.∴∠C=∠EPC,∴∠P:∠EPC-∠EP A=∠C-∠A.图1证明过程:过点P作EF//AB,∴EF//AB//CD,∴∠A=∠EP A,∠C=∠FPC,∴∠P=∠APE+∠CPE=∠A+∠C.图3证明过程:过点P作EF//AB,∴EF//AB//CD,∴∠C+∠CPF=180°,∠A+∠APF=180°,∴∠CPF=180°-∠C,∠APF=180°-∠A,∴∠P=∠CPF-∠APF=180°-∠C-(180°-∠A).=∠A-∠C.30、如图,已知AB//CD,分别探讨下面的四个图形中∠APC、∠P AB和∠PCD的关系,并请你从所得的五个关系中的图2,图5,说明成立的理由.(1)图①的关系是______.(2)图②的关系是______.(3)图③的关系是______.(4)图④的关系是______.(5)图⑤的关系是______.答案:(1)∠APC+∠P AB+∠PCD=360°(2)∠APC=∠P AB+∠PCD(3)∠P AB+∠APC=∠PCD(4)∠APC+∠P AB=∠PCD(5)∠APC+∠P AB-∠PCD=180°解答:(1)作PE//AB,易证AB//PE//CD,∴∠1+∠2=180°,∠3+∠4=180°,∠2+∠3=∠APC,∴∠1+∠2+∠3+∠4=360°,即∠APC+∠P AB+∠PCD=360°.(2)作PE//AB,易证AB//PE//CD,∴∠P AB=∠1,∠PCD=∠2,∠1+∠mathbf2=∠APC,∴∠APC=∠P AB+∠PCD.(3)同理:∠PCD=∠1,∠P AB=∠2,∠1-∠2=∠APC,∴∠P AB+∠APC=∠PCD.(4)同理:∠P AB=∠2,∠PCD=∠1,∠1-∠2=∠APC,∴∠APC+∠P AB=∠PCD. (5)同理:∠P AB+∠1=180°,即∠1=180°-∠P AB,∠PCD=∠2,∠1+∠2=∠APC,∴∠APC=180°-∠P AB+∠PCD,即∠APC+∠P AB-∠PCD=180°.。
平行线中的模型-初中数学常见的模型方法专题

5.如图,已知AB∥DE,∠1=30°,∠2=35°,则∠BCE的度数为( )
A. 70°B. 65°C. 35°D. 5°
【答案】B
【解析】
【分析】作CF∥AB,根据平行线的性质可以得到∠1=∠BCF,∠FCE=∠2,从而可得∠BCE的度数,本题得以解决.
【详解】作CF∥AB,
∵AB∥DE,
=180°-[180°-(4x°+4y°)]
=4x°+4y°
=4(x°+y°),
∠AFC=180°-(∠FAC+∠FCA)
=180°-[180°-(3x°+3y°)]
=3x°+3y°
=3(x°+y°),
∴∠AFC= ∠AEC.
【点睛】本题考查了平行线性质和三角形内角和定理的应用,解题时注意:两直线平行,同旁内角互补.
【详解】证明:连接AC,
设∠EAF=x°,∠ECF=y°,∠EAB=4x°,∠ECD=4y°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠CAE+4x°+∠ACE+4y°=180°,
∴∠CAE+∠ACE=180°-(4x°+4y°),∠FAC+∠FCA=180°-(3x°+3y°)
∴∠AEC=180°-(∠CAE+∠ACE)
∴∠BCD+∠DCF=∠B+∠F,
即∠C=∠B+∠F.
(3)∠1+∠3+∠5=∠2+∠4,
如图,
作MN∥AB,
由(2)的结论得到∠2=∠1+∠6,∠4=∠5+∠7,
∴∠2+∠4=∠1+∠6+∠5+∠7=∠1+∠3+∠5.
专题01 平行线的四大模型(解析版)-【常考压轴题】2023-2024学年七年级数学下册压轴题攻略

专题01平行线的四大模型平行线的性质和判定是证明角相等、研究角的关系的重要依据,是研究几何图形位置关系与数量关系的基础,是平面几何的一个重要内容和学习简单的逻辑推理的素材。
它不但为三角形的内角和定理的证明提供了转化的方法,而且也是今后学习三角形、四边形知识的基础.本节课重点学习平行线的基础模型的应用迁移.模型一“铅笔”模型点P在EF右侧,在AB、CD内部“铅笔”模型结论1:若AB∥CD,则∠P+∠AEP+∠PFC=360°;结论2:若∠P+∠AEP+∠PFC=360°,则AB∥CD.【典例1】(2023秋•南岗区校级期中)已知,射线FG分别交射线AB、DC于点F、G,点E为射线FG上一点.(1)如图1,若∠A+∠D=∠AED,求证:AB∥CD.(2)如图2,若AB∥CD,求证:∠A﹣∠D=∠AED.专题分析模型分类模型分析典例分析(3)如图3,在(2)的条件下,DI交AI于点Ⅰ,交AE于点K,∠EDI=∠CDE,∠BAI=∠EAI,∠I=∠AED=25°,求∠EKD的度数.【答案】(1)(2)证明见解析;(3)95°.【解答】(1)证明:如图所示:过点E作EH∥AB,∴∠A=∠AEF,∵∠A+∠D=∠AED,∠AED=∠AEF+∠DEF,∴∠D=∠DEF,∴EF∥CD,∴AB∥CD;(2)证明:∵AB∥CD,∴∠A=∠EHG,∵∠EHG=∠D+∠AED,∴∠A=∠D+∠AED,∴∠A﹣∠D=∠AED;(3)解:设AE与CD交于点H,∠EAI=x,则∠BAI=,,∵AB∥CD,∴∠EHC=∠EAB=,∵∠I=∠AED=25°,∠EKI=∠EAI+∠I=∠EDI+∠AED,∴x+25°=∠EDI+25°,∴∠EDI=x,∵∠EDI=∠CDE,∴∠CDI=,∵∠CHE=∠CDE+∠AED,∴,解得:x=60°,∴∠EKD=∠AKI=180°﹣∠EAI﹣∠I=180°﹣60°﹣25°=95°.【变式1-1】(2023•渝中区校级模拟)如图,已知直线a∥b,∠BAC=90°,∠1=40°,则∠2的度数为()A.40°B.50°C.130°D.140°【答案】B【解答】解:如图,∵∠1+∠3+90°=180°,∠1=40°,∴∠3=50°,∵a∥b,∴∠2=∠3,∴∠2=50°,故选:B.【变式1-2】(2023•金安区一模)如图,已知a∥b,∠1=45°,∠2=125°,则∠ABC的度数为()A.100°B.105°C.115°D.125°【答案】A【解答】解:解法一:如图,过点B作DE∥a,∴∠DBA=∠1=45°,∵a∥b,DE∥a,∴DE∥b,∴∠2+∠DBC=180°,∴∠DBC=180°﹣∠2=180°﹣125°=55°,∴∠ABC=∠DBA+∠DBC=45°+55°=100°.解法二:如图,延长AB交b于点F,∵a∥b,∴∠1=∠3=45°,∵∠2=125°,∵∠2=∠3+∠CBF,∴∠CBF=∠2﹣∠3=125°﹣45°=80°,∴∠ABC=180°﹣∠CBF=180°﹣80°=100°.故选:A.【变式1-3】(2022春•肇州县期末)如图,AB∥CD,∠C=110°,∠B=120°,则∠BEC =()A.110°B.120°C.130°D.150°【答案】C【解答】解:∵过点E作EF∥AB,∵AB∥CD,∴EF∥AB∥CD,∴∠1+∠B=180°,∠2+∠C=180°,∵∠C=110°,∠B=120°,∴∠1=60°,∠2=70°,∴∠BEC=∠1+∠2=130°.故选:C.【变式1-4】(2023春•巴南区月考)已知直线MN∥PQ,点C、B分别在直线MN、PQ上,点A在直线MN和PO之间.(1)如图1,求证:∠CAB﹣∠MCA=∠PBA;(2)如图2,CD∥AB,点E在直线PQ上,且∠MCA=∠DCE,求证:∠ECN=∠CAB;(3)如图3,BF平分∠PBA,CG平分∠ACN,且AF∥CG.若∠CAB=50°,直接写出∠AFB的度数.【答案】(1)见解答.(2)见解答.(3)115°.【解答】(1)证明:过点A作AH∥MN,如图:∴AH∥MN∥PQ,∴∠MCA=∠CAH,∠PBA=∠BAH,∴∠CAB=∠CAH+∠BAH=∠MCA+∠PBA,∴:∠CAB﹣∠MCA=∠PBA.(2)证明:∵∠MCA=∠DCE.∴∠ACD=∠MCE,∵CD∥AB,∴∠CAB+∠ACD=180°,∴∠CAB=180°﹣∠ACD=180°﹣∠MCE,=∠ECN,∴∠ECN=∠CAB.(3)解:∵AF∥CG.∴∠GCA+∠FAC=180°,∵∠CAB=50°,∴∠GCA+∠CAB+∠FAC=180°,∴∠FAB=130°﹣∠GCA,∵BF平分∠PBA,CG平分∠ACN,∴∠ACN=2∠GCA,∠ABP=2∠ABF,又∵∠MCA=180°﹣∠ACN,∴∠CAB=180°﹣2∠GCA+2∠ABF=50°,∴∠GCA﹣∠ABF=65°,∵∠ABF+∠AFB+∠FAB=180°,∴∠AFB=180°﹣∠ABF﹣∠FAB=180°﹣(130°﹣∠GCA)﹣∠ABF=50°+∠GCA﹣∠ABF=50°+65°=115°.∴∠AFB=115°.【变式1-5】(2023春•遂宁期末)如图,直线PQ∥MN,两个三角形如图①放置,其中∠ABC=∠CDE=90°,∠ACB=30°,∠BAC=60°,∠DCE=∠DEC=45°,点E在直线PQ上,点B,C均在直线MN上,且CE平分∠ACN.(1)求∠DEQ的度数;(2)如图②,若将△ABC绕B点以每秒3°的速度按逆时针方向旋转(A,C的对应点分别为F,G).设旋转时间为t秒,当t=10时,边BG与CD有何位置关系?请说明理由.【答案】(1)60°;(2)BG∥CD,理由见解析.【解答】解:(1)∵∠ACB=30°,∴∠ACN=180°﹣∠ACB=150°,∵CE平分∠ACN,∴∠ECN=75°,∵PQ∥MN,∴∠ECN+∠CEQ=180°,∴∠CEQ=105°,∵∠DEC=45°,∴∠DEQ=∠CEQ﹣∠DEC=60°;(2)BG∥CD,理由如下:当t=10时,BC转动了3×10°=30°,即∠CBG=30°,由(1)可知∠ECN=75°,∠DCE=45°,∴∠DCN=∠ECN﹣∠DCE=30°,∴∠CBG=∠DCN,∴BG∥CD.模型分析结论1:若AB∥CD,则∠P=∠AEP+∠CFP;结论2:若∠P=∠AEP+∠CFP,则AB∥CD.典例分析【典例2】(2023春•邵阳县期末)如图,直线AB∥CD,连接EF,直线AB,CD及线段EF 把平面分成①②③④四个部分,规定:线上各点不属于任何部分.当动点G落在某个部分时,连接GE,GF,构成∠EGF,∠GEB,∠GFD三个角.(1)当动点G落在第③部分时,如图一,试说明:∠EGF,∠GEB,∠GFD三者的关系;(2)当动点G落在第②部分时,如图二,思考(1)中三者关系是否仍然成立若不成立,说明理由.【答案】(1)∠EGF=∠GEB+∠GFD,理由见解答;(2)(1)中三者关系不成立,理由见解答.【解答】解:(1)∠EGF=∠GEB+∠GFD,理由:过点G作GM∥AB,∴∠GEB=∠EGM,∵AB∥CD,∴CD∥GM,∴∠GFD=∠FGM,∵∠EGF=∠EGM+∠FGM,∴∠EGF=∠GEB+∠GFD;(2)(1)中三者关系不成立,理由:过点G作GN∥AB,∴∠GEB+∠EGN=180°,∵AB∥CD,∴CD∥GN,∴∠GFD+∠FGN=180°,∴∠GEB+∠EGN+∠FGN+∠GFD=360°,即∠GEB+∠EGF+∠GFD=360°.【变式2-1】(2023•盘锦)如图,直线AB∥CD,将一个含60°角的直角三角尺EGF按图中方式放置,点E在AB上,边GF,EF分别交CD于点H,K,若∠BEF=64°,则∠GHC等于()A.44°B.34°C.24°D.14°【答案】B【解答】解:因为AB∥CD,且∠BEF=64°,所以∠DKF=∠BEF=64°.又三角形EFG为直角三角形,且∠G=90°,∠GEF=60°,所以∠F=30°.所以∠KHF=64°﹣30°=34°.又∠GHC=∠KHF,所以∠GHC=34°.故选:B.【变式2-2】(2023•盘锦)如图,直线AB∥CD,将一个含60°角的直角三角尺EGF按图中方式放置,点E在AB上,边GF,EF分别交CD于点H,K,若∠BEF=64°,则∠GHC等于()A.44°B.34°C.24°D.14°【答案】B【解答】解:因为AB∥CD,且∠BEF=64°,所以∠DKF=∠BEF=64°.又三角形EFG为直角三角形,且∠G=90°,∠GEF=60°,所以∠F=30°.所以∠KHF=64°﹣30°=34°.又∠GHC=∠KHF,所以∠GHC=34°.故选:B.【变式2-3】(2023•海南模拟)如图,已知AB∥DE,∠B=20°,∠D=130°,那么∠BCD 等于()A.60°B.70°C.80°D.90°【答案】B【解答】解:过点C作CF∥AB,∵AB∥DE,∴AB∥DE∥CF;∴∠B=∠BCF,∠FCD+∠D=180°,∴∠BCD=180°﹣∠D+∠B=180°﹣130°+20°=70°.故选:B.【变式2-4】(2023春•覃塘区期末)如图,AB∥CD,将一副直角三角板作如下摆放,∠GEF =60°,∠MNP=45°.下列结论:①GE∥MP;②∠EFN=150°;③∠BEF=65°;④∠AEG=35°,其中正确的个数是()A.1B.2C.3D.4【答案】B∴∠HFN=∠MNP=45°,∴∠EFH=∠EFN﹣∠HFN=105°,∴∠BEF=180°﹣∠EFH=75°,故③错误;④∵∠GEF=60°,∠BEF=【解答】解:①由题意得:∠G=∠MPN=90°,∴GE∥MP,故①正确;②由题意得∠EFG=30°,∴∠EFN=180°﹣∠EFG=150°,故②正确;③过点F作FH∥AB,如图,∵AB∥CD,∴∠BEF+∠EFH=180°,FH∥CD,75°,∴∠AEG=180°﹣∠GEF﹣∠BEF=45°,故④错误.综上所述,正确的有2个.故选:B.【变式2-5】(2023春•赣县区期末)【问题背景】:同学们,观察小猪的猪蹄,你会发现一个熟悉的几何图形,我们就把这个图形的形象称为“猪蹄模型”,猪蹄模型中蕴含着角的数量关系.【问题探究】:(1)如图1,AB∥CD,E为AB、CD之间一点,连接BE、DE,得到∠BED 与∠B、∠D之间的数量关系,并说明理由;【类比迁移】:(2)请你利用上述“猪蹄模型”得到的结论或解题方法,完成下面的问题:如图2,直线AB∥CD,若∠B=23°,∠G=35°,∠D=25°,求∠BEG+∠GFD的度数;【灵活应用】:(3)如图3,直线AB∥CD,若∠E=∠B=60°,∠F=85°,则∠D=25度.【答案】(1)∠BED=∠B+∠D,理由见解答;(2)∠BEG+∠GFD的度数为83°;(3)25.【解答】解:(1)∠BED=∠B+∠D,理由:过点E作EP∥AB,∴∠B=∠BEP,∵AB∥CD,∴CD∥EP,∴∠D=∠DEP,∵∠BED=∠BEP+∠DEP,∴∠BED=∠B+∠D;(2)过点G作GM∥AB,由(1)可得:∠BEG=∠B+∠EGM,∵AB∥CD,∴GM∥CD,由(1)可得:∠GFD=∠D+∠FGM,∵∠B=23°,∠EGF=35°,∠D=25°,∴∠BEG+∠GFD=∠B+EGM+∠D+∠FGM =∠B+∠D+∠EGF=23°+25°+35°=83°,∴∠BEG+∠GFD的度数为83°;(3)如图:∵∠B=60°,∠F=85°,∴∠BNF=180°﹣∠B﹣∠F=35°,∴∠ANE=∠BNF=35°,∵AB∥CD,∴由(1)可得:∠DEN=∠ANE+∠D,∴∠D=∠DEN﹣∠ANE=60°﹣35°=25°,故答案为:25.【变式2-6】(2023春•邵阳期末)如图1,直线AB∥CD,P是截线MN上的一点.(1)若∠MNB=45°,∠MDP=20°,求∠MPD;(2)如图1,当点P在线段MN上运动时,∠CDP与∠ABP的平分线交于Q,问是否为定值,若是定值,请求出;若不是定值,请说明理由;(3)如图2,若T是直线MN上且位于M点的上方的一点,如图所示,当点P在射线MT上运动时,∠CDP与∠ABP的平分线交于Q,问的值是否和(2)问中的情况一样呢?请你写出探究过程,说明理由.【答案】(1)∠MPD的度数25°;(2)是定值,=;(3)是定值,=.【解答】解:(1)∵AB∥CD,∠MNB=45°,∴∠DMP=180°﹣∠MNB=135°,∵∠MDP=20°,∴∠MPD=180°﹣∠DMP﹣∠MDP=25°,∴∠MPD的度数为25°;(2)是定值,理由:过点P作PG∥CD,∴∠CDP=∠DPG,∵CD∥AB,∴PG∥AB,∴∠ABP=∠BPG,∵∠DPB=∠DPG+∠BPG,∴∠DPB=∠CDP+∠ABP,同理可得:∠Q=∠CDQ+∠ABQ,∵DQ平分∠CDP,BQ平分∠ABP,∴∠CDQ=∠CDP,∠ABQ=∠ABP,∴∠Q=∠CDQ+∠ABQ=∠CDP+∠ABP=(∠CDP+∠ABP)=∠DPB,∴=;(3)是定值,理由:过点P作PG∥CD,∴∠CDP=∠DPG,∵CD∥AB,∴PG∥AB,∴∠ABP=∠BPG,∵∠DPB=∠BPG﹣∠DPG,∴∠DPB=∠ABP﹣∠CDP,同理可得:∠Q=∠ABQ﹣∠CDQ,∵DQ平分∠CDP,BQ平分∠ABP,∴∠CDQ=∠CDP,∠ABQ=∠ABP,∴∠Q=∠ABQ﹣∠CDQ=∠ABP﹣∠CDP=(∠ABP﹣∠CDP)=∠DPB,∴=.【变式2-7】(2023春•防城港期末)阅读下面材料:(1)小亮同学遇到这样一个问题:已知:如图甲,AB∥CD,E为直线AB,CD之间一点,连接BE、DE得到∠BED.求证:∠BED=∠B+∠D.下面是小亮写出了该问题的证明,请你帮他把证明过程补充完整.证明:过点E作EF∥AB,则有∠BEF=∠B,∵AB∥CD,∴CD∥EF,∴∠FED=∠D,∴∠BED=∠BEF+∠FED=∠B+∠D.(2)请你参考小亮思考问题的方法,解决问题:如图乙,直线a∥b,BE平分∠ABC,DE平分∠ADC,若∠ABC=50°,∠ADC=60°,求∠BED的度数,(温馨提示:过点E作EF∥AB)【答案】(1)∠B,CD,∠D;(2)∠BED=55°.【解答】(1)证明:过点E作EF∥AB,则有∠BEF=∠B,∵AB∥CD,∴CD∥EF,∴∠FED=∠D,∴∠BED=∠BEF+∠FED=∠B+∠D,故答案为:∠B,CD,∠D;(2)解:如图乙,过点E作EF∥AB,∴∠BEF=∠ABE,∵a∥b,即AB∥CD,∴CD∥EF,∴∠DEF=∠CDE,∴∠BED=∠BEF+∠DEF=∠ABE+∠CDE,∵BE平分∠ABC,DE平分∠ADC,∴∠ABE=∠ABC,∠CDE=∠ADC,又∵∠ABC=50°,∠ADC=60°,∴∠ABE=25°,∠CDE=30°,∴∠BED=∠ABE+∠CDE=25°+30°=55°.结论1:若AB ∥CD ,则∠P =∠AEP -∠CFP 或∠P =∠CFP -∠AEP ;结论2:若∠P =∠AEP -∠CFP 或∠P =∠CFP -∠AEP ,则AB ∥CD .【典例3】(2023春•中山区期末)如图,∠ABE +∠BED =∠CDE .(1)如图1,求证AB ∥CD ;(2)如图2,点P 在AB 上,∠CDP =∠EDP ,BF 平分∠ABE ,交PD 于点F ,探究∠BFP ,∠BED 的数量关系,并证明你的结论;(3)在(2)的条件下,如图3,PQ 交ED 延长线于点Q ,∠DPQ =2∠APQ ,∠PQD =80°,求∠CDE 的度数.【答案】(1)答案见解答过程;模型三“臭脚”模型点P 在EF 右侧,在AB 、CD 外部“臭脚”模型模型分析典例分析(2)∠BED=2∠BFP,理由见解答过程;(3)120°.【解答】(1)证明:延长CD交BE于点H,∴∠CDE=∠DHE+∠BED,∵∠ABE+∠BED=∠CDE,∴∠DHE=∠ABE,∴AB∥CD,(2)解:∠BFP,∠BED的数量关系是:∠BED=2∠BFP,理由如下:设∠EBF=α,∠CDP=β,∵BF平分∠ABE,∠CDP=∠EDP,∴∠EBF=∠ABF=α,∠CDP=∠EDP=β,∴∠PBE=2∠EBF=2α,由(1)可知:AB∥CD,∴∠DPB=∠CDP=β,∴∠APD=180°﹣∠∠DPB=180°﹣β,∵∠APD=∠ABF+∠BFP,∴180°﹣β=α+∠BFP,∴∠BFP=180°﹣(α+β),由四边形的内角和等于360°得:∠BED+∠EDP+∠DPB+∠PBE=360°,即:∠BED+β+β+2α=360°,∴∠BED=360°﹣2(α+β),∴∠BED=2∠BFP.(3)解:设∠APQ=θ,∴∠DPQ=2∠APQ=2θ,∴∠APD=∠APQ+∠DPQ=3θ,由(1)可知:AB∥CD,∴∠CDP+∠APD=180°,∴∠CDP=180°﹣∠APD=180°﹣3θ,∵∠PQD=80°,∴∠EDP=∠PQD+∠DPQ=80°+2θ,∵∠CDP=∠EDP,∴180°﹣3θ=80°+2θ,解得:θ=20°,∴∠CDP=180°﹣3θ=120°,∠EDP=80°+2θ=120°,根据周角的定义得:∠CDE+∠CDP+∠EDP=360°,∴∠CDE=360°﹣(∠CDP+∠EDP)=360°﹣(120°+120°)=120°.【变式3-1】已知AB∥CD.(1)如图1,求证:∠ABE+∠DCE﹣∠BEC=180°;(2)如图2,∠DCE的平分线CG的反向延长线交∠ABE的平分线BF于F.若BF∥CE,∠BEC=26°,求∠BFC.【答案】(1)详见解析;(2)103°.【解答】(1)证明:如图,过E作EF∥AB,∵AB∥CD,∴DC∥EF,∴∠B=∠BEF,∠C+∠CEF=180°,∴∠C+∠B=∠BEC=180°,即:∠ABE+∠DCE﹣∠BEC=180°;(2)解:∵FB∥CE,∴∠FBE=∠BEC=26°,∵BF平分∠ABE,∴∠ABE=2∠FBE=52°,由(1)得:∠DCE=180°﹣∠ABE+∠BEC=180°﹣52°+26°=154°,∵CG平分∠ECD,∴∠DCG=77°,过点F作FN∥AB,如图:∵AB∥CD,∴FN∥CD,∴∠BFN=∠ABF=26°,∠NFC=∠DCG=77°,∴∠BFC=∠BFN+∠NFC=103°.模型分析·结论1:若AB∥CD,则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP;结论2:若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP,则AB∥CD.典例分析【典例4】(2022秋•朝阳区校级期末)已知AB∥CD,点E在AB上,点F在DC上,点G 为射线EF上一点.(1)【基础问题】如图1,试说明:∠AGD=∠A+∠D.(完成图中的填空部分)证明:过点G作直线MN∥AB,又∵AB∥CD,∴MN∥CD∵MN∥AB,∴∠A=∠MGA.∵MN∥CD,∴∠D=DGM(两直线平行,内错角相等)∴∠AGD=∠AGM+∠DGM=∠A+∠D.(2)【类比探究】如图2,当点G在线段EF延长线上时,请写出∠AGD、∠A、∠D三者之间的数量关系,并说明理由.(3)【应用拓展】如图3,AH平分∠GAE,DH交AH于点H,且∠GDH=2∠HDF,∠HDF=22°,∠H=32°,直接写出∠DGA的度数为°.【答案】(1)MN;∠A;∠DGM;两直线平行,内错角相等;(2)∠AGD=∠A﹣∠D.理由见解析;(3)42°.【解答】解:(1)过点G作直线MN∥AB,又∵AB∥CD,∴MN∥CD(平行于同一条直线的两条直线平行),∵MN∥AB,∴∠A=∠AGM(两直线平行,内错角相等),∵MN∥CD,∴∠D=∠DGM(两直线平行,内错角相等),∴∠AGD=∠AGM+∠DGM=∠A+∠D.故答案为:MN;∠A;∠DGM;两直线平行,内错角相等.(2)如图所示,过点G作直线MN∥AB,又∵AB∥CD,∴MN∥CD,∵MN∥AB,∴∠A=∠AGM,∵MN∥CD,∴∠D=∠DGM,∴∠AGD=∠AGM﹣∠DGM=∠A﹣∠D.(3)如图所示,过点G作直线MN∥AB,过点H作直线PQ∥AB,又∵AB∥CD,∴MN∥CD,PQ∥CD∵MN∥AB,PQ∥AB,∴∠BAG=∠AGM,∠BAH=∠AHP,∵MN∥CD,PQ∥CD,∴∠CDG=∠DGM,∠CDH=∠DHP,∵∠GDH=2∠HDC,∠HDC=22°,∠AHD=32°,∴∠GDH=44°,∠DHP=22°,∴∠CDG=66°,∠AHP=54°,∴∠DGM=66°,∠BAH=54°,∵AH平分∠GAE,∴∠BAG=2∠BAH=108°,∴∠AGM=108°,∴∠AGD=∠AGM﹣∠DGM=42°.【变式4-1】(2022秋•肃州区校级期末)如图(1),AB∥CD,∠AEP=40°,∠PFD=130°,求∠EPF的度数.小明想到了以下方法:解:如图(1),过点P作PM∥AB,∴∠1=∠AEP=40°(两直线平行,内错角相等)∵AB∥CD(已知)∴PM∥CD(平行于同一条直线的两直线平行)∴∠2+∠PFD=180°(两直线平行,同旁内角互补)∵∠PFD=130°(已知)∴∠2=180°﹣130°=50°∴∠EPF=∠1+∠2=40°+50°=90°即∠EPF=90°【探究】如图(2),AB∥CD,∠AEP=50°,∠PFC=120°,求∠EPF的度数.【应用】如图(3),在【探究】的条件下,∠PEA的平分线和∠PFC的平分线交于点G,求∠G的度数.【答案】[探究]70°;[应用]35°.【解答】[探究]如图②,过点P作PM∥AB,∴∠MPE=∠AEP=50°(两直线平行,内错角相等)∵AB∥CD(已知),∴PM∥CD(平行于同一条直线的两直线平行),∴∠PFC=∠MPF=120°(两直线平行,内错角相等).∴∠EPF=∠MPF﹣∠MPE=120°﹣50°=70°(等式的性质).[应用]如图③所示,∵EG是∠PEA的平分线,FG是∠PFC的平分线,∴∠AEG=AEP=25°,∠GFC=PFC=60°,过点G作GM∥AB,∴∠MGE=∠AEG=25°(两直线平行,内错角相等)∵AB∥CD(已知),∴GM∥CD(平行于同一条直线的两直线平行),∴∠GFC=∠MGF=60°(两直线平行,内错角相等).∴∠EGF=∠MGF﹣∠MGE=60°﹣25°=35°.【变式4-2】(2022春•朝阳县期末)学习完平行线的性质与判定之后,我们发现借助构造平行线的方法可以帮我们解决许多问题.(1)小明遇到了下面的问题:如图1,l1∥l2,点P在l1,l2内部,探究∠A,∠APB,∠B的关系,小明过点P作l1的平行线,可得∠APB,∠A,∠B之间的数量关系是:∠APB=∠A+∠B.(2)如图2,若AC∥BD,点P在AC,BD外部,∠A,∠B,∠APB的数量关系是否发生变化?请写出证明过程.【答案】(1)∠APB=∠A+∠B;(2)发生变化,∠APB=∠B﹣∠A,证明见解答过程.【解答】解:(1)∵记过点P作l1的平行线为PC,∵PC∥l1,∴∠A=∠APC,∵l1∥l2,∴PC∥l2,∴∠B=∠BPC,∴∠APB=∠APC+∠BPC=∠A+∠B,故答案为:∠APB=∠A+∠B;(2)发生变化,如图,过点PF∥AC,则∠APF=∠A,∵AC∥BD,∴PF∥BD,∴∠B=∠BPF,∴∠APB=∠BPF﹣∠APF=∠B﹣∠A.【变式4-3】(2020春•乳山市期中)【信息阅读】材料信息:如图①,AB∥DE,点C是直线AB,DE外任意一点,连接BC,DC.方法信息:如图②,在“材料信息”的条件下,∠B=55°,∠D=35°,求∠BCD的度数.解:过点C作CF∥AB.∴∠BCF=∠B=55°.∵AB∥DE,∴CF∥DE.∴∠DCF=∠D=35°.∴∠BCD=55°﹣35°=20°.【问题解决】(1)通过【信息阅读】,猜想:∠B,∠D,∠BCD之间有怎样的等量关系?请直接写出结论:∠BCD=∠B﹣∠D;(2)如图③,在“材料信息”的条件下,改变点C的位置,∠B,∠D,∠BCD之间的等量关系是否改变?若不改变,请写出理由;若改变,请写出新的等量关系及理由.【答案】∠BCD=∠B﹣∠D,∠BCD=∠D﹣∠B【解答】解(1)过C作CF∥ED,∵AB∥ED,∴AB∥CF,∴∠B=∠BCF,∠D=∠DCF,∵∠BCD=∠BCF﹣∠DCF,∴∠BCD=∠B﹣∠D,故答案为:∠BCD=∠B﹣∠D.(2)过点C作CF∥AB,∴∠BCF=∠B,∵AB∥DE,∴CF∥DE.∴∠DCF=∠D,∵∠BCD=∠DCF﹣BCF,∴∠BCD=∠D﹣∠B.1.(2023春•建昌县期末)如图,将一个含30°角的直角三角板的直角顶点C放在直尺的两边MN,PQ之间,则下列结论中:①∠1=∠3;②∠2=∠3;③∠1+∠3=90°;④若∠3=60°,则AB⊥PQ,其中正确结论的个数是()A.1个B.2个C.3个D.4个【答案】C【解答】解:设BC与PQ交于点F,AB与PQ交于点G,AB与MN交于点H,延长AC 交PQ于点E,∵MN∥PQ,∴∠3=∠AEG,∵∠1≠∠AEG,∴∠3≠∠1,故①不正确;根据对顶角相等可得:∠2=∠3,故②正确;∵∠ACB是△CEF的一个外角,∠ACB=90°,∴∠ACB=∠AEB+∠1=90°,∵∠AEB=∠3,∴∠3+∠1=90°,故③正确;∵∠A=30°,∠3=60°,∴∠AHM=180°﹣∠A﹣∠3=90°,∵MN∥PQ,∴∠AHM=∠AGP=90°,∴AB⊥PQ,故④正确;所以,上列结论中,其中正确结论的个数是3个,故选:C.2.(2023春•芜湖期末)如图所示是汽车灯的剖面图,从位于O点灯发出光照射到凹面镜上反射出的光线BA,CD都是水平线,若∠ABO=α,∠DCO=60°,则∠BOC的度数为()A.180°﹣αB.120°﹣αC.60°+αD.60°﹣α【答案】C【解答】解:连接BC,∵AB∥CD,∴∠ABO+∠CBO+∠BCO+∠OCD=180°,而∠CBO+∠BCO+∠O=180°,∴∠O=∠ABO+∠DCO=60°+α.故选:C.3.(2022•恩施州)已知直线l1∥l2,将含30°角的直角三角板按如图所示摆放.若∠1=120°,则∠2=()A.120°B.130°C.140°D.150°【答案】D【解答】解:过含30°角的直角三角板的直角顶点B作BF∥l1,交AC于点F,∵∠C=30°,∴∠A=90°﹣∠C=60°.∵∠1=∠A+∠ADE,∴∠ADE=60°.∵BF∥l1,∴∠ABF=∠ADE=60°,∴∠FBG=90°﹣∠ABF=30°.∵BF∥l1,l1∥l2,∴BF∥l2,∴∠BGH+∠FBG=180°,∴∠BGH=180°﹣∠FBG=150°,∴∠2=∠BGH=150°.故选:D.4.(2022•博山区一模)如图,直线a∥b,点M、N分别在直线a、b上,P为两平行线间一点,那么∠1+∠2+∠3等于()A.360°B.300°C.270°D.180°【答案】A【解答】解:如图,过点P作PA∥a,则a∥b∥PA,∴∠3+∠NPA=180°,∠1+∠MPA=180°,∴∠1+∠2+∠3=180°+180°=360°.故选:A.5.(2021春•椒江区校级月考)如图,已知AB∥CD,∠BAD和∠BCD的平分线交于点E,∠FBC=n°,∠BAD=m°,则∠AEC等于()度.A.90﹣+m B.90﹣﹣C.90﹣D.90﹣+【答案】D【解答】解:如图,过点E作EM∥AB,∵AB∥CD,EM∥AB,∴AB∥EM∥CD,∴∠BAE=∠AEM,∠MEC=∠ECD,∠FBC+∠BCD=180°,∴∠BCD=180°﹣∠FBC=180°﹣n°,∵∠BAD和∠BCD的平分线交于点E,∴∠BAE=∠BAD=m°,∠ECD=∠BCD=(180°﹣n°),∴∠AEC=∠AEM+∠MEC=∠BAE+∠ECD=m°+(180°﹣n°)=90°+m°﹣n°,故选:D.6.(2023春•赫山区期末)【问题情景】(1)如图1,AB∥CD,∠PAB=135°,∠PCD=115°,求∠APC的度数;【问题迁移】(2)如图2,已知∠MON,AD∥BC,点P在射线OM上运动,当点P在A,B两点之间运动时,连接PD,PC,∠ADP=∠α,∠BCP=∠β,求∠CPD与∠α,∠β之间的数量关系,并说明理由;【知识拓展】(3)在(2)的条件下,若将“点P在A,B两点之间运动”改为“点P在A,B两点外侧运动(点P与点A,B,O三点不重合)”其他条件不变,请直接写出∠CPD 与∠α,∠β之间的数量关系.【答案】(1)∠APC的度数为110°;(2)∠CPD=∠α+∠β,理由见解答;(3)当P在BA延长线时,∠CPD=∠β﹣∠α;当P在AB延长线时,∠CPD=∠α﹣∠β.【解答】解:(1)过点P作PE∥AB,∴∠APE=180°﹣∠A=45°,∵AB∥CD,∴PE∥CD,∴∠CPE=180°﹣∠C=65°,∴∠APC=∠APE+∠CPE=45°+65°=110°,∴∠APC的度数为110°;(2)∠CPD=∠α+∠β,理由:过P作PE∥AD交CD于E,∴∠ADP=∠DPE=∠α,∵AD∥BC,∴PE∥BC,∴∠BCP=∠CPE=∠β,∴∠CPD=∠DPE+∠CPE=∠α+∠β;(3)分两种情况:当P在BA延长线时,∠CPD=∠β﹣∠α,理由:如图3,过P作PE∥AD交CD于E,∴∠ADP=∠DPE=∠α,∵AD∥BC,∴PE∥BC,∴∠BCP=∠CPE=∠β,∴∠CPD=∠CPE﹣∠DPE=∠β﹣∠α;当P在AB延长线时,∠CPD=∠α﹣∠β,理由:如图4,过P作PE∥AD交OD于E,∴∠ADP=∠DPE=∠α,∵AD∥BC,∴PE∥BC,∴∠BCP=∠CPE=∠β,∴∠CPD=∠DPE﹣∠CPE=∠α﹣∠β,综上所述,∠CPD=∠β﹣∠α或∠CPD=∠α﹣∠β.7.(2022春•良庆区校级期中)已知AM∥CN,点B为平面内一点,AB⊥BC于B.(1)如图1,直接写出∠A和∠C之间的数量关系∠A+∠C=90°;(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB=∠CFD,∠BFC=3∠DBE,求∠EBC的度数.【答案】(1)∠A+∠C=90°;(2)见解答;(3)105°.【解答】解:(1)如图1,AM与BC的交点记作点O,∵AM∥CN,∴∠C=∠AOB,∵AB⊥BC,∴∠A+∠AOB=90°,∴∠A+∠C=90°,故答案为:∠A+∠C=90°;(2)如图2,过点B作BG∥DM,∵BD⊥AM,∴DB⊥BG,即∠ABD+∠ABG=90°,又∵AB⊥BC,∴∠CBG+∠ABG=90°,∴∠ABD=∠CBG,∵AM∥CN,BG∥AM,∴CN∥BG,∴∠C=∠CBG,∴∠ABD=∠C;(3)如图3,过点B作BG∥DM,∵BF平分∠DBC,BE平分∠ABD,∴∠DBF=∠CBF,∠DBE=∠ABE,由(2)可得∠ABD=∠CBG,∴∠ABF=∠GBF,设∠DBE=α,∠ABF=β,则∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=3∠DBE=3α,∴∠AFC=3α+β,∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,∴∠FCB=∠AFC=3α+β,△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+3α+(3α+β)=180°,①由AB⊥BC,可得β+β+2α=90°,②由①②联立方程组,解得α=15°,∴∠ABE=15°,∴∠EBC=∠ABE+∠ABC=15°+90°=105°.8.(2021秋•平昌县期末)如图,AD∥BC,∠BAD的平分线交BC于点G,∠BCD=90°.(1)试说明:∠BAG=∠BGA;(2)如图1,点F在AG的反向延长线上,连接CF交AD于点E,若∠BAG﹣∠F=45°,求证:CF平分∠BCD.(3)如图2,线段AG上有点P,满足∠ABP=3∠PBG,过点C作CH∥AG.若在直线AG上取一点M,使∠PBM=∠DCH,求的值.【答案】(1)证明过程见解答;(2)证明过程见解答;(3)5或.【解答】(1)证明:∵AD∥BC,∴∠GAD=∠BGA,∵AG平分∠BAD,∴∠BAG=∠GAD∴∠BAG=∠BGA;(2)解:∵∠BGA=∠F+∠BCF,∴∠BGA﹣∠F=∠BCF,∵∠BAG=∠BGA,∴∠∠BAG﹣∠F=∠BCF,∵∠BAG﹣∠F=45°,∴∠BCF=45°,∵∠BCD=90°,∴CF平分∠BCD;(3)解:有两种情况:①当M在BP的下方时,如图5,设∠ABC=4x,∵∠ABP=3∠PBG,∴∠ABP=3x,∠PBG=x,∵AG∥CH,∴∠BCH=∠AGB==90°﹣2x,∵∠BCD=90°,∴∠DCH=∠PBM=90°﹣(90°﹣2x)=2x,∴∠ABM=∠ABP+∠PBM=3x+2x=5x,∠GBM=2x﹣x=x,∴∠ABM:∠GBM=5x:x=5;②当M在BP的上方时,如图6,同理得:∠ABM=∠ABP﹣∠PBM=3x﹣2x=x,∠GBM=2x+x=3x,∴∠ABM:∠GBM=x:3x=.综上,的值是5或.9.(2023春•黑山县期中)问题情境我们知道,“两条平行线被第三条直线所截,同位角相等,内错角相等,同旁内角互补”,所以在某些探究性问题中通过“构造平行线”可以起到转化的作用.已知三角板ABC中,∠BAC=60°,∠B=30°,∠C=90°,长方形DEFG中,DE∥GF.问题初探(1)如图(1),若将三角板ABC的顶点A放在长方形的边GF上,BC与DE相交于点M,AB⊥DE于点N,求∠EMC的度数.分析:过点C作CH∥GF.则有CH∥DE,从而得∠CAF=∠HCA,∠EMC=∠MCH,从而可以求得∠EMC的度数.由分析得,请你直接写出:∠CAF的度数为30°,∠EMC的度数为60°.类比再探(2)若将三角板ABC按图(2)所示方式摆放(AB与DE不垂直),请你猜想写∠CAF 与∠EMC的数量关系,并说明理由.(3)请你总结(1),(2)解决问题的思路,在图(3)中探究∠BAG与∠BMD的数量关系?并说明理由.【答案】(1)30°,60°;(2)∠EMC+∠CAF=90°,理由见解答;(3)∠BAG﹣∠BMD=30°,理由见解答.【解答】解:(1)由题可得,∠CAF=∠BAF﹣∠BAC=90°﹣60°=30°,∠EMC=∠BCH=90°﹣30°=60°;故答案为:30°,60°;(2)∠EMC+∠CAF=90°,理由:证明:如图,过C作CH∥GF,则∠CAF=∠ACH,∵DE∥GF,CH∥GF,∴CH∥DE,∴∠EMC=∠HCM,∴∠EMC+∠CAF=∠MCH+∠ACH=∠ACB=90°;(3)∠BAG﹣∠BMD=30°,理由:证明:如图,过B作BK∥GF,则∠BAG=∠KBA,∵BK∥GF,DE∥GF,∴BK∥DE,∴∠BMD=∠KBM,∴∠BAG﹣∠BMD=∠ABK﹣∠KBM=∠ABC=30°.10.(2022春•龙亭区校级期末)如图,已知AB∥CD,E、F分别在AB、CD上,点G在AB、CD之间,连接GE、GF.(1)当∠BEG=40°,EP平分∠BEG,FP平分∠DFG时:①如图1,若EG⊥FG,则∠P的度数为45°;②如图2,在CD的下方有一点Q,EG平分∠BEQ,FD平分∠GFQ,求∠Q+2∠P的度数;(2)如图3,在AB的上方有一点O,若FO平分∠GFC.线段GE的延长线平分∠OEA,则当∠EOF+∠EGF=100°时,请直接写出∠OEA与∠OFC的数量关系.【答案】(1)①45°;②120°;(2)∠OEA+2∠PFC=160°.【解答】解:(1)①如图,分别过点G,P作GN∥AB,PM∥AB,∴∠BEG=∠EGN,∵AB∥CD,∴∠NGF=∠GFD,∴∠EGF=∠BEG+∠GFD,同理可得∠EPF=∠BEP+∠PFD,∵EG⊥FG,∴∠EGF=90°,∵EP平分∠BEG,FP平分∠DFG;∴∠BEP=BEG,∠PFD=GFD,∴∠EPF=(∠BEG+∠GFD)=EGF=45°,故答案为:45°;②如图,过点Q作QR∥CD,∵∠BEG=40°,∵EG恰好平分∠BEQ,FD恰好平分∠GFQ,∠GEQ=∠BEG=40°,∠GFD=∠QFD,设∠GFD=∠QFD=α,∵QR∥CD,AB∥CD,∴∠EQR=180°﹣∠QEB=180°﹣2∠QEG=100°,∵CD∥QR,∴∠DFQ+∠FQR=180°,∴α+∠FQR=180°,∴α+∠FQE=80°,∴∠FQE=80°﹣α,由①可知∠G=2∠P=∠BEG+∠GFD=40°+α,∴∠FQE+2∠P=80°﹣α+40°+α=120°;(2)结论:∠OEA+2∠PFC=160°.理由:∵在AB的上方有一点O,若FO平分∠GFC,线段GE的延长线平分∠OEA,设H为线段GE的延长线上一点,∴∠OFC=∠OFG,∠OEH=∠HEA,设∠OFC=∠OFG=β,∠OEH=∠HEA=α,如图,过点O作OT∥AB,则OT∥CD,∴∠TOF=∠OFC=β,∠TOE=∠OEA=2α,∴∠EOF=β﹣2α,∵∠HEA=∠BEG=a,∠GFD=180°﹣2β,由(1)可知∠G=∠BEG+∠GFD=α+180°﹣2β,∵∠EOF+∠EGF=100°,∴β﹣2α+α+180°﹣2β=100°,∴α+β=80°,∴∠OEA+∠OFC=80°,∴∠OEA+2∠PFC=160°.11.(2023春•孝义市期末)综合与探究数学活动课上,老师以“一个含45°的直角三角板和两条平行线”为背景展开探究活动,如图1,已知直线m∥n,直角三角板ABC中,∠ACB=90°,∠BAC=∠ABC=45°.(1)如图1,若∠2=65°,则∠1=20°;(直接写出答案)(2)“启航”小组在图1的基础上继续展开探究:如图2,调整三角板的位置,当三角板ABC的直角顶点C在直线n上,直线m与AB,AC相交时,他们得出的结论是:∠1﹣∠2=135°,你认为启航小组的结论是否正确,请说明理由;(3)如图3,受到“启航”小组的启发,“睿智”小组提出的问题是:在图2的基础上,继续调整三角板的位置,当点C不在直线n上,直线m与AC,BC相交时,∠1与∠2有怎样的数量关系?请你用平行线的知识说明理由.【答案】(1)20°;(2)正确,理由见解析;(3))∠1+∠2=90°,理由见解析.【解答】解:(1)∵直线m∥n,∴∠1+∠ABC=∠2=65°,∵∠ABC=45°,∴∠1=20°,故答案为:20°;(2)正确,理由如下:如图所示:过点B作BD∥m,∴∠1+∠ABD=180°,∴∠ABD=180°﹣∠1,∵m∥n,∴∠CBD=∠2,∵∠ABC=45°,∴∠ABC=∠ABD+∠CBD=45°∴180°﹣∠1+∠2=45°,∴∠1﹣∠2=135°;(3)∠1+∠2=90°,理由如下:如图所示,过点C作EF∥m,∴∠1=∠ACE,∠2=∠BCF,∵∠ACB=90°,∴∠ACE+∠BCF=180°﹣∠ACB=180°﹣90°=90°,∴∠1+∠2=90°.12.(2023春•安化县期末)在课后学习中,小红探究平行线中的线段与角的数量关系,如图,直线AB∥CD,点N在直线CD上,点P在直线AB上,点M为平面上任意一点,连接MP,MN,PN.(1)如图1,点M在直线CD上,PM平分∠APN,试说明∠PMN=∠MPN;(2)如图2,点M在直线AB,CD之间,∠PMN=70°,∠MNC=30°,求∠APM的度数;(3)如图3,∠APM和∠MNC的平分线交于点Q,∠PQN与∠PMN有何数量关系?并说明理由.【答案】(1)说明见解析;(3)2∠PQN=∠PMN,理由见解析.【解答】解:(1)∵AB∥CD,∴∠APM=∠PMN.∵PM平分∠APN,∴∠APM=∠MPN,∴∠PMN=∠MPN;(2)如图,过点M作ME∥CD,∴∠EMN=∠MNC=30°,∵AB∥CD,ME∥CD,∴ME∥AB,∴∠APM=∠PME,∴∠PMN=∠PME+∠EMN=∠APM+∠MNC,∵∠PMN=70°,∴∠APM=∠PMN﹣∠MNC=70°﹣30°=40°;(3)2∠PQN=∠PMN,理由如下:由(2)可知∠PMN=∠APM+∠MNC,同理可得:∠PQN=∠APQ+∠QNC,∵PQ和NQ分别是∠APM和∠MNC的平分线,∴,∴∠PQN=∠APQ+∠QNC,=,∴2∠PQN=∠PMN.12.(2023春•甘井子区期末)如图1,点M在射线BA,CD之间,0°<∠ABM<30°,连接BM,过点M作ME⊥BM交射线CD于点E,且∠MED﹣∠B=90°.(1)求证:AB∥CD;(2)过点C作∠ECN=∠B,交直线ME于点N,先按要求画图,再解决下列问题.①当CN在CD上方,满足∠CNE=5∠B时,在图2中画图,求∠B的度数;②作∠BME的角平分线交射线CD于点K,交∠ECN的角平分线于点F,请直接写出∠MKC与∠MFC之间的数量关系=45..【答案】(1)证明见解析;(2)①18°;②=45.【解答】解:(1)如图所示:过点M作MN∥AB,∴∠B=∠BMN,∵ME⊥BM,∴∠BMN+∠NME=90°,∴∠NME=90°﹣∠BMN,∵∠MED﹣∠B=90°,∴∠MED=90°+∠B,∴∠NME+∠MED=90°﹣∠BMN+90°+∠B=180°,∴MN∥CD,∴AB∥CD;(2)①当CN在CD上方,如图所示:过点M作MN∥AB,设∠B=x,则∠CNE=5∠B=5x,∠ECN=∠B=x,∵MN∥AB,∴∠BMH=∠B=x,∵∠MED=∠ECN+∠CNE,∴∠MED=6x,由(1)得AB∥CD∴MH∥CD,∴∠HME+∠MED=180°,∴∠HME=180°﹣∠MED=180°﹣6x,∵ME⊥BM,∴∠BMH+∠HME=90°,∴x+180°﹣6x=90°,5x=90°,x=18°,即∠B=18°;②如图所示:设∠B=x,则∠ECN=∠B=x,∵ME⊥BM,∴∠BME=90°,∵∠BME的角平分线交射线CD于点K,交∠ECN的角平分线于点F ∴∠FCE=∠ECN=,∠BMK=∠EMH=∵MH∥AB,∴∠BMH=∠B=x,∴∠HMK=∠BMK﹣∠BMH=45°﹣x°,由(1)得AB∥CD∴MH∥CD,∴∠HMK=∠MKC,∵∠MFC=∠MKC+∠FCE==45.。
平行线模型练习题(含解析)

平行线模型练习题1.如图,l1∥l2,将一副直角三角板作如下摆放,图中点A、B、C在同一直线上,∠1=80°,则∠2的度数为()A.100°B.120°C.130°D.150°【答案】C【解答】解:如图,过点A作AD∥l1,∵l1∥l2,∴AD∥l2,∴∠FNA+∠NAD=180°,∵AD∥l1,∴∠EMA+∠MAD=180°,∴∠EMA+∠MAD+∠DAN+∠ANF=180°+180°=360°,∵∠EMA=∠EMC+∠CMA=80°+60°=140°,∠MAD+∠DAN=90°,∴∠FNA=360°﹣140°﹣90°=130°,即∠2=130°,故选:C.2.将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置,如果∠CDE =40°,那么∠BAF的大小为()A.25°B.20°C.15°D.10°【答案】D【解答】解:由题意知:∠CAB=60°,∠C=90°.∵∠CDE=40°,∴∠CED=50°.∵DE∥AF,∴∠F AE=∠CED=50°.∴∠BAF=∠CAB﹣F AE=60°﹣50°=10°.故选:D.3.如图,AB∥EF,∠C=90°,则α、β、y的关系是()A.β+γ﹣α=90°B.α+β+γ=180°C.α+β﹣γ=90°D.β=α+γ【答案】C【解答】解:如图,过点C、D分别作AB的平行线CG、DH,∵AB∥EF,∴AB∥CG∥DH∥EF,∴∠1=∠α,∠2=∠3,∠4=∠γ,∵∠2=90°﹣∠1=90°﹣∠α,∠3=∠β﹣∠4=∠β﹣∠γ,∴90°﹣∠α=∠β﹣∠γ,∴α+β﹣γ=90°.故选:C.4.如图,AB∥EF,∠C=90°,则α、β、γ的关系为()A.β=α+γB.α+β﹣γ=90°C.α+β+γ=180°D.β+γ﹣α=90°【答案】B【解答】解:延长DC交AB于G,延长CD交EF于H.直角△BGC中,∠1=90°﹣α;△EHD中,∠2=β﹣γ,∵AB∥EF,∴∠1=∠2,∴90°﹣α=β﹣γ,即α+β﹣γ=90°.故选:B.5.如图,AB与HN交于点E,点在直线CD上,GF交AB于点M,∠FMA=∠FGC,∠FEN=2∠NEB,∠FGH=2∠HGC,下列四个结论:①AB∥CD;②∠EHG=2∠EFM;③∠EHG+∠EFM=90°;④3∠EHG﹣∠EFM=180°.其中正确的结论是()A.①②③B.②④C.①②④D.①④【答案】D【解答】解:∵∠FMA=∠FGC∴AB∥CD∴①正确;过点F作FP∥AB,HQ∥AB,∵AB∥CD,∴FP∥AB∥HQ∥CD,设∠NEB=x,∠HGC=y,则∠FEN=2x,∠FGH=2y∴∠EHG=∠EHQ+∠GHQ=∠AEH+∠HGC=∠NEB+∠HGC=x+y,∠EFM=∠BEF﹣∠FME=∠BEF﹣∠AMG=∠BEF﹣(180°﹣∠FGC)=x+2x﹣(180°﹣y﹣y)=3x+3y﹣180°,∴2∠EFM=6x+6y﹣360°,∴∠EHG≠2∠EFM∴②错误;∴∠EHG+∠EFM=x+y+3x+3y﹣180°=4x+4y﹣180°≠90°,∴③错误;∴3∠EHG﹣∠EFM=3(x+y)﹣(3x+3y﹣180°)=180°,∴④正确.综上所述,正确答案为①④.故选:D.6.如图,AB∥CD,EMNF是直线AB、CD间的一条折线.若∠1=40°,∠2=60°,∠3=70°,则∠4的度数为()A.55°B.50°C.40°D.30°【答案】B【解答】解:如图2,过M作OM∥AB,PN∥AB,∵AB∥CD,∴AB∥OM∥PN∥CD,∴∠1=∠EMO,∠4=∠PNF,∠OMN=∠PNM,∴∠EMN﹣∠MNF=(∠1+∠MNP)﹣(∠MNP+∠4)=∠1﹣∠4,∴60°﹣70°=40°﹣∠4,∴∠4=50°.故选:B.7.为了落实“双减”政策,促进学生健康成长,各学校积极推行“5+2”模式,立足学生的认知成长规律,满足学生多样化的需求,打造特色突出、切实可行的体育锻炼内容.晋中市的某学校将“抖空竹”引入阳光体育一小时活动,如图1是一位同学抖空竹时的一个瞬间,小丽把它抽象成图2的数学问题:已知AB∥CD,∠EAB=80°,∠ECD=110°,则∠E的度数是30°.【答案】30°【解答】解:延长DC交AE于点F,∵AB∥CD,∴∠EFC=∠A=80°,由外角的性质得,∠DCE=∠E+∠EFC,∴∠E=110°﹣80°=30°.故答案为:30°.8.如图,直线PQ∥MN,直角三角尺ABC的∠BAC=30°,∠ACB=90°.(1)若把三角尺按图甲方式放置,则∠MAC+∠PBC=90°;(2)若把三角尺按图乙方式放置,点D,E,F是三角尺的边与平行线的交点,若∠AEN =∠A,求∠BDF的值;(3)如图丙,三角尺的直角顶点C始终在两条平行线之间,点G在线段CD上,连接EG,适当转动三角尺,使得CE恰好平分∠MEG,求的值.【解答】解:(1)延长BC交MN于点D,∵PQ∥MN,∴∠PBC=∠ADC,∵∠ACB是△ACD的一个外角,∴∠ACB=∠ADC+∠MAC,∴∠ACB=∠PBC+∠MAC=90°,故答案为:90;(2)∵∠AEN=∠A,∠BAC=30°,∴∠AEN=∠A=30°,∴∠CEM=∠AEN=30°,利用(1)的结论可得:∠ACB=∠PDC+∠MEC,∴∠PDC=∠ACB﹣∠MEC=60°,∴∠BDF=∠PDC=60°,∴∠BDF的度数为60°;(3)∵CE平分∠MEG,∴∠CEM=∠CEG,设∠CEM=∠CEG=x,∴∠GEN=180°﹣∠CEM﹣∠CEG=180°﹣2x,利用(1)的结论可得:∠ACB=∠PDC+∠MEC,∴∠PDC=∠ACB﹣∠MEC=90°﹣x,∴∠BDF=∠PDC=90°﹣x,∴==2,∴的值为2.9.如图,AB∥CD,点E为两直线之间的一点.(1)如图1,若∠BAE=35°,∠DCE=20°,则∠AEC=;(2)如图2,试说明,∠BAE+∠AEC+∠ECD=360°;(3)①如图3,若∠BAE的平分线与∠DCE的平分线相交于点F,判断∠AEC与∠AFC 的数量关系,并说明理由;②如图4,若设∠E=m,∠BAF=∠F AE,∠DCF=∠FCE,请直接用含m、n的代数式表示∠F的度数.【解答】解:(1)55°如图所示,过点E作EF∥AB,∵AB∥CD∴AB∥CD∥EF,∴∠BAE=∠1,∠ECD=∠2,∴∠AEC=∠1+∠2=∠BAE+∠ECD=35°+20°=55°,故答案为55°.(2)如图所示,过点E作EG∥AB,∵AB∥CD∴AB∥CD∥EG,∴∠A+∠1=180°,∠C+∠2=180°,∴∠A+∠1+∠2+∠C=360°,即∠BAE+∠AEC+∠ECD=360°.(3)①2∠AFC+∠AEC=360°,理由如下:由(1)可得,∠AFC=∠BAF+∠DCF,∵AF平分∠BAE,CF平分∠DCE,∴∠BAE=2∠BAF,∠DCE=2∠DCF,∴∠BAE+∠DCE=2∠AFC,由(2)可知,∠BAE+∠AEC+∠DCE=360°,∴2∠AFC+∠AEC=360°.②由①知∠F+∠F AE+∠E+∠FCE=360°,∵∠BAF=∠F AE,∠DCF=∠FCE,∠BAF+∠DCF=∠F,∴∠F=(∠F AE+∠FCE),∴∠F AE+∠FCE=n∠F,∴∠F+∠E+n∠F=360°,∴(n+1)∠F=360°﹣∠E=360°﹣m,∴∠F=.10.问题情境我们知道,“两条平行线被第三条直线所截,同位角相等,内错角相等,同旁内角互补”,所以在某些探究性问题中通过“构造平行线”可以起到转化的作用.已知三角板ABC中,∠BAC=60°,∠B=30°,∠C=90°,长方形DEFG中,DE∥GF.问题初探(1)如图(1),若将三角板ABC的顶点A放在长方形的边GF上,BC与DE相交于点M,AB⊥DE于点N,求∠EMC的度数.分析:过点C作CH∥GF.则有CH∥DE,从而得∠CAF=∠HCA,∠EMC=∠MCH,从而可以求得∠EMC的度数.由分析得,请你直接写出:∠CAF的度数为,∠EMC的度数为.类比再探(2)若将三角板ABC按图(2)所示方式摆放(AB与DE不垂直),请你猜想写∠CAF 与∠EMC的数量关系,并说明理由.(3)请你总结(1),(2)解决问题的思路,在图(3)中探究∠BAG与∠BMD的数量关系?并说明理由.【解答】解:(1)由题可得,∠CAF=∠BAF﹣∠BAC=90°﹣60°=30°,∠EMC=∠BCH=90°﹣30°=60°;故答案为:30°,60°;(2)∠EMC+∠CAF=90°,理由:证明:如图,过C作CH∥GF,则∠CAF=∠ACH,∵DE∥GF,CH∥GF,∴CH∥DE,∴∠EMC=∠HCM,∴∠EMC+∠CAF=∠MCH+∠ACH=∠ACB=90°;(3)∠BAG﹣∠BMD=30°,理由:证明:如图,过B作BK∥GF,则∠BAG=∠KBA,∵BK∥GF,DE∥GF,∴BK∥DE,∴∠BMD=∠KBM,∴∠BAG﹣∠BMD=∠ABK﹣∠KBM=∠ABC=30°.11.已知AM∥CN,点B在直线AM、CN之间,AB⊥BC于点B.(1)如图1,请直接写出∠A和∠C之间的数量关系:.(2)如图2,∠A和∠C满足怎样的数量关系?请说明理由.(3)如图3,AE平分∠MAB,CH平分∠NCB,AE与CH交于点G,则∠AGH的度数为45°.【解答】解:(1))过点B作BE∥AM,如图,∵BE∥AM,∴∠A=∠ABE.∵BE∥AM,AM∥CN,∴BE∥CN.∴∠C=∠CBE.∵AB⊥BC,∴∠ABC=90°.∴∠A+∠C=∠ABE+∠CBE=∠ABC=90°.故答案为:∠A+∠C=90°;(2)∠A和∠C满足:∠C﹣∠A=90°.理由:过点B作BE∥AM,如图,∵BE∥AM,∴∠A=∠ABE.∵BE∥AM,AM∥CN,∴BE∥CN.∴∠C+∠CBE=180°.∴∠CBE=180°﹣∠C.∵AB⊥BC,∴∠ABC=90°.∴∠ABE+∠CBE=90°.∴∠A+180°﹣∠C=90°.∴∠C﹣∠A=90°.(3)设CH与AB交于点F,如图,∵AE平分∠MAB,∴∠GAF=∠MAB.∵CH平分∠NCB,∴∠BCF=∠BCN.∵∠B=90°,∴∠BFC=90°﹣∠BCF.∵∠AFG=∠BFC,∴∠AFG=90°﹣∠BCF.∵∠AGH=∠GAF+∠AFG,∴∠AGH=∠MAB+90°﹣∠BCN=90°﹣(∠BCN﹣∠MAB).由(2)知:∠BCN﹣∠MAB=90°,∴∠AGH=90°﹣45°=45°.故答案为:45°.12.已知直线EF分别与直线AB,CD相交于点G,M,并且∠AGE+∠CHF=180°.(1)如图1,求证:AB∥CD;(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;(3)如图3,在(2)的条件下,若射线GH恰好是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,则∠M、∠N、∠FGN的数量关系是(直接写答案).【解答】(1)证明:∵∠AGE=∠BGF,∠CHF=∠EHD,又∠AGE+∠CHF=180°,∴∠BGF+∠EHD=180°,∴AB∥CD;(2)证明:过点M作MK∥CD,则∠KMH=∠CHM,又AB∥CD;∴AB∥MK;∴∠AGM=∠GMK,∵∠GMH=∠AGM+∠KMH∴∠GMH=∠AGM+∠CHM.(3)解:如图3,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β,∵射线GF是∠BGM的平分线,∴∠FGM=∠BGM=(180°−∠AGM)=90°−α,∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,∵∠GMH=∠N+∠FGN,∴2α+β=2α+∠FGN,∴∠FGN=2β,∴∠M=2α+β=∠N+∠FGN,即:∠M=∠N+∠FGN.。
平行线之猪脚模型(M模型)-【压轴必刷】中考数学压轴大题之经典模型(解析版)
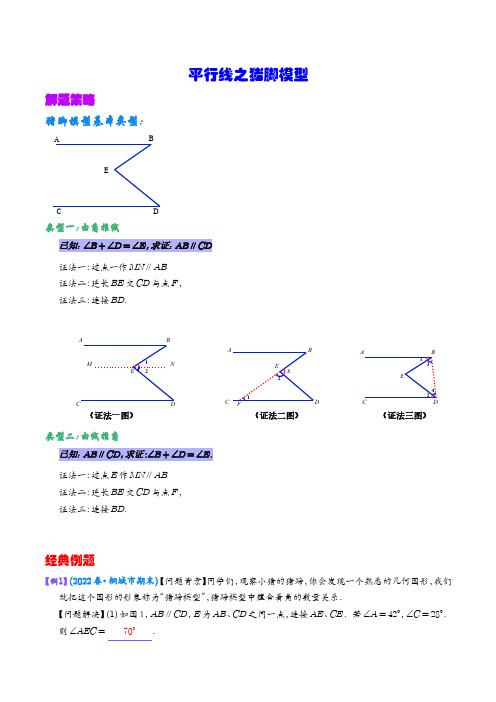
平行线之猪脚模型解题策略猪脚模型基本类型:A BC DE类型一:由角推线已知:∠B +∠D =∠E ,求证:AB ∥CD证法一:过点一作MN ∥AB 证法二:延长BE 交CD 与点F ,证法三:连接BD .A BC D E MN AB C D EF A B C DE 121231234(证法一图)(证法二图)(证法三图)类型二:由线推角已知:AB ∥CD ,求证:∠B +∠D =∠E .证法一:过点E 作MN ∥AB证法二:延长BE 交CD 与点F ,证法三:连接BD .经典例题【例1】(2022春•桐城市期末)【问题背景】同学们,观察小猪的猪蹄,你会发现一个熟悉的几何图形,我们就把这个图形的形象称为“猪蹄模型”,猪蹄模型中蕴含着角的数量关系.【问题解决】(1)如图1,AB ∥CD ,E 为AB 、CD 之间一点,连接AE 、CE .若∠A =42°,∠C =28°.则∠AEC = 70° .【问题探究】(2)如图2,AB∥CD,线段AD与线段BC交于点E,∠A=36°,∠C=54°,EF平分∠BED,求∠BEF的度数.【问题拓展】(3)如图3.AB∥CD,线段AD与线段BC相交于点G,∠BCD=56°,∠GDE=20°,过点D作DF∥CB交直线AB于点F,AE平分∠BAD,DG平分∠CDF,求∠AED的度数.【分析】(1)延长CE交AB于点F,利用平行线的性质可得∠AFC=28°,然后再利用三角形的外角可得∠AEC=∠A+∠C,进行计算即可解答;(2)利用猪蹄模型可得:∠AEC=∠A+∠C=90°,再利用对顶角相等可得∠BED=90°,然后利用角平分线的定义进行计算即可解答;(3)利用平行线的性质可求出∠CDF的度数,从而利用角平分线的定义求出∠CDG的度数,进而利用平行线的性质可求出∠BAD的度数,然后根据角平分线的定义求出∠BAE的度数,再利用平角定义求出∠EDH的度数,最后根据猪蹄模型可得∠AED=∠BAE+∠EDH,进行计算即可解答.【解答】解:(1)延长CE交AB于点F,∵AB∥CD,∴∠AFC=∠C=28°,∵∠AEC是△AEF的一个外角,∴∠AEC=∠A+∠AFC=∠A+∠C=70°,故答案为:70°;(2)利用(1)的结论可得:∠AEC=∠A+∠C=36°+54°=90°,∴∠AEC=∠BED=90°,∵EF平分∠BED,∠BED=45°,∴∠BEF=12∴∠BEF的度数为45°;(3)∵BC∥DF,∴∠CDF=180°-∠BCD=124°,∵DG平分∠CDF,∴∠CDG=1∠CDF=62°,2∵AB∥CD,∴∠BAG=∠CDG=62°,∵AE平分∠BAD,∠BAD=31°,∴∠BAE=12∵∠GDE=20°,∴∠EDH=180°-∠CDG-∠GDE=98°,利用(1)的结论可得:∠AED=∠BAE+∠EDH=31°+98°=129°,∴∠AED的度数为129°.【例2】(2022春•南京期中)已知直线AB∥CD,点E,F分别在AB,CD上,O是平面内一点(不在直线AB、CD、EF上),OG平分∠EOF,射线OH∥AB,交EF于点H.(1)如图①,若∠AEO=45°,∠CFO=75°,则∠HOG= 15° ,(2)如图②,若∠AEO=150°,∠HOG=20°,则∠CFO= 110° ;(3)直接写出点O在不同位置时∠AEO、∠CFO和∠HOG三个角之间满足的数量关系.【分析】(1)由AB∥CD,OH∥AB可得AB∥OH∥CD,利用平行线的性质可得∠AEO=∠EOH,∠CFO=∠FOH,由∠EOF=∠EOH+∠FOH,等量代换可得∠AEO+∠CFO=∠EOF,根据已知条件和角平分线的定义求出∠EOG=60°,即可得到∠HOG的度数;(2)同(1)类似,利用平行线的性质和角平分线的定义计算可以得出∠CFO的度数;(3)由(1)和(2)的计算方法可以得出结论.【解答】解:(1)∵AB∥CD,OH∥AB,∴AB∥OH∥CD,∴∠AEO=∠EOH,∠CFO=∠FOH,∴∠AEO+∠CFO=∠EOH+∠FOH,即∠AEO+∠CFO=∠EOF,∵∠AEO=45°,∠CFO=75°,∴∠EOF=120°,∵OG平分∠EOF,∴∠EOG=60°,∴∠HOG=∠EOG-∠EOH=15°,故答案为:15°;(2)∵AB∥CD,OH∥AB,∴AB∥OH∥CD,∴∠AEO+∠EOH=180°,∠CFO+∠FOH=180°,∴∠AEO+∠CFO+∠EOH+∠FOH=360°,即∠AEO+∠CFO+∠EOF=360°,∵AB∥OH,∴∠AEO+∠EOH=180°,∵∠AEO=150°,∴∠EOH=30°,∵∠HOG=20°,∴∠EOG=∠EOH+∠HOG=30°+20°=50°,∵OG平分∠EOF,∴∠EOF=2∠EOG=100°,∵∠AEO+∠CFO+∠EOF=360°,∠AEO=150°,∴∠CFO=360°-150°-100°=110°,故答案为:110°;(3)①若点O在直线AB与CD之间,则有|∠AEO-∠CFO|=2∠HOG;②若点O在直线AB与CD之外,且在直线EF的左侧,则有∠AEO+∠CFO=2∠HOG;若点O在直线AB与CD之外,且在直线EF的右侧,则有360°-∠AEO-∠CFO=2∠HOG.【例3】(2022春•上城区校级期中)如图,一副三角板,其中∠EDF=∠ACB=90°,∠E=45°,∠A=30°.(1)若这副三角板如图摆放,EF∥CD,求∠ABF的度数.(2)将一副三角板如图1所示摆放,直线GH∥MN,保持三角板ABC不动,现将三角板DEF绕点D以每秒2°的速度顺时针旋转,如图2,设旋转时间为t秒,且0≤t≤180,若边BC与三角板的一条直角边(边DE,DF)平行时,求所有满足条件的t的值.(3)将一副三角板如图3所示摆放,直线GH∥MN,现将三角板ABC绕点A以每秒1°的速度顺时针旋转,同时三角板DEF绕点D以每秒2°的速度顺时针旋转.设旋转时何为t秒,如图4,∠BAH= t°,∠FDM=2t°,且0≤t≤150,若边BC与三角板的一条直角边(边DE,DF)平行时,请直接写出满足条件的t的值.【分析】(1)由题意得,∠EBF=90°,∠E=45°,∠ABC=60°,利用平行线的性质可得∠CDE=∠E=45°,即可求得答案;(2)①当DE∥BC时,延长AC交MN于点P,分两种情况:当DE在MN上方时或当DE在MN下方时,分别运用平行线的性质即可;②当BC∥DF时,延长BC交MN于点T,分两种情况:当DF在MN上方时或当DF在MN下方时,分别运用平行线的性质即可;(3)当DE∥BC时,延长AC交MN于点P,分两种情况讨论:①DE在MN上方时,②DE在MN下方时,∠FDP=2t°-180°,列式求解即可;(2)当BC∥DF时,延长AC交MN于点I,①DF在MN上方时,∠FDN=180°-2t°,②DF在MN下方时,∠FDN=180°-2t°,列式求解即可.【解答】解:(1)如图,由题意得,∠EBF=90°,∠E=45°,∠ABC=60°,∵EF∥CD,∴∠CDE=∠E=45°,∴∠ABE=∠ABC-∠CDE=60°-45°=15°,∴∠ABF=∠EBF-∠ABE=90°-15°=75°;(2)如图,①当DE∥BC时,延长AC交MN于点P,当DE在MN上方时,∵DE∥BC,DE⊥DF,AC⊥BC,∴AP∥DF,∴∠FDM=∠MPA,∵MN∥GH,∴∠MPA=∠HAC,∴∠FDM=∠HAC,即2t°=30°,∴t=15;当DE在MN下方时,∠F′DP=2t°-180°,∵DE′∥BC,DE′⊥DF′,AC⊥BC,∴AP∥DF′,∴∠F′DP=∠MPA,∵MN∥GH,∴∠MPA=∠HAC,∴∠F′DP=∠HAC,即2t°-180°=30°,∴t=105;②当BC∥DF时,当DF在MN上方时,BC∥DF,如图,延长BC交MN于点T,根据题意得:∠FDN=180°-2t°,∵DF∥BC,∴∠FDN=∠BTN,∵GH∥MN,∴∠BTN=∠ABC=60°,∴∠FDN=60°,即180°-2t°=60°,∴t=60;当DF在MN下方时,如图,延长BC交MN于点T,根据题意可知:∠FDN=2t°-180°,∵DF∥BC,∴∠FDN=∠BTM,∵GH∥MN,∴∠BTN=∠ABC=60°,∴∠BTM=180°-∠BTN=120°,∴∠NDF=120°,即2t°-180°=120°,∴t=150,综上所述:所有满足条件的t的值为15或60或105或150;(3)由题意得,∠HAC=∠BAH+∠BAC=t°+30°,∠FDM=2t°,①如图,当DE∥BC时,延长AC交MN于点P,当DE在MN上方时,∵DE∥BC,DE⊥DF,AC⊥BC,∴AP∥DF,∴∠FDM=∠MPA,∵MN∥GH,∴∠MPA=∠HAC,∴∠FDM=∠HAC,即2t°=t°+30°,∴t=30,当DE′在MN下方时,∠F′DP=2t°-180°,∵DE′∥BC,DE′⊥DF′,AC⊥BC,∴AP∥DF′,∴∠F′DP=∠MPA,∵MN∥GH,∴∠MPA=∠HAC,∴∠F′DP=∠HAC,即2t°-180°=t°+30°,∴t=210(不符合题意,舍去),②当BC∥DF时,延长AC交MN于点I,当DF在MN上方时,BC∥DF,如图,根据题意得:∠FDN=180°-2t°,∵DF∥BC,AC⊥BC,∴CI⊥DF,∴∠FDN+∠MIC=90°,即180°-2t°+t°+30°=90°,∴t=120,∴2t=240°>180°,此时DF应该在MN下方,不符合题意,舍去;当DF在MN下方时,如图,根据题意可知:∠FDN=2t°-180°,∵DF∥BC,∴∠MIC=∠NDF,∴∠NDF=∠AQI=t+30°-90°=t-60°,即2t°-180°=t°-60°,∴t=120,综上所述:所有满足条件的t的值为30或120.【例4】(2021春•梅江区期末)如图(1),AB∥CD,点E在AB、CD之间,连接EA、EC;如图(2),AB∥CD.点M、N分别在AB、CD上,连接MN.(1)在图(1)中,若∠A=30°,∠C=50°,则∠AEC= 80° ;若∠A=25°,∠C=40°,则∠AEC= 65° .(2)图(1)的条件下,猜想∠EAB、∠ECD、∠AEC的关系,并说明你的结论.(3)如图(2),点E是四边形ACDB内(不含边界和MN)任意一点,请说明∠EMB、∠END、∠MEN的关系.【分析】(1)过点E作EF∥AB,如图1,根据平行线的性质,两直线平行,内错角相等可得∠AEG=∠A,∠CEG=∠C,由∠AEC=∠AEG+∠CEG,可得∠AEC=∠A+∠C,代入计算即可得出答案;(2)过点E作EF∥AB,如图1,根据平行线的性质可得,∠AEG=∠EAB,∠CEG=∠ECD.由∠AEC=∠AEG+∠CEG,即可得出答案;(3)根据题意画图,如图2,过点E作EF∥AB,根据平行线的性质,两直线平行,同旁内角互补可得,∠EMB+∠MEF=180°,∠NEF+∠END=180°,由∠EMB+∠MEF+∠NEF+∠END=360°,根据∠MEN=∠MEF+∠NEF,即可得出答案.【解答】解:(1)过点E作EF∥AB,如图1,∵AB∥CD,∴GF∥CD,∴∠AEG=∠A,∠CEG=∠C,∴∠AEC=∠AEG+∠CEG,∴∠AEC=∠A+∠C,若∠A=30°,∠C=50°,则∠AEC=30°+50°=80°,若∠A=25°,∠C=40°,则∠AEC=25°+40°=65°;故答案为:80°,65°;(2)∠AEC=∠EAB+∠ECD.理由如下:过点E作EF∥AB,如图1,∵AB∥CD,∴GF∥CD,∴∠AEG=∠EAB,∠CEG=∠ECD.∵∠AEC=∠AEG+∠CEG,∴∠AEC=∠EAB+∠ECD;(3)∠ENB+∠NEN+∠END=360°.理由如下:根据题意画图,如图2,过点E作EF∥AB,∴∠EMB+∠MEF=180°,∵AB∥CD,∴GF∥CD,∴∠NEF+∠END=180°,∴∠EMB+∠MEF+∠NEF+∠END=360°,∵∠MEN=∠MEF+∠NEF,∴∠ENB+∠NEN+∠END=360°.培优训练一、选择题1.(2022•黔东南州)一块直角三角板按如图所示方式放置在一张长方形纸条上,若∠1=28°,则∠2的度数为()A.28°B.56°C.36°D.62°【分析】过直角的顶点E作MN∥AB,利用平行线的性质解答即可.【解答】解:如下图所示,过直角的顶点E作MN∥AB,交AD于点M,交BC于点N,则∠2=∠3.∵四边形ABCD是矩形,∴AB∥CD,∵AB∥MN,∴MN∥CD,∴∠4=∠1=28°,∵∠3+∠4=90°,∴∠3=90°-∠4=62°.∴∠2=∠3=62°.故选:D.2.(2022•临清市二模)如图,若AB∥CD,CD∥EF,那么∠BCE=()A.180°-∠2+∠1B.180°-∠1-∠2C.∠2=2∠1D.∠1+∠2【分析】先利用平行线的性质说明∠3、∠1、∠4、∠2间关系,再利用角的和差关系求出∠BCA【解答】解:∵AB∥CD,CD∥EF,∴∠1=∠3,∠2+∠4=180°.∴∠BCE=∠3+∠4=∠1+180°-∠2.故选:A.3.(2021春•硚口区月考)如图,AB与HN交于点E,点G在直线CD上,GF交AB于点M,∠FMA=∠FGC,∠FEN=2∠NEB,∠FGH=2∠HGC,下列四个结论:①AB∥CD;②∠EHG=2∠EFM;③∠EHG+∠EFM=90°;④3∠EHG-∠EFM=180°.其中正确的结论是()A.①②③B.②④C.①②④D.①④【分析】过点F作FP∥AB,HQ∥AB,设∠NEB=x,∠HGC=y,利用猪脚模型、锯齿模型表示出∠EHG、∠EFM,即可分析出答案.【解答】解:∵∠FMA=∠FGC∴AB∥CD∴①正确;过点F作FP∥AB,HQ∥AB,∵AB∥CD,∴FP∥AB∥HQ∥CD,设∠NEB=x,∠HGC=y,则∠FEN=2x,∠FGH=2y∴∠EHG=∠EHQ+∠GHQ=∠AEH+∠HGC=∠NEB+∠HGC=x+y,∠EFM=∠BEF-∠FME=∠BEF-∠AMG=∠BEF-(180°-∠FGC)=x+2x-(180°-y-y) =3x+3y-180°,∴2∠EFM=6x+6y-360°,∴∠EHG≠2∠EFM∴②错误;∴∠EHG+∠EFM=x+y+3x+3y-180°=4x+4y-180°≠90°,∴③错误;∴3∠EHG-∠EFM=3(x+y)-(3x+3y-180°)=180°,∴④正确.综上所述,正确答案为①④.故选:D.4.(2018春•南昌期中)如图,AB∥CD,∠1=30°,∠2=90°,则∠3的度数是()A.30°B.45°C.50°D.60°【分析】作辅助线,过点O做OP∥AB∥CD,再结合两直线平行内错角相等的性质,即可得出∠3的度数.【解答】解:过点O做OP∥AB∥CD,∴∠A=∠AOP=30°,∠D=∠POC,∵∠2=90°,即∠AOC=90°,∴∠POC=60°,∴∠3=60°.故选:D.5.(2018春•沂源县期末)如图,AB∥CD,∠ABF=23∠ABE,∠CDF=23∠CDE,则∠E:∠F=()A.2:1B.3:1C.3:2D.4:3【分析】本题主要利用两直线平行,内错角相等作答.【解答】解:过点E、F分别作AB的平行线EG、FH,由平行线的传递性可得AB∥EG∥FH∥CD,∵AB∥FH,∴∠ABF=∠BFH,∵FH∥CD,∴∠CDF=∠DFH,∴∠BFD=∠DFH+∠BFH=∠CDF+∠ABF;同理可得∠BED=∠DEG+∠BEG=∠ABE+∠CDE;∵∠ABF=23∠ABE,∠CDF=23∠CDE,∴∠BFD=∠DFH+∠BFH=∠CDF+∠ABF=23(∠ABE+∠CDE)=23∠BED,∴∠BED:∠BFD=3:2.故选:C.6.(2022春•诸暨市期末)从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出,已知入射光线OA的反射光线为AB,∠OAB=∠COA=72°.在如图中所示的截面内,若入射光线OD经反光罩反射后沿DE射出,且∠ODE=27°.则∠AOD的度数是 45°或99° .【分析】分两种情况:如果∠AOD是锐角,∠AOD=∠COA-∠COD;如果∠AOD是钝角,∠AOD=∠COA+∠COD,由平行线的性质求出∠COA,∠COD,从而求出∠AOD的度数.【解答】解:∵DE∥CF,∴∠COD=∠ODE.(两直线平行,内错角相等)∵∠ODE=22°,∴∠COD=22°.在图1的情况下,∠AOD=∠COA-∠COD=72°-27°=45°.在图2的情况下,∠AOD=∠COA+∠COD=72°+27°=99°.∴∠AOD的度数为45°或99°.故答案为:45°或99°.7.(2022春•潜山市月考)如图,AB∥CD,点E,F分别是AB,CD上的点,点M位于AB与CD之间且在EF的右侧.(1)若∠M=90°,则∠AEM+∠CFM= 270° ;(2)若∠M=n°,∠BEM与∠DFM的角平分线交于点N,则∠N的度数为 1n° .(用含n的2式子表示)【分析】(1)过点M 作MP ∥AB ,则AB ∥CD ∥MP ,根据两直线平行,内错角相等可得答案;(2)过点N 作NQ ∥AB ,则AB ∥CD ∥NQ ,根据两直线平行内错角相等和角平分线的定义可得答案.【解答】解:(1)过点M 作MP ∥AB ,∵AB ∥CD ,∴AB ∥CD ∥MP ,∴∠1=∠MEB ,∠2=∠MFD ,∵∠M =∠1+∠2=90°,∴∠MEB +∠MFD =90°,∵∠AEM +∠MEB +∠CFM +∠MFD =180°+180°=360°,∴∠AEM +∠CFM =360°-90°=270°.故答案为:270°;(2)过点N 作NQ ∥AB ,∵AB ∥CD ,∴AB ∥CD ∥NQ ,∴∠3=∠NEB ,∠4=∠NFD ,∴∠NEB +∠NFD =∠3+∠4=∠ENF ,∵∠BEM 与∠DFM 的角平分找交于点N ,∵∠NEB =12∠MEB ,∠DFN =12∠MFD ,∴∠3+∠4=∠BEN +∠DFN =12(∠MEB +∠MFD ),由(1)得,∠MEB +∠MFD =∠EMF ,∴∠ENF =12∠EMF =12n °.故答案为:12n °.8.(2019•大丰区一模)如图,已知:AB ∥CD ,∠1=50°,∠2=113°,则∠3= 63 度.【分析】如图,作EF ∥AB .证明基本结论;∠AEC =∠1+∠3即可解决问题.【解答】解:如图,作EF ∥AB .∵AB ∥CD ,AB ∥EF ,∴EF ∥CD ,∴∠1=∠AEF,∠3=∠CEF,∴∠AEC=∠1+∠3,∴113°=50°+∠3,∴∠3=63°.故答案为63;9.(2019秋•福田区校级期末)如图,AB∥CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD= 125° .【分析】首先过点E作EM∥AB,过点F作FN∥AB,由AB∥CD,即可得EM∥AB∥CD∥FN,然后根据两直线平行,同旁内角互补,由∠BED=110°,即可求得∠ABE+∠CDE=250°,又由BF平分∠ABE,DF平分∠CDE,根据角平分线的定义,即可求得∠ABF+∠CDF的度数,又由两直线平行,内错角相等,即可求得∠BFD的度数.【解答】解:过点E作EM∥AB,过点F作FN∥AB,∵AB∥CD,∴EM∥AB∥CD∥FN,∴∠ABE+∠BEM=180°,∠CDE+∠DEM=180°,∴∠ABE+∠BED+∠CDE=360°,∵∠BED=110°,∴∠ABE+∠CDE=250°,∵BF平分∠ABE,DF平分∠CDE,∴∠ABF=12∠ABE,∠CDF=12∠CDE,∴∠ABF+∠CDF=12(∠ABE+∠CDE)=125°,∵∠DFN=∠CDF,∠BFN=∠ABF,∴∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=125°.故答案为125°10.(2022春•交城县期中)如图,已知AB∥CD,AE和CF分别平分∠BAF和∠DCE,若∠AEC=57°,∠AFC=63°,则∠BAF的度数为 46° .【分析】延长AE 交CD 于点H ,延长AF 交CD 于点G ,设∠BAE =x ,∠FCG =y ,根据角平分线的定义可得∠BAF =2x ,∠ECG =2y ,然后利用平行线的性质可得∠AGC =2x ,∠AHC =x ,,再利用三角形的外角性质可得∠AEC =x +2y ,∠AFC =2x +y ,最后列出关于x ,y 的方程组,进行计算即可解答.【解答】解:延长AE 交CD 于点H ,延长AF 交CD 于点G ,设∠BAE =x ,∠FCG =y ,∵AE 和CF 分别平分∠BAF 和∠DCE ,∴∠BAF =2∠BAE =2x ,∠ECG =2∠FCG =2y ,∵AB ∥CD ,∴∠BAF =∠AGC =2x ,∠BAH =∠AHC =x ,∵∠AEC 是△EHC 的一个外角,∴∠AEC =∠AHC +∠ECG =x +2y ,∵∠AFC 是△GCF 的一个外角,∴∠AFC =∠AGC +∠FCG =2x +y ,∵∠AEC =57°,∠AFC =63°,∴x +2y =57o2x +y =63o ,解得:x =23o y =17o ,∴∠BAF =46°,故答案为:46°.11.(2022春•濠江区期末)已知直线AB ∥CD ,直线EF 分别截AB 、CD 于点G 、H ,点M 在直线AB 、CD 之间,连接MG ,MH .(1)如图1,求证:∠M =∠AGM +∠MHC ;(2)如图2,若HM 平分∠GHC ,在HM 上取点Q ,使得∠HGQ =∠AGM ,求证:∠M +∠GQH =180°;(3)如图3,若GH 平分∠MGB ,N 在为HD 上一点,连接GN ,且∠GNH =∠M ,∠HGN =2∠MHC ,求∠MHG 的度数.【分析】(1)过点M作MN∥AB,利用平行线的猪脚模型,即可解答;(2)根据角平分线的定义可得∠MHG=∠CHM,再利用(1)的结论可得∠GMH=∠AGM+∠MHC,从而可得∠GMH=∠HGQ+∠MHG,然后利用三角形内角和定理进行计算即可解答;(3)设∠AGM=2α,∠CHM=β,从而可得∠HGN=2β,再利用(1)的结论可得∠GMH=2α+β,从而可得∠GNH=2α+β,然后利用角平分线的定义可得∠MGH=90°-α,再利用三角形的外角可得∠CHG= 3β+2α,最后利用平行线的性质可得∠AGH+∠CHG=180°,从而可得α+β=30°,再利用角的和差关系进行计算即可解答.【解答】(1)证明:过点M作MN∥AB,∴∠AGM=∠GMN,∵AB∥CD,∴MN∥CD,∴∠NMH=∠CHM,∵∠GMH=∠GMN+∠NMH,∴∠GMH=∠AGM+∠MHC;(2)证明:∵HM平分∠GHC,∴∠MHG=∠CHM,由(1)得:∠GMH=∠AGM+∠MHC,∵∠HGQ=∠AGM,∴∠GMH=∠HGQ+∠MHG,∵∠GQH+∠HGQ+∠MHG=180°,∴∠GMH+∠GQH=180°;(3)解:设∠AGM=2α,∠CHM=β,由(1)可得:∠GMH=∠AGM+∠MHC,∴∠GMH=2α+β,∵∠GNH=∠M,∴∠GNH=2α+β,∵∠HGN=2∠MHC,∴∠HGN=2β,∵GH平分∠MGB,∴∠MGH=12∠BGM=12(180°-∠AGM)=90°-α,∵∠CHG是△GHN的一个外角,∴∠CHG=∠HGN+∠GNH=2β+2α+β=3β+2α,∵AB∥CD,∴∠AGH+∠CHG=180°,∴∠AGM+∠MGH+∠CHG=180°,∴2α+90°-α+3β+2α=180°,∴α+β=30°,∴∠MHG=∠CHG-∠CHM=3β+2α-β=2β+2α=60°,∴∠MHG的度数为60°.12.(2022春•沂源县期末)在综合与实践课上,同学们以“一个含30°的直角三角尺和两条平行线”为背景开展数学活动如图,已知两直线a,b且a∥b和直角三角形ABC,∠BCA=90°,∠BAC=30°,∠ABC=60°.操作发现:(1)在图1中,∠1=46°,求∠2的度数.(2)某同学把直线a向上平移,并把∠2的位置改变,如图2,发现∠2-∠1=120°,说明理由.【分析】(1)根据直角三角形的性质求出∠3,根据平行线的性质解答;(2)过点B作BD∥a,根据平行线的性质得到∠ABD=180°-∠2,∠DBC=∠1,结合图形计算,证明结论.【解答】解:(1)∵∠BCA=90°,∴∠3=90°-∠1=44°,∵a∥b,∴∠2=∠3=44°.(2)理由如下:过点B作BD∥a,则∠ABD=180°-∠2,∵a∥b,BD∥a,∴BD∥b,∴∠DBC=∠1,∵∠ABC=60°∴180°-∠2+∠1=60°,∴∠2-∠1=120°.13.(2022春•无棣县期末)如图1,已知∠BAE=∠AEC-∠ECD,点E在直线AB,CD之间.(1)求证:AB∥CD;(2)若AH平分∠BAE,FG∥CE.①如图2,若∠AEC=84°,FH平分∠DFG,求∠AHF的度数;②如图3,若FH平分∠CFG,试判断∠AHF与∠AEC的数量关系并说明理由.【分析】(1)过E作EN∥AB,可得∠BAE=∠AEN,∠BAE=∠AEC-∠ECD,证得∠ECD=∠CEN,故EF∥CD∥AB;(2)①HF平分∠DFG,设∠GFH=∠DFH=x,根据平行线的性质可以得到∠AHF的度数;②设∠GFD=2x,∠BAH=∠EAH=y,根据角平分线的性质以及平行线的性质即可得到∠AHF与∠AEC的数量关系.【解答】解:(1)如图1,过点E作直线EN∥AB,∴∠BAE=∠AEN,∵∠BAE=∠AEC-∠ECD,∴∠BAE+∠ECD=∠AEC,∵∠AEN+∠CEN=∠AEC,∴∠ECD=∠CEN,∴EN∥CD,∴CD∥AB;(2)∵AH平分∠BAE,∴∠BAH=∠EAH,①∵HF平分∠DFG,设∠GFH=∠DFH=x,又CE∥FG,∴∠ECD=∠GFD=2x,又∠AEC=∠BAE+∠ECD,∠AEC=84°,∴∠BAH=∠EAH=42°-x,如图2,过点H作HM∥AB,∴∠BAH=∠AHM,∵HM∥AB,∴HM∥CD,∴∠DFH=∠MHF,∴∠AHF=∠BAH+∠DFH=42°-x+x=42°;②设∠GFD=2x,∠BAH=∠EAH=y,∵HF平分∠CFG,∴∠GFH=∠CFH=90°-x,由(1)知∠AEC=∠BAE+∠ECD=2x+2y,如图3,过点H作HK∥AB,∴∠BAH=∠AHK,∵HK∥AB,∴HK∥CD,∴∠KHF+∠CFH=180°,∴∠AHF-y+∠CFH=180°,即∠AHF-y+90°-x=180°,∠AHF=90°+(x+y),∴∠AHF=90°+1∠AEC.214.(2022春•墨玉县期末)问题情景:(1)如图①,已知AB∥DE.试∠B、∠E、∠BCE有什么关系?小明添加了一条辅助线.解决了这道题.得到的结果是∠B+∠E=∠BCE.请你帮他完善证明过程:如图②,过点C作CF∥AB∴ ∠B = ∠1 ( 两直线平行,内错角相等 )∵AB∥DE,AB∥CF∴ DE ∥ CF .∴∠E= ∠2 ( 两直线平行,内错角相等 )∴∠B+∠E=∠1+∠2即∠B+∠E=∠BCE.(2)在图①中.若BC⊥CE,且∠B=52°,请你计算∠E的度数等于 38° .(3)问题迁移:如图③.AD∥BC.当点P在射线AM上运动时,∠ADP=∠α,∠BCP=∠β请你猜想∠α、∠β与∠CPD之间有怎样的数量关系?并说明理由.【分析】(1)根据两直线平行,内错角相等即可求解;(2)由(1)可知∠B+∠E=90°,即可求解;(3)由三角形外角性质可得∠CPD+∠CDP=∠OCP,从而可得∠CPD+∠α+∠ADO=∠β+∠BCO,由AD∥BC可得∠ADO=∠BCO,即可得出∠CPD+∠α=∠β.【解答】解:(1)过点C作CF∥AB,∴∠B=∠1(两直线平行,内错角相等),∵AB∥DE,AB∥CF,∴DE∥CF,∴∠E=∠2(两直线平行,内错角相等),∴∠B+∠E=∠1+∠2,即∠B+∠E=∠BCE,故答案为:∠B=∠1;两直线平行,内错角相等;DE;CF;∠2;两直线平行,内错角相等;(2)由(1)可知∠B+∠E=∠BCE,∵∠BCE=90°,∠B=52°,∴∠E=∠BCE-∠B=38°,故答案为:38°;(3)∠CPD+∠α=∠β,理由如下:∵∠CPD+∠CDP=∠OCP,∴∠CPD+∠α+∠ADO=∠β+∠BCO,∵AD∥BC,∴∠ADO=∠BCO,∴∠CPD+∠α=∠β.15.(2022春•抚远市期末)如图,已知AD∥BC,AB∥CD,点E在线段BC的延长线上,AE平分∠BAD,连接DE,∠ADC=2∠CDE,∠AED=60°.(1)求证∠ABC=∠ADC;(2)求∠CDE的度数.【分析】(1)根据平行线的性质即可得到答案.(2)根据∠ADE=3∠CDE,设∠CDE=x,∠ADE=3x,∠ADC=2x,根据平行线的性质得出方程90°-x+60°+3x=180°,求出x即可.【解答】(1)证明:∵AB∥CD,∴∠ABC=∠DCE,∵AD∥BC,∴∠ADC=∠DCE,∴∠ABC=∠ADC.(2)解:设∠CDE=x,则∠ADC=2x,∵AB∥CD,∴∠BAD=180°-2x,∵AE平分∠BAD,∴∠EAD=12∠BAD=90°-x,∵AD∥BC,∴∠BEA=∠EAD=90°-x,∴∠BED+∠ADE=180°,∴90°-x+60°+3x=180°,∴x=15°,∴∠CDE=15°.16.(2022春•来宾期末)如图,直线PQ∥MN,直角三角尺ABC的∠BAC=30°,∠ACB=90°.(1)若把三角尺按图甲方式放置,则∠MAC+∠PBC= 90 °;(2)若把三角尺按图乙方式放置,点D,E,F是三角尺的边与平行线的交点,若∠AEN=∠A,求∠BDF的值;(3)如图丙,三角尺的直角顶点C始终在两条平行线之间,点G在线段CD上,连接EG,适当转动三角尺,使得CE恰好平分∠MEG,求∠GEN∠BDF的值.【分析】(1)延长BC交MN于点D,根据平行线的性质可得∠PBC=∠ADC,再利用三角形的外角可得∠ACB=∠ADC+∠MAC,然后利用等量代换即可解答;(2)根据已知可得∠AEN=∠A=30°,再利用对顶角相等可得∠CEM=30°,然后利用(1)的结论可得:∠PDC=60°,最后利用对顶角相等即可解答;(3)利用角平分线的定义设∠CEM=∠CEG=x,从而利用平角定义可得∠GEN=180°-2x,再利用(1)的结论可得:∠PDC=90°-x,然后利用对顶角相等可得∠BDF=90°-x,进行计算即可解答.【解答】解:(1)延长BC交MN于点D,∵PQ∥MN,∴∠PBC=∠ADC,∵∠ACB是△ACD的一个外角,∴∠ACB=∠ADC+∠MAC,∴∠ACB=∠PBC+∠MAC=90°,故答案为:90;(2)∵∠AEN=∠A,∠BAC=30°,∴∠AEN=∠A=30°,∴∠CEM=∠AEN=30°,∠ACB=∠PDC+∠MEC,∴∠PDC=∠ACB-∠MEC=60°,∴∠BDF=∠PDC=60°,∴∠BDF的度数为60°;(3)∵CE平分∠MEG,∴∠CEM=∠CEG,设∠CEM=∠CEG=x,∴∠GEN=180°-∠CEM-∠CEG=180°-2x,利用(1)的结论可得:∠ACB =∠PDC +∠MEC ,∴∠PDC =∠ACB -∠MEC =90°-x ,∴∠BDF =∠PDC =90°-x ,∴∠GEN ∠BDF =180O -2x 90o -x=2,∴∠GEN ∠BDF的值为2.17.(2022春•咸安区期末)(1)如图1,已知AB ∥CD ,∠AEP =40°,∠PFD =110°,求∠EPF 的度数.(2)如图2,AB ∥CD ,点P 在AB 的上方,问∠PEA ,∠PFC ,∠EPF 之间有何数量关系?并说明理由;(3)如图3,在(2)的条件下,已知∠EPF =60°,∠PEA 的平分线和∠PFC 的平分线交于点G ,求∠G 的度数.【分析】(1)延长EP 交CD 于点G ,利用平行线的性质可得∠PGF =40°,再利用平角定义可得∠PFG =70°,然后利用三角形的外角进行计算即可解答;(2)设AB 与PF 交于点M ,先利用三角形的外角可得∠PMA =∠PEA +∠EPF ,再利用平行线的性质可得∠PMA =∠PFC ,然后利用等量代换可得∠PFC =∠PEA +∠EPF ,即可解答;(3)利用(2)的结论可得∠EPF =∠PFC -∠PEA =60°,再利用角平分线的性质可得∠GEA =12∠AEP ,∠GFC =12∠PFC ,然后利用(2)的结论可得∠G =∠GFC -∠GEA =12(∠PFC -∠AEP ),进行计算即可解答.【解答】解:(1)延长EP 交CD 于点G ,∵AB ∥CD ,∴∠AEG =∠PGF =40°,∵∠PFD =110°,∴∠PFG =180°-∠PFD =70°,∵∠EPF 是△PFG 的一个外角,∴∠EPF =∠PGF +∠PFG =110°,∴∠EPF 的度数为110°;(2)∠PFC =∠PEA +∠EPF ,理由:如图:设AB 与PF 交于点M ,∵∠PMA 是△PME 的一个外角,∴∠PMA =∠PEA +∠EPF ,∵AB ∥CD ,∴∠PMA =∠PFC ,∴∠PFC =∠PEA +∠EPF ;(3)由(2)可得:∠PFC =∠PEA +∠EPF ,∴∠EPF =∠PFC -∠PEA =60°,∵EG 平分∠AEP ,FG 平分∠PFC ,∴∠GEA =12∠AEP ,∠GFC =12∠PFC ,由(2)得:∠GFC =∠G +∠GEA ,∴∠G =∠GFC -∠GEA=12∠PFC -12∠AEP =12(∠PFC -∠AEP )=12×60°=30°,∴∠G 的度数为30°.18.(2022春•上虞区期末)如图1,已知点E ,F 分别是直线AB ,CD 上的点,点M 在AB 与CD 之间,且AB ∥CD .(1)若∠EMF =80°,则∠AEM +∠CFM = 80° .(2)如图2,在图1的基础上,作射线EN ,FN 交于点N ,使∠AEN =13∠AEM ,∠CFN =13∠CFM ,设∠EMF =α,猜想∠ENF 的度数(用α表示),并说明理由.(3)如图3,在图1的基础上,分别作射线EP ,FP 交于点P ,作射线EQ ,FQ 交于点Q ,若∠AEP =1m ∠AEM ,∠CFP =1m ∠CFM ,∠BEQ =1n ∠BEM ,∠DFQ =1n∠DFM ,请直接写出∠P 与∠Q 间的数量关系.【分析】(1)过点M 作MP ∥AB ,利用平行线的性质,把∠AEM +∠CFM 转化为∠EMF ,从而求得度数.(2)过点M 作MP ∥AB ,过点N 作NQ ∥AB ,利用平行线的性质,把∠EMF 转化为∠AEM +∠CFM ,把∠ENF 转化为∠AEN +∠CFN ,得出∠ENF =13∠EMF ,从而用α表示出∠ENF 的度数.(3)利用(2)的结论,同时利用两直线平行,同旁内角互补得出∠BEM +∠DFM +∠M =360°,进而找到∠P 与∠Q 间的数量关系.【解答】解:(1)过点M 作MG ∥AB ,∵AB ∥CD ,∴AB ∥CD ∥MG ,∴∠AEM =∠EMG ,∠GMF =∠CFM ,∴∠AEM +∠CFM =∠EMG +∠GMF =∠EMF =80°.故答案为:80°.(2)∠ENF =13α.理由如下:过点M 作MG ∥AB ,由(1)知,∠EMF =∠AEM +∠CFM ,过点N 作NH ∥AB ,∵AB ∥CD ,∴AB ∥CD ∥NH ,∴∠AEN =∠ENH ,∠HNF =∠CFN ,∴∠ENF =∠ENH +∠HNF =∠AEN +∠CFN ,∵∠AEN =13∠AEM ,∠CFN =13∠CFM ,∴∠ENF =13∠AEM +13∠CFM =13(∠AEM +∠CFM )=13∠EMF ,∵∠EMF =α,∴∠ENF=13α.(3)n∠Q+m∠P=360°.理由如下:由(2)的结论可知,∠P=1m∠M,∠Q=∠BEQ+∠DFQ,∠BEM+∠DFM+∠M=360°,∵∠BEQ=1n ∠BEM,∠DFQ=1n∠DFM,∴∠Q=1n ∠BEM+1n∠DFM,=1n(∠BEM+∠DFM)=1n(360°-∠M),∴∠M=360°-n∠Q,∵∠M=m∠P,∴360°-n∠Q=m∠P,即n∠Q+m∠P=360°.19.(2022春•西岗区期末)如图1,AB∥CD,点P,Q分别在AB,CD上,点E在AB,CD之间.连接PE,QE,PE⊥QE.(1)直接写出∠BPE与∠DQE的数量关系为 ∠BPE+∠DQE=90° ;(2)如图2,∠APE的平分线PG和∠CQE的平分线QH的反向延长线相交于点G,求∠G的度数;(3)如图3,M为线段PE上一点,连接QM,∠BPE和∠MQD的平分线相交于点N,直接写出∠PNQ和∠MQE的数量关系为 2∠PNQ-∠MQE=90° .【分析】(1)延长PE交CD于点F,根据垂直定义可得∠PEQ=90°,根据平行线的性质可得∠BPE=∠PFC,然后再利用三角形的外角可得∠DQE+∠PFC=90°,即可解答;(2)过点G作GF∥CD,从而可得∠HQC=∠HGF,再利用平行线的性质可得∠PGF=180°-∠APG,利用(1)的结论可得∠APE+∠CQE=270°,然后利用角平分线的定义可得∠APG+∠CQH=135°,最后根据∠HGP=∠PGF-∠HGF=180°-∠APG-∠HQC,进行计算即可解答;(3)根据角平分线的定义可得∠BPE=2∠BPN,∠MQN=∠DQN,再利用猪脚模型可得∠BPE+∠DQE=90°,∠BPN+∠DQN=∠PNQ,再利用角的和差关系进行计算即可解答.【解答】解:(1)延长PE交CD于点F,∵PE ⊥QE ,∴∠PEQ =90°,∵AB ∥CD ,∴∠BPE =∠PFC ,∵∠PEQ 是△QEF 的一个外角,∴∠PEQ =∠DQE +∠PFC =90°,∴∠BPE +∠DQE =90°,故答案为:∠BPE +∠DQE =90°,(2)过点G 作GF ∥CD ,∴∠HQC =∠HGF ,∵AB ∥CD ,∴AB ∥FG ,∴∠PGF =180°-∠APG ,由(1)得:∠BPE +∠DQE =90°,∴∠APE +∠CQE =360°-(∠BPE +∠DQE )=270°,∵PG 平分∠APE ,QH 平分∠CQE ,∴∠APG =12∠APE ,∠CQH =12∠CQE ,∴∠APG +∠CQH =12(∠APE +∠CQE )=135°,∵∠HGP =∠PGF -∠HGF=180°-∠APG -∠HQC=45°,∴∠HGP 的度数为45°;(3)2∠PNQ -∠MQE =90°,理由:∵PN 平分∠BPE ,QN 平分∠MQD ,∴∠BPE =2∠BPN ,∠MQN =∠DQN ,由(1)可得:∠BPE +∠DQE =90°,∴2∠BPN +∠DQN +∠EQN =90°,由(1)可得:∠BPN +∠DQN =∠PNQ ,∴∠PNQ +∠BPN +∠MQN -∠MQE =90°,∴∠PNQ +∠BPN +∠DQN -∠MQE =90°,∴∠PNQ+∠PNQ-∠MQE=90°,∴2∠PNQ-∠MQE=90°,故答案为:2∠PNQ-∠MQE=90°.20.(2022春•宜春期末)问题:已知线段AB∥CD,在AB、CD间取一点P(点P不在直线AC上),连接PA、PC,试探索∠APC与∠A、∠C之间的关系.(1)端点A、C同向:如图1,点P在直线AC右侧时,∠APC-(∠A+∠C)= 0 度;如图2,点P在直线AC左侧时,∠APC+(∠A+∠C)= 360 度;(2)端点A、C反向:如图3,点P在直线AC右侧时,∠APC与∠A-∠C有怎样的等量关系?写出结论并证明;如图4,点P在直线AC左侧时,∠APC-(∠A-∠C)= 180 度.【分析】(1)过点P作PE∥AB,分别利用猪脚模型,铅笔模型即可解答;(2)过点P作PE∥CD,利用平行线的性质,以及角的和差关系进行计算即可解答.【解答】解:(1)如图:过点P作PE∥AB,∴∠A=∠APE,∵AB∥CD,∴PE∥CD,∴∠C=∠EPC,∵∠APC=∠APE+∠EPC,∴∠APC=∠A+∠C,∴∠APC-(∠A+∠C)=0度,故答案为:0;如图:过点P作PE∥AB,∴∠A+∠APE=180°,∵AB∥CD,∴PE∥CD,∴∠C+∠EPC=180°,∴∠A+∠APE+∠C+∠EPC=360°,∴∠APC+∠A+∠C=360°,∴∠APC+(∠A+∠C)=360度,故答案为:360;(2)∠APC+∠A-∠C=180°,证明:过点P作PE∥CD,∴∠C=∠EPC,∵AB∥CD,∴PE∥AB,∴∠A+∠APE=180°,∴∠A+∠APC-∠EPC=180°,∴∠A+∠APC-∠C=180°,∴∠APC+∠A-∠C=180°;如图:过点P作PE∥AB,∴∠A=∠APE,∵AB∥CD,∴PE∥CD,∴∠C+∠EPC=180°,∴∠C+∠APC-∠APE=180°,∴∠C+∠APC-∠A=180°,∴∠APC-(∠A-∠C)=180°,故答案为:180.。
平行线常考经典较难题、压轴题例题和巩固练习

平行线例1 翻折1、如图,把一张长方形纸带沿着直线GF 折叠,∠CGF=30°,则∠1的度数是.2、如图,生活中将一个宽度相等的纸条按图所示折叠一下,如果∠2=100°,那么∠1的度数为 .例2 旋转1、将一副直角三角尺ABC 和CDE 按如图方式放置,其中直角顶点C 重合,∠D=45°,∠A=30°.将三角形CDE 绕点C 旋转,若DE ∥BC,则直线AB 与直线CE 的较大的夹角∠1的大小为 度.1A EDBC例3 平行线的性质1、已知,直线AB ∥DC ,点P 为平面上一点,连接AP 与CP .(1)如图1,点P 在直线AB 、CD 之间,当∠BAP=60°,∠DCP=20°时,求∠APC .(2)如图2,点P 在直线AB 、CD 之间,∠BAP 与∠DCP 的角平分线相交于点K ,写出∠AKC 与∠APC 之间的数量关系,并说明理由.(3)如图3,点P 落在CD 外,∠BAP 与∠DCP 的角平分线相交于点K ,∠AKC 与∠APC 有何数量关系?并说明理由.2、如图,两直线AB、CD平行,则∠1+∠2+∠3+∠4+∠5= .3、已知直线AB∥CD.(1)如图1,直接写出∠BME、∠E、∠END的数量关系为;(2)如图2,∠BME与∠CNE的角平分线所在的直线相交于点P,试探究∠P与∠E之间的数量关系,并证明你的结论;(3)如图3,∠ABM=∠MBE,∠CDN=∠NDE,直线MB、ND交于点F,则= .例4 平移1、如图1所示,已知BC∥OA,∠B=∠A=120°(1)说明OB∥AC成立的理由.(2)如图2所示,若点E,F在BC上,且∠FOC=∠AOC,OE平分∠BOF,求∠EOC的度数.(3)在(2)的条件下,若左右平移AC,如图3所示,那么∠OCB:∠OFB的比值是否随之发生变化?若变化,请说明理由;若不变,请求出这个比值.(4)在(3)的条件下,当∠OEB=∠OCA时,求∠OCA的度数.2、如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.(1)求∠CBD的度数;(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是.例5 作图—应用1、(1)如图1,一个牧童从P点出发,赶着羊群去河边喝水,则应当怎样选择饮水路线,才能使羊群走的路程最短?请在图中画出最短路线.(2)如图2,在一条河的两岸有A,B 两个村庄,现在要在河上建一座小桥,桥的方向与河岸方向垂直,桥在图中用一条线段CD表示.试问:桥CD建在何处,才能使A到B的路程最短呢?请在图中画出桥CD的位置.图2图1BA2、如图,平面上有直线a及直线a外的三点A、B、P.(1)过点P画一条直线m,使得m∥a;(2)过B作BH⊥直线m,并延长BH至B′,使得BB′为直线a、m之间的距离;(3)若直线a、m表示一条河的两岸,现要在这条河上建一座桥(桥与河岸垂直),使得从村庄A经桥过河到村庄B的路程最短,试问桥应建在何处?画出示意图.【巩固练习】1、如图,AB∥DE,∠ABC的角平分线BP和∠CDE的角平分线DK的反向延长线交于点P且∠P﹣2∠C=57°,则∠C等于( )A.24° B.34° C.26° D.22°第1题图第2题图2、如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K ﹣∠H=27°,则∠K=()A.76° B.78° C.80° D.82°3、在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()A.平行 B.垂直C.平行或垂直 D.无法确定4、如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值,其中结论正确的有()A.1个 B.2个C.3个 D.4个第4题图第5题图5、如图所示,AB∥CD,则∠A+∠E+∠F+∠C等于( )A.180° B.360° C.540° D.720°6、如图所示,AB∥EF,∠B=35°,∠E=25°,则∠C+∠D的值为.第7题图第8题图第9题图7、如图所示,AB∥CD,∠E=35°,∠C=20°,则∠EAB的度数为.8、如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B﹣∠D=24°,则∠GEF= .9、已知D是△ABC的边BC所在直线上的一点,与B,C不重合,过D分别作DF∥AC交AB所在直接于F,DE ∥AB交AC所在直线于E.若∠A=80°,则∠FDE的度数是.10、如图1,MN∥PQ,直线AD与MN、PQ分别交于点A、D,点B在直线PQ上,过点B作BG⊥AD,垂足为点G.(1)求证:∠MAG+∠PBG=90°;(2)若点C在线段AD上(不与A、D、G重合),连接BC,∠MAG和∠PBC的平分线交于点H,请在图2中补全图形,猜想并证明∠CBG与∠AHB的数量关系;(3)若直线AD的位置如图3所示,(2)中的结论是否成立?若成立,请证明;若不成立,请直接写出∠CBG 与∠AHB的数量关系.11、已知AM∥CN,点B为平面内一点,AB⊥BC于B.(1)如图1,直接写出∠A和∠C之间的数量关系;(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.12、如图1,AB∥CD,E是AB、CD之间的一点.(1)判定∠BAE,∠CDE与∠AED之间的数量关系,并证明你的结论;(2)如图2,若∠BAE、∠CDE的两条平分线交于点F.写出∠AFD与∠AED之间的数量关系;(3)将图2中的射线DC沿DE翻折交AF于点G得图3,若∠AGD的余角等于2∠E的补角,求∠BAE的大小.13、已知:如图,BC∥OA,∠B=∠A=100°,试回答下列问题:(1)如图①所示,求证:OB∥AC.(注意证明过程要写依据)(2)如图②,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.(ⅰ)求∠EOC的度数; (ⅱ)求∠OCB:∠OFB的比值;(ⅲ)如图③,若∠OEB=∠OCA.此时∠OCA度数等于.(在横线上填上答案即可)14、已知直线AB∥CD.(1)如图1,直接写出∠ABE,∠CDE和∠BED之间的数量关系是.(2)如图2,BF,DF分别平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.(3)如图3,点E在直线BD的右侧,BF,DF仍平分∠ABE,∠CDE,请直接写出∠BFD和∠BED的数量关系.。
平行线有关模型汇总

直线平行的条件和性质1. 猪蹄模型已知:如图,AB ∥CD ,求证:∠B+∠D=∠BED 。
2. 铅笔模型如图,已知: CD AB ∥,求证: ∠+B ∠D +∠=BED 360°. (至少用三种方法)3. 其他4. 角平分线如图1,在ABC ∆中,BE 平分,ABC CE ∠平分ACB ∠.若80A ∠=︒,则BEC ∠= ;若A n ∠=︒,求BEC ∠用含n 的代数式表示)如图3,在ABC ∆中,BO 平分外角,CBD CO ∠平分外角BCE ∠.若A n ∠=︒,求BOC ∠.如图5,在ABC ∆中,BE 平分ABC ∠, CE 平分外角ACM ∠.若A n ∠=︒,求BEC ∠.5. “8”字形 如图b 所示的“”字型,其也存在着一个等式:1+2=3+4∠∠∠∠,请证明;6. “A ”字型如图a 所示的“”字型,我们可称其为“A 字型”或“塔形”,其存在一个等式:1+2=3+4∠∠∠∠,请证明;7. 燕尾形如图c所示,其也存在着如下等式:D A B C∠=∠+∠+∠,请证明一.考点:平行线的性质,角度的计算与证明.二.重难点:常见的几种两条直线平行的结论1.两条平行线被第三条直线所截,一组同位角的角平分线平行;2.两条平行线被第三条直线所截,一组内错角的角平分线平行;3.两条平行线被第三条直线所截,一组同旁内角的角平分线垂直.三.易错点:1.性质是由图形的“位置关系”决定“数量关系”;2.两条平行线之间的距离其实可看成点到直线的距离.题型一:猪蹄模型例1. 如图,直线a∥b,直角三角形ABC的顶点B在直线a上,∠C=90°,∠β=55°,则∠α的度数为()A. 15° B. 25° C. 35° D. 55°题型二:铅笔模型∠+∠+∠+∠=()例2. 如图,AB∥CD,A E F CA . 180°B . 360°C . 540°D . 720°题型三:铅笔、猪蹄模型综合压轴例3. 某学习小组发现一个结论:已知直线a ∥b ,若直线c ∥a ,则c ∥b .他们发现这个结论运用很广,请你利用这个结论解决以下问题:已知直线AB ∥CD ,点E 在AB 、CD 之间,点P 、Q 分别在直线AB 、CD 上,连接PE 、EQ . (1)如图1,运用上述结论,探究∠PEQ 与∠APE +∠CQE 之间的数量关系,并说明理由; (2)如图2,PF 平分∠BPE ,QF 平分∠EQD ,当∠PEQ =140°时,求出∠PFQ 的度数; (3)如图3,若点E 在CD 的下方,PF 平分∠BPE ,QH 平分∠EQD ,QH 的反向延长线交PF 于点F .当∠PEQ =70°时,请求出∠PFQ 的度数.题型三:其他例4. (周练)如图,已知AB ∥CD ,则∠A 、∠C 、∠P 的关系为.FE DCBA练习1. 如图,若AB∥CD,则α、β、γ之间的关系为.题型四:翻折例5. 如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65°,则∠AED′等于______例6. 如图,将四边形纸片ABCD沿MN折叠,点A、D分别落在点A1、D1处.若∠1+∠2=140°,则∠B+∠C=°.题型五:角平分线例7. 如图,在△ABC中,∠ABC与∠ACB的平分线交于点O.(1)如图1,已知∠ABC=40°,∠ACB=60°,求∠BOC的度数.(2)如图2,已知∠A=90°,求∠BOC的度数.(3)如图1,设∠A=m°,求∠BOC的度数.例8. 如图13, 1BA 和1CA 分别是ABC ∆的内角平分线和外角平分线,2BA 是1A BD ∠的角平分线,2CA 是1A CD ∠的角平分线,3BA 是2A BD ∠的角平分线,3CA 是2A CD ∠的角平分线,若A α∠=,则2018A ∠为 .1. 如图,∠A +∠B +∠C +∠D +∠E +∠F 的度数为( )A .180°B .360°C .540°D .720°2. 如图,将ABC ∆纸片沿DE 折叠,使点A 落在点'A 处,且'A B 平分ABC ∠,'A C 平分ACB ∠,若'110BA C ∠=︒,则12∠+∠的度数为( ) A. 80° B. 90° C. 100° D. 110°3. 如图,将矩形纸带ABCD ,沿EF 折叠后,C 、D 两点分别落在C ′、D ′的位置,经测量得∠EFB=65°,则∠AED ′的度数是( )A . 65°B . 55°C . 50°D . 25°4. 如图,已知30B ∠=︒,55BCD ∠=︒,45CDE ∠=︒,20E ∠=︒,求证:AB ∥CD .AFBC ED3.5. 如图,已知AB ∥DE ,BF ,EF 分别平分∠ABC 与∠CED ,若140BCE ∠=︒,求BFE ∠的度数.1. 如图,ABCDE 是封闭折线,则∠A 十∠B +∠C +∠D +∠E 为_______度.2. 如图,△ABE 和△ACD 是△ABC 分别沿着AB ,AC 边翻折180°形成的,若∠BAC =150°,则∠θ的度数是_______.3. 如图,在△ABC 中,∠C =90°.若BD ∥AE ,∠DBC =20°,则∠CAE 的度数是A .40°B .60°C .70°D .80° 4. 如图,把矩形沿对折后使两部分重合,若,则=( )A .110°B .115°C .120°D .130°A BCD E1.如图所示,将△ABC沿着DE翻折,若∠1+∠2=80°,则∠B=____度.2. 如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=70o,则∠BFD=________.3. 将一张长方形纸片如图所示折叠后,再展开.如果∠1=55o,那么∠2等于( )A.55o B.60o C.65o D.70o4. 问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.问题迁移:(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP =∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.5. 在△ABC中,∠A=40°(1)如图1,若两内角∠ABC、∠ACB的角平分线交于点P,则∠P=,∠A与∠P 之间的数量关系是.为什么有这样的关系?请证明它;(2)如图2,若内角∠ABC、外角∠ACE的角平分线交于点P,则∠P=,∠A与∠P 之间的数量关系是;(3)如图3,若两外角∠EBC、∠FCB的角平分线交于点P,则∠P=,∠A与∠P 之间的数量关系是.6. 【探究发现】如图1,在△ABC中,点P是内角∠ABC和外角∠ACD的角平分线的交点,试猜想∠P与∠A 之间的数量关系,并证明你的猜想.【迁移拓展】如图2,在△ABC中,点P是内角∠ABC和外角∠ACD的n等分线的交点,即∠PBC=∠ABC,∠PCD=∠ACD,试猜想∠P与∠A之间的数量关系,并证明你的猜想.【应用创新】已知,如图3,AD、BE相交于点C,∠ABC、∠CDE、∠ACE的角平分线交于点P,∠A=35°,∠E=25°,则∠BPD=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行线模型经典例题
几何学有形象化的好处,几何会给人以数学直觉,不能把几何学等同于逻辑推理,只会推理,缺乏数学直觉,是不会有创造的。
现在初一的学生刚刚开始接触几何的证明,普遍会出现证明步骤不规范,在书写的时候也会出现无从下手的情况,做题速度也普遍变慢,只有少数学生能够在规定时间内正确作答。
所以,只要学生能够学会利用平行线的性质和判定的几个基本模型去解决实际问题,会起到事半功倍的效果。
下面,我就平行线的判定与性质中的一个经典题型为例,引导学生来掌握最基本的平行线的模型,为以后的学习打好一个坚实的基础。
探究:
(1)如图a,若AB∥CD,则∠B+∠D=∠E,你能说明为什么吗?
(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?请证明;(3)若将点E移至图b所示位置,此时∠B、∠D、∠E之间有什么关系?请证明;
(4)若将E点移至图c所示位置,情况又如何?
(5)在图d中,AB∥CD,∠E+∠G与∠B+∠F+∠D又有何关系?
(6)在图e中,若AB∥CD,又得到什么结论?
名师点拨:已知AB∥CD,连接AB、CD的折线内折或外折,或改变E点位置、或增加折线的条数,通过适当地改变其中的一个条件,就能得出新的结论,给我们创造性的思考留下了极大的空间,解题的关键是过E点作AB(或CD)的平行线,把复杂的图形化归为基本图形.
解:(1)过E作EF∥AB,则
∠B=∠BEF,
∵AB∥CD,
∴EF∥CD,
∴∠D=∠DEF,
∴∠BED=∠BEF+∠DEF=∠B+∠D.
(2)若∠B+∠D=∠E,由EF∥AB,∴∠B=∠BEF,
∵∠E=∠BEF+∠DEF=∠B+∠D,
∴∠D=∠DEF,∴EF∥CD,
∴AB∥CD;
(3)若将点E移至图b所示位置,过E作EF∥AB,
∴∠BEF+∠B=180°,∵EF∥CD,∴∠D+∠DEF=180°,
∠E+∠B+∠D=360°;
(4)∵AB∥CD,∴∠B=∠BFD,
∵∠D+∠E=∠BFD,
∴∠D+∠E=∠B;
(5)∵AB∥CD,∴∠E+∠G=∠B+∠F+∠D;
(6)由以上可知:∠E
1+∠E
2
+…+∠E
n
=∠B+∠F
1
+∠F
2
+…+∠F
n-1
+∠D;
方法总结:本题是一类夹在两平行线间的折线问题,考查了平行线的性质与判定,属于基础题,关键是过E点作AB(或CD)的平行线,把复杂的图形化归为基本图形。
