第八章 点的合成运动
08-点的合成运动

第八章 点的合成运动8-1 如图所示,光点M 沿y 轴作谐振动,其运动方程为:0=x , )cos(β+=kt a y 如将点M 投影到感光记录纸上,此纸以等速e v 向左运动。
求点M 在记录纸上的轨迹。
解:把动坐标系'''y x O 固连在纸上,M 点的相对运动的运动方程为 t v x e '=,)cos('β+=kt a y 消去t 即可得到M 点在记录纸上的轨迹方程)'cos('eβ+=x v ka y8-3 水流在水轮机工作轮入口处的绝对速度m/s 15a =v ,并与直径成︒=60β角,如图所示,工作轮的半径m 2=R ,转速r/min 30=n 。
为避免水流与工作轮叶片相冲击,叶片应恰当地安装,以使水流对工作轮的相对速度与叶片相切。
求在工作轮外缘处水流对工作轮的相对速度的大小方向。
解:取水轮机工作轮入口处的一滴水为动点M ,动坐标系建立在工作轮上,速度分析图(a ),设θ为r v 与'x 轴的夹角。
M 点的牵连速度为m/s 283.630π2e =⨯==n R v ω 方向与'y 轴平行,由图(a )︒=-︒=+︒sin30)sin(90)sin(60ra e v v v θθ 前一等式得)60sin(cos a e θθ+︒=v v即 ︒︒-=60cos 60sin tan a a e v v v θ把m/s 283.6e =v 及m/s 15a =v 代入解得'4841︒=θ后一等式得m/s 1.10cos 30sin a r =︒=v v θ8-5 杆OA 长l ,由推杆推动而在图面内绕点O 转动,如图所示。
假定推杆的速度为v ,其弯头高为a 。
试求杆端A 的速度的大小(表示为推杆至点O 的速度x 的函数)。
解:取推杆上与AO 杆接触的B 点为动点,动系固连在AO 上,B 点速度分析如图。
设OA 角速度为ωv v =a ,ϕωsin a e v OB v =⋅=,ϕωsin v OB =⋅ 以 22sin a x aOBa +==ϕ代入上式得,22ax va+=ω 最终得 22a ax lavl v +==ω,方向如图8-7 在图a 和b 所示的两种机构中,已知mm 20021==a O O ,rad/s 31=ω。
同济大学 理论力学 孙杰 第八章 点的合成运动 课件
dr r 其中 dt dt
o dr
va vr vo e r o 牵连点M’的速度( 动系 其中: vo e r ve 上与动点M重合的点 )
a e r
v v r dr dr dro o e e M’ e r dt dt dt r v o
ee : x :x : r r r e r e 0 0 0 sin e r r sin sin e sinsin sin
R
a e r
例4
图示刨床的滑道摇杆机构,已知O为匀角速度
(曲杆OA)。 r r , 1 OO131r3r ,OrC C 12 2r3 ,2 r ,3r , 30 OA OAr , ,OO r3 , 3 1, 1 O 13 2r 3 3030 30 OA ,OA OO1 OO, r O C C, O 。 求:当曲杆水平时,杆O1D的角速度、CE的速度。 Be Ba 解: 动点: 滑块A 动系: 杆O1D 1 1 1 Aa Br sin Ae Aasin Ae 0OA sin 0 OA sin0 r0 Aa sin Aa OA sin 30 rr30 00 Ae 0 Ae Ar 2 2 2 Ae11 Ae 1 1O1 D Ae O1D00 A 4 0 1 OD O1D O1 O AA 44 O1
3、传动机构类零件 ——
P30 习题:3、4
动点:两物体的接触点 ( 在接触点不变的物体上 ), 动系:另一物体。
例3
已知:凸轮以匀速度v向左移动。 求: =30 时,顶杆的速度。
哈工大第七版理论力学__点的合成运动课件

第八章 点的合成运动
Resultant Motion of a Particle
运动学
运
动
演
示
第八章 点的合成运动
Resultant Motion of a Particle
运动学
(2) 选择动点,动系与定系 情况一
视频
第八章 点的合成运动
Resultant Motion of a Particle
即为相对运动方程,也就是笔尖相对纸带的运动方程。
上二式消去时间t 得相对轨迹方程:
y A cos
v
x
余弦曲线
第八章 点的合成运动
Resultant Motion of a Particle
运动学
§8-2 点的速度合成定理 Theorem of Composition of the Velocities of a Particle
第八章 点的合成运动
Resultant Motion of a Particle
运动学
视频
牵连点、 牵连点的运动轨迹?动点的相对运动轨迹?绝对运动轨迹?
第八章 点的合成运动
Resultant Motion of a Particle
运动学
视频
牵连点的运动轨迹?动点的相对运动轨迹?绝对运动轨迹?
第八章 点的合成运动 视频
第八章 点的合成运动
Resultant Motion of a Particle
运动学
B
由三角形关系,AB 杆速度大小为:
y
vr
y ' va R
va ve cot v0 cot 60 0.577v0
ve
v0 x'
3理论力学 第八章点的合成运动解析

? ? tg ?1 v?
v平
[例8-2] 曲柄摆杆机构
φ
已知:OA= r , ? , OO1=l 图示瞬时OA? O
求:摆杆O1B角速度? 1
解:取套筒A点为动点,摆杆O1B为动系.基座为静系。
绝对速度va = r ?
相对速度vr = ?
方向? OA 方向//O1B
牵连速度ve = ?
方向? O1B
由速度合成定理 va ? vr ? ve 作出速度平行四边形 如图示。
r
ve ? va sin? ? r? ?
r2? l2
又?ve ? O1 A?? 1,
? ? 1 ? Ov1eA?
1? r 2 ?l2
r 2?
r2?
l2
?
r
r 2?
2 ? l2
(
)
[例8-3]圆盘凸轮机构
已知:OC=e , R ? 3e , ? (匀角速度)
vr
va
A veva
B
aa
ar
va
A
Baen
ae?
练习三
解:
A
?
?
o
B
A
? ?
o
ve ? OB??
va
B
vr
动系:OA杆; 动点:滑块B
A
? ?
arn
o
aen ? OB?? 2
ar?
B
aa
a?e ? OB??
[例8-1] 桥式吊车。 已知:小 车水平运行,速度为v平, 物块A相对小车垂直上升 的速度为v? 。求物块A的运 行速度。
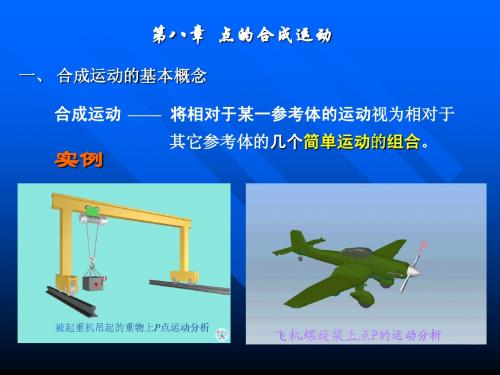
一、实例 : M点运动
地面: 摆线, 车箱: 圆。
二、复合运动的一般模型
第八章 点的合成运动

潍坊学院机电系讲稿专用纸如车轮上的点P的运动,如果以地面作为参考系,点的轨迹是旋轮线,而如果以小车作为参考系,点的轨迹则是一个圆。
相对于地面是直线运动,相对于旋转的工件,是,因此,车刀在工件的表面上切出螺旋线。
在实际问题中,往往不仅要知道物体相对地球的运动,而且有时要知道被观察物体相对于地面运动着的参考系的运动情况。
例如在运动着的飞机、车船上观察飞机、车船潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸动系上与动点相重合的点相对于定系的速度、加速度称为牵连速度、牵连加速度。
6. 动点和动系的选择基本原则:(1)动点对动系要有相对运动。
(2)动点的相对运动轨迹要明确、容易确定。
具体选择方法:(1)选择持续接触点为动点。
(2)对没有持续接触点的问题,一般不选择接触点为动点。
根据选择原则具体问题具体分析。
实例见PPT。
潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸内的绝对位移绕固定轴O limlim11M M MM '+='M M MMM M '+='11潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸在定系和动系中的矢径分别用r 和r ′表示。
k z j y i x r r ''+''+''+='r潍坊学院机电系讲稿专用纸和为未知量,暂设潍坊学院机电系讲稿专用纸当牵连运动是定轴转动时,动点的绝对加速度并不等于牵连加速度与相对加速之矢量和。
牵连运动是定轴转动时点的加速度合成定理和角加速度α 绕定系Oxyz 的轴z 转动;动系)分析动系的单位矢量k j i''',,对时间的一阶导数以角速度e ω绕定轴z 转动,则角速度矢e ω沿潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸0=r v ③ r e v//ω r e v⊥, 此时 e k a =ω2是由于牵连运动和相对运动的相互影响而产生的潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸潍坊学院机电系讲稿专用纸。
第8章 点的合成运动

vr
Dj
Dt
evr
,
方向 vr 。
这一项表明由于牵连转动而引起 相对速度方向改变的加速度。
26
由于第二项和第四项所表示的加速度分量的大小,方向都
相同,可以合并为一项,用 aC 表示,称为科里奥利加速度,简
称科氏加速度。是由牵连运动为转动时,牵连运动与相对运动的 相互影响而产生的。
aC 2evr , 方向 vr , 指向顺ωe 转动的一边
14
例 题 8-3
解:
1. 选择动点,动系与定系。
动点-滑块 A 。
y'
动系-O1x'y',固连于摇杆 O1B。
2. 运动分析。 绝对运动-以O为圆心的圆周运动。
x'
相对运动-沿O1B的直线运动。
牵连运动-摇杆绕O1轴的摆动。
15
例 题 8-3
3. 速度分析。
绝对速度va:va=OA ·ω =r ω ,方 向垂直于OA,沿铅垂 方向向上。
x
2. 运动分析。
绝对运动- 平面曲线运动。
相对运动-沿动直管的直线运动。
牵连运动-直管绕O作定轴转动。
29
例 题 8-4
va
y
y'
ve=vaφ
x' vr=var
M
Oj
x
3. 速度分析。
绝对速度va: 大小和方向未知。
牵连速度ve:大小
ve
r
dj
dt
,
方向垂直于向直管向左上。
相对速度vr: 大小
2
§8-1 相对运动•牵连运动•绝对运动
运动是绝对的,但运动的描述则是相对的。同一物体的运动 在不同的参考系中是不一样的。例如车轮上的点P的运动, 如果以地面作为参考系,点的轨迹是旋轮线,而如果以小车 作为参考系,点的轨迹则是一个圆。
理论力学第八章点的合成运动

运动学/点的合成运动
运动学/点的合成运动
运动学/点的合成运动
运动学/点的合成运动
▼动点和动系的选择
基本原则: 1.动点对动系要有相对运动。 2.动点的相对运动轨迹要明确、容易确定。 具体选择方法: 1.选择持续接触点为动点。
(1)绝对运动方程: x x(t), y y(t)
运动学/点的合成运动
第八章
点的合成运动
§8-1 点的合成运动的概念
§8-2 点的速度合成定理
§8-3 牵连运动为平移时
点的加速度合成定理
§8-4
牵连运动为转动时
点的加速度合成定理
本章中点的速度合成是重点,点的加速度合成是难点。
运动学/点的合成运动
§8-1 点的合成运动的概念
一、坐标系 ●定坐标系:建立在固定参
考物上的坐标系,简称定系。 一般将定系固结在地面上。
建立在相对于定系运动着的物体上的坐
标系,简称动系。图示原点在轮心与车厢固连的坐标系
o`x`y` 汽车车厢相对于
运动,如果将 坐标系固
结于车厢上,则形成了相对于定系运动的坐标系
。
运动学/点的合成运动
二、动点 ●动点是指相对于定系和动系均 有运动的点,本章就是研究动点 相对于定系和动系的运动。
牵连运动: 直线平移
运动学/点的合成运动
▼凸轮机构运动分析
动点:凸轮圆心点O 动系:摇杆 静系:地面 绝对运动:直线 相对运动:直线
牵连运动:定轴转动
●注意的问题:
▼三种运动的分析必须明确什么物体相对什么参考体的
运动。 ▼相对、绝对运动指点的运动,可以是直线或曲线运动 ;牵连运动是指参考体的运动,是刚体的运动,可以是 平移或定轴转动以及刚体的其他运动形式。
理论力学第八章 点的合成运动

I) 动系作平动时,动系上各点速度都相等。
II) 动系作转动时,ve必须是该瞬时动系上与 动点相重合点的速度。
第二节 点的速度合成定理
点的速度合成定理是瞬时矢量式,共包括大小‚方向 六个元素, 已知任意四个元素,就能求出其他两个。 二.应用举例 [例8-1] 桥式吊车 已知: 小车水平运行,速度为v平, 物块A相对小车垂直上升
第一节 点的合成运动的概念
三.三种运动及三种速度与三种加速度。 1.绝对运动:动点对静系的运动。 点的运动 2.相对运动:动点对动系的运动。 例如:人在行驶的汽车里走动。 3.牵连运动:动系相对于静系的运动 刚体的运动 例如:行驶的汽车相对于地面的运动。
绝对运动中,动点的速度与加速度称为绝对速度 va 与绝对加速度
第八章 点的合成运动
主要研究内容
§8–1 点的合成运动的概念
§8–2 点的速度合成定理
§8–3点的速度合成定理合成定理
第一节 点的合成运动的概念
一.坐标系: 1.静坐标系:把固结于地面上的坐标系称为静坐标系, 简称静系。 2.动坐标系:把固结于相对于地面运动物体上的坐标 系,称为动坐标系,简称动系。例如在行驶的汽车。 二.动点:所研究的点(运动着的点)。
v A v a v e v r v平 v
2
2
2
2
t g1
v v平
第二节 点的速度合成定理
[例8-2] 曲柄摆杆机构 已知:OA= r , , OO1=l 求:摆杆O1B角速度1 图示瞬时OAOO1
解:取OA杆上A点为动点,摆杆O1B为动系, 基座为静系。 绝对速度va = r 方向 OA 相对速度vr = ? 方向//O1B 牵连速度ve = ? 方向O1B 由速度合成定理 va= vr+ ve 作出速度平行四边形 如图示。 r r 2 sin ,ve va sin r 2 l 2 r 2 l 2 ve 1 r 2 r 2 又ve O1 A1 ,1 2 l 2 ( 2 2 O1 A r 2 2 r l r l
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C
ω
A θ O e ve
ε R vr
θ
va
3)求BCD杆的加速度 A点的相对加速度沿水平方向。 A点的牵连加速度亦即杆BCD的加速度,沿铅垂向下。 因aa = ar + ae 故aax + aay = arx + ary + aex + aey D 故aay = ary + aey = ae 即A点的牵连加速度大小为 A点的绝对加速度沿铅垂方 向的投影。 ae= aancosθ+ aatsinθ aBCD= eω2cosθ+ eεsinθ
A x' z O x y z' M O' B y'
ω
动系的选择要确保动点与之有相对运动且相对运动状 态易判断,故动点和动系不能在同一物体上。
3.三种运动 3.三种运动 •相对运动:动点相对于动系的运动。 相对运动: •牵连运动:动系相对于定系的运动,是刚体的运动。 牵连运动: •绝对运动:动点相对于定系的运动。 绝对运动: 4.两种轨迹 4.两种轨迹 •相对轨迹:动点相对于动系的轨迹。 相对轨迹: •绝对轨迹:动点相对于定系的轨迹。 绝对轨迹: 5.牵连点 5.牵连点 在某瞬时,动系上与动点相重合 的点为动点在该瞬时的牵连点 牵连点。 牵连点 牵连点相对于动系静止不动。
则位移: rM = rO'+ r' 动系上与动点重合的点 (牵连点)记为M',它 牵连点) 在定系中的矢径为rM' 。 图示瞬时: rM = rM'
二、点的速度 相对速度
~ ~ d r ′ d ( x′i ′ + y′j ′ + z ′k ′) = vr = dt dt
M z M' O’ i' O x y
三、相对运动、牵连运动与绝对运动间的关系 相对运动、 在平面运动情况下,设动 点M的相对运动方程为: x'= x' (t), y'= y' (t) 设动系O'x'y'相对于定系 Oxy的牵连运动方程为: xO'= xO' (t), yO' = yO' (t), φ = φ(t)—从x轴正向到x'轴 正向逆时针转的角为正。 设M的绝对运动方程为: x= x (t), y= y (t) 则相对运动、牵连运动与 绝对运动间的关系为:
第八章 点的合成运动
§ 8-1 § 8-2 § 8-3 相对运动·牵连运动 绝对运动 相对运动 牵连运动·绝对运动 牵连运动 点的速度合成定理 点的加速度合成定理
§ 8-1 相对运动·牵连运动·绝对运动 相对运动·牵连运动·
一、问题的引出 一水平放置的圆板绕过中心 O的铅 直轴以角速度ω旋转,在圆板上有 一光滑直槽AB,槽内放一小球 M。 AB M 1)若以圆板为参考系,小球M将 如何运动? 2)若以地面为参考系,小球M将 如何运动?
ve C θ eθ O vr
BD 杆作水平平动,其速度为C点的牵连速度 vBD = ve = va cosθ =eω cosθ
B
D
ar
a C θ e e O
ω
aa A
3)求BD 杆的加速度 C点绕O点作匀速圆周运动, 其绝对加速度aa= eω2 C点的相对加速度:ar= aa cosθ =eω2 cosθ BD 杆作水平平动,其加速度为C点的牵连加速度 aBD = ae = aa sinθ =eω2 sinθ
B
B va ve vr P C
A
C va
ve vr A O
先选杆AC上的点A为动点,动系建立 于杆O1D上; 绝对运动:沿杆AC的水平直线运动; 相对运动:为沿杆O1D的直线运动; vAe 牵连运动:杆O1D的转动。
vAa
D A vAr vBr C
再选杆OB上的点B为动点, vBa 动系仍建立于杆O1D上; 绝对运动:以O为圆心、 vBe 以OB为半径的圆周运动; 相对运动:沿杆O1D的直线运动; ω 牵连运动:杆O1D的转动。 O
O x y A x' z z' M B O' M' y'
ω
6.三种速度 6.三种速度 •相对速度(vr):动点相对于动系的速度。 相对速度( •牵连速度(ve):牵连点相对于定系的速度。 牵连速度( •绝对速度(va):动点相对于定系的速度。 绝对速度( 7.三种加速度 7.三种加速度 •相对加速度(ar):动点相对于动系的加速度。 相对加速度( •牵连加速度(ae):牵连点相对于定系的加速度。 牵连加速度( •绝对加速度(aa):动点相对于定系的加速度。 绝对加速度(
x z M M' O' i’ O y
动点M的绝对加速度
d r M d (r O′ + r ′) = aa = 2 dt d t2 && = &&O′ + ( x′&&′ + y′&&′ + z ′k ′) i j r + ( &&′i ′ + &&′j ′ + &&′k ′) x y z && &j & & + 2( x′i ′ + y′&′ + z ′k ′)
B O1
【例8-2】曲柄导杆机构如图示。 已知OA=r,曲杆BCD速度为vD。 求该瞬时杆 OA转动的角速度ω。 【解】1)取滑块A为动点,曲 杆BCD为动系。 绝对运动:以O为圆心r为半 径的圆周运动。 va = rω 相对运动: 水平直线运动。 牵连运动:沿铅垂直线 平动。 ve = vD
va =
2 2
考虑到 & i ′ = ωe × i ′
&′ = ωe × j ′ k ′ = × k ′ & ωe j
ωe
&& &j & & 则2( x′i ′ + y′&′ + z ′k ′) & & & = 2 ωe × ( x′i ′ + y′j ′ + z ′k ′) = 2 ωe × v r
令aC=2ωe×vr—科氏加速度 科氏加速度 科氏加速度是由于动系为 转动时,牵连运动与相对 运动互相影响产生的, 其方向按右手定则确定。
ωe vr θ aC
z
M M'
O' i’ y
O x
aa = ar + ae + ac
点的加速度合成定理: 点的加速度合成定理: 动点在某瞬时的绝对加速 度等于该瞬时它的相对加 速度、牵连加速度与科氏 加速度的矢量和。 牵连运动为平动时aC=0。
aC=2ωevrsinθ
【例8-4】 半径为r、偏心距为e的偏心圆凸轮以等角 速度 ω绕定轴O逆时针转动,并带动拨叉A和固接于A 的控制杆 BD沿水平作往复运动,拨叉与凸轮接触表 面铅垂。 D B 用角θ表示杆BD的 速度和加速度。 【解】1)取轮心C为动点, 杆BD为动系。 A ω 2)求BD 杆的速度 C点绕O点作匀速圆周运动, 其绝对速度va= eω C点的相对速度: vr= va sinθ =eω sinθ
动点和动系不能选在同一 物体上,动点与动系之间 要有容易识别的相对运动。 分析三种运动和三种速度。 明确动点的绝对运动和相 对运动、动系的牵连运动。
运用速度合成定理,作出 选取动点、动系和定系。 速度平行四边形。确保绝 所选的参考系应能将动点 对运动速度为平行四边形 的运动分解成相对运动和 的对角线。 牵连运动。动点、动系须 运用速度平行四边形中的 指明,动系可不画出,定 几何关系求解未知数。 系可不用指明也不必画出。
绝对速度
d r M d (r O′ + r ′) = va = dt dt
& & = r O′ + [( x′i ′ + y′&′ + z ′k ′) j & & & & + ( x′i ′ + y′j ′ + z ′k ′)]
va = ve + v r
点的速度合成定理: 点的速度合成定理: 动点在某瞬时的绝对速度 等于它在该瞬时的牵连速 度与相对速度的矢量和。 三、解题步骤
l O1
ω θ
ve φ vr B
va
A
ω1 φ
O2
绝对运动:以O1为圆心 r为半径的 圆周运动。va = rω 2 ω r2 r ω ⇒ ω1 = 2 2 ve = va sin ϕ ⇒ l 2 + r 2ω1 = 求解: 2 2
l +r
l +r
§ 8-3 点的加速度合成定理
一、动系中单位矢量对时间的导数 设动系绕定系的z轴作定轴 转动,转动角速度矢为ωe。
& & & = x′i ′ + y′j ′ + z ′k ′
牵连速度 牵连速度是牵连点M'相对 于定系的速度,该点是动 系上的点,它相对于动系 静止不动,故它在动系上 的坐标x'、y'、z'是常量。
d r M ′ d (r O′ + r ′) = 故 ve = dt dt
& & = r O′ + x′i ′ + y′&′ + z ′k ′ j &
ω
M A
B
二、基本概念 1.合成运动: 1.合成运动:物体相对于某一参考体的运动由相对 合成运动 于其他参考体的几个运动组合而成。 2.两个坐标系 2.两个坐标系 •定参考系:习惯上把固定在地球 定参考系: 上的坐标系称为定参考系,简称 定系,以Oxyz坐标系表示。 定系 •动参考系:把固定在相对于地球 动参考系: 运动的参考体上的坐标系称为动 参考系,简称动系 动系,以O'x'y'z'坐 动系 标系表示。
