历年全国卷高考数学真题大全解析版

合集下载

全国统一高考数学试卷及解析

202X年全国统一高考数学卷子〔文科〕〔新课标版〕参考答案与真题解析一、选择题：本大题共12小题，每题5分，在每题给同的四个选项中，只有一项为哪一项符合题目要求的．1．〔5分〕〔202X•新课标〕已知集合A={x|x2﹣x﹣2＜0}，B={x|﹣1＜x＜1}，则〔〕A．A⊊B B．B⊊A C．A=B D．A∩B=∅2．〔5分〕〔202X•新课标〕复数z=的共轭复数是〔〕A．2+i B．2﹣i C．﹣1+i D．﹣1﹣i3．〔5分〕〔202X•新课标〕在一组样本数据〔x1，y1〕，〔x2，y2〕，…，〔x n，y n〕〔n≥2，x1，x2，…，x n不全相等〕的散点图中，假设全部样本点〔x i，y i〕〔i=1，2，…，n〕都在直线y=x+1上，则这组样本数据的样本相关系数为〔〕A．﹣1 B．0 C．D．14．〔5分〕〔202X•新课标〕设F1、F2是椭圆的左、右焦点，P 为直线x=上一点，△F2PF1是底角为30°的等腰三角形，则E的离心率为〔〕A．B．C．D．5．〔5分〕〔202X•新课标〕已知正三角形ABC的顶点A〔1，1〕，B〔1，3〕，顶点C在第一象限，假设点〔x，y〕在△ABC内部，则z=﹣x+y的取值范围是〔〕A．〔1﹣，2〕 B．〔0，2〕C．〔﹣1，2〕D．〔0，1+〕6．〔5分〕〔202X•新课标〕如果执行右边的程序框图，输入正整数N〔N≥2〕和实数a1，a2，…，a n，输出A，B，则〔〕A．A+B为a1，a2，…，a n的和B．为a1，a2，…，a n的算术平均数C．A和B分别是a1，a2，…，a n中最大的数和最小的数D．A和B分别是a1，a2，…，a n中最小的数和最大的数7．〔5分〕〔202X•新课标〕如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为〔〕A．6 B．9 C．12 D．188．〔5分〕〔202X•新课标〕平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，则此球的体积为〔〕A．π B．4πC．4πD．6π9．〔5分〕〔202X•新课标〕已知ω＞0，0＜φ＜π，直线x=和x=是函数f〔x〕=sin〔ωx+φ〕图象的两条相邻的对称轴，则φ=〔〕A．B．C．D．10．〔5分〕〔202X•新课标〕等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线y2=16x 的准线交于A，B两点，，则C的实轴长为〔〕A．B． C．4 D．811．〔5分〕〔202X•新课标〕当0＜x≤时，4x＜log a x，则a的取值范围是〔〕A．〔0，〕B．〔，1〕C．〔1，〕D．〔，2〕12．〔5分〕〔202X•新课标〕数列{a n}满足a n+1+〔﹣1〕n a n=2n﹣1，则{a n}的前60项和为〔〕A．3690 B．3660 C．1845 D．1830二．填空题：本大题共4小题，每题5分．13．〔5分〕〔202X•新课标〕曲线y=x〔3lnx+1〕在点〔1，1〕处的切线方程为．14．〔5分〕〔202X•新课标〕等比数列{a n}的前n项和为S n，假设S3+3S2=0，则公比q=．15．〔5分〕〔202X•新课标〕已知向量夹角为45°，且，则=．16．〔5分〕〔202X•新课标〕设函数f〔x〕=的最大值为M，最小值为m，则M+m=．三、解答题：解容许写出文字说明，证明过程或演算步骤．17．〔12分〕〔202X•新课标〕已知a，b，c分别为△ABC三个内角A，B，C的对边，〔1〕求A；〔2〕假设a=2，△ABC的面积为，求b，c．18．〔12分〕〔202X•新课标〕某花店每天以每枝5元的价格从农场购进假设干枝玫瑰花，然后以每枝10元的价格出售．如果当天卖不完，剩下的玫瑰花做垃圾处理．〔Ⅰ〕假设花店一天购进17枝玫瑰花，求当天的利润y〔单位：元〕关于当天需求量n〔单位：枝，n∈N〕的函数解析式．〔Ⅱ〕花店记录了100天玫瑰花的日需求量〔单位：枝〕，整理得下表：日需求量n 14 15 16 17 18 19 20频数10 20 16 16 15 13 10〔i〕假设花店在这100天内每天购进17枝玫瑰花，求这100天的日利润〔单位：元〕的平均数；〔ii〕假设花店一天购进17枝玫瑰花，以100天记录的各需求量的频率作为各需求量发生的概率，求当天的利润不少于75元的概率．19．〔12分〕〔202X•新课标〕如图，三棱柱ABC﹣A1B1C1中，侧棱垂直底面，∠ACB=90°，AC=BC=AA1，D是棱AA1的中点．〔Ⅰ〕证明：平面BDC1⊥平面BDC〔Ⅱ〕平面BDC1分此棱柱为两局部，求这两局部体积的比．20．〔12分〕〔202X•新课标〕设抛物线C：x2=2py〔p＞0〕的焦点为F，准线为l，A∈C，已知以F为圆心，FA为半径的圆F交l于B，D两点；〔1〕假设∠BFD=90°，△ABD的面积为，求p的值及圆F的方程；〔2〕假设A，B，F三点在同一直线m上，直线n与m平行，且n与C只有一个公共点，求坐标原点到m，n距离的比值．21．〔12分〕〔202X•新课标〕设函数f〔x〕=e x﹣ax﹣2．〔Ⅰ〕求f〔x〕的单调区间；〔Ⅱ〕假设a=1，k为整数，且当x＞0时，〔x﹣k〕f′〔x〕+x+1＞0，求k的最大值．22．〔10分〕〔202X•新课标〕如图，D，E分别为△ABC边AB，AC的中点，直线DE交△ABC 的外接圆于F，G两点，假设CF∥AB，证明：〔1〕CD=BC；〔2〕△BCD∽△GBD．23．〔202X•新课标〕选修4﹣4；坐标系与参数方程已知曲线C1的参数方程是〔φ为参数〕，以坐标原点为极点，x轴的正半轴为极轴建立坐标系，曲线C2的坐标系方程是ρ=2，正方形ABCD的顶点都在C2上，且A，B，C，D依逆时针次序排列，点A的极坐标为〔2，〕．〔1〕求点A，B，C，D的直角坐标；〔2〕设P为C1上任意一点，求|PA|2+|PB|2+|PC|2+|PD|2的取值范围．24．〔202X•新课标〕已知函数f〔x〕=|x+a|+|x﹣2|〔1〕当a=﹣3时，求不等式f〔x〕≥3的解集；〔2〕假设f〔x〕≤|x﹣4|的解集包含[1，2]，求a的取值范围．202X年全国统一高考数学卷子〔文科〕〔新课标版〕参考答案与真题解析一、选择题：本大题共12小题，每题5分，在每题给同的四个选项中，只有一项为哪一项符合题目要求的．1．〔5分〕【专题】集合．【分析】先求出集合A，然后依据集合之间的关系可推断【解答】解：由题意可得，A={x|﹣1＜x＜2}，∵B={x|﹣1＜x＜1}，在集合B中的元素都属于集合A，但是在集合A中的元素不肯定在集合B中，例如x=∴B⊊A．应选B．【点评】此题主要考查了集合之间关系的推断，属于根底真题．2．〔5分〕【专题】计算题．【分析】利用复数的分子、分母同乘分母的共轭复数，把复数化为a+bi的形式，然后求法共轭复数即可．【解答】解：复数z====﹣1+i．所以复数的共轭复数为：﹣1﹣i．应选D．【点评】此题考查复数的代数形式的混合运算，复数的根本概念，考查计算能力．3．〔5分〕【专题】规律型．【分析】全部样本点〔x i，y i〕〔i=1，2，…，n〕都在直线y=x+1上，故这组样本数据完全正相关，故其相关系数为1．【解答】解：由题设知，全部样本点〔x i，y i〕〔i=1，2，…，n〕都在直线y=x+1上，∴这组样本数据完全正相关，故其相关系数为1，应选D．【点评】此题主要考查样本的相关系数，是简单题．4．〔5分〕【专题】计算题．【分析】利用△F2PF1是底角为30°的等腰三角形，可得|PF2|=|F2F1|，依据P为直线x=上一点，可建立方程，由此可求椭圆的离心率．【解答】解：∵△F2PF1是底角为30°的等腰三角形，∴|PF2|=|F2F1|∵P为直线x=上一点∴∴应选C．【点评】此题考查椭圆的几何性质，解题的关键是确定几何量之间的关系，属于根底题．5．〔5分〕【专题】计算题．【分析】由A，B及△ABC为正三角形可得，可求C的坐标，然后把三角形的各顶点代入可求z的值，进而推断最大与最小值，即可求解范围【解答】解：设C〔a，b〕，〔a＞0，b＞0〕由A〔1，1〕，B〔1，3〕，及△ABC为正三角形可得，AB=AC=BC=2即〔a﹣1〕2+〔b﹣1〕2=〔a﹣1〕2+〔b﹣3〕2=4∴b=2，a=1+即C〔1+，2〕则此时直线AB的方程x=1，AC的方程为y﹣1=〔x﹣1〕，直线BC的方程为y﹣3=〔〕〔x﹣1〕当直线x﹣y+z=0经过点A〔1，1〕时，z=0，经过点B〔1，3〕z=2，经过点C〔1+，2〕时，z=1﹣∴应选A【点评】考查学生线性规划的理解和认识，考查学生的数形结合思想．属于基此题型．6．〔5分〕【专题】算法和程序框图．【分析】分析程序中各变量、各语句的作用，再依据流程图所示的顺序，可知：该程序的作用是求出a1，a2，…，a n中最大的数和最小的数．【解答】解：分析程序中各变量、各语句的作用，再依据流程图所示的顺序，可知，该程序的作用是：求出a1，a2，…，a n中最大的数和最小的数其中A为a1，a2，…，a n中最大的数，B为a1，a2，…，a n中最小的数应选：C．【点评】此题主要考查了循环结构，解题的关键是建立数学模型，依据每一步分析的结果，选择恰当的数学模型，属于中档题．7．〔5分〕【专题】计算题．【分析】通过三视图推断几何体的特征，利用三视图的数据求出几何体的体积即可．【解答】解：该几何体是三棱锥，底面是俯视图，三棱锥的高为3；底面三角形斜边长为6，高为3的等腰直角三角形，此几何体的体积为V=×6×3×3=9．应选B．【点评】此题考查三视图与几何体的关系，考查几何体的体积的求法，考查计算能力．8．〔5分〕【专题】计算题．【分析】利用平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，求出球的半径，然后求解球的体积．【解答】解：因为平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，所以球的半径为：=．所以球的体积为：=4π．应选B．【点评】此题考查球的体积的求法，考查空间想象能力、计算能力．9．〔5分〕【专题】计算题．【分析】通过函数的对称轴求出函数的周期，利用对称轴以及φ的范围，确定φ的值即可．【解答】解：因为直线x=和x=是函数f〔x〕=sin〔ωx+φ〕图象的两条相邻的对称轴，所以T==2π．所以ω=1，并且sin〔+φ〕与sin〔+φ〕分别是最大值与最小值，0＜φ＜π，所以φ=．应选A．【点评】此题考查三角函数的解析式的求法，注意函数的最值的应用，考查计算能力．10．〔5分〕【专题】计算题；压轴题．【分析】设等轴双曲线C：x2﹣y2=a2〔a＞0〕，y2=16x的准线l：x=﹣4，由C与抛物线y2=16x 的准线交于A，B两点，，能求出C的实轴长．【解答】解：设等轴双曲线C：x2﹣y2=a2〔a＞0〕，y2=16x的准线l：x=﹣4，∵C与抛物线y2=16x的准线l：x=﹣4交于A，B两点，∴A〔﹣4，2〕，B〔﹣4，﹣2〕，将A点坐标代入双曲线方程得=4，∴a=2，2a=4．应选C．【点评】此题考查双曲线的性质和应用，解题时要认真审题，认真解答，注意挖掘题设中的隐含条件，合理地进行等价转化．11．〔5分〕【专题】计算题；压轴题．【分析】由指数函数和对数函数的图象和性质，将已知不等式转化为不等式恒成立问题加以解决即可【解答】解：∵0＜x≤时，1＜4x≤2要使4x＜log a x，由对数函数的性质可得0＜a＜1，数形结合可知只需2＜log a x，∴即对0＜x≤时恒成立∴解得＜a＜1应选B【点评】此题主要考查了指数函数和对数函数的图象和性质，不等式恒成立问题的一般解法，属根底题12．〔5分〕【专题】等差数列与等比数列．【分析】由题意可得a2﹣a1=1，a3+a2=3，a4﹣a3=5，a5+a4=7，a6﹣a5=9，a7+a6=11，…a50﹣a49=97，变形可得a3+a1=2，a4+a2=8，a7+a5=2，a8+a6=24，a9+a7=2，a12+a10=40，a13+a11=2，a16+a14=56，…利用数列的结构特征，求出{a n}的前60项和．【解答】解：由于数列{a n}满足a n+1+〔﹣1〕n a n=2n﹣1，故有a2﹣a1=1，a3+a2=3，a4﹣a3=5，a5+a4=7，a6﹣a5=9，a7+a6=11，…a50﹣a49=97．从而可得a3+a1=2，a4+a2=8，a7+a5=2，a8+a6=24，a11+a9=2，a12+a10=40，a15+a13=2，a16+a14=56，…从第一项开始，依次取2个相邻奇数项的和都等于2，从第二项开始，依次取2个相邻偶数项的和构成以8为首项，以16为公差的等差数列．{a n}的前60项和为15×2+〔15×8+〕=1830，应选D．【点评】此题主要考查数列求和的方法，等差数列的求和公式，注意利用数列的结构特征，属于中档题．二．填空题：本大题共4小题，每题5分．13．〔5分〕【专题】计算题．【分析】先求导函数，求出切线的斜率，再求切线的方程．【解答】解：求导函数，可得y′=3lnx+4，当x=1时，y′=4，∴曲线y=x〔3lnx+1〕在点〔1，1〕处的切线方程为y﹣1=4〔x﹣1〕，即y=4x﹣3．故答案为：y=4x﹣3．【点评】此题考查导数的几何意义，考查点斜式求直线的方程，属于根底题．14．〔5分〕【专题】计算题．【分析】由题意可得，q≠1，由S3+3S2=0，代入等比数列的求和公式可求q【解答】解：由题意可得，q≠1∵S3+3S2=0∴∴q3+3q2﹣4=0∴〔q﹣1〕〔q+2〕2=0∵q≠1∴q=﹣2故答案为：﹣2【点评】此题主要考查了等比数列的求和公式的应用，解题中要注意公比q是否为1 15．〔5分〕【专题】计算题；压轴题．【分析】由已知可得，=，代入|2|====可求【解答】解：∵，=1∴=∴|2|====解得故答案为：3【点评】此题主要考查了向量的数量积定义的应用，向量的数量积性质||=是求解向量的模常用的方法16．〔5分〕【专题】综合题；压轴题．【分析】函数可化为f〔x〕==，令，则为奇函数，从而函数的最大值与最小值的和为0，由此可得函数f〔x〕=的最大值与最小值的和．【解答】解：函数可化为f〔x〕==，令，则为奇函数，∴的最大值与最小值的和为0．∴函数f〔x〕=的最大值与最小值的和为1+1+0=2．即M+m=2．故答案为：2．【点评】此题考查函数的最值，考查函数的奇偶性，解题的关键是将函数化简，转化为利用函数的奇偶性解题．三、解答题：解容许写出文字说明，证明过程或演算步骤．17．〔12分〕【专题】计算题．【分析】〔1〕由正弦定理及两角和的正弦公式可得sinAcosC+sinAsinC=sinB+sinC=sin 〔A+C〕+sinC=sinAcosC+sinCcosA+sinC，整理可求A〔2〕由〔1〕所求A及S=可求bc，然后由余弦定理，a2=b2+c2﹣2bccosA=〔b+c〕2﹣2bc﹣2bccosA可求b+c，进而可求b，c【解答】解：〔1〕∵acosC+asinC﹣b﹣c=0∴sinAcosC+sinAsinC﹣sinB﹣sinC=0∴sinAcosC+sinAsinC=sinB+sinC=sin〔A+C〕+sinC=sinAcosC+sinCcosA+sinC∵sinC≠0∴sinA﹣cosA=1∴sin〔A﹣30°〕=∴A﹣30°=30°∴A=60°〔2〕由由余弦定理可得，a2=b2+c2﹣2bccosA=〔b+c〕2﹣2bc﹣2bccosA即4=〔b+c〕2﹣3bc=〔b+c〕2﹣12∴b+c=4解得：b=c=2【点评】此题综合考查了三角公式中的正弦定理、余弦定理、三角形的面积公式的综合应用，诱导公式与辅助角公式在三角函数化简中的应用是求解的根底，解题的关键是熟练掌握根本公式18．〔12分〕【专题】综合题；概率与统计．【分析】〔Ⅰ〕依据卖出一枝可得利润5元，卖不出一枝可得赔本5元，即可建立分段函数；〔Ⅱ〕〔i〕这100天的日利润的平均数，利用100天的销售量除以100即可得到结论；〔ii〕当天的利润不少于75元，当且仅当日需求量不少于16枝，故可求当天的利润不少于75元的概率．【解答】解：〔Ⅰ〕当日需求量n≥17时，利润y=85；当日需求量n＜17时，利润y=10n﹣85；〔4分〕∴利润y关于当天需求量n的函数解析式〔n∈N*〕〔6分〕〔Ⅱ〕〔i〕这100天的日利润的平均数为元；〔9分〕〔ii〕当天的利润不少于75元，当且仅当日需求量不少于16枝，故当天的利润不少于75元的概率为P=0.16+0.16+0.15+0.13+0.1=0.7．〔12分〕【点评】此题考查函数解析式确实定，考查概率知识，考查利用数学知识解决实际问题，属于中档题．19．〔12分〕【专题】计算题；证明题．【分析】〔Ⅰ〕由题意易证DC1⊥平面BDC，再由面面垂直的判定定理即可证得平面BDC1⊥平面BDC；〔Ⅱ〕设棱锥B﹣DACC1的体积为V1，AC=1，易求V1=××1×1=，三棱柱ABC﹣A1B1C1的体积V=1，于是可得〔V﹣V1〕：V1=1：1，从而可得答案．【解答】证明：〔1〕由题设知BC⊥CC1，BC⊥AC，CC1∩AC=C，∴BC⊥平面ACC1A1，又DC1⊂平面ACC1A1，∴DC1⊥BC．由题设知∠A1DC1=∠ADC=45°，∴∠CDC1=90°，即DC1⊥DC，又DC∩BC=C，∴DC1⊥平面BDC，又DC1⊂平面BDC1，∴平面BDC1⊥平面BDC；〔2〕设棱锥B﹣DACC1的体积为V1，AC=1，由题意得V1=××1×1=，又三棱柱ABC﹣A1B1C1的体积V=1，∴〔V﹣V1〕：V1=1：1，∴平面BDC1分此棱柱两局部体积的比为1：1．【点评】此题考查平面与平面垂直的判定，着重考查线面垂直的判定定理的应用与棱柱、棱锥的体积，考查分析，表达与运算能力，属于中档题．20．〔12分〕【专题】综合题；压轴题．【分析】〔1〕由对称性知：△BFD是等腰直角△，斜边|BD|=2p点A到准线l的距离，由△ABD的面积S△ABD=，知=，由此能求出圆F的方程．〔2〕由对称性设，则点A，B关于点F对称得：，得：，由此能求出坐标原点到m，n距离的比值．【解答】解：〔1〕由对称性知：△BFD是等腰直角△，斜边|BD|=2p点A到准线l的距离，∵△ABD的面积S△ABD=，∴=，解得p=2，所以F坐标为〔0，1〕，∴圆F的方程为x2+〔y﹣1〕2=8．〔2〕由题设，则，∵A，B，F三点在同一直线m上，又AB为圆F的直径，故A，B关于点F对称．由点A，B关于点F对称得：得：，直线，切点直线坐标原点到m，n距离的比值为．【点评】此题考查抛物线与直线的位置关系的综合应用，具体涉及到抛物线的简单性质、圆的性质、导数的应用，解题时要认真审题，认真解答，注意合理地进行等价转化．21．〔12分〕【专题】综合题；压轴题；分类商量；转化思想．【分析】〔Ⅰ〕求函数的单调区间，可先求出函数的导数，由于函数中含有字母a，故应按a 的取值范围进行分类商量研究函数的单调性，给出单调区间；〔II〕由题设条件结合〔I〕，将不等式，〔x﹣k〕f´〔x〕+x+1＞0在x＞0时成立转化为k＜〔x＞0〕成立，由此问题转化为求g〔x〕=在x＞0上的最小值问题，求导，确定出函数的最小值，即可得出k的最大值；【解答】解：〔I〕函数f〔x〕=e x﹣ax﹣2的定义域是R，f′〔x〕=e x﹣a，假设a≤0，则f′〔x〕=e x﹣a≥0，所以函数f〔x〕=e x﹣ax﹣2在〔﹣∞，+∞〕上单调递增．假设a＞0，则当x∈〔﹣∞，lna〕时，f′〔x〕=e x﹣a＜0；当x∈〔lna，+∞〕时，f′〔x〕=e x﹣a＞0；所以，f〔x〕在〔﹣∞，lna〕单调递减，在〔lna，+∞〕上单调递增．〔II〕由于a=1，所以，〔x﹣k〕f´〔x〕+x+1=〔x﹣k〕〔e x﹣1〕+x+1故当x＞0时，〔x﹣k〕f´〔x〕+x+1＞0等价于k＜〔x＞0〕①令g〔x〕=，则g′〔x〕=由〔I〕知，当a=1时，函数h〔x〕=e x﹣x﹣2在〔0，+∞〕上单调递增，而h〔1〕＜0，h〔2〕＞0，所以h〔x〕=e x﹣x﹣2在〔0，+∞〕上存在唯一的零点，故g′〔x〕在〔0，+∞〕上存在唯一的零点，设此零点为α，则有α∈〔1，2〕当x∈〔0，α〕时，g′〔x〕＜0；当x∈〔α，+∞〕时，g′〔x〕＞0；所以g〔x〕在〔0，+∞〕上的最小值为g〔α〕．又由g′〔α〕=0，可得eα=α+2所以g〔α〕=α+1∈〔2，3〕由于①式等价于k＜g〔α〕，故整数k的最大值为2．【点评】此题考查利用导数求函数的最值及利用导数研究函数的单调性，解题的关键是第一小题应用分类的商量的方法，第二小题将问题转化为求函数的最小值问题，此题考查了转化的思想，分类商量的思想，考查计算能力及推理推断的能力，综合性强，是高考的重点题型，难度大，计算量也大，极易出错．22．〔10分〕【专题】证明题．【分析】〔1〕依据D，E分别为△ABC边AB，AC的中点，可得DE∥BC，证明四边形ADCF 是平行四边形，即可得到结论；〔2〕证明两组对应角相等，即可证得△BCD～△GBD．【解答】证明：〔1〕∵D，E分别为△ABC边AB，AC的中点∴DF∥BC，AD=DB∵AB∥CF，∴四边形BDFC是平行四边形∴CF∥BD，CF=BD∴CF∥AD，CF=AD∴四边形ADCF是平行四边形∴AF=CD∵，∴BC=AF，∴CD=BC．〔2〕由〔1〕知，所以．所以∠BGD=∠DBC．因为GF∥BC，所以∠BDG=∠ADF=∠DBC=∠BDC．所以△BCD～△GBD．【点评】此题考查几何证明选讲，考查平行四边形的证明，考查三角形的相似，属于根底题．23．〔202X•新课标〕【专题】综合题；压轴题．【分析】〔1〕确定点A，B，C，D的极坐标，即可得点A，B，C，D的直角坐标；〔2〕利用参数方程设出P的坐标，借助于三角函数，即可求得|PA|2+|PB|2+|PC|2+|PD|2的取值范围．【解答】解：〔1〕点A，B，C，D的极坐标为点A，B，C，D的直角坐标为〔2〕设P〔x0，y0〕，则为参数〕t=|PA|2+|PB|2+|PC|2+|PD|2=4x2+4y2+16=32+20sin2φ∵sin2φ∈[0，1]∴t∈[32，52]【点评】此题考查极坐标与直角坐标的互化，考查圆的参数方程的运用，属于中档题．24．〔202X•新课标〕【专题】计算题；压轴题．【分析】〔1〕不等式等价于，或，或，求出每个不等式组的解集，再取并集即得所求．〔2〕原命题等价于﹣2﹣x≤a≤2﹣x在[1，2]上恒成立，由此求得求a的取值范围．【解答】解：〔1〕当a=﹣3时，f〔x〕≥3 即|x﹣3|+|x﹣2|≥3，即①，或②，或③．解①可得x≤1，解②可得x∈∅，解③可得x≥4．把①、②、③的解集取并集可得不等式的解集为{x|x≤1或x≥4}．〔2〕原命题即f〔x〕≤|x﹣4|在[1，2]上恒成立，等价于|x+a|+2﹣x≤4﹣x在[1，2]上恒成立，等价于|x+a|≤2，等价于﹣2≤x+a≤2，﹣2﹣x≤a≤2﹣x在[1，2]上恒成立．故当1≤x≤2时，﹣2﹣x的最大值为﹣2﹣1=﹣3，2﹣x的最小值为0，故a的取值范围为[﹣3，0]．【点评】此题主要考查绝对值不等式的解法，关键是去掉绝对值，化为与之等价的不等式组来解，表达了分类商量的数学思想，属于中档题．。

历年全国高考数学考试试卷附详细解析.doc

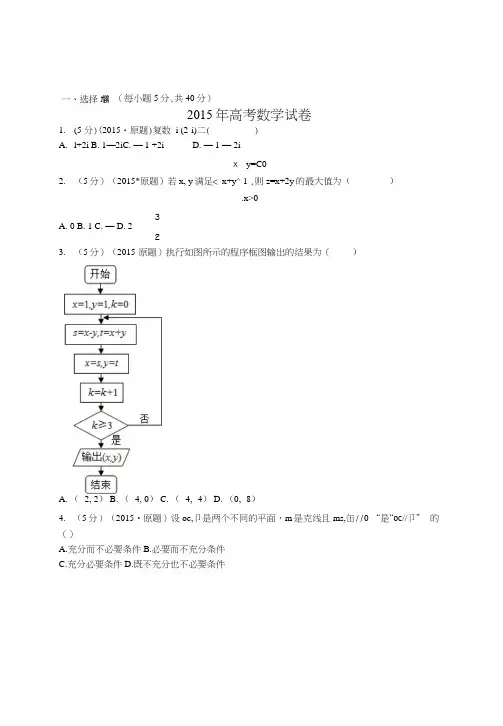
2015年高考数学试卷1. (5 分)(2015・原题)复数 i (2-i)二( )A. l+2iB. 1—2iC. — 1 +2iD. — 1 — 2ix - y=C02. （5分）（2015*原题）若x, y 满足< x+y^ 1 ,则z=x+2y 的最大值为（） .x>03A. 0B. 1C. —D. 2 23. （5分）（2015-原题）执行如图所示的程序框图输出的结果为（）A. （ -2, 2）B. （ -4, 0）C. （ -4, -4）D. （0, -8）4. （5分）（2015•原题）设oc,卩是两个不同的平面，m 是克线且ms,缶//0“是“oc //卩” 的（）A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件一、选择J （每小题5分,共40分）5.（5分）（2015•原题）某三棱锥的三视图如图所示，则该三棱锥的表面积是（）6. （5分）（2015・原题）设{%}是等差数列，下列结论屮正确的是（）八・若 a 1+a 2>0,贝!j a 2+a 3>0 B.若 a 1+a 3<0> 贝lj a]+a 2<07. （5分）（2015•原题）如图，函数f （x ）的图象为折线ACB,则不等式f （x ） >1<）& （x+1）A. {x| -l<x<0}B. {x| -Kx<l}C. {x| - 1<x<1}D. {x| -l<x<2}8. （5分）（2015-原题）汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程，如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况，下列叙述中正确的是（）C.若 0<ai <a 2,则 2〉寸8护3D.若 2]V0,贝lj (a 2-a 1) (a 2-a 3) >0 A. 2+V5 B. 4+^5 C. 2+2A /5 D ・ 5A.消耗1升汽油，乙车最多可行驶5千米B.以相同速度行驶相同路程，三辆车屮，甲车消耗汽油最多C.甲车以80千米/小时的速度行驶1小时，消耗10升汽油D. 某城市机动车最高限速80千米/小时，相同条件下，在该市用丙车比用乙车更省油9. （5分）（2015•原题）在（2+x ）'的展开式中，J 的系数为 __________ （用数字作答）10. （5分）（2015-原题）已知双曲线岭-y2=l （a >0）的一条渐近线为V3x+y=0，贝911. （5分）（2015-原题）在极坐标系中，点（2,牛）到直线° （cosO+V3sinO ） =6的距离为 ____________ •12. （5 分）（2015・原题）在AABC 中，a=4, b=5, c=6,则二 ____________________ .sinC在AABC 中，点 M, N 满足 AM=2MC, BN=NC,若MN=xAB+yAC,① 若汗1,则f （x ）的最小值为 _____________ ；② 若f （x ）恰有2个零点，则实数a 的取值范围是 ____________15. （13 分）（2015・原题）已矢U 函数 F （x ） =V2sin —cos — - V2sin ^―.2 2 2（I ）求f （x ）的最小正周期；（H ）求F （x ）在区间［■心0］上的最小值.16. （13分）（2015-原题）A, B 两组各有7位病人，他们服用某种药物后的康复时间（单位: 天）记录如下：A 组:10, 11, 12, 13, 14, 15, 16B 组;12, 13, 15, 16, 17, 14, a假设所有病人的康复时间相互独立，从八，B 两组随机各选1人，八组选出的人记为甲，B 组选出的人记为乙.（I ）求甲的康复时间不少于14天的概率；（U ）如果沪25,求甲的康复时间比乙的康复时间长的概率；（HI ）当a 为何值时，A, B 两组病人康复时间的方差相等？（结论不要求证明）17. （14分）（206原题）如图，在四棱锥A-EFCB 中，AAEF 为等边三角形，平面AEF 丄平面 EFCB, EF//BC, BC=4, EF=2a,上EBC 二上FCB 二60° , O 为 EF 的中点.（I ）求证：AO1BE.二、填空题侮小丿 5分,共30分）13. （5 分）（2015*原题）14. （5分）（2015•原题）设函数f （x ）= 2x-a, 4（x - a ）（x _ 2 a ）,x<l 三、解答］（共6小题 ,共80分）（U）求二面角F-AE-B的余弦值；（HI）若BE丄平面AOC,求a的值.18. (13分)(2015*原题)已知函数f (x)二1门丿注，(I )求曲线尸f (X )在点(0, f (0))处的切线方程; 3(H) 求证,当*€ (0, 1)时，f (x) >2(x+^-)；3(m)设实数k 使得f (x) >k(x+专-)对乂€ (o, 1)恒成立，求k 的最大值.19. (14分)(2015•原题)已知椭圆C:三+笃二1 (a>b>0)的离心率为李，点P (0, 1)/ b ， 2和点A (m, n) (mHO)都在椭圆C±,直线PA 交x 轴于点M.(I) 求椭圆C 的方程，并求点M 的坐标(用n 表示)；(U )设O 为原点，点B 与点A 关于x 轴对称，直线PB 交x 轴于点N,问：y 轴上是否存在点Q,使得ZOQM=ZONQ?若存在，求点Q 的坐标，若不存在，说明理由.2(). (13 分)(2013 •原题)已知数列｛%｝满足： , a t <36，且 a n+1 = (n=l, 2,…)，记集合 M ={a n |n€N +}.(I)若引二6,写出集合M 的所有元素；(n )如集合M 存在一个元素是3的倍数，证明：M 的所有元素都是3的倍数; (111)求集合M 的元索个数的最大值.2%,a n <18 2%-36, %>182015年原题市高考数学试卷（理科）1. （5 分）（2015-原题）复数 i （2-i ）二（）A. l+2iB. 1 -2iC. —l+2iD. - 1 - 2i【分析】利用复数的运算法则解答.【解答】解:原式=2i - i 2=2i - (-1) =l+2i;故选：A.【点评】本题考查了复数的运算；关键是熟记运算法则.注意i 2=-l. &-y<02. （5分）（2015•原题）若x, y 满足《 x+yCl ,则z=x+2y 的最大值为（）、x>03A. 0B. 1C. —D. 2 2【分析】作出题中不等式组表示的平面区域，再将目标函数z 二x+2y 对应的直线进行平移, 即可求出z 取得最大值."x-y<0【解答】解：作出不等式组x+y< 1表示的平面区域，.xi>0当1经过点B 时，目标函数z 达到最大值 z 煨大值二0+2X1 —2・【点评】本题给出二元一次不等式组，求目标函数Z 二x+2y 的最大值，着重考查了二元一次不一、选择题（每小, 5分，共40分）等式组表示的平面区域和简单的线性规划等知识，属于基础题•3.（5分）（2015•原题）执行如图所示的程序框图输出的结果为（）A. (—2, 2)B. (一4, 0) C- (一4, -4) D. (0, -8)【分析】模拟程序框图的运行过程，即可得出程序运行后输出的结果.【解答】解：模拟程序框图的运行过程，如下；x=l, y=l,k=0 时,s=x - y=0, t=x+y=2 ；x=s=0, y=t=2,k二1 时，s=x - y= - 2, t二x+y二2;x二s二一2，y二t二2，k=2 吋,s=x - y= ~ 4, t=x+y=0 ；x=s= -4, y=t=0,k=3时，循环终止，输出(x, y)是(-4, 0).故选：B.【点评】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，是基础题目•4.(5分)(2015-原题)设冷卩是两个不同的平面，口是直线且muoc, //0 “是、//卩” 的()A.充分而不必耍条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【分析】m // p并得不到a II ,3,根据面面平行的判定定理，只有a内的两相交直线都平行于P，而a//0,并且mua,显然能得到这样即可找出正确选项.【解答】解：mca, 口//(3得不到00”(3,因为oc, 0可能相交，只要m和a,卩的交线平行即可得到m" (3；a // P，mCa, m 和0 没有公共点,.'.m//p,即oc//0 能得到m//0；二“m/邙”是、/人3”的必要不充分条件.故选B.【点评】考查线面平行的定义，线面平行的判定定理，面面平行的定义，面面平行的判定定理，以及充分条件、必要条件，及必要不充分条件的概念.5. （5分）（2015-原题）某三棱锥的三视图如图所示，则该三棱锥的表面积是（）A. 2+^^/5B. 4+A /5C. 2+2A /5D. 5【分析】根据三视图可判断克观图为：（）A 丄面ABC,AC=AB,E 为BC 中点,EA=2,E/\=EB=1, OA二 1,: BC 丄 ffi AEO, AC=V5, OE=V5判断儿何体的各个面的特点，计算边长，求解面积.【解答】解：根据三视图可判断立观图为：（）八丄面ABC, AC 二AB, E 为BC 屮点，EA=2, EC=EB=1, ()A 二 1,•••可彳导/\E 丄BC, BC 丄OA,运用£［线平面的垂立得岀：BC 丄面AEO, AC=V5, OR=V5S/XBCO 二专 X2x V5-V5.故该三棱锥的表面积是2+2丽, 故选：C.【点评】本题考查了空间几何体的三视图的运用，空间想象能力，计算能力，关键是恢复直观图，得出几何体的性质.6. （5分）（2015•原题）设｛%｝是等差数列，下列结论中正确的是（）• • ^AABCX2X2 二 2, S AO/\C =^AOAB-^ XV5>< 1=^^-A.若引+玄2>0,贝lj a2+a3>0B.若卯+%<0,贝lj a1+a2<0C.若0<旬<近，则阴D・若吗<0,贝lj (a2-aj) (a2-a3) >0【分析】对选项分别进行判断，即可得岀结论.【解答】解：若a1+a2>0,则2a]+d>0, a2+a3=2a]+3d>2d, d>0时,结论成立，即A不正确；若吗+%<(),贝lj a1+a2=2a1+d<0, a2+a3=2a1+3d<2d, dV()日寸，结论丿成立，即B 不止确；{%}是詩差数列，0<则<^2，2屯二引+%>2寸3]阴,；•耳>勺a]巧，即C止确；若引V0,贝I」(迈—吗)(a2-a3) =-d2<0,即D不正确.故选：C.【点评】本题考查等差数列的通项，考查学生的计算能力，比较基础.7.(5分)(2015•原题)如图,函数f (x)的图象为折线ACB,则不等式f(x) >lo& (x+1)-l<x<l}C. {x| - l<x<l}D. {x| -l<x<2}【分析】在已知坐标系内作IB y=log2 (x+1)的图象，利用数形结合得到不等式的解集.【解答】解：由已知F(x)的图象，在此坐标系内作出y二1。

2024年全国甲卷数学(理)高考真题(含解析)

2024年普通高等学校招生全国统一考试全国甲卷（理科数学）（使用范围：陕西、宁夏、青海、内蒙古、四川）注意事项：1．答题前，务必将自己的姓名、考籍号填写在答题卡规定的位置上．2．答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦擦干净后，再选涂其它答案标号．3．答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上．4．所有题目必须在答题卡上作答，在试题卷上答题无效．5．考试结束后，只将答题卡交回．一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1.设5i z =+，则()i z z +=（）A .10iB.2iC.10D.2-2.集合{}{}1,2,3,4,5,9,A B A ==，则()A A B ⋂=ð（）A.{}1,4,9 B.{}3,4,9 C.{}1,2,3 D.{}2,3,53.若实数,x y 满足约束条件43302202690x y x y x y --≥⎧⎪--≤⎨⎪+-≤⎩，则5z x y =-的最小值为（）A.5B.12C.2- D.72-4.等差数列{}n a 的前n 项和为n S ，若510S S =，51a =，则1a =（）A.2- B.73C.1D.25.已知双曲线的两个焦点分别为(0,4),(0,4)-，点(6,4)-在该双曲线上，则该双曲线的离心率为（）A.4B.3C.2D.6.设函数()2e 2sin 1x xf x x+=+，则曲线()y f x =在()0,1处的切线与两坐标轴围成的三角形的面积为（）A.16B.13C.12D.237.函数()()2e esin xxf x x x -=-+-在区间[ 2.8,2.8]-的大致图像为（）A.B.C. D.8.已知cos cos sin ααα=-πtan 4α⎛⎫+= ⎪⎝⎭（）A.1+ B.1- C.32D.19.已知向量()()1,,,2a x x b x =+=，则（）A.“3x =-”是“a b ⊥”的必要条件B.“3x =-”是“//a b”的必要条件C.“0x =”是“a b ⊥ ”的充分条件D.“1x =-+”是“//a b”的充分条件10.设αβ、是两个平面，m n 、是两条直线，且m αβ= .下列四个命题：①若//m n ，则//n α或//n β②若m n ⊥，则,n n αβ⊥⊥③若//n α，且//n β，则//m n ④若n 与α和β所成的角相等，则m n⊥其中所有真命题的编号是（）A.①③B.②④C.①②③D.①③④11.在ABC 中内角,,A B C 所对边分别为,,a b c ，若π3B =，294b ac =，则sin sin A C +=（）A.32B.C.72D.212.已知b 是,a c 的等差中项，直线0ax by c ++=与圆22410x y y ++-=交于,A B 两点，则AB 的最小值为（）A.2B.3C.4D.二、填空题：本题共4小题，每小题5分，共20分．13.1013x ⎛⎫+ ⎪⎝⎭的展开式中，各项系数的最大值是______．14.已知甲、乙两个圆台上、下底面的半径均为1r 和2r ，母线长分别为()212r r -和()213r r -，则两个圆台的体积之比=V V 甲乙______．15.已知1a >，8115log log 42a a -=-，则=a ______．16.有6个相同的球，分别标有数字1、2、3、4、5、6，从中不放回地随机抽取3次，每次取1个球.记m 为前两次取出的球上数字的平均值，n 为取出的三个球上数字的平均值，则m 与n 差的绝对值不超过12的概率是______．三、解答题：共70分．解答应写出文字说明，证明过程或演算步骤．第17题~第21题为必考题，每个考题考生必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17.某工厂进行生产线智能化升级改造，升级改造后，从该工厂甲、乙两个车间的产品中随机抽取150件进行检验，数据如下：优级品合格品不合格品总计甲车间2624050乙车间70282100总计96522150（1）填写如下列联表：优级品非优级品甲车间乙车间能否有95%的把握认为甲、乙两车间产品的优级品率存在差异？能否有99%的把握认为甲，乙两车间产品的优级品率存在差异？（2）已知升级改造前该工厂产品的优级品率0.5p=，设p为升级改造后抽取的n件产品的优级品率.如果p p>+150件产品的数据，能否认为12.247≈）附：22()()()()()n ad bcKa b c d a c b d-=++++()2P K k≥0.0500.0100.001k 3.841 6.63510.82818.记n S为数列{}n a的前n项和，且434n nS a=+．（1）求{}n a的通项公式；（2）设1(1)nn nb na-=-，求数列{}n b的前n项和为n T．19.如图，在以A，B，C，D，E，F为顶点的五面体中，四边形ABCD与四边形ADEF均为等腰梯形，//,//BC AD EF AD，4,2AD AB BC EF====，ED FB==M为AD的中点．（1）证明：//BM平面CDE；（2）求二面角F BM E --的正弦值．20.设椭圆2222:1(0)x y C a b a b+=>>的右焦点为F ，点31,2M ⎛⎫ ⎪⎝⎭在C 上，且MF x ⊥轴．（1）求C 的方程；（2）过点()4,0P 的直线与C 交于,A B 两点，N 为线段FP 的中点，直线NB 交直线MF 于点Q ，证明：AQ y ⊥轴．21.已知函数()()()1ln 1f x ax x x =-+-．（1）当2a =-时，求()f x 的极值；（2）当0x ≥时，()0f x ≥恒成立，求a 的取值范围．（二）选考题：共10分，请考生在第22、23题中任选一题作答，并用2B 铅笔将所选题号涂黑，多涂、错涂、漏涂均不给分，如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]22.在平面直角坐标系xOy 中，以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为cos 1ρρθ=+.（1）写出C 的直角坐标方程；（2）设直线l ：x ty t a =⎧⎨=+⎩（t 为参数），若C 与l 相交于A B 、两点，若2AB =，求a 的值.[选修4-5：不等式选讲]23.实数,a b 满足3a b +≥．（1）证明：2222a b a b +>+；（2）证明：22226a b b a -+-≥．参考答案（含解析）一、选择题题号123456789101112答案ADDBCABBCACC1.【答案】A【解析】由5i 5i,10z z z z =+⇒=-+=，则()i 10i z z +=，故选：A2.【答案】D【解析】因为{}{}1,2,3,4,5,9,A B A ==，所以{}1,4,9,16,25,81B =，则{}1,4,9A B = ，(){}2,3,5A A B = ð，故选：D3.【答案】D【解析】实数,x y 满足43302202690x y x y x y --≥⎧⎪--≤⎨⎪+-≤⎩，作出可行域如图：由5z x y =-可得1155y x z =-，即z 的几何意义为1155y x z =-的截距的15-，则该直线截距取最大值时，z 有最小值，此时直线1155y x z =-过点A ，联立43302690x y x y --=⎧⎨+-=⎩，解得321x y ⎧=⎪⎨⎪=⎩，即3,12A ⎛⎫ ⎪⎝⎭，则min 375122z =-⨯=-.故选：D.4.【答案】B【解析】由105678910850S S a a a a a a -=++++==，则80a =，则等差数列{}n a 的公差85133a a d -==-，故151741433a a d ⎛⎫=-=-⨯-= ⎪⎝⎭.故选：B.5.【答案】C【解析】设()10,4F -、()20,4F 、()6,4-P ，则1228F F c ==，110PF ==，26PF ==，则1221064a PF PF =-=-=，则28224c e a ===.故选：C.6.【答案】A 【解析】()()()()()222e 2cos 1e 2sin 21xx x x x xf x x ++-+⋅'=+，则()()()()()2e 2cos 010e 2sin 000310f ++-+⨯'==+，即该切线方程为13y x -=，即31y x =+，令0x =，则1y =，令0y =，则13x =-，故该切线与两坐标轴所围成的三角形面积1111236S =⨯⨯-=.故选：A.7.【答案】B【解析】()()()()()22ee sin e e sin xx x x f x x x x x f x ---=-+--=-+-=，又函数定义域为[]2.8,2.8-，故该函数为偶函数，可排除A 、C ，又()11πe 11111e sin11e sin 10e e 622e 42e f ⎛⎫⎛⎫=-+->-+-=-->-> ⎪ ⎪⎝⎭⎝⎭，故可排除D.故选：B.8.【答案】B【解析】因为cos cos sin ααα=-，所以11tan =-α，tan 13⇒α=-，所以tan 1tan 11tan 4α+π⎛⎫==α+⎪-α⎝⎭，故选：B .9.【答案】C【解析】对A ，当a b ⊥ 时，则0a b ⋅=，所以(1)20x x x ⋅++=，解得0x =或3-，即必要性不成立，故A 错误；对C ，当0x =时，()()1,0,0,2a b == ，故0a b ⋅=，所以a b ⊥ ，即充分性成立，故C 正确；对B ，当//a b时，则22(1)x x +=，解得1x =±，即必要性不成立，故B 错误；对D ，当1x =-+时，不满足22(1)x x +=，所以//a b不成立，即充分性不立，故D 错误.故选：C.10.【答案】A【解析】对①，当n ⊂α，因为//m n ，m β⊂，则//n β，当n β⊂，因为//m n ，m α⊂，则//n α，当n 既不在α也不在β内，因为//m n ，,m m αβ⊂⊂，则//n α且//n β，故①正确；对②，若m n ⊥，则n 与,αβ不一定垂直，故②错误；对③，过直线n 分别作两平面与,αβ分别相交于直线s 和直线t ，因为//n α，过直线n 的平面与平面α的交线为直线s ，则根据线面平行的性质定理知//n s ，同理可得//n t ，则//s t ，因为s ⊄平面β，t ⊂平面β，则//s 平面β，因为s ⊂平面α，m αβ= ，则//s m ，又因为//n s ，则//m n ，故③正确；对④，若,m n αβ⋂=与α和β所成的角相等，如果//,//αβn n ，则//m n ，故④错误；综上只有①③正确，故选：A.11.【答案】C 【解析】因为29,34B b ac π==，则由正弦定理得241sin sin sin 93A CB ==.由余弦定理可得:22294b ac ac ac =+-=，即:22134a c ac +=，根据正弦定理得221313sin sin sin sin 412A C A C +==，所以2227(sin sin )sin sin 2sin sin 4A C A C A C +=++=，因为,A C 为三角形内角，则sin sin 0A C +>，则7sin sin 2A C +=.故选：C.12.【答案】C【解析】因为,,a b c 成等差数列，所以2b a c =+，2c b a =-，代入直线方程0ax by c ++=得20ax by b a ++-=，即()()120a x b y -++=，令1020x y -=⎧⎨+=⎩得12x y =⎧⎨=-⎩，故直线恒过()1,2-，设()1,2P -，圆化为标准方程得：()22:25C x y ++=，设圆心为C ，画出直线与圆的图形，由图可知，当PC AB ⊥时，AB 最小，1,PC AC r ===24AB AP ====.故选：C二、填空题13.【答案】5【解析】由题展开式通项公式为101101C 3rr r r T x -+⎛⎫= ⎪⎝⎭，010r ≤≤且r ∈Z ，设展开式中第1r +项系数最大，则1091101010111101011C C 3311C C 33r rr r r rr r --+---⎧⎛⎫⎛⎫≥⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎨⎛⎫⎛⎫⎪≥ ⎪ ⎪⎪⎝⎭⎝⎭⎩，294334r r ⎧≥⎪⎪⇒⎨⎪≤⎪⎩，即293344r ≤≤，又r ∈Z ，故8r =，所以展开式中系数最大的项是第9项，且该项系数为28101C 53⎛⎫= ⎪⎝⎭.故答案为：5.14.【答案】64【解析】由题可得两个圆台的高分别为)12h r r ==-甲，)12h r r ==-乙，所以((2121163143S S h V h V h S S h ++-===++甲甲甲乙乙乙.故答案为：64.15.【答案】64【解析】由题28211315log log log 4log 22a a a a -=-=-，整理得()2225log 60log a a --=，2log 1a ⇒=-或2log 6a =，又1a >，所以622log 6log 2a ==，故6264a ==故答案为：64.16.【答案】715【解析】从6个不同的球中不放回地抽取3次，共有36A 120=种，设前两个球的号码为,a b ，第三个球的号码为c ，则1322a b c a b +++-≤，故2()3c a b -+≤，故32()3c a b -≤-+≤，故323a b c a b +-≤≤++，若1c =，则5a b +≤，则(),a b 为：()()2,3,3,2，故有2种，若2c =，则17a b ≤+≤，则(),a b 为：()()()()()1,3,1,4,1,5,1,6,3,4，()()()()()3,1,4,1,5,1,6,1,4,3，故有10种，当3c =，则39a b ≤+≤，则(),a b 为：()()()()()()()()1,2,1,4,1,5,1,6,2,4,2,5,2,6,4,5，()()()()()()()()2,1,4,1,5,1,6,1,4,2,5,2,6,2,5,4，故有16种，当4c =，则511a b ≤+≤，同理有16种，当5c =，则713a b ≤+≤，同理有10种，当6c =，则915a b ≤+≤，同理有2种，共m 与n 的差的绝对值不超过12时不同的抽取方法总数为()22101656++=，故所求概率为56712015=.故答案为：715.三、解答题（一）必考题17.【答案】（1）答案见解析；（2）答案见解析；【解析】（1）根据题意可得列联表：优级品非优级品甲车间2624乙车间7030可得()2215026302470754.687550100965416K ⨯-⨯===⨯⨯⨯，因为3.841 4.6875 6.635<<，所以有95%的把握认为甲、乙两车间产品的优级品率存在差异，没有99%的把握认为甲，乙两车间产品的优级品率存在差异.（2）由题意可知：生产线智能化升级改造后，该工厂产品的优级品的频率为960.64150=，用频率估计概率可得0.64p =，又因为升级改造前该工厂产品的优级品率0.5p =，则0.50.50.5 1.650.56812.247p +=+≈+⨯≈，可知p p >+所以可以认为生产线智能化升级改造后，该工厂产品的优级品率提高了.18.【答案】（1）14(3)n n a -=⋅-；（2）(21)31nn T n =-⋅+【解析】（1）当1n =时，1114434S a a ==+，解得14a =．当2n ≥时，11434n n S a --=+，所以1144433n n n n n S S a a a ---==-即13n n a a -=-，而140a =≠，故0n a ≠，故13nn a a -=-，∴数列{}n a 是以4为首项，3-为公比的等比数列，所以()143n n a -=⋅-.（2）111(1)4(3)43n n n n b n n ---=-⋅⋅⋅-=⋅,所以123n n T b b b b =++++ 0211438312343n n -=⋅+⋅+⋅++⋅ ，故1233438312343nn T n =⋅+⋅+⋅++⋅ ，所以1212443434343n nn T n --=+⋅+⋅++⋅-⋅ ()1313444313n nn --=+⋅-⋅-()14233143n nn -=+⋅⋅--⋅(24)32n n =-⋅-，(21)31n n T n ∴=-⋅+.19.【答案】（1）证明见解析；（2）4313【解析】（1）因为//,2,4,BC AD EF AD M ==为AD 的中点，所以//,BC MD BC MD =，四边形BCDM 为平行四边形，所以//BM CD ，又因为BM ⊄平面CDE ，CD ⊂平面CDE ，所以//BM 平面CDE ；（2）如图所示，作BO AD ⊥交AD 于O ，连接OF ，因为四边形ABCD 为等腰梯形，//,4,BC AD AD =2AB BC ==，所以2CD =，结合（1）BCDM 为平行四边形，可得2BM CD ==，又2AM =，所以ABM 为等边三角形，O 为AM中点，所以OB =，又因为四边形ADEF 为等腰梯形，M 为AD 中点，所以,//EF MD EF MD =，四边形EFMD 为平行四边形，FM ED AF ==，所以AFM △为等腰三角形，ABM 与AFM △底边上中点O 重合，OF AM ⊥，3OF =，因为222OB OF BF +=，所以OB OF ⊥，所以,,OB OD OF 互相垂直，以OB 方向为x 轴，OD 方向为y 轴，OF 方向为z 轴，建立O xyz -空间直角坐标系，()0,0,3F，)()(),0,1,0,0,2,3BM E，()(),BM BF ==，()2,3BE = ，设平面BFM 的法向量为()111,,m x y z =，平面EMB 的法向量为()222,,n x y z =，则00m BM m BF ⎧⋅=⎪⎨⋅=⎪⎩，即1111030y z ⎧+=⎪⎨+=⎪⎩，令1x =113,1y z ==，即)m =，则00n BM n BE ⎧⋅=⎪⎨⋅=⎪⎩，即222220230y y z ⎧+=⎪⎨++=⎪⎩，令2x =，得223,1y z ==-，即)1n =-，11cos ,13m n m n m n ⋅===⋅，则43sin ,13m n =，故二面角F BM E --的正弦值为13.20.【答案】（1）22143x y +=；（2）证明见解析【解析】（1）设(),0F c ，由题设有1c =且232b a =，故2132a a -=，故2a =，故b =，故椭圆方程为22143x y +=.（2）直线AB 的斜率必定存在，设:(4)AB y k x =-，()11,A x y ，()22,B x y，由223412(4)x y y k x ⎧+=⎨=-⎩可得()2222343264120k x k x k +-+-=，故()()422Δ102443464120k kk=-+->，故1122k -<<，又22121222326412,3434k k x x x x k k -+==++，而5,02N ⎛⎫ ⎪⎝⎭，故直线225:522y BN y x x ⎛⎫=-⎪⎝⎭-，故22223325252Qy y y x x --==--，所以()1222112225332525Q y x y y y y y x x ⨯-+-=+=--()()()12224253425k x x k x x -⨯-+-=-()222212122264123225825834342525k k x x x x k k k k x x -⨯-⨯+-++++==--2222212824160243234025k k k k k x --+++==-，故1Q y y =，即AQ y ⊥轴.21.【答案】（1）极小值为0，无极大值；（2）12a ≤-.【解析】（1）当2a =-时，()(12)ln(1)f x x x x =++-，故121()2ln(1)12ln(1)111x f x x x x x +'=++-=+-+++，因为12ln(1),11y x y x=+=-++在()1,∞-+上为增函数，故()f x '在()1,∞-+上为增函数，而(0)0f '=，故当10x -<<时，()0f x '<，当0x >时，()0f x '>，故()f x 在0x =处取极小值且极小值为()00f =，无极大值.（2）()()()()11ln 11ln 1,011a x axf x a x a x x x x+-=-+'+-=-+->++，设()()()1ln 101a xs x a x x x+=-+->+，则()()()()()()222111211111a a x a a ax a s x x x x x ++++-++=-=-=-+++'+，当12a ≤-时，()0s x '>，故()s x 在()0,∞+上为增函数，故()()00s x s >=，即()0f x '>，所以()f x 在[)0,∞+上为增函数，故()()00f x f ≥=.当102a -<<时，当210a x a+<<-时，()0s x '<，故()s x 在210,a a +⎛⎫-⎪⎝⎭上为减函数，故在210,a a +⎛⎫- ⎪⎝⎭上()()0s x s <，即在210,a a +⎛⎫-⎪⎝⎭上()0f x '<即()f x 为减函数，故在210,a a +⎛⎫- ⎪⎝⎭上()()00f x f <=，不合题意，舍.当0a ≥，此时()0s x '<在()0,∞+上恒成立；同理可得在()0,∞+上()()00f x f <=恒成立，不合题意，舍；综上，12a ≤-.（二）选考题[选修4-4：坐标系与参数方程]22.【答案】（1）221y x =+；（2）34a =.【解析】（1）由cos 1ρρθ=+，将ρρθ⎧⎪=⎨=⎪⎩cos 1ρρθ=+，1x =+，两边平方后可得曲线的直角坐标方程为221y x =+.（2）对于直线l 的参数方程消去参数t ，得直线的普通方程为y x a =+.法1：直线l 的斜率为1，故倾斜角为π4，故直线的参数方程可设为222x s y a s⎧=⎪⎪⎨⎪=+⎪⎩，s ∈R .将其代入221y x =+中得()221)210s a s a +-+-=设,A B 两点对应的参数分别为12,s s，则)()212121,21s s a s s a +=--=-，且()()22Δ818116160a a a =---=->，故1a <，12AB s s ∴=-=2==，解得34a =.法2：联立221y x ay x =+⎧⎨=+⎩，得22(22)10x a x a +-+-=，()22Δ(22)41880a a a =---=-+>，解得1a <，设()()1122,,,A x y B x y ,2121222,1x x a x x a ∴+=-=-，则AB ==2=，解得34a =.[选修4-5：不等式选讲]23.实数,a b 满足3a b +≥．（1）证明：2222a b a b +>+；（2）证明：22226a b b a -+-≥．【答案】（1）证明见解析；（2）证明见解析.【解析】（1）因为()()2222222022a b a ab b a b b a -+=--++=≥，当a b =时等号成立，则22222()a b a b +≥+，因为3a b +≥，所以22222()a b a b a b +≥+>+;（2）222222222222()a b b a a b b a a b a b -+-≥-+-=+-+22222()()()()(1)326a b a b a b a b a b a b =+-+≥+-+=++-≥⨯=.。

高考数学历年真题及答案详解

高考数学历年真题及答案详解一、选择题1. 题目描述：在平面直角坐标系中，点A(-3, 4)关于y轴的对称点是（）。

A. (3, -4)B. (-3, -4)C. (-3, 4)D. (3, 4)答案解析：点关于y轴对称即x取相反数，所以答案为A.(3, -4)。

2. 题目描述：已知函数 f(x) = 2^(2x-3)，则当 x = 1 时，f(x) 的值是（）。

A. 1B. 2C. 4D. 8答案解析：将x=1代入函数中，即f(1) = 2^(2*1-3)，化简得f(1)= 2^(-1) = 1/2，所以答案为A. 1。

二、填空题1. 题目描述：已知三角形ABC中，∠B = 90°，AC = 5 cm，BC =12 cm，求AB的长度。

答案解析：根据勾股定理，AB^2 + BC^2 = AC^2，代入已知数据得AB^2 + 12^2 = 5^2，化简得AB^2 = 25 - 144 = -119，由于长度不能为负数，所以不存在满足要求的三角形ABC。

2. 题目描述：若a1, a2, a3为等差数列的前三项，且满足a1 + a3 = 18，a2 - a3 = 4，求a1, a2和a3的值。

答案解析：由等差数列的性质可知，a2 = (a1 + a3) / 2，代入已知数据得a2 = 9.5，将a2带入a2 - a3 = 4解得a3 = 5.5，再将a3带入a1 +a3 = 18解得a1 = 12.5，所以a1 = 12.5，a2 = 9.5，a3 = 5.5。

三、解答题1. 题目描述：设函数f(x) = cos(x + 1) - sin(x - 1)，求f(x)的单调递增区间。

答案解析：对f(x)求导得f'(x) = -sin(x + 1) - cos(x - 1)，令f'(x) = 0，解方程得x = 1/4 (4πn + 3π/2) - 1，其中n为整数。

通过二阶导数的符号判断可知，当x < -1或x > -3/4 + 4πn，f(x)单调递增；当-3/4 + 4πn < x< -1，f(x)单调递减。

2024年高考数学真题分类汇编(三角函数篇,解析版)

专题三角函数1(新课标全国Ⅰ卷)已知cos (α+β)=m ,tan αtan β=2，则cos (α-β)=()A.-3mB.-m3C.m 3D.3m【答案】A【分析】根据两角和的余弦可求cos αcos β,sin αsin β的关系，结合tan αtan β的值可求前者，故可求cos α-β 的值.【详解】因为cos α+β =m ，所以cos αcos β-sin αsin β=m ，而tan αtan β=2，所以=12×2b ×kb ×sin A 2+12×kb ×b ×sin A2，故cos αcos β-2cos αcos β=m 即cos αcos β=-m ，从而sin αsin β=-2m ，故cos α-β =-3m ，故选：A .2(新课标全国Ⅰ卷)当x ∈[0,2π]时，曲线y =sin x 与y =2sin 3x -π6 的交点个数为()A.3B.4C.6D.8【答案】C【分析】画出两函数在0,2π 上的图象，根据图象即可求解【详解】因为函数y =sin x 的的最小正周期为T =2π，函数y =2sin 3x -π6 的最小正周期为T =2π3，所以在x ∈0,2π 上函数y =2sin 3x -π6有三个周期的图象，在坐标系中结合五点法画出两函数图象，如图所示：由图可知，两函数图象有6个交点.故选：C3(新课标全国Ⅱ卷)设函数f (x )=a (x +1)2-1，g (x )=cos x +2ax ，当x ∈(-1,1)时，曲线y =f (x )与y =g (x )恰有一个交点，则a =()A.-1B.12C.1D.22024年高考数学真题分类汇编——三角函数篇【分析】解法一：令F x =ax 2+a -1,G x =cos x ，分析可知曲线y =F (x )与y =G (x )恰有一个交点，结合偶函数的对称性可知该交点只能在y 轴上，即可得a =2，并代入检验即可；解法二：令h x =f (x )-g x ,x ∈-1,1 ，可知h x 为偶函数，根据偶函数的对称性可知h x 的零点只能为0，即可得a =2，并代入检验即可.【详解】解法一：令f (x )=g x ，即a (x +1)2-1=cos x +2ax ，可得ax 2+a -1=cos x ，令F x =ax 2+a -1,G x =cos x ，原题意等价于当x ∈(-1,1)时，曲线y =F (x )与y =G (x )恰有一个交点，注意到F x ,G x 均为偶函数，可知该交点只能在y 轴上，可得F 0 =G 0 ，即a -1=1，解得a =2，若a =2，令F x =G x ，可得2x 2+1-cos x =0因为x ∈-1,1 ，则2x 2≥0,1-cos x ≥0，当且仅当x =0时，等号成立，可得2x 2+1-cos x ≥0，当且仅当x =0时，等号成立，则方程2x 2+1-cos x =0有且仅有一个实根0，即曲线y =F (x )与y =G (x )恰有一个交点，所以a =2符合题意；综上所述：a =2.解法二：令h x =f (x )-g x =ax 2+a -1-cos x ,x ∈-1,1 ，原题意等价于h x 有且仅有一个零点，因为h -x =a -x 2+a -1-cos -x =ax 2+a -1-cos x =h x ，则h x 为偶函数，根据偶函数的对称性可知h x 的零点只能为0，即h 0 =a -2=0，解得a =2，若a =2，则h x =2x 2+1-cos x ,x ∈-1,1 ，又因为2x 2≥0,1-cos x ≥0当且仅当x =0时，等号成立，可得h x ≥0，当且仅当x =0时，等号成立，即h x 有且仅有一个零点0，所以a =2符合题意；故选：D .4(全国甲卷数学(理)(文))已知cos αcos α-sin α=3，则tan α+π4=()A.23+1 B.23-1C.32D.1-3【答案】B【分析】先将cos αcos α-sin α弦化切求得tan α，再根据两角和的正切公式即可求解.【详解】因为cos αcos α-sin α=3，所以11-tan α=3，⇒tan α=1-33，所以tan α+π4 =tan α+11-tan α=23-1，故选：B .5(新高考北京卷)已知f x =sin ωx ω>0 ，f x 1 =-1，f x 2 =1，|x 1-x 2|min =π2，则ω=()A.1B.2C.3D.4【分析】根据三角函数最值分析周期性，结合三角函数最小正周期公式运算求解.【详解】由题意可知：x 1为f x 的最小值点，x 2为f x 的最大值点，则x 1-x 2 min =T 2=π2，即T =π，且ω>0，所以ω=2πT=2.故选：B .6(新高考天津卷)已知函数f x =sin3ωx +π3ω>0 的最小正周期为π．则函数在-π12,π6 的最小值是()A.-32B.-32C.0D.32【答案】A【分析】先由诱导公式化简，结合周期公式求出ω，得f x =-sin2x ，再整体求出x ∈-π12,π6时，2x 的范围，结合正弦三角函数图象特征即可求解.【详解】f x =sin3ωx +π3 =sin 3ωx +π =-sin3ωx ，由T =2π3ω=π得ω=23，即f x =-sin2x ，当x ∈-π12,π6 时，2x ∈-π6,π3，画出f x =-sin2x 图象，如下图，由图可知，f x =-sin2x 在-π12,π6上递减，所以，当x =π6时，f x min =-sin π3=-32故选：A7(新高考上海卷)下列函数f x 的最小正周期是2π的是()A.sin x +cos xB.sin x cos xC.sin 2x +cos 2xD.sin 2x -cos 2x【答案】A【分析】根据辅助角公式、二倍角公式以及同角三角函数关系并结合三角函数的性质一一判断即可 .【详解】对A ，sin x +cos x =2sin x +π4，周期T =2π，故A 正确；对B ，sin x cos x =12sin2x ，周期T =2π2=π，故B 错误；对于选项C ，sin 2x +cos 2x =1，是常值函数，不存在最小正周期，故C 错误；对于选项D ，sin 2x -cos 2x =-cos2x ，周期T =2π2=π，故D 错误，故选：A ．8(新课标全国Ⅱ卷)对于函数f(x)=sin2x和g(x)=sin2x-π4，下列说法正确的有() A.f(x)与g(x)有相同的零点 B.f(x)与g(x)有相同的最大值C.f(x)与g(x)有相同的最小正周期D.f(x)与g(x)的图像有相同的对称轴【答案】BC【分析】根据正弦函数的零点，最值，周期公式，对称轴方程逐一分析每个选项即可.【详解】A选项，令f(x)=sin2x=0，解得x=kπ2,k∈Z，即为f(x)零点，令g(x)=sin2x-π4=0，解得x=kπ2+π8,k∈Z，即为g(x)零点，显然f(x),g(x)零点不同，A选项错误；B选项，显然f(x)max=g(x)max=1，B选项正确；C选项，根据周期公式，f(x),g(x)的周期均为2π2=π，C选项正确；D选项，根据正弦函数的性质f(x)的对称轴满足2x=kπ+π2⇔x=kπ2+π4,k∈Z，g(x)的对称轴满足2x-π4=kπ+π2⇔x=kπ2+3π8,k∈Z，显然f(x),g(x)图像的对称轴不同，D选项错误.故选：BC9(新课标全国Ⅱ卷)已知α为第一象限角，β为第三象限角，tanα+tanβ=4，tanαtanβ=2+1，则sin(α+β)=.【答案】-22 3【分析】法一：根据两角和与差的正切公式得tanα+β=-22，再缩小α+β的范围，最后结合同角的平方和关系即可得到答案；法二：利用弦化切的方法即可得到答案.【详解】法一：由题意得tanα+β=tanα+tanβ1-tanαtanβ=41-2+1=-22，因为α∈2kπ,2kπ+π2,β∈2mπ+π,2mπ+3π2，k,m∈Z，则α+β∈2m+2kπ+π,2m+2kπ+2π，k,m∈Z，又因为tanα+β=-22<0，则α+β∈2m+2kπ+3π2,2m+2kπ+2π，k,m∈Z，则sinα+β<0，则sinα+βcosα+β=-22，联立sin2α+β+cos2α+β=1，解得sinα+β=-223.法二：因为α为第一象限角，β为第三象限角，则cosα>0,cosβ<0,cosα=cosαsin2α+cos2α=11+tan2α，cosβ=cosβsin2β+cos2β=-11+tan2β，则sin(α+β)=sinαcosβ+cosαsinβ=cosαcosβ(tanα+tanβ)=4cosαcosβ=-41+tan2α1+tan2β=-4(tanα+tanβ)2+(tanαtanβ-1)2=-442+2=-223故答案为：-22 3.10(全国甲卷数学(文))函数f x =sin x-3cos x在0,π上的最大值是．【答案】2【分析】结合辅助角公式化简成正弦型函数，再求给定区间最值即可.【详解】f x =sin x -3cos x =2sin x -π3 ，当x ∈0,π 时，x -π3∈-π3,2π3，当x -π3=π2时，即x =5π6时，f x max =2.故答案为：2一、单选题1(2024·宁夏石嘴山·三模)在平面直角坐标系中，角θ的顶点与原点重合，始边与x 轴的非负半轴重合，终边经过点P 1,2 ，则7cos 2θ-2sin2θ=()A.-15B.15C.-2D.2【答案】A【分析】由题意可知：tan θ=2，根据倍角公式结合齐次化问题分析求解.【详解】由题意可知：tan θ=2，所以7cos 2θ-2sin2θ=7cos 2θ-4sin θcos θsin 2θ+cos 2θ=7-4tan θtan 2θ+1=7-4×222+1=-15.故选：A .2(2024·广东茂名·一模)已知cos α+π =-2sin α，则sin 2α-3cos α+π2cos αcos2α+1=()A.-1B.-25C.45D.78【答案】D【分析】根据给定条件，求出tan α，再结合诱导公式及二倍角的余弦公式，利用正余弦齐次式法计算得解.【详解】由cos α+π =-2sin α，得cos α=2sin α，则tan α=12，所以sin 2α-3cos α+π2 cos αcos2α+1=sin 2α+3sin αcos α2cos 2α=12tan 2α+32tan α=18+34=78.故选：D3(2024·河北保定·二模)函数f (x )=1-e x1+e xcos2x 的部分图象大致为()A. B.C. D.【答案】A【分析】根据函数的奇偶性判断即可.【详解】设g x =1-e x1+e x，则g-x=1-e-x1+e-x=e x-11+e x=-g x ，所以g x 为奇函数，设h x =cos2x，可知h x 为偶函数，所以f x =1-e x1+e xcos2x为奇函数，则B，C错误，易知f0 =0，所以A正确，D错误．故选：A.4(2024·山东济宁·三模)已知函数f(x)=(3sin x+cos x)cos x-12，若f(x)在区间-π4,m上的值域为-3 2,1，则实数m的取值范围是()A.π6,π2B.π6,π2C.π6,7π12D.π6,7π12【答案】D【分析】利用二倍角公式、辅助角公式化简函数f(x)，再借助正弦函数的图象与性质求解即得.【详解】依题意，函数f(x)=3sin x cos x+cos2x-12=32sin2x+12cos2x=sin2x+π6，当x∈-π4,m时，2x+π6∈-π3,2m+π6，显然sin-π3=sin4π3=-32,sinπ2=1，且正弦函数y=sin x在π2,4π3上单调递减，由f(x)在区间-π4,m上的值域为-32,1，得π2≤2m+π6≤4π3，解得π6≤m≤7π12，所以实数m的取值范围是π6,7π12.故选：D5(2024·江西景德镇·三模)函数f x =cosωx x∈R在0,π内恰有两个对称中心，fπ=1，将函数f x 的图象向右平移π3个单位得到函数g x 的图象.若fα +gα =35，则cos4α+π3=()A.725B.1625C.-925D.-1925【答案】A【分析】根据y轴右边第二个对称中心在0,π内，第三个对称中心不在0,π内可求得32≤ω<52，结合fπ=1可得ω=2，再利用平移变换求出g x ，根据三角变换化简fα +gα =35可得sin2α+π6=35，然后由二倍角公式可解.【详解】由x∈0,π得ωx∈0,ωπ，因为函数f x 在0,π内恰有两个对称中心，所以3π2≤ωπ5π2>ωπ，解得32≤ω<52，又fπ=cosωπ=1，所以ωπ=kπ,k∈Z，即ω=k,k∈Z，所以ω=2，将函数f x 的图象向右平移π3个单位得到函数y=cos2x-π3=cos2x-2π3，即g x =cos2x-2π3，因为fα +gα =cos2α+cos2α-2π3=32sin2α+12cos2α=sin2α+π6=35，所以cos4α+π3=1-2sin22α+π6=1-2×35 2=725.故选：A6(2024·安徽马鞍山·三模)已知函数f(x)=sin2ωx+cos2ωx(ω>1)的一个零点是π2，且f(x)在-π6,π16上单调，则ω=()A.54B.74C.94D.114【答案】B【分析】整理可得f(x)=2sin2ωx+π4，以2ωx+π4为整体，根据单调性分析可得1<ω≤2，再结合零点分析求解.【详解】因为f(x)=sin2ωx+cos2ωx=2sin2ωx+π4，x∈-π6,π16，且ω>1时，可得2ωx+π4∈-π3ω+π4,π8ω+π4，且-π3ω+π4<0<π8ω+π4，若f(x)在-π6,π16上单调，则-π3ω+π4≥-π2π8ω+π4≤π2，解得1<ω≤2，又因为f(x)的一个零点是π2，则πω+π4=kπ,k∈Z，解得ω=k-14,k∈Z，所以k=2,ω=7 4 .故选：B.7(2024·山东临沂·二模)已知函数f x =sin2x+φϕ <π2图象的一个对称中心为π6,0，则()A.f x 在区间-π8,π3上单调递增B.x=5π6是f x 图象的一条对称轴C.f x 在-π6,π4上的值域为-1,32D.将f x 图象上的所有点向左平移5π12个长度单位后，得到的函数图象关于y轴对称【答案】D【分析】借助整体代入法结合正弦函数的性质可得A、B；结合正弦函数最值可得C；得到平移后的函数解析式后借助诱导公式即可得D.【详解】由题意可得2×π6+φ=kπk∈Z，解得φ=-π3+kπk∈Z，又ϕ <π2，故φ=-π3，即f x =sin2x-π3；对A ：当x ∈-π8,π3 时，2x -π3∈-7π12,π3，由函数y =sin x 在-7π12,π3上不为单调递增，故f x 在区间-π8,π3上不为单调递增，故A 错误；对B ：当x =5π6时，2x -π3=4π3，由x =4π3不是函数y =sin x 的对称轴，故x =5π6不是f x 图象的对称轴，故B 错误；对C ：当x ∈-π6,π4 时，2x -π3∈-2π3,π6，则f x ∈-1,12，故C 错误；对D ：将f x 图象上的所有点向左平移5π12个长度单位后，可得y =sin 2x +2×5π12-π3 =sin 2x +π2=cos2x ，该函数关于y 轴对称，故D 正确.故选：D .8(2024·广东广州·二模)已知函数f (x )=2sin (ωx +φ)ω>0,|φ|<π2的部分图象如图所示，若将函数f (x )的图象向右平移θ(θ>0)个单位后所得曲线关于y 轴对称，则θ的最小值为()A.π8B.π4C.3π8D.π2【答案】A【分析】根据给定的图象特征，结合五点法作图列式求出ω和φ，再根据图象的平移变换，以及图象的对称性即可得解.【详解】由f π4=1，得sin π4ω+φ =22，又点π4,1 及附近点从左到右是上升的，则π4ω+φ=π4+2k π,k ∈Z ，由f 5π8 =0，点5π8,0 及附近点从左到右是下降的，且上升、下降的两段图象相邻，得5π8ω+φ=π+2k π,k ∈Z ，联立解得ω=2，φ=-π4+2k π,k ∈Z ，而|φ|<π2，于是φ=-π4，f (x )=2sin 2x -π4，若将函数f (x )的图像向右平移θ(θ>0)个单位后，得到y =sin 2x -2θ-π4，则-2θ-π4=π2-k π,k ∈Z ，而θ>0，因此θ=-3π8+k π2,k ∈N ，所以当k =1时，θ取得最小值为π8.故选：A9(2024·四川雅安·三模)已知函数f x =sin ωx +3cos ωx (ω>0)，则下列说法中正确的个数是()①当ω=2时，函数y =f x -2log πx 有且只有一个零点；②当ω=2时，函数y =f x +φ 为奇函数，则正数φ的最小值为π3；③若函数y =f x 在0,π3 上单调递增，则ω的最小值为12；④若函数y =f x 在0,π 上恰有两个极值点，则ω的取值范围为136,256.A.1 B.2C.3D.4【答案】B【分析】利用辅助角公式化简函数，由图象分析判断①；由正弦函数的性质判断②③；由极大值的意义结合正弦函数的性质判断④.【详解】依题意，ω>0，函数f (x )=212sin ωx +32cos ωx =2sin ωx +π3，对于①：f (x )=2sin 2x +π3，令y =f x -2log πx =0，即f x =2log πx ，作出函数y =f (x )和函数y =2log πx 的图象，如图，观察图象知，两个函数在0,7π12 上只有一个零点，f 13π12 =2sin 5π2=2，当x =13π12时，y =2log π13π12=2log π1312+2log ππ=2+2log π1312>2，当x >13π12时，2log πx >2≥f (x )，因此函数y =f x 与函数y =2log πx 的图象有且只有一个交点，①正确；对于②：f (x +φ)=2sin 2x +2φ+π3 为奇函数，则2φ+π3=k π,k ∈Z ，φ=-π6+k π2,k ∈Z ，即正数φ的最小值为π3，②正确；对于③：当x ∈0,π3 时，ωx +π3∈π3,π(ω+1)3，由y =f x 在0,π3 上单调递增，得π(ω+1)3≤π2ω>0，解得0<ω≤12，正数ω有最大值12，③错误；对于④：当x ∈(0,π)时，ωx +π3∈π3,ωπ+π3，而y =f x 在(0,π)上恰有两个极值点，由正弦函数的性质得3π2<ωπ+π3≤5π2，解得76<ω≤136，因此ω的取值范围是76,136，④错误.综上，共2个正确，故选：B .10(2024·河北保定·二模)已知tan α=3cos αsin α+11，则cos2α=()A.-78B.78C.79D.-79【答案】B【分析】利用切化弦和同角三角函数的关系，解出sin α，再结合二倍角公式即可求解.【详解】因为sin αcos α=3cos αsin α+11，所以4sin 2α+11sin α-3=0，解得sin α=14或sin α=-3(舍去)，所以cos2α=1-2sin 2α=78．故选：B .11(2024·河北衡水·三模)已知sin (3α-β)=m sin (α-β)，tan (2α-β)=n tan α，则m ，n 的关系为()A.m =2nB.n =m +1mC.n =m m -1D.n =m +1m -1【答案】D【分析】利用和差角的正弦公式化简，结合已知列出方程即可求解.【详解】依题意，sin (3α-β)=sin [(2α-β)+α]=sin (2α-β)cos α+cos (2α-β)sin α，sin (α-β)=sin [(2α-β)-α]=sin (2α-β)cos α-cos (2α-β)sin α，则sin (2α-β)cos α+cos (2α-β)sin α=m sin (2α-β)cos α-m cos (2α-β)sin α，即sin (2α-β)cos αcos (2α-β)sin α=m +1m -1，即tan (2α-β)tan α=m +1m -1=n .故选：D12(2024·辽宁沈阳·三模)已知tan α2=2，则sin 2α2+sin α的值是()A.25B.45C.65D.85【答案】D【分析】利用二倍角公式和同角之间的转化，进行求解判断选项【详解】当tan α2=2，则sin 2α2+sin α=sin 2α2+2sin α2cos α2sin 2α2+cos 2α2=tan 2α2+2tan α2tan 2α2+1=22+2×222+1=85故选：D13(2024·贵州黔东南·二模)已知0<α<β<π，且sin α+β =2cos α+β ，sin αsin β-3cos αcos β=0，则tan α-β =()A.-1 B.-32C.-12D.12【答案】C【分析】找出tan α和tan β的关系，求出tan α和tan β即可求解.【详解】∵sin αsin β-3cos αcos β=0，∴sin αsin β=3cos αcos β，∴tan αtan β=3①，∵sin α+β =2cos α+β ，∴tan α+β =2⇒tan α+tan β1-tan αtan β=2⇒tan α+tan β1-3=2，∴tan α+tan β=-4②，由①②解得tan α=-1tan β=-3或tan α=-3tan β=-1 ，∵0<α<β<π，∴tan α<tan β，∴tan α=-3tan β=-1 ，∴tan α-β =tan α-tan β1+tan αtan β=-12.故选：C .二、多选题14(2024·河北张家口·三模)已知函数f (x )=23cos 2x +2sin x cos x ，则下列说法正确的是()A.函数f (x )的一个周期为2πB.函数f (x )的图象关于点π3,0 对称C.将函数f (x )的图象向右平移φ(φ>0)个单位长度，得到函数g (x )的图象，若函数g (x )为偶函数，则φ的最小值为5π12D.若f 12α-5π24 -3=12，其中α为锐角，则sin α-cos α的值为6-308【答案】ACD【分析】利用三角恒等变换公式化简，由周期公式可判断A ；代入验证可判断B ；根据平移变化求g (x )，由奇偶性可求出φ，可判断C ；根据已知化简可得sin α-π12 =14，将目标式化为2sin α-π12 -π6 ，由和差角公式求解可判断D .【详解】对于A ，因为f (x )=31+cos2x +sin2x =2sin 2x +π3+3，所以f (x )的最小值周期T =2π2=π，所以2π是函数f (x )的一个周期，A 正确；对于B ，因为f π3 =2sin 2×π3+π3 +3=3，所以，点π3,0 不是函数f (x )的对称中心，B 错误；对于C ，由题知，g x =f (x -φ)=2sin 2(x -φ)+π3 +3=2sin 2x +π3-2φ +3，若函数g (x )为偶函数，则π3-2φ=π2+k π,k ∈Z ，得φ=-π12-k π2,k ∈Z ，因为φ>0，所以φ的最小值为5π12，C 正确；对于D ，若f 12α-5π24-3=2sin 212α-5π24 +π3 =2sin α-π12 =12，则sin α-π12 =14，因为α为锐角，-π12<α-π12<5π12，所以cos α-π12 =154，所以sin α-cos α=2sin α-π4 =2sin α-π12 -π6=232sin α-π12 -12cos α-π12=232×14-12×154=6-308，D 正确.故选：ACD 15(2024·辽宁鞍山·模拟预测)已知函数f x =sin x ⋅cos x ，则()A.f x 是奇函数B.f x 的最小正周期为2πC.f x 的最小值为-12D.f x 在0,π2上单调递增【答案】AC【分析】首先化简函数f x =12sin2x ，再根据函数的性质判断各选项.【详解】f x =sin x ⋅cos x =12sin2x ，函数的定义域为R ，对A ，f -x =-12sin2x =-f x ，所以函数f x 是奇函数，故A 正确；对B ，函数f x 的最小正周期为2π2=π，故B 错误；对C ，函数f x 的最小值为-12，故C 正确；对D ，x ∈0,π2 ，2x ∈0,π ，函数f x 不单调，f x 在0,π4 上单调递增，在π4,π2上单调递减，故D 错误.故选：AC16(2024·安徽·三模)已知函数f x =sin x -3cos x ，则()A.f x 是偶函数B.f x 的最小正周期是πC.f x 的值域为-3,2D.f x 在-π,-π2上单调递增【答案】AC【分析】对于A ，直接用偶函数的定义即可验证；对于B ，直接说明f 0 ≠f π 即可否定；对于C ，先证明-3≤f x ≤2，再说明对-3≤u ≤2总有f x =u 有解即可验证；对于D ，直接说明f -5π6>f -2π3 即可否定.【详解】对于A ，由于f x 的定义域为R ，且f -x =sin -x -3cos -x =-sin x -3cos x =sin x -3cos x =f x ，故f x 是偶函数，A 正确；对于B ，由于f 0 =sin0 -3cos0=-3，f π =sinπ -3cosπ=3，故f 0 ≠f π ，这说明π不是f x 的周期，B 错误；对于C ，由于f x =sin x -3cos x ≤sin x +3cos x =sin x +3cos x 2≤sin x +3cos x 2+3sin x -cos x 2=sin 2x +3cos 2x +23sin x cos x +3sin 2x +cos 2x -23sin x cos x =4sin 2x +4cos 2x =4=2，且f x =sin x -3cos x ≥-3cos x ≥-3，故-3≤f x ≤2.而对-3≤u ≤2，有f 0 =-3≤u ，f 5π6 =2≥u ，故由零点存在定理知一定存在x ∈0,5π6使得f x =u .所以f x 的值域为-3,2 ，C 正确；对于D ，由于-π<-5π6<-2π3<-π2，f -5π6 =2>3=f -2π3 ，故f x 在-π,-π2上并不是单调递增的，D 错误.故选：AC .17(2024·山西太原·模拟预测)已知函数f x =sin 2x +φ 0<φ<π2 的图象关于直线x =π12对称，且h x =sin2x -f x ，则()A.φ=π12B.h x 的图象关于点π6,0中心对称C.f x 与h x 的图象关于直线x =π4对称 D.h x 在区间π6,5π12内单调递增【答案】BCD【分析】根据正弦函数的对称性求解φ判断A ，先求出h x =sin 2x -π3，然后利用正弦函数的对称性求解判断B ，根据对称函数的性质判断C ，结合正弦函数的单调性代入验证判断D .【详解】由题意得2×π12+φ=π2+k π，k ∈Z ，解得φ=π3+k π，k ∈Z ，又因为0<φ<π2，所以φ=π3，A 错误；由φ=π3可知f x =sin 2x +π3，则h x =sin2x -sin 2x +π3 =12sin2x -32cos2x =sin 2x -π3，令2x -π3=k π，k ∈Z ，解得x =π6+k π2，k ∈Z ，令k =0，得x =π6，所以点π6,0 是曲线y =h x 的对称中心，B 正确；因为f π2-x =sin 2π2-x +π3 =sin 4π3-2x =sin 2x -π3=h x ，所以f x 与h x 的图象关于直线x =π4对称，C 正确；当x ∈π6,5π12 时，2x -π3∈0,π2 ，故h x 在区间π6,5π12内单调递增，D 正确.故选：BCD 18(2024·浙江金华·三模)已知函数f x =sin2ωx cos φ+cos2ωx sin φω>0,0<φ<π2的部分图象如图所示，则()A.φ=π6B.ω=2C.f x +π6为偶函数 D.f x 在区间0,π2的最小值为-12【答案】ACD【分析】先由正弦展开式，五点法结合图象求出f x =sin 2x +π6，可得A 正确，B 错误；由诱导公式可得C 正确；整体代入由正弦函数的值域可得D 正确.【详解】由题意得f x =sin 2ω+φ ，由图象可得f 0 =12⇒sin φ=12，又0<φ<π2，所以φ=π6，由五点法可得ω×4π3+π6=3π2⇒ω=1，所以f x =sin 2x +π6 .A ：由以上解析可得φ=π6，故A 正确；B ：由以上解析可得ω=1，故B 错误；C ：f x +π6 =sin 2x +π6 +π6=cos2x ，故C 正确；D ：当x ∈0,π2 ⇒2x +π6∈π6,7π6 时，sin 2x +π6 ∈-12,1，所以最小值为-12，故D 正确；故选：ACD .19(2024·浙江温州·二模)已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，P -3,4 为其终边上一点，若角β的终边与角2α的终边关于直线y =-x 对称，则()A.cos π+α =35B.β=2k π+π2+2αk ∈Z C.tan β=724D.角β的终边在第一象限【答案】ACD【分析】根据三角函数的定义，可求角α的三角函数，结合诱导公式判断A 的真假；利用二倍角公式，求出2α的三角函数值，结合三角函数的概念指出角2α的终边与单位圆的交点，由对称性确定角β终边与单位圆交点，从而判断BCD 的真假.【详解】因为角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边经过点P -3,4 ，所以：OP =5，所以sin α=45，cos α=-35，所以cos π+α =-cos α=35，故A 对；又sin2α=2sin α⋅cos α=2×45×-35 =-2425，cos2α=cos 2α-sin 2α=-35 2-45 2=-725，所以2α的终边与单位圆的交点坐标为：-725,-2425 ，因为角β的终边与角2α的终边关于直线y =-x 对称，所以角β的终边与单位圆的交点为2425,725，所以tan β=724，且β的终边在第一象限，故CD 正确；又因为终边在直线y =-x 的角为：k π-π4,k ∈Z ，角2α的终边与角β的终边关于y =-x 对称，所以2α+β2=k π-π4⇒β=2k π-π2-2αk ∈Z ，故B 错误.故选：ACD20(2024·广东佛山·二模)已知函数f x =sin x +cos2x 与g x =sin2x +cos x ，记h x =λf x +μg x ，其中λ，μ∈R 且λ2+μ2≠0．下列说法正确的是()A.h x 一定为周期函数B.若λ⋅μ>0，则h x 在0,π2上总有零点C.h x 可能为偶函数 D.h x 在区间0,2π 上的图象过3个定点【答案】ABD【分析】对于A ：计算h x +2π ，化简即可；对于B ：求出h x ，然后计算h 0 h π2的正负即可；对于C ：计算h x ,h -x 是否恒相等即可；对于D ：令f x =0g x =0，求解x 即可.【详解】对于A ，∀x ∈R ，h x +2π =λf x +2π +μg x +2π =λf x +μg x =h x ，A 正确；对于B ，h x =λcos x -2sin2x +μ2cos2x -sin x ，则h 0 =λ+2μ，h π2=-3μ，因为λμ>0，即λ，μ同号，所以h 0 h π2<0，由零点存在定理知h x 在0,π2上总有零点，故B 正确；对于C ，h x =λsin x +λcos2x +μsin2x +μcos x ，h -x =-λsin x +λcos2x -μsin2x +μcos x ，由h x =h -x 得2λsin x +2μsin2x =2λsin x +2μ⋅2sin x cos x =2sin x λ+2μcos x =0对x ∈R 恒成立，则λ=μ=0与题意不符，故C 错误；对于D ，令f x =0g x =0 ，则sin x +cos2x =1-2sin 2x +sin x =-sin x -1 2sin x +1 =0sin2x +cos x =cos x 2sin x +1 =0 ⇒sin x =1或sin x =-12cos x =0或sin x =-12，即x ∈-π6+2k π,π2+2k π,7π6+2k π ，k ∈Z ，故所有定点坐标为-π6+2k π,0 ，π2+2k π,0 ，7π6+2k π,0 ，k ∈Z ，又因为x ∈0,2π ，所以函数h x 的图象过定点π2,0 ，7π6,0 ，11π6,0 ，故D 正确；故选：ABD ．21(2024·湖南·二模)已知函数f x =12cos 2x -π3 ，把y =f x 的图象向右平移π3个单位长度，得到函数y =g x 的图象，以下说法正确的是()A.x =π6是y =f x 图象的一条对称轴B.f x 的单调递减区间为k π+π6,k π+2π3k ∈Z C.y =g x 的图象关于原点对称D.f x +g x 的最大值为12【答案】ABD【分析】根据题意，求得g x =-12cos2x 的图象，结合三角函数的图象与性质，以及两角差的正弦公式，逐项判定，即可求解.【详解】将函数f x =12cos 2x -π3 的图象向右平移π3个单位长度，得到函数y =g x =12cos 2x -π =-12cos2x 的图象，对于A 中，令x =π6，求得f x =12，即为函数y =f x 最大值，所以直线x =π6是函数f x 图象的一条对称轴，所以A 正确；对于B 中，令2k π≤2x -π3≤2k π+π,k ∈Z ，解得k π+π6≤x ≤k π+2π3,k ∈Z ，可得f x 的单调减区间为k π+π6,k π+2π3,k ∈Z ，所以B 正确.对于C 中，由于g x =-12cos2x 是偶函数，可得函数g x 的图象关于y 轴对称，所以C 错误.对于D 中，由f x +g x =12cos 2x -π3 +-12cos2x =1212cos2x +32sin2x -12cos2x =34sin2x -14cos2x =12sin 2x -π6 ≤12，即f x +g x 的最大值为12，所以D 正确.故选：ABD .22(2024·广东江门·一模)已知函数f (x )=sin 2ωx +π3 +sin 2ωx -π3+23cos 2ωx -3(ω>0)，则下列结论正确的是()A.若f x 相邻两条对称轴的距离为π2，则ω=2B.当ω=1，x ∈0,π2时，f x 的值域为-3,2 C.当ω=1时，f x 的图象向左平移π6个单位长度得到函数解析式为y =2cos 2x +π6D.若f x 在区间0,π6上有且仅有两个零点，则5≤ω<8【答案】BCD【分析】根据三角恒等变换化简f x =2sin 2ωx +π3，进而根据周期可判断A ，根据整体法求解函数的值域判断B ，根据函数图象的平移可判断C ，根据零点个数确定不等式满足的条件可判断D .【详解】f (x )=sin 2ωx +π3 +sin 2ωx -π3+23cos 2ωx -3=sin2ωx cos π3+cos2ωx sin π3+sin2ωx cos π3-cos2ωx sin π3+3cos2ωx=sin2ωx +3cos2ωx =2sin 2ωx +π3，对于A ，若f x 相邻两条对称轴的距离为π2，则T =2×π2=π=2π2ω,故ω=1，A 错误，对于B ，当ω=1，f x =2sin 2x +π3 ，当x ∈0,π2 时，2x +π3∈π3,4π3，则f x 的值域为-3,2 ，B 正确，对于C ，当ω=1，f x =2sin 2x +π3，f x 的图象向左平移π6个单位长度得到函数解析式为f x +π6 =2sin 2x +π6 +π3 =2sin 2x +2π3 =2cos 2x +π6，C 正确，对于D ，当x ∈0,π6 时，2ωx +π3∈π3,2ωπ6+π3，若f x 在区间0,π6 上有且仅有两个零点，则2π≤2ωπ6+π3<3π，解得5≤ω<8，故D 正确，故选：BCD 三、填空题23(2024·北京·三模)已知函数f (x )=sin x cos ωx ,x ∈R ．①若ω=1，则f (x )的最小正周期是；，②若ω=2，则f (x )的值域是．【答案】π[-1,1]【分析】把ω=1代入，t 明智二倍角的正弦，结合正弦函数的周期求出f (x )的最小正周期；把ω=2代入，利用二倍角的余弦公式，借助换元法，利用导数求出f (x )的值域.【详解】当ω=1时，f (x )=sin x cos x =12sin2x ，函数f (x )的最小正周期为2π2=π；当ω=2时，f (x )=sin x cos2x =sin x (1-2sin 2x )，令sin x =t ∈[-1,1]，g (t )=t (1-2t 2)=-2t 3+t ，求导得g (t )=-6t 2+1，当-1≤t <-66或66<t ≤1时，g (t )<0，当-66<t <66时，g (t )>0，函数g (t )在-1,-66 ，66,1 上单调递减，在-66,66上单调递增，g (-1)=1,g 66 =69，g (1)=-1,g -66 =-69，所以g (t )min =-1,g (t )max =1，f (x )的值域是[-1,1].故答案为：π；[-1,1]24(2024·北京·模拟预测)已知函数f (x )=sin ωx -2cos ωx (ω>0)，且f α+x =f α-x .若两个不等的实数x 1,x 2满足f x 1 f x 2 =5且x 1-x 2 min =π，则sin4α=.【答案】-45/-0.8【分析】利用辅助角公式化简f (x )的解析式，再由题意可得函数关于x =α对称，且最小正周期T =π，即可求出ω的值，从而得到2α=φ+π2+k π,k ∈Z ，再由二倍角公式及同角三角函数的基本关系计算可得．【详解】因为f (x )=sin ωx -2cos ωx =5sin ωx -φ ，其中tan φ=2，由f α+x =f α-x ，可得f x 关于x =α对称，又两个不等的实数x 1,x 2满足f x 1 f x 2 =5且x 1-x 2 min =π，所以f x 的最小正周期T =π，又ω>0，所以2πω=π，解得ω=2，所以f x =5sin 2x -φ ，所以2α-φ=π2+k π,k ∈Z ，则2α=φ+π2+k π,k ∈Z ，所以sin4α=sin2φ+π2+k π =sin 2φ+π+2k π =-sin2φ=-2sin φcos φsin 2φ+cos 2φ=-2tan φtan 2φ+1=-2×222+1=-45.故答案为：-4525(2024·湖北荆州·三模)设0<α<β<π2，tan α=m tan β，cos α-β =35，若满足条件的α与β存在且唯一，则m =，tan αtan β=.【答案】191【分析】由tan α=m tan β得到sin αcos β=m cos αsin β，再结合cos α-β =35，利用sin α-β =-45，得到cos αsin β=-45m -1 ，sin αcos β=-4m5m -1 ，从而sin α+β =-4m +1 5m -1，再由满足条件的α与β存在且唯一，得到α+β唯一，从而sin α+β =-4m +15m -1=1，求得m 即可.【详解】解：由tan α=m tan β，得sin αcos α=m sin βcos β，即sin αcos β=m cos αsin β，因为0<α<β<π2，tan α=m tan β，所以-π2<α-β<0，0<m <1，又cos α-β =35，所以sin α-β <0，从而sin α-β =sin αcos β-cos αsin β=m -1 cos αsin β=-45，所以cos αsin β=-45m -1，所以sin αcos β=m cos αsin β=-4m5m -1，所以sin α+β =sin αcos β+cos αsin β=-4m +15m -1，因为α,β∈0,π2，所以α+β∈0,π ，因为满足条件的α与β存在且唯一，所以α+β唯一，所以sin α+β =-4m +1 5m -1=1，所以m =19，经检验符合题意，所以tan α=19tan β，则tan α-β =-43=tan α-tan β1+tan αtan β=tan α-9tan α1+9tan 2α，解得tan α=13，所以tan αtan β=9tan 2α=1.故答案为：19，1【点睛】关键点点睛：关键是结合已知得出sin α+β =-4m +15m -1 =1，求出m ，由此即可顺利得解.。

全国统一高考数学试卷理科参考答案与试题解析

全国统一高考数学试卷（理科）参考答案与试题解析一、选择题（共15小题，110每小题4分,1115每小题5分，满分65分）1．（4分）设集合M={x|0≤x＜2}，集合N={x|x2﹣2x﹣3＜0}，集合M∩N=（）A ．{x|0≤x＜1}B．{x|0≤x＜2}C．{x|0≤x≤1}D．{x|0≤x≤2}考点：交集及其运算．分析：解出集合N中二次不等式，再求交集．解答：解：N={x|x2﹣2x﹣3＜0}={x|﹣1＜x＜3}，∴M∩N={x|0≤x＜2}，故选B点评：本题考查二次不等式的解集和集合的交集问题，注意等号，较简单．2．（4分）如果直线ax+2y+2=0与直线3x﹣y﹣2=0平行，那么实数a等于（）A ．﹣6B．﹣3C．D．考点：直线的一般式方程与直线的平行关系．专题：计算题．分析：根据它们的斜率相等，可得=3，解方程求a的值．解答：解：∵直线ax+2y+2=0与直线3x﹣y﹣2=0平行，∴它们的斜率相等，∴=3，∴a=﹣6．故选A．点评：本题考查两直线平行的性质，两直线平行，斜率相等．3．（4分）函数y=tan （）在一个周期内的图象是（）A ．B．C．D．考点：正切函数的图象．专题：综合题．分析：先令tan （）=0求得函数的图象的中心，排除C，D；再根据函数y=tan （）的最小正周期为2π，排除B．解答：解：令tan （）=0，解得x=kπ+，可知函数y=tan （）与x 轴的一个交点不是，排除C，D∵y=tan （）的周期T==2π，故排除B故选A点评：本题主要考查了正切函数的图象．要熟练掌握正切函数的周期，单调性，对称中心等性质．4．（4分）已知三棱锥P﹣ABC的三个侧面与底面全等，且AB=AC=，BC=2．则二面角P﹣BC﹣A的大小为（）A ．B．C．D．考点：平面与平面之间的位置关系；与二面角有关的立体几何综合题．专题：计算题．分析：要求二面角P﹣BC﹣A的大小，我们关键是要找出二面角P﹣BC﹣A的大小的平面角，将空间问题转化为平面问题，然后再分析二面角P﹣BC﹣A的大小的平面角所在的三角形的其它边与角的关系，解三角形进行求解．解答：解：如图所示，由三棱锥的三个侧面与底面全等，且AB=AC=，得PB=PC=，PA=BC=2，取BC的中点E，连接AE，PE，则∠AEP即为所求二面角的平面角．且AE=EP=，∵AP2=AE2+PE2，∴∠AEP=，故选C．点评：求二面角的大小，一般先作出二面角的平面角．此题是利用二面角的平面角的定义作出∠AEP为二面角P﹣BC﹣A的平面角，通过解∠AEP所在的三角形求得∠AEP．其解题过程为：作∠AEP→证∠AEP是二面角的平面角→计算∠AEP，简记为“作、证、算”．5．（4分）函数y=sin （）+cos2x的最小正周期是（）A ．B．πC．2πD．4π考点：三角函数的周期性及其求法．分析：先将函数化简为：y=sin（2x+θ），即可得到答案．解答：解：∵f（x）=sin （）+cos2x=cos2x ﹣sin2x+cos2x=（+1）cos2x ﹣sin2x=sin（2x+θ）∴T==π故选B．点评：本题主要考查三角函数的最小正周期的求法．属基础题．6．（4分）满足arccos（1﹣x）≥arccosx的x的取值范围是（）A ．[﹣1，﹣]B．[﹣，0]C．[0，]D．[，1]考点：反三角函数的运用．专题：计算题．分析：应用反函数的运算法则，反函数的定义及性质，求解即可．解答：解：arccos（1﹣x）≥arccosx 化为cos[arccos（1﹣x）]≤cos[arccosx]所以1﹣x≤x，即：x，又x∈[﹣1，1]，所以x的取值范围是[，1]故选D．点评：本题考查反余弦函数的运算法则，反函数的定义域，考查学生计算能力，是中档题．7．（4分）将y=2x的图象____________再作关于直线y=x对称的图象，可得到函数y=log2（x+1）的图象（）A ．先向左平行移动1个单位B．先向右平行移动1个单位C ．先向上平行移动1个单位D．先向下平行移动1个单位考点：反函数；函数的图象与图象变化．分析：本题考查函数图象的平移和互为反函数的函数图象之间的关系两个知识点，作为本题，可以用逐一验证的方法排除不合题意的选项，验证的个数在1到3个，对于本题，这不是最佳选择，建议逆推得到平移后的解析式，这样就可以方便的观察到平移的方向及单位数．解答：解：利用指数式和对数式的互化，由函数y=log2（x+1）解得：x=2y﹣1则函数y=log2（x+1）（x＞﹣1）的反函数为y=2x﹣1（x∈R）即函数y=2x平移后的函数为y=2x﹣1，易见，只需将其向下平移1个单位即可．故选D点评：本题采用先逆推获取平移后的解析式的方法，得到解析式后平移的方向和单位便一目了然，简便易行，值得尝试．8．（4分）长方体的一个顶点上三条棱长为3、4、5，且它的八个顶点都在一个球面上，这个球的表面积是（）A ．20πB．25πC．50πD．200π考点：球的体积和表面积．专题：计算题．分析：设出球的半径，由于直径即是长方体的体对角线，由此关系求出球的半径，即可求出球的表面积．解答：解：设球的半径为R，由题意，球的直径即为长方体的体对角线，则（2R）2=32+42+52=50，∴R=．∴S球=4π×R2=50π．故选C点评：本题考查球的表面积，球的内接体，考查计算能力，是基础题．9．（4分）曲线的参数方程是（t是参数，t≠0），它的普通方程是（）A ．（x﹣1）2（y﹣1）=1B．y=C．D．考点：参数方程的概念．专题：计算题．分析：由题意知x=1﹣，可得x﹣1=﹣，将方程两边平方，然后与y﹣1=﹣t2，相乘消去t即可求解．解答：解：∵曲线的参数方程是（t是参数，t≠0），∴，∴将两个方程相乘可得，（x﹣1）2（1﹣y）=1，∴y=，故选B．点评：此题考查参数方程与普通方程的区别和联系，两者要会互相转化，根据实际情况选择不同的方程进行求解，这也是每年高考必考的热点问题．10．（4分）函数y=cos2x﹣3cosx+2的最小值为（）A ．2B．0C．D．6考点：函数的值域；余弦函数的定义域和值域．专题：计算题．分析：先进行配方找出对称轴，而﹣1≤cosx≤1，利用对称轴与区间的位置关系求出最小值．解答：解：y=cos2x﹣3cosx+2=（cosx﹣）2﹣∵﹣1≤cosx≤1∴当cosx=1时ymin=0，故选B点评：本题以三角函数为载体考查二次函数的值域，属于求二次函数的最值问题，属于基本题．11．（5分）椭圆C与椭圆关于直线x+y=0对称，椭圆C的方程是（）A ．B．C．D．考点：直线与圆锥曲线的综合问题．专题：计算题．分析：依题意可知椭圆C关于直线x+y=0对称，长轴和短轴不变，主要椭圆的中心即可．根据原椭圆方程可求得其中心坐标，进而求得其关于直线x+y=0对称点，则椭圆方程可得．解答：解：依题意可知椭圆C关于直线x+y=0对称，长轴和短轴不变，主要椭圆的中心即可．∵椭圆的中心为（3，2）关于直线x+y=0对称的点为（﹣2，﹣3）故椭圆C的方程为故选A．点评：本题主要考查了直线与椭圆的关系及点关于直线对称的问题．属基础题．12．（5分）圆台上、下底面面积分别是π、4π，侧面积是6π，这个圆台的体积是（）A ．πB．2πC．πD．π考点：旋转体（圆柱、圆锥、圆台）．专题：计算题．分析：通过圆台的底面面积，求出上下底面半径，利用侧面积公式求出母线长，然后求出圆台的高，即可求得圆台的体积．解答：解：S1=π，S2=4π，∴r=1，R=2，S=6π=π（r+R）l，∴l=2，∴h=．∴V=π（1+4+2）×=π．故选D点评：本题是基础题，通过底面面积求出半径，转化为求圆台的高，是本题的难点，考查计算能力，常考题．13．（5分）（•碑林区一模）定义在区间（﹣∞，+∞）的奇函数f（x）为增函数；偶函数g（x）在区间[0，+∞）的图象与f（x）的图象重合，设a＞b＞0，给出下列不等式：①f（b）﹣f（﹣a）＞g（a）﹣g（﹣b）；②f（b）﹣f（﹣a）＜g（a）﹣g（﹣b）；③f（a）﹣f（﹣b）＞g（b）﹣g（﹣a）；④f（a）﹣f（﹣b）＜g（b）﹣g（﹣a），其中成立的是（）A ．①与④B．②与③C．①与③D．②与④考点：函数奇偶性的性质．分析：根据f（﹣a）=﹣f（a），f（﹣b）=﹣f（b），g（﹣a）=g（a）=f（a），g（﹣b）=g（b）=f （b），对①②③④进行逐一验证即可得答案．解答：解：由题意知，f（a）＞f（b）＞0又∵f（﹣a）=﹣f（a），f（﹣b）=﹣f（b），g（﹣a）=g（a）=f（a），g（﹣b）=g（b）=f（b）；∴①f（b）﹣f（﹣a）＞g（a）﹣g（﹣b）⇔f（b）+f（a）＞f（a）﹣f（b）⇔f（b）＞﹣f（b），故①对②不对．③f（a）﹣f（﹣b）＞g（b）﹣g（﹣a）⇔f（b）+f（a）＞f（b）﹣f（a）⇔f（a）＞﹣f（a），故③对④不对．故选C．点评：本题主要考查函数奇偶性的应用．14．（5分）不等式组的解集是（）A ．{x|0＜x＜2}B．{x|0＜x＜2.5}C．D．{x|0＜x＜3}考点：其他不等式的解法．专题：压轴题．分析：可以直接去绝对值解不等式，比较复杂；可结合答案用特值法解决．解答：解：取x=2满足不等式，排除A；再取x=2.5，不满足，排除B、D故选C点评：本题考查解绝对值不等式和分式不等式问题，要注意选择题的特点，选择特殊做法解决．15．（5分）四面体的顶点和各棱中点共10个点，在其中取4个不共面的点，则不同的取法共有（）A ．150种B．147种C．144种D．141种考点：排列、组合的实际应用；计数原理的应用．专题：计算题；压轴题．分析：由题意知从10个点中任取4个点有C104种取法，减去不合题意的结果，4点共面的情况有三类，取出的4个点位于四面体的同一个面上；取任一条棱上的3个点及该棱对棱的中点；由中位线构成的平行四边形，用所有的结果减去不合题意的结果即可得答案．解答：解：从10个点中任取4个点有C104种取法，其中4点共面的情况有三类．第一类，取出的4个点位于四面体的同一个面上，有4C64种；第二类，取任一条棱上的3个点及该棱对棱的中点，这4点共面，有6种；第三类，由中位线构成的平行四边形（其两组对边分别平行于四面体相对的两条棱），它的4顶点共面，有3种．以上三类情况不合要求应减掉，∴不同的取法共有C104﹣4C64﹣6﹣3=141种．故选D．点评：本题考查分类计数原理，考查排列组合的实际应用，是一个排列组合同立体几何结合的题目，解题时注意做到不重不漏．二、填空题（共4小题，每小题4分，满分16分）16．（4分）已知的展开式中x3的系数为，常数a的值为4．考点：二项式定理；二项式系数的性质．专题：计算题．分析：利用二项展开式的通项公式求出第r+1项，令x的指数为3求出展开式中x3的系数，列出方程解得．解答：解：的展开式的通项为=令解得r=8∴展开式中x3的系数为∵展开式中x3的系数为∴解得a=4故答案为4点评：本题考查二项展开式的通项公式是解决二项展开式的特定项问题的工具．17．（4分）（•陕西模拟）已知直线的极坐标方程为，则极点到该直线的距离是．考点：简单曲线的极坐标方程；与圆有关的比例线段；不等式的基本性质．专题：计算题；压轴题．分析：先将原极坐标方程中的三角函数式展开后两边同乘以ρ后化成直角坐标方程，再利用直角坐标方程进行求解即得．解答：解：将原极坐标方程，化为：ρsinθ+ρcosθ=1，化成直角坐标方程为：x+y﹣1=0，则极点到该直线的距离是=．故填；．点评：本题考查点的极坐标和直角坐标的互化，利用直角坐标与极坐标间的关系，即利用ρcosθ=x，ρsinθ=y，ρ2=x2+y2，进行代换即得．18．（4分）的值为．考点：角的变换、收缩变换．专题：计算题；压轴题．分析：先将分式中的15°化为7°+8°，利用两角和的余弦、正弦展开，分子、分母分组提取sin7°，cos7°，再用同角三角函数的基本关系式，化简，然后，就会求出tan15°，利用两角差的正切，求解即可．解答：解：=======tan15°=tan（45°﹣30°）===，故答案为：点评：本题考查角的变换，两角和的正弦、余弦，同角三角函数的基本关系式，考查学生运算能力，是中档题．19．（4分）已知m、l是直线，α、β是平面，给出下列命题：①若l垂直于α内两条相交直线，则l⊥α；②若l平行于α，则l平行于α内所有的直线；③若m⊊α，l⊊β且l⊥m，则α⊥β；④若l⊊β且l⊥α，则α⊥β；⑤若m⊊α，l⊊β且α∥β，则l∥m．其中正确命题的序号是①④．考点：空间中直线与直线之间的位置关系；空间中直线与平面之间的位置关系．专题：压轴题．分析：对于①，考虑直线与平面垂直的判定定理，符合定理的条件故正确；对于②，考虑直线与平面平行的性质定理以及直线与平面的位置关系，故错误；对于③考虑α⊥β的判定方法，而条件不满足，故错误；对于④符合面面垂直的判定定理，故正确；对于⑤不符合线线平行的判定，故错误．正确命题的序号是①④解答：解：①，符合定理的条件故正确；②，若l平行于α，则l与α内的直线有两种：平行或异面，故错误；③m⊊α，l⊊β且l⊥m，则α与β可以相交但不垂直；④符合面面垂直的判定定理，故正确；⑤若m⊊α，l⊊β且α∥β，则l∥m或者异面，错误，故正确命题的序号是①④．点评：本题考查立体几何中线线关系中的平行、线面关系中的垂直、面面关系中的垂直的判定方法，要注意对比判定定理的条件和结论，同时要注意性质定理、空间直线与直线、直线与平面、平面与平面的位置关系的应用．三、解答题（共6小题，满分69分）20．（10分）已知复数，．复数，z2ω3在复数平面上所对应的点分别为P，Q．证明△OPQ是等腰直角三角形（其中O为原点）．考点：复数代数形式的混合运算．分析：利用复数三角形式，化简复数，．然后计算复数，z2ω3，计算二者的夹角和模，即可证得结论．解答：解法一：，于是，，=因为OP与OQ的夹角为，所以OP⊥OQ．因为，所以|OP|=|OQ|由此知△OPQ有两边相等且其夹角为直角，故△OPQ为等腰直角三角形．解法二：因为，所以z3=﹣i．因为，所以ω4=﹣1于是由此得OP⊥OQ，|OP|=|OQ|．由此知△OPQ有两边相等且其夹角为直角，故△OPQ为等腰直角三角形．点评：本小题主要考查复数的基本概念、复数的运算以及复数的几何意义等基础知识，考查运算能力和逻辑推理能力，是中档题．21．（11分）已知数列{an}，{bn}都是由正数组成的等比数列，公比分别为p、q，其中p＞q，且p≠1，q≠1．设cn=an+bn，Sn为数列{cn}的前n项和．求．考点：等比数列的通项公式；极限及其运算；数列的求和．专题：计算题．分析：先根据等比数列的通项公式分别求出an和bn，再根据等比数列的求和公式，分别求得Sn和Sn﹣1的表达式，进而可得的表达式，分p＞1和p＜1对其进行求极限．解答：解：，．分两种情况讨论．（Ⅰ）p＞1．∵，====p．（Ⅱ）p＜1．∵0＜q＜p＜1，==点评：本小题主要考查等比数列的概念、数列极限的运算等基础知识，考查逻辑推理能力和运算能力．22．（12分）甲、乙两地相距S千米，汽车从甲地匀速行驶到乙地，速度不得超过c千米/时．已知汽车每小时的运输成本（以元为单位）由可变部分和固定部分组成：可变部分与速度v（千米/时）的平方成正比，比例系数为b；固定部分为a元．（1）把全程运输成本y（元）表示为速度v（千米/时）的函数，并指出这个函数的定义域；（2）为了使全程运输成本最小，汽车应以多大速度行驶？考点：根据实际问题选择函数类型；基本不等式在最值问题中的应用．专题：应用题．分析：（1）全程运输成本有两部分组成，将其分别分别表示出来依题意建立起程运输成本y（元）表示为速度v（千米/时）的函数，由题设条件速度不得超过c千米/时．故定义域为v∈（0，c]．（2）由（1）知，全程运输成本关于速度的函数表达式中出现了积为定值的情形，由于等号成立的条件有可能不成立，故求最值的方法不确定，对对速度的范围进行分类讨论，如等号成立时速度值不超过c，则可以用基本不等式求求出全程运输成本的最小值，若等号成立时速度值大于最高限速v，可以判断出函数在（0，c]上的单调性，用单调性求出全程运输成本的最小值．解答：解：（1）依题意知汽车从甲地匀速行驶到乙地所用时间为，全程运输成本为故所求函数及其定义域为（2）依题意知S，a，b，v都为正数，故有当且仅当，．即时上式中等号成立若，则当时，全程运输成本y最小，若，即a＞bc2，则当v∈（0，c]时，有==因为c﹣v≥0，且a＞bc2，故有a﹣bcv≥a﹣bc2＞0，所以，且仅当v=c时等号成立，也即当v=c时，全程运输成本y最小．综上知，为使全程运输成本y最小，当时行驶速度应为；当时行驶速度应为v=c．点评：本小题主要考查建立函数关系、不等式性质、最大值、最小值等基础知识，考查综合应用所学数学知识、思想和方法解决实际问题的能力．23．（12分）如图，在正方体ABCD﹣A1B1C1D1中，E、F分别是BB1、CD的中点．（1）证明AD⊥D1F；（2）求AE与D1F所成的角．考点：异面直线及其所成的角．专题：计算题；证明题．分析：（1）证明线线垂直可先证线面垂直，欲证AD⊥D1F，可先证AD⊥面DC1，即可证得；（2）先通过平移将两条异面直线平移到同一个起点，取AB的中点G，将D1F平移到A1G，AB与A1G构成的锐角或直角就是异面直线所成的角，利用三角形全等求出此角即可．解答：解：（Ⅰ）∵AC1是正方体，∴AD⊥面DC1．又D1F⊂面DC1，∴AD⊥D1F．（Ⅱ）取AB中点G，连接A1G，FG．因为F是CD的中点，所以GF、AD平行且相等，又A1D1、AD平行且相等，所以GF、A1D1平行且相等，故GFD1A1是平行四边形，A1G∥D1F．设A1G与AE相交于点H，则∠AHA1是AE与D1F所成的角，因为E是BB1的中点，所以Rt△A1AG≌Rt△ABE，∠GA1A=∠GAH，从而∠AHA1=90°，即直线AE与D1F所成角为直角．点评：本小题主要考查异面直线及其所成的角，考查逻辑推理能力和空间想象能力，属于基础题．25．（12分）（•北京模拟）设圆满足：①截y轴所得弦长为2；②被x轴分成两段圆弧，其弧长的比为3：1，在满足条件①、②的所有圆中，求圆心到直线l：x﹣2y=0的距离最小的圆的方程．考点：直线与圆的位置关系．专题：压轴题．分析：圆被x轴分成两段圆弧，其弧长的比为3：1，劣弧所对的圆心角为90°，设圆的圆心为P（a，b），圆P截X轴所得的弦长为，截y轴所得弦长为2；可得圆心轨迹方程，圆心到直线l：x﹣2y=0的距离最小，利用基本不等式，求得圆的方程．解答：解法一：设圆的圆心为P（a，b），半径为r，则点P到x轴，y轴的距离分别为|b|，|a|．由题设知圆P截x轴所得劣弧对的圆心角为90°，知圆P截X轴所得的弦长为，故r2=2b2，又圆P截y轴所得的弦长为2，所以有r2=a2+1．从而得2b2﹣a2=1．又点P（a，b）到直线x﹣2y=0的距离为，所以5d2=|a﹣2b|2=a2+4b2﹣4ab≥a2+4b2﹣2（a2+b2）=2b2﹣a2=1，当且仅当a=b时上式等号成立，此时5d2=1，从而d取得最小值．由此有解此方程组得或由于r2=2b2知．于是，所求圆的方程是（x﹣1）2+（y﹣1）2=2，或（x+1）2+（y+1）2=2．解法二：同解法一，得∴得①将a2=2b2﹣1代入①式，整理得②把它看作b的二次方程，由于方程有实根，故判别式非负，即△=8（5d2﹣1）≥0，得5d2≥1．∴5d2有最小值1，从而d有最小值．将其代入②式得2b2±4b+2=0．解得b=±1．将b=±1代入r2=2b2，得r2=2．由r2=a2+1得a=±1．综上a=±1，b=±1，r2=2．由|a﹣2b|=1知a，b同号．于是，所求圆的方程是（x﹣1）2+（y﹣1）2=2，或（x+1）2+（y+1）2=2．点评：本小题主要考查轨迹的思想，求最小值的方法，考查综合运用知识建立曲线方程的能力．易错的地方，P到x轴，y轴的距离，不能正确利用基本不等式．24．（12分）设二次函数f（x）=ax2+bx+c（a＞0），方程f（x）﹣x=0的两个根x1，x2满足0＜x1＜x2＜．（1）当x∈（0，x1）时，证明x＜f （x）＜x1；（2）设函数f（x）的图象关于直线x=x0对称，证明x0＜．考点：一元二次方程的根的分布与系数的关系；不等式的证明．专题：证明题；压轴题；函数思想；方程思想；作差法．分析：（1）方程f（x）﹣x=0的两个根x1，x2，所以构造函数，当x∈（0，x1）时，利用函数的性质推出x＜f （x），然后作差x1﹣f（x），化简分析出f（x）＜x1，即可．（2）．方程f（x）﹣x=0的两个根x1，x2，函数f（x）的图象，关于直线x=x0对称，利用放缩法推出x0＜；解答：证明：（1）令F（x）=f（x）﹣x．因为x1，x2是方程f（x）﹣x=0的根，所以F（x）=a（x﹣x1）（x﹣x2）．当x∈（0，x1）时，由于x1＜x2，得（x﹣x1）（x﹣x2）＞0，又a＞0，得F（x）=a（x﹣x1）（x﹣x2）＞0，即x＜f（x）．x1﹣f（x）=x1﹣[x+F（x）]=x1﹣x+a（x1﹣x）（x﹣x2）=（x1﹣x）[1+a（x﹣x2）]因为所以x1﹣x＞0，1+a（x﹣x2）=1+ax﹣ax2＞1﹣ax2＞0．得x1﹣f（x）＞0．由此得f（x）＜x1．（2）依题意知因为x1，x2是方程f（x）﹣x=0的根，即x1，x2是方程ax2+（b﹣1）x+c=0的根．∴，因为ax2＜1，所以．点评：本小题主要考查一元二次方程、二次函数和不等式的基础知识，考查综合运用数学知识分析问题和解决问题的能力．高考理科数学试题及答案（考试时间：120分钟试卷满分：150分）一、选择题：本题共12小题，每小题5分，共60分。

历年全国卷高考数学真题汇编(解析版)

全国卷历年高考真题汇编三角1 (2017全国I卷9题)已知曲线G : y cosx , C2: y sin2 n2x —，则下面结论正确的3是()A .把G上各点的横坐标伸长到原来的2倍, 纵坐标不变, 再把得到的曲线向右平移上个单6位长度，得到曲线C2B.把C上各点的横坐标伸长到原来的2倍, 纵坐标不变, 再把得到的曲线向左平移单位长度，得到曲线C2C.把C上各点的横坐标缩短到原来的纵坐标不变, 再把得到的曲线向右平移丄个单6位长度，得到曲线C2D .把G上各点的横坐标缩短到原来的2倍, 纵坐标不变, 再把得到的曲线向左平移单位长度，得到曲线C2【答案】D【解析】C1: y cosx , C2: y sin 2x首先曲线G、C2统一为一三角函数名，可将G：y cosx用诱导公式处理.y cosx cos xsinsin x .横坐标变换需将2 2 21C1上各点横坐标缩短它原来一2ynsin 2x —2注意根据1变成y sin 2x 8 sin23的系数，在右平移需将2提到括号外面，这时"左加右减”原则，“I卷17题)nsin 2 x —4亍平移至n ”到“ x字需加上，即再向左平移n122 (2017全国2的面积为—3sin A(1 )求sin Bsin C ;(2 )若6cos B cosC 1 ,△ABC的内角A , B , C的对边分别为a, b , c，已知△ABC a 3，求△ABC的周长.【解析】本题主要考查三角函数及其变换，正弦定理，余弦定理等基础知识的综合应用(1) •/ △ ABC 面积S2a3sinA.且S ^bcsinA2^bcsin A 3sin A 2严2 A23 2••由正弦定理得 sin A —sin BsinCsin A ,2 2由 sin A 0 得 si n Bsi nC— 2,cosB cosC3•/ ABC n又A 0, n2, a.bc l sin A 由①②得b c——.a b c ———，即△ ABC 周长为———3. （2017 •新课标全国n 卷理 17）17. （12分）2 BABC 的内角A,B,C 的对边分别为a,b,c ,已知sin （A C ） 8si n 2—.2（1）求 cosB⑵若a c 6 , ABC 面积为2,求b.【命题意图】本题考查三角恒等变形，解三角形.【试题分析】在第（I ）中，利用三角形内角和定理可知A C B ,将2B 2 Bsin （A C ） 8sin —转化为角B 的方程，思维方向有两个：①利用降幕公式化简 sin 2—,2 222Q B结合sin B cos B 1求出cosB ；②利用二倍角公式，化简 sinB 8sin 2 ，两边约去2B Bsin ，求得tan，进而求得cosB .在第（n ）中，利用（I ）中结论，禾U 用勾股定理和22面积公式求出a c 、ac ，从而求出b . （I ）【基本解法1】(2)由(1)得 sin Bsin C cos A cos n B Ccos B C sin BsinC cosBcosC二 A 60 , sin A由余弦定理得 2 b 2 c 2cos A -2 bc由正弦定理得-sin B , sin Ac — sin C sin Asin BsinC 8、2 B由题设及A B C , si nB 8si n ，故20，si nB 4(1-cosB )上式两边平方，整理得217cos B-32cosB+15=0【基本解法2】由余弦定理及所以b=2【知识拓展】解三角形问题是高考高频考点，形的内角和定理，正、余弦定理、三角形面积公式等知识解题，解题时要灵活利用三角形的边角关系进行“边转角” “角转边”，另外要注意a c, ac,a 2 c 2三者的关系，这样的题目小而活，备受老师和学生的欢迎. 4 (2017全国卷3理)17.( 12分)ABC 的内角A , B , C 的对边分别为a , b, c ,已知sin A 3cosA 0 , a 2 H , b 2 .(1) 求 c ；(2) 设D 为BC 边上一点，且 ADAC ,求△ ABD 的面积【解析】 (1)由 si nA3 cos An0 得 2sin A —0 ,3即Ank n k Z , 又A0, n ,3冗n ,得A2n二 A -33 •由余弦定理a 2 b 2 c 2 2bc cosA •又T a 2 7, b 2,cosA —代入并整理2/口2得 c 1 25，故 c 4 •解得cosB= 1 (舍去),cosB=^17由题设及ABC,sin B 8sin2-，所以 2B B 2 BB 2sin cos 8sin ，又 sin - 2 2 2 所以 tan B 1, cosB2 415(n)由 cosB=得 sin B174 + 2 B1 tan -_____ 2 + 2 B tan — 2—，故1715 17SABC1acsin B 24 ac 17又 S ABC =2, 则ac17 2.2 2 2b a c(a+c )2 : 2accosB36 22ac(1 口(12cosB)鸟17命题大多放在解答题的第一题，主要利用三角(2) •/ AC 2,BC Z 7, AB 4 ,2 2 2由余弦定理cosC a b— ^7. 2ab 7 ••• AC AD ，即△ ACD 为直角三角形,cosC ，得 CD 7. 贝U AC CD由勾股定理AD 』CD | |AC73.n2 n n n 又 A ，贝V DAB -33 2 6 1n S A ABD AD AB sin §35 （2017全国卷文1） 14已知a10（法一） 0,2,tan又 sin 2 cos 21 ,辽 (cos sincos 42(cos2（法二） cos( 7)21sin coscos —4 2sin cos sin cos・2 2 sin cos 由 0,- 知 - __ — 2 4 4 【答案】 n (0,—),tana,=2U cos(-)=24sin22 sin 2coscos解得sin2、553 10)10 •sin ).又tan2tan22cos — tan1 5 4cos— 0,故 cos49 10， —3怖4 1056.( 2017全国卷2 文)3.函数f(x) A. 4 n B. 2 n C. n D. 【答案】C nsin （2x -）的最小正周期为3n2【解析】由题意T —2 【考点】正弦函数周期 ,故选C.【名师点睛】函数 y Asin （ x )B(A 0, 0）的性质(1)y max =A+B, y min A B .⑵周期Tn⑶由x — k M k Z)求对称轴2⑷由上2k n x n 2k^k Z) 求增区间；由2 2n 3 n-2k n x 2k n(k Z)求减区间；2 27 ( 2017 全国卷2 文)13.函数f(x) 2cosx sinx 的最大值为【答案】「5【解析】‘㈤乞Q+1 =/【考点】三角函数有界性【名师点睛】通过SB公式把三角函数化为—小i贰处+劝我的形式再借助三角函數團象研究性质,解题时注意观察角、函数名，结构等特征，一般可利用七如兀十处"•审后每求最值8 ( 2017全国卷2文)16. ABC的内角代B,C的对边分别为a,b,c ,若2bccosB acosC ccosA,贝U B【答案】—3【解析】由正弦定理可得2 sin^cos5 =5in. J：4CO5 C+ 5inCco5.4 = win(J. + C)=血占=ccs^ = —=>5 =—23［考点】正弦定理【宕师点睛】解三角形问題』多为边和角的求值问風遠就需要根抿正、余弦走理结合已知S件灵活转化边和角之间的关系，从而达到解决冋题的目的一其基本歩靈d第一步：定条件‘艮嚥定三角形中的已infMff求』在團形中标岀来，然后确主转化的方向第二宦走工具，即根揭臬件和所求合理选揺专化的工具，实S4边角之间的互亿第三步：求结果一9 （2017全国卷3文）4.已知Sin COS 43，则sin2=（）7A.9C. D. 【答案】A【解析】気3“吐口W帥—町一'工-1 9本题选择A选顶10 （2017全国卷3文）6.函数f(x)=-sin( x+ )+cos( x-)的最大值为(5 3 6A. 65 B. 1 C.-5D.【答案】A【解析】由诱导公式可得: cos cos 一2sin小 1则：f x sin x —5 3 sin6 .Sin x5函数的最大值为65本题选择A选项•7•函数丫=1+*+里器的部分图像大致为（xh/丿-/ /■XA11F 1 ■十41\11 X\）【答案】D【解析】士= 1时,/(1)=1+1 + 511]1=2+3111>2, ®排除民G当工T+H时』PT1+•故科除昆满足条件的只有D故选D1、(2016全国I卷12题)已知函数f(x) sin( x+ )( 0, n，X P f(X)的n n 5 n零点，x 为y f (x)图像的对称轴，且f (x)在(一，二)单调，则的最大值为4 18 36(A) 11 ( B)9 ( C) 7 ( D) 5【答案】B【解析】JT TT JT T r趣另析；因为$为/XE的寧気。

以来历年全国高考数学试卷全试题标准答案解析

1951年普通高等学校招生全国统一考试数学第一部分：1．设有方程组x+y=8，2x-y=7，求x ，y.解略：⎩⎨⎧==35y x2．若一三角形的重心与外接圆圆心重合，则此三角形为何种三角形？证：设△ABC 的重心与外接圆的圆心均为O （图1）∵OA=OC ，E 为AC 的中点，∴BE ⊥AC ；同理，CD ⊥AB ，AF ⊥BC 在Rt △ABE 与Rt △ACD 中，∠A 为公共角，BE=CD=R+21R=23R （R 为外接圆半径），所以△ABE ≌△ACD ，AB=AC ，同理可得AB=BC 由此可知△ABC 为等边三角形3．当太阳的仰角是600时，若旗杆影长为1丈，则旗杆长为若干丈？解略：3丈0)()()(:)()(,)(,,:?,,,,.4=-+-+-=++-=-=-==-=-=-=++-=-=-t a c t c b t b a z y x t a c tz c b y t b a x t ac zc b y b a x z y x c b a a c zc b y b a x 由此可得则有设解则各不相等而若5．试题10道，选答8道，则选法有几种？解略：45810=c 6．若一点P 的极坐标是（r,θ），则它的直角坐标如何？解：x=r θcos ,y=r θsin7．若方程x 2+2x+k=0的两根相等，则k=？解：由Δ=b 2-4ac=0,得k=18．列举两种证明两个三角形相似的方法OABCEFD答：略9．当（x+1)(x-2)＜0时，x 的值的范围如何？解略：-1＜x ＜210．若一直线通过原点且垂直于直线ax+by+c=0，求直线的方程解略：bx-ay=011．（x +x1)6展开式中的常数项如何？解：由通项公式可求得是T 4=2012．02cos =θ的通解是什么？解：).(4为整数k k π±π=θ13．系数是实数的一元三次方程，最少有几个根是实数，最多有几个根是实数？答：最少是一个，最多是三个14．解：原式=1003)5(4)2(4550554)5(55430)2(=⋅-⋅--⋅⋅-⋅⋅-⋅⋅-+⋅⋅+⋅⋅- 15．x 2-4y 2=1的渐近线的方程如何？解略：02=±y x?345505542=--16．三平行平面与一直线交于A ，B ，C 三点，又与另一直线交于A ＇，B ＇，C ＇三点，已知AB=3，BC=7及A ＇B ＇=9求A ＇C ＇解：如图易证:3011=''∴''''==C A C A B A AC AB AC AB 17．有同底同高的圆柱及圆锥，已知圆柱的体积为18立方尺，求圆锥的体积略：6立方尺18．已知lg2=0.3010,求lg5. 略：lg5=1-lg2=0.699019．二抛物线y 2=12x 与2x 2=3y 的公共弦的长度是多少？解略：解方程组得两公共点为（0，0）及（3，6）故其公共弦长为：5320．国旗上的正五角星的每一个顶角是多少度？解：由图可知：∠AFG=∠C+∠E=2∠C, ∠AGF=∠B+∠D=2∠B,∴∠A+∠AFG+∠AGF=∠A+2∠C+2∠B=5∠A ∴5∠A=1800，∴∠A=360 第二部分：A A ＇ αB B ＇ βB 1γ C C ＇C 1FGAC EBD1．P ，Q ，R 顺次为△ABC 中BC ，CA ，AB 三边的中点，求证圆ABC 在A 点的切线与圆PQR 在P 点的切线平行证：如图：由AD 是大圆的切线，可得： ∠1=∠2由RQ ∥BC ，可得：∠2=∠3，由QP ∥AB ，可得：∠3=∠4由PE 是小圆的切线，可得： ∠4=∠5由RP ∥AC ，可得：∠5=∠6综上可得：∠1=∠6，故AD ∥PE2．设△ABC 的三边BC=4pq,CA=3p 2+q 2,AB=3p 2+2pq-q 2,求∠B ，并证∠B 为∠A 及∠C 的等差中项解：由余弦定理可得：.C A B A,-B 60)180(60B 214)23(2)3()4()23(2cos 222222222222的等差中项与是∠∠∠∴∠∠=∠-︒=∠-∠-∠-︒=∠-∠︒=∠∴=⋅-+--+-+=⋅-+=A B B A B C pqq pq p q p pq q pq p BC AB CA BC AB B 3．（1）求证，若方程x 3+ax 2+bx+c=0的三根可排成等比数列，则a 3c=b 3.证：设α，β，γ是方程x 3+ax 2+bx+c=0的三根，由根与系数关系可知：α+β+γ=-aαβ+βγ+γα=b αβγ=-c564321E QPRA BC又因α，β，γ排成等比数列，于是β2=αγ33333233a )()()(bc c a b ==αβγ-=β-=⎥⎦⎤⎢⎣⎡γ+β+αβγ+β+α-=⎥⎦⎤⎢⎣⎡γ+β+αβ+βγ+α-=⎥⎦⎤⎢⎣⎡γ+β+α-γα+βγ+αβ=⎪⎭⎫⎝⎛此即（2）已知方程x 3+7x 2-21x-27=0的三根可以排成等比数列，求三根解：由⑴可知β3=-c ，∴β3=27，∴β=3代入α+β+γ=-7可得α+γ=-10，又由α，β，γ成等比数列，∴β2=αγ，即αγ=9，故可得方程组：⎩⎨⎧--=γ--=α=αγ-=γ+α.91,19,910或或可得解之于是，所求之三根为-9，3，-1或-1，3，-94．过抛物线顶点任做互相垂直的两弦，交此抛物线于两点，求证此两点联线的中点的轨迹仍为一抛物线证：设抛物线方程为y 2=2px ……………①过抛物线顶点O 任作互相垂直的二弦OA 和 OB ，设OA 的斜率为k ，则直线OB 的斜率为 -k 1，于是直线OA 的方程为： y =kx ………………………②直线OB 的方程为：x k y 1-=③ 设点A （x 1 ,y 1),点B(x 2 ,y 2)由①，②可得： .2,2121k p y k p x ==由①，③可得：YA·P （x,y)O XBx 2=2pk 2, y 2=-2pk设P （x ，y ）为AB 的中点，由上可得： ④ ⑤ 由⑤可得： ⑥ 由④可知：px 2222k p kp +=,代入⑥,2p -px y 22222222222=-=-⎪⎪⎭⎫ ⎝⎛+=即p px p k p k p y 所以，点P 的轨迹为一抛物线1952年普通高等学校招生全国统一考试数学第一部分：1.因式分解x 4 – y 4 =？解：x 4 – y 4 =(x 2+y 2)(x+y)(x-y)2.若lg2x=21lgx ，问x=？解：2x=x 21，x ≠0，∴202=X3.若方程x 3+bx 2+cx+d=0的三根为1,-1,21,则c=？解：由根与系数的关系可知：c=1·（-1）+（-1）·21+21·1=1pk kpy y y pk kp x x x -=+=+=+=222122212222222k p p kp y +-=4.若x x 求,0472=-+解：两边平方，得：x 2 +7=16，∴3±=x5.解:原式=-246.两个圆的半径都是4寸,并且一个圆过另一个圆的圆心，则此两圆的公共弦长是多少寸？解：设两圆O 1及O 2之公共弦为AB 连结O 1O 2交AB 于点C ，则AB垂直平分O 1O 2∴O 1C=21O 1O 2=2（寸）).(342),(3224222121寸寸==∴=-=-=AC AB C O AO AC连结AO 1，则△ACO 1为直角三角形， 7.三角形ABC 的面积是60平方寸，M 是AB 的中点，N 是AC 的中点，△AMN 的面积是多少？解：∵MN ∥BC ，∴41ABC AMN 22==∆∆ANAM 的面积的面积， △AMN 的面积=41△ABC 的面积=15（平方寸）8.正十边形的一个内角是多少度？解：由公式,)2(180nn -︒此处n=10于是一个内角为：︒144AO 1 O 2CB?123054321=9.祖冲之的圆周率π=？答：22/7，355/13310.球的面积等于大圆面积的多少倍？解：球的面积4πR 2为大圆面积πR 2的4倍11.直圆锥之底半径为3尺，斜高为5尺，则其体积为多少立方尺？解：圆锥高h=4（尺），故此直圆锥的体积：V 锥 =31πR 2h=12π（立方尺） 12.正多面体有几种？其名称是什么？答：共有五种，其名称为：正四面体，正六面体，正八面体，正十二面体和正二十面体13.已知 sin θ=31,求cos2θ=？解：cos2θ=1-2sin 2θ=97 14.方程tg2x=1的通解x=？解：).(82为整数k k x π+π=15.太阳的仰角为300时，塔影长为5丈，求塔高是多少？解：塔高=5×tg300=335（寸） 16．△ABC 的b 边为3寸，c 边为4寸，A 角为300，问△ABC 的面积为多少平方寸？解：).(330sin 4321sin 21平方寸的面积=︒⋅⋅⋅==∆A bc ABC17.已知一直线经过（2，3），其斜率为-1，则此直线方程如何？解：即x+y –5=018.若原点在一圆上，而此圆的圆心为（3，4）则此圆的方程如何？解：圆的半径.54322=+=R所以，圆的方程为：(x-3)2+(y-4)2=25，也即：x 2+y 2-6x-8y=019.原点至3x+4y+1=0的距离是什么？解：.51431040322=++⋅+⋅=d 20.抛物线y 2-8x+6y+17=0的顶点坐标是什么？解：原方程可变形为：(y+3)2=8(x-1), 故顶点坐标为（1，-3）第二部分：1.解方程x 4+5x 3-7x 2-8x-12=0解：左式=(x 4+5x 3-6x 2）-（x 2+8x+12）=(x+6)[x 2(x-1)-(x+2)] =(x+6)(x 3-x 2-x-2) =(x+6)[(x 3-2x 2)+(x 2-x-2)] =(x+6)(x-2)(x 2+x+1)=0 可得原方程的四根为：.231,231,2,64321ix i x x x --=+-==-= 2.△ABC 中，∠A 外角的平分线与此三角形外接圆相交于P ，求证：BP=CP证：如图，∠CBP=∠CAP=∠PAD 又∠1=∠2由∠CAD=∠ACB+∠CBA=∠ACB+∠CBP+∠2=∠ACB+∠1+∠CBP =∠BCP+∠CBP∴∠BCP=∠CBP ，∴BP=CP 3.设三角形的边长为a =4，b=5，c=6，其对角依次为A ，B ，C 求A B C C sin ,sin ,sin ,cos .问A ，B ，C 三角为锐角或钝角？解：应用余弦定理，可得： .812cos 222=-+=ab c b a C由此可知C 为锐角；另外，由已知条件，三边边长适合关系式a ＜b ＜c ，从而可知∠A ＜∠B ＜∠C 由于C 为锐角，故A ，B 亦为锐角.741c asinC sinA .7165sin sin ,.783)81(-1sinC cos -1sinC 22=======c C b B C 可得应用正弦定理可得由 4.一椭圆通过（2，3）及（-1，4）两点，中心为原点，长短轴重合于坐标轴，试求其长轴，短轴及焦点解：由于椭圆过（2，3）及（-1，4）两点，所以将此两点代入标准方程可得：C1P2D A B.75522,35522,355,755,1161194222222==∴==⎪⎩⎪⎨⎧=+=+a b b a b ab a 短轴长轴解之 .2155221220,22222==-=∴-=a b c a b c 又 ).21552,0(),21552,0(21F F -故焦点坐标为1954年普通高等学校招生全国统一考试数学1．甲、化简.])()()[(317212131223b ab b a --- 解：原式=.)()(32310231272321223a b a b b a b a ==--乙、解c b a x lg lg 2lg 31lg 61++= 解略：x=a 2b 12c 6.丙、用二项式定理计算（3.02）4，使误差小于千分之一.,,,001.0)1002()1002(34)1002(36100234310023)02.3(:43223444千分之一其误差必小于计算可到第三项为止所以可知第四项之值已小于解+⋅⋅+⋅⋅+⋅⋅+=⎪⎭⎫ ⎝⎛+=.182.830216.016.281)02.3(4=++=丁、试证直角三角形弦上的半圆的面积，等于勾上半圆的面积与股上半圆的面积的总和证：由c 2 =a 2+b 2∴弦上半圆的面积= 22222221221421221⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=+=⎪⎭⎫ ⎝⎛b a b a c ππππ=勾上半圆的面积+股上半圆的面积戊、已知球的半径等于r ，试求内接正方形的体积解：内接正方体的中心即该球的球心正方体过中心的对角线为该球的直径，故其长为2r 若设内接正方体的边长为a ，则有3a 2=4r 2，.398332.332333r r a r a =⎪⎭⎫⎝⎛==∴=内接正方体的体积己、已知a 是三角形的一边，β及γ是这边的两邻角，试求另一边b 的计算公式解：由正弦定理可知.)sin(sin )](180sin[sin ,sin )](180sin[γββγβββγβ+=--︒=∴=--︒a a b b a2.描绘y=3x 2-7x-1的图象，并按下列条件分别求x 的值所在的范围： 1）y ＞0， 2）y ＜0).1261(31)67(:2+=-y x 将原方程变形可得解 ).1261,67(,-抛物线顶点为于是)0,6617(,)0,6617(:+-N M x 轴的交点为与).,6617(),6617,(,0+∞+--∞>的值所在范围为时当x y ).6617,6617(,0+-<的值所在范围为时当x y YM O N X)1261,67(-3.假设两圆互相外切，求证用连心线做直径的圆，必与前两圆的外公切线相切证：设⊙O 1及⊙O 2为互相外切之二圆，其一外公切线为A 1A 2，切点为A 1及A 2令点O 为连心线O 1O 2的中点，过O 作OA ⊥A 1A 2∵OA=21（O 1A 1+O 2A 2）=21O 1O 2，∴以O 1O 2为直径，即以O 为圆心，OA 为半径的圆必与直线A 1A 2相切同理可证，此圆必切于⊙O 1及⊙O 2的另一条外公切线4．试由.,2sin 111通值求的x x tgxtgx+=-+ )(0sin 4,1,0sin cos ,0sin )sin (cos 20)sin cos 1)(sin (cos )sin (cos sin cos sin cos :22222为整数或者即或者所以解k k x x k x tgx x x x x x x x x x x x x x x x π=∴=π-π=∴-==+=⋅+=+-++=-+由检验可知，均为其通解5．有一直圆锥，另外有一与它同底同高的直圆柱，假设a 是圆锥的全面积，a ＇是圆柱的全面积，试求圆锥的高与母线的比值解：设直圆锥的高为h ，底面半径为R ，母线长为L ，则,)(2)(2)(h R L R h R R L R R a a ++=++='ππ .2)2(),()(2,).()(222222222ah L a h L a a L h L a h h L a h L R L R a h R a -'=-'-+-'=+--=+'=+∴代入可得由A 2AA 1O 1 O O 2,.21)2(,2等式两边平方可得两边同除以L h a a L h a a L -'=⎪⎭⎫⎝⎛-'-.)2(4)2()2(22])2(4[2)2()2(44)48(2)2(164:,,0)2(16)4)(48(4)4(.0)4(4)48(,441)44(2222223322222222222222a a a a a a a a a a a a a a a a a a a a a a a a a a a a a L h a a a a a a a a a a a a Lha a a L h a a L h a a a a L h a L h a a a L h a a a a '-+'-'-±'='-+'-'-±'='+'-'-±'=∴>'-='+''+'--'-=∆='+'+'-⎪⎭⎫⎝⎛'+'-⎪⎭⎫⎝⎛+⋅'-'=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-'+'-母线的比此二实根即圆锥的高与实根该一元二次方程有二个式的一元二次方程的判别这个关于1958年普通高等学校招生全国统一考试数学1．甲、求二项式5)21(x +展开式中3x 的系数解：设求的项为.802,32)2(333354551x x C T r x C x C T r r r r r r ==∴===+今乙、求证.sin 88sin 4cos 2cos cos xxx x x =⋅⋅ 证：x x x 4cos 4sin 28sin =xx x x xx x 4cos 2cos cos sin 84cos 2cos 2sin 4=⌒ ⌒⌒ ⌒ ⌒ ⌒ .sin 88sin 4cos 2cos cos xxx x x =⋅⋅∴ 丙、设AB ，AC 为一个圆的两弦，D 为AB 的中点，E 为AC 的中点，作直线DE 交AB 于M ，交AC 于N ，求证：AM=AN证：联结AD 与AE （如图） ∵∠AMN=∠DAM+∠MDA ， ∠ANM=∠EAN+∠NEA ，又∵AD=DB ，∠DAB=∠AED ，AE=EC ，∠ADE=∠EAC ， ∴∠AMN=∠ANM ， AM=AN.丁、求证正四面体ABCD 中相对的两棱（即异面的两棱）互相垂直证：因ABCD 是正四面体，各个面都是等边三角形，过A 作AE ⊥BC ，联结DE ，则DE ⊥BC ， ∴BC 垂直平面AED ，而AD 在此平面内， ∴BC ⊥AD同理可证AB ⊥DC ，AC ⊥DB戊、求解.cos 3sin x x = 解：,cos 3sin x x =AD EM NBCDCA EB).(3,3为整数k k x tgx π+π==∴ 2．解方程组⎪⎪⎩⎪⎪⎨⎧=++=-+++)2(9122)1(4121 y y x y x y x v y x u yx y x y x =-+=+=-+++12,1,8)12()1()2(:设式变形为由解则原方程变形为⎩⎨⎧=+=+)4(8)3(422 v u v u 解方程组，可得.2,2==v u 将v u ,的值代回所设，可得⎪⎩⎪⎨⎧-==⎩⎨⎧====-==∴=--=--⎪⎩⎪⎨⎧=-+=+⎪⎩⎪⎨⎧=-+=+.21,6;1,3.6,3),5(.21,1,01,112)5()6()6(412)5(41,21221221121212y x y x x x y y y y y y y x y x y x y x 由检验可知代入即得得两边平方都是原方程组的解3．设有二同心圆，半径为R ，r(R>r ），今由圆心O 作半径交大圆于A ，交小圆于A ＇，由A 作直线AD 垂直大圆的直径BC ，并交BC 于D;由A ＇作直线A ＇E 垂直AD ，并交AD 于E ，已知∠OAD= α，求OE 的长解：在直角△OAD 中， OD=Rsin α，AD=Rcos α 在直角△A ＇AE 中， AE=（R-r ）cos α ∴DE=AD-AE=Rcos α-（R-r ）cos α=rcos α. OE=.cos sin 222222α+α=+r R DE OD4．已知三角形ABC ，求作圆经过A 及AB 中点M ，并与BC 直线相切已知：M 为△ABC 的AB 的中点.求作：一个经过A 、M 两点且与BC 直线相切的圆.AA ＇ EB O D C分析：设⊙O 即为合于要求的圆（如图）因⊙O 经过A 、M 两点且与直线BC 相切于点P ，这样，BP 为⊙O 的切线，BA 为⊙O 的割线，所以，应有 BP 2=BM ·BA而BM ，BA 均为已知，因此，BP 的长度可以作出，由此可得点P ，于是过A 、M 、P 三点就可确定所求之圆作法：1）作线段A ＇B ＇M ＇，使A ＇B ＇=AB ，B ＇M ＇=BM2）以A ＇M ＇为直径作半圆3）过B ＇作A ＇M ＇的垂线B ＇P ＇交半圆于点P ＇ 4）在△ABC 的边BC 上截取BP=B ＇P ＇ 5）经过A 、M 、P 三点作⊙O 即为所求证明：由作图可知B ＇P ＇2= A ＇B ＇·B ＇M ＇，A ＇B ＇=AB ，B ＇M ＇=BM ，所以BP 2=BM ·BA ，即BP 为⊙O 的切线，BMA 为其割线，且⊙O 经过A 、M 、P 三点，故⊙O 适合所要求的条件5．已知直角三角形的斜边为2，斜边上的高为23，求证此直角三角形的两个锐角是下列三角方程的根CPOA BMP ＇A ＇B ＇ M ＇043sin 231sin 2=++-x x 证：设AD=k （如图） ∵AB=2，∴DB=2-k. 由CD 2=AD ·DB ，.2123,0432),2()23(22或==+--=∴k k k k k在直角△ACD 中，当23==k AD 时，,332323===AD CD tgA ∴A=300，B=600.当21==k AD 时，,32123===AD CD tgA ∴A=600，B=300. 总之，两锐角一为300，一为600. 当x=300时，代入原方程中得;04321231)21(4330sin 23130sin 22=+⋅+-=+︒+-︒ 当x=600时，代入原方程中得.04323231)23(4360sin 23160sin 22=+⋅+-=+︒+-︒ 故这个直角三角形的两个锐角是原三角方程的根CA D B1959年普通高等学校招生全国统一考试数学1．甲、已知lg2=0.3010,lg7=0.8451,求lg35解：原式=2lg 10lg 7lg 2107lg 270lg-+=⨯= =0.8451+1-0.3010=1.5441.乙、求ii +-1)1(3的值.解：.21)1(21221331133132-=++-=+--=++--=+-+-=ii i i i i i i i i i 原式丙、解不等式.3522<-x x 解：原式移项得,03522<--x x ∴原不等式的解为.321<<-x 丁、求︒165cos 的值解：)3045cos(15cos )15180cos(165cos ︒-︒-=︒-=︒-︒=︒.426)21222322()30sin 45sin 30cos 45(cos +-=⋅+⋅-=︒︒+︒︒-=戊、不在同一平面的三条直线c b a ,,互相平行，A 、B 为b 上两定点，求证另两顶点分别在c a 及上的四面体体积为定值证：因为A 、B 为直线b 上两定点，而直线b ∥直线c ，所以，不论点C 在直线c 的什么位置上，△ABC 的面积均为一定值（同底等高的三角形等积）又因直线a 平行于直线 c b ,，所以，直线a ∥平面α（已知c b a ,,不在同一平面内），因此，不论点D 在直线a 的什么位置上，从点D 到平面α的距离h 为一定值，故四面体ABCD 的体积=定值高底面积=⋅⋅=⨯⨯∆h S ABC 3131己、圆台上底面积为225cm π，下底直径为cm 20，母线为cm 10，求圆台的侧面积解：设此圆台上底半径为r ，下底半径为R ，由已知条件,252π=πr 所以r=5(cm).又下底半径R=10cm ，母线,10cm l =圆台侧面积=πl （R+r)=π·10·（10+5）=150π（cm 2). 2．已知△ABC 中，∠B=600，AC=4，面积为3，求AB 和BC. 解：设AB=c ，BC=a ，则有⎪⎩⎪⎨⎧︒-+==︒),(60cos 24)(360sin 21222余弦定理两边夹角求面积公式ac c a ac D ahA B bOα cC.37,37.32,12)(,72,28)(,,1642222=±=∴±=-∴=-=+∴=+⎩⎨⎧=-+=c a c a c a c a c a ac c a ac 由由解之即故所求AB ，BC 之长为⎩⎨⎧+=-=⎩⎨⎧-=+=.37,37;37,37BC AB BC AB 3．已知三个数成等差数列，第一第二两数的和的3倍等于第三个数的2倍，如果第二个数减去2，则成等比数列，求这三个数解：设所求之三数为d a a d a +-,,则根据题意有⎩⎨⎧==⎪⎩⎪⎨⎧==⎩⎨⎧=-=⎩⎨⎧+-=-+=+-.45;1,45:4454).)(()2(),(2])[(3221122d a d a d a d a d a d a a d a a d a 解得化简后得故所求三数为.9,5,149,45,41或4．已知圆O 的两弦AB 和CD 延长相交于E ，过E 点引EF ∥CB 交AD 的延长线于F ，过F 点作圆O 的切线FG ，求证：EF=FG. 证：∵FG 为⊙O 的切线，而FDA 为⊙O 的割线，∴FG 2=FD ·FA …………① 又∵EF ∥CB ，∴∠1=∠2.而∠2=∠3， ∴∠1=∠3，∠EFD=∠AFE 为公共角 ∴△EFD ∽△AFE ，,FAEF EF FD =即EF 2=FD ·FA …………②由①，②可得EF 2=FG 2 ∴EF=FG.5．已知A 、B 、C 为直线l 上三点，且AB=BC=a ;P 为l 外一点，且∠APB=900，∠BPC=450，求（1）∠PBA 的正弦、余弦、正切; （2）PB 的长; （3）P 点到l 的距离.解：过P 点作PD ⊥AB 交AB 于点D （如图）（1）过点B 作BE ∥AP 交PC 于点E 则∠PBE=900，∠PEB=450，PB=BE. ∵△CPA ∽△CEB ∴,22==a aBE PA 因PB=BE ， ∴.2,2=∠=PBA tg PBPA C G2 FO D1A 3 EBP450 EA a DB a C又∵,sec 122PBA PBA tg ∠=∠+∠PBA 为锐角， ∴,51sec 2=∠+=∠PBA tg PBA.552cos sin ,5551cos =∠⋅∠=∠==∠PBA PBA tg PBA PBA（2）.55cos a PBA AB PB =∠⋅= （3）,552sin ,55=∠=PBA a PB ∴.52sin a PBA PB PD =∠⋅= 综上，所求为（1）∠PBA 的正弦、余弦、正切分别是2,551,552 （2）PB 的长为;551a （3）P 点到l 的距离为.52a1957年普通高等学校招生全国统一考试数学1．甲、化简32221)27102(1.0)972(--++解：原式=.481110216910035)2764()101()925(32221=++=++--乙、求适合不等式22<+x x 的实数x 的范围解：原式为022<-+x x 解为：-2<x<1. 故x 的范围为-2<x<1. 丙、求证.210322+='︒ctg 证：.2145sin 45cos 12450322+=︒︒+=︒='︒ctgctg丁、在四面体ABCD 中，AC=BD ，P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点，求证：PQRS 为一个菱形证：由于点P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点，根据三角形两边中点连线的性质可得.////,21////BD SP RQ AC RS PQ ====而由题设，AC=BD ， ∴PQ=QR=RS=SP ，故 PQRS 为一个菱形戊、设b a ,为异面直线，EF 为ba ,的公垂线，α为过EF 的中点且与b a ,平行的平面，M 为a 上任一点，N 为b 上任一点求证线段MN 被平面α二等分证：过直线b 作平面β//α（如图）过直线a 及公垂线EF 作一平面，在此平面内作MC ∥EF ，且与平面α，β分别交于B 、C 两点设EF 、MN 分别与平面α交于点A 、D∵点A 是EF 的中点，ASPDRC BQM E aB Aα DC bN F β又ME ∥BA ∥CF ， ∴点B 是MC 的中点又∵DB ∥NC ， ∴D 是MN 的中点另法：如图，连接EN ，AB,BD 由AB b BD a b a //,////,//⇒αα由A 是EF 的中点得,D 为MN 的中点此即线段MN 被平面α二等分 2．解方程组⎩⎨⎧⋅==-++)2(101010)1(1)2lg()12lg( yx xy y x 解：由（1）可得,10)2)(12(=-+y x)3(01242 =-+-y x xy由（2）可得)4( y x xy +=将（4）代入（3）可得,012422=-+-+y x y x,01232=-+-y x)5(3212 xy +=再将（5）代入（4）可得,32123212xx x x ++=+⋅ 化简，得,012722=-+x x.41457±-=∴x 将x 值代入（5）.6145173212±=+=x y abαEFAMNBD此即⎪⎪⎩⎪⎪⎨⎧-=--=⎪⎪⎩⎪⎪⎨⎧+=+-=.614517,41457;614517,414572211y x y x 因为,0122<+x 所以（1）式无意义（负数无对数），故原方程组的解仅为⎪⎪⎩⎪⎪⎨⎧+=+-=.614517,41457y x 3．设△ABC 的内切圆半径为r ，求证BC 边上的高.2sin2cos 2cos 2A CB r AD ⋅⋅=证：在直角△ABC 中，2cos2sin 2sin B B c Bc AD ⋅⋅=⋅=另外，EB AE c +=)22(Bctg A ctgr += 2sin2sin )22sin()2sin 2cos 2sin 2cos (B A B A r B B A A r ⋅+⋅=+=AEc r bOB Ca D.2sin2cos2cos 22cos 2sin2sin 2sin2cos22sin 2sin2cosA CB r B B BA Cr AD B A C r ⋅⋅=⋅⋅⋅⋅=∴⋅⋅= 4．设△ABC 为锐角三角形，以BC 为直径作圆，并从A 作此圆的切线AD 与圆切于D 点，由在AB 边上取AE=AD ，并过E 作AB 的垂线与AC 边的延长线交于F ，求证：（1）AE:AB=AC:AF.（2）△ABC 的面积=△AEF 的面积.证（1）：设AB 与⊙O 相交于点G ，联结EC ，CG ，BF.∵EF ⊥AB ，CG ⊥AB ，∴GC ∥EF ，AC:AF=AG:AE ………………① 又∵AD 是⊙O 的切线，∴AD 2=AG ·AB ，也即AG:AD=AD:AB但∵AD=AE ，∴AG:AE=AE:AB ……………② 由①、②可得AE:AB=AC:AF证（2）：由（1）AE:AB=AC:AF ，则EC ∥BF ，△EBC 的面积=△EFC 的面积 ∴△ABC 的面积=△AEC 的面积+△EBC 的面积=△AEC 的面积+△EFC 的面积 =△AEF 的面积5．求证方程0)2()12(23=+-++-Q x Q x x 的一个根是1设这个方程的三个根是△ABC 的三个内角的正弦,sin ,sin ,sin C B A 求A 、B 、C 的度数以及Q 的值解：将x=1代入这个方程式，则01)2(1)12(123=+⋅-+⋅+-Q Q ，故知1是原方程的一个根由于1是原方程的一个根，所以方程左边能被x-1整除AGE DB GOF用x-1除方程左边后得商式.022=--Q x x根据题设条件（即有一个根为1，不妨设1sin =C ）及根与系数的关系可得⎪⎩⎪⎨⎧-=⋅=+=)3(sin sin )2(2sin sin )1(1sin Q B A B A C 由（1）可知C=900，于是A+B=900，B=900-A ，代入（2）得.212222sin sin )3(45459045,045,1)45cos(,1cos 45cos sin 45sin ,1cos 22sin 22,2cos sin ,2)90sin(sin -=⋅-=⋅-=︒=︒-︒=︒=∴=︒-∴=︒-=⋅︒+⋅︒=+∴=+=-︒+B A Q B A A A A A A A A A A A 式可得从即1957年普通高等学校招生全国统一考试数学1．甲、化简32221)27102(1.0)972(--++解：原式=.481110216910035)2764()101()925(32221=++=++--乙、求适合不等式22<+x x 的实数x 的范围解：原式为022<-+x x 解为：-2<x<1. 故x 的范围为-2<x<1. 丙、求证.210322+='︒ctg证：.2145sin 45cos 12450322+=︒︒+=︒='︒ctgctg 丁、在四面体ABCD 中，AC=BD ，P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点，求证：PQRS 为一个菱形证：由于点P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点，根据三角形两边中点连线的性质可得.////,21////BD SP RQ AC RS PQ ====而由题设，AC=BD ， ∴PQ=QR=RS=SP ，故 PQRS 为一个菱形戊、设b a ,为异面直线，EF 为ba ,的公垂线，α为过EF 的中点且与b a ,平行的平面，M 为a 上任一点，N 为b 上任一点求证线段MN 被平面α二等分证：过直线b 作平面β//α（如图）过直线a 及公垂线EF 作一平面，在此平面内作MC ∥EF ，且与平面α，β分别交于B 、C 两点设EF 、MN 分别与平面α交于点ASPDRC BQM E aB Aα DC bN FβA 、D∵点A 是EF 的中点，又ME ∥BA ∥CF ， ∴点B 是MC 的中点又∵DB ∥NC ， ∴D 是MN 的中点另法：如图，连接EN ，AB,BD 由AB b BD a b a //,////,//⇒αα由A 是EF 的中点得,D 为MN 的中点此即线段MN 被平面α二等分 2．解方程组⎩⎨⎧⋅==-++)2(101010)1(1)2lg()12lg( yx xy y x 解：由（1）可得,10)2)(12(=-+y x)3(01242 =-+-y x xy由（2）可得)4( y x xy +=将（4）代入（3）可得,012422=-+-+y x y x,01232=-+-y x)5(3212 xy +=再将（5）代入（4）可得,32123212xx x x ++=+⋅ 化简，得,012722=-+x x.41457±-=∴x abαEFAMNBD将x 值代入（5）.6145173212±=+=x y 此即⎪⎪⎩⎪⎪⎨⎧-=--=⎪⎪⎩⎪⎪⎨⎧+=+-=.614517,41457;614517,414572211y x y x 因为,0122<+x 所以（1）式无意义（负数无对数），故原方程组的解仅为⎪⎪⎩⎪⎪⎨⎧+=+-=.614517,41457y x 3．设△ABC 的内切圆半径为r ，求证BC 边上的高.2sin2cos 2cos 2A CB r AD ⋅⋅=证：在直角△ABC 中，2cos2sin 2sin B B c Bc AD ⋅⋅=⋅=另外，EB AE c +=)22(Bctg A ctgr += 2sin2sin )22sin()2sin 2cos 2sin 2cos (B A B A r B B A A r ⋅+⋅=+=AEc r bOB Ca D.2sin2cos2cos 22cos 2sin2sin 2sin2cos22sin 2sin2cosA CB r B B BA Cr AD B A C r ⋅⋅=⋅⋅⋅⋅=∴⋅⋅= 4．设△ABC 为锐角三角形，以BC 为直径作圆，并从A 作此圆的切线AD 与圆切于D 点，由在AB 边上取AE=AD ，并过E 作AB 的垂线与AC 边的延长线交于F ，求证：（1）AE:AB=AC:AF.（2）△ABC 的面积=△AEF 的面积.证（1）：设AB 与⊙O 相交于点G ，联结EC ，CG ，BF.∵EF ⊥AB ，CG ⊥AB ，∴GC ∥EF ，AC:AF=AG:AE ………………① 又∵AD 是⊙O 的切线，∴AD 2=AG ·AB ，也即AG:AD=AD:AB但∵AD=AE ，∴AG:AE=AE:AB ……………② 由①、②可得AE:AB=AC:AF证（2）：由（1）AE:AB=AC:AF ，则EC ∥BF ，△EBC 的面积=△EFC 的面积 ∴△ABC 的面积=△AEC 的面积+△EBC 的面积=△AEC 的面积+△EFC 的面积 =△AEF 的面积5．求证方程0)2()12(23=+-++-Q x Q x x 的一个根是1设这个方程的三个根是△ABC 的三个内角的正弦,sin ,sin ,sin C B A 求A 、B 、C 的度数以及Q 的值解：将x=1代入这个方程式，则01)2(1)12(123=+⋅-+⋅+-Q Q ，故知1是原方程的一个根由于1是原方程的一个根，所以方程左边能被x-1整除AGE DB GOF用x-1除方程左边后得商式.022=--Q x x根据题设条件（即有一个根为1，不妨设1sin =C ）及根与系数的关系可得⎪⎩⎪⎨⎧-=⋅=+=)3(sin sin )2(2sin sin )1(1sin Q B A B A C 由（1）可知C=900，于是A+B=900，B=900-A ，代入（2）得.212222sin sin )3(45459045,045,1)45cos(,1cos 45cos sin 45sin ,1cos 22sin 22,2cos sin ,2)90sin(sin -=⋅-=⋅-=︒=︒-︒=︒=∴=︒-∴=︒-=⋅︒+⋅︒=+∴=+=-︒+B A Q B A A A A A A A A A A A 式可得从即1957年普通高等学校招生全国统一考试数学1．甲、化简32221)27102(1.0)972(--++解：原式=.481110216910035)2764()101()925(32221=++=++--乙、求适合不等式22<+x x 的实数x 的范围解：原式为022<-+x x 解为：-2<x<1. 故x 的范围为-2<x<1. 丙、求证.210322+='︒ctg证：.2145sin 45cos 12450322+=︒︒+=︒='︒ctgctg 丁、在四面体ABCD 中，AC=BD ，P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点，求证：PQRS 为一个菱形证：由于点P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点，根据三角形两边中点连线的性质可得.////,21////BD SP RQ AC RS PQ ====而由题设，AC=BD ， ∴PQ=QR=RS=SP ，故 PQRS 为一个菱形戊、设b a ,为异面直线，EF 为ba ,的公垂线，α为过EF 的中点且与b a ,平行的平面，M 为a 上任一点，N 为b 上任一点求证线段MN 被平面α二等分证：过直线b 作平面β//α（如图）过直线a 及公垂线EF 作一平面，在此平面内作MC ∥EF ，且与平面α，β分别交于B 、C 两点设EF 、MN 分别与平面α交于点ASPDRC BQM E aB Aα DC bN FβA 、D∵点A 是EF 的中点，又ME ∥BA ∥CF ， ∴点B 是MC 的中点又∵DB ∥NC ， ∴D 是MN 的中点另法：如图，连接EN ，AB,BD 由AB b BD a b a //,////,//⇒αα由A 是EF 的中点得,D 为MN 的中点此即线段MN 被平面α二等分 2．解方程组⎩⎨⎧⋅==-++)2(101010)1(1)2lg()12lg( yx xy y x 解：由（1）可得,10)2)(12(=-+y x)3(01242 =-+-y x xy由（2）可得)4( y x xy +=将（4）代入（3）可得,012422=-+-+y x y x,01232=-+-y x)5(3212 xy +=再将（5）代入（4）可得,32123212xx x x ++=+⋅ 化简，得,012722=-+x x.41457±-=∴x abαEFAMNBD将x 值代入（5）.6145173212±=+=x y 此即⎪⎪⎩⎪⎪⎨⎧-=--=⎪⎪⎩⎪⎪⎨⎧+=+-=.614517,41457;614517,414572211y x y x 因为,0122<+x 所以（1）式无意义（负数无对数），故原方程组的解仅为⎪⎪⎩⎪⎪⎨⎧+=+-=.614517,41457y x 3．设△ABC 的内切圆半径为r ，求证BC 边上的高.2sin2cos 2cos 2A CB r AD ⋅⋅=证：在直角△ABC 中，2cos2sin 2sin B B c Bc AD ⋅⋅=⋅=另外，EB AE c +=)22(Bctg A ctgr += 2sin2sin )22sin()2sin 2cos 2sin 2cos (B A B A r B B A A r ⋅+⋅=+=AEc r bOB Ca D.2sin2cos2cos 22cos 2sin2sin 2sin2cos22sin 2sin2cosA CB r B B BA Cr AD B A C r ⋅⋅=⋅⋅⋅⋅=∴⋅⋅= 4．设△ABC 为锐角三角形，以BC 为直径作圆，并从A 作此圆的切线AD 与圆切于D 点，由在AB 边上取AE=AD ，并过E 作AB 的垂线与AC 边的延长线交于F ，求证：（1）AE:AB=AC:AF.（2）△ABC 的面积=△AEF 的面积.证（1）：设AB 与⊙O 相交于点G ，联结EC ，CG ，BF.∵EF ⊥AB ，CG ⊥AB ，∴GC ∥EF ，AC:AF=AG:AE ………………① 又∵AD 是⊙O 的切线，∴AD 2=AG ·AB ，也即AG:AD=AD:AB但∵AD=AE ，∴AG:AE=AE:AB ……………② 由①、②可得AE:AB=AC:AF证（2）：由（1）AE:AB=AC:AF ，则EC ∥BF ，△EBC 的面积=△EFC 的面积 ∴△ABC 的面积=△AEC 的面积+△EBC 的面积=△AEC 的面积+△EFC 的面积 =△AEF 的面积5．求证方程0)2()12(23=+-++-Q x Q x x 的一个根是1设这个方程的三个根是△ABC 的三个内角的正弦,sin ,sin ,sin C B A 求A 、B 、C 的度数以及Q 的值解：将x=1代入这个方程式，则01)2(1)12(123=+⋅-+⋅+-Q Q ，故知1是原方程的一个根由于1是原方程的一个根，所以方程左边能被x-1整除AGE DB GOF用x-1除方程左边后得商式.022=--Q x x根据题设条件（即有一个根为1，不妨设1sin =C ）及根与系数的关系可得⎪⎩⎪⎨⎧-=⋅=+=)3(sin sin )2(2sin sin )1(1sin Q B A B A C 由（1）可知C=900，于是A+B=900，B=900-A ，代入（2）得.212222sin sin )3(45459045,045,1)45cos(,1cos 45cos sin 45sin ,1cos 22sin 22,2cos sin ,2)90sin(sin -=⋅-=⋅-=︒=︒-︒=︒=∴=︒-∴=︒-=⋅︒+⋅︒=+∴=+=-︒+B A Q B A A A A A A A A A A A 式可得从即1957年普通高等学校招生全国统一考试数学1．甲、化简32221)27102(1.0)972(--++解：原式=.481110216910035)2764()101()925(32221=++=++--乙、求适合不等式22<+x x 的实数x 的范围解：原式为022<-+x x 解为：-2<x<1. 故x 的范围为-2<x<1. 丙、求证.210322+='︒ctg 证：.2145sin 45cos 12450322+=︒︒+=︒='︒ctgctg丁、在四面体ABCD 中，AC=BD ，P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点，求证：PQRS 为一个菱形证：由于点P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点，根据三角形两边中点连线的性质可得.////,21////BD SP RQ AC RS PQ ====而由题设，AC=BD ， ∴PQ=QR=RS=SP ，故 PQRS 为一个菱形戊、设b a ,为异面直线，EF 为ba ,的公垂线，α为过EF 的中点且与b a ,平行的平面，M 为a 上任一点，N 为b 上任一点求证线段MN 被平面α二等分证：过直线b 作平面β//α（如图）过直线a 及公垂线EF 作一平面，在此平面内作MC ∥EF ，且与平面α，β分别交于B 、C 两点设EF 、MN 分别与平面α交于点A 、D∵点A 是EF 的中点，ASPDRC BQM E aB Aα DC bN F β又ME ∥BA ∥CF ， ∴点B 是MC 的中点又∵DB ∥NC ， ∴D 是MN 的中点另法：如图，连接EN ，AB,BD 由AB b BD a b a //,////,//⇒αα由A 是EF 的中点得,D 为MN 的中点此即线段MN 被平面α二等分 2．解方程组⎩⎨⎧⋅==-++)2(101010)1(1)2lg()12lg( yx xy y x 解：由（1）可得,10)2)(12(=-+y x)3(01242 =-+-y x xy由（2）可得)4( y x xy +=将（4）代入（3）可得,012422=-+-+y x y x,01232=-+-y x)5(3212 xy +=再将（5）代入（4）可得,32123212xx x x ++=+⋅ 化简，得,012722=-+x x.41457±-=∴x 将x 值代入（5）.6145173212±=+=x y abαEFAMNBD此即⎪⎪⎩⎪⎪⎨⎧-=--=⎪⎪⎩⎪⎪⎨⎧+=+-=.614517,41457;614517,414572211y x y x 因为,0122<+x 所以（1）式无意义（负数无对数），故原方程组的解仅为⎪⎪⎩⎪⎪⎨⎧+=+-=.614517,41457y x 3．设△ABC 的内切圆半径为r ，求证BC 边上的高.2sin2cos 2cos 2A CB r AD ⋅⋅=证：在直角△ABC 中，2cos2sin 2sin B B c Bc AD ⋅⋅=⋅=另外，EB AE c +=)22(Bctg A ctgr += 2sin2sin )22sin()2sin 2cos 2sin 2cos (B A B A r B B A A r ⋅+⋅=+=AEc r bOB Ca D.2sin2cos2cos 22cos 2sin2sin 2sin2cos22sin 2sin2cosA CB r B B BA Cr AD B A C r ⋅⋅=⋅⋅⋅⋅=∴⋅⋅= 4．设△ABC 为锐角三角形，以BC 为直径作圆，并从A 作此圆的切线AD 与圆切于D 点，由在AB 边上取AE=AD ，并过E 作AB 的垂线与AC 边的延长线交于F ，求证：（1）AE:AB=AC:AF.（2）△ABC 的面积=△AEF 的面积.证（1）：设AB 与⊙O 相交于点G ，联结EC ，CG ，BF.∵EF ⊥AB ，CG ⊥AB ，∴GC ∥EF ，AC:AF=AG:AE ………………① 又∵AD 是⊙O 的切线，∴AD 2=AG ·AB ，也即AG:AD=AD:AB但∵AD=AE ，∴AG:AE=AE:AB ……………② 由①、②可得AE:AB=AC:AF证（2）：由（1）AE:AB=AC:AF ，则EC ∥BF ，△EBC 的面积=△EFC 的面积 ∴△ABC 的面积=△AEC 的面积+△EBC 的面积=△AEC 的面积+△EFC 的面积 =△AEF 的面积5．求证方程0)2()12(23=+-++-Q x Q x x 的一个根是1设这个方程的三个根是△ABC 的三个内角的正弦,sin ,sin ,sin C B A 求A 、B 、C 的度数以及Q 的值解：将x=1代入这个方程式，则01)2(1)12(123=+⋅-+⋅+-Q Q ，故知1是原方程的一个根由于1是原方程的一个根，所以方程左边能被x-1整除AGE DB GOF用x-1除方程左边后得商式.022=--Q x x根据题设条件（即有一个根为1，不妨设1sin =C ）及根与系数的关系可得⎪⎩⎪⎨⎧-=⋅=+=)3(sin sin )2(2sin sin )1(1sin Q B A B A C 由（1）可知C=900，于是A+B=900，B=900-A ，代入（2）得.212222sin sin )3(45459045,045,1)45cos(,1cos 45cos sin 45sin ,1cos 22sin 22,2cos sin ,2)90sin(sin -=⋅-=⋅-=︒=︒-︒=︒=∴=︒-∴=︒-=⋅︒+⋅︒=+∴=+=-︒+B A Q B A A A A A A A A A A A 式可得从即1957年普通高等学校招生全国统一考试数学1．甲、化简32221)27102(1.0)972(--++解：原式=.481110216910035)2764()101()925(32221=++=++--乙、求适合不等式22<+x x 的实数x 的范围解：原式为022<-+x x 解为：-2<x<1. 故x 的范围为-2<x<1. 丙、求证.210322+='︒ctg证：.2145sin 45cos 12450322+=︒︒+=︒='︒ctgctg 丁、在四面体ABCD 中，AC=BD ，P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点，求证：PQRS 为一个菱形证：由于点P 、Q 、R 、S 依次为棱AB 、BC 、CD 、DA 的中点，根据三角形两边中点连线的性质可得.////,21////BD SP RQ AC RS PQ ====而由题设，AC=BD ， ∴PQ=QR=RS=SP ，故 PQRS 为一个菱形戊、设b a ,为异面直线，EF 为ba ,的公垂线，α为过EF 的中点且与b a ,平行的平面，M 为a 上任一点，N 为b 上任一点求证线段MN 被平面α二等分证：过直线b 作平面β//α（如图）过直线a 及公垂线EF 作一平面，在此平面内作MC ∥EF ，且与平面α，β分别交于B 、C 两点设EF 、MN 分别与平面α交于点ASPDRC BQM E aB Aα DC bN FβA 、D∵点A 是EF 的中点，又ME ∥BA ∥CF ， ∴点B 是MC 的中点又∵DB ∥NC ， ∴D 是MN 的中点另法：如图，连接EN ，AB,BD 由AB b BD a b a //,////,//⇒αα由A 是EF 的中点得,D 为MN 的中点此即线段MN 被平面α二等分 2．解方程组⎩⎨⎧⋅==-++)2(101010)1(1)2lg()12lg( yx xy y x 解：由（1）可得,10)2)(12(=-+y x)3(01242 =-+-y x xy由（2）可得)4( y x xy +=将（4）代入（3）可得,012422=-+-+y x y x,01232=-+-y x)5(3212 xy +=再将（5）代入（4）可得,32123212xx x x ++=+⋅ 化简，得,012722=-+x x.41457±-=∴x abαEFAMNBD。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

全国卷历年高考真题汇编三角1（2017全国I 卷9题）已知曲线1:cos C y x =，22π:sin 23C y x ⎛⎫=+⎪⎝⎭，则下面结论正确的是（） A ．把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线2CB ．把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线2CC ．把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线2CD ．把1C 上各点的横坐标缩短到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线2C【答案】D【解析】1:cos C y x =，22π:sin 23⎛⎫=+ ⎪⎝⎭C y x【解析】首先曲线1C 、2C 统一为一三角函数名，可将1:cos C y x =用诱导公式处理．【解析】πππcos cos sin 222⎛⎫⎛⎫==+-=+ ⎪ ⎪⎝⎭⎝⎭y x x x ．横坐标变换需将1=ω变成2=ω，【解析】即112πππsin sin 2sin 2224⎛⎫⎛⎫⎛⎫=+−−−−−−−−−→=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭C 上各坐短它原y x y x x 点横标缩来【解析】2ππsin 2sin 233⎛⎫⎛⎫−−→=+=+ ⎪ ⎪⎝⎭⎝⎭y x x ．【解析】注意ω的系数，在右平移需将2=ω提到括号外面，这时π4+x 平移至π3+x ，【解析】根据“左加右减”原则，“π4+x ”到“π3+x ”需加上π12，即再向左平移π122 （2017全国I 卷17题）ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，已知ABC △的面积为23sin a A．（1）求sin sin B C ；（2）若6cos cos 1B C =，3a =，求ABC △的周长．【解析】本题主要考查三角函数及其变换，正弦定理，余弦定理等基础知识的综合应用. 【解析】（1）∵ABC △面积23sin a S A=.且1sin 2S bc A =【解析】∴21sin 3sin 2a bc A A = 【解析】∴223sin 2a bc A =【解析】∵由正弦定理得223sin sin sin sin 2A B C A =，由sin 0A ≠得2sin sin 3B C =.（2）由（1）得2sin sin 3B C =，1cos cos 6B C =∵πA B C ++=∴()()1cos cos πcos sin sinC cos cos 2A B C B C B B C =--=-+=-=又∵()0πA ∈，∴60A =︒，sin A =1cos 2A =由余弦定理得2229a b c bc =+-= ①由正弦定理得sin sin a b B A =⋅，sin sin a c C A=⋅ ∴22sin sin 8sin a bc B C A=⋅= ②由①②得b c +=∴3a b c ++=+ABC △周长为3+3. (2017·新课标全国Ⅱ卷理17)17.（12分）ABC ∆的内角,,A B C 的对边分别为,,a b c ,已知2sin()8sin 2B AC +=． (1)求cos B(2)若6a c += , ABC ∆面积为2,求.b 【命题意图】本题考查三角恒等变形，解三角形．【试题分析】在第（Ⅰ）中，利用三角形内角和定理可知A C B π+=-，将2sin 8)sin(2BC A =+转化为角B 的方程，思维方向有两个：①利用降幂公式化简2sin 2B，结合22sin cos 1B B +=求出cos B ；②利用二倍角公式，化简2sin 8sin 2B B =，两边约去2sin B ，求得2tan B ，进而求得B cos .在第（Ⅱ）中，利用（Ⅰ）中结论，利用勾股定理和面积公式求出a c ac +、，从而求出b ．（Ⅰ）【基本解法1】由题设及2sin8sin ,2BB C B A ==++π，故上式两边平方，整理得 217cos B-32cosB+15=0解得 15cosB=cosB 171（舍去），= 【基本解法2】由题设及2sin8sin ,2B BC B A ==++π，所以2sin 82cos 2sin 22B B B =，又02sin ≠B ，所以412tan =B ，17152tan 12tan 1cos 22=+-=B BB （Ⅱ）由158cosB sin B 1717==得，故14a sin 217ABC S c B ac ∆==又17=22ABC S ac ∆=，则由余弦定理及a 6c +=得所以b=2【知识拓展】解三角形问题是高考高频考点，命题大多放在解答题的第一题，主要利用三角形的内角和定理，正、余弦定理、三角形面积公式等知识解题，解题时要灵活利用三角形的边角关系进行“边转角”“角转边”，另外要注意22,,a c ac a c ++三者的关系，这样的题目小而活，备受老师和学生的欢迎． 4 （2017全国卷3理）17．（12分）ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c，已知sin 0A A =，a =2b =．（1）求c ；（2）设D 为BC 边上一点，且AD AC ⊥，求ABD △的面积．【解析】（1）由sin 0A A =得π2sin 03A ⎛⎫+= ⎪⎝⎭，即()ππ3A k k +=∈Z ，又()0,πA ∈，∴ππ3A +=，得2π3A =.由余弦定理2222cos a b c bc A =+-⋅.又∵12,cos 2a b A ===-代入并整理得()2125c +=，故4c =.（2）∵2,4AC BC AB ===，由余弦定理222cos 2a b c C ab +-==. ∵AC AD ⊥，即ACD △为直角三角形，则cos AC CD C =⋅，得CD =由勾股定理AD =又2π3A =，则2πππ326DAB ∠=-=，1πsin 26ABD S AD AB =⋅⋅=△5 （2017全国卷文1）14 已知π(0)2a ∈，,tan α=2，则πcos ()4α-=__________。

（法一）Θ0,2πα⎛⎫∈ ⎪⎝⎭，sin tan 22sin 2cos cos ααααα=⇒=⇒=，又22sin cos 1αα+=，解得sin 5α=，cos 5α=，cos (cos sin )4210πααα⎛⎫∴-=+=⎪⎝⎭．（法二）)sin cos (22)4cos(ααπα+=-21cos sin cos 42πααα⎛⎫∴-=+ ⎪⎝⎭．又Θtan 2α=222sin cos tan 2sin cos sin cos tan 15αααααααα∴===++，29cos 410πα⎛⎫∴-= ⎪⎝⎭，由0,2πα⎛⎫∈ ⎪⎝⎭知444πππα-<-<，cos 04πα⎛⎫∴-> ⎪⎝⎭，故cos 410πα⎛⎫-=⎪⎝⎭ 6.（2017全国卷2 文） 3.函数π()sin(2)3f x x =+的最小正周期为A.4πB.2πC. πD.π2【答案】C 【解析】由题意22T ππ==，故选C. 【考点】正弦函数周期【名师点睛】函数sin()(A 0,0)y A x B ωϕω=++>>的性质 (1)max min =+y A B y A B =-，. (2)周期2.T πω=(3)由 ππ()2x k k ωϕ+=+∈Z 求对称轴 (4)由ππ2π2π()22k x k k ωϕ-+≤+≤+∈Z 求增区间; 由π3π2π2π()22k x k k ωϕ+≤+≤+∈Z 求减区间;7（2017全国卷2文）13.函数()2cos sin f x x x =+的最大值为 .8（2017全国卷2文）16.ABC ∆的内角,,A B C 的对边分别为,,a b c ,若2cos cos cos bc B a C c A =+,则B = 【答案】3π 9（2017全国卷3文） 4．已知4sin cos 3αα-=，则sin 2α=（） A ．79-B ．29-C ．29D ．79【答案】A10 （2017全国卷3文）6．函数f (x )=15sin(x +3π)+cos(x ?6π)的最大值为（）A ．65B ．1C ．35D ．15【答案】A【解析】由诱导公式可得：cos cos sin 6233x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫-=-+=+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦ ，则：()16sin sin sin 53353f x x x x πππ⎛⎫⎛⎫⎛⎫=+++=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ , 函数的最大值为65. 本题选择A 选项. 7．函数y =1+x +2sin xx 的部分图像大致为（） A BD ．C D 【答案】D1、（2016全国I 卷12题）已知函数ππ()sin()(0),24f x x+x ，ωϕωϕ=>≤=-为()f x 的零点，π4x =为()y f x =图像的对称轴，且()f x 在π5π()1836，单调，则ω的最大值为（A ）11?????? ??（B ）9????? （C ）7??????? ?（D ）5 【答案】B考点：三角函数的性质2、（2016全国I 卷17题）（本小题满分12分）ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，已知2cos (cos cos ).C a B+b A c =（I ）求C ；（II）若c ABC △=ABC △的周长．【答案】（I ）C 3π=（II）5【解析】试题解析：（I ）由已知及正弦定理得，()2cosC sin cos sin cos sinC A B+B A =，()2cosCsin sinC A+B =．故2sinCcosC sinC =．可得1cosC 2=，所以C 3π=．考点：正弦定理、余弦定理及三角形面积公式3、（2015全国I 卷2题）sin20°cos10°-con160°sin10°=（A）（B（C ）12- （D ）12【答案】D 【解析】试题分析：原式=sin20°cos10°+cos20°sin10°=sin30°=12，故选D.考点：诱导公式；两角和与差的正余弦公式4、（2015全国I 卷8题）函数()f x =cos()x ωϕ+的部分图像如图所示，则()f x 的单调递减区间为(A)（kπ−14,kπ+34,）,k ∈z (b)（2kπ−14,2kπ+34）,k ∈z (C)（k −14,k +34）,k ∈z (D)（2k −14,2k +34）,k ∈z 【答案】D 【解析】试题分析：由五点作图知，1+4253+42πωϕπωϕ⎧=⎪⎪⎨⎪=⎪⎩，解得=ωπ，=4πϕ，所以()cos()4f x x ππ=+，令22,4k x k k Z πππππ<+<+∈，解得124k -＜x ＜324k +，k Z ∈，故单调减区间为（124k -，324k +），k Z ∈，故选D. 考点：三角函数图像与性质5、（2015全国I 卷16题）在平面四边形ABCD 中，∠A=∠B=∠C=75°，BC=2，则AB 的取值范围是【答案】（【解析】试题分析：如图所示，延长BA ，CD 交于E ，平移AD ，当A 与D 重合与E 点时，AB 最长，在△BCE 中，∠B=∠C=75°，∠E=30°，BC=2，由正弦定理可得sin sin BC BEE C=∠∠，即o o2sin 30sin 75BE=，解得BE AD ，当D 与C 重合时，AB 最短，此时与AB 交于F ，在△BCF 中，∠B=∠BFC=75°，∠FCB=30°，由正弦定理知，sin sin BF BCFCB BFC=∠∠，即o o2sin 30sin 75BF =，解得AB ）. 考点：正余弦定理；数形结合思想 6. （2014全国I 卷8题）设(0,)2πα∈，(0,)2πβ∈，且1sin tan cos βαβ+=，则 A .32παβ-=B .22παβ-=C .32παβ+=D .22παβ+=【答案】：Ｂ【解析】：∵sin 1sin tan cos cos αβααβ+==，∴sin cos cos cos sin αβααβ=+ ()sin cos sin 2παβαα⎛⎫-==- ⎪⎝⎭，,02222ππππαβα-<-<<-<∴2παβα-=-，即22παβ-=，选B7、（2014全国I 卷16题）已知,,a b c 分别为ABC ∆的三个内角,,A B C 的对边，a =2，且(2)(sin sin )()sin b A B c b C +-=-，则ABC ∆面积的最大值为 .【答案】【解析】：由2a =且 (2)(sin sin )()sin b A B c b C +-=-，即()(sin sin )()sin a b A B c b C +-=-，由及正弦定理得：()()()a b a b c b c +-=-∴222b c a bc +-=，故2221cos 22b c a A bc +-==，∴060A ∠=，∴224b c bc +-= 224b c bc bc =+-≥，∴1sin 32ABC S bc A ∆=≤，8、（2013全国I 卷15题）设当x =θ时，函数f (x )＝sin x －2cos x 取得最大值，则cosθ=______【命题意图】本题主要考查逆用两角和与差公式、诱导公式、及简单三角函数的最值问题，是难题. 【解析】∵()f x =sin 2cos x x -=5255(sin cos )x x - 令cos ϕ=55，25sin 5ϕ=-，则()f x =5(sin cos sin cos )x x ϕϕ+=5sin()x ϕ+，当x ϕ+=2,2k k z ππ+∈，即x =2,2k k z ππϕ+-∈时，()f x 取最大值，此时θ=2,2k k z ππϕ+-∈，∴cos θ=cos(2)2k ππϕ+-=sin ϕ=255-. 9、（2013全国I 卷17题）（本小题满分12分）如图，在△ABC 中，∠ABC ＝90°，AB= 3 ，BC=1，P 为△ABC 内一点，∠BPC ＝90°(1)若PB=12，求PA ；(2)若∠APB ＝150°，求tan ∠PBA【命题意图】本题主要考查利用正弦定理、余弦定理解三角形及两角和与差公式，是容易题.【解析】（Ⅰ）由已知得，∠PBC=o60，∴∠PBA=30o，在△PBA 中，由余弦定理得2PA =o 11323cos3042+-⨯⨯=74，∴PA=7；（Ⅱ）设∠PBA=α，由已知得，PB=sin α，在△PBA 中，由正弦定理得，o 3sin sin(30)αα=-，化简得，3cos 4sin αα=，∴tan α=34，∴tan PBA ∠=34.10、（2016全国II 卷7题）若将函数y =2sin 2x 的图像向左平移π12个单位长度，则平移后图象的对称轴为（A ）()ππ26k x k =-∈Z （B ）()ππ26k x k =+∈Z （C ）()ππ212Z k x k =-∈ （D ）()ππ212Z k x k =+∈【解析】B平移后图像表达式为π2sin 212y x ⎛⎫=+ ⎪⎝⎭，令ππ2π+122x k ⎛⎫+= ⎪⎝⎭，得对称轴方程：()ππ26Z k x k =+∈，故选B ．11、（2016全国II 卷9题）若π3cos 45α⎛⎫-= ⎪⎝⎭，则sin 2α=（A ）725 （B ）15（C ）15-（D ）725-【解析】D∵3cos 45πα⎛⎫-= ⎪⎝⎭，2ππ7sin 2cos 22cos 12425ααα⎛⎫⎛⎫=-=--= ⎪ ⎪⎝⎭⎝⎭，故选D ．12、（2016全国II 卷13题）ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，若4cos 5A =，5cos 13C =，1a =，则b = ．【解析】2113∵4cos 5A =，5cos 13C =，3sin 5A =，12sin 13C =， ()63sin sin sin cos cos sin 65B AC A C A C =+=+=，由正弦定理得：sin sin b a B A =解得2113b =． 13、（2015全国II 卷17题）?ABC 中，D 是BC 上的点，AD 平分∠BAC，?ABD 是?ADC 面积的2倍。