浮力习题中的液面变化问题-2019年文档
浮力整体法分析液面变化及冰化水问题

浮力整体法分析液面变化及冰化水问题第一篇:浮力整体法分析液面变化及冰化水问题捞放货物问题1、一艘船漂浮在湖面上,将船上的货物扔进湖里,请问船体将沉一些),湖面将(上升、下降或不变)。
2、一艘船漂浮在湖面上,将船上的货物用钢丝吊在船下,请问船体将(上浮一些或下沉一些),湖面将(上升、下降或不变)。
冰化水问题3、容器里装满水,水面上漂浮着一块冰,问,并在融化后水面将或不变)。
冰包物问题1、容器里盛满水,一块冰包木块浮在水面上,溶化后液面怎么变化降或不变)。
2、容器里盛满水,一块冰包铁块浮在水面上,溶化后液面怎么变化降或不变)。
3、容器里盛满水,一块冰包气泡浮在水面上,溶化后液面怎么变化降或不变)。
1.有一个烧杯,烧杯中的冰块漂浮在水中,烧杯中的水面恰好与烧杯口相平。
待这些冰全部融化后,水是否会溢出,或水面是否会下降?解析:因为冰块处于漂浮状态,故有G冰=F浮,∴ρ冰V冰g=ρ水V排g化解得ρ冰V冰=ρ水V排∵冰融化成水后质量不变,故有m冰=m水融∴ρ冰V冰=ρ水V 水融综合两式:ρ冰V冰=ρ水V排,ρ冰V冰=ρ水V水融可得ρ水V排=ρ水V水融∴V排=V水融,∴水面既不会升高也不会降低答:。
还有以下的几种类型的浮冰问题:1.冰在果汁中浮着,叫你判断冰融化后液面的变化,其实这时冰融化后水面时会变化的。
2.冰中含有杂质小石块,冰此时可能悬浮也可能漂浮,然后让你计算一些数据,比如压强,密度(石块的),等等!我在举个例子:2.一杯浓橘汁加了冰块后,刚好不会溢出,如果冰块融化,则液面将怎么变化?解析:(我要偷懒了)和上面那个题一样的方法,可以得出如下结论ρ冰V冰=ρ汁V 排,ρ冰V冰=ρ水V水融综合可得:ρ汁V排=ρ水V水融因为ρ汁>ρ水所以V排<V水融所以会溢出。
答:.........浮冰问题种种冰、水是同种物质的不同状态,冰可由水凝固而成,水由冰熔化可得。
由于冰、水密度不等,带来了一些需要我们探究的问题。
1、冰山一角到底是冰山的多少?解析:设冰山体积为V,浮在水面上的冰山体积为V1,因为冰漂浮在水面上,F浮=G冰,即ρ水g(V-V1)= ρ冰 gV1化简得V1=V冰(ρ水-ρ冰)/ρ水=V冰/10,即浮于水面的冰山一角是冰山的十分之一。
总复习浮力液面高度变化专题(定稿)闫

V排
Δh
F浮
G
A
h1 h2
ΔP
ΔF压
甲
乙
情景一:V排变化导致液面高度变化
A
Δh液升 Δh物降
A
甲
乙
液面上升的高度Δh液升与Δh物降的关系? S物Δh物降=(S容-S物)Δh液升
情景一:V排变化导致液面高度变化
A
Δh液降 Δh物升
A
甲
乙
液面下降高度Δh液降与Δh物升的关系?
S物Δh物升=(S容-S物)Δh液降
若注入液体的过程中细线对物块的拉力F随液 体深度h的变化关系图像如图丙所示。 请问:能从图像中得到什么信息?
(1)
(2)
F浮=G物
h=30cm
h’=35cm F拉=8N
(4)
( 5)
H=60cm
(3)
绳恰好拉直
恰好浸没
例3.如图10甲所示,圆柱形平底容器置于水平桌面上, 其底面积为500cm2。在容器内放入一个底面积为 200cm2、高为20cm的圆柱形物块,物块底部的中心通 过一段细线与容器底部相连。向容器内缓慢注入某种 液体直至将其注满,如图10乙所示。已知在注入液体 的过程中细线对物块的拉力F随液体深度h的变化关系 图像如图10丙所示。若将细线剪断,当物块静止时, 液体对容器底部的压强为 Pa。(g=10N/kg)
S容=500cm2
S物= 200cm2、h物= 20cm
h=30cm h’=35cm h容=60cm Δh
(1)
(2)
刚好F浮=G物 F浮=G物
(3)
(4)
(5) 绳恰好直 F拉=0N F浮=G物
(6) 恰好浸没 F浮不变 F拉=8N
浮力液面变化(经典推荐)
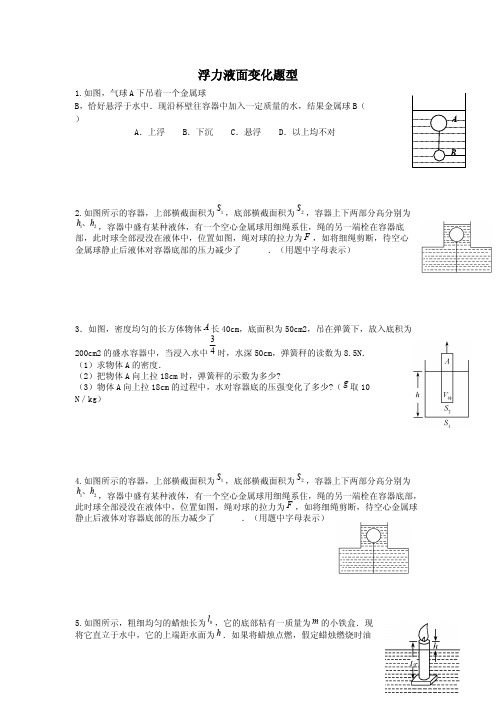
1.如图,气球 A 下吊着一个金属球 B,恰好悬浮于水中.现沿杯壁往容器中加入一定质量的水,结果金属球 B( ) A.上浮 B.下沉 C.悬浮 D.以上均不对
A
B
2.如图所示的容器,上部横截面积为 S1 ,底部横截面积为 S2 ,容器上下两部分高分别为 h1、h2 ,容器中盛有某种液体,有一个空心金属球用细绳系住,绳的另一端栓在容器底 部,此时球全部浸没在液体中,位置如图,绳对球的拉力为 F ,如将细绳剪断,待空心 金属球静止后液体对容器底部的压力减少了 .(用题中字母表示)
x
∴ 因每分钟烧去的蜡烛长为 l , 1h 1h x t l () 1 l (分).答案: () 1 l (分) ∴
1h 1
6.
<解析> 按题意,刻度线 a 和 b 所表示的密度分别为
a 1 103 kg/m3 ……………………①
b 2 103 kg/m3 ………………………②
3.如图,密度均匀的长方体物体 A 长 40cm,底面积为 50cm2,吊在弹簧下,放入底积为 3 200cm2 的盛水容器中,当浸入水中 4 时,水深 50cm,弹簧秤的读数为 8.5N. (1)求物体 A 的密度. (2)把物体 A 向上拉 18cm 时,弹簧秤的示数为多少? (3)物体 A 向上拉 18cm 的过程中,水对容器底的压强变化了多少?( g 取 10 N/kg)
4.如图所示的容器,上部横截面积为 S1 ,底部横截面积为 S2 ,容器上下两部分高分别为 h1、h2 ,容器中盛有某种液体,有一个空心金属球用细绳系住,绳的另一端栓在容器底部, 此时球全部浸没在液体中,位置如图,绳对球的拉力为 F ,如将细绳剪断,待空心金属球 静止后液体对容器底部的压力减少了 .(用题中字母表示)
2019年中考物理试题专题训练——浮力实验专题(word版含答案)

(2)分析图丙、丁可知,浮力大小跟物体浸没在水中的深度(选填“有关”或“无关”)。
(3)分析两图可知,浸在液体中的物体所受浮力大小跟液体密度有关。戊图中盐水的密度是kg/m3.如果在实验中不小心使戊图中的金属块接触了容器底且与容器底有力的作用,此时测量出的盐水密度值将如何变化,并分析原因。
(2)将合金块分别浸没在水和某液体中(如图1乙、丙所示),比较图1甲、乙、丙可知:。
(3)合金块的密度为ρ合金=g/cm3。
(4)若用此合金块制成一空心合金球,当合金球恰好能悬浮于图1丙所示液体中时,空心部分的体积是cm3。
12.(2019赤峰,20)如图所示,是探究同一物体所受浮力大小于哪些因素有关的实验过程。
(1)两次实验证明物体所受浮力随物体排开液体积的变化而变化(选填实验序号)
(2)进行乙、丙两次实验是为了探究物体所受浮力大小与关系。
(3)由丙、丁两次实验可知:完全浸没在同种液体中的物体,所受浮力大小与无关
13.(2019重庆A卷,18)小薇同学制作了如图1所示的探头进行了液体压强和浮力的综合探究。
3.(2019上海,26)某小组同学在“探究物体在液体中所受向上的力与哪些因素有关”实验中,用弹簧测力计拉着一个圆柱体,测力计示数为F0.现将圆柱体悬空放置在一个烧杯中,倒入液体A,圆柱体的下表面到液面的深度为 h,记录下此时弹簧测力计的示数为F,以及F0和F 的差为△F.接着,将液体A 钟换为液体B,重复上述实验,记录数据如下表二所示.
(1)金属块完全浸没在水中受到的浮力为N。
(2)金属块的密度是kg/m3。
(3)你还能求出有关金属块的哪些物理量:(写出三个物理量即可,不需要计算结果)
2.(2019 青岛,21)测量盐水的密度,方案如下:
浮力专题:浮力习题中的液面变化问题(有答案)

浮力专题:浮力习题中的液面变化问题【例1】(纯冰熔于液体)容器内分别装有水和盐水,在液面上浮着一块冰,问:(1)冰在水中熔化后,水面如何变化?(2)冰在盐水中熔化后,液面如何变化?【答案】(1)不变;(2)上升【解析】液面是否变化,关键是看V排是否等于V化水。
(1)①当冰漂浮时,依漂浮条件知,F浮=G冰即ρ水ɡV排= G冰= m冰g ∴V排=m冰/ρ水②冰化成水后,冰的质量与水的质量没有变化即m化水= m冰∴V化水=m冰/ρ水③所以V排=V化水即冰块完全熔化后水面高度不变。
(2)同理:纯冰浮在盐水液面上,当冰熔化后液面将上升。
练习1:若一冰块在水中,冰块与容器底部相接触并相互间有压力,则当冰块完全熔化后,容器内的水面将怎样变化?【答案】上升【解析】冰块没有漂浮在水面上,冰块所受浮力小于冰块所受重力,∴熔化前F浮<G冰,即ρ水g V排<G冰,故得V排<m冰/ρ水。
熔化为水的体积V化水=m水/ρ水= m冰/ρ水,∴V排<V化水,即熔化后水面要上升。
【例2】(冰中有杂质)在盛水的烧杯中漂浮着一块冰,冰中夹着一小木块,问:(1)当冰完全熔化为水时,水面将如何变化?(2)若冰中夹杂着一小石块,冰熔化后液面如何变化?【答案】(1)不变;(2)下降【解析】方法一:比较体积变化法①冰块漂浮时:F浮=G冰+G木即ρ水gV排= G冰+G木,V前排= (m冰+m木)/ ρ水=m冰/ρ水+m木/ρ水②当冰块化成水时:m化水= m冰∴V化水=m冰/ρ水又因为木块仍漂浮,F木浮= G木即ρ水gV木排= m木g ∴V木排=m木/ρ水V后排=V化水+V木排= m冰/ρ水+ m木/ρ水 (2)由(1)(2)得:V前排= V后排故当冰完全熔化成水时,水面不变。
方法二:比较浮力变化法熔化前冰块和木块都漂浮∴F前浮= G冰+ G木熔化后熔化成的水悬浮,木块仍漂浮∴F后浮= G化水+ G木又G化水= G冰所以F前浮=F后浮,即熔化前后所受浮力不变,所以液面将不变。
3 浮力——液面升降问题(原卷版)

B.A的一半浸入水中前后,台秤的示数变化了
C.若剪断细线,A物体下表面受到的压强先变大后不变
D.若剪断细线,待液面静止后,水对容器底的压强为
11、小科在水盆中洗碗,发现一个大碗正漂浮在水盆中,如图所示。他将水盆中的一些水放入大碗中,但大碗仍然漂浮。与原先相比,水盆中的水面将会(填“上升”、“不变”或“下降”),一不小心倾斜沉入水底,水盆底受水的压强将会(填“变大”、“不变”或“变小”)。
一、液面升降的三种情形
1、物体浸没
2、物体部分浸入
方法一:
方法二:
V1=2V2
V3+V1=V3+2V2
3、剪断绳子
液面升降:
二、液体和固压变化量:Δp水、ΔF水、ΔF桌、Δp桌
柱形容器中装有0.2m深的水,容器底面积为0.02m2,将重为10N,体积为1×10-3m3的正方体A放入上述液体中,A完全浸没且完全没有水溢出,求:
(1)水对容器底部压强变化量Δp水;
(2)水对容器底部压力变化量ΔF水;
(3)容器对桌面压力变化量ΔF桌;
(4)容器对桌ρ水gΔh=1.0×103kg/m3×10N/kg×0.05m=500Pa
(2)ΔF=ΔpS=500Pa×0.02m2=10N
(3)F压1=F支1=G液+G容F压2=F支2=G液+G容+G物ΔF桌= F压2-F压1=G物=10N
A.下降B.上升C.不变D.无法判断
7、如图所示,柱形容器的底面积为500cm2,重为5N的木块A在水中处于静止状态,此时绳子的拉力为3N。若绳子突然断了,待木块再次静止时,容器中水面将下降的高度是( )
A.4.0×103mB.6.0×10-3mC.1.0×10-2mD.1.6×10-2m
初中物理:浮力-液面升降问题

G总
F浮总
乙图中
(2)冰熔化问题
思路:
冰漂浮
液面不变h1=h
点题:实际就是比较V排和V化水
S
h
水
S
h1
水
液面上升h1〉h
S S 淡盐水
S
盐水
盐水
1
2
3
(3)冰中物,冰熔化问题
S
h
水
S
h1
水
S
h
水
等效
熔化
液面不变h1=h
S 水 S 水 熔化 液面下降
h
h
h1
水
S
等效
4、浮力与压力、压强相结合问题
—总体积变化?
—物体排开液体的总体积变化?
—浮力变化?
思路:液面升降?
3、液面升降问题
S
h
S
h1
思路:整体法
船和物均漂浮
G总不变
F总浮不变
V排总不变
液面不变h1=h
(1)船中物问题
1
第一部分
2
第二部分
思路:
S
h
S
h2
甲图中 船和物漂浮
F总浮变小
V排总变小
液面下降
甲图
乙图
G球
N
F球浮
G船
h
S
h1
S
甲
h1
S
乙
h1
S
丙
h1
S
丁
液体对容器底的压力变化
从无到有
4、浮力与压力、压强相结合问题
S
h1
S
h2
液体对容器的压力变化
有中有变
01
边审题边画图,明确物理状态、过程和条件
浮力专题:液面升降问题

(3)
.
橡皮泥密度的表达式:
.
2.小红的妈妈有一只翠玉手镯,她想知道手镯的密度。现在只有如
下器材:一个水槽和足量的水、细线、刻度尺、一个正方体木块。请你
按照下面的实验设计思路,把实验步骤补充完整,并利用测量中的表
示符号和水的密度ρ水,写出测量翠玉手镯密度的数学表达式。实验 步骤:
①水槽中装入适量水,将木块放入水槽中,用刻度尺测出木块下表面到水面的距离 h1;
5
【浮力与密度实验练习】
1.用图所示的方法可以粗测出橡皮泥的密度.请你将李明同学测橡皮泥密度的实验步
骤补充完整,并用测得的物理量表示出橡皮泥密度的表达式.实验步骤:
(1)将适量的水倒入烧杯中,用刻度尺测出烧杯中水的深度 h1. (2)将橡皮泥捏成球状后放入烧杯中(如图甲所示),用刻度尺
测出此时烧杯中水的深度 h2.
9.下图是常见的厕所自动冲水装置原理图,水箱内有质量 m1=0.4kg,体积 V1=3×10-3m3 的浮筒 P,另有一厚度不计,质量 m2=0.2kg,面积 S2=8×10-3m2 的盖板 Q 盖在水箱底部 的排水管上,用细线将 P、Q 连接,当供水管上流进水箱的水使浮筒刚好浸没时,盖板 Q 恰好被拉开,水通过排水管流出冲洗厕所,当盖板 Q 恰好被拉开 的瞬间,求:(1)浮筒受到的浮力大小。 (2)细线对浮筒 P 的拉力大小。(3)水箱中水的深度。
量△V 水=
。
,加入水
*若木块被按压又下降 h(水未溢出),则水面升高高度△h2=
。
2、将木块(密度为ρ,底面积 S0,高为 h0)立放于容器中(容器底面积 S0),
向 容 器 中 加 水( ,密 度 为 ρ 水 ),水 面 高 度 为 h ,木 块 未 浮 起 ,则 V 排
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浮力习题中的液面变化问题
浮力是初中物理教学中的重点和难点。
在浮力习题教学中经常会涉及到求液面变化的问题。
这种问题的综合性较强,是对学生综合运用物理知识分析并解决相关问题的考查。
本文由生活中初春开化时河面将如何变化这一问题引入,对漂浮于水面的冰块融化后液面将如何变化这一问题做了讨论并以此展开联想,分别论述了浮力习题中经常涉及到的求解液面变化的几种情况。
每当初春河开化时,我们都会发现河面上漂浮着很多冰排,那么当这些冰排融化后,河面将如何变化呢?我们可以把漂浮在河面上的冰排看作是漂浮在量杯中的冰块,计算冰块融化后量杯内液面示数的变化,并对冰中混有石子、汽泡、油滴、蜡块这四种情况加以讨论。
例:纯冰漂在水面的情形
水槽中装有体积为V的水,水面上漂浮着重为G的一块冰。
求冰融化后,液面示数将如何变化?
分析:设冰块的重力为G,其质量为m,所受浮力为F1,排开水的体积为V1,冰块的体积为V2,冰块未融化时液面以下的体积为V12,冰块融化成水的体积为V3,冰块融化后液面以下的体积为V13,水的密度为P1,冰的密度为P2。
在冰块未融化之前,由于冰块是漂浮在水面上的,故
F1=G
根据阿基米德原理F1=P1gV1
G=mg=P2gV2
整理可得P1gV1=P2gV2
当冰块熔化后,冰块融化成水的体积为V3
此时
故
也就是说,漂浮在水面上的冰排开水的体积恰好等于冰化成水的体积,所以冰融化后液面保持不变。
从这道题可以看出当纯冰漂浮在水面时冰融化后液面不变化。
但是漂浮的冰的内部混有其他物质时,液面将如何变化呢?下面我们对以下几种情况对该题进行讨论。
变试1:冰中混有石子的情形
量杯中装有体积为V的水,水面上漂浮着重为G的一混有小石子的冰块,小石子的重力为G0。
求冰融化后,液面示数将如何变化?
分析:设冰块的总重力为G,其质量为m,纯冰部分重力为G1,所受浮力为F1,排开水的体积为V1,冰块的体积为V2,冰块未融化时液面以下的体积为V12,冰块融化成水的体积为V3,冰块融化后液面以下的体积为V13,水的密度为P1,冰的密度为P2,小石子的质量为m0,小石子的体积为V0,密度为P0。
在冰块未融化之前,由于冰块是漂浮在水面上的,故
F1=G
根据阿基米德原理
F1=P1gV1
而G=G1+G0=P2g(V2V0)+G0
所以P1gV1=P2g(V2V0)+G0
整理可得
当冰块融化后,冰块融化成水的体积为V3
当冰块融化后,石子落入水中,此时石子排开水的体积为石子的体积V0。
因为P0>P1
故V12>V13
也就是说,当冰块中含有石块时,冰块融化后液面下降。
当然,这道题除了计算以外,还有一种简便的解法。
石块单独放入水中是要沉入水底的,但由于外面包裹了冰块而漂浮在水面上。
我们可以看做是石块借助冰增加了自身的体积,从而增大了浮力使自身漂浮在水面上。
当冰融化后这种凭借消失,浮力变小,石块下沉,排开水的体积变小,故液面下降。
变试2:冰中混有汽泡的情形
量杯中装有体积为V的水,水面上漂浮着重为G的一混有汽泡的冰块,汽泡的重力为G0。
求冰融化后,液面示数将如何变化?
分析:设冰块的总重力为G,其质量为m,纯冰部分重力为G1,所受浮力为F1,排开水的体积为V1,冰块的体积为V2,冰
块未融化时液面以下的体积为V12,冰块融化成水的体积为V3,冰块融化后液面以下的体积为V13,水的密度为P1,冰的密度为P2,汽泡的质量为m0,汽泡的体积为V0,密度为P0。
在冰块未融化之前,由于冰块是漂浮在水面上的,故
F1=G
根据阿基米德原理F1=P1gV1
而G=G1+G0=P2g(V2V0)+G0
所以P1gV1=P2g(V2V0)+G0
整理可得
当冰块融化后,冰块融化成水的体积为V3
当冰块融化后,气体释放,
V12>V13
故液面下降。
也就是说,当冰块中含有汽泡时,冰块融化之后气体释放,液面下降。
我们可以将冰块、水、汽泡看作一个整体。
由于纯冰化成水后液面不变,当冰块中含有汽泡时,冰块融化之后气体要从整体中释放出去,故液面下降。
变试3:冰中混有油滴的情形
量杯中装有体积为V的水,水面上漂浮着重为G的一混有油滴的冰块,油滴的重力为G0。
求冰融化后,液面示数将如何变化?
分析:设冰块的总重力为G,其质量为m,纯冰部分重力为
G1,所受浮力为F1,排开水的体积为V1,冰块的体积为V2,冰块未融化时液面以下的体积为V12,冰块融化成水的体积为V3,冰块融化后油平铺于水面总体积为V13,水的密度为P1,冰的密度为P2,油滴的质量为m0,油滴的体积为V0,密度为P0。
在冰块未融化之前,由于冰块是漂浮在水面上的,故
F1=G
根据阿基米德原理F1=P1gV1
而G=G1+G0=P2g(V2V0)+G0
所以P1gV1=P2g(V2V0)+G0
因为m0=P0V0
所以
当冰块融化后,冰块融化成水的体积为V3
当冰块融化后,由于油的密度比水小,所以油会平铺于水面因为P0<P1
所以V12<V13 因为纯冰融化成水后液面不变。
本题相当于把原题中冰内的一部分变成油,如图2所示。
我们可以假定为将图甲中虚线部分的冰变为油。
在图甲中虚线部分为冰,当冰化成水后,虚线部分的冰体积变小而液面不变。
而图乙中虚线部分为等体积的油,油体积不变而平铺于液面。
既当冰化成水后,虚线部分的油体积不变故液面升高。
变试4:冰中混有蜡块的情形
量杯中装有体积为V的水,水面上漂浮着重为G的一混有蜡
块的冰块,如图3所示。
蜡块的重力为G0。
求冰融化后,液面示数将如何变化?
分析:设冰块的总重力为G,其质量为m,纯冰部分重力为G1,所受浮力为F1,排开水的体积为V1,冰块的总体积为V2,冰块未融化时液面以下的总体积为V12,冰块融化成水的体积为V3,冰块融化后蜡块仍然漂浮,所受浮力为F2,冰块融化后蜡块在液面以下的体积为V30,液面以下的总体积为V13,水的密度为P1,冰的密度为P2,蜡块的质量为m0,蜡块的体积为V0,密度为P0。
在冰块未融化之前,由于冰块是漂浮在水面上的,故
F1=G
根据阿基米德原理F1=P1gV1
而G=G1+G0=P2g(V2V0)+G0
所以P1gV1=P2g(V2V0)+G0
因为m0=P0V0
所以
当冰块融化后,冰块融化成水的体积为V3
当冰块融化后,由于蜡的密度比水小,所以蜡块会漂浮于水面
此时F2=G0
根据阿基米德原理F2=P1gV30
而G0=m0g=P0gV0
所以P1gV30=P0gV0
冰块融化后液面以下的总体积
所以V13=V12
故冰融化后液面不变。
由于蜡块无需借助冰块也能漂浮在水面上,所以冰的融化对蜡块没有影响,故冰融化后液面不变。
我们对上题及其几个变式比较后不难发现这样的结论:纯冰漂浮在水面上融化后液面不变,当冰中混有石子或汽泡时融化后液面下降,当冰中混有油滴时融化后液面上升,当冰中混有蜡块时融化后液面不变。
在解决浮力习题中的液面变化问题时,首先要对所研究对象的初始状态进行受力分析,列出平衡方程。
根据阿基米德原理将方程展开。
然后再分析当条件变化后的情形,并对两种情形加以比较,或进行相关的讨论得出结论。
同时要注意分析所得结论的物理意义以及与实际生活之间的联系。
除了理论计算分析以外,还可以用一些简便方法分析,即从定性的角度加以分析比较。
在分析了基本问题的基础上,再对该问题采用变换题设条件的方式进行变式,从而对该问题进行进一步拓展。
2.哈尔滨师范大学物理与电子工程学院)。
