201x年中考数学专题复习小训练 专题1 实数
中考数学复习《实数》专项测试卷(带答案)

中考数学复习《实数》专项测试卷(带答案)学校:___________班级:___________姓名:___________考号:___________一、单选题 1.与2(9)-结果相同的是( )A.3±B.|3|C.23D.方程281x =的解2.下列说法正确的是( )A.81-平方根是-B.81的平方根是9C.平方根等于它本身的数是1和0D.21a +一定是正数3.一个正方体的棱长为a ,体积为b ,则下列说法正确的是( )A.b 的立方根是a ±B.a 是b 的立方根C.a b =D.b a =4.下列关于5说法错误的是( ) A.5是无理数 B.数轴上可以找到表示5的点C.5相反数是5-D.53>5.估计11832的运算结果介于( )A.2与3之间B.3与4之间C.4与5之间D.5与6之间6.若实数a ,b 满足13a b +=( )A.a ,b 都是有理数B.a b -的结果必定为无理数C.a ,b 都是无理数D.a b -的结果可能为有理数7.如图,在ABC △中90ACB ∠=︒,AC=3,BC=1,AC 在数轴上,点A 所表示的数为1,以点A 为圆心,AB 长为半径画弧,在点A 左侧交数轴于点D ,则点D 表示的数是( )10 B.10- C.110-1018.若1014M -=,12N =则M ,N 的大小关系是( )A.M N <B.M N =C.M N >D.无法比较9.已知实数tan30sin 45cos60a b c =︒=︒=︒,,,则下列说法正确的是( )A.b a c >>B.a b c >>C.b c a >>D.a c b >>10.定义运算:若,则,例如328=,则2log 83=.运用以上定义,计算:53log 125log 81-=( )A.1-B.2C.1D.411.在下列计算中,正确的是( )A.()56+-=-B.122=C.()26⨯-=D.3sin 30︒= 12.式子52的倒数是( ) A.52 B.52- C.25+ D.52213.对于实数a 、b ,定义22()*2()a b ab a b a b ab a b a b +-≥⎧=⎨--<⎩,则结论正确的有( )①5*31=;②22272(1)*(21)451(1)m m m m m m m m ⎧-+-<-=⎨-+≥⎩; ③若1x ,2x 是方程2560x x --=的两个根,则12*16x x =或17-;④若1x ,2x 是方程210x mx m +--=的两个根12*4x x =,则m 的值为3-或.A.1个B.2个C.3个D.4个二、填空题14.在实数: 中无理数有______个.15a 是一个无理数,且13a <<,请写出一个满足条件的a 值_____.16.011|3|(3π)()tan 45162--+-+-+︒+=______. 17.若m 为7的整数部分,n 为7的小数部分,则)7m n =______. 18.实数a ,b ,c 在数轴上的点如图所示,化简222()()a a b b c +-=____________.三、解答题19.计算m a b =log (0)a b m a =>6-(1)11233- (2)12632322⨯- (3)2245tan 30cos60︒+⋅︒︒20.计算:)102cos6031(16)27--︒-+-. 21.设5a 是一个两位数,其中a 是十位上的数字(9a ≤≤).例如,当a =时5a 表示的两位数是45.尝试:①当1a =时2152251210025=⨯⨯+=;①当2a =时2256252310025==⨯⨯+;①当3a =时2351225==______;…… 归纳:()25a 与()100125a a ++有怎样的大小关系? 验证:请论证“归纳”中的结论正确.22.若正整数a 是4的倍数,则称a 为“四倍数”,例如:8是4的倍数,所以8是“四倍数”.(1)已知p 是任意三个连续偶数的平方和,设中间的数为2n (n 为整数),判断p 是不是“四倍数”,并说明理由;(2)已知正整数k 是一个两位数,且10k x y =+(19x y ≤<≤,其中x ,y 为整数),将其个位上的数字与十位上的数字交换,得到新数m .若m 与k 的差是“四倍数”,求出所有符合条件的正整数k . 参考答案1.答案:C 解析:2(9)819-==33=239=方程281x =的解为9x =±. 故选C.2.答案:D解析:A 、81-是负数,负数没有平方根,不符合题意;B 、819= 9的平方根是3±,不符合题意;C 、平方根等于它本身的数是0,1的平方根是1±,不符合题意;D 、21>0a + 正数的算术平方根大于0,符合题意.故选:D.3.答案:B 解析:一个正方体的棱长为a ,体积为b∴3b a =,即:3a b =∴a 是b 的立方根故选:B.4.答案:D 解析:①5 2.2365857......≈属于无限不循环小数 ①5是无理数,故A 选项正确;①数轴上可以表示任意实数 ①数轴上可以找到表示5的点,故B 选项正确;①5相反数是5,故C 选项正确; ①5 2.2365857......≈①53<,故D 选项错误,符合题意故选:D.5.答案:C 解析:1183232223=+33=+; 132<<4335∴<<;故选:C.6.答案:D解析:A 、当2a =时13213b ==--a 是有理数,b 是无理数,故A 错误;B 、当1322a b ==-,那么0a b -=,所以B 错误; C 、当2a =时13b =-,a 是有理数,故选项C 错误;D 、当1322a b ==-,那么0a b -=,所以选项正确,D 正确. 故选:D.7.答案:C 解析:在Rt ABC △中3AC =,BC=1 22223110AB AC BC ∴=++=∴点D 表示的数为:110故选:C.8.答案:C 解析:1014M -=12= 1011103424M N ∴-=-=103> 0M N ∴->M N ∴>.故选C.9.答案:A 解析:321tan 30sin 45cos 602a b c =︒==︒==︒= 132232<< ∴b a c >> 故选:A.10.答案:A解析:35125= 4381=5log 1253∴= 3log 814=53log 125log 81∴-34=-1=-.故选:A.11.答案:A解析:A 、5(6)561+-=-=-正确,符合题意; B 、1222=原计算错误,不符合题意; C 、3(2)6⨯-=-原计算错误,不符合题意;D 、1sin 302=︒原计算错误,不符合题意. 故选: A.12.答案:A 解析:()()1521 52525252⨯==--+式子5的倒数是52式子5的倒数是52,故选:A.13.答案:C 解析:①5*32523531=⨯+⨯-⨯=,故①正确;②当21m m ≥-时即1m ≤时()()()22*212221212422272m m m m m m m m m m m m -=+---=+--+=-+-当21m m <-时即1m >时 ()()()22*21221214221451m m m m m m m m m m m m -=----=---+=-+()()222721*21451(1)m m m m m m m m ⎧-+-≤∴-=⎨-+>⎩,故②错误; ③1x ,2x 是方程2560x x --=的两个根 125x x ∴+= 126x x =-当12x x ≥时()()121212*225616x x x x x x =+-=⨯--= 当12x x <时()()121212*226517x x x x x x =-+=⨯--=-,故③正确;④1x ,2x 是方程210x mx m +--=的两个根12x x m ∴+=- 121x x m =--当12x x ≥时()()121212*22114x x x x x x m m m =+-=----=-+= 解得:3m =-当12x x <时()()121212*221()24x x x x x x m m m =-+=⨯----=--=解得:6m =-综上可知:①③④正确 故选:C.14.答案:4 解析:3644= 其中8 ⋯ π -2是无理数,共4个 故答案为:4.15.答案:2解析:2123<< 2a ∴=.故答案:2(答案不唯一).16.答案:7 解析:0113(3π)()tan 45162-+-+-+︒+31(2)14=++-++7=.17.答案:3 解析:479<<273∴<2m ∴= 72n = )7(72)(72)743m n ==-=∴故答案为3.18.答案:0解析:由数轴可知0b c a <<<则0a b +< 0b c -<222()||()a a b c b c +---()()a a b c b c =-+++-a abc b c =--++-0=.故答案为:0.19.答案:(1)1(2)5 (3)76解析:(1)(133********===; (2)12632322⨯- 22126322⨯=+632=-+5=;(3)2245tan 30cos60︒+⋅︒︒2312222=+⨯⎝⎭ 21113=+⨯ 76=. 20.答案:532 解析:)102cos6031(16)27--︒-+- 1113133222=-+=53.21.答案:尝试3410025⨯⨯+ 归纳()()25100125a a a =++ 验证:见解析解析:尝试:当3a =时2351225==3410025⨯⨯+; 归纳:()()25100125a a a =++; 验证:等号左边222(5)(105)10010025a a a a =+=++ 等号右边2100(1)2510010025a a a a ++=++ 所以,等号左边=等号右边,等式成立,即证.22.答案:(1)p 是“四倍数”;理由见解析(2)15,19,26,37,48,59解析:(1)p 是“四倍数”,理由如下:①()()()22222222p n n n ++=+-()22128432n n =+=+①p 是“四倍数”;(2)由题意得10m y x =+,则()()10109m k y x x y y x -=+-+=-. ①19x y ≤<≤,其中x ,y 为整数①18y x ≤-≤.若()9y x -.是4的倍数,则4y x -=或8y x -=.当4y x -=时符合条件的k 是15,26,37,48,59; 当8y x -=时符合条件的k 是19.①所有符合条件的正整数k 是15,19,26,37,48,59.。
2023年九年级数学中考复习《实数的计算》常考题型专题训练+

2022-2023学年九年级数学中考复习《实数的计算》常考题型专题训练(附答案)1.计算:(﹣48)×(﹣).2.计算:﹣32÷(﹣2)2×|﹣1|×6+(﹣2)3.3.计算:|﹣2|+tan60°﹣()﹣1﹣(+2023)0.4.计算:.5.计算:(1)++﹣(π﹣3.14)0;(2).6.若一个整数能写成a2+b2(a,b都是整数)的形式,则称这个数为“航天数”,例如:因为2=12+12,所以2是“航天数”,再如T=m2+2m+1+n2=(m+1)2+n2(m,n为整数),所以T也是“航天数”.(1)判断13是否是“航天数”,并说明理由.(2)若M=x2+6x+9+4y2+8y+k(x,y都是整数,k为常数),要使M为“航天数”,请求出常数k的值.(3)若P=2x2+6x+5是“航天数”,且P=(x+2)2+A2,求整式A.7.对于有理数x,y,a,t,若|x﹣a|+|y﹣a|=t,则称x和y关于a的“美好关联数”为t,例如,|2﹣1|+|3﹣1|=3,则2和3关于1的“美好关联数”为3.(1)﹣3和5关于2的“美好关联数”为;(2)若x和2关于3的“美好关联数”为4,求x的值;(3)若x0和x1关于1的“美好关联数”为1,x1和x2关于2的“美好关联数”为1,x2和x3关于3的“美好关联数”为1,…,x40和x41关于41的“美好关联数”为1,….①x0+x1的最小值为;②x1+x2+x3+……+x40的最小值为.8.计算:﹣12+2sin260°﹣﹣3tan45°+(tan30°)﹣1.9.计算:×(﹣)+÷2﹣(π﹣1)0.10.阅读下面的文字,解答问题.例如:因为<<,即2<<3,所以的整数部分为2,小数部分为﹣2.请解答下列各题:(1)的整数部分是,小数部分是.(2)已知9﹣小数部分是m,9+小数部分是n,且x2=m+n,请求出满足条件的x的值.11.计算(1)+﹣(2)﹣++12.观察下列运算过程:22=2×2=4,;,=;…(1)根据以上运算过程和结果,我们发现:22=;()2=;(2)仿照(1)中的规律,判断()3与()﹣3的大小关系;(3)求(﹣)﹣4×()4÷()﹣3的值.13.已知2x+7y+1的算术平方根是6,8x+3y的立方根是5,求x+y的平方根.14.最近李老师家刚买了一辆小轿车,他连续记录了7天中小轿车每天行驶的路程(如表),以50千米为标准,多于50千米的记为“+”,不足50千米的记为“﹣”,刚好50千米记为“0”.第一天第二天第三天第四天第五天第六天第七天路程(千米)﹣8﹣11﹣140﹣16+41+8(1)求出这七天中平均每天行驶多少千米?(2)若每行驶100千米需用汽油6升,汽油价7.7元每升,请计算李老师家一个月(按30天算)的油费是多少元?15.计算:(1)sin60°﹣tan30°﹣2﹣1+(﹣cos45°)0.(2)3tan30°﹣(cos60°)﹣1+cos45°+.16.先阅读材料,再解答问题.计算:﹣5﹣(+9)﹣(﹣17)+(﹣3)解:﹣5﹣(+9)﹣(﹣17)+(﹣3)=﹣5+(﹣9)+(+17)+(﹣3)=[(﹣5)+(﹣)]+[(﹣9)+(﹣)]+(17+)+[(﹣3)+(﹣)]=[(﹣5)+(﹣9)+17+(﹣3)]+[﹣+(﹣)++(﹣)]=0+(﹣1)=﹣1.上面的解题方法叫做拆项法.仿照上面的方法,计算:(﹣2023)+(﹣2022)+4046+(﹣1).17.在有些情况下,不需要计算出结果也能把绝对值符号去掉.例如:例如:|6+7|=6+7;|6﹣7|=7﹣6;|7﹣6|=7﹣6;|﹣6﹣7|=6+7;(1)根据上面的规律,把下列各式写成去掉绝对值符号的形式:①|7﹣21|=;②=;③=;④=;(2)用合理的方法计算:;(3)用简便的方法计算:.18.阅读材料一:21=2,22=4,23=8,24=16,25=32,…材料二:求1+2+22+23+…+22019+22020的值.解:设S=1+2+22+23+…+22019+22020①,将等式①的两边同乘以2,得2S=2+22+23+24+…+22020+22021②,用②﹣①得,2S﹣S=22021﹣1,即S=22021﹣1.即1+2+22+23+…+22019+22020=22021﹣1.根据以上材料回答:(1)27的个位数字为;(2)1+2+22+23+…+22021+22022结果的个位数字为;(3)请计算1+7+72+73+…+799+7100的值.19.某一出租车一天下午以鹿鸣路初级中学为出发地在东西方向营运,向东为正,向西为负,行车里程(单位:km)依先后次序记录如下,+9,﹣3,﹣5,+4,﹣8,+6,﹣3,﹣6,﹣4,+12.(1)将最后一名乘客送到目的地,出租车离鹿鸣路初级中学出发点多远?在鹿鸣路初级中学的什么方向?(2)出租车在行驶过程中,每千米耗油0.08升,求这辆出租车共耗油多少升?(3)出租车在行驶过程中,离鹿鸣路初级中学最远的距离是多少?(4)出租车按物价部门规定,起步价(不超过3千米)为8元,超过3千米的部分每千米的价格为1.4元,司机一个下午的营业额是多少?20.有一种“24点”的游戏,其游戏规则是这样的:将4个1至13之间的数进行加减乘除四则运算(每个数只能用一次),使其结果为24,例如1,2,3,4可作如下运算:如(1+2+3)×4=24.(1)现有4个有理数:3,4,﹣6,10,运用上述规则,写出两种不同方法的算式,使其结果为24;(2)现有4个有理数:1,2,4,﹣8,再多给你一种乘方运算,请你写出一个含乘方的算式,使其结果为24;(3)现有4个有理数:1,5,5,5,请你写出一个算式,使其结果为24.参考答案1.解:(﹣48)×(﹣)=48×+48×﹣48×=24+30﹣28=26.2.解:﹣32÷(﹣2)2×|﹣1|×6+(﹣2)3=﹣9÷4××6+(﹣8)=﹣9×××6+(﹣8)=﹣18+(﹣8)=﹣26.3.解:|﹣2|+tan60°﹣()﹣1﹣(+2023)0=2+×﹣2﹣1=2+3﹣2﹣1=2.4.解:原式=2﹣1+2+2=5.5.解:(1)原式=2﹣++3﹣1=4﹣;(2)原式=12﹣6﹣4×÷=12﹣6﹣=12﹣6﹣3=6﹣3.6.解:(1)∵13=22+32,∴13是“航天数”;(2)∵M=x2+6x+9+4y2+8y+k,∴M=(x+3)2+(2y+2)2﹣4+k,∵M为“航天数”,∴﹣4+k=0,∴k=4;(3)∵P=2x2+6x+5是“航天数”,P=(x+2)2+A2,∴A2=2x2+6x+5﹣(x+2)2,∴A2=2x2+6x+5﹣x2﹣4x﹣4=x2+2x+1=(x+1)2,∴A=x+1.7.解:(1)|﹣3﹣2|+|5﹣2|=8,故答案为:8;(2)∵x和2关于3的“美好关联数”为4,∴|x﹣3|+|2﹣3|=4,∴|x﹣3|=3,解得x=6或x=0;(3)①∵x0和x1关于1的“美好关联数”为1,∴|x0﹣1|+|x1﹣1|=1,∴在数轴上可以看作数x0到1的距离与数x1到1的距离和为1,∴只有当x0=0,x1=1时,x0+x1有最小值1,故答案为:1;②由题意可知:|x1﹣2|+|x2﹣2|=1,x1+x2的最小值1+2=3;|x3﹣4|+|x4﹣4|=1,x3+x4的最小值3+4=7;|x5﹣6|+|x6﹣6|=1,x5+x6的最小值5+6=11;|x7﹣8|+|x8﹣8|=1,x7+x8的最小值7+8=15;.......|x39﹣40|+|x40﹣40|=1,x39+x40的最小值39+40=79;∴x1+x2+x3+……+x40的最小值:3+7+11+15+...+79==820.故答案为:820.8.解:﹣12+2sin260°﹣﹣3tan45°+(tan30°)﹣1=﹣1+2×()2﹣(﹣1)﹣3×1+()﹣1=﹣1+2×﹣+1﹣3+=﹣1+﹣+1﹣3+=﹣.9.解:原式=+22﹣1=3﹣+1=1=3﹣3+1﹣1=3﹣3.10.解:(1)∵<,即4<<5,∴的整数部分是4,小数部分是﹣4,故答案为:4,﹣4;(2)∵的整数部分是4,∴9﹣小数部分是m=9﹣﹣4=5﹣,9+小数部分是n=9+﹣13=﹣4,∴x2=m+n=5﹣+﹣4=1,∴x=±1,即满足条件的x的值是±1.11.解:(1)+﹣=3﹣4﹣2=﹣1﹣2;(2)﹣++=﹣5﹣++=﹣.12.解:(1)∵22=2×2=4,,∴;∵,=,∴,故答案为:;;(2)()3=()﹣3,理由:∵==,==,∴()3=()﹣3.(3)原式=×÷23=×=16×=2.13.解:∵2x+7y+1的算术平方根是6,∴2x+7y+1=36,即2x+7y=35,∵8x+3y的立方根是5,∴8x+3y=125,解,得,∴x+y=16,∴x+y的平方根为±4.14.解:(1)50+[(﹣8)+(﹣11)+(﹣14)+0+(﹣16)+(+41)+(+8)]÷7=50+0=50(千米),答:这七天平均行驶50千米.(2)30×50×6÷100×7.7=90×7.7=693(元),答:李老师家一个月的油费是693元.15.解:(1)sin60°﹣tan30°﹣2﹣1+(﹣cos45°)0=﹣×﹣+1=﹣1﹣+1=﹣;(2)3tan30°﹣(cos60°)﹣1+cos45°+=3×﹣()﹣1+2×+=﹣2+2+(﹣1)=+﹣1=2﹣1.16.解:原式=(﹣2023﹣)+(﹣2022﹣)+(4046+)+(﹣1﹣)=﹣2023﹣﹣2022﹣+4046+﹣1﹣=(﹣2023﹣2022﹣1)+4046+()﹣﹣=﹣4046+4046+0﹣()=﹣=﹣.17.解:(1)①|7﹣21|=21﹣7;②|﹣+0.8|=0.8﹣;③||=;④|3.2﹣2.8﹣|=2.8+﹣3.2;故答案为:①21﹣7;②0.8﹣;③;④2.8+﹣3.2;(2)原式=+﹣=(﹣)+()﹣=﹣;(3)原式=+++•+===.18.解:(1)由题意可得27的个位数字为:8;故答案为:8;(2)1+2+22+23+…+22021+22022=22023﹣1,22023个位上的数为8,∴22023﹣1的个位上的数就是7.故答案为:7.(3)阅读材料二可知,设S=1+7+72+73+…+799+7100①,将等式①的两边同乘以7,得7S=7+72+73+…+799+7100+7101②,②﹣①得,6S=7101﹣1,1+7+72+73+…+799+7100=.19.解:(1)∵+9﹣3﹣5+4﹣8+6﹣3﹣6﹣4+12=2(km),∴出租车离鹿鸣路初级中学出发点2km,在鹿鸣路初级中学的正东方向;(2)∵|+9|+|﹣3|+|﹣5|+|+4|+|﹣8|+|+6|+|﹣3|+|﹣6|+|﹣4|+|+12|=60(km),∴60×0.08=4.8(升),∴这辆出租车共耗油4.8升;(3)第一次距离鹿鸣路初级中学4(km),第二次距离鹿鸣路初级中学|9﹣3|=6(km),第三次距离鹿鸣路初级中学|9﹣3﹣5|=1(km),第四次距离鹿鸣路初级中学|9﹣3﹣5+4|=5(km),第五次距离鹿鸣路初级中学|9﹣3﹣5+4﹣8|=3(km),第六次距离鹿鸣路初级中学|9﹣3﹣5+4﹣8+6|=3(km),第七次距离鹿鸣路初级中学|9﹣3﹣5+4﹣8+6﹣3|=0(km),第八次距离鹿鸣路初级中学|9﹣3﹣5+4﹣8+6﹣3﹣6|=6(km),第九次距离鹿鸣路初级中学|9﹣3﹣5+4﹣8+6﹣3﹣6﹣4|=10(km),第十次距离鹿鸣路初级中学|9﹣3﹣5+4﹣8+6﹣3﹣6﹣4+12|=2(km),∴离鹿鸣路初级中学最远的距离是10km;(4)第一个乘客收费8+(9﹣3)×1.4=16.4(元),第二个乘客收费8(元),第三个乘客收费8+(5﹣3)×1.4=10.8(元),第四个乘客收费8+(4﹣3)×1.4=9.4(元),第五个乘客收费8+(8﹣3)×1.4=15(元),第六个乘客收费8+(6﹣3)×1.4=12.2(元),第七个乘客收费8(元),第八个乘客收费8+(6﹣3)×1.4=12.2(元),第九个乘客收费8+(4﹣3)×1.4=9.4(元),第十个乘客收费8+(12﹣3)×1.4=20.6(元),∴16.4+8+10.8+9.4+15+12.2+8+12.2+9.4+20.6=122(元),∴司机一个下午的营业额是122元.20.解:(1)3×[10+4+(﹣6)]=3×8=24,(10﹣4)﹣3×(﹣6)=6+18=24;(2)42﹣(﹣8)×1=16﹣(﹣8)×1=16+8=24;(3)5×(5﹣1÷5)=5×(5﹣)=5×=24。
中考数学专题复习《实数的运算》测试卷-附带答案

中考数学专题复习《实数的运算》测试卷-附带答案学校:___________班级:___________姓名:___________考号:___________一、选择题1.下列说法中正确的是()A.√25的值是±5B.两个无理数的和仍是无理数C.-3没有立方根.D.√a2−b2是最简二次根式.2.实数m,n在数轴上的对应点的位置如图所示,下列结论中正确的是()A.|m|<|n|B.m+n>0C.m−n<0D.mn>0 3.计算:|−2|+3sin30°−2−1−(2022−π)0等于()A.-2B.−12C.2D.04.观察下列各式:√1+112+122=1+11×2√1+122+132=1+12×3√1+132+142=1+13×4…请利用你所发现的规律计算√1+112+122+√1+122+132+√1+132+142+⋯⋯+√1+192+1102其结果为()A.8910B.9910C.989D.8895.估计√2(√23−√2)的值应在()A.2和3之间B.3和4之间C.4和5之间D.5和6之间.6.秦兵马俑的发现被誉为“世界第八大奇迹” 兵马俑的眼睛到下巴的距离与头顶到下巴的距离之比为√5−12下列各数中最接近于√5−12的是()A.25B.12C.35D.347.若x为实数在“(√3+1)◯ x”的“◯”中添上一种运算符号(在“+-× ÷”中选择)后其运算的结果为有理数则不可能是()A.√3−1B.1−√3C.3√3D.1+√38.计算sin60°⋅tan30°−sin45°⋅cos30°的结果是()A.−12+√62B.√32+12C.−√32+12D.12−√649.下列运算正确的是()A .√3+√2=√5B .|3.14−π|=π−3.14C .a 2⋅a 3=a 6D .(a −1)2=a 2−2a −110.今年“十一”期间 广州部分公园举行游园活动 据统计 天河公园早晨6时30分有2人进入公园 接下来的第一个30分钟内有4人进去1人出来 第二个30分钟内有8人进去2人出来 第三个30分钟内有16人进去3人出来 第四个30分钟内有32人进去4人出来.按照这种规律进行下去 到上午11时30分公园内的人数是( )A .211−47B .212−57C .213−68D .214−80二 填空题11.(√3−1.732)0+(−14)−2= .12.【中考变形】已知a =(12)−1+(−√3)0,b =(√3+√2)(√3−√2) 则√a +b = .13.计算:|−5|+(3−π)0−6×3−1+√3−1−2sin60°= 。
中考数学专题复习1实数的运算(原卷版)

实数的运算复习考点攻略考点01 有理数1.整数和分数统称为有理数。
(有限小数与无限循环小数都是有理数。
)2.正整数、0、负整数统称为整数。
正分数、负分数统称分数。
3.正数和零统称为非负数,负数和零统称为非正数,正整数和零统称为非负整数,负整数和零统称为非正整数。
4.正数和负数表示相反意义的量。
【注意】0既不是正数,也不是负数。
【例1】.在下列各组中,哪个选项表示互为相反意义的量()A.足球比赛胜5场与负5场B.向东走3千米,再向南走3千米C.增产10吨粮食与减产﹣10吨粮食D.下降的反义词是上升【例2】已知某快递公司的收费标准为:寄一件物品不超过5千克,收费13元;超过5千克的部分每千克收2元。
圆圆在该快递公司寄一件8千克的物品,需要付费( )。
A.17元B.19元C.21元D.23元考点02 数轴1.数轴的三要素:原点、正方向、单位长度。
数轴是一条直线。
2.所有有理数都可以用数轴上的点来表示,但数轴上的点不一定都是有理数。
3.数轴上,右边的数总比左边的数大;表示正数的点在原点的右侧,表示负数的点在原点的左侧。
【例3】如图,数轴上的点A,B分别表示数﹣2和1,点C是线段AB的中点,则点C 表示的数是()A.﹣0.5B.﹣1.5C.0D.0.5考点03 相反数、绝对值和倒数1.在数轴上表示数a的点与原点的距离,叫做a的绝对值,记作:a。
2.一个正数的绝对值等于本身,一个负数的绝对值等于它的相反数,0的绝对值是0.即(0)0(0)(0)a a a a a a >⎧⎪==⎨⎪-<⎩3. 乘积为1的两个数互为倒数。
正数的倒数为正数,负数的倒数为负数,0没 有倒数。
倒数是本身的只有1和-1。
4. 倒数性质:(1)若a 与b 互为倒数,则a·b=1;反之,若a·b=1,则a 与b 互为倒数。
(2)若a 与b 互为负倒数,则a·b=-1;反之,若a·b= -1则a 与b 互为倒数。
专题01 实数及其运算(31题)(解析版)--2024年中考数学真题好题汇编

专题01实数及其运算(31题)一、单选题1(2024·广东深圳·中考真题)如图,实数a ,b ,c ,d 在数轴上表示如下,则最小的实数为()A.aB.bC.cD.d【答案】A【分析】本题考查了根据数轴比较实数的大小.根据数轴上右边的数总比左边的大即可判断.【详解】解:由数轴知,a <b <0<c <d ,则最小的实数为a ,故选:A .2(2024·甘肃临夏·中考真题)下列各数中,是无理数的是()A.π2B.13C.327D.0.13133【答案】A【分析】本题考查无理数的定义,根据无理数是无限不循环小数结合立方根的定义,进行判断即可.【详解】解:A 、π2是无理数,符合题意;B 、13是有理数,不符合题意;C 、327=3是有理数,不符合题意;D 、0.13133是有理数,不符合题意;故选A .3(2024·福建·中考真题)下列实数中,无理数是()A.-3B.0C.23 D.5【答案】D【分析】无理数就是无限不循环小数,理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数,由此即可判定选择项.本题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001....,等数.【详解】根据无理数的定义可得:无理数是5故选:D .4(2024·四川内江·中考真题)16的平方根是()A.-4 B.4C.2D.±4【答案】D【分析】题考查了平方根,熟记定义是解题的关键.根据平方根的定义计算即可.【详解】解:16的平方根是±4,故选:D .5(2024·四川泸州·中考真题)下列各数中,无理数是()A.-13B.3.14C.0D.π【答案】D【分析】本题考查了无理数的识别,无限不循环小数叫无理数,初中范围内常见的无理数有三类:①π类,如2π,π3等;②开方开不尽的数,如2,35等;③虽有规律但却是无限不循环的小数,如0.1010010001⋯(两个1之间依次增加1个0),0.2121121112⋯(两个2之间依次增加1个1)等.【详解】解:根据无理数的定义可知,四个数中,只有D 选项中的数π是无理数,故选:D .6(2024·山东·中考真题)下列实数中,平方最大的数是()A.3B.12C.-1D.-2【答案】A【分析】本题考查的是实数的大小比较,乘方运算,先分别计算各数的乘方,再比较大小即可.【详解】解:∵32=9,122=14,-1 2=1,-2 2=4,而14<1<4<9,∴平方最大的数是3;故选A7(2024·山东烟台·中考真题)下列实数中的无理数是()A.23B.3.14C.15D.364【答案】C【分析】本题考查无理数,根据无理数的定义:无限不循环小数,叫做无理数,进行判断即可.【详解】解:A 、23是有理数,不符合题意;B 、3.14是有理数,不符合题意;C 、15是无理数,符合题意;D 、364=4是有理数,不符合题意;故选C .8(2024·四川眉山·中考真题)下列四个数中,无理数是()A.-3.14B.-2C.12D.2【答案】D【分析】本题考查的是无理数的概念,无理数即无限不循环小数,它的表现形式为:开方开不尽的数,与π有关的数,无限不循环小数.根据无理数的定义,即可得出符合题意的选项.【详解】解:-3.14,-2,12是有理数,2是无理数,故选:D .9(2024·广东·中考真题)完全相同的4个正方形面积之和是100,则正方形的边长是()A.2B.5C.10D.20【答案】B【分析】本题主要考查了算术平方根的应用,先求出一个正方形的面积,再根据正方形的面积计算公式求出对应的边长即可.【详解】解:∵完全相同的4个正方形面积之和是100,∴一个正方形的面积为100÷4=25,∴正方形的边长为25=5,故选:B .10(2024·天津·中考真题)估算10的值在()A.1和2之间B.2和3之间C.3和4之间D.4和5之间【答案】C【分析】本题考查无理数的估算,根据题意得9<10<16,即可求解.【详解】解:∵9<10<16∴3<10<4,∴10的值在3和4之间,故选:C .11(2024·四川自贡·中考真题)在0,-2,-3,π四个数中,最大的数是()A.-2B.0C.πD.-3【答案】C【分析】此题主要考查了实数大小比较的方法,正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,据此判断即可,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.【详解】解:根据实数比较大小的方法,可得:-2<-3<0<π,∴在0,-2,-3,π四个数中,最大的数是π,故选:C .12(2024·四川南充·中考真题)如图,数轴上表示2的点是()A.点AB.点BC.点CD.点D【答案】C【分析】本题考查了实数与数轴,无理数的估算.先估算出2的范围,再找出符合条件的数轴上的点即可.【详解】解:∵1<2<2,∴数轴上表示2的点是点C ,故选:C .13(2024·北京·中考真题)实数a ,b 在数轴上的对应点的位置如图所示,下列结论中正确的是()A.b >-1B.b >2C.a +b >0D.ab >0【答案】C【分析】本题考查了是实数与数轴,绝对值的意义,实数的运算,熟练掌握知识点是解题的关键.由数轴可得-2<b <-1,2<a <3,根据绝对值的意义,实数的加法和乘法法则分别对选项进行判断即可.【详解】解:A 、由数轴可知-2<b <-1,故本选项不符合题意;B 、由数轴可知-2<b <-1,由绝对值的意义知1<b <2,故本选项不符合题意;C 、由数轴可知2<a <3,而-2<b <-1,则a >b ,故a +b >0,故本选项符合题意;D 、由数轴可知2<a <3,而-2<b <-1,因此ab <0,故本选项不符合题意.故选:C .14(2024·黑龙江绥化·中考真题)下列计算中,结果正确的是()A.-3 -2=19B.a +b 2=a 2+b 2C.9=±3D.-x 2y 3=x 6y 3【答案】A【分析】本题考查了负整数指数幂,完全平方公式,算术平方根,积的乘方,据此逐项分析计算,即可求解.【详解】解:A . -3 -2=19,故该选项正确,符合题意;B. a+b2=a2+2ab+b2,故该选项不正确,不符合题意;C. 9=3,故该选项不正确,不符合题意;D. -x2y3=-x6y3,故该选项不正确,不符合题意;故选:A.15(2024·内蒙古包头·中考真题)若2m-1,m,4-m这三个实数在数轴上所对应的点从左到右依次排列,则m的取值范围是()A.m<2B.m<1C.1<m<2D.1<m<53【答案】B【分析】本题考查实数与数轴,求不等式组的解集,根据数轴上的数右边的比左边的大,列出不等式组,进行求解即可.【详解】解:由题意,得:2m-1<m<4-m,解得:m<1;故选B.二、填空题16(2024·内蒙古赤峰·中考真题)请写出一个比5小的整数【答案】1(或2)【详解】试题分析:先估算出5在哪两个整数之间,即可得到结果.∵2=4<5<9=3,满足条件的数为小于或等于2的整数均可.考点:本题考查的是无理数的估算点评:解答本题的关键是熟知用“夹逼法”估算无理数是常用的估算无理数的方法.17(2024·四川广安·中考真题)3-9=.【答案】0【分析】本题考查的是实数的混合运算,先计算算术平方根,再计算减法运算即可.【详解】解:3-9=3-3=0,故答案为:018(2024·广西·中考真题)写一个比3大的整数是.【答案】2(答案不唯一)【分析】本题考查实数大小比较,估算无理数的大小是解题的关键.先估算出3的大小,再找出符合条件的整数即可.【详解】解:∵1<3<4,∴1<3<2,∴符合条件的数可以是:2(答案不唯一).故答案为:2.19(2024·内蒙古包头·中考真题)计算:38+-1 2024=.【答案】3【分析】本题考查实数的混合混算,先进行开方和乘方运算,再进行加法运算即可.【详解】解:原式=2+1=3;故答案为:3.20(2024·四川成都·中考真题)若m ,n 为实数,且m +4 2+n -5=0,则m +n 2的值为.【答案】1【分析】本题考查非负数的性质,根据平方式和算术平方数的非负数求得m 、n 值,进而代值求解即可.【详解】解:∵m +4 2+n -5=0,∴m +4=0,n -5=0,解得m =-4,n =5,∴m +n 2=-4+5 2=1,故答案为:1.21(2024·安徽·中考真题)我国古代数学家张衡将圆周率取值为10,祖冲之给出圆周率的一种分数形式的近似值为227.比较大小:10227(填“>”或“<”).【答案】>【分析】本题考查的是实数的大小比较,先比较两个正数的平方,从而可得答案.【详解】解:∵227 2=48449,10 2=10=49049,而48449<49049,∴2272<10 2,∴10>227;故答案为:>22(2024·黑龙江绥化·中考真题)如图,已知A 11,-3 ,A 23,-3 ,A 34,0 ,A 46,0 ,A 57,3 ,A 69,3 ,A 710,0 ,A 811,-3 ⋯,依此规律,则点A 2024的坐标为.【答案】2891,-3【分析】本题考查了点坐标的规律探究.解题的关键在于根据题意推导出一般性规律.根据题意可知7个点坐标的纵坐标为一个循环,A 7n 的坐标为10n ,0 ,据此可求得A 2024的坐标.【详解】解:∵A 11,-3 ,A 23,-3 ,A 34,0 ,A 46,0 ,A 57,3 ,A 69,3 ,A 710,0 ,A 811,-3 ⋯,,∴可知7个点坐标的纵坐标为一个循环,A 7n 的坐标为10n ,0 ,A 7n +110n +1,-3 ∵2024÷7=289⋅⋅⋅1,∴A 2023的坐标为2890,0 .∴A 2024的坐标为2891,-3 故答案为:2891,-3 .三、解答题23(2024·广东·中考真题)计算:20×-13+4-3-1.【答案】2【分析】本题主要考查了实数的运算,零指数幂,负整数指数幂,先计算零指数幂,负整数指数幂和算术平方根,再计算乘法,最后计算加减法即可.【详解】解:20×-13+4-3-1=1×13+2-13=13+2-13=2.24(2024·甘肃临夏·中考真题)计算:-4 -13-1+20250.【答案】0【分析】本题考查实数的混合运算,先进行开方,去绝对值,零指数幂和负整数指数幂的运算,再进行加减运算即可.【详解】解:原式=2-3+1=0.25(2024·福建·中考真题)计算:(-1)0+-5 -4.【答案】4【分析】本题考查零指数幂、绝对值、算术平方根等基础知识,熟练掌握运算法则是解题的关键.根据零指数幂、绝对值、算术平方根分别计算即可;【详解】解:原式=1+5-2=4.26(2024·江苏连云港·中考真题)计算|-2|+(π-1)0-16.【答案】-1【分析】本题考查实数的混合运算,零指数幂,先进行去绝对值,零指数幂和开方运算,再进行加减运算即可.【详解】解:原式=2+1-4=-127(2024·江苏苏州·中考真题)计算:-4+-20-9.【答案】2【分析】本题考查了实数的运算,利用绝对值的意义,零指数幂的意义,算术平方根的定义化简计算即可.【详解】解:原式=4+1-3=2.28(2024·陕西·中考真题)计算:25--70+-2×3.【答案】-2【分析】本题考查了实数的运算.根据算术平方根、零次幂、有理数的乘法运算法则计算即可求解.【详解】解:25--70+-2×3=5-1-6=-2.29(2024·四川乐山·中考真题)计算:-3+π-20240-9.【答案】1【分析】本题考查了绝对值,零指数幂,算术平方根.熟练掌握绝对值,零指数幂,算术平方根是解题的关键.先分别计算绝对值,零指数幂,算术平方根,然后进行加减运算即可.【详解】解:-3+π-20240-9=3+1-3=1.30(2024·浙江·中考真题)计算:1 4-1-38+-5【答案】7【分析】此题考查了负整数指数幂,立方根和绝对值,解题的关键是掌握以上运算法则.首先计算负整数指数幂,立方根和绝对值,然后计算加减.【详解】1 4-1-38+-5=4-2+5=7.31(2024·湖北·中考真题)计算:-1×3+9+22-20240【答案】3【分析】本题主要考查了实数混合运算,根据零指数幂运算法则,算术平方根定义,进行计算即可.【详解】解:-1×3+9+22-20240水不撩不知深浅=-3+3+4-1=3.。
专题01实数的有关概念及计算(测试)-2023年中考数学一轮复习讲练测(浙江专用)(解析版)

2023年中考数学总复习一轮讲练测(浙江专用)第一单元数与式专题01实数的有关概念及计算(测试)班级:________ 姓名:__________ 得分:_________注意事项:本试卷满分120分,试题共23题,其中选择10道、填空6道、解答7道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.本试卷所选题目为浙江地区中考真题、模拟试题、阶段性测试题.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2022•台州)计算﹣2×(﹣3)的结果是( )A.6B.﹣6C.5D.﹣5【分析】根据有理数的乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘即可得出答案.【解析】﹣2×(﹣3)=+(2×3)=6.故选:A.2.(2022•宁波)﹣2022的相反数是( )A.―12022B.12022C.﹣2022D.2022【分析】根据相反数的定义直接求解.【解析】﹣2022的相反数是2022,故选:D.3.(2022•杭州)国家统计局网站公布我国2021年年末总人口约1412600000人,数据1412600000用科学记数法可以表示为( )A.14.126×108B.1.4126×109C.1.4126×108D.0.14126×1010【分析】根据科学记数法的规则,进行书写即可.【解析】1412600000=1.4126×109,故选:B.4.(2022•金华)在﹣2,12,2中,是无理数的是( )A .﹣2B .12CD .2【分析】利用有理数,无理数的概念对每个选项进行判断即可得出结论.【解析】﹣2,12,2故选:C .5.(2022•A .1和2之间B .2和3之间C .3和4之间D .4和5之间【分析】根据无理数的估算分析解题.【解析】∵4<6<9,∴23.故选:B .6.(2022秋•杭州期中)在数2,0,﹣2,―A .―B .0C .﹣2D .2【分析】根据正数、0、负数比较大小的办法得结论.【解析】∵正数>0>负数,∴数2,0,﹣2,―2.故选:D .7.(2022•富阳区一模)已知a ,b 是两个连续整数,a ―1<b ,则a ,b 分别是( )A .﹣1,0B .0,1C .1,2D .2,3【分析】估算无理数的大小即可得出答案.【解析】∵4<5<9,∴23,∴1―1<2,∴a =1,b =2,故选:C .8.(2022秋•杭州期中)以下几种说法:①每一个无理数都可以用数轴上的点来表示;②近似数1.70所表示的准确数x 的范围是1.695≤x <1.705;③在数轴上表示的数在原点的左边;④立方根是它本身的数是0和1;其中正确的有( )A.1个B.2个C.3个D.4个【分析】①数轴上的点与实数是一一对应关系,每一个无理数都可以用数轴上的点来表示;②根据四舍五入来判定x的取值范围;③在数轴上表示的数可以在原点的左边右边或原点上;④根据立方根的定义解答.【解析】①数轴上的点与实数是一一对应关系,每一个无理数都可以用数轴上的点来表示;②根据四舍五入来判定近似数1.70所表示的准确数x的范围是1.695≤x<1.705;③在数轴上表示的数可以在原点的左边右边或原点上;④立方根是它本身的数为0,1,﹣1.故选B.9.(2020秋•拱墅区期末)一个物体自由下落时,它所经过的距离h(米)和时间t(秒)之间的关系我们可以用t假设物体从超过10米的高度自由下落,小明要计算这个物体每经过1米所需要的时间,则经过第5个1米时所需要的时间最接近( )A.1秒B.0.4秒C.0.2秒D.0.1秒【分析】用经过5米所用的时间减去经过4米所用的时间计算即可.【解析】当h=5时,t=1,当h=4时,t=≈0.9,∴1﹣0.9=0.1(秒),∴经过第5个1米时所需要的时间最接近0.1秒,故选:D.10.(2021秋•秀洲区校级期中)对于实数a、b,定义min{a,b}的含义为:当a<b时,min{a,b}=a;当a>b时,min{a,b}=b,例如:min{1,﹣2}=﹣2.已知min a}=a,min b}=a 和b为两个连续正整数,则2a﹣b的值为( )A.1B.2C.3D.4【分析】根据a,b的范围,然后再代入求出2a﹣b的值即可.【解析】∵min a}=a,min b}=∴a b∵a,b是两个连续的正整数.∴a=5,b=6.∴2a﹣b=2×5﹣6=4.故选:D.二.填空题(共6小题)11.(2022•宁波)请写出一个大于2【分析】首先2【解析】大于2的无理数有:须使被开方数大于4.12.(2021秋•余杭区期中)若(x﹣1)3=8,则x= 3 .【分析】直接利用立方根的定义得出x的值,进而得出答案.【解析】∵(x﹣1)3=8,∴x﹣1=2,解得:x=3.故答案为:3.13.(2022秋•萧山区校级期中)已知6―a,小数部分b,则a= 2 ,2a﹣b【分析】先估算6―a和小数部分b,最后代入计算2a﹣b.34,∴﹣4<――3,∴6﹣4<6―6﹣3,即2<63.∴a=2,b=62=4―∴2a﹣b=2×2﹣(4=4﹣4+=故答案为:214.(2016秋•嵊州市校级期中)有一个数值转换器,流程如下:当输入的x值为64时,输出的y【分析】依据运算程序进行计算即可.8,是有理数,8的立方根是2,是有理数,215.(2017春•梁子湖区期中)对于任何实数a ,可用[a ]表示不超过a 的最大整数,如[4]=4,=1.现对72进行如下操作:72第一次→=8第二次→=2第三次→=1,类似地,只需进行3次操作后变为1的所有正整数中,最大的是 255 .【分析】根据规律可知,最后的取整是1,得出前面的一个数字最大是3,再向前一步推取整是3的最大数为15,继续会得到取整是15的最大数为255;反之验证得出答案即可.【解析】∵=1,=3,=15;所以只需进行3次操作后变为1的所有正整数中,最大的是255.故答案为:255.16.(2020秋•柯桥区期中)如图,Rt △OAB 的直角边OA =2,AB =1,OA 在数轴上,在OB 上截取BC =BA ,以原点O 为圆心,OC 为半径画弧,交数轴于点P ,则OP 的中点D 对应的实数是 2 .【分析】根据勾股定理求出OB ,进而求出OC ,最后求出OD 即可.【解析】∵Rt △OAB 的直角边OA =2,AB =1,∴OB =又∵BA =BC ,∴OC =OB ﹣BC =1=OP ,∵点D 是OP 的中点,∴OD =12OP =即点D 所表示的数为:2,故答案为:2.三.解答题(共7小题)17.(2022秋•上城区校级期中)计算:(1)(―79+56―118)×(﹣18);(2)﹣24―17×[2﹣(﹣3)2];(3)8.4×103﹣4.8×104.【分析】(1)根据乘法分配律计算即可;(2)先计算乘方,再计算乘法,最后计算减法,有括号的先计算括号内的;(3)根据科学记数法的表示方法计算即可.【解析】(1)(―79+56―118)×(﹣18)=79×18―56×18+118×18=14﹣15+1=0;(2)﹣24―17×[2﹣(﹣3)2]=―16―17×(2―9)=―16―17×(―7)=﹣16+1=﹣15;(3)8.4×103﹣4.8×104.=8400﹣48000=﹣39600.18.(2021•金华)计算:(﹣1)2021+―4sin45°+|﹣2|.【分析】先分别计算有理数的乘方,二次根式的化简,代入特殊角三角函数值,绝对值的化简,然后再计算.【解析】原式=﹣1+4×+2=﹣2=1.19.(2022•杭州)计算:(﹣6)×(23―■)﹣23.圆圆在做作业时,发现题中有一个数字被墨水污染了.(1)如果被污染的数字是12,请计算(﹣6)×(23―12)﹣23.(2)如果计算结果等于6,求被污染的数字.【分析】(1)将被污染的数字12代入原式,根据有理数的混合运算即可得出答案;(2)设被污染的数字为x,根据计算结果等于6列出方程,解方程即可得出答案.【解析】(1)(﹣6)×(23―12)﹣23=(﹣6)×16―8=﹣1﹣8=﹣9;(2)设被污染的数字为x,根据题意得:(﹣6)×(23―x)﹣23=6,解得:x=3,答:被污染的数字是3.20.(2020•拱墅区模拟)计算:已知|x|=23,|y|=12,且x<y<0,求6÷(x﹣y)的值.【分析】直接利用绝对值的性质结合有理数混合运算法则计算得出答案.【解析】∵|x|=23,|y|=12,且x<y<0,∴x=―23,y=―12,∴6÷(x﹣y)=6÷(―23+12)=﹣36.21.(2020•西湖区二模)(1)若a=cos45°,b=(π+1)0,c=d=(―12)﹣1,化简得a= 2 ,b= 1 ,c= 12 ,d= ﹣2 ;(2)在(1)的条件下,试计算a―cd.【分析】(1)根据cos45°=a0=1(a≠0),负整数指数幂:a﹣p=1a p(a≠0,p为正整数),算术平方根分别计算即可;(2)把(1)中的数据代入进行计算即可.【解析】(1)a=cos45°b=(π+1)0=1,c=12,d=(―12)﹣1=﹣2,故答案为:2;1;12;﹣2;(2)a―cd―(﹣1)=2+1=3.22.(2021•宁波模拟)规定一种新运算a※b=a2﹣2b.(1)求(﹣1)※2的值;(2)这种新运算满足交换律吗?若不满足请举反例,若满足请说明理由.【分析】(1)把a=(﹣1),b=2,代入所给运算中计算就可以了;(2)不满足,举出反例,例如:1※2≠2※1等.【解析】(1)(﹣1)※2=(﹣1)2﹣2×2=1﹣4=﹣3;(2)不满足.例如:∵1※2=﹣3,2※1=2.∴1※2≠2※1.23.(2022秋•温州期中)操作探究:已知在纸面上有一数轴(如图所示),(1)折叠纸片,使表示1的点与表示﹣1的点重合,则表示﹣2的点与表示 2 的点重合;(2)折叠纸片,使表示﹣1的点与表示3的点重合,回答以下问题:①表示5的点与表示 ﹣3 的点重合;②若数轴上A、B两点之间的距离为13(A在B的左侧),且A、B两点经折叠后重合,此时点A表示的数是 ―112 ;点B表示的数是 152 .③(3)已知数轴上P,Q两点表示的数分别为﹣1和3,有一只电子小蜗牛从P点出发以每秒2个单位的速度向右移动,运动多少秒时,它到点P的距离是到点Q的距离的2倍?【分析】(1)根据题意确定纸片是沿着0点进行折叠的,再求解即可;(2)①由题意确定纸片是沿着表示1的点进行折叠的,再求解即可;②设点A表示的数是x,则点B表示的数是x+13,根据折叠的性质可得x x132=1,求出x的值再求解即可;③由①2―(3)设运动时间为t 秒,小电子小蜗牛运动的点表示的数为x ,则x =﹣1+2t ,根据题意列出方程|x +1|=2|x ﹣2|,求出x 后再求t 的值即可求解.【解析】(1)∵表示1的点与表示﹣1的点重合,∴纸片是沿着0点进行折叠的,∴表示﹣2的点与表示2的点重合,故答案为:2;(2)①∵表示﹣1的点与表示3的点重合,又∵132=1,∴纸片是沿着表示1的点进行折叠的,∴表示5的点与表示﹣3的点重合,故答案为:﹣3;②设点A 表示的数是x ,则点B 表示的数是x +13,∵A 、B 两点经折叠后重合,∴x x 132=1,解得x =―112,∴―112+13=152,∴点A 表示的数是―112,点B 表示的数是152,故答案为:―112,152;③∵纸片是沿着表示1的点进行折叠的,2―故答案为:2(3)设运动时间为t 秒,小电子小蜗牛运动的点表示的数为x ,∴x =﹣1+2t ,∵它到点P 的距离是到点Q 的距离的2倍,∴|x +1|=2|x ﹣2|,解得x=1或x=5,当x=1时,2t﹣1=1,解得t=1,当x=5时,2t﹣1=5,解得t=3,∴运动1秒或3秒时,它到点P的距离是到点Q的距离的2倍.。
中考数学专题复习一实数及其运算

专题01有理数考点一:有理数之正数和负数◎基础巩固1.正数和负数的定义:大于0的数叫做正数,小于0的数叫做负数。
0既不是正数也不是负数。
2.正数和负数的意义:表示具有相反意义的两个量。
3.正负号的化简:同号为正,异号为负。
◎同步练习1.下列各数是负数的是()A .0B .21C .﹣(﹣5)D .﹣52.下列各数为负数的是()A .﹣2B .0C .3D .53.四个实数﹣2,1,2,31中,比0小的数是()A .﹣2B .1C .2D .314.在﹣3,1,21,3中,比0小的数是()A .﹣3B .1C .21D .35.若气温上升2℃记作+2℃,则气温下降3℃记作()A .﹣2℃B .+2℃C .﹣3℃D .+3℃6.如果将“收入50元”记作“+50元”,那么“支出20元”记作()A .+20元B .﹣20元C .+30元D .﹣30元7.在东西向的马路上,把出发点记为0,向东与向西意义相反.若把向东走2km 记做“+2km ”,那么向西走1km 应记做()A .﹣2km B .﹣1km C .1km D .+2km8.中国是最早采用正负数表示相反意义的量,并进行负数运算的国家.若零上10℃记作+10℃,则零下10℃可记作()A .10℃B .0℃C .﹣10℃D .﹣20℃9.(如果水位升高2m 时水位变化记作+2m ,那么水位下降2m 时水位变化记作.10.负数的概念最早出现在中国古代著名的数学专著《九章算术》中,负数与对应的正数“数量相等,意义相反”,如果向东走5米,记作+5米,那么向西走5米,可记作米.考点二:有理数之相反数◎基础巩固1.相反数的定义:只有符号不同的两个数互为相反数。
我们说其中一个数是另一个数的相反数。
0的相反数还是0。
2.相反数的性质:互为相反数的两个数和为0。
即a 与b 互为相反数⇔0=+b a ⇔()a b b a -=-=◎同步练习11.实数9的相反数等于()A .﹣9B .+9C .91D .﹣9112.下列各数中,﹣1的相反数是()A .﹣1B .0C .1D .213.﹣2022的相反数是.14.如图,数轴上点A 表示的数的相反数是()A .﹣2B .﹣21C .2D .3考点三:有理数之绝对值◎基础巩固1.绝对值的定义:数轴上表示数a 的点到原点的距离用数a 的绝对值来表示。
中考数学 专题01 实数的有关概念及运算(原卷版)
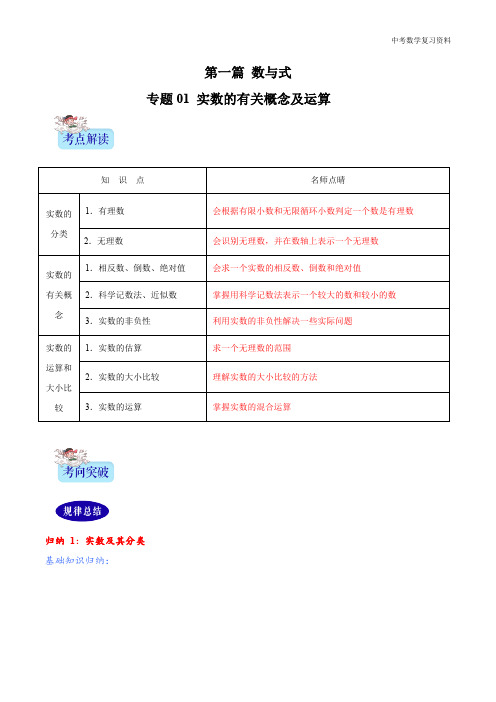
归纳 4:科学记数法与近似数 基础知识归纳:根据科学记数法的定义,科学记数法的表示形式为 a×10n,其中 1≤|a|<10,n 为整数, 表示时关键要正确确定 a 的值以及 n 的值. 基本方法归纳:利用科学记数法表示一个数,在确定 n 的值时,看该数是大于或等于 1 还是小于 1.当该 数大于或等于 1 时,n 为它的整数位数减 1;当该数小于 1 时,-n 为它第一个有效数字前 0 的个数(含小
中考数学复习资料
的克数记为负数,下面检测过的四个排球,在其上方标注了检测结果,其中质量最接近标准的一个是 ( )A.B.Fra bibliotek C.D.
3.(2019 内蒙古通辽市,第 1 题,3 分) 1 的相反数是( ) 2019
A.2019 B. 1 C.﹣2019 D. 1
( )
A.5×106 B.107 C.5×107 D.108 14.(2019 重庆 A,第 8 题,4 分)按如图所示的运算程序,能使输出 y 值为 1 的是( )
A.m=1,n=1 B.m=1,n=0 C.m=1,n=2 D.m=2,n=1
归纳 5:实数的混合运算 基础知识归纳:实数混合运算时,将运算分为三级,加减为一级运算,乘除为二级运算,乘方为三级运 算.同级运算时,从左到右依次进行;不是同级的混合运算,先算乘方,再算乘除,而后才算加减;运算 中如有括号时,先做括号内的运算,按小括号、中括号、大括号的顺序进行 基本方法归纳:实数的混合运算经常涉及到零指数幂、负整数指数幂、特殊角的三角函数值、绝对值的化 简、二次根式等内容,要熟练掌握这些知识. 注意问题归纳:实数的混合运算经常以选择、填空和解答的形式出现,是中考是热点,也是比较容易出错 的地方,在解答此类问题时要注意基本性质和运算的顺序.
