相角裕度幅值裕度
王划一-自动控制原理-5-3稳定裕度
= 37.4
当(g) = 180时
180 = arctang 180 2arctan0.1g
求得
arctang =2arctan0.1g g = 8.94
20 lg h
20 lg A(g )
20
lg
k g g2 12
9.03dB
因为 > 0，所以闭环系统是稳定旳。
0
0 20 40 60 80
能够看出，调整时间与相角裕度和幅值穿越频率都有 关系。假如两个二阶系统旳相同，则它们旳超调量也相同， 这时比较大旳系统，调整时间较短。
17
例5-19 一单位反馈控制系统，其开环传递函数
G(s)
7
s(0.087s 1)
试用相角裕度估算过渡过程指标p% 与ts。
解：系统开环伯德图如图示
33
四 、奈奎斯特稳定判据
内容 应用
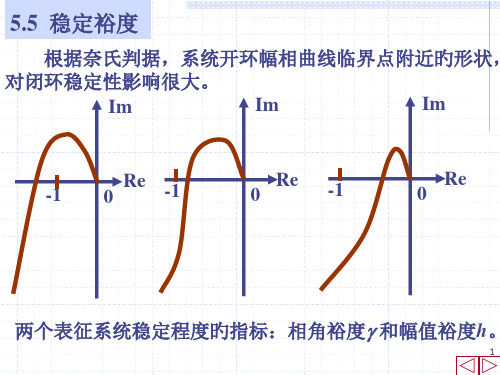
5.5 稳定裕度
根据奈氏判据，系统开环幅相曲线临界点附近旳形状，
对闭环稳定性影响很大。
Im
Im
Im
-1
Re 0
-1
Re 0
-1
Re 0
两个表征系统稳定程度旳指标：相角裕度 和幅值裕度h。
1
（1）幅值裕度h ：令相角为180时相应旳频率为g （相角穿越频率），频率为g 时相应旳幅值A(g)旳倒数，
定义为幅值裕度h ，即 h 1 A(g )
10 11.5
0
1
20
40dB/dec
()/()
0
90
180
19
2) 高阶系统
近似旳关系式
p
0.16 0.4( 1
16 第十六讲 伯德图分析-稳定性-及幅值和相角裕度
作业： P339 P339 16.1 a. 16.3 e.
当 k > k1时， 系统是稳定的
Im
ω =0
-1
ω=∞
Re
图.16.14
稳定系统的奈奎斯特图
例题 16.1
问题: 如图所示的系统， 画出当K=45时 的伯德图， 并确定增益裕度和相位裕度。 计算使系统稳定的最大K值， 并用劳斯阵 列验证其结果。
R +
⊕
-
C
K
1 ( s + 2)( s + 3)3
Mdb
log10 ω
GM
0db
φ
−1800
PM
log10 ω
图.16.3 增益裕度和相位裕度
系统的型和从伯德图得到 稳态误差
一般开环传递函数
Kb (1+ s / z1 )(1+ s / z2 )L(1+ s / zm ) GH(s) = n s (1+ s / p1 )(1+ s / p2 )L(1+ s / pk )
GM 1 = K1db GM 2 = K 2 db
图.16.11 系统的根轨迹图
单一频率穿越点: 增加相位 考虑下面的例子
(1+ s / 2) GH(s) =
s3
2
相位裕度是负的，表明系统是不稳定的。 增益裕度是正的，表明系统是稳定的。 考虑相位裕度，系统是稳定的。
0.1 40
1
10
100
ω
M db
伯德图中的相位裕度： - 相位裕度是使相角曲线向下移动 直到 增益和相角穿越点发生在同一频率时 的纯相角滞后量 。 - 在图16.1中
PM = 54
幅值裕度和相角裕度计算
幅值裕度和相角裕度计算幅值裕度和相角裕度计算，这可真是个有趣又烧脑的事儿啊。
我在实验室里研究控制系统的时候，就老得琢磨这俩玩意儿。
周围那些仪器啊，闪着小灯，嗡嗡响着，就像一群小虫子在叫。
我的搭档，是个眼睛小小的家伙，戴着个黑框眼镜，那镜片厚得像酒瓶底儿。
他拿着计算草稿，眉头皱得像麻花，嘟囔着：“这幅值裕度和相角裕度可真不好算呐。
”咱先说这幅值裕度计算。
这就像在走迷宫，得找到那个关键的出口。
你得先把开环传递函数搞清楚，那函数就像一团乱麻，得一点点梳理。
这函数里的参数啊，有的像调皮的小鬼，稍不注意就把你带偏了。
我们在计算的时候，拿着计算器按个不停，那计算器的按键声，哒哒哒的，就像小马蹄在跑。
有次我算着算着，算错了一个数，结果那数值差得离谱，我气得直拍脑袋，像个傻瓜一样。
相角裕度计算也不简单。
它和幅值裕度就像一对难兄难弟。
得先找到截止频率，这就像在大海里找一颗珍珠一样。
要画出伯德图，那伯德图的线啊，弯弯绕绕的，就像山路一样。
我拿着尺子在纸上比划着，想把线画准，眼睛都看花了。
我问搭档：“你看这线对不？” 他凑过来，眼睛瞪得老大，看了半天说：“好像不太对，再量量。
”这幅值裕度和相角裕度计算啊，得细心又细心。
要是算错了，那控制系统可就出大问题了，就像火车跑错了轨道一样。
不过呢，当你好不容易算对了，那种感觉就像打了胜仗一样，心里美美的。
而且这俩概念在实际中用处可大了，就像给控制系统上了保险，让它稳稳当当的，不会出乱子。
咱搞这行的，就得把这些计算吃透，就像老虎咬住猎物不松口一样，这样才能把控制系统设计得更好，让那些机器啊、设备啊都乖乖听话。
相角裕度幅值裕度知识讲解
h2l0g
20
2l0g 20
x 1x2 10.0•1x2
x 0x2
2l0g3.212 066.0d2B
P198
5-13
已知系统的开环传递函数 G(s 试计算K=4、10的稳定裕度。
A (c)G (jc)H (jc)1
n2
1
c c2 2n2
10 8 G 0 jc H jc
1800 900 arctan c 2n
＝arctan2n c
cn 14422
arctan 2 144 22
P200 例5-14（图解法、近似计算法、精确计算法）
已知系统的开环传递函数，试计算 G(s)
为了使最小相位系统稳定，相角裕度必须为正。 在对数坐标图上的临界稳定点为0dB和－1800
幅值裕度又称增益裕度(Gain Margin)
相角为-180°点所对应的频率为穿越频率
(x ) G jx H jx 10 80
定义幅值裕度为
h
1
GjxHjx
幅值裕度h的物理意义：
对于闭环稳定系统，如果系统开环幅频特性再增大h
4
h 1 2l0 g G (j x) 2l0 g 3 6 (d)B (31 )2
G (j)j K 1 3(2 K 1 )2 3ex j( 3 p t g 1 )
K=10时：
10
( c21)2 3 1,
c1
1
03011.9
1
2 1 0 8 c 0 1 0 3 8 t 1 1 g . 9 0 7 1 0
=0+
G(j)j(jT 1K 1)(jT 21)
第六章-5-相角裕度和幅值裕度以及闭环频率特性指标
1/h < 1,
h>1
LmG(jω) ωΦ 幅值裕度, Lm (+) ) h(
Lmh Lm G ( j x ) 0
1/h -1 ωx
-90°
Φ γ(+) ω ωΦ G(jω)
-135 135° -180° -225 225° -270°
ωx 相位裕度, γ(+)
ω→
G(jω)的极坐标图 G(jω)的对数幅频曲线和相频曲线 9
1 h 1.25 0.8
1
1 h
Im j
GH
1 Re
x
0
A
j
0
例6-20 的极坐标图
浙江大学控制科学与工程学系
15
Phase Margin and Gain Margin
相角裕度和幅值裕度的求解方法——Bode图法 Bode图法
（三）Bode图法 画出系统的Bode图，由开环对数幅频特性与零分贝线（即 轴）的交 点频率 ，求出对应的相频特性与－ 求出对应的相频特性与 1800线的相移量，即为相角裕度 线的相移量 为相角裕度
G(jω)
ω
-225° -270°
G(jω)的极坐标图
G(jω)的对数幅频曲线和相频曲线 6 浙江大学控制科学与工程学系
Phase Margin and Gain Margin
相角裕度和幅值裕度以及与稳定性的关系
对于闭环稳定系统，如果系统的开环相频特性再滞后 相角裕度γ 度，则系统将处于临界稳定状态. 滞后该角度将使得极坐标图穿越–1 1点 对于最小相位系统来说，相角裕度为正，系统稳定，负的相角裕 度表示系统是不稳定的. 相角裕度与系统阻尼比 有关，一般来讲，相角裕度在 有关 一般来讲 相角裕度在45°到 到 60°之间的系统响应是能令人满意的。
一、幅值裕度
为了获得满意的过渡过程，通常要求系统有 45°－70°的相角裕度。这可以通 过减小开环增益K的办法来达到。
但是，减小K一般会使斜坡输入时稳态误差变大。因此有必要应用校正技术，使 系统兼顾稳态误差和过渡过程的要求。
L 对数幅值稳定裕度或对数增益稳定裕度。 g
二、相角裕度
定义 : 在幅相曲线上，相角180 加开环幅相曲线幅值等于1时的
相角, 称为控制系统的相角裕度。
即
＝1 8 0 ＋ (c）
式中c－截止频率或剪切频率。在c处，A(c）＝1。
物理意义 : 如果系统在频率c处的相角迟后再增大度，则系统
将处于临界稳定状态。
求ωc 和相角裕度γ的另一种方法
由已知的开环传递函数得
A()
K
1 2 1 ( )2
5
按定义由 A (ω)＝1就可以求出ωc来，但系统阶数高时，由A (ω)＝1求 ωc是很麻烦的。可以采用近似处理的办法求ωc 。
由图可知因1＜ωc＜5，故可取1 2 ，(认为 2 1)
c
c
c
1
( )2 1 [认为( )2。则 1]
§5-5 控制系统的相对稳定性
一、幅值裕度
定义 : 在幅相曲线上，相角等于－180 时对应幅值的倒数, 称为
控制系统的幅值裕度。
1
即
h
A( g )
式中 g－相角交接频率。在 g 处， ( g）
180。
物理意义 : 稳定系统在相角交界频率 g 处, 若幅值增大h倍，系统
将处于临界稳定状态。
令
L g 20 log h(dB)
由曲线2和3可知，K ＝2时，相角裕度和幅值裕度分别是
24 , L 20 log h 10(dB)
伯德图分析-稳定性-及幅值和相角裕度
0.01
0.1
1.0
10
增益穿 越点
相位穿
图16.1 例子系统的伯德图
越点
增加K 将使幅值曲线向上平移动，从 而使幅值穿越点向右移。但是相角穿越点 保持不变。 系统最终处在临界不稳定点上。
▽ 计算临界不稳定时系统的幅值。
20 lg NK 20 lg K 20 lg N
20 lg NK KdB NdB
渐近线的延长线求出。
M db
20 log10 Kv
-
20d
b/d
log10
eca1
图.16.6 1 型系统的另一种伯德图
2型系统
GHs
Kb s2
GH
j
Ka
j 2
如果 ka=1。对数幅频特性在当ω =1时，其低频段或它的延长线会以– 40db/decade 的斜率穿过 零分贝线 。
Ka 的值可以通过测量ω = 1 处的 增益值来获得。
PM 54
▽ 在伯德图中获得增益裕度和相位裕 度:
增益裕度是通过相角穿越频率得出的。 它是该频率处的幅值分贝值与0dB线之间
的差值(用分贝表示) 。 相角裕度是通过增益穿越频率得出的， 它是此频率处的相角与-180o线之间的差值。
M db
0 d b
1800
log10
G M
P
log10
M
图.16.3 增益裕度和相位裕度
线性控制系统工程
第16章
伯德图分析，稳 定性，
及幅值和相角 裕度
第16章 伯德图分析,稳定性 及幅值和相角裕度
伯德图中的增益裕度和相角裕度
g c
(g c)
(g c)
GM Kc
简述幅值裕度的概念
简述幅值裕度的概念幅值裕度是一个工程学术语，它是指在幅值的基础上再留有一定余地的程度，即允许存在的最大偏差。
这个概念常用于数学、物理等学科以及电流、电磁、机械等领域。
幅值就是幅度，指的是偏离平衡位置的最大距离。
例如，在一个周期内，交流电出现的最大绝对值，称为交流电的幅值，也叫最大值、振幅、峰值。
幅值裕度表示了系统在幅值方面的稳定储备量。
它与系统的稳定性密切相关。
在开环系统中，如果幅值裕度h大于2（h(dB)大于0），则系统是稳定的；如果h小于2（h(dB)小于0），则系统是不稳定的。
在相角裕度方面，一般要求相角裕度γ大于40°（γ大于0），表示奈奎斯特曲线未包围(-1,j0)点，系统是稳定的；如果γ小于0，表示奈奎斯特曲线包围了(-1,j0)点，系统是不稳定的；如果γ等于0，表示奈奎斯特曲线通过了(-1,j0)点，系统是临界稳定的。
在设计控制系统时，为了使系统具有足够的稳定裕度和获得良好的动态性能，一般要求相角裕度γ=30~70度，幅值裕度h=2~2.5或h(dB)=6~8。
在电路设计中，幅值裕度也是一个重要的概念，它可以用来描述信号的稳定性和可靠性。
幅值裕度越大，信号的稳定性和可靠性就越高。
幅值裕度在工程领域中具有重要的应用价值。
首先，它代表了系统在面对外部扰动时的稳定性。
当系统受到外部干扰时，幅值裕度可以保证系统不会立即失去稳定性，而是会在一定范围内波动。
其次，幅值裕度可以用来衡量系统的鲁棒性。
具有较大幅值裕度的系统，通常更加稳定。
1.在控制系统设计中，幅值裕度是一个关键的性能指标。
它表示了系统在幅值方面的稳定储备量，是评估系统稳定性的重要依据。
为了使系统具有足够的稳定裕度和获得良好的动态性能，一般要求相角裕度γ=30~70度，幅值裕度h=2~2.5或h(dB)=6~8。
2.在电路设计中，幅值裕度也是一个重要的概念，它可以用来描述信号的稳定性和可靠性。
幅值裕度越大，信号的稳定性和可靠性就越高。
相角裕度和幅值裕度定义
相角裕度和幅值裕度定义
相角裕度和幅值裕度是电路稳定性和控制系统设计中常用的概念。
相角裕度是指系统的相位差与临界相位差之间的差距，幅值裕度是指系统的增益与临界增益之间的差距。
相角裕度和幅值裕度的目的是保证系统在不同工作条件下仍能保持稳定性和良好的性能。
在控制系统设计中，相角裕度和幅值裕度是非常重要的概念。
相角裕度是指系统相位差与临界相位差之间的差距，临界相位差是系统稳定的临界条件。
相角裕度越大，系统的稳定性就越好。
在频率响应曲线上，相角裕度可以通过相角裕度曲线来表示。
相角裕度曲线是系统传递函数的相角与频率的函数。
幅值裕度是指系统增益与临界增益之间的差距，临界增益是系统稳定的临界条件。
幅值裕度越大，系统的稳定性就越好。
在频率响应曲线上，幅值裕度可以通过幅值裕度曲线来表示。
幅值裕度曲线是系统传递函数的幅值与频率的函数。
在电路稳定性分析中，相角裕度和幅值裕度也是非常重要的概念。
相角裕度和幅值裕度可以通过极点和零点的位置来判断系统的稳定性。
如果系统的极点或零点在右半平面，那么系统就是不稳定的。
如果系统的极点或零点在虚轴上，那么系统就是边缘稳定的。
如果系统的极点或零点在左半平面，那么系统就是稳定的。
综上所述，相角裕度和幅值裕度是控制系统设计和电路稳定性分析中非常重要的概念。
通过相角裕度和幅值裕度的分析，可以确保系统在不同工作条件下仍能保持稳定性和良好的性能。
相角裕度和幅值裕度的一种估算方法
相角裕度和幅值裕度的一种估算方法刘美侠;孙延永【摘要】Phase angle margin and amplitude margin are important indicators of the relative stability in the automatic control system. A method to estimate phase angle and amplitude margin is proposed. The cut-off frequency of seeking an approximate method is introduced, and the definition to equate phase angle margin is used; then the solution of the amplitude margin by using the routh stability of the system to equate the critical open-loop gain is introduced, and the meaning of amplitude margin to derive is re-used. Thus the approximate method to calculate the crossover frequency is drawled. The estimation methods are simple and practical and the examples prove that these methods have higher calculation accuracy.%相角裕度和幅值裕度是自动控制系统中反应系统的相对稳定性的重要指标。
本文提出了求解相角裕度和幅值裕度一种估算方法,首先介绍了截止频率的一种估算求法,再利用相角裕度定义求出相角裕度;其次是先通过劳斯判据求出系统临界稳定时的开环增益,再利用幅值裕度的含义求出,最后用估算法求出穿越频率。
幅值裕度和相角裕度
幅值裕度和相角裕度
幅值裕度和相角裕度是控制系统设计中非常重要的两个指标。
幅值裕度是指系统增益的变动范围，即输入信号变化时系统输出信号的最大变化范围与输入信号幅值的比值。
相角裕度是指系统相位的变动范围，即输入信号变化时系统输出信号相位的最大变化范围与输入信号相位的比值。
幅值裕度和相角裕度的大小直接影响系统的稳定性和性能。
幅值裕度越大，系统对于幅度变化的容忍度也就越大，系统的稳定性越好；相角裕度越大，系统对于相位变化的容忍度也就越大，系统的稳定性也越好。
因此，在系统设计中，需要根据具体的要求和控制目标，合理地选择幅值裕度和相角裕度的大小，以确保系统的稳定性和性能。
在实际的控制系统中，一般采用控制理论中的方法来计算幅值裕度和相角裕度，并根据计算结果进行系统设计和调节。
同时，也需要进行系统的实验和测试，以验证系统的稳定性和性能是否符合设计要求。
- 1 -。
相角裕度和幅值裕度
相角裕度和幅值裕度
通过实验，确定了电机励磁级的相角裕度和幅值裕度。
可利用这些参数进行电机参数优化，降低电动机运行中的失速概率，提高运行稳定性和可靠性；可以修正电机损耗，改善满负荷时的功率损失，从而提高电机运行时的效率；可以根据工况变化实时调节电机励磁级，改善电机负荷变化的影响。
此外，可通过更改电机励磁级，改变电机特性从而满足特定应用需求，如改善行程控制精度或者改变电机的旋转方向等。
通过相角裕度和幅值裕度的调整，可以大大降低电机的振荡，提高电机的功率密度、性能和可靠性，从而改善整个系统的性能。
此外，可以通过相角裕度和幅值裕度的调整，较为精确的检测出各类故障状态，如漏电流，过热电机和电机控制器故障等，从而更有效的排除问题，提高电机系统故障诊断精度。
通过调整相角裕度和幅值裕度参数，实时优化电机参数，可使被控电机在变化的工况下保持最佳的工作性能，从而为用户节约能源，缩短预热时间和延长运行时间。
裕度 PPT
2.相角裕度
相角裕度是指开环幅相频率G(jω)的幅值A(ω)= |G(jω)|=1时的向量与负实轴的夹角，常用希腊字母γ表示。 在平面G上画出以原点为圆心的单位圆，G(jω)曲线与单 位圆相交，交点频率 称为截止频率。
在波特图中，相角裕度表现为L(ω)=0时相角与 -180°水 平线之间的角度差。
4.波特图
波特图（Bode plots）是线性非时变系统的传递函数对 频率的半对数坐标图，其横轴频率以对数尺度（Log scale） 表示，利用波特图可以看出系统的频率响应。又称幅频响 应和相频响应曲线图。 利用波特图可以看出
在不同频率下，系统增 益的大小及相位，也可 以看出大小及相位随频 率变化的趋势。
裕度
统计学术语
裕度是指留有一定余地的程度，允许有一定的误差的程 度。 裕度的应用范围很广，多用于各学科的测量和检测等 方面。
பைடு நூலகம்
1.稳定裕度
控制系统稳定与否是绝对稳定性的概念，而对于一个稳 定的系统而言，还存在一个稳定的程度，即相对稳定性的 概念。相对稳定性与系统的动态性能指标有着密切的关系。
在设计一个控制系统时，不能保证系统的绝对稳定，那 么就需要在系统参数小范围漂移时系统的性能依然优秀并 保持稳定，这即是稳定裕度。
3.幅值裕度
幅值裕度是指在幅值的基础上再留有一定余地的程度， 即允许存在的最大偏差。 幅值就是幅度，指的是偏离平衡位置的最大距离。 幅值裕度是G(jω)与负实轴交点至虚轴距离的倒数常用 h表示。
在控制科学中，常用波特图来描述频率响应，对于稳定 性的判定会有两个参数 ，那就是幅值裕度和相角裕度，通 常情况下，利用后者进行判定，即相角裕度大于零，系统 是稳定的，反之不稳定，但是对于幅值裕度，指的是相角 为-180度时对应的幅值。
控制系统的相对稳定性
K s ( s 1)( s / 5 1)
解：系统的开环对数频率特性如图所示：
由曲线2和3可知，K ＝2时，相角裕度和幅值裕度分别是
因为 γ＞0，Lg ＞0，故对应的闭环系统是稳定的。
24 ,
Lg 20log h 10(dB)
K＝20时，由曲线1和3看到
24 ,
γ 0 结论： 欲使系统稳定 , 需h 1 L 0 g
γ和h越大，系统稳定程度越 好。 γ＝0，h＝ 1时系统处于临界稳定状 态； γ 0，h 1时系统处于不稳定状态 。
例：某单位反馈系统的开环传递函数为 求相角裕度和幅值裕度，并判断闭环系统的稳定性。
Gk ( s )
Lg 20logh 10(dB)
因为 γ＜0，Lg ＜ 0，故对应的闭环系统是不稳定的。
求ωc 和相角裕度γ的另一种方法
由已知的开环传递函数得
A( )
K
1
2
1 ( )2 5
按定义由 A (ω)＝1就可以求出ωc来，但系统阶数高时，由A (ω)＝1求 ωc是很麻烦的。可以采用近似处理的办法求ωc 。
，(认为 2 1) 1 c2 c c 。 K 2 2。则 A( ) 1 1 ( ) 1 [认为( ) 1] c 。 1 当 。当K＝2时， 5K＝20时， 5 c c 2 1.414 c 20 4.47 知道了ωc后，便可利用如下公式求相角裕度。 由图可知因1＜ωc＜5，故可取
§5-5
一、幅值裕度
控制系统的相对稳定性
定义 : 在幅相曲线上，相角等 于－180 时对应幅值的倒数 , 称为 控制系统的幅值裕度。 即 h 1 A ( g )
第五章5 5 相角裕度和幅值裕度以及闭环频率特性自动控制原理 浙江大学考研资料
-90° -135° -180°
-225° -270°
ωΦ ωc
ω→
Phase margin angle, γ(–)
G(jω)的对数幅频曲线和10相频曲线
Phase Margin and Gain Margin
相角裕度和幅值裕度的求解方法——解析法
通常有三种求解系统相角裕度和幅值裕度的方法，即解析法、极坐标 图法和伯德图法。下面通过实例进行说明。
则系统将处于临界稳定状态。可以用频率点ωx处的传递函数来表示，
即 G( jx ) h 1
在G(jω)极坐标图上，频率点 ωx对应的幅值
G(
jx )
1 h
在对数幅频曲线上, Lmh Lm G( jx )
8
Phase Margin and Gain Margin
相角裕度和幅值裕度以及与稳定性的关系
如果稳定性不够？？－－校正。
2
主要内容
Phase Margin and Gain Margin
简介 Bode 图 (对数坐标图) 极坐标图 Nyquist稳定判据- 1 Nyquist稳定判据- 2 相角裕度和幅值裕度以及与稳定性的关系 闭环频率特性 补偿 ………
LmG(jω)
ωΦ
-1 γ(–) Φ
G(jω) ω G(jω)的极坐标图
-90°
-135° -180° -225° -270°
ωΦ
ω→ Phase margin
angle, γ(–)
G(jω)的对数幅频曲线6 和相频曲线
Phase Margin and Gain Margin
相角裕度和幅值裕度以及与稳定性的关系
（一） 解析法 根据系统的开环频率特性，由 G( j )H ( j ) 1 (0 )
自动控制原理 第五章(第六次)
• 指开环幅相特性曲线在截止频率 附c 近的区段。
22
从开环频率特性研究闭环系统性能
自动控制原理
(1)截止频率 的c 斜率为-20dB/dec 宽度2 c 3
系统是稳定的，并近似认为整个开环特性为-20dB/dec
则，开环传递函数为 G(s) K c
ss
相位裕度约为90°，幅值裕度为无穷大，超调量 为零，调节时间 3 。
n2
1
c2 4 2n2
29
从开环频率特性研究闭环系统性能
自动控制原理
A(c ) c
n2
1
c 2
4
2 2 n
n4 c2 (c2 4
2 2 n
)
1
n4
c4
1
4
2
n2 c2
1
c ( 4 2 1 2 2 )1/ 2 n
阻尼比一定，截止频率随自然频率的增大 而增大。
30
从开环频率特性研究闭环系统性能
A( jc )
(
K 1
1 c2 )3
c
K
1/
3
1
1.233, K 1.908, K
4 10
相角裕度:
180
K=4时:
() 180 3arctgc Kg>1, γ>0 闭环系统稳定
27.1 7.0
K=10时: Kg<1,γ <0 闭环系统不稳定
K 4 K 10
பைடு நூலகம்10
5.6 频域稳定裕度—相对稳定性
幅值裕度为
Kg
1
G jg H jg
1 4
0.34
0.98 1 0.982
该闭环系统不稳定。
伯德图分析-稳定性-及幅值和相角裕度
作业： P339 16.1 a. P339 16.3 e.
sys=tf([1 1],[0.2 1 0 0]); bode(sys) pause
用根轨迹来验证： Im
Re
-10
-1
图.16.9 系统的根轨迹图
▽ 多个频率穿越点：
考虑下面的例子
GH s
K
s 3 1
1 s1 s s /1001
/10 s /1000
增益穿越频率在ω =1处, 相角裕度为 -45º, 可判断出系统是不稳定的。
它是该频率处的幅值分贝值与0db线之间的差值用分贝表示相角裕度是通过增益穿越频率得出的它是此频率处的相角与180线之间的差值
线性控制系统工程
第16章
伯德图分析，稳定性， 及幅值和相角裕度
第16章 伯德图分析,稳定性 及幅值和相角裕度
伯德图中的增益裕度和相角裕度
M ( pc)
g c
(g c)
20 lg NK KdB NdB
M db
－90 －180 －270
K3 Kc K2
K1
log10
Im
Kc
K1 K2
K3
Re
Im
－1 K1
Kc K2 K3
Re
图.16.2 具有变化K的系统伯德图、奈奎斯特图和根轨迹
在相位-180°时， K dB 幅值约为 – 18dB， 如果系统不稳定：
如果k=1 ，那么当ω = 1 时，图形经过
Mdb= 0dB线。
M db -20db/decade
20 log10 Kv
1800
图.16.5
1
1型系统的伯德图
log10
相角裕度幅值裕度
19
5-5 从开环频率特性研究闭环系统性能
(2)截止频率c 处的斜率为-40dB/dec
并近似认为整个开环特性为-40dB/dec 则，开环传递函数为G(s)=K/s2 相位裕度为0°，系统处于临界稳定状态。
(3)通过截止频率 c 的斜率为-60dB/dec
相位裕度为-90°,系统不稳定
20
5-5 从开环频率特性研究闭环系统性能
0
c
负幅值裕度 h
0
正h 幅值裕度
c
90 180 270
＋
x
正相角裕度
(a)稳定系统
90
180 270
x －
负相角裕度
（b）不稳定系统
相角裕度和幅值裕度小结：
相角裕度和幅值裕度是系统的极坐标图对(-1,j0)点 靠近程度的度量。这两个裕度可以作为设计准则。
只用相角裕度或幅值裕度，都不能说明系统的相对 稳定性。系统的相对稳定性必须同时给出这两个量。
K=10时：
10
(c 2
3
1) 2
1,
c
1
1003 1 1.91
2 180 0 c 180 0 3tg11.91 70
(x ) 3tg1x 1800 , x 3
h2
1
G( jx )
8 0.8 10
h2
20 lg G( jx )
10
20 lg
3
(3 1) 2
2(dB)
0
t
t
(c)
(d)
c、d系统稳定
幅相曲线越远离临界点
系统的稳定程度越好
▪相角裕度又称相位裕度(Phase Margin)
设系统的截止频率为 c
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
控制系统正常工作的首要条件是系统稳定，同时 还必须满足一定的相对稳定性要求，相对稳定性反映 出系统稳定程度的好坏。闭环控制系统相对稳定性 （时域中，超调量 % ，根与虚轴距离）可以通过 开环频率特性加以描述。奈氏（幅相）曲线与临界点 （－1，j0）的靠近程度，可以用来度量稳定裕度， 在实际工程系统（控制、电子、通信系统）中常用相 角（位）裕度（量）和幅值裕度（量）h表示。
20lg
x 1 x2 1 0.01• x2
x 0x2
20 20lg 3.162 6.02dB
P198
5-13
已知系统的开环传递函数 G(s) 试计算K=4、10的稳定裕度。
s
K
13
G( j)
K=4时：
K
j 13
K
( 2
3
1) 2
exp j(3tg1 )
j
4
(c 2
3
1) 2
1
相角裕度: =1800+ ∠ G(jc)
稳定裕度的定义续2
20lgG( jc )H( jc ) 0dB
1800 G jc H jc
00
dB h 0dB
(x ) G jx H j x 1800
h 20lg G( jx ) dB
00
dB h 0dB
0
c
负幅值裕度 h
j
G(j )曲线过(-1,j0)点时
G(j) =1
-1
∠ G(j) = -180o G(j)
0
同时成立！
此时，截止频率等于穿越频率
=0+
G( j )
K
j( jT1 1)( jT2 1)
1 =0
幅值裕度: hdB=－20lgG(jx )
c
0dB
20lg G( jx )
c
x
∠ G(jc)
-180o
最小相位系统的相位裕度和增益裕度都是正值时， 系统才是稳定的。负的裕度表示系统不稳定。
适当的相角裕度和幅值裕度可以防止系统参数变化 造成的影响，并且指明了频率值。
工程（实践）上满足: 控制系统的性能要求:
相角裕度: 300 ~ 600
幅值裕度: h 6～10dB
对数幅频曲线以 20dBdec 穿越0分贝线
一般来说，相角裕度和幅值裕度概念只适用于 最小相位控制系统(但可含滞后环节)。
举例 说明
Im
-1
0 Re
G( j)
K
j( jT1 1)( jT2 1)
Im
Im
Im
-1
0 Re
-1
0 Re
-1
0 Re
h(t)
h(t)
h(t)
h(t)
0
t
(a)
a系统不稳定
0
0
t
(b)
b系统临界稳定
(-1,j0)为临界点
试分别计算K=5、20的相角裕度和幅值裕度。
解：G( j )
K
e j 900 arctan arctan0.1
1 2 1 0.01 2
计算K=5：由图读出相角裕度和幅值裕度; 辅助计算
A( )
5
1 2 1 0.01 2
5
12
5 1,
02
c
5
0
180
900 arctan
P199 例5-13
已知二阶系统的开环传递函数为G(s) n2 试计算相位裕量与阻尼比 的关系。 s(s 2n )
解：
G( j)
2 n
j( j 2 n )
2
2 n
2 n 2
exp
j
900
arctan
2 n
A(c ) G( jc )H( jc ) 1
n2
1
c c2 2 n 2
定义幅值裕度为
h
1
G jx H jx
幅值裕度h的物理意义：
对于闭环稳定系统，如果系统开环幅频特性再增大h
倍，则系统将变为临界稳定状态。h 值越大，保证系统稳
定工作的前提下，允许开环增益值变化越大。若以分贝表
示，则有：
h
20lg
G
j x
1
H
j x
20lg G jx H jx (dB)
系统临界稳定，见右图：
0
正h 幅值裕度
c
90 180 270
＋
x
正相角裕度
(a)稳定系统
90
180 270
x －
负相角裕度
（b）不稳定系统
相角裕度和幅值裕度小结：
相角裕度和幅值裕度是系统的极坐标图对(-1,j0)点 靠近程度的度量。这两个裕度可以作为设计准则。
只用相角裕度或幅值裕度，都不能说明系统的相对 稳定性。系统的相对稳定性必须同时给出这两个量。
A()
20
1 2 1 0.01 2
20
12
20 1,
02
c
20
0
180
900 arctan
20 arctan0.1•
20 900 77.40 24.10 11.50
(x )
900
arctan x
arctan
0.1 x
0
180
x
3.16 rads
20
20
h 20lg
5 arctan0.1•
5 900 65.90 12.60
11.50
(x ) 900 arctan x arctan 0.1x 1800 x 3.16 rads
5
5
5
h 20lg
x
1 x2
20lg
1 0.01•x2
x
0 x2 20lg 3.162 6.02dB
计算K=20：由图读出相位裕量和幅值裕量 辅助计算
相位裕度的物理意义：
对于闭环稳定系统，如果开环相频特性再滞后 度，则系统将由稳定变为临界稳定。
为了使最小相位系统稳定，相角裕度必须为正。 在对数坐标图上的临界稳定点为0dB和－1800
幅值裕度又称增益裕度(Gain Margin)
相角为-180°点所对应的频率为穿越频率
(x ) G jx H j x 1800
0
t
t
(c)
(d)
c、d系统稳定
幅相曲线越远离临界点
系统的稳定程度越好
▪相角裕度又称相位裕度(Phase Margin)
设系统的截止频率为 c
A(c ) G( jc )H( jc ) 1, L(c ) 0dB
定义相角裕度为 G jc H jc 1800
1800 G jc H jc
0 4 0 10
1
-1
c 163 1 1.23
1 1800 c
G ( j )
1800 3tg11.23 27.10
(x ) 3tg1x 0 , x 3
h1 20lg G( jx ) 20lg
1800 G jc H jc
1800 900 arctan c 2 n
＝arctan 2n c
c n 1 4 4 2 2
arctan
2
1 4 4 2 2
P200 例5-14（图解法、近似计算法、精确计算法）
已知系统的开环传递函数，试计算 G(s)
K
s(s 1)(0.1s 1)