精密机械设计(裘祖荣) 第七章答案 齿轮传动
机械原理课后答案——第七章--齿轮系及其设计PPT课件

-
6
11-17 解:此轮系为一个3K型周转轮 系,即有三个中心轮(1、3和4)。
i1H1i1 H 3 1(z z1 2 z z2 3 ')15 6 71.5 0 i4 H 1 i4 H 3 1 (z z2 4 'z z2 3) 1 5 2 6 5 5 2 7 5 5 16 i14 ii1 4H H1.5 0(5)6 58(n1 8 与 n4转向 ) 相反
齿轮系及其设计
习题11-11 习题11-16 习题11-17 习题11-18- Nhomakorabea1
11-11 解:
i1 5zz 1 2 zz 2 '3 z z3 4 'z z5 4 ' 5 2 0 3 0 1 0 4 5 1 1 0 58 25.7 77 8
-
2
-
3
11-16 解:此轮系为一复合轮系。
在1-2(3)-4定轴轮系中
画箭头表示的是构件在转化轮系中的转向关系,而不 是在周转轮系中的转向关系。 n1Hn1nH18.461r5/min n1=200r/min
n3Hn3nH11.538r5/min n3= -100r/min
n1H与n3H反向,与图中箭 方头 向所 相示 同。
若转化轮系传动比的“”判断错误,不仅会影响到 周转轮系传动比的大小,还会影响到周转轮系中构件的转
i 1 H i 1 i 4 ' 7 i 7 H 3 . 5 2 5 . 8 1 2 9 . 7 9 2 7 . 5 8 7 87
故 n H n 1 /i 1 H 3/ 5 2 .5 4 8 8 1 9 .1 7 2 (5 r 4转 /m 4 转 向 in) ) 向 与
-
4
11-16 解:1) 图a: i1 H3 n n 1 3 n n H Hz z1 2zz2 3 ' 2 2 0 4 4 3 0 01.6
精密机械设计基础(1-2章) (裘祖荣 著) 机械工业出版社 1-2章课后答案

FC α α D T E Q C FDY FDX
代入已知参数,解得: FDX=2Q , FDY=0.25Q 1-9 解 : 取 杆 点受滑 D)T 和 程:
y
= 0 = FB ⋅ cos α − F
d FA’ FA O A M
即
FB = F / cos α
3)取 OA 杆进行受力分析。OA 杆在 A 点受力 FA(和 FA’是一对作用力和反作 用力) 。对 O 点取矩, 根据平衡条件合力 矩为 0:
M O ( F ) = 0 = FA ⋅ d − M
2
即: M = FA ⋅ d = FA '⋅ d = FB '⋅ d = FB ⋅ d = Fd / cos α 又:d=(200+100)sinα tanα=100/200 解得:M=60000N.mm=60N.m
1-8 解:1)BC 杆是二力杆,受力在 杆沿线上。 2) 取 CD 杆和滑轮为一体进行受 力分析。 其中滑轮受力可简化到中心E (如图,T=Q) 。 C 点受力 FC(方向 由二力杆 BC 确定) 。列平衡方程:
1-6 解:1)取整体结构为行受力分析,在外力(重 力 P、 在 B 点的正压力 FB 和在 C 点的正压力 FC) 作用下平衡,则对 B 点取矩,合力矩为 0:
M B (F ) = 0 = FC ⋅ 2l ⋅ cos α − P (2l cos α − a cos α )
FC
a a 解得 FC = P (1 − ) , FB = P − FC = P 2l 2l
精密机械设计基础课件(合肥工业大学)第七章(齿轮1)详解

分度圆压力角()
rb r cos
齿顶高(ha)齿根高(hf)
图7-6a
齿宽(b)
分度圆是计算齿轮各部分尺寸的基准圆,具有标准模数和压力角。
正常齿制
m>=1, ha *=1, c* =0.25 m<=1, ha *=1, c* =0.35 短齿制 m>=1, ha *=0.8, c* =0.3
法节Pn 相邻两齿同侧齿廓间沿法线量得的距离 它与基圆周节Pb相等
⒊ 齿廓上各点压力角相同,等于齿廓的倾斜角
⒋ 齿廓上各点齿距相同
第四节 渐开线齿轮的基本参数
三、渐开线圆柱齿轮任意圆上的齿厚
任意圆齿厚:(7-9)
si
ri
s
ri r
2ri (invi
inv )
式中 任意圆上压力角:
i
arccos
rb ri
计算齿顶圆、节圆和基圆上
的齿ห้องสมุดไป่ตู้时,只要把式中的ri和
i进行相应的替换即可。
⑶N为渐开线上K点的曲率中 心,NK为曲率半径。
⑷渐开线的形状取决于基圆 的大小。
⑸基圆内无渐开线。
第三节 渐开线齿廓曲线
图7-3
图8-4
二、渐开线方程式
rk
rb
cos k
第三节 渐开线齿廓曲线
压力角
k invk tank k
tan k
NK rb
AN rb
rb
k k
rb
k
k
图8-3
第三节 渐开线齿廓曲线
1、插齿 一把刀具可加工各种齿数齿轮;确保被 加工齿轮有相同的模数和压力角;可加工内齿轮; 效率偏低。
图7-14
图7-15
精密机械设计基础习题答案(裘祖荣)
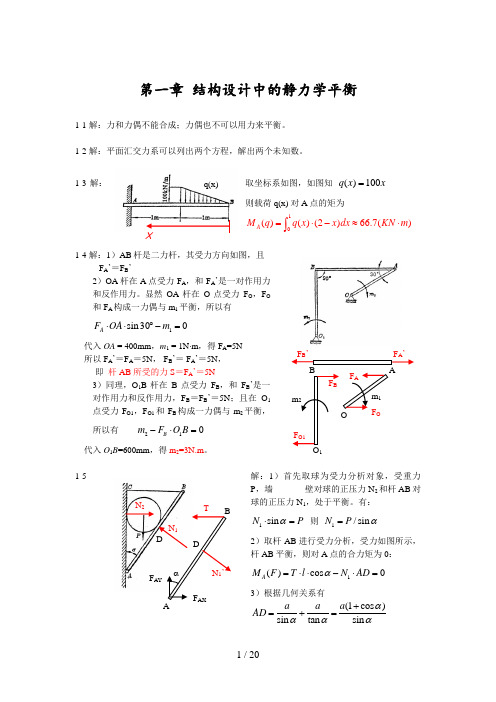
第一章 结构设计中的静力学平衡1-1 解:力和力偶不能合成;力偶也不可以用力来平衡。
1-2 解:平面汇交力系可以列出两个方程,解出两个未知数。
取坐标系如图,如图知 ()100q x x = 1-3 解:则载荷q(x) 对A 点的矩为1()()(2)66.7()A M q q x x dx KN m =⋅-≈⋅⎰1-4 解:1)AB 杆是二力杆,其受力方向如图,且 F A ’=F B ’2)OA 杆在A 点受力F A ,和F A ’是一对作用力和反作用力。
显然OA 杆在O 点受力F O ,F O 和F A 构成一力偶与m 1平衡,所以有 1sin 300A F OA m ⋅⋅︒-=代入OA = 400mm ,m 1 = 1N ⋅m ,得 F A =5N 所以F A ’=F A =5N , F B ’= F A ’=5N ,即 杆AB 所受的力S =F A ’=5N3)同理,O 1B 杆在B 点受力F B ,和F B ’是一对作用力和反作用力,F B =F B ’=5N ;且在O 1点受力F O1,F O1和F B 构成一力偶与m 2平衡,所以有 210B m F O B -⋅= 代入O 1B =600mm ,得 m 2=3N.m 。
解:1)首先取球为受力分析对象,受重力1-5P ,墙 壁对球的正压力N 2和杆AB 对球的正压力N 1,处于平衡。
有:1sin N P α⋅= 则 1/sin N P α=2)取杆AB 进行受力分析,受力如图所示,杆AB 平衡,则对A 点的合力矩为0:1()cos 0A M F T l N AD α=⋅⋅-⋅=3)根据几何关系有(1cos )sin tan sin a a a AD αααα+=+=Xq(x)F B ’ ABF A ’ F Am 1 OFm 21F BF O1N 1 N 2A D N 1’TαBD F AYF AX最后解得:2211/cos 1sin cos cos Pa Pa T l l αααα+=⋅=⋅- 当2cos cos αα-最大,即α=60°时,有T min =4Pa l。
精密传动答案汇总(万)

1.谐波齿轮传动的组成、工作原理和特点。
三个基本构件:(1)谐波发生器(简称波发生器)(2)柔性齿轮(简称柔轮)(3)刚性齿轮(简称刚轮)工作原理:谐波齿轮传动的运动转换,是依靠挠性构件的弹性变形来实现的,这种运动转换原理称为变形原理特点:传动特点:(1)结构简单,体积小,重量轻;(2)传动比范围大(3)同时啮合齿数多(4)运动精度高。
(5)承载能力大。
(6)传动效率高。
(7)齿侧间隙可以调整。
(8)运动平稳,无冲击,噪声小。
(9)同轴性好。
(10)可实现向密闭空间传递运动及动力。
(11)可实现高增速运动。
(12)方便的实现差速传动。
2.谐波齿轮传动的分类方法和类型。
(1)按啮合类型可分为1)径向啮合式谐波齿轮传动2)端面啮合式谐波齿轮传动(2)按变形波数可分为1)单波(U=1)传动。
刚轮与柔轮的齿数之差为1,在国内外均研究得较少。
单波传动不仅具有谐波齿轮传动所具有的一切优点,而且在传动比和模数相同的情况下,其径向尺寸分别比双波和三波传动小一倍到两倍。
2)双波(U=2)传动。
其齿差为2。
由于变形时柔轮的表面应力较小,结构比较简单,且易于获得大的传动比,因而是目前最常用的一种。
3)三波(U=3)传动。
其齿数差为3。
这种传动的元件虽然对中性好,偏心误差较小,但是在相同的传动比和模数的情况下,径向尺寸比上两种传动都大;采用凸轮式波发生器时,波发生器凸轮廓线的加工复杂;同时由于柔轮中的应力较大(约比双波传动大两倍)和波发生器转一圈时,柔轮反复弯曲的次数增加,因而对柔轮的疲劳寿命提出了较高的要求。
故一般情况下,这种传动应用较少。
(3)按波发生器与柔轮相互作用原理的不同可分为1)依靠波发生器与柔轮之间的机械连系以产生相互作用的传动。
例如,机械波发生器(常用的有触头型、双圆盘型和采用柔性轴承的凸轮型波发生器等),液压波发生器和气动波发生器等,均籍机械力使柔轮产生移动的可控弹性变形波以实现啮合运动的传递;2)依靠波发生器与柔轮之间的电磁耦合以产生相互作用的传动。
机械原理课后答案第七章作业
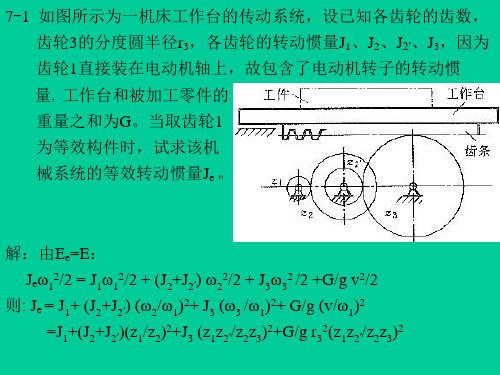
=J1+(J2+J2′)(z1/z2)2+J3 (z1z2′/z2z3)2+G/g r32(z1z2′/z2z3)2
7-5 某内燃机的曲轴输出力矩Md随曲柄转角ψ的变化曲线如图a所示,
其运动周期ψT=π,曲柄的平均转速 nm=620r/min,当用该内燃
机驱动一阻抗力为常数的机械时,如果要求运转不均匀系数 δ=0.01,试求:
1)曲柄最大转速nmax和相应的曲柄转角ψ(max ) ;
2)装在曲轴上的飞轮转动惯量JF(不计其余构件的转动惯量)。 解:1)确定阻抗力矩 因一个运动循环内驱动功应等 于阻抗功,有
ψTMr = Md(ψ)dψ=200(π/6+π)/2
0
π
a)
故Mr =200(π/6+π)/π=116.7(Nm)
7-1 如图所示为一机床工作台的传动系统,设已知各齿轮的齿数,
齿轮3的分度圆半径r3,各齿轮的转动惯量J1、J2、J2′、J3,因为
齿轮1直接装在电动机轴上,故包含了电动机转子的转动惯 量,工作台和被加工零件的
重量之和为G。当取齿轮1
为等效构件时,试求该机 械系统的等效转动惯量Je 。
解:由Ee=E: Jeω12/2 = J1ω12/2 + (J2+J2′) ω22/2 + J3ω32 /2 +G/g v2/2 则: Je = J1+ (J2+J2′) (ω2/ω1)2+ J3 (ω3 /ω1)2+ G/g (v/ω1)2
2)求nmax及ψ(max ) ab/20=116.7/200 ∴ ab=11.7° x/130=(200-116.7)/200 ∴ x =54.2° Wab = -11.7×π/180×116.7/2= -11.9(Nm) Wca′= -(130-54.2)×π/180×116.7= -77.2(Nm) a) Wbc = +[30+(20-11.7+30+54.2)]×π/180×(200-116.7)/2=+89.1(Nm)
精密机械设计基础_裘祖荣_齿轮传动

1、什么是啮合角?啮合角与压力角有何关系?
2、基圆上渐开线的曲率半径是多少?压力角多大?
3、齿轮的齿顶圆是否一定大于齿根圆?有没有基圆大于分
度圆的情况?
4、由于齿轮传动中要留有径向间隙,因此,齿根圆附近径
向距离为 c*m 的一段齿廓不是渐开线,其他齿廓段皆为渐
开线,这种说法对吗?
5、任意圆上的齿厚公式对齿轮任意圆上的齿廓都使用吗?
6、如图所示是一对齿数分别为 z 1 、 z 2 的齿轮互相啮合,设模数为 m ,压力角α。
试求实际啮合线 B 1 B 2 的长度,基节 P b 和重合度ε的表达式,并求轮 1 上的牙齿自开始啮合至脱开啮合(即齿廓与 B 1 B 2 有相交之处)过程中所转过的角φ 1 。
7、如例图所示,已知各轮齿数为 z1 , z2 , z3 , z4 , z5 , z6 , z1为主动件,转向如图箭头所示,试求:( 1 )传动比 i 1H =w 1 /w H =? ( 列出表达式 );( 2 )若已知各齿轮齿数 z 1 =z 2 =z 4 =z 5 =20 、 z 3 =40,z 6 =60, 求 i 1H 的大小及转向。
8、如例图所示轮系,已知各轮齿数为: z 1 =25, z 2 =50, z 2' =25, z
H =100,z 4 =50, 各齿轮模数相同。
求传动比i(14) 。
精密机械设计习题答案

精密机械设计习题答案精密机械设计习题答案在精密机械设计中,习题是我们提高技能和理解能力的重要方式。
通过解答习题,我们可以加深对机械设计原理的理解,培养解决问题的能力。
在这篇文章中,我将为您提供一些精密机械设计习题的答案,希望能够帮助您更好地掌握这一领域的知识。
1. 问题:如何设计一个精密的齿轮传动系统?答案:设计精密齿轮传动系统需要考虑许多因素,包括齿轮的模数、齿轮的齿数、齿轮的硬度等。
首先,我们需要选择合适的材料,如高强度合金钢或硬质合金。
然后,根据传动比和载荷要求,计算出齿轮的模数和齿数。
接下来,进行齿轮的绘制和加工,确保齿轮的精度和表面质量。
最后,进行齿轮的装配和调试,确保传动系统的稳定性和精度。
2. 问题:如何设计一个高精度的直线导轨系统?答案:设计高精度直线导轨系统需要考虑导轨的材料、导轨的精度和导轨的润滑等因素。
首先,我们需要选择高硬度和高耐磨性的材料,如硬质铝合金或工具钢。
然后,根据导轨的长度和载荷要求,计算出导轨的精度和尺寸。
接下来,进行导轨的制造和加工,确保导轨的平整度和表面质量。
最后,进行导轨的润滑和调试,确保导轨系统的稳定性和精度。
3. 问题:如何设计一个高精度的光学仪器?答案:设计高精度光学仪器需要考虑光学元件的选择、光路的设计和光学系统的调试等因素。
首先,我们需要选择高质量的光学元件,如高透射率的镜片和透镜。
然后,根据光学系统的要求,设计出合适的光路,包括准直、聚焦和成像等过程。
接下来,进行光学元件的安装和调试,确保光学系统的稳定性和精度。
最后,进行光学仪器的性能测试和校准,确保其满足实际应用的要求。
4. 问题:如何设计一个高精度的测量仪器?答案:设计高精度测量仪器需要考虑测量原理、传感器的选择和测量系统的调试等因素。
首先,我们需要选择合适的测量原理,如激光测距、电阻测量或光学测量等。
然后,根据测量要求,选择合适的传感器,如激光传感器、压力传感器或光学传感器等。
接下来,进行测量系统的设计和调试,确保测量系统的稳定性和精度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7-19 图7-71所示为一大传动比的减速器。
已知其各齿轮的齿数为Z1=100,Z2=101,Z2′=100,Z3=99,求原动件对从动件1的传动比i H1 .又当Z1=99而其他齿轮齿数均不变,求传动比i H1。
试分析该减速器有何变化。
图7-71 1)解法一:
这是一个简单行星轮系。
其转化机构的传动比为:
()100100991011'213223131
13⨯⨯=
-=--==z z z z i H H H H
H ωωωωωω
100100991010113
3⨯⨯=
--==H H H
i ωωωω所以:
由于
10000
100
1009910111
11=⨯⨯-
==∴ωωH H i
解法二:
10000
/110000
1100100991011z
z z z 1111213213
1==∴=
⨯⨯-=-=-='H H H
H i i i i )(上式直接用公式:
2)将Z1=99代入,求得i H1= -100.
3)齿轮1的转向从与原动件H 相同变为与原动件H 相反。
7-20 在图
7-72
示双螺旋桨飞机的减速器中,已知
18,30,20,265421====z z z z ,及1n =15000r/min ,试求Q P n n 和的大小
和方向。
(提示:先根据同心,求得3z 和6z 后再求解。
)
图7-72
解:由图可知n 3=n 6=0 根据同心条件:
66202262213=⨯+=+=z z z 64253021866z z z =+=+⨯=
1)1-2-3-P(H)组成行星轮系 i 13
P
=
n 1−n p n 3−n p
=
15000−n p 0−n p
=−
z 3z 1
=−
6626
解得n p =4239.5r/min (与n 1同向) n 4=n p =4239.5r/min 2)4-5-6-Q(H)组成行星轮系 i 46
Q
=
n 4−n Q n 6−n Q
=
4239.5−n Q
−n Q
=−z 6
z 4
=−66
30
解得min /737.1324r n Q =(与n 1同向).
7-21 在图7-73所示输送带的行星减速器中,已知:z 1=10, z 2=32, z 3=74, z 4=72, z 2,=30 及电动机的转速为1450r/min ,求输出轴的转速n 4。
解:
1-2-3-H 行星轮系; 3-2-2’-4-H 行星轮系;
1-2―2’-4-H 差动轮系;(由于n4未知,且无法利用n3=0的条件,故不讨论) 这两个轮系是独立的。
)1(3
1
113z z
n n n i H H H -=--=
)2(2
43
2443z z z z n n n i H H H
'=--=
3
1
11z z i H
+==8.4
2
43
241z z z z i H
'-
==0.0365
3
12
432144111z z z z z z i i H
H +
-=
='=n 4n1 = n 41450
解得n4=6.31r/min(与
1
n转向相同)。
7-22 在题图7-74所示的自行车里程表机构中,C为车轮轴,P为里程表指针。
已知各轮齿数为z1=17,z3=23,z4=19,z4'=20,z5=24。
设轮胎受压变形后车轮的有效直径为0.7m,当自行车行驶1km时,表上的指针刚好回转一周。
试求齿轮2的齿数。
7-23 已知图4-4所示车床尾架套筒的微动进给机构中Z
1 = Z
2
= Z
4
= 16
Z
3
= 48 ,丝杆的螺距 t = 4 mm 。
慢速给时齿轮1和齿轮2啮合;快速退回时齿轮1插入内齿轮4。
求慢速进给过程中和快速退回过程中手轮回转一周时,
套筒移动的距离各为多少?
解:
1)慢进时:1-2-3-H 为行星轮系
416
48
1111313
1=+=--=-=)(z z i
i H H
4
1
41==n n H
移动距离 mm L n S H 144
1
=⨯==
2)快进时:1、4为一整体。
114===n n n H
移动距离
mm
L n S H 441=⨯==。
