三角函数特殊角值表(完整版)资料
(完整版)三角函数特殊角值表

角度 函数 0 30 45 60 90 120 135 150 180 270 360 角a 的弧度0 π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π 3π/2 2π sin 0 1/2 √2/2 √3/2 1 √3/2 √2/2 1/2 0 -1 0 cos 1 √3/2 √2/2 1/2 0 -1/2 -√2/2 -√3/2 -1 0 1 tan√3/31√3-√3-1-√3/31、图示法:借助于下面三个图形来记忆,即使有所遗忘也可根据图形重新推出: sin30°=cos60°=21,sin45°=cos45°=22, tan30°=cot60°=33, tan 45°=cot45°=1正弦函数 sinθ=y/r 余弦函数 cosθ=x/r 正切函数 tanθ=y/x 余切函数 cotθ=x/y 正割函数 secθ=r/x 余割函数 cscθ=r/y2、列表法:说明:正弦值随角度变化,即0˚ 30˚ 45˚ 60˚ 90˚变化;值从02122 23 1变化,其余类似记忆.3、规律记忆法:观察表中的数值特征,可总结为下列记忆规律:① 有界性:(锐角三角函数值都是正值)即当0°<α<90°时,则0<sin α<1; 0<cos α<1 ; tan α>0 ; cot α>0。
②增减性:(锐角的正弦、正切值随角度的增大而增大;余弦、余切值随角度的增大而减小),即当0<A <B <90°时,则sin A <sin B ;tan A <tan B ; cos A >cos B ;cot A >cot B ;特别地:若0°<α<45°,则sin A <cos A ;tan A <cot A 若45°<A <90°,则sin A >cos A ;tan A >cot A . 4、口决记忆法:观察表中的数值特征 正弦、余弦值可表示为2m 形式,正切、余切值可表示为3m 形式,有关m 的值可归纳成顺口溜:一、二、三;三、二、一;三九二十七.30˚ 123145˚ 1212 60˚ 3函数名正弦余弦正切余切正割余割符号sin cos tan cot sec csc正弦函数sin(A)=a/c余弦函数cos(A)=b/c正切函数tan(A)=a/b余切函数cot(A)=b/a其中a为对边,b为邻边,c为斜边三角函数对照表三角函数SIN COS TAN 三角函数SIN COS TAN 0°0 1 0 90° 1 0 无1°0.0174 0.9998 0.0174 89°0.9998 0.0174 57.2899 2°0.0348 0.9993 0.0349 88°0.9993 0.0348 28.6362 3°0.0523 0.9986 0.0524 87°0.9986 0.0523 19.0811 4°0.0697 0.9975 0.0699 86°0.9975 0.0697 14.3006 5°0.0871 0.9961 0.0874 85°0.9961 0.0871 11.4300 6°0.1045 0.9945 0.1051 84°0.9945 0.1045 9.5143 7°0.1218 0.9925 0.1227 83°0.9925 0.1218 8.1443 8°0.1391 0.9902 0.1405 82°0.9902 0.1391 7.1153 9°0.1564 0.9876 0.1583 81°0.9876 0.1564 6.3137 10°0.1736 0.9848 0.1763 80°0.9848 0.1736 5.6712 11°0.1908 0.9816 0.1943 79°0.9816 0.1908 5.1445 12°0.2079 0.9781 0.2125 78°0.9781 0.2079 4.7046 13°0.2249 0.9743 0.2308 77°0.9743 0.2249 4.3314 14°0.2419 0.9702 0.2493 76°0.9702 0.2419 4.0107 15°0.2588 0.9659 0.2679 75°0.9659 0.2588 3.7320二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin 22sin cos cos 2cos 2sin 22cos 2112sin 2αααααααα==-=-=-2tan tan 21tan 2ααα=--sin 33sin 4sin 3cos34cos33cos .3tan tan 3tan 313tan 2αααααααααα=-=--=--三角函数的和差化积公式 三角函数的积化和差公式sin sin 2sincos 22sin sin 2cos sin22cos cos 2cos cos22cos cos 2sin sin22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=⋅+--=⋅+-+=⋅+--=-⋅[][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=++-⋅=+--⋅=++-⋅=-+--化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)22sin cos sin()a x b x a b x φ±=+±其中φ角所在的象限由a 、b 的符号确定,φ角的值由tan ba φ=确定六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
特殊三角函数值对照表(特殊角的三角函数值)

特殊三角函数值对照表(特殊角的三角函数值)《特殊角的三角函数值》是人教版数学九年级下册第二十八章的内容,特殊三角函数值一般指在0,30°,45°,60°,90°,180°角下的正余弦值。
这些角度的三角函数值是经常用到的。
并且利用两角和与差的三角函数公式,可以求出一些其他角度的三角函数值。
具体的三角函数值如下表:扩展资料:黄金三角函数介绍:α=18°(π/10) sinα=(√5-1)/4 cosα=√(10+2√5)/4tαnα=√(25-10√5)/5cscα=√5+1 secα=√(50-10√5)/5 cotα=√(5+2√5)α=36°(π/5) sinα=√(10-2√5)/4 cosα=(√5+1)/4tαnα=√(5-2√5)cscα=√(50+10√5)/5 secα=√5-1 cotα=√(25+10√5)/5α=54°(3π/10) sinα=(√5+1)/4 cosα=√(10-2√5)/4 tαnα=√(25+10√5)/5是数学中属于初等函数中的超越函数的一类函数。
它们的本质是任意角的集合与一个比值的集合的变量之间的映射。
通常的三角函数是在平面直角坐标系中定义的,其定义域为整个实数域。
另一种定义是在直角三角形中,但并不完全。
扩展资料:三角函数在复数中有重要的应用。
三角函数也是物理学中的常用工具。
它有六种基本函数函数名正弦余弦正切余切正割余割符号 sin cos tan cot sec csc正弦函数sin(A)=a/c余弦函数cos(A)=b/c正切函数tan(A)=a/b余切函数cot(A)=b/a其中a为对边,b为邻边,c为斜边特殊角的值如下表:在直角三角形中,任意一锐角∠A的对边与斜边的比叫做∠A 的正弦,记作sinA(由英语sine一词简写得来),即sinA=∠A的对边/斜边。
扩展资料:sinα = tanα × cosα(即sinα / cosα = tanα )cosα = cotα × sinα (即cosα / sinα = cotα)tanα = sinα × secα (即tanα / sinα = secα)sin ( α ± β ) = sinα · cosβ ± cosα · sinβsin ( α + β + γ ) = sinα · cosβ · cosγ +cosα · sinβ · cosγ + cosα · cosβ · sinγ - sinα · sinβ · sinγcos ( α ± β ) = cosα cosβ ∓ sinβ sinαtan ( α ± β ) = ( tanα ± tanβ ) / ( 1 ∓ tanα tanβ )完整初中三角函数值表如下图所示:常见的三角函数有正弦函数、余弦函数和正切函数。
三角函数特殊角值表
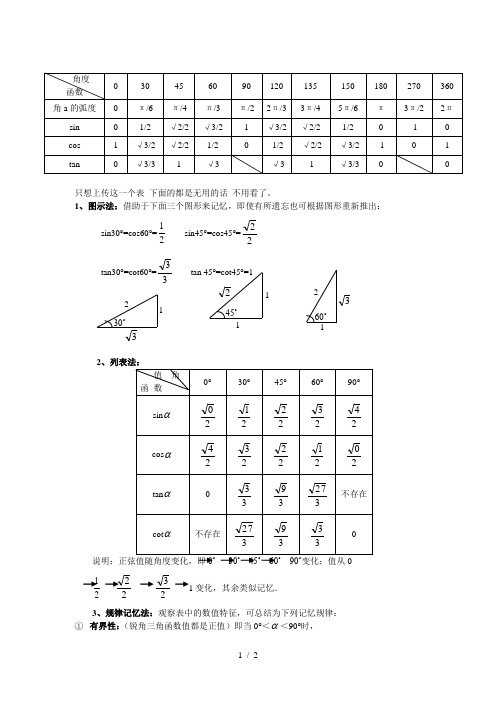
只想上传这一个表 下面的都是无用的话 不用看了。
1、图示法:借助于下面三个图形来记忆,即使有所遗忘也可根据图形重新推出: sin30°=cos60°=
21 sin45°=cos45°=2
2
tan30°=cot60°=3
3
tan 45°=cot45°=1
2说明:正弦值随角度变化,即0˚ 30˚ 45˚ 60˚ 90˚变化;值从0 23 1变化,其余类似记忆. 3、规律记忆法:观察表中的数值特征,可总结为下列记忆规律: ① 有界性:(锐角三角函数值都是正值)即当0°<α<90°时,
30˚ 1
2
3 1
45˚ 1
2 1
2 60˚ 3
则0<sin α<1; 0<cos α<1 ; tan α>0 ; cot α>0。
②增减性:(锐角的正弦、正切值随角度的增大而增大;余弦、余切值随角度的增大而减小),即当0<A <B <90°时,则sin A <sin B ;tan A <tan B ; cos A >cos B ;cot A >cot B ;特别地:若0°<α<45°,则sin A <cos A ;tan A <cot A 若45°<A <90°,则sin A >cos A ;tan A >cot A . 4、口决记忆法:观察表中的数值特征 正弦、余弦值可表示为
2m 形式,正切、余切值可表示为3
m 形式,有关m 的值可归纳成顺口溜:一、二、三;三、二、一;三九二十七.
注:资料可能无法思考和涵盖全面,最好仔细浏览后下载使用,感谢您的关注!。
特殊三角函数数值表

特殊三角函数数值表两角和公式sin(A+B = sinAcosB+cosAsinBsin(A-B = sinAcosB-cosAsinBcos(A+B = cosAcosB-sinAsinB cos(A-B = cosAcosB+sinAsinBtan(A+B = (tanA+tanB/(1-tanAtanB tan(A-B = (tanA-tanB/(1+tanAtanB cot(A+B = (cotAcotB-1/(cotB+cotA cot(A-B = (cotAcotB+1/(cotB-cotA三倍角公式sin3A = 3sinA-4(sinA^3;cos3A = 4(cosA^3 -3cosAtan3a = tan a · tan(π/3+a· tan(π/3-a半角公式sin(A/2 = √{(1--cosA/2}cos(A/2 = √{(1+cosA/2}tan(A/2 = √{(1--cosA/(1+cosA}cot(A/2 = √{(1+cosA/(1-cosA}tan(A/2 = (1--cosA/sinA=sinA/(1+cosA 和差化积sin(a+sin(b = 2sin[(a+b/2]cos[(a-b/2] sin(a-sin(b = 2cos[(a+b/2]sin[(a-b/2] cos(a+cos(b = 2cos[(a+b/2]cos[(a-b/2] cos(a-cos(b = -2sin[(a+b/2]sin[(a-b/2] tanA+tanB=sin(A+B/cosAcosB积化和差sin(asin(b = -1/2*[cos(a+b-cos(a-b] cos(acos(b = 1/2*[cos(a+b+cos(a-b] sin(acos(b = 1/2*[sin(a+b+sin(a-b]cos(asin(b = 1/2*[sin(a+b-sin(a-b]诱导公式sin(-a = -sin(acos(-a = cos(asin(π/2-a = cos(acos(π/2-a = sin(asin(π/2+a = cos(acos(π/2+a = -sin(asin(π-a = sin(acos(π-a = -cos(asin(π+a = -sin(acos(π+a = -cos(atgA=tanA = sinA/cosA万能公式sin(a = [2tan(a/2] / {1+[tan(a/2]^2}cos(a = {1-[tan(a/2]^2} / {1+[tan(a/2]^2}tan(a = [2tan(a/2]/{1-[tan(a/2]^2}a·sin(a+b·cos(a = [√(a^2+b^2]*sin(a+c [其中,tan(c=b/a]a·sin(a-b·cos(a = [√(a^2+b^2]*cos(a-c [其中,tan(c=a/b]1+sin(a = [sin(a/2+cos(a/2]^2;1-sin(a = [sin(a/2-cos(a/2]^2;;这是高考用的正割函数与余割函数正割函数在y=secx中,以x的任一使secx有意义的值与它对应的y值作为(x,y.在直角坐标系中作出的图形叫正割函数的图像,也叫正割曲线. y=secx的性质:(1定义域,{x|x≠π/2+kπ,k∈Z}(2值域,|secx|≥1.即secx≥1或secx≤-1;(3y=secx是偶函数,即sec(-x=secx.图像对称于y轴;(4y=secx是周期函数.周期为2kπ(k∈Z,且k≠0,最小正周期T=2π.并附上很难找到的正割图像.(正割函数图像中值域在-1到1之间的图像不包括。
三角函数特殊角值表
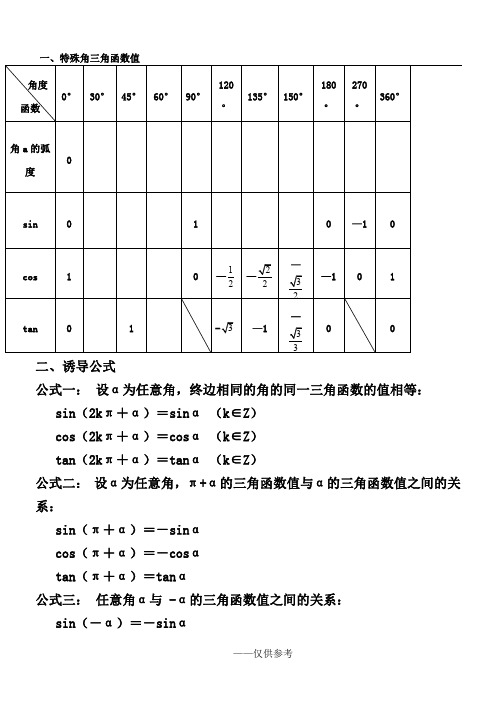
一、特殊角三角函数值
角度
120
180
0° 30° 45° 60° 90°
135° 150°
函数
°
°
270 360°
°
角 a 的弧 0
度
sin
0
1
0 —1 0
cos
1
0 —1 — 2
2
2
— 3
—1
0
1
2
tan
0
1
二、诱导公式
—
- 3 —1
0 3
0
3
公式一: 设α为任意角,终边相同的角的同一三角函数的值相等:
sin(2kπ+α)=sinα (k∈Z)
cos(2kπ+α)=cosα (k∈Z)
tan(2kπ+α)=tanα (k∈Z)
公式二: 设α为任意角,π+α的三角函数值与α的三角函数值之间的关
系:
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
公式三: 任意角α与 -α的三角函数值之间的关系:
关系:
sin(2π-α)=-sinα
cos(2π-α)=cosα
tan(2π-α)=-tanα
公式六: π/2±α及 3π/2±α与α的三角函数值之间的关系:
sin(π/2+α)=cosα
sin(π/2-α)=cosα
cos(π/2+α)=-sinα
cos(π/2-α)=sinα
tan(π/2+α)=-cotα
sin(-α)=-sinα
——仅供参考
cos(-α)=cosα
tan(-α)=-tanα
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
说明:正弦值随角度变化,即0˚30˚ 45˚ 60˚ 90˚变化;值从0
1变化,其余类似记忆.
3、规律记忆法:观察表中的数值特征,可总结为下列记忆规律:
1有界性:(锐角三角函数值都是正值)即当0°< <90°时,
则0<sin <1; 0<cos <1 ; tan >0 ; cot >0。
②增减性:(锐角的正弦、正切值随角度的增大而增大;余弦、余切值随角度的增大而减小),即当0<A<B<90°时,则sinA<sinB;tanA<tanB; cosA>cosB;cotA>cotB;特别地:若0°< <45°,则sinA<cosA;tanA<cotA
《三角函数的应用》
研究性学习开题报告
数学研究性学习小组
2021年11月
一、课题名称:三角函数的应用
二、课题提出的背景:
高一的数学重点是三角函数。他在生活中应用非常广泛,与物理,地理等学科也有密切的关系。为使学生更好的了解数学与生活的联系,以此为研究的课题:
三、课题研究的目的与意义:
1、研究性学习的原因:
若45°<A<90°,则sinA>cosA;tanA>cotA.
4、口决记忆法:观察表中的数值特征
正弦、余弦值可表示为 形式,正切、余切值可表示为 形式,有关m的值可归纳成顺口溜:一、二、三;三、二、一;三九二十七.
巧记特殊角的三角函数值
初学三角函数,记忆特殊角三角函数值易错易混。若在理解掌握的基础上,经过变形,使其呈现某种规律,再配以歌诀,则可浅显易记,触目成诵。
(2)教学课件,网站、文字网站
ENDFOR(3)学生研究活动记录,研究论文及研究报告等。
最终成果形式:(小论文、调查报告、课件、图片等)
(1)sin260°+cos260 (2) -tan450
(3)cos45°-sin30° (4)sin2300+cos2300
(5)tan45°-sin30°·cos60° (6)
(7)2sin300-cos450(6)sin600cos600(8)2sin30°+3cos60°-4tan45°
(9)cos30°sin45°+sin30°cos45° (10)
(11) cos30°+ sin45° (12)2sin300+3sin600-4tan450
(13)tan300sin450+tan600cos450(14)
2、研究目的意义:
⑴以三角函数史为开端,了解三角函数的生活应用,丰富学生对自然科学的认识和提高学生研究生活中的数学知识的兴趣。
⑵通过研究活动,丰富学生的研究体验,发展学生发现问题、提出问题、分析问题和解决问题的创新精神和研究能力,通过实地调查研究、查阅资料、完成本组的研究任务,培养学生积极参加研究活动的意识、积极与他人协作,善于听取、采纳他人的建议以及正确对待不同意见等协作学习的能力。
(15) ;
仔细观察表1,你会发现重要的规律。
表1
α
三角函数
30°
45°
60°
表1中,三角函数值的前三行,分子被开方数排列特征依次为“1,2,3,3,2,1,3,9,27”。“一二三,三二一,三九二十七”。记此歌诀即可。
观察表2也可发现重要的规律。
表2
α
三角函数
30°
45°
60°
表2中,弦函数分子被开方数分别为1,2,3,3,2,1,分母都是2;切函数分子的幂指数分别是1,2,3,3,2,1,分母都是3。据此概括歌诀为:“一二三,三二一,弦内切外莫忘记。分母弦二切为三,正、余只把顺序翻。”这两个歌诀记住一个即可,两歌诀一起记应用更方便。
六、研究所需的条件
1、
2、case n=8图书资料、有关数学学的书籍及科普资料。
3、
4、11. 顺序查询对表的记录没有任何要求,但查找速度较慢;而索引查询要求表的记录是???????????的,查找速度较快。设备:计算机及网络资源
5、
6、交通工具:公交车,自行车。
CONTINUE七、预期的成果
(1)研究报告,系列论文(含调查报告等)学生汇报课
四、研究内容:
1、三角函数的历史
2、三角函数的物理应用
【答案】D3、三角函数的生活应用
use4、实际测量旗杆的高度。
31、FTP五、研究方法:
DO WHILE x!=0“培养学生通过阅读、实验、大众传媒、调查访问等多种途径,培养学生收集、鉴别、处理信息的能力、获取新知识的能力”
1、查询法:通过调查访问方式了解与数学研究性学习有关的信息与内容。
三角函数特殊值
角度
函数
0
30
45
60
90
120
135
150
180
270
360
角a的弧度
0
π/6
π/4
π/3
π/2
2π/3
3π/4
5π/6
π
3π/2
2π
sin
0
1/2
√2/2
√3/2
1
√3/2
√2/2
1/2
0
-1
0
cos
1√3Βιβλιοθήκη 2√2/21/20
-1/2
-√2/2
-√3/2
-1
0
1
tan
0
√3/3
1
√3
高中教育要进一步提高学生的思想品德、文化科学、劳动技能、审美情趣和身体心理素质,培养学生创新精神、实践能力、终身学习的能力和适应社会的能力,促进学生个性的健康发展。在高中开展研究性学习,是全面培养学生综合运用所学知识的能力、收集和处理信息的能力、分析和解决问题的能力、语言文字表达能力以及团结协作能力的重要环节。这项活动还有利于培养学生独立思考的习惯,激发学生的创新意识。
-√3
-1
-√3/3
0
0
1、图示法:借助于下面三个图形来记忆,即使有所遗忘也可根据图形重新推出:
sin30°=cos60°= sin45°=cos45°=
tan30°=cot60°= tan 45°=cot45°=1
2、列表法:
值 角
函 数
0°
30°
45°
60°
90°
sin
cos
tan
0
不存在
cot
3、双绞线、同轴电缆、光纤 4、局域网、城域网2、经验筛选法: 利用计算机网络进行研究资料的查找、分析与收集,探索与研究性学习有关的相关知识,在研究分析、收集前人或相关研究结论的基础上,进行理论分析,比较筛选出与本课题有关的知识与结论。
3、行动研究法:本课题研究主要运用行动,在实际的教育教学和管理工作中寻找开展研究性学习活动的策略、方法、途径与措施,在具体的研究工作情境中认真进行行动过程的研究,行动者参与研究,研究者参与实践,并根据研究中遇到的具体情况,边实践,边探索,边完善,使理论与实践,成果与应用有机的统一起来。
