晶体结构课后练习
课后作业27晶体结构与性质2025年高考化学一轮复习
— 7—
解析
— 返回 —
4. (2024·北京东城区模拟)干冰(固态二氧化碳)在－78 ℃时可直接升华为气体，其晶胞 结构如图所示。下列说法不正确的是( )
A．CO2 中有 C===O 键，中心原子 C 是 sp2 杂化 B．每个晶胞中含有 4 个 CO2 分子 C．每个 CO2 分子周围有 12 个紧邻的 CO2 分子 D．干冰升华时需克服分子间作用力
— 19 —
— 返回 —
[B 组 能力提升] 8．(2023·重庆沙坪坝模拟)氮化铬的晶胞结构如图所示，A 点分数坐标为(0,0,0)。氮 化铬的晶体密度为 d g·cm－3，摩尔质量为 M g·mol－1，晶胞参数为 a nm，NA 代表阿伏加 德罗常数的值。下列说法正确的是( ) A．铬原子的价电子排布图为
— 12 —
答案
— 返回 —
【解析】 周期表中基态原子的最外层均有 2 个未成对电子的元素在第ⅣA 族和第ⅥA 族，短周期中符合此条件的有碳、硅、氧、硫四种元素，由图中看出，一个 A 原子周围有 2 个 B，一个 B 原子周围有 4 个 A，A、B 原子个数比应该是 2∶1，可以形成 CO2、CS2、SiO2 等物质，又知 A、B 原子序数依次增大，只有 A 是 O 元素，B 是 Si 元素符合，形成的化合 物是 SiO2。SiO2 是原子晶体，故 A 错误；由图可知晶胞中 B 原子(即 Si 原子)所在位置有 4 个在棱上，2 个在面上，1 个在晶胞内，该晶胞中含有 Si 原子个数为 4×14＋2×12＋1＝3，按 照 Si 与 O 原子 1∶2，所以含有 6 个氧原子，故 B 正确；SiO2 中 Si 原子和 O 原子都是 sp3 杂化，杂化方式相同，故 C 错误；硅最外层有 4 个电子，一个硅与周围 4 个氧原子形成共价 键，O 原子最外层有 6 个电子，与 2 个硅形成共价键，因此 Si 原子和 O 原子都满足 8 电子 稳定结构，故 D 错误。
晶体学基础与晶体结构习题与答案
晶体学基础与晶体结构习题与答案1. 由标准的(001)极射赤面投影图指出在立方晶体中属于[110]晶带轴的晶带，除了已在图2-1中标出晶面外，在下列晶面中哪些属于[110]晶带？(1-12)，(0-12)，(-113)，(1-32)，(-221)。
图2-12. 试证明四方晶系中只有简单立方和体心立方两种点阵类型。
3. 为什么密排六方结构不能称作为一种空间点阵？4. 标出面心立方晶胞中（111）面上各点的坐标。
5. 标出具有下列密勒指数的晶面和晶向：a)立方晶系(421)，(-123)，(130)，[2-1-1]，[311]；b)六方晶系(2-1-11)，(1-101)，(3-2-12)，[2-1-11]，[1-213]。
6. 在体心立方晶系中画出{111}晶面族的所有晶面。
7. 在立方晶系中画出以[001]为晶带轴的所有晶面。
8. 已知纯钛有两种同素异构体，密排六方结构的低温稳定的α-Ti和体心立方结构的高温稳定的β-Ti，其同素异构转变温度为882.5℃，使计算纯钛在室温(20℃)和900℃时晶体中(112)和(001)的晶面间距(已知aα20℃=0.29506nm，cα20℃=0.46788nm，aα900℃=0.33065nm)。
9. 试计算面心立方晶体的(100)，(110)，(111)，等晶面的面间距和面致密度，并指出面间距最大的面。
10.平面A在极射赤平面投影图中为通过NS及核电0°N，20°E的大圆，平面B的极点在30°N，50°W处，a)求极射投影图上两极点A、B间的夹角；b)求出A绕B顺时针转过40°的位置。
11. a)说明在fcc的(001)标准极射赤面投影图的外圆上，赤道线上和0°经线上的极点的指数各有何特点，b)在上述极图上标出(-110)，(011)，(112)极点。
12. 图2-2为α-Fe的x射线衍射谱，所用x光波长λ=0.1542nm，试计算每个峰线所对应晶面间距，并确定其晶格常数。
无机化学第二版课后练习题含答案
无机化学第二版课后练习题含答案
第一章晶体结构与晶体化学
练习题
1.什么是晶体结构？
2.描述组成配位数和形貌相同的正交晶系、四方晶系和六方晶系的特点。
3.TaCl5的结构类型是什么？给出TaCl5的点阵参数。
4.描述共价晶体和离子晶体的结构特点并给出两个例子。
答案
1.晶体结构是指对于一种给定的化学元素或化合物，其原子或离子分别
按一定的规律有序排列，形成具有规则重复的空间排列的结构。
–正交晶系：组成配位数为8，形貌倾向于长方体或正方体，一般相互垂直，如NaCl、MgO等。
–四方晶系：组成配位数为8，形貌为正方形或长方形板状，沿着一个轴和对角线对称。
如ZnS、TiO2、CaF2等。
–六方晶系：组成配位数为12，形貌为六边形柱状或针状，有沿着一个轴对称的等边六边形截面。
如α-石墨、SiC等。
2.TaCl5的结构类型是正交晶系。
TaCl5的点阵参数为a = 5.73 Å，b
= 5.28 Å，c = 11.85 Å，α = β = γ= 90°。
–共价晶体：由原子间较强的共价键构成，如金刚石、氧化硅（SiO2）。
–离子晶体：由阳离子和阴离子通过电滑移力相互结合而成，如NaCl、MgO。
1。
人教版高中化学选择性必修第2册课后习题 第3章晶体结构与性质 第1节 第2课时 晶胞 晶体结构的测定
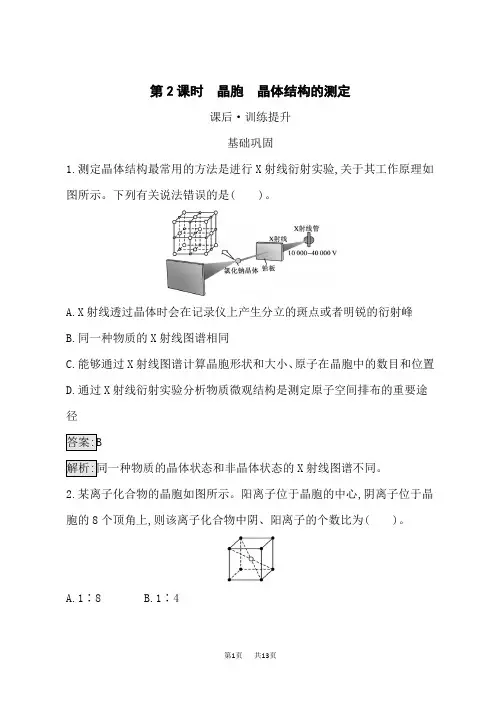
第2课时晶胞晶体结构的测定课后·训练提升基础巩固1.测定晶体结构最常用的方法是进行X射线衍射实验,关于其工作原理如图所示。
下列有关说法错误的是( )。
A.X射线透过晶体时会在记录仪上产生分立的斑点或者明锐的衍射峰B.同一种物质的X射线图谱相同C.能够通过X射线图谱计算晶胞形状和大小、原子在晶胞中的数目和位置D.通过X射线衍射实验分析物质微观结构是测定原子空间排布的重要途径X射线图谱不同。
2.某离子化合物的晶胞如图所示。
阳离子位于晶胞的中心,阴离子位于晶胞的8个顶角上,则该离子化合物中阴、阳离子的个数比为( )。
A.1∶8B.1∶4C.1∶2D.1∶1=1,阳离子8个顶角,晶胞中阴离子的个数为8×18位于晶胞的中心,晶胞中阳离子的个数为1。
3.已知X、Y、Z三种元素组成的化合物的晶胞如图所示,则下面表示该化合物的化学式正确的是( )。
A.ZXY3B.ZX2Y6C.ZX4Y8D.ZX8Y12=1;Y占X占据8个顶角,属于该晶胞的X的数目为8×18=3;Z占据该晶胞的体心,据12条棱的中间,属于该晶胞的Y的数目为12×14属于该晶胞的Z的数目为1。
故该化合物的化学式为Zs等在1957年使Mn 和Bi形成的晶体薄膜磁化并用光读取之后开始的。
如图是Mn和Bi形成的某种晶体的结构示意图,则该晶体物质的化学式可表示为( )。
A.Mn2BiB.MnBiC.MnBi3D.Mn4Bi3Mn 的个数为12×16+6×13+2×12+1=6,含有Bi 的个数为6,则该晶体物质的化学式为MnBi 。
5.已知某晶体的晶胞如图所示,则该晶体的化学式为( )。
A.XYZB.X 2Y 4ZC.XY 4ZD.X 4Y 2Z原子位于晶胞顶角,该晶胞含有的X 原子数目为8×18=1;Y 原子位于该晶胞内,共有4个,因此该晶胞中含有的Y 原子数目为4;Z 只有1个,位于晶胞的体心上,故该晶体的化学式为XY 4Z 。
四种晶体练习题及答案
四种晶体练习题及答案在化学和物理学科中，晶体是一种具有规律排列的原子、离子或分子组成的固体。
晶体结构的类型对于材料的物理性质有着重要的影响。
以下是四种常见晶体结构的练习题及答案。
练习题1：请描述简单立方晶体的排列特征，并说明其晶格常数的计算方法。
答案1：简单立方晶体中，原子或分子在立方体的每个顶点上排列，每个顶点的原子属于相邻的八个立方体共享。
晶格常数a可以通过测量立方体的边长来确定。
练习题2：面心立方（FCC）晶体和体心立方（BCC）晶体有何区别？请用原子填充率来说明。
答案2：面心立方晶体中，除了立方体的每个顶点上有一个原子外，每个面的中心也有一个原子。
体心立方晶体则在立方体的中心有一个原子，而顶点上没有原子。
FCC的原子填充率大约为74.05%，而BCC的原子填充率大约为68%。
练习题3：金刚石晶体是一种什么类型的晶体结构？请简述其原子排列方式。
答案3：金刚石晶体是一种面心立方晶体结构，但它的每个原子都与四个其他原子以四面体的方式连接，形成了一个非常稳定的三维网络。
练习题4：石墨的晶体结构是怎样的？请描述其层与层之间的连接方式。
答案4：：石墨具有六角晶系的层状结构，每个碳原子与其三个最近邻的碳原子以sp²杂化形成平面六角网状结构，层与层之间通过范德华力连接。
练习题5：为什么说晶体的缺陷会影响其物理性质？答案5：晶体的缺陷，如点缺陷、线缺陷（位错）和面缺陷（晶界），会打断原子的规律排列，从而影响晶体的机械强度、导电性和光学性质等。
例如，位错的存在可以降低晶体的强度，而晶界的增加可以降低晶体的电导率。
结束语：通过以上练习题及答案，我们可以看到晶体结构的多样性及其对材料性质的重要影响。
了解和掌握不同晶体结构的特点对于材料科学和化学领域的研究至关重要。
希望这些练习题能帮助你更好地理解晶体结构的基本概念。
晶体结构课后习题含答案
晶体结构1、解释下列概念晶系、晶胞、晶胞参数、空间点阵、米勒指数（晶面指数）、离子晶体的晶格能、原子半径与离子半径、配位数、离子极化、同质多晶与类质同晶、正尖晶石与反正尖晶石、反萤石结构、铁电效应、压电效应.2、（1）一晶面在x、y、z轴上的截距分别为2a、3b、6c，求出该晶面的米勒指数；（2）一晶面在x、y、z轴上的截距分别为a/3、b/2、c，求出该晶面的米勒指数。
3、在立方晶系的晶胞中画出下列米勒指数的晶面和晶向：（001）与[210]，（111）与[112]，（110）与[111]，（322）与[236]，（257）与[111]，（123）与[121]，（102），（112），（213），[110]，[111]，[120]，[321]4、写出面心立方格子的单位平行六面体上所有结点的坐标。
5、已知Mg2+半径为0.072nm，O2-半径为0.140nm，计算MgO晶体结构的堆积系数与密度。
6、计算体心立方、面心立方、密排六方晶胞中的原子数、配位数、堆积系数。
7、从理论计算公式计算NaC1与MgO的晶格能。
MgO的熔点为2800℃，NaC1为80l℃, 请说明这种差别的原因。
8、根据最密堆积原理，空间利用率越高，结构越稳定，金钢石结构的空间利用率很低(只有34.01％)，为什么它也很稳定?9、证明等径圆球面心立方最密堆积的空隙率为25．9％；10、金属镁原子作六方密堆积，测得它的密度为1.74克/厘米3，求它的晶胞体积。
11、根据半径比关系，说明下列离子与O2—配位时的配位数各是多?r o2-=0.132nm r Si4+=0.039nm r K+=0.133nm r Al3+=0.057nm r Mg2+=0.078n m12、为什么石英不同系列变体之间的转化温度比同系列变体之间的转化温度高得多？13、有效离子半径可通过晶体结构测定算出。
在下面NaCl型结构晶体中，测得MgS 和MnS的晶胞参数均为a=0.52nm(在这两种结构中，阴离子是相互接触的)。
固体物理课后习题答案
(
)
⎞ 2π k⎟= −i + j + k 同理 ⎠ a
(
)
(
)
(
)
2π ⎧ ⎪b1 = a −i + j + k ⎪ 2π ⎪ i− j+k ⎨b 2 = a ⎪ 2π ⎪ ⎪b3 = a i + j − k ⎩
(
)
(
)
(
)
由此可得出面心立方格子的倒格子为一体心立方格子； 所以体心立方格子和面心立方格子互为正倒格子。 2.2 在六角晶系中，晶面常用四个指数（hkil）来表示，如图 所示，前三个指数表示晶面族中最靠近原点的晶面在互成 1200的 共面轴 a1 , a2 , a3 上的截距为
设两法线之间的夹角满足
K 1 i K 2 = K1 i K 2 cos γ
K 1iK 2 cos γ = = K1 i K 2 2π 2π (h1 i + k1 j + l1 k )i (h2 i + k2 j + l2 k ) a a 2π 2π 2π 2π (h1 i + k1 j + l1 k )i (h1 i + k1 j + l1 k ) i (h2 i + k2 j + l2 k )i (h2 i + k2 j + l2 k ) a a a a
a1 a2 a3 , , ，第四个指数表示该晶面 h k i
在六重轴c上的截距为
c 。证明： l
i = −(h + k )
并将下列用（hkl）表示的晶面改用（hkil）表示：
2
第一章 晶体的结构
( 001) , (133) , (110 ) , ( 323) , (100 ) , ( 010 ) , ( 213) .
晶体结构课后练习
1．立方晶系中为什么不存在底心立方晶胞？为什么不带电荷的原子或分子都不以简单立方形成晶体？为什么对于相同的单质而言，六方紧密堆积（hcp）结构和立方紧密堆积（ccp）具有相同的密度？在这两种紧密堆积中，原子的配位数是多少？2．已知Cu为立方面心结构，其原子量为63.54，密度ρ = 8.936g/cm3，晶胞参数为3.165Ǻ，试求：（1）阿佛加德罗数，（2）铜的金属半径3．铁存在几种晶型：体心立方的α型和面心立方的γ型等等，在910℃时，α型可以转变成γ型。
假设在转变温度条件下，最相邻的两个铁原子之间的距离是相同的，试计算在转变温度条件下，α型对γ型的密度之比为多少？4．金属Cu属于立方面心结构(1)分别画出（111）、（110）和（100）晶面上Cu原子的分布情况(2)计算这些面上的原子堆积系数（= 球数×球面积/球占面积）5．下列几种具有NaCl结构的化合物，它们之间的阳—阴离子距离列表如下：MgO 2.10ǺMgS 2.60 ǺMgSe 2.73 ǺMnO 2.24 ǺMnS 2.59 ǺMnSe 2.73 Ǻ(1)你如何解释这些数据？(2)从这些数据中，计算S2–离子的半径。
6．金属钛属于立方面心晶体。
它与碳或氢气反应，形成碳化物或氢化物，外来的原子分别占满金属钛晶体存在的不同类型的空隙。
(1)氢原子、碳原子分别占有什么样的空隙？对你的判断解释之。
(2)写出钛化碳和钛化氢的化学式7．一个Ca和C的二元化合物具有四方晶胞：a = b = 3.87Ǻ，c = 6.37Ǻ，（α = β = γ = 90˚），晶胞图如右图，图中钙原子用较大的黑圆圈表示（●），碳原子用空心圆圈表示（○）。
在位于原点的钙原子上面的碳原子的坐标为为x = 0，y = 0，z = 0.406。
（1Ǻ = 10–8cm）(1) 导出这个化合物的化学式为，(2) 一个晶胞中所含的化学式单位的数目为，(3) C2基团中C—C键长为Ǻ，(4) 最短的Ca—C距离为Ǻ，(5) 两个最短的非键C C间距离为、Ǻ，(6) 这一结构与型离子化合物的结构密切相关。
固体物理学课后题答案
固体物理学课后题答案 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第一章 晶体结构1.1、 如果将等体积球分别排成下列结构，设x 表示钢球所占体积与总体积之比，证明：结构 X简单立方52.06=π体心立方68.083≈π 面心立方74.062≈π 六角密排74.062≈π 金刚石34.063≈π解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。
因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1） a=2r ， V=3r 34π，Vc=a 3，n=1 ∴52.06834343333====πππrra r x（2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)334(3423423333≈=⨯=⨯=πππr r a r x （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 374.062)22(3443443333≈=⨯=⨯=πππr r a r x（4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062)22(3443443333≈=⨯=⨯=πππr r a r x （5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.06333834834833333≈=⨯=⨯=πππr r a r x 1.3、证明：面心立方的倒格子是体心立方；体心立方的倒格子是面心立方。
晶体结构练习参考答案
（3）
8． （1）NiAs（3 分）
（2）
（3）Ni 在 6 个 As 的八面体中，As 在 6 个 Ni 的三方柱体中 3 （4）7.88g/cm （3 分） （5）砷化镍晶体中 Ni－Ni 只有 250pm（c 轴方向） ，与金属镍中的距离一致（c＝4rNi） 9． 解： （1） 或
本小题建议给分 3 分 (2)根据晶体密度公式
心构成正四棱柱，设小球半径为 r，则正四棱柱边长为 2r，高为 r，共包括 1 个小球（4 个 1/4，1 个 1/2） ，空间利用率为 (5)正八面体空隙为 0.414r，正四面体空隙为 0.225r。 （6）8.91g/cm3 －23cm3。 （7）H－填充在正四面体空隙，占有率为 50% 正四面体为 4 配位，正八面体 根据第（4）题，正四棱柱质量为 58.70/NAg，体积为 1.094× 10
可得：
MZ NV
Z
NV
M 4.64 6.02 10 23 (5.148 5.148 13.863 10 24 sin60) (6.94 92.91 16.00 3) 6
所以每个晶胞中包含 6 个 LiNbO3 单位，有 6 个 Nb 原子，每个 Nb 原子占据一个（NbO6） 八面体中心，所以每个晶胞中含有 6 个（NbO6）八面体。 本小题建议给分 4 分 （3）简单六方晶胞
晶体结构练习参考答案
1． （1）简单正交晶胞 2．(1) 1︰1︰2 (2) 1︰1︰2 一个球参与六个正八面体空隙， 一个正八面体空隙由六个球围成； （2）0.71 g· cm-3 （3）1.32 Å
一个球参与八个正四面体空隙，一个正四面体空隙由四个球围成。 (3)小球的配位数为 12 个，共 12 个。 （4）74.05% 以 4 个相邻小球中心构成底面，空隙上小球的中心为上底面的中 平面已配位 4 个，中心球周围的四个空隙上下各堆积 4
晶体学课后习题参考答案
晶体学课后习题参考答案第⼀章习题1.晶体与⾮晶体最本质的区别是什么?准晶体是⼀种什么物态?答：晶体和⾮晶体均为固体，但它们之间有着本质的区别。
晶体是具有格⼦构造的固体，即晶体的内部质点在三维空间做周期性重复排列。
⽽⾮晶体不具有格⼦构造。
晶体具有远程规律和近程规律，⾮晶体只有近程规律。
准晶态也不具有格⼦构造，即内部质点也没有平移周期，但其内部质点排列具有远程规律。
因此，这种物态介于晶体和⾮晶体之间。
2.在某⼀晶体结构中，同种质点都是相当点吗?为什么?答：晶体结构中的同种质点并不⼀定都是相当点。
因为相当点是满⾜以下两个条件的点：a.点的内容相同；b.点的周围环境相同。
同种质点只满⾜了第⼀个条件，并不⼀定能够满⾜第⼆个条件。
因此，晶体结构中的同种质点并不⼀定都是相当点。
3.从格⼦构造观点出发，说明晶体的基本性质。
答：晶体具有六个宏观的基本性质，这些性质是受其微观世界特点，即格⼦构造所决定的。
现分别变述：a.⾃限性晶体的多⾯体外形是其格⼦构造在外形上的直接反映。
晶⾯、晶棱与⾓顶分别与格⼦构造中的⾯⽹、⾏列和结点相对应。
从⽽导致了晶体在适当的条件下往往⾃发地形成⼏何多⾯体外形的性质。
b.均⼀性因为晶体是具有格⼦构造的固体，在同⼀晶体的各个不同部分，化学成分与晶体结构都是相同的，所以晶体的各个部分的物理性质与化学性质也是相同的。
c.异向性同⼀晶体中，由于内部质点在不同⽅向上的排布⼀般是不同的。
因此，晶体的性质也随⽅向的不同有所差异。
d.对称性晶体的格⼦构造本⾝就是质点周期性重复排列，这本⾝就是⼀种对称性；体现在宏观上就是晶体相同的外形和物理性质在不同的⽅向上能够有规律地重复出现。
e.最⼩内能性晶体的格⼦构造使得其内部质点的排布是质点间引⼒和斥⼒达到平衡的结果。
⽆论质点间的距离增⼤或缩⼩，都将导致质点的相对势能增加。
因此，在相同的温度条件下，晶体⽐⾮晶体的内能要⼩；相对于⽓体和液体来说，晶体的内能更⼩。
f.稳定性内能越⼩越稳定，晶体的稳定性是最⼩内能性的必然结果。
第二章晶体的结构习题和答案
由晶面间距 d hkl 与倒格矢 K hkl 的关系式
d hkl =
2π K hkl
得
d hkl =
a h + k2 + l2
2
。
（2）对于正交晶系，晶胞基矢 a ， b ， c 相互垂直，但晶格常数 a ≠ b ≠ c ，设沿晶轴 a ， b ， c 的 单位矢量分别为 i ， j ， k ，则正格子基矢为 a = ai ， b = bj ， c = ck ，
* *
图 2.8
六角晶胞
其中利用了矢量混合积的循环关系
A • ( B × C ) = B • (C × A) = C • ( A × B)
及关系式
A × ( B × C ) = B( A • C ) − C ( A • B) 。
因为 (a × b) 矢量平行于 c ，所以
a* • c* =
4π 2 [(b × c) • (a × b)] = 0 ， Ω2 4π 2 [(c × a ) • (a × b)] = 0 。 Ω2
b3 =
（1）
设 b1 与 b2 的交角为 θ 12 ， b2 与 b3 的交角为 θ 23 , b3 与 b1 的交角为 θ 31 ,则有
4π 2 4π 2 b1 • b2 = b cos θ12 = 2 [(a2 × a3 ) • (a3 × a1 )] = 2 a1 • [(a 2 × a3 ) × a3 ] Ω Ω 2 2 4 4π 4π a = 2 [(a1 • a3 )(a 2 • a3 ) − (a1 • a 2 )a 2 ] = (cos 2 θ − cos θ ) Ω Ω2
0A 的长度等于 a1 长度，0B 的长度等于 a 2 的长度的 1/2 ，0C 的长度等于 a3 的长度的 1/3 ，所以只有 A 点
北师大结构化学 第九章 晶体结构 习题答案
北师大结构化学第九章晶体结构习题答案习题解析9.1 若平面周期性结构系按下列单位并置重复堆砌而成，试画出它们的点阵结构，并指出结构基元。
●○●○●○●○●○○○○○○○○○○○○●●●○○○●●○●●○○●○●○○●○○○○○●●○○○●●○○●○○○○解：用实线画出点阵结构如下图9.1，各结构基元中圈和黑点数如下表：●○●○●○1○○○○5○○○○○●○●○○○●●●2●●○●●○○○○3○○○●●○○○7●●○○●○●○○●○○○●4○○○6○图9.1号数黑点数圈数1 1 12 1 13 1 19.2 有一AB型晶体，晶胞中A和B的坐标参数分别为(0，0，0)和(1/2，1/2，1/2).指明该晶体的空间点阵型式和结构基元。
解：不论该晶体属于哪一个晶系，均为简单的空间点阵，结构基元为AB。
9.3 已知金刚石立方晶胞的晶胞参数a=356.7pm, 写出其中碳原子的分数坐标,并计算C―C键的键长和晶胞密度。
解：金刚石中碳原子分数坐标为：0，0，0；1/2，1/2，0；1/2，0，1/2；0，1/2，1/2；1/4，1/4，1/4；3/4，3/4，1/4；3/4，1/4，3/4；1/4，3/4，3/4。
C－C键长可由（0，0，0）及（1/4，1/4，1/4）两个原子的距离求出；因为立方金刚石4 1 25 0 36 2 17 4 3a=b=c=356.7pmrc-c =(a)+(b)+(c)142142142=33×356.7pm a=44= 154.4pm 密度D =ZM/NAV8醋12.0gmol-1= -10323-1(356.7创10cm)(6.022 10mol) = 3.51 g・cm-39.4 立方晶系的金属钨的粉末衍射线指标如下：110，200，211，220，310，222，321，400，试问：(a)钨晶体属于什么点阵形式？(b)X-射线波长为154.4pm, 220衍射角为43.62°，计算晶胞参数。
无机化学——晶体结构习题解答
无机化学——晶体结构习题解答第9章习题解答一、是非题1. 具有相同电子层结构的单原子离子，阳离子的半径往往小于阴离子的半径。
（）解：对2. 离子半径是离子型化合物中相邻离子核间距的一半。
（）解：错3. 同种元素离子的半径随离子电荷代数值增大而减小。
（）解：对4. 仅依据离子晶体中正负离子半径的相对大小即可决定晶体的晶格类型。
（）解：错5. NaCl晶体中配位数比是6：6，因此每个晶胞中含有6个Na+和6个Cl-。
（）解：错6. NaCl晶体是由Na+和Cl-组成的面心立方晶格交错（重叠1/2）排列而成。
（）解：对7. CsCl晶体是由Cs+和Cl-的简单立方交错（重叠1/8）排列而成。
（）解：对8. 每个CsCl晶胞中含有1个Cs+和1个Cl-。
（）解：对9. 每个NaCl晶胞中含有4个Na+和4个Cl-。
（）解：对10. 固体物质可以分为晶体和非晶体两类。
（）解：对11. 所有无机盐都是离子晶体。
（）解：错12. 任何晶体都存在晶格能，晶格能越大则物质的熔点越高。
（）解：错13. 所有原子晶体的熔点均比离子晶体的熔点高。
（）解：错14. 在常温常压下，原子晶体物质的聚集状态只可能是固体。
（）解：对15. 分子晶体的物质在任何情况下都不导电。
（）解：错16. 分子晶体的特性之一是熔点均相对较低。
（）解：对17. 原子晶体的特性之一是熔点高。
（）解：对18. 所有层状晶体均可作为润滑剂和导电体使用。
（）解：错19. 某物质可生成两种或两种以上的晶体，这种现象叫做类质多晶现象。
（）解：错20. 石墨晶体层与层之间的主要结合力为金属键。
（）解：错21. 无定形物质都是由微小的晶粒组成的。
（）解：错22. 自然界存在的晶体或人工制备的晶体中，所有粒子都是按照一定规律有序排列的，没有任何缺陷。
（）解：错23. 一般来说，离子晶体的晶格能越大，该晶体的热稳定性就越低。
（）解：错24. 离子晶体的晶格能越大，熔点越低。
金属的晶体结构习题答案
第一章金属的晶体结构（一）填空题3.金属晶体中常见的点缺陷是空位、间隙原子和置换原子，最主要的面缺陷是。
4.位错密度是指单位体积中所包含的位错线的总长度，其数学表达式为一。
V 5.表示晶体中原子排列形式的空间格子叫做晶格，而晶胞是指从晶格中选取一个能够完全反应晶格特征的最小几何单元。
6.在常见金属晶格中，原子排列最密的晶向，体心立方晶格是[111],而面心立方晶格是」110]。
7晶体在不同晶向上的性能是不同的，这就是单晶体的各向异性现象。
一般结构用金属为多晶体,在各个方向上性能相同，这就是实际金属的伪等向性现象。
8实际金属存在有点缺陷、线缺陷和面缺陷三种缺陷。
位错是线缺陷。
9.常温下使用的金属材料以细晶粒为好。
而高温下使用的金属材料在一定范围内以>晶粒为好。
10.金属常见的晶格类型是面心立方、体心立方、密排六方。
11.在立方晶格中，各点坐标为：A（1,0,1）,B（0,1,1）,0（1,1,1/2）,D（1/2,1,1/2）,-那么AB晶向指数为[110],OC晶向指数为[221]—,OD晶向指数为[121]。
12.铜是面心结构的金属,它的最密排面是7111},若铜的晶格常数a=，那么最密排面上原子间距为。
13a-Fe丫-Fe、Al、Cu、Ni、Cr、V、Mg、Zn中属于体心立方晶格的有_a-Fe、Cr、V_,属于面心立方晶格的有丫-FeAl、Cu、Ni、,属于密排六方晶格的有_Mg、Zn。
14.已知Cu的原子直径为0.256nm,那么铜的晶格常数为。
1mm3Cu中的原子数为。
15.晶面通过（0,0,0）、（1/2、1/4、0）和（1/2,0,1/2）三点，这个晶面的晶面指数为.16.在立方晶系中，某晶面在x轴上的截距为2,在y轴上的截距为1/2;与z轴平行，则该晶面指数为（140）.17.金属具有良好的导电性、导热性、塑性和金属光泽主要是因为金属原子具有金属键的结合方式。
18.同素异构转变是指当外部条件（如温度和压强）改变时，金属内部由一种金属内部由一种晶体结构向另一种晶体结构的转变。
晶体结构练习及参考答案
专题10 晶体结构一、选择题：1、下列个组物质的晶体中，化学键类型相同，晶体类型也相同的是（）A、SO2和SiO2B、CO2和H2OC、NaCl和HClD、CCl4和KCl2、下列晶体中，不属于原子晶体的是（）A、干冰B、水晶C、晶体硅D、金刚石3、下列晶体，属于分子晶体，且分子内只含极性键的是（）A、I2B、CH3COONaC、CO2D、NH4Cl4、共价键、离子键、分子间作用力都是构成物质微粒间的作用,含有以上两种作用的是（）A、SiO2B、干冰C、食盐D、蔗糖5、固体融化时，必须破坏非极性共价键的是（）A、冰B、晶体硅C、溴D、二氧化硅6、下列个物质气化或熔化时，所克服的微粒见的作用，属同种类型的是（）A、碘和干冰的升华B、二氧化硅和生石灰的熔化C、氯化钠和铁的熔化D、苯和环己烷的蒸发7、下列个组物质中，按熔点由低到高排列正确的是（）A、O2、I2、HgB、CO2、KCl、SiO2C、Na、K、RbD、SiC、NaCl、SO28、碳化硅（SiC）的一种晶体有类似金刚石的结构，其中碳原子和硅原子的位置是交替的。
在下列三种晶体（1）金刚石（2）晶体硅（3）碳化硅中，它们的熔点由高到低的顺序是（）A、（1）（3）（2）B、（2）（3）（1）C、（3）（1）（2）D、（2）（1）（3）9、某共价化合物C、H、N三种元素，其分子内有4个氮原子，且4个单原子排列成内空的四面体，如同白磷的分子结构，每两个氮原子见都有一个碳原子，已知此分子内碳原子与碳原子之间不直接形成化学键，则该化合物的分子式为：（）A、CH4N4B、C6H12N4C、C6H10N4D、C4H8N410、关于晶体的下列说法正确的是（）A、在晶体中只要有阴离子就一定有阳离子B、在晶体中只要有阳离子就一定有阴离子C、原子晶体的熔点一定比金属晶体高D、分子晶体的熔点一定比金属晶体的低二、填空题：11、在金刚石的网状结构中，含有由共价键形成的碳原子环，其中最小的环上有____________（填数字）个碳原子，每个碳原子上任意两个C－C键的夹角都是_____________（填角度）12、右图是石英晶体平面示意图，它实际上是立体的网状结构，其中硅氧原子数之比为____________________。
2023年高考化学---晶胞结构的分析与计算课后作业练习(含答案)
2023年高考化学---晶胞结构的分析与计算课后作业练习（含答案）1．(2021·济南模拟)(1)某种氮化铝晶体属六方晶系，晶胞结构如图所示。
晶体内与氮原子距离最近且相等的铝原子的数目是________，若晶胞参数为a pm 、a pm 、c pm ，则氮化铝晶体的密度为________g·cm －3(用代数式表示，N A 为阿伏加德罗常数的值，sin 60°＝32)。
(2)汞钡铜氧晶体的晶胞如图A 所示，通过掺杂Ca 2＋获得的具有更高临界温度的超导材料如图B 所示。
汞钡铜氧晶体的密度为________g·cm －3(设N A 为阿伏加德罗常数的值)。
图A 晶胞中钡离子的分数坐标为⎝ ⎛⎭⎪⎫12，12，1＋x 2和________。
掺杂Ca 2＋所得超导材料的化学式为________________。
解析：(1)由题图可知Al 配位数为4，晶胞中Al 原子数目＝1＋8×18＝2；N 原子数目＝1＋4×14＝2，故二者配位数相同为4，即晶体内与氮原子距离最近且相等的铝原子的数目是4；晶体密度＝2×27＋14N Ag÷(a ×10－10 cm ×a ×10－10 cm ×sin 60°×c ×10－10 cm)＝1.64×10323a 2cN A g·cm －3。
(2)根据汞钡铜氧晶体的结构可知，晶胞中Hg 有8×18＝1个、Ba有2个、Cu 有4×14＝1个、O 有8×14＋4×12＝4个，其密度为ρ＝N ×M N A ×V ＝6.02×1032a 2cN Ag·cm－3，图A 晶胞中钡离子的分数坐标为⎝ ⎛⎭⎪⎫12，12，1＋x 2和⎝ ⎛⎭⎪⎫12，12，1－x 2，根据掺杂Ca 2＋所得超导材料的结构可知，晶胞中含有1个Ca 、1个Hg 、2个Ba 、2个Cu 、6个O ，化学式为HgBa 2CaCu 2O 6。
材料科学基础课后练习题含答案
材料科学基础课后练习题含答案1. 什么是晶格？晶格是指晶体结构中原子、离子、分子在空间排列有一定的规律，按照特定的对称性排列而形成的空间点阵。
2. 什么是晶体？晶体是指结晶体系中具有高度有序的排列而洛美斯密度一致、呈现清晰晶体面，和具有代表性的晶体内部结构的无穷大固体。
3. 简述晶体结构分类原则晶体结构可以根据原子位置的对称性分为14种布拉维格子，每个布拉维格子又可以对应多种晶体结构类型，例如简单晶体、体心立方、面心立方、钻石晶体等。
4. 什么是晶体缺陷？晶体缺陷是指晶体结构中原子、离子或分子位置不完全精确、规则的现象。
根据缺陷在晶体中的分布情况，可以将晶体缺陷分为线缺陷、点缺陷和面缺陷。
5. 简述热力学条件下晶体生长的三个步骤热力学条件下的晶体生长过程可以分为三个步骤：•核心形成：当过饱和度达到一定值时，就可形成微小的晶核，晶核数量随着过饱和度的增加而增大；•晶体生长：当核心生成后，溶液中的各种离子、分子会沉积在晶核上，促使气 / 液 / 溶液中的原子、离子、分子在晶面上排列组成更完整的晶体结构；•晶体成长：当溶液中的原子、离子、分子全部沉积在晶核上时，晶体成长过程就会停止。
6. 简述表面能的概念和意义表面能是指单位面积内表面上两种不同的物质相互接触时所表现出的相互吸引和相互排斥的能量。
表面能在化学键合、材料表面能、液体表面张力等方面都具有重要的意义。
7. 什么是结晶方向？结晶方向是指晶体的晶体学位置和方向散布，其决定了晶体内部原子、离子、分子排列的方向和空间位置。
8. 简述晶体缺陷的种类晶体缺陷根据出现的位置、性质不同可分为点缺陷、线缺陷和面缺陷。
其中点缺陷包括空位缺陷和杂质原子缺陷，线缺陷包括位错和螺旋差排，面缺陷包括晶界和附加缺陷。
9. 什么是位错？位错是晶体中原子排列从理论完美晶体位置发生的某种不规则畸变，是由于晶体内部发生畸变所产生的一类线缺陷，可分为Edge位错、Screw位错和Mixed位错。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1． 立方晶系中为什么不存在底心立方晶胞？为什么不带电荷的原子或分子都不以简单立方形成晶体？为什么对于相同的单质而言，六方紧密堆积（hcp ）结构和立方紧密堆积（ccp ）具有相同的密度？在这两种紧密堆积中，原子的配位数是多少？2． 已知Cu 为立方面心结构，其原子量为63.54，密度ρ = 8.936g/cm 3，晶胞参数为3.165Ǻ，试求：（1）阿佛加德罗数，（2）铜的金属半径3． 铁存在几种晶型：体心立方的α型和面心立方的γ型等等，在910℃时，α型可以转变成γ型。
假设在转变温度条件下，最相邻的两个铁原子之间的距离是相同的，试计算在转变温度条件下，α型对γ型的密度之比为多少？4． 金属Cu 属于立方面心结构(1) 分别画出（111）、（110）和（100）晶面上Cu 原子的分布情况(2) 计算这些面上的原子堆积系数（= 球数×球面积/球占面积）5． 下列几种具有NaCl 结构的化合物，它们之间的阳—阴离子距离列表如下：MgO 2.10Ǻ MgS 2.60 Ǻ MgSe 2.73 ǺMnO 2.24 Ǻ MnS 2.59 Ǻ MnSe 2.73 Ǻ(1) 你如何解释这些数据？(2) 从这些数据中，计算S 2–离子的半径。
6． 金属钛属于立方面心晶体。
它与碳或氢气反应，形成碳化物或氢化物，外来的原子分别占满金属钛晶体存在的不同类型的空隙。
(1) 氢原子、碳原子分别占有什么样的空隙？对你的判断解释之。
(2) 写出钛化碳和钛化氢的化学式7． 一个Ca 和C 的二元化合物具有四方晶胞：a = b = 3.87Ǻ，c = 6.37Ǻ，（α = β = γ = 90˚），晶胞图如右图，图中钙原子用较大的黑圆圈表示（●），碳原子用空心圆圈表示（○）。
在位于原点的钙原子上面的碳原子的坐标为为x = 0，y = 0，z = 0.406。
（1Ǻ = 10–8cm ）(1) 导出这个化合物的化学式为 ，(2) 一个晶胞中所含的化学式单位的数目为 ，(3) C 2基团中C —C 键长为 Ǻ， (4) 最短的Ca —C 距离为 Ǻ，(5) 两个最短的非键C C 间距离为 、 Ǻ，(6) 这一结构与 型离子化合物的结构密切相关。
8． 晶体是质点（分子、离子或原子）在空间有规则地排列而成的，具有整备的外形，以多面体出现的固体物质，在空间里无限地周期性的重复能成为晶体具有代表性的最小单位，称为单元晶胞。
一种Al-Fe 合金的立方晶胞如右图所示，请回答：(1) 导出此晶体中Fe 原子与Al 原子的个数比，并写出此种合金的化学式。
(2) 若此晶胞的边长a = 0.578nm ，计算此合金的密度(3) 试求Fe-Al 原子之间的最短距离（相对原子的质量：Al:27 Fe:56） 9． 有一种镧（La ）、镍合金，属六方晶系，晶胞参数为a= 511pm ，c= 397pm●Al ○Fe(1) 参考右图，试画出该合金的晶胞(2) 根据此晶胞，试导出该晶胞的化学式(3) 该合金能储存氢气，每个晶胞填6个氢原子比较稳定，试求此合金中氢气的密度（假定吸氢后，体积不便）(4) 试求它与在标准状态下氢气的密度之比(5) H 2能够为镧镍合金所吸收，H 2首先需要原子化H 2→2H ，这是由于H 2与合金表面的Ni 相互作用所致，试用分子轨道理论解释之。
10．铜矿是最重要的铜矿，全世界约三分之二的铜是由它提炼的。
(1) 右图为黄铜矿的晶胞，计算该晶胞中各种原子的数目，写出黄铜矿的化学式(2) 在黄铜矿的晶胞中，化学和空间环境都相同的硫原子、铁原子、铜原子各有几个？在黄铜矿晶胞中含几个结构基元（周期性重复的最小单位）？每个结构基元代表什么？(3) 在高温下，黄铜矿晶胞中的金属原子可以发生迁移。
若铁原子与铜原子发生完全无序的置换，可将它们视为等同的金属原子，请画出它的晶胞，每个晶胞中环境相同的硫原子有几个？(4) 在无序的高温结构中，硫原子作什么代表类型的堆积？金属原子占据什么类型的空隙，该类型的空隙被金属原子占据的分数是多少？(5) 实验表明，CuGaS 2和Cu 2FeSnS 4与黄铜矿的结构类型相同，请据此推测黄铜矿与铁的氧化数。
11．将一定量的纯粹的NiO 晶体在氧气中加热，部分Ni 2+被氧化为Ni 3+，得到氧化物Ni x O ，测得该氧化物的密度为6.47g ·cm –3，已知Ni 的相对原子质量为58.70，纯粹的NiO 晶体具有NaCl 型结构，核间Ni —O 的距离为207.85pm ，O 2–的离子半径为140pm(1) 画出纯粹的NiO 立方晶胞(2) 计算Ni x O 的晶胞参数(3) 计算x 值，并写出该氧化物的化学式（要求标明Ni 元素的价态）(4) 在Ni x O 的晶体中，O 2–采取何种堆积方式？Ni 在此堆积中占据哪种空隙？占据的百分比是多少？(5) 在Ni x O 的晶体中，Ni —Ni 间的最短距离是多少？(6) 将Ni x O 的晶与NiO 晶体比较，Ni 和O 2–的配位数有何变化（指平均情况）12．金刚石的立方晶胞如右图所示，晶胞边长a = 356.6pm(1) 列式计算C —C 键长(2) 列式计算碳原子的空间利用率(3) 说明金刚石硬度大的原因13．C 60分子晶体属于NaCl 型，根据C 60分子晶体的晶胞图，回答下列问题：(1) C 60分别占据立方体的什么位置？(2) 在晶胞中C 60分子可以围成哪几类空隙？(3) C 60分子数与这些类型空隙数之比（最简单整数比）为多少？(4) 当碱金属元素全部占满C 60晶体中所有空隙，这类C 60掺杂物才有超导性。
若用金属铯填满后，请写出该掺杂物的化学式。
(5) 室温下，C 60晶体的晶胞参数a = 14.20Å(1Å = 10–8cm)，计算金属填隙前，C 60分子晶体的密度是多少？填满Cs 后，该晶体的密度是多少？（Cs 的相对原子质量：132.9）14．金属单晶的结构可用等径圆球的密堆积模拟。
常见的最紧密堆积型式有立方最密堆积和六方密堆积。
(1) 立方最密堆积的晶胞如图一。
请用“X ”和“Δ”分别标出其中的正四面体空隙和正八面体空隙的中心位置，计算晶体中球数、四面体空隙数和八面体空隙数之比，并计算此种堆积的空间利用率。
(2) 六方密堆积如图二所示。
请用“X ”和“Δ”分别标出其中的正四面体空隙和正八面体空隙的中心位置，计算此晶体中球数、四面体空隙数和八面体空隙数之比，并计算此种堆积的空间利用率。
(3) 已知离子半径的数据：r Ti 3+ = 77pm ，r Cl – = 181pm ；在β-TiCl 3晶体中，取Cl –六方密堆积的排列，Ti 3+则是填隙离子，请回答：Ti 3+离子应填入由Cl –离子围成的哪种多面体空隙？它占据该种空隙的百分数为多少（写出推算过程）？它填入空隙的可能方式有几种？15．今年3月发现硼化镁在39K 呈超导性，可能是人类对超导认识的新里程碑。
在硼化镁晶体的理想模型中，镁原子和硼原子是分层排布的，像维夫饼干，一层镁一层硼地相间，右图是该晶体微观空间取出的部分原子沿c 轴方向的投影，白球是镁原子投影，黑球是硼原子投影，图中的硼原子和镁原子投影在同一平面上。
（a = b ≠c ，c 轴向上）(1) 根据右图确定硼化镁的化学式。
(2) 画出硼化镁的一个晶胞的透视图，标出该晶胞内、面、棱、顶角上可能存在的所有硼原子和镁原子（镁原子用大白球，硼原子用小黑球表示）。
16．石墨晶体由层状石墨“分子”按ABAB 方式堆积而成，如图一所示，图中用虚线标出了石墨的一个六方晶胞。
(1) 试确定该晶胞的碳原子个数。
(2) 写出晶胞内各碳的原子坐标。
(3) 已知石墨的层间距为334.8pm ，C —C 键长为142pm ，计算石墨晶体的密度。
17．石墨可用作锂离子电池的负极材料，充电时发生下述反应：Li 1－x C 6 + x Li + + x e －LiC 6其结果是，Li +嵌入石墨的A 、B 层间，导致石墨的层堆积方式发生改变，形成化学式为LiC 6的嵌入化合物。
(1) 图二给出了一个Li +沿c 轴投影在A 层上的位置，试在图上标出与该离子临近的其它六个Li +的投影位置。
(2) 在LiC 6中，Li +与相邻石墨六元环的作用力属何种键型？(3) 假想石墨每个六元环下都对应一个Li +，写出其化学式，画出晶胞图（c 轴向上）。
18．锂离子电池的正极材料为层状结构的LiNiO 2。
已知LiNiO 2中Li +和Ni 3+均处于氧离子组成的正八面体体心位置，但处于不同层中。
(1) 将化学计量的NiO 和LiOH 在空气中加热到700℃可得LiNiO 2，试写出反应方程式。
(2) 写出LiNiO 2正极的充电反应方程式。
(3) 锂离子完全脱嵌时LiNiO 2的层状结构变得不稳定，用铝离子取代部分镍离子形成LiNi 1－y Al y O 2，可防止锂离子完全脱嵌而起到稳定结构的作用，为什么？19．固体电解质是具有与强电解质水溶液的导电性相当的一类无机固体。
这类固体通过其中的离子迁移进行电荷传递，因此又称为固体离子导体。
固体电解质取代液体电解质，可以做成全固态电池及其它传感器、探测器等，在电化学、分析化学等领域的应用日益广泛。
碘化银具有α、β和γ等多种晶型。
在水溶液中Ag +与I －沉淀形成的是γ-AgI 和β-AgI的混合物，升温至136℃全变为β-AgI ，至146℃变为α-AgI 。
α-AgI 是一种固体电解质，导电率为1.31Ω–1·cm –1（注：强电解质水溶液导电率为10–3～1Ω–1·cm –1）。
y = 0 y = 41a y = 21a y = 43a(1) γ-AgI 和β-AgI 晶体的导电性极差。
其中γ-AgI 晶体属立方晶体，其晶胞截面图如上所示。
图中实心圆和空心圆分别表示Ag +和I －，a 为晶胞边长。
试指出和γ-AgI 晶体的点阵型式和Ag +、I －各自的配位数（已知通常I －，Ag +的半径为100～150pm ）。
(2) α-AgI 晶体中，I －离子取体心立方堆积，Ag +填充在其空隙中。
试指出α-AgI 晶体的晶胞中，八面体空隙、四面体空隙各有多少？(3) 通常Ag +离子半径有一个变化范围，为什么？(4) 实验发现，α-AgI 晶体中能够迁移的全是Ag +，试分析Ag +能够发生迁移的可能原因。
(5) 用一价正离子部分取代α-AgI 晶体中的Ag +离子，得通式为MAg x I 1+x 的化合物。
如RbAg 4I 5晶体，室温导电率达0.271Ω–1·cm –1。
其中迁移的物种仍全是Ag +。
利用RbAg 4I 5晶体，可以制成电化学气敏传感器，下图是一种测定O 2含量的气体传感器示意图。