晶体结构
合集下载
第一章晶体的结构
求晶面指数的方法
OA1 ra1, OA2 sa2 , OA3 ta3
h1 : h2 : h3 1 1 1 : : r s t
n
N
a3
O
d
a2
A2 A1
a1
设 a 1 , a 2 , a 3的末端上的格点分别在离原点距离h1d、h2d、
h3d的晶面上，这里 h1、h2、h3为整数 。 基矢
格点只在顶角上，内部和面上都不包含其他格点，整个原胞 只包含一个格点。
3、晶胞
原胞往往不能反映晶体的对称性
晶胞：能反映晶体对称性的最小结构重复单元
是原胞的数倍。晶胞的基矢用 a b c
原胞:
表示
a1 a2 a3
*几种典型晶体结构的原胞和晶胞
每种原子都各自构成一种相同的Bravais格子，这些Bravais 格子相互错开一段距离，相互套构而形成的格子。即复式 格子是由若干相同的Bravais格子相互位移套构而成的。
*几种典型的复式晶格
NaCl结构（Sodium Chloride structure ） 复式面心立方
例：MgO、KCl、AgBr 等
用来描述晶体中原子排列的紧密程度，原子排 列越紧密，配位数越大
简单立方（简立方）(simple cubic, sc)
配位数
6
晶胞内有 1 个原子
体心立方( body-centered cubic, bcc )
排列：ABABAB……
配位数
8
晶胞内有 2 个原子 具有体心立方结构的金属晶体：LI、Na、K、Fe等
重复周期为二层。形成AB AB AB· · · · · · 方式排列。
具有六角结构的金属： Mg，Co，Zn等
晶体结构——精选推荐
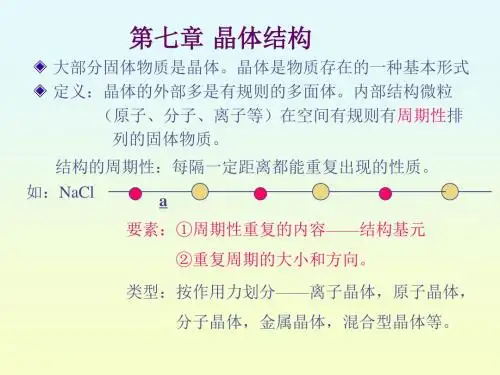
第七章晶体结构第一节晶体的点阵结构一、晶体及其特性晶体是原子（离子、分子）或基团（分子片段）在空间按一定规律周期性重复地排列构成的固体物质。
晶体中原子或基团的排列具有三维空间的周期性，这是晶体结构的最基本的特征，它使晶体具有下列共同的性质：(1)自发的形成多面体外形晶体在生长过程中自发的形成晶面，晶面相交成为晶棱，晶棱会聚成顶点，从而出现具有几何多面体外形的特点。
晶体在理想环境中应长成凸多面体。
其晶面数（F）、晶棱数（E）、顶点数（V）相互之间的关系符合公式：F+V=E+2 八面体有8个面，12条棱，6个顶点，并且在晶体形成过程中，各晶面生长的速度是不同的，这对晶体的多面体外形有很大影响：生长速度快的晶面在晶体生长的时候，相对变小，甚至消失，生长速度小的晶面在晶体生长过程中相对增大。
这就是布拉维法则。
(2)均匀性：晶体中原子周期性的排布，由于周期极小，故一块晶体各部分的宏观性质完全相同。
如密度、化学组成等。
(3)各向异性：由于晶体内部三维的结构基元在不同方向上原子、分子的排列与取向不同，故晶体在不同方向的性质各不相同。
如石墨晶体在与它的层状结构中各层相平行方向上的电导率约为与各层相垂直方向上电导率的410倍。
(4)晶体有明显确定的熔点二、晶体的同素异构由于形成环境不同，同一种原子或基团形成的晶体，可能存在不同的晶体结构，这种现象称为晶体的同素异构。
如：金刚石、石墨和C60是碳的同素异形体。
三、晶体的点阵结构理论1、基本概念（1）点阵：伸展的聚乙烯分子具有一维周期性，重复单位为2个C原子，4个H 原子。
如果我们不管其重复单位的内容，将它抽象成几何学上的点，那么这些点在空间的排布就能表示晶体结构中原子的排布规律。
这些没有大小、没有质量、不可分辨的点在空间排布形成的图形称为点阵。
构成点阵的点称为点阵点。
点阵点所代表的重复单位的具体内容称为结构基元。
用点阵来研究晶体的几何结构的理论称为点阵理论。
（2）直线点阵：根据晶体结构的周期性，将沿着晶棱方向周期的重复排列的结构单元，抽象出一组分布在同一直线上等距离的点列，称直线点阵。
14种晶体结构
14种晶体结构晶体是由原子、分子或福隔离子按照一定的空间规则排列而成的有序固体。
晶体结构是指晶体中原子、离子或分子排列的规则和顺序。
在固体物质中，晶体结构的种类有很多种，其中比较常见的有以下14种：1. 立方晶体结构：最简单的晶体结构之一，具有三个等长的边和六个等角，包括简单立方、体心立方和面心立方三种类型。
2. 六方晶体结构：其晶胞的基本结构是六方密堆，其中最典型的就是六方晶体和螺旋晶体。
3. 正交晶体结构：晶胞具有三个不相互垂直的晶轴，分别被称为a、b 和c 轴，是最常见的晶体结构之一。
4. 单斜晶体结构：晶胞具有两个不相互垂直的晶轴，是晶体结构中的一种。
5. 三方晶体结构：具有三个相等的轴，夹角为60度，最常见的晶体结构之一是石英。
6. 菱晶体结构：晶胞内部有四面体结构，是一种简单的晶体结构。
7. 钙钛矿晶体结构：一种具有钙钛矿结构的晶体，包括钙钛矿结构和螺旋钙钛矿结构。
8. 蜗牛晶体结构：晶胞的形状像一只蜗牛的壳，是晶体结构中的一种。
9. 立方密排晶体结构：晶胞的结构是立方密排，是晶体结构中的一种。
10. 体心立方晶体结构：晶体结构的晶胞中有一个原子位于晶体的中心，是晶体结构中的一种。
11. 面心立方晶体结构：晶体结构的晶胞的各个面的中心有一个原子，是晶体结构中的一种。
12. 钻石晶体结构：晶体结构的晶胞构成了一种钻石结构，是晶体结构中的一种。
13. 银晶体结构：晶体结构的晶胞构成了一种银结构，是晶体结构中的一种。
14. 锶钛矿晶体结构：晶体结构的晶胞构成了一种锶钛矿结构，是晶体结构中的一种。
晶体结构的种类繁多，每种晶体结构都有其独特的结构特点和性质，对晶体的物理和化学性质有着重要的影响。
研究晶体结构不仅可以帮助我们更好地了解晶体的构成和性质，还有助于我们在材料科学、物理化学等领域的应用和研究。
因此，对晶体结构的研究具有重要的科学意义和应用价值。
常见晶体结构
（5）FCC和HCP的两种间隙的相对大小相等。（原因见堆垛方式）
常见晶体结构
FCC和HCP ➢配位数是一样的 ➢间隙相对大小是一样的 ➢间隙数和原子数比是一样的 ➢堆垛密度（致密度）是一样的
0.155R<100>
常见晶体结构
三、常见晶体结构及其几何特征
4 常见晶体的堆垛方式 任何晶体都可以看成由任给的{hkl}原子面一层一层堆垛而成的。 主要讨论FCC和HCP的密排面的堆垛次序。
➢这里，“最邻近”是就同种元素的原子 相比较而言，而配位数则是一个原子周 围的各元素的最近邻原子数之和。 ➢ 配位数通常用 CN 表示。例如， CN 12 表示配位数为12。
体心立方结构 CN8常见晶 Nhomakorabea结构四 面 体 配 位4
立方 体配
位 8
常见晶体结构
八 面 体 配 位6
十 四 面 体 配 位 12
体中的原子看成是有一定直径的刚球，则紧密系 数可以用刚球所占空间的体积百分数来表示。
以一个晶胞为例，致密度就等于晶胞中原子所 占体积与晶胞体积之比 即： 致密度 ＝晶胞中原子所占体积之和/晶胞的体积。
=nv/V n: 晶胞原子数 v：每个原子所占的体积 V: 晶胞的体积
常见晶体结构
三、常见晶体结构及其几何特征
1 常见晶体结构 （1）体心立方结构 简写为BCC 例如：V Nb Ta Cr Mo W （2）面心立方结构 简写为FCC 例如：Al Cu Ag Au （3）密排六方结构 简写为HCP 例如：-Ti -Zr -Hf
常见晶体结构
2 几何特征 2.1 配位数 简写CN 一个原子周围最邻近的原子数 ➢ 纯元素金属 这些最邻近的原子到所论原子的距离是相等的 ➢ 多元素晶体 不同元素的最邻近原子到所论原子的距离不一定相等
常见晶体结构
FCC和HCP ➢配位数是一样的 ➢间隙相对大小是一样的 ➢间隙数和原子数比是一样的 ➢堆垛密度（致密度）是一样的
0.155R<100>
常见晶体结构
三、常见晶体结构及其几何特征
4 常见晶体的堆垛方式 任何晶体都可以看成由任给的{hkl}原子面一层一层堆垛而成的。 主要讨论FCC和HCP的密排面的堆垛次序。
➢这里，“最邻近”是就同种元素的原子 相比较而言，而配位数则是一个原子周 围的各元素的最近邻原子数之和。 ➢ 配位数通常用 CN 表示。例如， CN 12 表示配位数为12。
体心立方结构 CN8常见晶 Nhomakorabea结构四 面 体 配 位4
立方 体配
位 8
常见晶体结构
八 面 体 配 位6
十 四 面 体 配 位 12
体中的原子看成是有一定直径的刚球，则紧密系 数可以用刚球所占空间的体积百分数来表示。
以一个晶胞为例，致密度就等于晶胞中原子所 占体积与晶胞体积之比 即： 致密度 ＝晶胞中原子所占体积之和/晶胞的体积。
=nv/V n: 晶胞原子数 v：每个原子所占的体积 V: 晶胞的体积
常见晶体结构
三、常见晶体结构及其几何特征
1 常见晶体结构 （1）体心立方结构 简写为BCC 例如：V Nb Ta Cr Mo W （2）面心立方结构 简写为FCC 例如：Al Cu Ag Au （3）密排六方结构 简写为HCP 例如：-Ti -Zr -Hf
常见晶体结构
2 几何特征 2.1 配位数 简写CN 一个原子周围最邻近的原子数 ➢ 纯元素金属 这些最邻近的原子到所论原子的距离是相等的 ➢ 多元素晶体 不同元素的最邻近原子到所论原子的距离不一定相等
晶体结构
1、点阵：按连接其中任意两点的向量进行平移后，均能复原
的一组点。 如 等径密置球
. a. . . . . . . .
3a
特点:①点阵是由无限多个点组成;
②每个点周围的环境相同;
③同一个方向上相邻点之间的距离一样.
晶体结构 = 点阵+结构基元
1、直线点阵：一维点阵 如：结构 结构基元：
点阵
.
a
.
2a
六、晶面指标（符号）和有理指数定律： 由于不同方向的晶面结构微粒排列的情况不同，导致物理 性质不一样——各向异性。
用晶面表示不同的平面点阵组，那晶面在三个晶轴上的倒
易截数之比——晶面指标。 如图 某晶面在坐标轴上的截面 截距
z
4c
2a , 3b , 4c
y
c b 2 3 4 截数 a 3b 1 1 1 2a 倒易截数 （643） 2 3 4 x 倒易截数之比：1/2：1/3：1/4 = 6：4：3 ，为整数 1 1 1 符号化—倒易截数之比： : : h : k : l hkl 为晶面指标 r s t
a b c , 900
一个 6 或 6
一个 4 或 4 一个 3 或 3 三个 2 一个 2 无（仅有i ）
1200
a b c, 900
a b c, 900
a b c, 900
C2V , D2 , D2 h
, , ;
V , M r , Z , DC 等
Beq ,U eq
原子坐标及等效温度因子： x , y , z;
分子结构参数：键长，键角，最小二乘平面等 绘出分子结构图，晶胞堆积图等 分析结构特征，解释结构与性能之间的关系。
晶体结构
d100
4.6 晶胞
在晶格所属的空间内，引入点阵点的具体物 理内容（结构基元），构成晶胞。
NaCl 晶体中 的晶格 和晶胞。
晶胞＝晶格＋结构基元
（1）整个晶体结构可以
看成晶胞在空间堆砌形成的
，所以晶胞是晶体结构的最 晶
小单元。
胞 的
特
（2）晶胞中原子个数比与晶体的
点
化学式一致。
（3）晶胞对称性与晶体的对称性 一致。
图中的各点，平移周期是ta； 滑移面：先对镜面反映， 然后沿着与镜面平行的方 向平移ta/2，图形复原。
滑移面按平移向量的大小和方向的 不同，可分为：
轴线滑移面a,b,c：
对角线滑移面n： 菱形滑移面d：
2、230个空间群
无限图形：宏观对称元素＋微观对称元素， 这些对称元素进行组合，共有230种组合方式， 即230种空间对称类型，称为230个空间群。
点群可用Schönflies符号表示。
32个点群包括:
(1) 特殊群：Cs 、Ci 、S4、 C3i (4种） (2) 单轴群：C1 、C2 、C3 、C4 、C6 (5种）
C2v 、C3v 、C4v 、C6v (4种） C2h 、C3h 、C4h 、C6h (4种）
(3) 双面群：D2 、D3 、D4 、D6 (4种） D2h 、D3h 、D4h 、D6h (4种） D2d 、D3d 、 (2种）
晶面指标：点阵面在 三个晶轴的截长的倒数比， 记为（h* k* l*）。
晶面指标：互质的整数比
(111)晶面 r=3,s=3,t=3
相互平行的一族平面点阵, 其（h*k*l*)相同:
(010) (010)
（h*k*l*）代表一族平面点阵,相邻两个点阵面 的间距用 表示，称为面间距。
4.6 晶胞
在晶格所属的空间内，引入点阵点的具体物 理内容（结构基元），构成晶胞。
NaCl 晶体中 的晶格 和晶胞。
晶胞＝晶格＋结构基元
（1）整个晶体结构可以
看成晶胞在空间堆砌形成的
，所以晶胞是晶体结构的最 晶
小单元。
胞 的
特
（2）晶胞中原子个数比与晶体的
点
化学式一致。
（3）晶胞对称性与晶体的对称性 一致。
图中的各点，平移周期是ta； 滑移面：先对镜面反映， 然后沿着与镜面平行的方 向平移ta/2，图形复原。
滑移面按平移向量的大小和方向的 不同，可分为：
轴线滑移面a,b,c：
对角线滑移面n： 菱形滑移面d：
2、230个空间群
无限图形：宏观对称元素＋微观对称元素， 这些对称元素进行组合，共有230种组合方式， 即230种空间对称类型，称为230个空间群。
点群可用Schönflies符号表示。
32个点群包括:
(1) 特殊群：Cs 、Ci 、S4、 C3i (4种） (2) 单轴群：C1 、C2 、C3 、C4 、C6 (5种）
C2v 、C3v 、C4v 、C6v (4种） C2h 、C3h 、C4h 、C6h (4种）
(3) 双面群：D2 、D3 、D4 、D6 (4种） D2h 、D3h 、D4h 、D6h (4种） D2d 、D3d 、 (2种）
晶面指标：点阵面在 三个晶轴的截长的倒数比， 记为（h* k* l*）。
晶面指标：互质的整数比
(111)晶面 r=3,s=3,t=3
相互平行的一族平面点阵, 其（h*k*l*)相同:
(010) (010)
（h*k*l*）代表一族平面点阵,相邻两个点阵面 的间距用 表示，称为面间距。
晶体结构(共78张PPT)
多为无色透明，折 射率较高
山东大学材料科学基础
共价键结合，有方 向性和饱和性，键 能约80kJ/mol
Si,InSb, PbTe
金属键结合， 无方向性，配 位数高，键能 约80kJ/mol
Fe,Cu,W
范得华力结合 ，键能低， 约 8-40 kJ /mol
Ar,H2,CO2
熔点高
强度和硬度由中到 高，质地脆
闪锌矿〔立方ZnS〕结构 S
Zn
属于闪锌矿结构的晶体有β-SiC，GaAs，AlP，InSb
山东大学材料科学基础
•
•
•
•
萤石〔CaF2〕型结构
立方晶系Fm3m空间群，
a0=0.545nm， Z=4。 AB2型化合物， rc/ra>0.732〔0.975〕 配位数：8：4
Ca2+作立方紧密堆积，
F-填入全部四面体 空隙中。 注意：所有八面 体空隙都未被占据。
山东大学材料科学基础
钙钛矿〔CaTiO3〕结构
Ti
ABO3型
立方晶系：以
•
一个Ca2+和3个
O2-作面心立方
Ca
密堆积，
Ti4+占1/4八面体C空aT隙iO3。晶胞 配位多面体连接与Ca2+配位数
Ti4+配位数6，rc/ra=0.436(0.414-0.732)
Ca2+配位数12，rc/ra=0.96
O2-配位数6；
取决温度、组成、掺杂等条件，钙钛矿结构呈现立方、
四方、正交等结构形式。
山东大学材料科学基础
许多化学式为ABO3型的化合物，其中A与B两种阳 离子的半径相差颇大时常取钙钛矿型结构。在钙钛矿 结构中实际上并不存在一个密堆积的亚格子，该结构 可以看成是面心立方密堆积的衍生结构。较小的B离 子占据面心立方点阵的八面体格位，其最近邻仅是氧 离子。
山东大学材料科学基础
共价键结合，有方 向性和饱和性，键 能约80kJ/mol
Si,InSb, PbTe
金属键结合， 无方向性，配 位数高，键能 约80kJ/mol
Fe,Cu,W
范得华力结合 ，键能低， 约 8-40 kJ /mol
Ar,H2,CO2
熔点高
强度和硬度由中到 高，质地脆
闪锌矿〔立方ZnS〕结构 S
Zn
属于闪锌矿结构的晶体有β-SiC，GaAs，AlP，InSb
山东大学材料科学基础
•
•
•
•
萤石〔CaF2〕型结构
立方晶系Fm3m空间群，
a0=0.545nm， Z=4。 AB2型化合物， rc/ra>0.732〔0.975〕 配位数：8：4
Ca2+作立方紧密堆积，
F-填入全部四面体 空隙中。 注意：所有八面 体空隙都未被占据。
山东大学材料科学基础
钙钛矿〔CaTiO3〕结构
Ti
ABO3型
立方晶系：以
•
一个Ca2+和3个
O2-作面心立方
Ca
密堆积，
Ti4+占1/4八面体C空aT隙iO3。晶胞 配位多面体连接与Ca2+配位数
Ti4+配位数6，rc/ra=0.436(0.414-0.732)
Ca2+配位数12，rc/ra=0.96
O2-配位数6；
取决温度、组成、掺杂等条件，钙钛矿结构呈现立方、
四方、正交等结构形式。
山东大学材料科学基础
许多化学式为ABO3型的化合物，其中A与B两种阳 离子的半径相差颇大时常取钙钛矿型结构。在钙钛矿 结构中实际上并不存在一个密堆积的亚格子，该结构 可以看成是面心立方密堆积的衍生结构。较小的B离 子占据面心立方点阵的八面体格位，其最近邻仅是氧 离子。
第一章 晶体结构(Crystal Structure)
§1.3 晶格的周期性
一、布拉菲（Bravais）格子
布喇菲(A. Bravais)，法国学者，1850年提出。 定义: 各晶体是由一些基元（或格点）按一定规则, 周期重 复排列而成。任一格点的位矢均可以写成形式 R n a n a n a n 1 n 2 n 3 、 、 a1 a2 。其中， 、 、 取整数， n 1 1 2 2 3 3 a Rn 为基矢， 为布拉菲格子的格矢，或称 正格矢。 3 能用上式表示的空间点阵称为布拉菲点阵，相应的 空间格子称为布拉菲格子．
§1.2 空间点阵
空间点阵定义： 晶体的内部结构可以概括为是由一些相同的 点子在空间有规则地作周期性的无限分布，这 些点子的总体称为点阵。 X射线衍射技术从实验上证明。
1、格点与基元 如果晶体是由完全相同的一种原子所组成 的，则格点代表原子或原子周围相应点的位置, 如铜的晶体结构。 点阵（lattice） 在空间任何方向 上均为周期排列的无 限个全同点的集合。
基元（ basis）
构成晶体的基本结构单元。 基元是化学组成、空间结构、排列取向、周 围环境相同的原子、分子、离子或离子团的集 合。 可以是一个原子(如铜、金、银等)，可以是 两个或两个以上原子(如金刚石、氯化钠、磷化 镓等)，有些无机物晶体的一个基元可有多达 100个以上的原子，如金属间化合物NaCd2的基 元包含1000 多个原子，而蛋白质晶体的一个基 元包含多达10000 个以上的原子。
复式晶格：
如果晶体的基元中包含两种或两种以上的原 子。显然,每一种等价原子各构成与晶体基元代表 点的空间格子相同的网格 , 称为晶体的 子晶格 . 每 一种等价原子的子晶格具有相同的几何结构，整 个晶格可视为，子晶格相互位移套构而成。该晶 体晶格称为复式晶格． 例如：氯化钠晶体
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
熔点
m.p./oC
993 801 747 661 2852 2614 2430 1918
摩氏 硬度 3.2 2.5
>2.5 >2.5 6.5 4.5 3.5 3.3
一般而言，晶格能越高，离子晶体的熔点越高、 硬度越大。晶格能大小还影响着离子晶体在水中的溶 解度、溶解热等性质。 注：离子晶体在水中的溶解度与溶解热不但与晶 体中离子克服晶格能进入水中吸收的能量有关，还与 进入水中的离子发生水化放出的能量（水化热）有关。 晶格需用实验方法或理论方法估算，获得晶格能 的方法很多，常见的方法有：
○ ○+ ○
-
○ ○- + ○
+
○ ○+ ○
○ ○○
●
● -
+
●
○
○+
○-
○
○+
○
○-
○
4、金属晶体：晶格上结点是金属的原子或正离子。
金 属 晶 体
一、金属键 . . . .. . 金属晶体中原子之间的化学作用力叫做金属键。 ○ . . ○. . . ○ . . .○ . . ○ . ○ + + .+ + + + ○ . . ○ . ○ . .○ ○ .○ . + + + + + + . . . . . . . . . 金属键是一种遍布整个晶体的离域化学键。金属晶 . . . . . . . . . . . . + . ○. ○ . ○ . .○ ○ .○ . + ○ 体是以金属键为基本作用力的晶体。 . . + . .+ . + . + + . ○ . . ○ .. ○ ○ .○ + + + + + . . . . . ... . . . .. . . . . . . . . . . . . 二、电子气理论 ○ . . .○. . . ○. .. . ○. .. . ○. . .○. + + + + .+ .+ ○ . ○ . ○ . . .○ ○ ○ + + + + + + . . . .. . . . . . . . . . 经典的金属键理论叫做“电子气理论”。它把 . . . . . . . . ○ ○ ○ ○ ○ ○ + + + + + ○ 金属键形象地描绘成从金属原子上“脱落”下来的+ + .○ .○ . ○ ○ ○ + + + + + 受外力作用金属原子移位滑动不影响电子气对金属原子的维系作用 大量自由电子形成可与气体相比拟的带负电的“电 （电子气理论对金属延展性的解释） 子气”，金属原子则“浸泡”在“电子气”的“海 洋”之中。 电子气理论定性地解释金属的性质：例如：金 属具有延展性和可塑性；金属有良好的导电性；金 属有良好的导热性；等等。电子气理论的缺点是定
2、六方最密堆积 我们将第一层球称为A球，第二层球称为B球）。 得到ABABAB……的垛积（配位数为12）。这是两层为 一个周期的垛积。
3、立方面心最密堆积 如果上述三维垛积 取……ABCABCABCABC……三层为一周期的垛积 方式（配位数为12），这种三层为一周期的最密堆 积被称为面心立方最密堆积。
3、晶胞的参数 晶胞的边长和夹角 4、晶胞的类型 立方、四方、六方、正交、单斜、三斜、菱方 5、晶胞中原子坐标 6、晶胞中的粒子数目
a
c
a a
a a
c
c
b a
a
b
a
a a
c
c
120
o
a a
a
b
返回
7、素晶胞与复晶胞 ——体心晶胞、面心晶胞和底心晶胞
[问]什么是体心晶胞?如何判断?
(1)若在一个晶胞里只有2个原子,一个原子的坐 标为0,0,0,另一个原子坐标为1/2，1/2，1/2, 而且它 们是同种原子,这个晶胞就是体心晶胞.
化学与生命科学学院
专业基础课
无 机 化 学
------晶体结构
晶体结构
重点：离子晶体的几种典型类型，其中的粒 子如何排列的？何为空隙？
晶
一、晶体的宏观特征
体
通常人们说的“固体”可分为晶态和非晶态两大类。 晶态物质,即晶体，是真正意义的固体。
单一的晶体多面体叫做单晶。有时两个体积大致相
当的单晶按一定规则生长在一起，叫做双晶；许多单晶
组成晶体的质点（分子、原子、离子）以确定 位置的点在空间作有规则的排列，这些点群具有一 定的几何形状，称为结晶格子（简称晶格，有的资
料中称为点阵）。每个质点在晶格中所占有的位置
b
c
称为晶体的结点。 晶格中含有晶体结构中具有代表性的最小重复 单位，称为单元晶胞（简称晶胞）。
a
二、晶胞的基本特征 1、解理性 晶体是 由完全等同 的晶胞无隙 并置地堆积 而成的。 2、晶胞具 有平移性
波恩-哈伯循环：把离子晶体中的离子变成气态离 子的过程分解为若干过程之和，例如：
E(a) E(b) E(c) NaCl(s)→ Na (s) +1/2Cl2 (g) →Na (g) + Cl (g) → Na+ (g) +Cl–(g)
E(a)(由单质化合成离子晶体的生成热的负值)； E(b)[为1摩尔金属钠气化吸收的能量(升华热)与0.5摩 尔氯分子的解离能之和]；E(c)为金属钠的电离能与氯 原子的电子亲和能之和)：晶格能是这些能量项的加和： U={E(a)+E(b)+E(c)}。 由于以上各能项均可用实验方法测定，故这种由 波恩和哈伯设计的热化学循环可以估算出许多离子晶 体的晶格能。
钙钛矿 Ca2+ 12 Ti4+ 6
多面体的连接方式
共角? 共边(棱)?
无隙并置?完全地共面\共棱\共角 如氯化铯晶型
空 隙
离子在晶体微观空间里有尽可能高的空间利用率是离子晶体 结构重要制约因素之一。为了得到较高的空间利用率,离子晶体中 的大离(经常是阴离子)会在空间尽可能紧密地堆积起来，然后， 小离子(经常是阳离子)填入堆积球之间的空隙中去形成的，这种 具有先后逻辑顺序的晶体结构分析思想被称为堆积—填隙模型。
某些离子晶体的晶格能以及晶体中的离子电 荷、核间距、晶体的熔点、硬度AB型离子晶体最短核间 距ro/pm
NaF NaCl NaBr NaI MgO CaO SrO BaO
231 282 298 323 210 240 257 256
晶格能 U/kJ· – mol 1 923 786
747 704 3791 3401 3223 3054
3、离子半径
二、离子键 阴阳离子之间用库仑力相互作用形成的化学键叫 做离子键。
离子键—既没有方向性，又没有饱和性。
三、晶格能 离子晶体中离子间的化学作用力并不限于一对正、 负离子之间，而是遍及所有离子之间。 整个离子晶体中离子之间的静电作用力是所有这 些离子的静电吸引力和排斥力的总和，由此形成晶格 能。 晶格能(U)是指将1摩离子晶体里的正负离子（克 服晶体中的静电引力）完全气化而远离所需要吸收的 能量（数符为+）。例如： NaCl(s)→Na+(g)+Cl–(g) U=786kJ· –1 mol
.
三、金属晶体的堆积模型 把金属晶体看成是由直径相等的圆球状金属原 子在三维空间堆积构建而成的模型叫做金属晶体的 堆积模型。
金属晶体堆积模型有三种基本形式——体心立 方堆积、六方最密堆积和面心立方最密堆积。
1、体心立方堆积 体心立方堆积的晶胞。金属原子分别占据立方 晶胞的顶点位置和体心位置。每个金属原子周围原 子数(配位数)是8。
结构类型 阳离子配位数 配位多面体 阴离子配位数 配位多面体 CsCl 8 CsCl8立方体 8 ClCs8立方体
NaCl
ZnS CaF2
6
4 8
NaCl6八面体
ZnS4四面体 CaF8立方体 CaO12十四面体 TiO6八面体
6
4 4 6
ClNa6八面体
SZn4四面体 FCa4四面体 OTi2Ca4八面体
C C B C
A
C B B C
B B A B
C
离 子 晶 体
典型的离子晶体是指由带电的原子——阴离子和 阳离子通过离子键相互作用形成的晶体。 一、离子 简单离子可以看成带电的球体，它的特征主要有 离子电荷、离子的电子构型和离子半径3个方面。对 于复杂离子，还要讨论其空间构型等问题。 1、离子电荷 离子电荷是简单离子的核电荷(正电荷)与它的核 外电子的负电荷的代数和。 所谓离子电荷,在本质上只是离子的形式电荷。
在ZnS的面心立方晶胞中Zn2+堆积形成几个八面体空隙、 几个四面体空隙？填隙率是多少？
配位多面体 平面三角形 四面体 配位数 3 4 半径比(r+/r–)范围 0.155-0.225 0.225-0.414
八面体
立方体 立方八面体
6
8 12
0.414-0.732
0.732-1.000 1.000
配位多面体
配位多面体模型对于分析 离子晶体结构,特别是分析离子 在晶体中穿越多面体的面,研究快离子导体具有重要价值.
TiO2晶胞是体心晶胞吗?
(2)将晶胞的框架移至体心,得到的新晶胞与原晶胞 毫无差别时,是体心晶胞.如
(3)考察处于晶胞顶角的原子本身以及其周围环境与处于体心 的原子以及周围环境是否相同,相同则是体心晶胞.
如赤铜矿Cu2O不是体心晶胞,为什么?
[问]如何判断面心晶胞? 即晶胞面心上的原子必须完 全与框架顶角原子相同.环境也要相同.