固体结构晶体学基础
合集下载
材第二章_晶体学基础
25
12 简单立方点阵
a=b=c，α=β=γ =90°
26
13 体心立方点阵
a=b=c，α=β=γ =90°
27
14 面心立方点阵
a=b=c，α=β=γ =90°
28
2.3、晶向指数和晶面指数
晶向——通过晶体中任意两个原子中心连成直 线 来表示晶体结构的空间的各个方向。 晶面——晶体结构一系列原子所构成的平面。
8
2.2 布拉菲点阵
点阵（晶格）模型
晶胞
代表性的基本单元（最小平行六面体）
9
c
b
a
空间点阵及晶胞的不同取法
10
选取晶胞的原则： 1.要能充分反映整个空间点成的周期性和对称性； 2.在满足1的基础上，单胞要具有尽可能多的直角； 3.在满足上条件，晶胞应具有最小的体积。
1
2
6
3
4 5
晶体学选取晶胞的原则
47
描述晶胞从以下几个方面： 晶胞中原子的排列方式 (原子所处的位置) 点阵参数 (晶格常数和晶轴间夹角) 晶胞中原子数 原子半径 R(原子的半径和点阵常数关系) 配位数和致密度 密排方向和密排面 晶体结构中间隙 (大小和数量) 原子的堆垛方式
48
三种典型金属晶体结构刚球模型
间隙有两种:四面体间隙和八面体间隙 八面体间隙: 位于晶胞体中心和每个棱边的中点， 由 6 个面心原子所围成,大小rB=0.414R，rB为间隙半径， R为原子半径，间隙数量为4个。
面心立方八面体间隙
55
面心立方四面体间隙
四面体间隙:由一个顶点原子和三个面心原子围成，其大 小：rB=0.225R，间隙数量为8个。
42
晶带定理的应用
材料科学基础-固体的结构
晶带面和与晶带轴之间存在以下关系：
hu+kv+lw=0
此关系称为晶带定理。满足该关系的（hkl)晶面都属于以
[uvw]为晶带轴的晶带。
[uvw]
整理课件
32
第二章 固体结构
利用晶带定理：
①已知两个不平行的晶面(h1k1l1)和(h2k2l2)，求出其晶带 轴[uvw]。
u : v : w ( k 1 l 2 k 2 l 1 ) : ( l 1 h 2 l 2 h 1 ) : ( h 1 k 2 h 2 k 1 )
整理课件
16
第二章 固体结构
整理课件
17
第二章 固体结构
整理课件
18
第二章 固体结构
整理课件
19
第二章 固体结构
整理课件
20
第二章 固体结构
整理课件
21
第二章 固体结构
整理课件
22
第二章 固体结构
晶面族：原子排列规律、面间距完全相同，仅空间位向 关系不同的一组晶面（等价晶面），以｛h k l｝表示。
如六个柱面分别为： ( 1 0 0 ),(0 1 0 ),(1 1 0 ),(1 0 0 ),(0 1 0 ),( 1 1 0 ) c
(1 1 0)
(100)
a2
a1 [100 ]
[110 ]
整理课件
25
第二章 固体结构
根据六方晶系的对称特点，通常采用a1, a2, a3和c四个晶轴确
定六方晶系的晶面指数和晶向指数。
具有相同空间点阵的不同晶体结构
晶体结构相似而具有空间点阵不同
整理课件
13
第二章 固体结构
二、晶向指数和晶面指数
（Miller Indices of Crystallographic Direction and Planes） 1、晶向与晶向指数
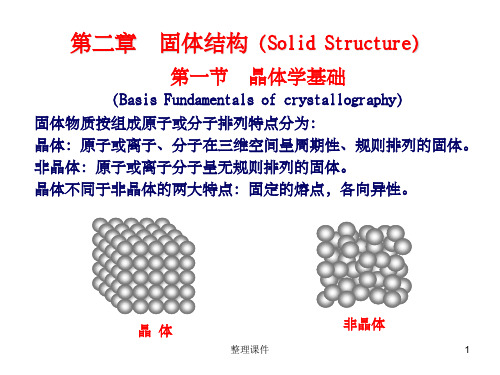
hu+kv+lw=0
此关系称为晶带定理。满足该关系的（hkl)晶面都属于以
[uvw]为晶带轴的晶带。
[uvw]
整理课件
32
第二章 固体结构
利用晶带定理：
①已知两个不平行的晶面(h1k1l1)和(h2k2l2)，求出其晶带 轴[uvw]。
u : v : w ( k 1 l 2 k 2 l 1 ) : ( l 1 h 2 l 2 h 1 ) : ( h 1 k 2 h 2 k 1 )
整理课件
16
第二章 固体结构
整理课件
17
第二章 固体结构
整理课件
18
第二章 固体结构
整理课件
19
第二章 固体结构
整理课件
20
第二章 固体结构
整理课件
21
第二章 固体结构
整理课件
22
第二章 固体结构
晶面族：原子排列规律、面间距完全相同，仅空间位向 关系不同的一组晶面（等价晶面），以｛h k l｝表示。
如六个柱面分别为： ( 1 0 0 ),(0 1 0 ),(1 1 0 ),(1 0 0 ),(0 1 0 ),( 1 1 0 ) c
(1 1 0)
(100)
a2
a1 [100 ]
[110 ]
整理课件
25
第二章 固体结构
根据六方晶系的对称特点，通常采用a1, a2, a3和c四个晶轴确
定六方晶系的晶面指数和晶向指数。
具有相同空间点阵的不同晶体结构
晶体结构相似而具有空间点阵不同
整理课件
13
第二章 固体结构
二、晶向指数和晶面指数
（Miller Indices of Crystallographic Direction and Planes） 1、晶向与晶向指数
固体无机化学-晶体学基础2
ree－ four－ three－index system four－index system
l） （h k l） l） （h k i l） i ＝ - h＋k ） （
[U V W] [u v t w] U = u - t, V = v - t, W = w 1 1 u = [2U - V], v = [2V - U], t = -(u + v), w = W 3 3
（Miller Indices of Crystallographic Direction and Planes） 前已指出，任何阵点的位置可由矢量ruvw和该点阵的坐标u,v,w来确定。 同样晶向OP可沿a,b,c三个方向分解为三个矢量，即 1．阵点坐标 op = xa + yb + zc 2.晶向指数（Orientation index）
宏观对称要素— 宏观对称要素—回转对称轴
二维晶胞的密排图形
宏观对称要素— 宏观对称要素—对称面
1 晶体通过某一平面作 镜像反映而能复原， 则该平面称为对称面 或镜面。 2 对称面用符号 m 表示。
宏观对称要素宏观对称要素-对称中心
1 如果位于晶体中心O点一边 的每点都可在中心的另一边 得到对应的等同点，且每对 点子的连线均通过O点并被 它所等分，则此中心点称为 晶体的对称中心 对称中心。或称为反 对称中心 演中心。即晶体的每一点都 可借以O点为中心的反演动 作而与其对应点重合。 2 对称中心用符号 z 表示。
1 对称要素构成一些动作，即晶体经过这些动作 之后所处的位置与其原始位置完全重合，也就 是晶体上每一点的新旧位置都完全重合。 2 晶体的对称要素可分为宏观和微观两类。宏观 对称要素反映出晶体外形和其宏观性质的对称 性。而微观对称要素与宏观对称要素配合运用 就能反映出晶体中原子排列的对称性。
l） （h k l） l） （h k i l） i ＝ - h＋k ） （
[U V W] [u v t w] U = u - t, V = v - t, W = w 1 1 u = [2U - V], v = [2V - U], t = -(u + v), w = W 3 3
（Miller Indices of Crystallographic Direction and Planes） 前已指出，任何阵点的位置可由矢量ruvw和该点阵的坐标u,v,w来确定。 同样晶向OP可沿a,b,c三个方向分解为三个矢量，即 1．阵点坐标 op = xa + yb + zc 2.晶向指数（Orientation index）
宏观对称要素— 宏观对称要素—回转对称轴
二维晶胞的密排图形
宏观对称要素— 宏观对称要素—对称面
1 晶体通过某一平面作 镜像反映而能复原， 则该平面称为对称面 或镜面。 2 对称面用符号 m 表示。
宏观对称要素宏观对称要素-对称中心
1 如果位于晶体中心O点一边 的每点都可在中心的另一边 得到对应的等同点，且每对 点子的连线均通过O点并被 它所等分，则此中心点称为 晶体的对称中心 对称中心。或称为反 对称中心 演中心。即晶体的每一点都 可借以O点为中心的反演动 作而与其对应点重合。 2 对称中心用符号 z 表示。
1 对称要素构成一些动作，即晶体经过这些动作 之后所处的位置与其原始位置完全重合，也就 是晶体上每一点的新旧位置都完全重合。 2 晶体的对称要素可分为宏观和微观两类。宏观 对称要素反映出晶体外形和其宏观性质的对称 性。而微观对称要素与宏观对称要素配合运用 就能反映出晶体中原子排列的对称性。
材料科学基础-第1章
晶面指数及晶面间距
现在广泛使用的用来表示晶面指数的密勒指数是由 英国晶体学家ler于1939年提出的。
z
确定晶面指数的具体步骤如下： 1.以各晶轴点阵常数为度量单位,求 出晶面与三晶轴的截距m,n,p； 2.取上述截距的倒数1/m,1/n,1/p； 3. 将以上三数值简为比值相同的三 个最小简单整数,即 1 1 1 h k l (553) : : : : h:k :l x m n p e e e 其中e为m,n,p三数的最小公倍数,h,k,l为简单整数； 4.将所得指数括以圆括号, (hkl)即为密勒指数。
13 体心立方点阵
a=b=c，α=β=γ =90°
14 面心立方点阵
a=b=c，α=β=γ =90°
§ 1.5 晶体结构的对称性
一、对称：对称是指物体相同部分作有规律的 重复。对称操作所依据的几何元素，亦即在对 称操作中保持不动的点、线、面等几何元素称 为对称元素。 二、对称性
1．晶体的宏观对称性 2. 晶体的32种点群 3. 晶体的微观对称性 4．230种空间群
晶体结构＝空间点阵+基元
注意：上式并不是一个数学关系式，而只是用来表示这三者之间的 关系。
二、晶体的点阵理论
1 、点阵(Lattice):
将晶体中重复出现的最小单元作为结构基元，用一个数 学上的点来代表 , 称为点阵点，整个晶体就被抽象成一组 点,称为点阵。 1 点阵点必须无穷多； 点阵必须具备的三个条件 2 每个点阵点必须处于相同的环境； 3 点阵在平移方向的周期必须相同。
c
b
a
空间点阵及晶胞的不同取法
选取晶胞的原则： 1.要能充分反映整个空间点阵的周期性和对称性； 2.在满足1的基础上，单胞要具有尽可能多的直角； 3.在满足上条件，晶胞应具有最小的体积。
材料科学基础2课件(1)
钠长石 Na[AlSi3O8]
绿柱石 Be3Al2(SiO3)6
硫
祖母绿
蓝宝石
放大1000倍的雪花
晶体概念的发展
几种不同外形的石英晶体——内部质点的规则排列形成规 则的多面体外形
晶体的棱角：面和棱的存在以及它们之间的规 则性是晶体的宏观特性之一。晶体自发生长成 规则几何外形的性质称为自限性。互相平行的 面之间的夹角是守恒的，这些平行的面称为对 应面，对应面的这种关系称为面角守恒定律。
立方晶系： <111>=[111]+[111]+[111]+[111]+[111]+[111]
+[111]+[111]
晶面指数
晶格中同一平面上的格 点构成一个晶面
整个晶格可以看成是由 无数互相平行且等距离 分布的全同的晶面构成
晶格的所有格点都处在 这族晶面上而无遗漏
晶格中存在无数取向不 同的晶面族
初基晶轴构成的平行六面体称为初基晶胞。 点阵平移矢量定义为：
T＝ u a＋v b＋w c 任意两个阵点都可以用这种形式的矢量连接
起来。 初基晶胞在空间无限重复构成空间点阵。
7个晶系 14种布拉菲点阵
根据六个点阵参数间的关系，可将全部空 间点阵归属于7种类型，即七个晶系
按照每个阵点周围环境相同的要求，用数 学方法可以推导出能够反映空间点阵全部 特征的单位平行六面体只有14种，称为14 种布拉菲点阵z c Nhomakorabeaa
x
by
晶胞、晶轴和点阵参数
晶胞的描述
图 空间点阵
点阵的描述
点阵平移矢量：
以任意一个阵点为原点，以矢 量a, b, c为坐标基矢，其他任 意阵点可表示为：
固体物理学的基础知识
固体物理学的基础知识固体物理学是物理学的一个重要分支，研究物质固态状态的性质和行为。
在这篇文章中，我们将介绍一些固体物理学的基础知识，包括晶体结构、晶格常数、晶体缺陷和固体力学性质等内容。
一、晶体结构晶体是指由周期性排列的原子、离子或分子组成的物质。
晶体结构描述了这些粒子在空间中的排列方式。
最基本的晶体结构是简单立方、面心立方和体心立方。
简单立方是最简单的结构，每个原子与其六个相邻原子相接触；面心立方在每个立方的面心上添加了一个原子；体心立方在每个简单立方的中心添加了一个原子。
除了这些基本结构，还存在许多复杂的晶体结构，如钻石和蓝宝石。
二、晶格常数晶格常数是描述晶体结构的一个重要参数。
它表示晶体中相邻原子之间的距离。
晶格常数可以通过实验或计算得到。
对于简单立方结构来说，晶格常数就是原子间距离；对于面心立方和体心立方结构，晶格常数与原子间距离有特定的关系。
三、晶体缺陷晶体缺陷是指晶体结构中的一些缺陷或杂质。
晶体缺陷可以分为点缺陷、线缺陷和面缺陷。
点缺陷包括空位、间隙原子和替位原子；线缺陷包括位错和螺旋位错；面缺陷包括晶界和界面。
晶体缺陷对晶体的性质有重要影响，如电导率、热导率和光学性质等。
四、固体力学性质固体力学性质描述了固体对外界力的响应和变形行为。
其中最基本的性质是弹性模量。
弹性模量分为压缩模量、剪切模量和杨氏模量，它们分别描述了固体对压力、剪切力和应力的响应。
除了弹性模量，还有塑性、断裂和疲劳等力学性质值得研究。
结论固体物理学的基础知识包括晶体结构、晶格常数、晶体缺陷和固体力学性质等内容。
通过对这些知识的研究，我们可以更深入地理解固体的性质和行为，为材料科学和工程技术的发展做出贡献。
希望本文对你对固体物理学的学习有所帮助。
参考文献：[1] Ashcroft N W, Mermin N D. Solid State Physics. Cengage Learning, 1976.[2] Kittel C. Introduction to Solid State Physics. John Wiley & Sons, 2005.[3] Rao C N R, Rao C N R, Omar Syed Ismail. Angular Momentum in Quantum Physics: Theory and Application. World Scientific, 2014.。
晶体几何学理论基础
周期平移是晶体学中最基本的对称操作。它通过平移操作使 晶体中的某个点或图形在某些晶体学方向上做有规律的周期 重复。晶体结构正是周期性平移操作的结果。
图3.1表示了周期平移对称性。将图中的一个星形的中心作为 原点A，则图中的其他星形图案均可通过对位于A的星形图案 的平移来获得。可以将图案从A平移到B和G，也可将图案从A 平移到C然后再平移至F。
4.4.2 等效点系
等效点系是利用一个空间群中所有对称要素的操作由一个原始点推导出来的规则点 系，由于原始点与空间群中对称要素的相对位置有区别，可用推导出数种等效点系。 一半等效点系：从原始点在一般位置上（也包括原始点在螺旋轴及滑移面上）推导 出来的等效点系称为一般等效点系。特殊等效点系：从与对称要所有特殊的位置关 系（如位于对称面、对称轴、对称要素的交点、对称中心或旋转反伸中心上）的点 所得到的等效点系称为特殊等效点系。由于各等效点系的对称要素的位置有别。其 本身的对称程度也有区别。一般等效点系的对称程度最低。一套等效点系在一个晶 胞中所具有的等效点系数称为该等效点系的重复点数。在一个空间群中等效点系可 在X射线结晶学国际表上查到。
晶体几何学理论基础
对称性是一种规律的重复，具有变化中的不变性，是自 然科学中一个重要的基本概念。晶体就是指原子或分子 在空间按一定规律重复排列构成的固体物质。晶体结构 的基本特征是其中的质点在三维空间作规律的重复排列。 晶体结构研究的就是揭示晶体内部原子和分子在空间排 列上的对称规律，这种规律只有在晶体结构中每个原子 在空间相对位置揭示出来时才能得到完整证明。
1.4 反伸
在反伸对称操作中，一个点或基本图案通过一个点做等距离投影来进行 重复。这个操作可以想象为通过一个点的反映。
1.5 复合对称操作
复合对称操作是基本对称操作的组合。当两个操作结合时，只有两个操作 都完成时基本图案才能被重复。对称操作的可能组合很多，但其中只有3 种组合产生的对称图样是独特的，它们不能用一组基本操作的一次作用而 复制出来。
图3.1表示了周期平移对称性。将图中的一个星形的中心作为 原点A，则图中的其他星形图案均可通过对位于A的星形图案 的平移来获得。可以将图案从A平移到B和G，也可将图案从A 平移到C然后再平移至F。
4.4.2 等效点系
等效点系是利用一个空间群中所有对称要素的操作由一个原始点推导出来的规则点 系，由于原始点与空间群中对称要素的相对位置有区别，可用推导出数种等效点系。 一半等效点系：从原始点在一般位置上（也包括原始点在螺旋轴及滑移面上）推导 出来的等效点系称为一般等效点系。特殊等效点系：从与对称要所有特殊的位置关 系（如位于对称面、对称轴、对称要素的交点、对称中心或旋转反伸中心上）的点 所得到的等效点系称为特殊等效点系。由于各等效点系的对称要素的位置有别。其 本身的对称程度也有区别。一般等效点系的对称程度最低。一套等效点系在一个晶 胞中所具有的等效点系数称为该等效点系的重复点数。在一个空间群中等效点系可 在X射线结晶学国际表上查到。
晶体几何学理论基础
对称性是一种规律的重复，具有变化中的不变性，是自 然科学中一个重要的基本概念。晶体就是指原子或分子 在空间按一定规律重复排列构成的固体物质。晶体结构 的基本特征是其中的质点在三维空间作规律的重复排列。 晶体结构研究的就是揭示晶体内部原子和分子在空间排 列上的对称规律，这种规律只有在晶体结构中每个原子 在空间相对位置揭示出来时才能得到完整证明。
1.4 反伸
在反伸对称操作中，一个点或基本图案通过一个点做等距离投影来进行 重复。这个操作可以想象为通过一个点的反映。
1.5 复合对称操作
复合对称操作是基本对称操作的组合。当两个操作结合时，只有两个操作 都完成时基本图案才能被重复。对称操作的可能组合很多，但其中只有3 种组合产生的对称图样是独特的，它们不能用一组基本操作的一次作用而 复制出来。
第2章 晶体学基础2.1
晶体与非晶体的区别：
1. 原子规排：晶体中原子（分子或离子）在三维空间呈周 期性重复排列，而非晶体的原子无规则排列的。 2. 固定熔点：晶体具有固定的熔点，非晶体无固定的熔点， 液固转变是在一定温度范围内进行。 3. 各向异性：晶体具有各向异性（anisotropy），非晶体为 各向同性。
二、空间点阵和晶胞
晶 格 常 数 示 意 图
3. 空间点阵类型（晶系）
根据６个参数间相关系可将全部空间点阵归为七大类，十四种（称为 布拉菲点阵）。
1）七大晶系
① ② ③ ④ ⑤ ⑥ ⑦
三斜晶系（Triclinic System） 单斜晶系（Monoclinic System） 正交晶系（斜方晶系，Orthogonal System） 四方晶系（正方晶系，Tetragonal System） 立方晶系（Cubic System） 六方晶系（Hexagonal System） 菱形晶系（Rhombohedral System）
晶体结构的微观特征 晶体可看作某种结构单元（基元）在三维空间作周期 性规则排列 质点或基元(basis)：原子、分子、离子或原子团 (组 成、位形、取向均同)
抽象为 质点 抽象为
阵点
质点的三维空间周期排列
空间点阵
1. 空间点阵
空间格子：把晶体中质点的中心用直线联起来构成的空 间格架即空间格子(Lattice)。 晶体点阵：由这些结点构成的空间总体称为晶体点阵。 晶体结点为物质质点的中心位置。 空间点阵中结点仅有几何意义，并不真正代表任何质点。
⑦菱形晶系（RHOMBOHEDRAL SYSTEM） 特点：对称轴和单胞的一个轴 （设a轴）夹角为某一角度α， 另外两个轴和对称轴夹角亦为 α并且长度相等。这三个轴构 成的六面体就是一个菱形单胞。 菱形晶系点阵常数间的关系为：
04-05 晶体几何学基础概述
晶体结构
萤石结构（ CaF2 ）
氯化钠结构(NaCl)
晶体结构
辉钼矿的化学成分：
MoS2,Mo 59.94%，S 40.06%；
辉钼矿的特征：
铅灰色，金属光泽， 硬度低，底面解理极 完全，比重大，光泽 强。
晶体结构
石墨的晶体结构
C60的晶体结构
金刚石的晶体结构
晶体结构X衍射图谱
石墨
金刚石
C60
b c c a * * a b (b c )(c a ) (c c )(b a ) V V cos * = * * = = abc2 sin a sin b | a b | bc sin a ca sin b V V cosa cos b cos = 同样可求 得α *, β *。 sin a sin b
a=bc, a=b==90
简单三角
四方 六角 立方
简单四方 体心四方
a=b, 六角 b==90, a=120 a=b=c, a=b==90 简单立方，体心立方 面心立方
七大晶系所要求最低的对称性
晶系 三斜 最低特征对称素 无对称素 晶胞形状 任意的平行六面体
单斜 正交 三角 四方 六角 立方
a = = d(200) 2 2 2 2 2 0 0
\ (200)
(110)
a
intersects with
a d(110) = 2 2 2 = 2 1 1 0
\ (110)
晶面间距
晶面间距(d)公式：
立方晶系：
1 d hkl
2
h k l = 2 a
2 2
2
h k l 四方晶系： = 2 2 2 a c d hkl 2 2 2 1 h k l 正交晶系： = 2 2 2 2 b c d hkl 1
(完整版)第1章 晶体学基础
第一篇 X射线衍射分析（15万字）1 晶体学基础1.1 晶体结构的周期性与点阵晶体是由原子、离子、分子或集团等物质点在三维空间内周期性规则排列构成的固体物质，这种周期性是三维空间的。
晶体中按周期重复的原子、分子或离子团称为结构基元，也就是重复单元。
为了描述晶体内部原子排列的周期性，总是把一个结构基元抽象地看成为一个几何点，而不考虑它的实际内容（指原子、离子或分子）。
这些几何点按结构周期排列，这种几何点的集合就称为点阵，将点阵中的每个点叫阵点。
要构成点阵，必须具备三个条件：（1）点阵点数无限多；（2）各点阵点所处的几何环境完全相同；（3）点阵在平移方向的周期必须相同。
凡是能够抽取出点阵的结构可称为点阵结构或晶体点阵。
点阵中每一阵点对应于点阵结构中的一个结构基元，在晶体中则是一些组成晶体的实物粒子，即原子、分子或离子等，或是这些微粒的集团。
这样，晶体结构与晶体点阵是两个不同的概念，其关系如图1-1所示，晶体结构可以表示为：晶体结构= 晶体点阵+ 结构基元图1-1晶体结构与点阵的关系根据点阵的性质，把分布在同一直线上的点阵称为直线点阵或一维点阵，分布在同一平面内的点阵称为平面点阵或二维点阵，分布在三维空间中的点阵称为空间点阵或三维点阵。
1.1.1 一维周期性结构与直线点阵图1-2（a）是聚乙烯分子链的结构示意图，具有一维周期结构，其结构基元（CH2CH2）周期性地排列在一个方向上。
每一个结构基元的等同位置抽象成一个几何点，可形成一条直线点阵，是等距离分布在一条直线上的无限点列，如图1-2（b）所示。
取任一阵点作为原点O ，A 为相邻的阵点，则矢量a=OA 表示重复的大小和方向，称为初基（单位）矢量或基矢，若以单位矢量a 进行平移，必指向另一阵点，而矢量的长度a a =ρ称为点阵参数。
图1-2晶体结构与点阵的关系（a ）聚乙烯分子链的结构示意图；（b ）等效的一维直线点阵直线点阵中任何两阵点的平移矢量称为矢径，可表示为T p = p a (0, ±1, ±2……)矢径T p 完整而概括地描述了一维结构基元排列的周期性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
固体结构晶体学基础
《材料科学基础》 第二章 固体结构
• 5.合金、合金系、相、组元、组织、显微组织、宏观组织； 合金相结构分类；影响相结构因素。
• 6.固溶体的分类、特点和性质，影响固溶体固溶度的因素。(置换固溶 体和间隙固溶体，有限固溶体和无限固溶体，有序固溶体和无序固溶体， 端部固溶体和中间固溶体，一次固溶体和二次固溶体)。 中间相的类型和特点。
3、准晶态(quasicrystalline state)：具有一般晶体不能有的 对称性（如五次对称轴）
4、液晶(liquid crystals)：有机物加热时所经历的某一不透明 的浑浊液态阶段（中间相），具有和晶体相似的性质，又称 中间相或介晶。
5、超晶格(点阵)(super lattice)：是将两种或两种以上不同材 料按照特定的迭代序列、沉积在衬底上而构成的（可是周期、 准周期、随机三种）；超晶格自然界不存在，人工生长出来 的，用于半导体薄膜。
• 晶体与非晶体的区别： １.原子规则排列：晶体中原子（分子或离子）在三维空间
呈周期性重复规则排列，存在长程有序，而非晶体的原子无 规则排列的。
２.是否有固定熔点：晶体具有固定的熔点，非晶体无固定 的熔点，液固转变是在一定温度范围内进行。
3.各向异(同)性：晶体具有各向异性（anisotropy），非晶 体为各向同性。 • 绝大部分陶瓷、少数高分子材料、金属及合金是晶体；多 数高分子材料、玻璃及结构复杂材料是非晶体。 注意： • 1. 实际金属为多晶体，伪各向同性; • 2. 晶体、非晶体间可相互转化。晶体在一定条件下可以转 化为晶体
个参数来表示，此即晶格特征参数，简
称晶胞参数。它们是3条棱边的长度a、
Z
b、c （称为点阵常数、晶格常数
(lattice constants /parameters))和
3条棱边的夹角、、 （称为晶轴间
[111] 132000
[100]
112000
[111] 41200
[100]
固体结构晶体学基础
《材料科学基础》 第二章 固体结构 晶态与科学基础》 第二章 固体结构
补充概念：
1、晶态(crystalline state)：各向异性，原子规排，固定熔点， 长程有序
2、非晶态(noncrystalline state)：各向同性，无固定熔点， 没规则外形，长程无序，短程有序（玻璃）
排列
距离 作用力 固定体积 形状
气态
(gas state)
无规律
远
小
无
无
液态
局部有序 较近 中等
有
无
(liquid state)
固态 结晶
(solid state)
非晶
有规律
小
强
局部有序 小
强
固体结构晶体学基础
有
有
有
有
《材料科学基础》 第二章 固体结构
• 晶体是内部质点在三维空间成周期性重复排列的固体，即 晶体是具有格子构造的固体。
• 1.晶体和非晶体的区别。 • 2.晶体结构与空间点阵、晶格、晶胞与原胞、晶系，布拉菲点阵，点阵
常数、七种晶系的各自特点。 • 3. 体心、面心立方和密排六方晶胞，根据原子半径计算出金属的晶胞常
数。掌握三种典型晶体结构的特征(包括：晶胞形状、晶格常数、晶胞原子 数、原子半径、配位数、致密度、各类间隙尺寸与个数，最密排面(滑移面) 和最密排方向的指数与个数，滑移系数目等) 。 • 4. 晶面指数、晶向指数，能标注体心、面心立方和密排六方晶胞的晶向 和晶面指数。晶面族，晶向族，晶带轴，晶面与晶向平行或垂直，晶向和 晶面指数的一些规律。求晶面间距d（hkl）、晶面夹角。晶带定理。
• 晶胞：从晶格中选取一个具有代表性的能完全反映晶格特 征的基本单元（最小平行六面体）作为点阵的组成单元，这 种最小的几何单元称晶胞(cell)。晶胞是晶体中的重复单元， 它平行堆积可充满三维空间，形成空间点阵。
晶
格
示
意
图
固体结构晶体学基础
《材料科学基础》 第二章 固体结构
晶胞大小和形状表示方法
• 晶胞参数：晶胞的形状和大小可以用6
固体结构晶体学基础
《材料科学基础》 第二章 固体结构
单晶体的异向性
金属
Cu Al Ag α-Fe Au
最大弹性模量 (MPa)
190000
晶向 [111]
最小弹性模量 晶向 (MPa)
66700
[100]
75500
[111] 62800
[100]
115000
[111] 43200
[100]
284000
《材料科学基础》 第二章 固体结构
第二章 固体结构
固体结构晶体学基础
《材料科学基础》 第二章 固体结构
本章主要内容
• 1、晶体学基础 • 2、金属的晶体结构 • 3、合金相结构 • 4、离子晶体的结构 • 5、共价晶体的结构 • 6、聚合物晶体结构 • 7、非晶态结构
固体结构晶体学基础
《材料科学基础》 第二章 固体结构 本章要求掌握的内容
• 空间格子：把晶体中质点的中心用直线联起来构成 的空间格架即晶体格子，简称晶格(space lattice)。 是用来描述晶体中原子排列规律的空间格架。
固体结构晶体学基础
《材料科学基础》 第二章 固体结构
• 点阵：将晶体中原子或原子团抽象为纯几何点即可得到一 个由无数几何点在三维空间排列成规则的空间格架(阵列)称 为空间点阵，简称点阵(space lattice) 。特征：每个阵点在 空间分布必须具有完全相同的周围环境(surrounding)
• 7.晶粒、晶界、各向同性与各向异性、同素异构转变(重结晶)和多晶型 性转变，单晶与多晶。
• 8.离子化合物的结构类型和特点，硅酸盐结构的一般特点。 • 9.共价晶体的特点。
固体结构晶体学基础
《材料科学基础》 第二章 固体结构
概述
物质按聚集状态分类有三种主要状态：气态、液态和固态
按原子或分子排列规律性分：晶体(crystal)和非晶体(noncrystal)
固体结构晶体学基础
《材料科学基础》 第二章 固体结构
2.１ 晶体学基础
2.1.1 空间点阵与晶胞
• 阵点：为了便于分析研究晶体中质点的排列规律性， 可先将实际晶体结构看成完整无缺的理想晶体并简 化，将其中每个质点抽象为规则排列于空间的几何 点，称之为阵点(lattice point)。它是纯粹的几何点， 各点周围环境相同。
《材料科学基础》 第二章 固体结构
• 5.合金、合金系、相、组元、组织、显微组织、宏观组织； 合金相结构分类；影响相结构因素。
• 6.固溶体的分类、特点和性质，影响固溶体固溶度的因素。(置换固溶 体和间隙固溶体，有限固溶体和无限固溶体，有序固溶体和无序固溶体， 端部固溶体和中间固溶体，一次固溶体和二次固溶体)。 中间相的类型和特点。
3、准晶态(quasicrystalline state)：具有一般晶体不能有的 对称性（如五次对称轴）
4、液晶(liquid crystals)：有机物加热时所经历的某一不透明 的浑浊液态阶段（中间相），具有和晶体相似的性质，又称 中间相或介晶。
5、超晶格(点阵)(super lattice)：是将两种或两种以上不同材 料按照特定的迭代序列、沉积在衬底上而构成的（可是周期、 准周期、随机三种）；超晶格自然界不存在，人工生长出来 的，用于半导体薄膜。
• 晶体与非晶体的区别： １.原子规则排列：晶体中原子（分子或离子）在三维空间
呈周期性重复规则排列，存在长程有序，而非晶体的原子无 规则排列的。
２.是否有固定熔点：晶体具有固定的熔点，非晶体无固定 的熔点，液固转变是在一定温度范围内进行。
3.各向异(同)性：晶体具有各向异性（anisotropy），非晶 体为各向同性。 • 绝大部分陶瓷、少数高分子材料、金属及合金是晶体；多 数高分子材料、玻璃及结构复杂材料是非晶体。 注意： • 1. 实际金属为多晶体，伪各向同性; • 2. 晶体、非晶体间可相互转化。晶体在一定条件下可以转 化为晶体
个参数来表示，此即晶格特征参数，简
称晶胞参数。它们是3条棱边的长度a、
Z
b、c （称为点阵常数、晶格常数
(lattice constants /parameters))和
3条棱边的夹角、、 （称为晶轴间
[111] 132000
[100]
112000
[111] 41200
[100]
固体结构晶体学基础
《材料科学基础》 第二章 固体结构 晶态与科学基础》 第二章 固体结构
补充概念：
1、晶态(crystalline state)：各向异性，原子规排，固定熔点， 长程有序
2、非晶态(noncrystalline state)：各向同性，无固定熔点， 没规则外形，长程无序，短程有序（玻璃）
排列
距离 作用力 固定体积 形状
气态
(gas state)
无规律
远
小
无
无
液态
局部有序 较近 中等
有
无
(liquid state)
固态 结晶
(solid state)
非晶
有规律
小
强
局部有序 小
强
固体结构晶体学基础
有
有
有
有
《材料科学基础》 第二章 固体结构
• 晶体是内部质点在三维空间成周期性重复排列的固体，即 晶体是具有格子构造的固体。
• 1.晶体和非晶体的区别。 • 2.晶体结构与空间点阵、晶格、晶胞与原胞、晶系，布拉菲点阵，点阵
常数、七种晶系的各自特点。 • 3. 体心、面心立方和密排六方晶胞，根据原子半径计算出金属的晶胞常
数。掌握三种典型晶体结构的特征(包括：晶胞形状、晶格常数、晶胞原子 数、原子半径、配位数、致密度、各类间隙尺寸与个数，最密排面(滑移面) 和最密排方向的指数与个数，滑移系数目等) 。 • 4. 晶面指数、晶向指数，能标注体心、面心立方和密排六方晶胞的晶向 和晶面指数。晶面族，晶向族，晶带轴，晶面与晶向平行或垂直，晶向和 晶面指数的一些规律。求晶面间距d（hkl）、晶面夹角。晶带定理。
• 晶胞：从晶格中选取一个具有代表性的能完全反映晶格特 征的基本单元（最小平行六面体）作为点阵的组成单元，这 种最小的几何单元称晶胞(cell)。晶胞是晶体中的重复单元， 它平行堆积可充满三维空间，形成空间点阵。
晶
格
示
意
图
固体结构晶体学基础
《材料科学基础》 第二章 固体结构
晶胞大小和形状表示方法
• 晶胞参数：晶胞的形状和大小可以用6
固体结构晶体学基础
《材料科学基础》 第二章 固体结构
单晶体的异向性
金属
Cu Al Ag α-Fe Au
最大弹性模量 (MPa)
190000
晶向 [111]
最小弹性模量 晶向 (MPa)
66700
[100]
75500
[111] 62800
[100]
115000
[111] 43200
[100]
284000
《材料科学基础》 第二章 固体结构
第二章 固体结构
固体结构晶体学基础
《材料科学基础》 第二章 固体结构
本章主要内容
• 1、晶体学基础 • 2、金属的晶体结构 • 3、合金相结构 • 4、离子晶体的结构 • 5、共价晶体的结构 • 6、聚合物晶体结构 • 7、非晶态结构
固体结构晶体学基础
《材料科学基础》 第二章 固体结构 本章要求掌握的内容
• 空间格子：把晶体中质点的中心用直线联起来构成 的空间格架即晶体格子，简称晶格(space lattice)。 是用来描述晶体中原子排列规律的空间格架。
固体结构晶体学基础
《材料科学基础》 第二章 固体结构
• 点阵：将晶体中原子或原子团抽象为纯几何点即可得到一 个由无数几何点在三维空间排列成规则的空间格架(阵列)称 为空间点阵，简称点阵(space lattice) 。特征：每个阵点在 空间分布必须具有完全相同的周围环境(surrounding)
• 7.晶粒、晶界、各向同性与各向异性、同素异构转变(重结晶)和多晶型 性转变，单晶与多晶。
• 8.离子化合物的结构类型和特点，硅酸盐结构的一般特点。 • 9.共价晶体的特点。
固体结构晶体学基础
《材料科学基础》 第二章 固体结构
概述
物质按聚集状态分类有三种主要状态：气态、液态和固态
按原子或分子排列规律性分：晶体(crystal)和非晶体(noncrystal)
固体结构晶体学基础
《材料科学基础》 第二章 固体结构
2.１ 晶体学基础
2.1.1 空间点阵与晶胞
• 阵点：为了便于分析研究晶体中质点的排列规律性， 可先将实际晶体结构看成完整无缺的理想晶体并简 化，将其中每个质点抽象为规则排列于空间的几何 点，称之为阵点(lattice point)。它是纯粹的几何点， 各点周围环境相同。