常用傅里叶变换表.
常用傅立叶变换表

弧频率表示的
傅里叶变换
注t)+b・h(t)
iGV) + b・H(f)
线性
2
g(f —q)
「如叮G(f)
时域平移
3
广勺(t)
W)
频域平移,变换2的频域对应
4
g(at)
如果hl值较大,则g(m)会收缩 到原点附近,而间丿会扩
散并变得扁平.当丨$丨趋向 无穷时,成为Delta函数。
2
由变换1和25得到,应用了:cos (at)=(尹 +e F)/2.
22
sin(at)
灯-刼-幻+知
21
由变换1和25得到
23
tn
(2;)网⑺
这里,n是一个.6®(3)是狄拉 克5函数分布的力阶微分。这个变换 是根据变换7和24得到的。将此变 换与1结合使用,我们可以变换所 有。
24
1
1
一沏•sgn(/)
Mrec,(0
变换10的频域对应。矩形函数是理 想的低通滤波器,是这类滤波器对冲 击的响应。
11
sine2(at)
右'trl(0
tri是
12
tri (at)
变换12的频域对应
13
e~°^
/7T(“2
低•…
exp(-a r)的傅里叶变换是他 本身.只有当Re(a)> 0时,这是 可积的。
14
cos(al2)
W)
15
sin (at2)
卜(卓)
16
e-a|t|
2a
3>0
a2H-47T2/2
17
1丽
1
丽
变换本身就是一个公式
18
完整版常用傅立叶变换表
xinc(出)
同
产(5
变换10的频域对应.矩形函数是理 想的低通滤波器,sinc函数是这类 滤波器对反因果冲击的响应.
11
siii〞(出
6'tri(0
tri是三角形函数
12
tri(tzZ)
Lsmc2图
变换12的频域对应
13
高斯函数exp( - at2)的傅里叶 变换是他本身.只有当Re( a) > 0时,这是可积的.
24
1
-f7T-sgn(/)
止匕处sgn(⑴)为符号函数;注意止匕变 换与变换7和24是一致的.
25
1
1
变换29的推广.
E(昌6gli0
26
后gn(£)
1i^L
变换29的频域对应.
27
U(Q
此处u(t)是单位阶跃函数;此变换 根据变换1和31得到.
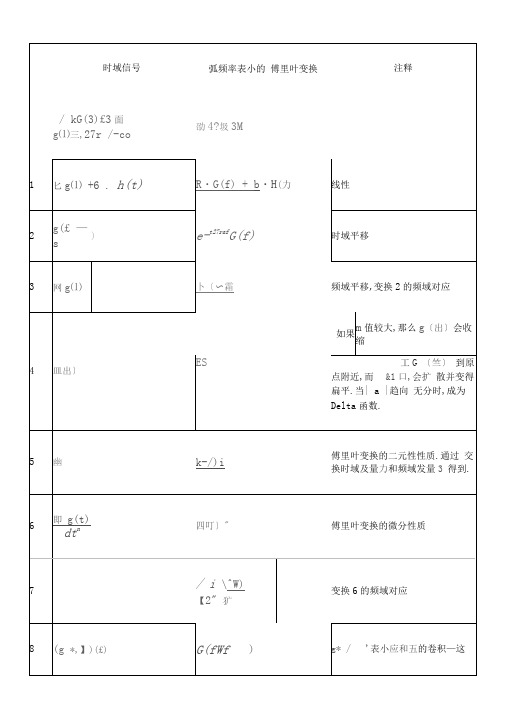
时域信号
弧频率表小的 傅里叶变换
注释
/ kG(3)£3面
g⑴三,27r /-co
劭4?圾3M
1
匕g⑴ +6.h(t)
R・G(f) +b・H(力
线性
2
g(£ —s
)
e-t27rafG(f)
时域平移
3
网g⑴
卜〔〜霜
频域平移,变换2的频域对应
4
皿出〕
如果
m值较大,那么g〔出〕会收缩
ES
工G〔竺〕到原点附近,而।&1口,会扩散并变得扁平.当|a|趋向 无分时,成为Delta函数.
5
幽
k-/)i
傅里叶变换的二元性性质.通过 交换时域及量力和频域发量3得到.
6
即g(t)dtn
常用傅里叶变换表

G ⑴ 1 2 3 g(M) 4 a a 5 6 7 2T T dt n 注释 5(0=| 盘・g ⑴+ b ・h(t\ 线性 QT 如吋G(f) 曲一。
) 时域平移 频域平移,变换2的频域对应 如果Ml 值较大,则ggt )会收缩到原 会扩散并变得 b (-f) 阳刀切 傅里叶变换的微分性质 变换6的频域对应弧频率表示的 傅里叶变换 傅里叶变换的二元性性质。
通过交换 时域变量f 和频域变量 3得到. '用 G(f) 时域信号 「gg 叫才 J _8 点附近,而kl 扁平.当| a |趋向无穷时,成为 Delta 函数。
18 S ( 3 )代表狄拉克S函数分布• 这个变换展示了狄拉克S函数的重要性:该函数是常函数的傅立叶变换19 变换23的频域对应20 由变换3和24得到.21 cos(at)2223242526 sgn(t)27 u(f) 咐-卸+刃十知由变换1和25得到,应用了欧拉公式:cos( at) = ( e iat + e - iat) / 2.卩(于一薛)一d"十盏) 2i-仙*Sgll:/)一卅黑;'唧(f)"(刀由变换1和25得到这里,n是一个自然数.S (n)( 3 ) 是狄拉克S函数分布的n阶微分。
这个变换是根据变换7和24得到的。
将此变换与1结合使用,我们可以变换所有多项式。
此处sgn( 3)为符号函数;注意此变换与变换7和24是一致的.变换29的推广.变换29的频域对应.此处u(t)是单位阶跃函数;此变换根据变换1和31得到.。
傅里叶变换性质及常见函数傅里叶变换总结,表格打印版
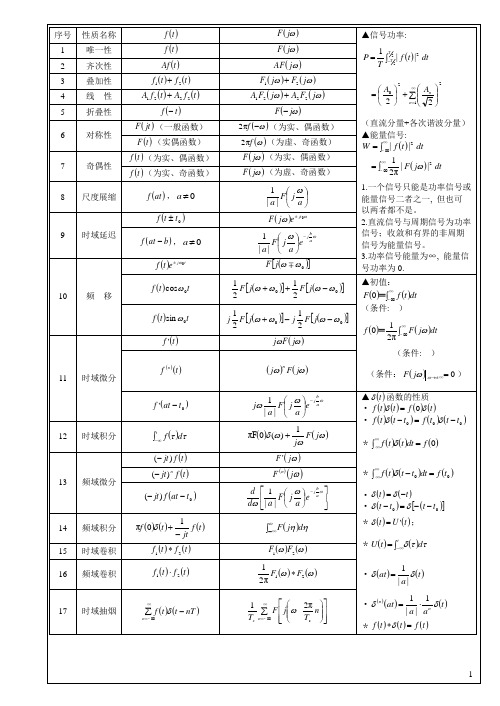
(为虚、奇函数)
7
奇偶性
(为实、偶函数)
(为实、偶函数)
(为实、奇函数)
(为虚、奇函数)
8
尺度展缩
,
9
时域延迟
,
10
频移
▲初值:
(条件:)
(条件:)
(条件: )
11
时域微分
▲ 函数的性质
·
·
*
*
·
·
* ;
*
·
·
*
*
·
12
时域积分
பைடு நூலகம்13
频域微分
14
频域积分
15
时域卷积
16
频域卷积
17
时域抽烟
序号
性质名称
▲信号功率:
(直流分量+各次谐波分量)
▲能量信号:
1.一个信号只能是功率信号或
能量信号二者之一,但也可
以两者都不是。
2.直流信号与周期信号为功率
信号;收敛和有界的非周期
信号为能量信号。
3.功率信号能量为∞,能量信
号功率为0.
1
唯一性
2
齐次性
3
叠加性
4
线性
5
折叠性
6
对称性
(一般函数)
(为实、偶函数)
18
频域抽样
常用时间信号傅里叶变换
常用非周期信号的傅里叶变换
周期信号的傅里叶变换
序号
↔
1
1
↔
2
↔
3
单位直流信号1
↔
4
5
6
一般周期信号
↔
其中
或,
或 ,
常用傅里叶变换表

时域信号弧频率表示的傅里叶变换注释1线性2时域平移3频域平移, 变换2的频域对应4如果值较大,则会收缩到原点附近,而会扩散并变得扁平. 当| a | 趋向无穷时,成为Delta函数。
5傅里叶变换的二元性性质。
通过交换时域变量和频域变量得到.6傅里叶变换的微分性质7变换6的频域对应8表示和的卷积—这就是卷积定理9矩形脉冲和归一化的sinc函数10变换10的频域对应。
矩形函数是理想的低通滤波器,sinc函数是这类滤波器对反因果冲击的响应。
11tri是三角形函数12变换12的频域对应13高斯函数exp( − αt2) 的傅里叶变换是他本身. 只有当Re(α) > 0时,这是可积的。
14 1518δ(ω) 代表狄拉克δ函数分布. 这个变换展示了狄拉克δ函数的重要性:该函数是常函数的傅立叶变换19变换23的频域对应20由变换3和24得到.21由变换1和25得到,应用了欧拉公式: cos(at) = (e iat + e−iat) / 2.22由变换1和25得到23这里, n是一个自然数. δ(n)(ω) 是狄拉克δ函数分布的n阶微分。
这个变换是根据变换7和24得到的。
将此变换与1结合使用,我们可以变换所16a>017变换本身就是一个公式有多项式。
此处sgn(ω)为符号函数;注意此变换24与变换7和24是一致的.25变换29的推广.26变换29的频域对应.此处u(t)是单位阶跃函数; 此变换根27据变换1和31得到.28u(t)是单位阶跃函数,且a > 0.狄拉克梳状函数——有助于解释或34理解从连续到离散时间的转变.。
常用傅里叶变换表

时域信号
弧频率表示的
傅里叶变换
注释
1
线性
2
时域平移
3
频域平移, 变换2的频域对应
4
如果
值较大,则会收缩到原
点附近,而会扩散并变得
扁平. 当 | a | 趋向无穷时,成为
Delta 函数。
5
傅里叶变换的二元性性质。
通过交换时域变量 和频域变量 得到.
6
傅里叶变换的微分性质
7
变换6的频域对应
表示和的卷积—这就是卷积定理
矩形脉冲和归一化的
变换
想的低通滤波器,
滤波器对反因果冲击的响应。
tri
变换
高斯函数
换是他本身
这是可积的。
a>0
变换本身就是一个公式δ
这个变换展示了狄拉克要性:
变换
由变换
由变换
式
由变换
这里
是狄拉克
这个变换是根据变换将此变换与
换所有多项式。
此处
换与变换
变换
变换
此处
根据变换
u
狄拉克梳状函数
理解从连续到离散时间的转变
Welcome !!! 欢迎您的下载,资料仅供参考!。
常用傅立叶变换表

18
δ(ω) 代表分布. 这个变换展示了狄拉克δ函数的重要性:该
时域信号
弧频率表示的
傅里叶变换
注释
1
线性
2
时域平移
3 频域平移, 变换2的频域对应 4
如果
值较大,则
会收缩
到原点附近,而会扩散并变得扁平. 当 | a | 趋向无穷时,成为 Delta 函数。
5 傅里叶变换的二元性性质。
通过交换时域变量 和频域变量 得到.
6 傅里叶变换的微分性质 7
变换6的频域对应
8
表示 和 的卷积 — 这
就是
9 和归一化的 10 变换10的频域对应。
矩形函数是理想的低通滤波器,是这类滤波器对冲击的响应。
11 tri 是
12
变换12的频域对应 13 exp( αt 2) 的傅里叶变换是
他本身. 只有当 Re(α) > 0时,这是可积的。
14
15 16 a>0
17 变换本身就是一个公式。
傅里叶变换简表

傅里叶变换简表
傅里叶变换(Fourier Transform)是一种将信号从时域(时间域)转换到频域(频率域)的数学方法。
傅里叶变换在信号处理、图像处理、通信等领域都有广泛的应用。
下面是傅里叶变换的简表:
傅里叶变换函数:
傅里叶变换F(k) = ∫[f(x) * e^(-2πikx)] dx
反变换函数:
反傅里叶变换f(x) = ∫[F(k) * e^(2πikx)] dk
常见信号的傅里叶变换:
1. 矩形函数(方波)的傅里叶变换:
F(k) = T * sin(πkT) / (πk)
2. 三角波的傅里叶变换:
F(k) = 2AT * sinc(2πATk)
3. 周期函数的傅里叶级数展开:
f(x) = a0 + Σ(an * cos(nωt) + bn * sin(nωt))
4. 高斯函数的傅里叶变换:
F(k) = σ * sqrt(2π) * e^(-π^2σ^2k^2)
5. 常见频率域运算的傅里叶变换:
a. 时移:f(x - x0) 的傅里叶变换F(k) * e^(2πikx0)
b. 频移:e^(2πik0x) 的傅里叶变换 F(k - k0)
c. 放大:f(ax) 的傅里叶变换 F(k/a) / a
d. 缩小:f(bx) 的傅里叶变换 F(k/b) * b
这只是一些傅里叶变换的简单例子,实际上傅里叶变换的应用十分广泛,还有很多复杂的数学关系和公式。
需要根据具体的问题和需求来进行深入研究和学习。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线性
时域平移
频域平移
如果值较大,则会收缩到原
点附近,而会扩散并变得扁平. 当 | a | 趋向无穷时,成为Delta函数。
傅里叶变换的二元性性质。
通过交换时域变量和频域变量得到.
傅里叶变换的微分性质
变换
表示和的卷积—这就是卷积定理
矩形脉冲
变换
想的低通滤波器,
滤波器对
tri
变换
高斯函数
换是他本身
这是可积的。
a>0
变换本身就是一个公式
δ(ω) 代表
这个变换展示了狄拉克要性:
变换
由变换
由变换
式
由变换
这里
是狄拉克
这个变换是根据变换将此变换与
换所有
此处
换与变换
变换
变换
此处
根据变换
u
狄拉克梳状函数理解从连续到。
