投资学(高级教程)-无风险投资
投资学概论(第五版)第07章风险投资

谢谢聆听
THANKS FOR YOUR ATTENTION
现代化经济体系、推动高质量
发展的生力军。
CHAPTER
ONE
第一节
风险投资概述
风险投资的概念
风险投资是指将资金投入具有巨大增长潜力,但同时在技术、市 场等各方面都存在巨大失败风险的高新技术产业的一种投资行为。 这主要是基于风险投资涉足的大多是高新技术产业领域,而高新 技术产业的突出特征就是:高投入、高风险,一旦成功,就会带 来高收益。风险投资家以专业知识主动参与经营,使被投资企业 (通常为高科技企业)能够稳健经营、迅速成长。风险投资家可 在被投资企业成功后,将所持股票卖出,收回资金,获得高额利 润,再投资于另一新创立企业,周而复始,进行中长期投资并参 与经营。风险投资家以获取股息、红利及资本利得为目的,其最 大特征是甘冒较大风险以获取巨额资本利润,故得此名。
风险投资机构参与风险企业管理与监控的方式分为三类,即积 极参与型、间接参与型和放任自由型。
风险投资的退出
风险投资的退出是风险投资活动的最后一个环节,也是非常重要 的一个环节。如前所述,风险投资公司是为卖而买,能够顺利套 现退出,并取得预期盈利,是风险投资公司投资的目的。顺利实 现退出又是风险投资公司进行下一轮投资的条件,如果不能顺利 退出,大量资本将被“套”在投资环节,长期下去,存量资本将 会枯竭,增量资本也会因此得不到补充,风险投资公司的投资将 难以为继。顺利实现退出还是衡量风险投资成败的标准,风险投 资是否成功是看其退出时的所得,所得越多,意味着越成功。
作为风险投资的对象,风险企业发展的不同阶段相应地对风险资 本有不同的融资需求。根据风险资本在企业不同发展阶段投资的 特性,可将风险投资分为前期融资投资、后期融资投资和投资转 型资本。
投资学-—第5章__无风险证券的投资价值

货币的时间价值
货币的时间价值是为取得货币单位时间内使用权支 付的价格,它是对投资者因投资而推迟消费所作出 牺牲支付的报酬,它是单位时间的报酬量与投资的 比率,即利息率。
二、名义利率与实际利率
名义利率
名义利率是指利息(报酬)的货币额与本金的货币 额的比率。
(三)到期收益率
1、含义:到期收益率,可以使投资购买债券获得的 未来现金流量的现值等于债券当前市价的贴现率。 它是投资者按照当前市场价格购买债券并且一直 持有到满期时可以获得的年平均收益率。
2、债券到期收益率的计算公式为:
P m(1C r)(1 C r)2....(C .1 .rF )n
一、即期利率、远期利率与到期收益率
3、有息债券的即期利率即为票面利率 4、无息债券的即期利率由以下公司计算:
其中: St为即期利率 Mt为票面面值 t为债券的期限
Pt
Mt (1ຫໍສະໝຸດ St )t 例1:设某2年期国债的票面面额为100元,投 资者以85.73元的价格购得,问该国债的即利 率是多少?
其中: F为债券的面值,C为按按票面利率每 年支付的利息,Pm为债券的当前市场价格,r为到 期收益率。
3、到期收益率计算标准是债券市场定价的基础, 建立统一、合理的计算标准是市场基础设施建设的重 要组成部分。计算到期收益率首先需要确定债券持有 期应计利息天数和付息周期天数,从国际金融市场来 看,计算应计利息天数和付息周期天数一般采用“实 际天数/实际天数”法、“实际天数/365”法、 “30/360”法等三种标准,其中应计利息天数按债 券持有期的实际天数计算、付息周期按实际天数计算 的“实际天数/实际天数”法的精确度最高。近年来, 许多采用“实际天数/365”法的国家开始转为采用 “实际天数/实际天数”法计算债券到期收益率。
无风险证券的投资价值(PPT 62张)

普通年金的终值是指一定时期每期期末等额收付款项的复利终值之和。 年金终值是将各年的年金分别按复利换算到期末,然后再求和。 复利终值是指每经过一个计息期,要将所生利息加入本金再计利息,逐期滚算, 到了期终的本利和即为复利终值。年金终值其实就是期内各个年金的复利终值 求和,它包含了多个复利终值。
• 普通年金现值
1 i 1 A n i 1 i
n
P为普通年金现值;A为年金数额; [(1+i)n-1] / i(1+i)n为年金现值系数; n为计算期数。
• 假设你需要在每年年末取出100元,连续取3年,在银行存 款利率为10%的情况下,你现在要向银行存入多少钱? • P=100×(1+10%)-1+100×(1+10%)-2+100× (1+10%)-3 • =248.68元
F=A+A(1+i)+A(1+i)2+……+A(1+i)n-2 +A(1+i)n-1
A
1 i n 1
i
F为普通年金终值;A为年金数额;n为计算期数;[(1+i)n-1]/i 为年金复利终值系数,可查表得出。
普通年金终值计算公式的推导
– 每年的支付金额为A;利率为I;期数为n; – 则按复利计算的普通年金终值F为:
无风险证券的投资价值
本章主要内容
• • • • 货币的时间价值 利率的决定 利率的期限结构 无风险条件下证券投资价值的评估
货币的时间价值
• 无风险收益与货币的时间价值 • 名义利率与实际利率
• 终值与现值
• 年金终值与现值
无风险收益与货币的时间价值
• 无风险收益
《投资学》试题及答案大全(二)

《投资学》试题及答案 试卷B注:需配备答题纸的考试,请在此备注说明“请将答案写在答题纸上,写在试卷上无效”。
一、单项选择题(共 15 题,请将正确答案的代号填写在指定位置,每小题 2分,共 30分)1.研究和发现股票的( ),并将其与市场价格相比较,进而决定投资策略是证券研究人员、投资管理人员的主要任务。
A .票面价值B .账面价值C .内在价值D .清算价值 2.下列不属于证券市场显著特征的选项是( )。
A .证券市场是价值直接交换的场所B .证券市场是价值实现增值的场所 C.证券市场是财产权利直接交换的场所 D .证券市场是风险直接交换的场所 3. A 股票的β系数为1.5,B 股票的β系数为0.8,则( )。
A .A 股票的风险大于B 股票 B .A 股票的风险小于B 股票 C .A股票的系统风险大于B 股票 D .A 股票的非系统风险大于B 股票4. 某只股票年初每股市场价值是30元,年底的市场价值是35元,年终分红5元,则该股票的收益率是( )。
A .10% B.14.3% C.16.67% D.33.3%5.某一国家借款人在本国以外的某一国家发行以该国货币为面值的债券属( )。
A .欧洲债券 B .扬基债券 C .亚洲债券 D .外国债券6、 市场风险也可解释为。
( )A. 系统风险,可分散化的风险B. 系统风险,不可分散化的风险C. 个别风险,不可分散化的风险D. 个别风险,可分散化的风险7.如果某可转换债券面额为l 000元,规定其转换比例为50,则转换价格为( )元。
A .10B .20C .50D .1008. 根据马柯威茨的证券组合理论,下列选项中投资者将不会选择( )组合作为投资对象。
A .期望收益率18%、标准差32%B .期望收益率12%、标准差16%C .期望收益率11%、标准差20%D .期望收益率8%、标准差11%9.就单根K 线而言,反映多方占据绝对优势的K 线形状是( )。
投资学:第5章 无风险借贷

下面,我们来计算这5个组合的预期收益率和风险,在上
述情况下,组合的预期收益率RP和风险P分别是:
N
Rp xi Ri x0rF x1R1 4%x0 16.2%x1 i 1
1
N
p
N
xi x j ij
2
x02
2 0
2x0 x1
01
x12
2 1
1 2
x12
2 1
1 2
12.08%x1
11
假设无风险资产的收益率是4%,某风险证券的预期收益 率和风险分别是16.2%和12.08%。
我们用x0表示投资于无风险资产的资金比例,用x1表示投 资于风险资产的资金比例,那么x0=1-x1。
如果投资者将全部资金投资于无风险资产,就有x0=1, x1=0。
相反,投资者也可以将全部资金投资于风险资产,这种情 况下就有x0=0,x1=1。
由于无风险资产的标准差为零,因此无风险资产的方 差也是0,其收益率与风险资产的收益率之间的协方 差也是0。
5
因为无风险资产具有确定的收益率,所以这种类型的 资产必定是某种具有固定收益,并且没有任何违约可 能的证券。
由于所有的公司证券从原则上讲都存在着违约的可能 性,因此无风险证券不可能由公司来发行,因而必须 是政府发行的证券。
22
5.3 无风险资产的借入
如果我们允许投资者借入资金,我们可以进一步扩 展前一节的分析。这意味着,当投资者在决定将多 少资金投资于风险资产时,他将不再受初始财富的 限制。
当然,当投资者借入资金时,他也必须为这笔贷款 付出利息。由于利率是已知的,而且偿还贷款也没 有任何不确定性,因此,投资者的这种行为常常被 称为“无风险借入” 。
如果一个证券组合P中,投资于组合PAB的比例是 xPAB,用x0=1- xPAB的比例投资于无风险资产,那么 该证券组合P的预期收益率和风险就分别是:
《投资学》课后习题参考答案

习题参考答案第2章答案:一、选择1、D2、C二、填空1、公众投资者、工商企业投资者、政府2、中国人民保险公司;中国国际信托投资公司3、威尼斯、英格兰4、信用合作社、合作银行;农村信用合作社、城市信用合作社;5、安全性、流动性、效益性三、名词解释:财务公司又称金融公司,是一种经营部分银行业务的非银行金融机构。
其最初是为产业集团内部各分公司筹资,便利集团内部资金融通,但现在经营领域不断扩大,种类不断增加,有的专门经营抵押放款业务,有的专门经营耐用消费品的租购和分期付款业务,大的财务公司还兼营外汇、联合贷款、包销证券、不动产抵押、财务及投资咨询服务等。
信托公司是指以代人理财为主要经营内容、以委托人身份经营现代信托业务的金融机构。
信托公司的业务一般包括货币信托(信托贷款、信托存款、养老金信托、有价证券投资信托等)和非货币信托(债权信托、不动产信托、动产信托等)两大类。
保险公司是一类经营保险业务的金融中介机构。
它以集合多数单位或个人的风险为前提,用其概率计算分摊金,以保险费的形式聚集资金建立保险基金,用于补偿因自然灾害或以外事故造成的经济损失,或对个人因死亡伤残给予物质补偿。
四、简答1、家庭个人是金融市场上的主要资金供应者,其呈现出的主要特点如下:(1)投资目标简单;(2)投资活动更具盲目性(3)投资规模较小,投资方向分散,投资形式灵活。
企业作为非金融投资机构,其行为呈现出了以下的显著特点:(1)资金需求者地位突现;(2)投资目标的多元化;(3)投资比较稳定;(4)短期投资交易量大。
2、商业银行在经济运行中主要的职能如下:(1)信用中介职能;(2)支付中介职能;(3)调节媒介职能;(4)金融服务职能;(5)信用创造职能;总的来说,商业银行业务可以归为以下三类:(1)负债业务:是指资金来源的业务;(2)资产业务:是商业银行运用资金的业务;(3)中间业务和表外业务:中间业务指银行不需要运用自己的资金而代客户承办支付和其他委托事项,并据以收取手续费的业务第3章答案:一、选择题1、D2、D3、B二、填空题1、会员制证券交易所和公司制证券交易所、会员制、公司制。
无风险证券的投资价值(PPT 62页)

– 基本观点:
• 由于存在法律、偏好或其他因素的限制,投资者和债券的发行者都 不能无成本地实现资金在不同期限的证券之间的自由转移,因此, 证券市场不是一个统一的无差别的市场,而是分别存在着短期市场、 中期市场和长期市场。
• 不同市场上的利率分别各市场的供给和需求决定。
• 当长期债券供给曲线与需求曲线的交点高于短期债券供给曲线与需 求曲线的交点时,债券的收益率曲线向上倾斜;反之则向下方倾斜。
• =248.68元
普通年金现值公式的推导:
• 由于:
P A1 i 1 A1 i 2 A1 i 3 ...... A1 i n
– 等式两边同乘(1+i):
1 iP A1 i0 A1 i 1 A1 i 2 ...... A1 i (n1)
– 上述两式相减(2)-(1):
• 当可贷资金需求大于供给时,利率就上升 • 当可贷资金需求小于供给时,利率就下降 • 当可贷资金需求等于供给时的利率就是市场均衡利率
西方经济学关于利率的决定
利率的期限结构
• 到期收益率、即期利率与远期利率 • 收益率曲线 • 利率的期限结构理论
到期收益率、即期利率与远期利率
• 考虑三种国债A、B、C,债券A一年到期,到期时 投资者得到100元;债券B两年到期,到期时投资 者得到100元;债券C是一个付息债券,从现在起 一年后,向投资者支付5元,两年后到期时,再支 付给投资者105元。这些债券现在在市场出售的价 格为:
• 债券利率的期限结构取决于投资者对未来利率的市场预期。 • 长期债券的利率等于长期债券到期之前人们对短期债券利率预期的平
均值。 • 投资者并不偏好于某种期限的债券,当某种债券的收益率低于期限不
同的另一债券时,投资者将不再持有这种债券,不同期限的债券具有 完全的可替代性,因而这些债券的预期收益率相等。
投资学习题
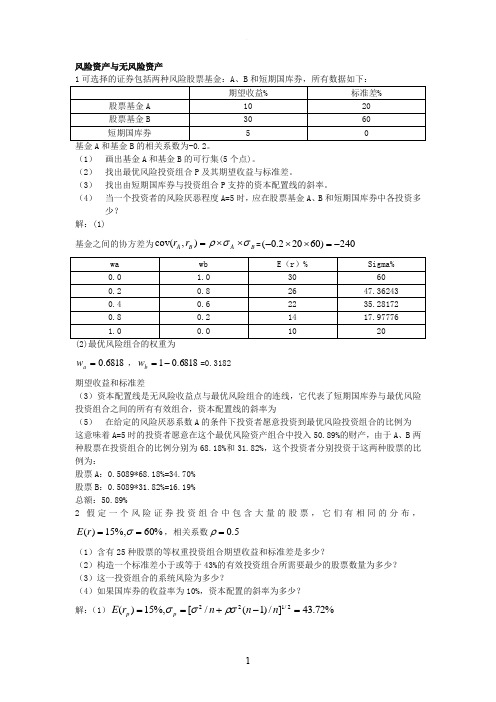
风险资产与无风险资产基金A 和基金B 的相关系数为-0.2。
(1) 画出基金A 和基金B 的可行集(5个点)。
(2) 找出最优风险投资组合P 及其期望收益与标准差。
(3) 找出由短期国库券与投资组合P 支持的资本配置线的斜率。
(4) 当一个投资者的风险厌恶程度A=5时,应在股票基金A 、B 和短期国库券中各投资多少?解:(1)基金之间的协方差为B A B A r r σσρ⨯⨯=),cov(=240)60202.0(-=⨯⨯-(2)最优风险组合的权重为6818.0=a w ,6818.01-=b w =0.3182期望收益和标准差(3)资本配置线是无风险收益点与最优风险组合的连线,它代表了短期国库券与最优风险投资组合之间的所有有效组合,资本配置线的斜率为(5) 在给定的风险厌恶系数A 的条件下投资者愿意投资到最优风险投资组合的比例为 这意味着A=5时的投资者愿意在这个最优风险资产组合中投入50.89%的财产,由于A 、B 两种股票在投资组合的比例分别为68.18%和31.82%,这个投资者分别投资于这两种股票的比例为:股票A :0.5089*68.18%=34.70% 股票B :0.5089*31.82%=16.19% 总额:50.89%2假定一个风险证券投资组合中包含大量的股票,它们有相同的分布,%60%,15)(==σr E ,相关系数5.0=ρ(1)含有25种股票的等权重投资组合期望收益和标准差是多少?(2)构造一个标准差小于或等于43%的有效投资组合所需要最少的股票数量为多少? (3)这一投资组合的系统风险为多少?(4)如果国库券的收益率为10%,资本配置的斜率为多少? 解:(1)%72.43]/)1(/[%,15)(2/122=-+==n n n r E p p ρσσσ(2)2%^43/)1(/22=-+n n n ρσσ即73.3649/1800,1849180018003600===-+n n n所以至少要37只股票组合才能达到目标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设风险证券组合期望收益率为 Rn ,其风险为σn , 如图中的点N;引入的无风险投资收益率为Rf , 则σf =0,如图中的点F。有设无风险投资与风险证券组
合的再组合比例系数分别为βf 和βn,有βf +βn=1,记 再组合期望收益率为 R,p 有
Rp f Rf n Rn
(5.1)
R
N
Rn
P
Rp
Rf
σp σn
σ
由于无风险投资的σf=0,则协方差σnf=σfn=0,再 组合投资的风险σp 满足下式:
2 p
[n, f
]
2 n
fn
nf
2 f
n
f
[n
,
f
]0n2
0 0
n f
n2
2 n
(5.2)
有
n
p n
将式(5.3)代入式(5.1), 得
Rp
(1
p n
)R
f
p n
Rn
p (m)
Rp Rm
Rf Rf
m
(5.13)
由无风险投资与其它风险证券组合(N)的再组合FN
确定的风险为
p (n)
Rp Rn
Rf Rf
n
(5.14)
p (m) p (n) (R p
R
f
)(
R
m m
R
f
n Rn Rf
)
(5.15)
由式(5.6)知,
dk d n
d Rn d n
n
Rn
Rf
Rn Rf n
p
Rf
性质得证。
(5.3) (5.4)
性质5.2:
(1) 无风险投资与风险证券组合的再组合的方程直线 与风险证券组合有效边界相切的切点(M)由下式确定:
Rm bRf a cRf b
2 m
ac
1 b2
2
(cRm
2bRm
a)
变量定义同前。
(5.5)
(2)当无风险投资与风险证券组合投资的再组合直线, 与风险证券组合有效边界相切时,该再组合切线即为 新的有效边界。
组合投资期望收益率与标准差关系:
Rp= rf + α(Ra- rf )= rf + (σp /σa) (Ra- rf )
=
rf
Ra rf
a
p
(CAL 方程)
借入
Ra
A
贷出
CAL
rf
k
σa
性质5.1:无风险投资与风险证券组合投资的再
组合的风险(标准差),与再组合的期望收益率 间呈线性关系。
证明:
d cR b
(5.9)
R
Rm
M
Rn
N
P
Rp
Rf
σp σmσn
σ
由性质5.1及式(5.6)知,上图中无风险投资(F)与风险证 券组合的再组合直线与风险证券组合有效边界在M点 相切时,满足:
dR d m
ac cR
b m
2
b
m
Rm Rf m
km
(5.10)
2 m
1 ac b2
2
[c R m
(cR f
如何确定资本结构变化、借贷利率变化条件下的 有效资产组合(边界)?
证明:
(1) 式(5.4)表示的直线的斜率为:
k dRn Rn Rf d n n
(5.6)
由性质4.5可知,风险证券组合有效边界可表示为:
2
ac
1
b2Βιβλιοθήκη (cR22bRa)
式(5.7)两边对σ求 d R,有
d
(5.7)
ac
1
b2
(cR
dR d
b
dR) d
(5.8)
即
d R ac b2
2 n
2
R
n R
2 n
f
0
(5.16)
式(5.4)所示直线的斜率随的增大而增大,切线FM 斜率达最大值,且有
Rm Rf Rn Rf ,
m
n
Rn Rf 0
(5.17)
p (m) p (n)
(5.18)
式(5.18)说明,对于一定的期望收益率,再组合FM确 定的投资风险最小,故再组合FM为新的有效边界,其 解析式为:
在均值-方差模型基础上引入无风险投资,若无风 险投资收益率为常数,则无风险投资于风险组合资 产的再组合,使组合资产选择转化为线性问题,使 决策简明化。
但利率的变化使常数条件消失,有效资产组合(边 界)的线性特征变为非线性特征;企业借贷比例变化 导致资本结构改变以及借贷利率的变化;投资风险 也将改变,将使有效资产组合(边界)随之变化。
记风险资产A的收益率为ra, R
其期望收益率为Ra,标准差为 Ra 12%
A
σa;无风险资产收益率为rf。
假定Ra=12%, σa =18%,
P
rf =5%。则风险资产溢价为 5%
Ra- rf =7%。
σa=18% σ
风险资产与无风险资产的组合P的收益率为:
rp =α ra +(1-α) rf =5%+ α(ra-5%) Rp=αRa +(1-α) rf = rf + α(Ra- rf ) 资产组合风险为: σp = α σa (或 α = σp /σa )。
p
m Rm Rf
(R p
Rf
)
(5.19)
证毕。
5.2 引入无风险资产的最优资产组合
不含无风险资产的资产组合选择
引入无风险借贷的资产组合选择
不同借贷利率条件下的资产组合选择
风险厌恶型(贷出)的最优资产组合选择
冒险型(借入)的最优资产组合选择
中性(不借不贷)的最优资产组合选择
思考问题:
b)Rm
bRf
]
(5.11)
令式(5.7)中 R Rm, m将, 式(5.7)与式(5.11)联立,解得
Rm bRf a
cRf b
(5.12)
2 m
1 ac b2
2
(cRm
2bRm
a)
式(5.12)表示切点M坐标。
(2) 对于一定的期望收益率,由式(5.5)知,再组
合FM确定的风险为
5 无风险资产 ---- 借入与贷出
5.1 无风险投资的引入
无风险投资指购买由政府或银行担保发行的债 券(如国库券)而进行的投资活动。无风险投资 收益率是稳定的,标准差为零。当在风险证券组 合中引入无风险投资时,其组合的期望收益率与 风险之间的关系将发生有趣的变化。
一种风险资产与一种无风险资产的组合
