2公式法,十字相乘法
十字相乘法
（4） 7 ( x y ) 5 ( x y ) 2 ( x y )
3 2
（5） ( a 8 a ) 22 ( a 8 a ) 120
2 2 2
-2-
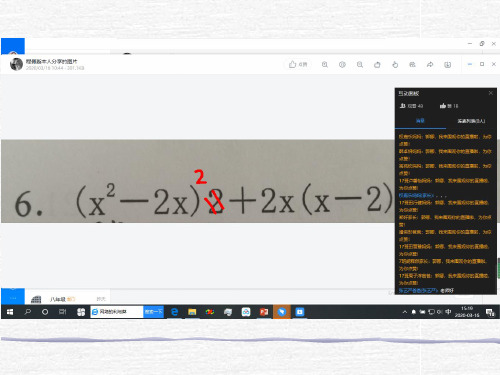
五、达标检测 1．分解因式： (1) x 5 x 6
2
(2) x 5 x 6
2
(3) x 5 x 6
2
(4) x 5 x 6
2பைடு நூலகம்
(5) x x 6
2
(6) x x 6
2
-1-
每一次的坚定都为你埋下成功的种子
(7) x 2 x 3
2
(8) x x 1 2
2
2
x
（2）因式分解的公式： x ( p q ) x p q ( x p )( x q ) -----方法特征：拆常数项，凑一次项 特别： ax bx c a 1 a 2 x ( a 1 c 2 a 2 c1 ) x c1 c 2 ( a 1 x c1 )( a 2 x c 2 ) -----方法特征：拆两头，凑中间
2
2
二、准备练习 （1） x 2 x 3 _ _ _ _ _ _ _ ; （3） x 4 x 2 _ _ _ _ _ _ _ ; 三、因式分解 （1） x 5 x 6 _ _ _ _ _ _ _ ;
2
（2） x 4 x 1 _ _ _ _ _ _ _ ; （4） x 5 x 3 _ _ _ _ _ _ _ ; （2） x 3 x 4 _ _ _ _ _ _ _ ;
每一次的坚定都为你埋下成功的种子
因式分解法(十字相乘法)
q>0时，q分解的因数a、b( 同号 )且（a、b符号）与p符 号相同 当q<0时， q分解的因数a、b( 异号) （其中绝对值较大 的因数符号）与p符号相同
把下列各式分解因式
（1）4x2 + 11x + 6 （2）3x2 + 10x + 8
2x
3
1x
4
2x×4+1x×3=11x
结果中一次项系数是分解 后十字交叉相乘所得的和
(2x+3)(x- 4) = 2x2-5x+12
2x
3
1x
-4
2x×（-4）+1x×3=-5x
结果中一次项系数是分解 后十字交叉相乘所得的和
十字相乘法（竖分常数交
叉验， 横写因式不能乱。 ）
例1、用十字相乘法分解因式 2x2-2x-12
法二：
2x2-2x-12 = （x+2）(2x-6)
x
2 = 2（x+2)(x-3)
2x
-6
x×（-6）+2x×2=-2x
(顺口溜：竖分常数交叉验，横写因式不能乱。)
例1、（2）
12x2 29x 15
3x
5
4x
3
(9x) (20x) 29x
所以： 原式 (3x 5)(4x 3)
将下列各式用十字相乘法进行因式分解
4x2- 7xy + 3y2
2x2 5xy 7 y2
2x
7y
x 1y
2xy 7xy 5xy
所以： 原式 (2x 7 y)(x y)
十字相乘法
十字相乘法虽然比较难学,但是一旦学会了它,用它来解题,会给我们带来很多方便,以下是我对十字相乘法提出的一些个人见解。
1、十字相乘法的方法：十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项系数。
2、十字相乘法的用处：（1）用十字相乘法来分解因式。
（2）用十字相乘法来解一元二次方程。
3、十字相乘法的优点：用十字相乘法来解题的速度比较快，能够节约时间，而且运用算量不大，不容易出错。
4、十字相乘法的缺陷：1、有些题目用十字相乘法来解比较简单，但并不是每一道题用十字相乘法来解都简单。
2、十字相乘法只适用于二次三项式类型的题目。
3、十字相乘法比较难学。
5、十字相乘法解题实例：1)、用十字相乘法解一些简单常见的题目，例子中的²是平方的意思例1把m²+4m-12分解因式分析：本题中常数项-12可以分为-1×12，-2×6，-3×4，-4×3，-6×2，-12×1当-12分成-2×6时，才符合本题解：因为 1 -21 ╳ 6所以m²+4m-12=（m-2）（m+6）例2把5x²+6x-8分解因式分析：本题中的5可分为1×5,-8可分为-1×8，-2×4，-4×2，-8×1。
当二次项系数分为1×5，常数项分为-4×2时，才符合本题解：因为 1 25 ╳ -4所以5x²+6x-8=（x+2）（5x-4）例3解方程x²-8x+15=0分析：把x²-8x+15看成关于x的一个二次三项式，则15可分成1×15，3×5。
解：因为 1 -31 ╳ -5所以原方程可变形（x-3）（x-5）=0所以x1=3 x2=5例4、解方程 6x²-5x-25=0分析：把6x²-5x-25看成一个关于x的二次三项式，则6可以分为1×6，2×3，-25可以分成-1×25，-5×5，-25×1。
十字相乘法口诀是什么乘法公式技巧
十字相乘法口诀是什么乘法公式技巧十字相乘法口诀十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项系数具体步骤：十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项系数原理：运用了乘法公式(x+a)(x+b)=x²+(a+b)x+ab的逆运算来进行因式分解。
十字相乘法能把二次三项式分解因式(不一定在整数范围内)。
对于形如ax²+bx+c=(a1x+c1)(a2x+c2)的整式计算步骤：⑴把二次项系数a分解成两个因数a1,a2的积a1·a2⑵把常数项c分解成两个因数c1,c2的积c1·c2⑶使a1c2+a2c1正好等于一次项的系数b⑷结果:ax²+bx+c=(a1x+c1)(a2x+c2)实质：二项式乘法的逆过程。
当首项系数不是1时，需注意各项系数的符号。
基本式子：x²+(p+q)x+pq=(x+p)(x+q)。
十字相乘顺口溜竖分常数交叉验，横写因式不能乱。
步骤注释①竖分二次项与常数项②交叉相乘，积相加③检验确定，横写因式十字相乘法对于二次三项式的分解因式，借用一个十字叉帮助我们分解因式，这种方法叫做十字相乘法。
【十字相乘法的方法】十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项系数。
【十字相乘法的用处】(1)用十字相乘法来分解因式。
(2)用十字相乘法来解一元二次方程。
因式分解的一般步骤(1) 如果多项式的各项有公因式时，应先提取公因式;(2) 如果多项式的各项没有公因式，则考虑是否能用公式法来分解;(3) 对于二次三项式的因式分解，可考虑用十字相乘法分解;(4) 对于多于三项的多项式，一般应考虑使用分组分解法进行。
在进行因式分解时，要结合题目的形式和特点来选择确定采用哪种方法。
以上这四种方法是彼此有联系的，并不是一种类型的多项式就只能用一种方法来分解因式，要学会具体问题具体分析。
因式分解题型提公因式法、公式法、分组分解法、十字相乘法
1.因式分解概念：把一个多项式化成几个整式的 的形式，这就叫做把这个多项式因式分解，也可称为将这个多项式分解因式，它与整式乘法互为逆运算。
2．常用的因式分解方法：（1）提公因式法：对于ma mb mc ++， 叫做公因式， 叫做提公因式法。
①多项式各项都含有的相同因式，叫做这个多项式各项的公因式。
②公因式的构成：系数：各项系数的 ；字母：各项都含有的相同字母； 指数：相同字母的最低次幂。
（2）公式法：①常用公式平方差： 完全平方：立方和：3322a b (a+b)(a -ab+b )+= 立方差：②常见的两个二项式幂的变号规律： 22()()n n a b b a -=-；2121()()n n a b b a ---=--．（n 为正整数）（3）十字相乘法①二次项系数为1的二次三项式q px x ++2中，如果能把常数项q 分解成两个因式b a ,的积，并且b a +等于一次项系数中p ，那么它就可以分解成②二次项系数不为1的二次三项式c bx ax ++2中，如果能把二次项系数a 分解成两个因数21,a a 的积，把常数项c 分解成两个因数21,c c 的积，并且1221c a c a +等于一次项系数b ，那么它就可以分解成：()=+++=++2112212212c c x c a c a x a a c bx ax ()()221c x a a x a ++。
（4）分组分解法①定义：分组分解法，适用于四项以上的多项式，例如22a b a b -+-没有公因式，又不能直接利用分式法分解，但是如果将前两项和后两项分别结合，把原多项式分成两组。
再提公因式或利用公式法，即可达到分解因式的目的。
例如22a b a b -+-=22()()()()()()(1)a b a b a b a b a b a b a b -+-=-++-=-++， 这种利用分组来分解因式的方法叫分组分解法。
②原则：分组后可直接提取公因式或可直接运用公式，但必须使各组之间能继续分解。
十字相乘法完整版
XX,a click to unlimited possibilities
十字相乘法完整版
目录
01
添加目录标题
02
十字相乘法的基本原理
03
十字相乘法的应用
04十字相乘法ຫໍສະໝຸດ 注意事项05十字相乘法的扩展应用
01
添加章节标题
02
十字相乘法的基本原理
定义与公式
定义：十字相乘法是一种解一元二次方程的方法，通过将方程的系数分解为两个因数的乘积，从而找到方程的解。
分解因式时，要注意符号的变化，特别是当多项式中含有括号时。
分解因式时，要注意符号的变化，特别是当多项式中含有分数时。
分解因式时要注意完全平方数的问题
分解因式时要注意完全平方数的问题，避免出现错误的结果。
分解因式时要注意符号问题，确保结果的正确性。
分解因式时要注意因式的分解是否彻底，避免出现不必要的错误。
应用场景：求解一元二次不等式时，当不等式的系数较大或较为复杂时，使用十字相乘法可以简化计算过程
注意事项：在使用十字相乘法时，需要确保分解后的两个一次项的乘积为正，否则会导致不等号方向错误
举例说明：通过具体的一元二次不等式实例，展示十字相乘法的应用和求解过程
求解一元二次函数极值
定义：一元二次函数极值是指函数在某点的导数为零，且该点两侧的函数值异号
代数方程：十字相乘法可用于解二次方程和一元高次方程
矩阵运算：十字相乘法在矩阵的乘法中也有应用
分式化简：十字相乘法可以用于化简分式，简化计算过程
在物理和工程领域的应用
线性代数方程组的求解
工程中的结构分析、流体动力学等领域
物理中的动力学方程求解
矩阵运算中的分块矩阵相乘
用十字相乘法解一元二次方程
回顾与复习 1
1.我们已经学过了几种解一元二次方程 的方法? X2=a (a≥0) 直接开平方法 2=n (n≥0) (x+m) 配方法 2 公式法 分解因式
3、横向写出两因式
(x+2)和(x+3)
2、x2-x-12=0
解：x2-x-12=0
(x+3)(x-4)=0 x+3=0 X=-3 x-4=0 X=4
x x
3 -4
3x -4x =-x
∴x1=-3, x2=4
3、x2-6x+8=0 解：x2-6x+8=0 (x-2)(x-4)=0
x
x
-2
-4
x-2=0 x=2 x-4=0 x=4
4、x2+6x-16=0
作业
用适当方法解下列方程
1、3x2-27=0
2、5x2-2x-7=0
3、4x2-27x-7=0 4、3x(x-2)=2x-4
-2x -4x = -6x
∴x1=2, x2=4
4、6x2-11x-35=0 解：6x2-11x-35=0 (2x-7)(3x+5) =0 2x-7=0
2x 3x
-7 5
-21x +10x = -11x
3x+5 =0 ∴
练习
用十字相乘法解下列方程
1、2x2+7x+3=0 2、2x2-7x+3=0 3、x2-8x+15=0
一元二次方程的解法-十字相乘法
首先观察一元二次方程的形式，确定二次 项系数和常数项系数。
根据二次项系数和常数项系数，将方程左 侧转化为两个一次项的乘积。
求解一次项系数
求解未知数
通过交叉相乘的方法，求解出一次项系数 。
将求得的一次项系数代入原方程，解出未 知数。
注意事项
适用范围
十字相乘法适用于解形式为 $ax^2+bx+c=0$的一元二次方
概念
十字相乘法基于因式分解的思想，通过将一元二次方程转化为两个一元一次方 程，进而求解未知数。
重要性及应用领域
重要性
十字相乘法是一元二次方程的重要解法之一，它能够直接求得方程的解，避免了 复杂的计算和求解过程。
应用领域
十字相乘法广泛应用于数学、物理、工程等领域，尤其在解决实际问题中，如代 数问题、几何问题、概率统计等，都经常需要使用到一元二次方程的解法，而十 字相乘法是其中的一种常用方法。
一元二次方程的解法-十相乘法原理 • 实例解析 • 与其他解法的比较 • 练习与巩固 • 总结与展望
01 引言
定义与概念
定义
十字相乘法是一种解一元二次方程的数学方法，通过将方程左侧的二次项和常 数项进行拆分，然后与右侧的一次项进行交叉相乘，得到两个一次方程，从而 求解一元二次方程。
02 十字相乘法原理
原理概述
十字相乘法是一种解一元二次方程的简便方法，通过将方程左侧的二次项和常数 项进行拆分，然后交叉相乘，得到两个一次项，从而找到方程的解。
该方法基于一元二次方程的因式分解，通过将方程左侧转化为两个一次项的乘积 ，简化了解的过程。
具体步骤
确定二次项系数和常数项系数
进行因式分解
与因式分解法的比较
适用范围
因式分解的七种常见方法
因式分解的七种常见方法因式分解是代数学中非常重要的一个基本概念，可以帮我们优化计算过程，得到简化的式子。
在因式分解的过程中，需要运用不同的方法来将一个给定的式子分解为若干个简单的乘积，本文将会介绍七种常见的因式分解方法。
1. 公式法公式法是一种较为常见的因式分解方法，它可以应用于一些特定的式子。
公式法常用的公式有两个：（1）$a^2-b^2=(a+b)(a-b)$该公式被称为"a二次减b二次"公式。
它告诉我们，一个平方数减另一个平方数的结果可以表示为两个因子的乘积，并分别是它们的和与差。
例如：$16-9=7\times5=(4+3)\times(4-3)$（2）$a^3+b^3=(a+b)(a^2-ab+b^2)$该公式被称为"a立方加b立方"公式。
它告诉我们一个立方数加另一个立方数的结果可以表示为两个因子的乘积，并分别是它们的和与差减去它们的积。
例如：$8^3+1^3=513=(8+1)\times(8^2-8+1)$2. 提公因式法提公因式法是一种常用的因式分解方法。
它的主要思想是将式子中的公因式先提出来，再对剩下的部分进行因式分解。
例如：$ax^2+bx=a(x^2+\frac{b}{a}x)$在上述式子中，$a$是公因式，$(x^2+\frac{b}{a}x)$是剩余部分的因式分解。
这样我们就把原始式子分解成了两个因子的乘积。
3. 十字相乘法十字相乘法主要用于二次三项式的因式分解。
该方法基于以下思想：将二次三项式分解为两个一次三项式的乘积，其中每个一次三项式的首项系数积等于原始式子的二次项系数，常数项积等于原始式子的常数项。
例如：$ax^2+bx+c$，首先将它分解为两个一次三项式$(px+q)(rx+s)$，然后进行十字相乘运算$(px+q)(rx+s)=px\times rx+px\times s+qrx+qs$，其中最后两项括号里的$c$是常数项。
专题：完全平方公式,十字相乘法
13
完成作业2.27作业
14
蓦然回首
对自己说，你有什么收获？ 对同学说，你有什么温馨提示？ 对老师说，你还有什么困惑？
15
＝(a＋2)2(a－2)2.
例4 已知x2－4x＋y2－10y＋29＝0，求x2y2＋2xy＋1的值．
解：∵x2－4x＋y2－10y＋29＝0，
x2 4x 22 y2 10 y 52 0
∴(x－2)2＋(y－5)2＝0.
∵(x－2)2≥0，(y－5)2≥0， 几个非负数的和为0， ∴x－2＝0，y－5＝0， 则这几个非负数都为0. ∴x＝2，y＝5，
∴x2y2＋2xy＋1＝(xy＋1)2
＝112＝121.
知识要点2
十字相乘法
十字相乘法公式：
x2 (a b)x ab (x a)(x b)
11
(1)X2-7x+12 x x
(3)x2+8x+12
(2)x2-4x-12 (4)x2-11x-12
(5) 2x2-7x+3
(6) 5x2+6xy-8y2
A . 11
B. 9 C. -11 D. -9
解析：根据完全平方式的特征，中间项-6x=2x×(-3),
故可知N=(-3)2=9.
变式训练 如果x2-mx+16是一个完全平方式,那么m的
值为___±__8___.
解析：∵16=(±4)2，故-m=2×(±4)，m=±8.
例2 分解因式：
（1）16x2+24x+9；
分析：(1)中有公因式3a,应先提出公因式，再进一步分解 因式；
解: (1)原式=3a（x2+2xy+y2） =3a（x+y）2；
因式分解_十字相乘法
一、提公因式法； 二、公式法； 三、十字相乘法； 四、换元法； 五、分组分解法；
方法一：提公因式法
这是因式分解的首选方法。在 分解因式时一定要首先认真观 察所给的多项式，尽可能地找 出它们的公因数（式）。
方法二：公式法
一、平方差公式： a2 b2 (a b)(a b) 二、完全平方公式： a2 2ab b2 (a b)2
（7）（a+b）2-4(a+b)+3 （8） x4-3x3 -28x2
(9) 2x2-7x+3 (10) 5x2+6xy-8y2
(6)x4+13x2+36
答案 (1). (x-1)(x+4) (2). (x+1)(x-4) (3). (x+8y)(x-2y) (4). (x-3y)(x-8y) (5). –(xy+9)(-xy+2) (6). (x²+4)(x²+9) (7). (a+b+1)(a+b+3) (8). (x+4)(x³-7x²) (9). (2x-1)(x-3) (10). (5x-4y)(x+2y)
(3) x2+5x-6； (4)x2-5x-6
(5) (x－y)2 ＋(x－y) －6
答案 (1). (x-3)(x-4) (2). (x-6)(x+2) (3). (x+2)(x+6) (4). (x-1)(x+12) (5). (x+1)(x+12) (6). (x-4)(x+3)
将下列多项式因式分解
(1)x2+3x-4 (2)x2-3x-4 (3)x2+6xy-16y2 (4)x2-11xy+24y2 (5)x2y2-7xy-18
人教版八年级数学--十字相乘法
竖分首末交叉验，
横写因式不能乱。
巩固3
a2-17ab+72b2
课堂小结
十字相乘法：借助十字交叉线分解因式的方法 竖分首末交叉验， 横写因式不能乱。 因式分解 方法小结： 提公因式 公式法 十字相乘法
随堂练习 因式分解：
（1） (a+b)2 – (a+b) – 20 （2）(x2+2x)2–7(x2+2x)–8 （3） 5x5–15x3y–20xy2
ቤተ መጻሕፍቲ ባይዱ
8x+15 = (x-3) (x-5)
-3
(x-3)
巩固1 因式分解：
竖分首末交叉验，
(1) y2–7y–30 (2) a2-6a+9 (3) –t2+4t–3
横写因式不能乱。
x2 + (p+q)x + pq =( x + p )( x + q ) 例2 因式分解：
(1) (
2+5 ( 2 ) y
横写因式不能乱。
（3） 2x2+13x+15
竖分首末交叉验， 横写因式不能乱。
2 y )+6
y4+5y2+6
(2) (
2- 5 ( ) a+b a+b )+6
巩固2 因式分解：
竖分首末交叉验，
(1) (a-b)2 + 2(a-b) – 15
横写因式不能乱。
(2) x4 – 20x2 + 91
(3) m2 x2 – 2mx -35
x2 + (p+q)x + pq =( x + p )( x + q )
十字相乘法
)x+( )
二 准备练习
（1）
( x + 2 )( x + 3) = _______; （3） ( x + 4 )( x − 2 ) = _______;
2
( x − 4 )( x + 1) = _______; （4） ( x − 5 )( x − 3 ) = _______;
三 因式分解
+ 5 x + 6 = _______; （2） x 2 − 3 x − 4 = _______; 2 2 （3） x + 2 x − 8 = _______; （4） x − 8 x + 15 = _______;
(6) x
2
− x−6
(7)
x2 − 2 x − 3
(8)
x 2 − x − 12
(9) x
2
+ 6x + 8
(10) x
2
− 7 x + 10
(11) x
2
− 6x − 7
（12） m
2
− 12m + 20;
(13)
p 2 − 5 p − 36
(14) t
2
− 2t − 8
(15) 10－3a－ a
（1） x
四 例题解析
例题 1 分解因式 （ 1） x
2
+ 11x + 24
（ 2） x
2
− 10 x + 24
（ 3） x
2
+ 5 x − 24
（ 4） x
2
− 10 x − 24
例题2 例题2、因式分解 （1） x 2 + 7 xy + 12 y 2 （2） x 2 − 8 xy + 12 y 2 （3） x 2 − 13 xy + 12 y 2
十字相乘法
仿照左边填写 5= × ；6= + 5= -6= -5= 4= -5= -4= 12= × + × + × + × ； ； ； ； ； ； ；7= +
在这个表格里你有什么发现?请说一说 在这个表格里你有什么发现 请说一说. 请说一说
如何把 x2－6x＋8 分解因式? ＋ 分解因式 说一说你是怎样理解下图的? 说一说你是怎样理解下图的
你能很快进行分解吗? 你能很快进行分解吗
(1) x2-6x-7 (2) x2+6x-7 (3) x2-8x+7 (4) x2+8x+7
= = = =
(x+1)(x-7) (x-1)(x+7) (x-1)(x-7) (x+1)(x+7)
连连看----找出对应的分解式 连连看----找出对应的分解式 ----
(1) x2+7x+12 (2) x2-7x+12 (பைடு நூலகம்) x2+8x+12 (4) x2-x-12 (5) x2+x-12
A. (x+2)(x+6) B. (x-3)(x+4) C. (x+3)(x+4) D. (x+3)(x-4) E. (x-3)(x-4)
高手们，有什么窍门么？救救我吧！ 高手们，有什么窍门么？救救我吧！
学过分解因式的方法有： 学过分解因式的方法有： 1、提公因式法 、 2、运用公式法： 、运用公式法： 平方差 完全平方公式
乘法运算
(x+2)(x+3)= x2+5x+6 (x-2)(x-3)= x2-5x+6 (x-1)(x+6)= x2+5x-6 (x+1)(x-6)= x2-5x-6 (x+p)(x+q)=
公式法和十字相乘法
公式法和十字相乘法概念回顾：1.公式法因式分解的平方差公式：a2-b2=(a+b)(a-b)因式分解的完全平方公式：a2+2ab+b2=(a+b)2,a2－2ab+b2=(a－b)22．十字相乘法定义：利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法.要将二次三项式x2+ px + q因式分解，就需要找到两个数a、b，使它们的积等于常数项q，和等于一次项系数p, 满足这两个条件便可以进行如下因式分解，即x2 + px + q = x2 +(a + b)x + ab = (x + a)(x + b).用十字交叉线表示: x +ax +bax + bx = (a + b)x由于把x2+ px + q中的q分解成两个因数有多种情况，怎样才能找到两个合适的数，通常要经过多次的尝试才能确定采用哪种情况来进行因式分解.将二次三项式x2+ 4x + 3因式分解，就需要将二次项x2分解为x·x，常数项3分解为3×1，而且3 + 1= 4，恰好等于一次项系数,所以用十字交叉线表示:x2+ 4x + 3 = (x + 3)(x + 1).x +3x +13x + x = 4x把x2 + px + q分解因式时，准确地找出a、b，使a ·b = q；a + b = p符号规律：当q＞0时，a、b同号，且a、b的符号与p的符号相同；当q＜0时，a、b异号，且绝对值较大的因数与p的符号相同。
例题精讲：基础训练：1. 用完全平方公式分解因式：2.用完全平方公式分解因式：3.用十字相乘法分解因式4.用十字相乘法分解因式5.用十字相乘法分解因式6.分解因式7.能力提高：1. 分解因式2.分解因式3. 分解因式4．解答题5.解答题6.解答题思维拓展：练习：一、选择题二．填空题。
十字相乘法
十字交叉法是公务员行政职业能力测验数学运算的一个重要方法，很多比例问题，都可以用十字交叉法来很快地解决，而在资料分析中，也能够派上很大用场，因此应该认真掌握，以便快速解题。
如果题目中给出两个平行的情况A，B，满足条件a，b，然后A和B按照某种条件混合在一起形成的情况C，满足条件ｃ，而且可以表示成。
那么此时就可以用十字交叉法，表示如下:由此可列比例式：。
采用十字交叉法时要注意比例的对应性以及减数与被减数的顺序。
十字相乘法使用时要注意几点：第一点：用来解决两者之间的比例关系问题。
第二点：得出的比例关系是基数的比例关系。
第三点：总均值放中央，对角线上，大数减小数，结果放对角线上。
下面我们一真题来具体说明十字交叉法的应用。
【例1】浓度为70％的酒精溶液100克与浓度为20％的酒精溶液400克混合后得到的酒精溶液的浓度是多少？（）A. 30％B. 32％C. 40％D. 45％【答案及解析】A。
解法一：这道题我们依旧可以按照传统的公式法来解：100克70％的酒精溶液中含酒精100×70％＝70克；400克20％的酒精溶液中含酒精400×20％＝80克；混合后的酒精溶液中含酒精的量＝70+80＝150克；混合后的酒精溶液的总重量＝100+400＝500克；混合后的酒精溶液的浓度＝150/500×100％＝30％，选择A。
解法二：十字相乘法：混合后酒精溶液的浓度为X%，运用十字交叉法：溶液Ⅰ70 X-20 100\ /X/ \溶液Ⅱ20 70-X 400我们可以采用带入法，把答案选项带入，结果就会一目了然。
【例2】甲容器中有浓度为4％的盐水250 克，乙容器中有某种浓度的盐水若干克。
现从乙中取出750 克盐水，放人甲容器中混合成浓度为8％的盐水。
问乙容器中的盐水浓度约是多少？（）A.9.78％B.10.14％C.9.33％D.11.27％【答案及解析】C。
设浓度为ｘ甲： 4 x-88乙：x 4（x -8）：4=250：750=1：3x =9.33%【例3】某市按以下规定收取燃气费：如果用气量60立方米，按每立方0.8元收费；如果用气量超过60立方米，则超过部分按每立方1.2元收费。
8、公式法、十字相乘法
辅导讲义1、上节课作业完成情况：2、主要学习内容：1）：因式分解：2）：提取公因式法：知识点1：因式分解（公式法）1、如果把乘法公式反过来，就可以把某些多项式分解因式，这种方法叫公式法。
平方差公式：22()()a b a b a b -=-+完全平方公式：2222()a ab b a b ±+=±知识点2：因式分解（十字相乘法）1、二次三项式多项式c bx ax ++2，称为字母x 的二次三项式，其中2ax 称为二次项，bx 为一次项，c 为常数项．例如，322--x x 和652++x x 都是关于x 的二次三项式．在多项式2286y xy x +-中，如果把y 看作常数，就是关于x 的二次三项式；如果把x 看作常数，就是关于y 的二次三项式．在多项式37222+-ab b a 中，把ab 看作一个整体，即3)(7)(22+-ab ab ，就是关于ab 的二次三项式．同样，多项式12)(7)(2++++y x y x ，把x ＋y 看作一个整体，就是关于x ＋y 的二次三项式．十字相乘法是适用于二次三项式的因式分解的方法．2、十字相乘法的依据和具体内容利用十字相乘法分解因式，实质上是逆用()()ax b cx d ＋＋竖式乘法法则．它的一般规律是：（1）对于二次项系数为1的二次三项式q px x ++2，如果能把常数项q 分解成两个因数a ，b 的积，并且a b ＋为一次项系数p ，那么它就可以运用公式 ))(()(2b x a x ab x b a x ++=+++分解因式．8.求证：当n 为自然数时，()()2231331n n n n -+-++是一个完全平方数.十字相乘法把下列各式分解因式：（1）1522--x x ； （2）2265y xy x +-．把下列各式分解因式：（1）3522--x x ； （2）3832-+x x ．把下列各式分解因式： 91024+-x x ； （2）)(2)(5)(723y x y x y x +-+-+；120)8(22)8(222++++a a a a ．1.二次项系数不等于1的二次三项式应用十字相乘法分解时，二次项系数的分解和常数项的分解随机性较大，往往要试验多次，这是用十字相乘法分解的难点，要适当增加练习，积累经验，才能提高速度和准确性．2.要深刻理解换元的思想，这可以帮助我们及时、准确地发现多项式中究竟把哪一个看成整体，才能构成二次三项式，以顺利地进行分解．同时要注意已分解的两个因式是否能继续分解，如能分解，要分解到不能再分解为止．我来试一试。
因式分解(十字相乘法)
十字相乘法
一、整式的有关概念
数与字母乘积，这样的代数式叫单项式。 1、单项式： 单独的一个数或字母也是单项式。
2、单项式的系数： 单项式中的数字因数。
3、单项式的次数： 单项式中所有的字母的指数和。 4、多项式： 几个单项式的和叫多项式。 5、多项式的项：组成多项式中的单项式叫多项式的项 6、多项式的次数： 多项式中次数最高的项的次数叫做这个多项式的次数。 7、整式：单项式与多项式统称整式。
2
Company Logo
因式分解：
8m 22mn 15n
2 2
Company Logo
2
1:计算: (1). (x+2)(x+3);
(2). (x+2)(x-3);
解 : 原式 x 2 2x 3x 2 3
x (2 3)x 6
2
x 5x 6
2
(3). (x-2)(x-3);
(4)(x+a)(x+b);
ax+bx+c=(a1 x+c1 )(a2 x+c 2)
a1
a2
1 2
c1
c2
a c +a c =b
2 1
Company Logo
因式分解：
(1)x2+8x+12
Company Logo
因式分解：
(2)x2-11x-12
Company Logo
因式分解： (3)x2+13x+12
Company Logo
因式分解：
(4)x2-x-12
Company Logo
因式分解：
公式法·十字相乘法
公式法·十字相乘法主备教师：学生：班学习目标1、初步了解用十字相乘法来分解二次三项式X2+px+q的方法。
2、进一步培养自己的观察、推理、联想及逆向思维的能力。
学习重点用十字相乘法来分解因式的方法。
学习难点掌握拆分常数项的规律。
学习过程一、学生自学1、计算：(x+5)(x+9）=(x-12)(x+5）=(x+a)(x+b）=2、分解因式：X2+14x+45=X2-7x-60=X2+(a+b)x+ab=3、根据上面第2题，你能在下列横线上填写适当的数吗？X2+14x+45=X2+( + )x+ ×X2-7x-60=X2+( + )x+ ×4、根据上面第3题右端的多项式能写成两个一次多项式的乘积吗？X2+14x+45=X2+( + )x+ ×=（x+ ）（x+ ）：X2-5x+6=X2+( + ）x+ ×=（x+ ）（x+ ）：X2-7x-60=X2+( + )x+ ×=（x+ ）（x+ ）；X2+x-2=X2+( + ）x+ ×=（x+ ）（x+ ）。
5、那么，对于X2+（a+b）x+ab又怎样分解呢？一般地，由多项式乘法（x+a）（x+b）=X2+（a+b）x+ab，反过来，就得到X2+（a+b）x+ab=（x+a）（x+b），这就是说，对于二次三项式X2+px+q，如果能够把常数项q分解成q=a×b，且a+b=p，那么X2+px+q= X2+（ + ）x+ ×=（x+ ）（x+ ）想一想：1）当q为正时， a、b 号，它们的符号与p的符号。
2）当q为负时，a、b 号，其中的符号与P的符号相同。
二、合作交流把下列二次三项式分解因式:(1) 232x x++ (2) 276x x-+小结: 当常数项为正数时,分解成两个同号因数,与一次项系数的符号相同.(3) 220m m+- (4) 2536p p--小结: 当常数项为负数时,分解成两个异号因数,其中绝对值较大的因数与一次项系数的符号相同。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一元二次解法：（1）公式法
【知识要点】
1．计算方法
一，先将方程变为标准形式)0(02
≠=++a c bx ax ，确认a ，b ，c 。
如何变：
① 通过移项或通分（如例一，例二，例三）注意：尽量使a 为正整数，方便计算
② 通过公式计算展开（如例四，例五） 注意：符号
③ 通过待定系数法结合①②（如例六） 注意：除了X ，其他均看做已知数
二，再计算△，当△=042≥-ac b ，有实数根。
如△＜0，则方程无解 三，根据求根公式，将a,b,c ,△代入公式，即得：2--4=2b b ac x a
±。
【典型例题】
领练：例一
例①4722=-x x 例②
02
122412=+-x x
例③05422=-+-x x 例④x x x x 6)1()12()12(2
2++=--+
例⑤2(3)2(1)7x x x --+=- 例⑥())1(03212
≠=+++-m m mx x m
测试：例二
1，x x 4212=- 2，11)2(5)31)(13(+-=-+x x x
3，(2)(3)
56x x --= 4，02222=-+-n m mx x
二，熟练掌握△，不解方程，能够判断方程根的情况。
方程有两个实数根→△≥0
方程有两个相等的实数根→△＝0
方程有两个不相等的实数根→△＞0
方程没有实数根→△＜0
例三，变式训练
①不解方程，请判别下列方程根的情况； （1）22340t t +-= ; （2）
2
16924x x += ; （3）25(1)70y y +-= ;
②方程242()0x a b x ab ---=的根的情况是 ;
③如果关于x 的方程222(41)210x k x k -++-=有两个不相等的实数根，那么k 的取值范
围是 .
④已知0,0,p q <<则一元二次方程20x px q ++=的根的情况是 ;
⑤已知关于x 的方程2(2)20x a x a b -++-=的判别式等于0,且12
x =是方程的根，则a b +的值为 ______________.
⑥若m =______ （m 为整数），方程22
x m x mx m +=-+有整数解.
（2）分解因式法，十字相乘法
【知识要点】
1，分解因式法：将一元二次方程利用因式分解把其变成因式乘积的形式。
① 利用完全平方公式分解（如例一，例二）
② 利用平方差公式分解（如例三，例四）
2，十字相乘法：将二次项，常数项拆开，交叉相乘，结果为一次项的因式分解特殊方法
① 二次项为1的方程（如例五，例六） 注意：一次项，常数项的符号
② 二次项不为1的方程（如例七，例八） 注意：当数字过大时，应用短除法找因数，
大胆尝试。
领练：例一
例①291240x x ++= 例②2
(1)2(1)10x x ---+=
例③22(3)(32)0x x ---= 例④22
4(21)9(2)x x -=-
例⑤2320x x -+= 例⑥22990x x --=
例⑦221527x x -=- 例⑧25521280x x -+=
测试:例二
1，2722420x x -+= 2，22
(3)4(21)x x +=-
3，01262=--x x 4，234(21)0x x ++=
5，2235+750x x -= 6，2
(1)2(1)150x x ----=
变式训练：
领练：例2.①如果二次三项式22
24x mx m ++-是关于x 的完全平方式，那么m = .
②若多项式2x px q ++分解因式的结果是()(),x m x n ++则方程2
0x px q ++= 的根为
③在等腰三角形ABC 中8,,BC AB AC =的长是关于x 的方程2
100x x m -+=的两个根,则m =
领练：例3.分别根据下面的条件求m 的值：
①方程2(2)40x m x -++=有一个根为1-；
③方程2310mx x -+=有两个不相等的实数根；
④方程2420mx x ++=没有实数根；
⑤方程2
20x x m --=有实数根.
领练：例4.
①试证：关于x 的一元二次方程2(1)2(2)0x a x a +++-=一定有两个不相等的实数根.
领练：②已知,αβ是关于x 的方程20x px q ++=的两个不相等的实数根，且32230,ααβαββ--+=求证：0,0.p q =<
领练：③已知方程2
(1)(2)x x m --= (m 为已知实数，且0m ≠)，不解方程证明：
(1)这个方程有两个不相等的实数根；
(2)一个根大于2，另一个根小于1.
领练：例5.①若两个方程22
2(1)(3)0x a x a --++=和222240x ax a a -+-+=中，至少有一个方程有实数根，求a 的取值范围.
领练：②设m 为整数，且440,m <<方程08144)32(22
2=+-+--m m x m x 有两个不相等的整数根，求m 的值及方程的根.
领练：③如图，在ABC ∆中，AD 是BAC ∠的平分线，EF 垂直平分,AD 垂足为,F 交BC 的延长线于点,,,.E BE a CE c DE b ===求证：关于x 的一元二次方程220x bx ac -+=有两个相等的实数根.
测试：【课后作业】
1.方程()()1231=+-x x 化为02
=++c bx ax 形式后，a 、b 、c 的值为（ ） A. 1，–2，–15 B. 1，–2，–15 C. 1，2，–15 D.–1，2，–15
2. 关于x 的方程2
210ax x -+=中，如果0,a <那么根的情况是（ ）
A 两个相等的实数根 B.有两个不相等的实数根 C.没有实数根 D.不能确定
3. 下列方程中，有两个相等的实数根的是（ ）
A.2256y y +=
B.25x += 220+= D.2310x -+= 4.方程()()1132=-+x x 的解的情况是（ ）
A.有两个不相等的实数根
B.没有实数根
C.有两个相等的实数根
D.有一个实数根
5.关于x 的一元二次方程2
10x kx +-=的根的情况是 （ ）
A.有两个不相等的同号实数根
B.有两个不相等的异号实数
C.有两个相等的实数根
D.没有实数根
6.若t 是一元二次方程20(0)ax bx c a ++=≠的根，则判别式24b ac ∆=-和完全平方公式2(2)M at b =+的关系是（ ）
A. M ∆=
B. M ∆<
C. M ∆>
D.大小关系不能确定
7.若一元二次方程20ax bx c ++=一个根是1，且,a b 满足等式 333+-+-=a a b ,
c =_________.
8.关于x 的方程2
(21)10kx k x k ++-+=的实根的情况是 .
9.如果关于x 的一元二次方程22(4)60x ax x --+=没有实数根，那么a 的最小整数值是__
10.若关于x 的二次方程28(10)70x a x a --+-=的根互为相反数，求a 的值.。