第二章 原子的结构和性质(2)
结构化学第二章

8h2224Z e20rE
精选可编辑ppt
17
球极坐标与笛卡儿坐标的关系
精选可编辑ppt
18
Schrödinger方程在球极坐标中的形式
精选可编辑ppt
19
2. 变数分离法
令 (r,)R( r())(),代入上式 r2si并 2n 乘以
R
s R 2 i r n r 2 R r s i n si n 1 2 2 8 h 2 2( E V ) r 2 s2 i 0 n
这样的原子称为Rydberg原子。在实验室里已造出n 约为105的H原子, n 约为104的Ba原子; 在宇宙中也观察到了n 从301到300之间的跃迁。
毋庸置疑, Rydberg原子是个大胖子。事实上, 它的半径大约相当于基态 原子的十万倍! 这样一个胖原子, 即使受到微弱的电场或磁场作用, 也会显著 变形。
第二章 原子的结构和性质
精选可编辑ppt
1
精选可编辑ppt
2
在本章中,将用Schrödinger方程处理真实的化学物种, 这自然要从最简单的H原子入手。为了更具一般性,也包括 类氢离子,如He+、Li2+等,它们的区别仅在于原子序数Z的 不同。
氢是化学中最简单的物种,也是宇宙中最丰富的元素。 无论在矿石、海洋或生物体内,氢无所不在。
精选可编辑ppt
20
2. 变量分离
设ψ(r,θ,φ)=R(r)Θ(θ)Φ(φ)= R(r) Y (θ,φ). 方程两边同乘以r2/(RΘΦ)
R方程:
Y方程:
Y=ΘΦ.方程两边同乘以 sin2θ/(ΘΦ)并移项
精选可编辑ppt
21
经变数分离得到的三个分别只含,和r变量的方程依次称 为方程、方程和R方程,将方程和方程合并,Y(,) =()(),代表波函数的角度部分。
2021届高考化学三轮考点突破训练:原子结构与性质(二)【含答案解析】

2021届高考化学三轮考点突破训练原子结构与性质(二)1.已知X、Y和Z三种元素的原子序数之和等于42。
X元素原子的4p轨道上有3个未成对电子,Y元素原子的最外层2p轨道上有2个未成对电子。
X与Y可形成化合物X Y,Z元素可形成负一价离子。
下列说法正确23的是( )A.X元素基态原子的电子排布式为23[Ar]4s4pB.X元素是第四周期第ⅤA族元素C.Y元素原子的轨道表示式为D.Z元素的单质2Z在氧气中不能燃烧2.“各能级最多能容纳的电子数是该能级原子轨道数的2倍”,支撑这一结论的理论是( )A.构造原理B.泡利原理C.洪特规则D.能量最低原理3.现在含有元素硒(Se)的保健品已经进入市场,已知硒与氧元素同族,与钾元素同周期。
下列关于硒的说法不正确的是( )A. Se的第一电离能比F大B.最高价氧化物对应水化物的化学式为H SeO24C.Br的电负性比Se大D.O和Se为p区元素,K为s区元素4.已知X、Y元素同周期,且电负性:X>Y,下列说法错误的是( )A.第一电离能:Y一定小于XB.气态氢化物的热稳定性:H Ym 小于H XnC.最高价氧化物对应水化物的酸性:X的强于Y的D.X和Y形成化合物时,X显负价,Y显正价5.下列关于元素原子核外电子排布的说法正确的是()A.Cr的价层电子排布式:423d4sB.基态氮原子的电子排布图是C.+Cu基态电子排布式为22626101s2s2p3s3p3dD.np电子的能量比(n-1)d电子的能量高,ns电子的能量不一定高于(n-1)p电子的能量6.在核电荷数为26的元素Fe的原子核外的3d、4s轨道内,下列电子排布图正确的是( )A. B.C. D.7.下列状态的镁中,电离最外层的一个电子所需能量最大的是( )A. B.C. D.8.下列关于物质结构与性质的说法,不正确的是( )A.36I AsF 晶体中存在3I +,3I +的几何构型为V 形B.C 、H 、O 三种元素的电负性由小到大的顺序为H<C<OC.水分子间存在氢键,故2H O 的熔沸点及稳定性均大于2H SD.第四周期元素中,Ga 的第一电离能低于Zn9.《天工开物》记载:“凡火药以硝石、硫黄为主,草木灰为辅……而后火药成声。
原子结构与性质知识点归纳
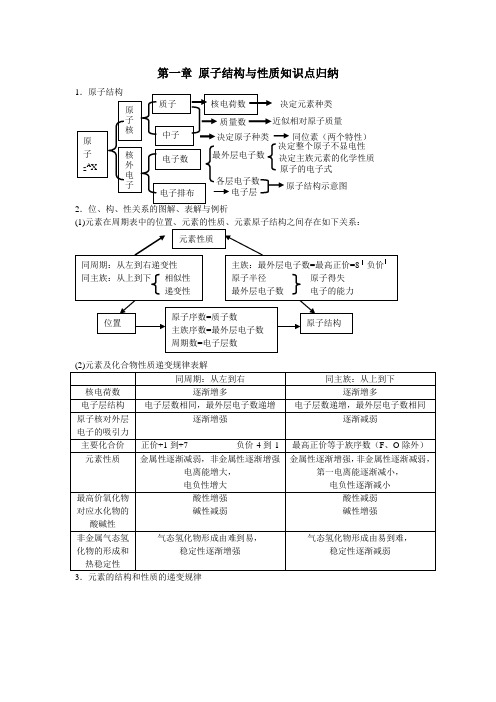
第一章 原子结构与性质知识点归纳2.位、构、性关系的图解、表解与例析3.元素的结构和性质的递变规律同位素(两个特性)4.核外电子构成原理(1)核外电子是分能层排布的,每个能层又分为不同的能级。
(2)核外电子排布遵循的三个原理:a .能量最低原理b .泡利原理c .洪特规则及洪特规则特例(3)原子核外电子排布表示式:a .原子结构简图 b .电子排布式 c .轨道表示式 5.原子核外电子运动状态的描述:电子云 6.确定元素性质的方法1.先推断元素在周期表中的位置。
2.一般说,族序数—2=本族非金属元素的种数(1 A 族 除外)。
3.若主族元素族序数为m ,周期数为n ,则: (1)m/n<1时为金属,m/n 值越小,金属性越强:(2)m/n>1时是非金属,m/n 越大,非金属性越强;(3)m/n=1时是两性元素。
随着原子序数递增① 原子结构呈周期性变化② 原子半径呈周期性变化③ 元素主要化合价呈周期性变化④ 元素的金属性与非金属形呈周期性变化⑤ 元素原子的第一电离能呈周期性变化⑥ 元素的电负性呈周期性变化元素周期律 排列原则① 按原子序数递增的顺序从左到右排列 ② 将电子层数相同的元素排成一个横行 ③ 把最外层电子数相同的元素(个别除外),排成一个纵行周期 (7个 横行) ① 短周期(第一、二、三周期)② 长周期(第四、五、六周期)③ 不完全周期(第七周期)性质递变 原子半径主要化合价元 素 周期表族(18 个纵行) ① 主族(第ⅠA 族—第ⅦA 族共七个) ② 副族(第ⅠB 族—第ⅦB 族共七个) ③ 第Ⅷ族(第8—10纵行) ④结构第二章 分子结构与性质复习1.微粒间的相互作用(2)共价键的知识结构2.分子构型与物质性质(1)微粒间的相互作用σ键π键 按成键电子云 的重叠方式极性键 非极性键一般共价键 配位键离子键 共价键 金属键 按成键原子的电子转移方式 化学键 范德华力氢键 分子间作用力本质:原子之间形成共用电子对(或电子云重叠) 特征:具有方向性和饱和性σ键特征 电子云呈轴对称(如s —s σ键、 s —p σ键、p —p σ键)π键 特征电子云分布的界面对通过键轴的一个平面对称(如p —p π键)成键方式共价单键—σ键共价双键—1个σ键、1个π键共价叁键—1个σ键、2个π键 规律 键能:键能越大,共价键越稳定键长:键长越短,共价键越稳定键角:描述分子空间结构的重要参数用于衡量共价键的稳定性 键参数 共 价 键定义:原子形成分子时,能量相近的轨道混合重新组合成一组新轨道sp 杂化 sp 2杂化sp 3杂化 分类 构型解释: 杂化理论sp 杂化:直线型sp 2杂化:平面三角形sp 3杂化:四面体型杂化轨道理论 价电子理论 实验测定 理论推测 构型判断 分 子 构 型共价键的极性 分子空间构型决定因素由非极性键结合而成的分子时非极性分子(O 3除外),由极性键组成的非对称型分子一般是极性分子,由极性键组成的完全对称型分子为非极性分子。
结构化学习题解答(第二章)

1(1 1) e 2 e
(c)设轨道角动量M和Z轴的夹角为θ,则:
h 0 Mz 2 0 cos h M 2 2
θ=900
(d) 电子离核的平均距离的表达式为:
r r d
* 2 pz 2 pz
2
2 2 pz
2
Li2+离子1s态的波函数为:
(a)
27 a e
1s 3 0
2 6 r a0 3 3 0 0
1 2
3 r a0
27 D 4r 4r e a
2 2 1s 1s 2 1s 3
108 re a
2
6 r a0
d 108 6 D 2r r e 0 dr a a 6 2 2r r 0 r a0 a0 r 又 r 0 3 a0 1s电子径向分布最大值在距核 处;
1 D1s / a0
r / a0
/ a
2 3 1s 0 1
1.60 2.00 2.30 2.50 3.00
3.50
4.00 4.50 5.00 — —
0.04 0.02 0.01 0.007 0.003 0.001< 0.001
1 D1s / a0
0.42 0.29 0.21 0.17
r r sin drdd
2
0
0
0
(e)
令
2 pz
0 r 0 , r , 90 , 得: 0
节面或节点通常不包括 r 0和r , 故 2 pz 的节 面只有一个,即x,y平面(当然,坐标原点也包含在xy 平面内)。亦可直接令函数的角度部分.
2014级大学化学 原子结构及元素性质的周期性(II)

氮原子中的各p电子,其量子数组合是
B. ⑴ ⑶ ⑸ 或⑵ ⑷ ⑹
D. ⑵ ⑷ ⑸
自测题:
原子序数为33的元素,其原子在 n=4,l=1,
m=0的轨道中的电子数为
A. 1 B. 2 D. 4 C. 3
自测题:
多电子原子中,各电子有以下量子数,其中能
量最高的是
A. 2, 1, 0, 1/2 C. 2, 1, 1, 1/2
B. 3, 2, 2, -1/2 D. 3, 1, -1, 1/2
特例:等价轨道处于全充满(p6、d10、f14)、半
充满(p3、d5、f7)或全空(p0、d0、f0)的状 态时,体系能量较低,状态较稳定。 例:
电子填入轨道的次序图
Filling the p Orbitals
Filling the d Orbitals
例:氦原子的1s 轨道中的两个电子
1 n 1, l 0, m 0, m s 2 1 n 1, l 0, m 0, m s 2
电子层中电子最大容量表
⑶ Hund 规则
电子分布到能量相同的等价轨道时, 总是尽先以自旋相同的方向,单独占据能 量相同的轨道,或者说成在等价轨道中自 旋相同的单电子越多,体系就越稳定。 等价轨道:n、l 相同的轨道,即同 一电子分层上的各个轨道。
4. 钻穿效应 主要是指 n 相同、l 不同的轨道,由于电子云径向 分布不同,电子穿过内层钻穿到核附近回避其它 电子屏蔽的能力不同,从而使其能量不同的现象。
用钻穿效应解释能级分裂现象:
如: E3s< E3p < E3d
电子钻得越深, 它受其它电子的 屏蔽作用就越小, 受核的吸引力越 强,因而能量也 越低。即钻穿作 用越大的电子的 能量越低。
结构化学课后答案第2章习题原子的结构与性质

1.简要说明原子轨道量子数及它们的取值范围解:原子轨道有主量子数 n ,角量子数|,磁量子数m 与自旋量子数s ,对类氢原子(单电子原子)来2说,原子轨道能级只与主量子数n 相关E Z R 。
对多电子原子,能级除了与n 相关,还要考虑电子n间相互作用。
角量子数|决定轨道角动量大小,磁量子数 m 表示角动量在磁场方向(z 方向)分量的大小,自旋量子数s 则表示轨道自旋角动量大小。
1n 取值为 1、2、3••…;| = 0、1、2、••…、n - 1; m = 0、±1 ±2 ……±l 取值只有一。
22.在直角坐标系下,Li 2+的Schr?dinger 方程为 ______________________ 。
解:由于Li 2+属于单电子原子,在采取 “-O'近似假定后,体系的动能只包括电子的动能,则体系的动量z 分量的平均值为多少(2)由于 |M I "J l(l1), l 1=1, l 2=1, l 3=1,又,210 ,211和 31 1 都是归一化的,2 h 2 h C 2 ■ l2 l 2 1 ——C3 ■ l3 l 3 1 o 2 2 2 ------------ h 2 ------------ hc 2 11 1 ——c 3 11 1 ——2 2 2h 222故C i 2 M iC 2 M1c ; M 2 C 3 M 3 能算符:T?h 2 8 2m2;体系的势能算符:\?Ze 2 3e 2 故Li 2+的 Schr?dinger 方程为:h 22式中:22 ____x 2y 23.对氢原子,C 1210的。
那么波函数所描述状态的(4 0r3e 22r = ( x 2+ y 2+ z 2F 2z 2C 2211C 331 能量平均值为多少( 1,其中4 0r211和 31 1都是归一化2)角动量出现在 ..2h 2的概率是多少,角动解:由波函数C 1210C 2211C 3 31 1 得:n 1=2, h=1,m 1=0; n 2=2, b=1,m 2=1;出=3,l 3=1,m 3=-1;(1)由于2210, 211 和 31 1都是归一化的,且单电子原子E 13.6―(eV )故E■i C 1 E12 2 C 2 E2C 3 E32 C 11 2 113.6 =eV 22 cf 13.6 peV22113.6 ?eV13.6 2 4 C1c ; eV 13.99c j eV 2 ---------------- hC 1 ■. l1 l 1 12c : J1 1 1 — 2则角动量为、、2h2出现的概率为: 1h,m1=0,m2=1,m3=-1;又210, 211和311都是归一化的,故M z' CMih2c|m22 c 2 * 2G 0 C2 1 C32 h°3 m3h1 -22 2C2 C34.已知类氢离子He+的某一状态波函数为:321 222re-2r2a。
大学《结构化学-原子的结构和性质》课件

对于每一个n值均有相应径向波函数
2Z 3 (n l 1)! 12 2 l 2l 1 Rn ,l ( ) [( ) ] e Ln l ( ) 3 n 0 2n[(n 1)!]
2Zr , n 0
2l 1 n 1 d d 2 l 1 n l Ln l e e 2l 1 n l d d
2 2 2 2 2 2 0
1 1 1 [ (sin ) ] ( , ) k ( , ) sin sin
2 2 2
——勒让德方程
将 Y ( , ) ( ).( ) 代入,整理得:
Sin 2 2 Sin k Sin m
3 2
Zr Z2 r 2 27 18 2 2 0 0 Zr e
m 1 im 1 i e cos m sin m 2 2 2
它们的线性组合也是方程的解,由此得到方程的实函数解:
2C C ( m m ) cos m 2 i2D sin m D ( m m ) sin m 2
2s 2p
Z 0 Z 0
Zr Zr 2 e 0 Zr e
20
20
3 2
Zr 0
3s 3p
Z 2 R 3 , 0 r 81 3 0 Z 4 R 3 ,1 r 81 6 0 4 R 3 , 2 r 81 30
Θ(θ) 方程的解:
2 1 d m 由原方程得: (sin ) k 0 2 sin d sin
第二章 原子的结构和性质习题课

第二章习题课主要概念:1、核固定近似(B-O近似)2、中心力场模型3、量子数的物理意义4、屏蔽效应,钻透效应5、原子轨道及电子云的径向分布和角度分布6、自旋量子数和原子的完全态函数7、原子核外电子排布5、态函数的角度分布和电子云的角度分布态函数的角度分布节面数为l电子云的角度分布形状与原子轨道角度分布相似,但没有正负之分原子轨道轮廓图(各类轨道标度不同)7、屏蔽效应8、电子自旋与保里原理自旋量子数:电子运动除了由n 、l 、m 三个量子数确定的轨道运动外,还有另外的且与轨道运动无关的自旋运动,由自旋量子数m s 决定。
m s 只能取±1/2两个数值原子的完全态态函数应是轨道态函数和自旋态函数的乘积:ii jσ=Σσs sn.l.m.m n.l.m m Ψ=Ψη9、原子核外电子排布(1)能量最低原理(2)保里原理(3)洪特规则二、填空题1、在氢原子及类氢原子体系中E 电子决定于。
2、氢原子的E 2简并态为、、、。
3、写出类氢原子的哈密顿算符。
4、4dxy 原子轨道角动量为,径向分布函数节面数为,角度分布节面数为,总节面数为。
5、在n=3、l=1原子轨道中,m 的取值有种,分别为。
6、对于类氢原子,与轨道角动量不同,能量相同的轨道还有;能量与角动量都相同的轨道有;7、的径向分布函数图为;有个峰,个节面;主峰位于离核较的范围。
8、径向分布函数D(r)= ;它表示。
9、n=3,l=2,m=0表示的原子轨道是。
10、n=4 的原子轨道数目为;最多可容纳的电子数为。
11、n=5 时其最大的轨道角动量M 为。
12、写出C 原子的哈密顿算符。
2.1.0Ψ3s Ψ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
I1 EHe EHe 54.4 (78.608 ) 24.208 (eV )
I2 EHe2 EHe 0 54.4 54.4(eV )
C 自洽场模型
与中心力场模型相似,认为电子i受到所有其
他电子的排斥的位能可近似看作是半径ri的函数
U (r ): i
N i 1
Ze2
4 0ri
1 2
i j
e2
4 0rij
i
ri rij
+Ze
j
rj
动能
吸引能
排斥能
若采用原子单位:ħ=1au, m=1au, e=1au, 4πε0=1au,则
Hˆ
1 2
N i1
i2
N i 1
Z ri
1 2
i j
1 rij
或 :
程所得能量公式为:
Ei
13.6 ( Z
i
n2
)2
13.6
Z *2 n2
( ev )
可见,多电子原子的状态能量不仅决定于主量子数n,
还决定于屏蔽常数σi,σi的大小与什么因素有关呢?电
子 i的屏蔽常数σi为原子中其他所有电子对它屏蔽作用 之总和,故可写成:
σi=∑σji σji ——电子j对电子i的屏蔽常数
Hˆ
1 2
N i 1
i2
N i 1
Z ri
N i 1
i j
1 rij
每个电子都在不停地高速运动,电子间存在着复杂 的瞬时相互作用,rij和电子i与电子j的瞬间坐标有关。 因此无法将e2/rij项严格进行变量分离,使之成为分别 与电子i的坐标以及j的坐标有关的两个部分。所以必 须采用近似处理的方法来解决求解薛定鄂方程。为此, 设计了一些近似模型来加以修正和改进。
• 例:计算He的第一、第二电离能。
解: He(g) →He+(g)+e
σ1s=0.3 ,
E1s
-13.6
(2 - 0.3) 2 12
39.304 (eV )
EHe=2E1s=2(-39.304)=-78.608(eV)
Z2
22
EHe 13.6 n2 -13.6 12 54.4( ev )
x, y, z, 称为自旋-轨道, 称为自旋波函数。
那么,如何求电子的自旋波函数呢?采用与轨道运动类 比的方法。
对轨道运动和自旋运动进行类比
轨道运动
自旋运动
Mˆ 2 12
Mˆ Z m
Mˆ s2 ss 12
Mˆ s,z ms
• 屏蔽效应指核外某个电子i受到核电荷的减 少,使能级升高的效应。
• 钻穿效应指电子i避开其余电子的屏蔽,其 电子云钻到近核区而感受到较大核电荷作 用,使能级降低的效应。
由屏蔽常数计算原子轨道能(Ei)
• C原子的基态电子组态为:1s22s22p2, 求1s、 2s、2p能。
解:●求1s能:
σ1s=0.3, Z*=6-0.3=5.7
1 2
N i1
i2
N i1
Z ri
N
Ui (ri )
i1
N i 1
1 2
i2
Z ri
Ui (ri )
N
Hˆ i i 1
多电子体系的单电子哈密顿算符为:Hˆ i
1 2
i2
Z ri
Ui
(ri
)
与单电子体系的哈密顿算符相比: Hˆ 1 2 Z
• 电离能:气态原子失去一个电子成为气态离子所需的 最低能量。
气态中性原子A失去一个电子成为气态+1价离子 (A+)所需的最低能量称为第一电离能;由气态 (A+)失去一个电子成为气态正二离子(A2+)所需 的最低能量称为第二电离能。
原子轨道能和电子结合能
• 原子轨道能是指和单电子波函数相应的能量Ei。
可用光谱等实验测定。
• 电子结合能是指在中性原子中当其他电子均 处在可能的最低能态时,某电子从指定的轨 道上电离时所需能量的负值,又称为原子轨 道能级。
• 电子结合能与原子轨道能互有联系:对单电 子原子两者数值相同;对最外层为单电子的 也相同;其他情况下就不相同了。说明电子 间存在互斥作用。
• 电子间的相互作用可从屏蔽效应和钻穿效 应两方面认识。
ll 1e
自旋磁矩和轨道磁矩作用,相当于一个小磁铁置于外 磁场中,会引起能级分裂。这说明在没有外磁场时, 能级分裂的原因和发生能级分裂的状态是角动量不 为零的状态(非s态)。
斯特恩(O.Stern)— 盖拉斯(W.Gerlach)实验
• 将碱金属原子束通过一个不均匀磁场后射到一个屏幕 上,射线束分裂并向两个方向偏转,说明碱金属原子 束有磁矩。碱金属原子在s轨道只有一个电子,它的 轨道磁矩为零,故碱金属的磁矩只能由电子自旋产生。 于是证实自旋磁矩的存在。而原子束只向两个方向偏 转,说明自旋磁矩在磁场中只有两个分量,这与氢光 谱、钠光谱的双线结构相一致。证实了自旋假设与实 验一致。
理称为单电子近似。常用中心力场方法和自洽场方法。
B 中心力场模型
• 把其他所有电子对电子i的平均作用看作是由 原子中心(即原子核位置)发出的球对称电 子云的作用。则电子i受到所有其他电子的排 斥 的 位 能 就 可 近 似 看 作 是 半 径 ri 的 函 数 Ui (ri)。
得到:
Hˆ
i
Hˆ
1 2
N i1
i2
N i1
Z ri
N
Ui (ri )
i1
N
Hˆ i
i 1
单电子哈密顿算符则为:Hˆ i
1 2
i2
Z ri
Ui (ri )
与中心力场不同的是,估算Ui(ri)的方法不同。
自洽场模型认为:其它电子对 i 电子的排斥是
这些电子的“电子云”的静电势的作用。
• 对氢原子光谱:
2p
2p
1s (a)
1s (b)
轨道能级由n和l决定(在外磁场中则还与m有关), 那么,当n和l确定后,能级也就确定,因此,能级的 分裂并不是电子的轨道运动引起的。即电子除了轨道 运动外,一定还有其他运动。究竟是什么运动?
1925年,乌仑贝克—哥希密特提出了电子自旋运动的 假设,即电子具有不依赖轨道运动的固有磁矩和固有 角动量。这可解释光谱精细结构:既然电子自旋有自 旋磁矩,当电子轨道运动角动量不为零(如p,d态) 时,轨道磁矩也不为零。
电子自旋
• 电子自旋问题的提出 • 斯特恩—盖拉斯实验 • 自旋波函数和自旋—轨道(自旋量子数) • 全同粒子和保里不相容原理
电子自旋问题的提出
• H原子由1s向2p跃迁,看到的不是一条而是两条靠 得很近的谱线。
• Na原子由3p向3s跃迁,看到的也是两条靠的很近的 谱线。
• 既然发生了谱线的分裂,那一定是始态或终态能级 发生了分裂。因此有必要探讨:是什么原因引起能 级分裂?是哪个状态(s态或p态)能级发生分裂?
2r
N
Hˆ 0 Hˆ i
Hˆ i类似于单电子哈密顿算符
i 1
所以,Schrodinger方程为:
令Ψ= ψ1 ψ2 … ψn
N i 1
(
1 2
i2
Z ri
)
E
则Schrodinger方程可分解为 n 个单电子Schrodinger方程:
Hˆ ii Eii
A 电子独立运动模型(零级近似)
电子独立运动模型:假定电子间相互作用为零。
则哈密顿算符为:
1
i2
N i1
Z ri
N i 1
(
1 2
2 i
Z ri
)
N i 1
Hˆ i
单电子:
^
H
2
2
Ze2
2m
4 0r
1 2 Z
i
ri
σi :电子i的屏蔽常数
Hˆ i
1 2
i2
Z ri
i
ri
1 2
i2
Z
i
ri
Z*=Z-σi:有效核电荷
代入单电子的Schrodinger方程: Hˆ ii Eii
得:
(
1 2
i2
Z* ri
) i
Ei i
与单电子体系薛定格方程比较,差别在于以Z-σi=Z*代 替了Z,即以有效核电荷代替原来的核电荷。解此方
σi既与电子i本身所处状态(由n,l决定)有关,也和其
他电子的数目和状态有关。因此,能量Ei不单取决于主 量子数 n ,也取决于角量子数 l 。 σi值由光谱实验数据得到。Slater提出估算屏蔽常数的 方法:
▲由内到外分组:1s|2s,2p|3s,3p|3d|4s,4p|4d|4f|5s,5p|… ▲外层电子对内层电子屏蔽作用较小,σij=0 ; ▲同层电子之间为0.35(1s的σij= 0.30); ▲内层电子对外层电子屏蔽作用较大:
E1s -13.6
●求2s能:
5.70 12
2
442 (eV )
σ2s= 2*0.85+3*0.35=2.75, Z*=6-2.75=3.25
E 2s
-13.6
3.25 2 22
35.9(eV )
●求2p能(按Slater法,E2p=E2s)
