浙大控制考研-845试卷-10A
浙江大学研究生考研845自动控制原理考试大纲

浙江大学845自动控制原理考研考试大纲《自动控制原理》(科目代码845)考试大纲参考书目:(1)各出版社出版的各种自动控制原理教材及习题集(2)胡寿松主编. 自动控制原理(第四版、第五版). 分别于2001年2月、2007年6月由科学出版社的(该书初版于1979年,前三版均由国防工业出版社出版,前三版亦可作为参考书)特别提醒:本考试大纲仅适合报考2015年控制科学与工程学系、专业课考<自动控制原理>课程的考生。
该门课程的满分为150分。
一、总的要求全面掌握自动控制的基本概念与原理,深入理解与掌握自动控制系统分析、综合设计的基本方法,并能用这些基本的原理与方法去分析问题、解决问题。
二、基本要求(1)自动控制的一般概念:自动控制的基本原理与自动控制系统组成、分类,能将系统物理的结构图抽象表示成系统方块图,分析其中各种物理量、信息流间的关系。
(2)动态系统的数学模型:能建立给定典型系统的数学模型,包括微分方程模型、传递函数模型、状态空间模型等;能熟练地通过方块图简化与信号流图等获得系统总的传递函数;能根据需要进行各种数学模型之间的相互转换。
(3)线性时不变连续系统的时域分析:系统微分方程模型的求解,LAPLACE变换在时域分析中的应用,一阶、二阶及高阶系统的时域分析;状态空间模型的求解与分析;系统时间响应的性能指标及计算;系统的稳定性分析、稳态误差计算。
(4)根轨迹: 根轨迹法的基本概念;根轨迹绘制的基本法则及推广法则;利用根轨迹进行系统性能的分析。
(5)频率分析:系统的频率特性基本概念;开环系统的典型环节分解与开环频率特性曲线及其分析;频率域稳定判据以及稳定裕度分析。
(6)线性系统的超前及滞后校正:一般性了解线性系统的超前及滞后校正方法,理解并能简单的应用。
(7)线性时不变离散系统的分析与校正:离散系统的基本概念与Z变换;离散系统的数学模型;稳定性与稳态误差分析;离散系统的动态性能分析。
(8)线性系统的状态空间分析与综合:线性系统的能控性与能观测性;线性定常系统的线性变换与标准型;线性定常系统的状态反馈控制器与状态观测器。
浙江大学《839控制理论》历年考研真题专业课考试试题

2012年浙江大学控制理论考研真题(回忆 版)
2011年浙江大学839控制理论考研真题
2010年浙江大学839控制理论考研真题
2009年浙江大学839控制理论考研真题
2008年浙江大学839控制理论考研真题
2007年浙江大学436控制理论考研真题
2006年浙江大学436控制理论考研真题
2005年浙江大学436控制理论考研真题
2004年浙江大学436控制理论考研真题
2003年浙江大学440控制理论考研真题
目 录
2012年浙江大学控制理论考研真题(回忆版) 2011年浙江大学839控制理论考研真题 2010年浙江大学839控制理论考研真题 2009年浙江大学839控制理论考研真题 2008年浙江大学839控制理论考研真题 2007年浙江大学436控制理论考研真题 2006年浙江大学436控制理论考研真题 2005年浙江大学436控制理论考研真题 2004年浙江大学436控制理论考研真题 2003年浙江大学440控制理论考研真题
浙大控制845自动控制原理大纲

《自动控制原理》参考书与考试大纲2014-06-26一:参考书目:《自动控制原理》,厉玉鸣等主编,化学工业出版社,2009年《自动控制原理》,孙优贤,王慧主编,化学工业出版社,2011年《自动控制原理》,胡寿松主编,科学出版社,2007年二:考试大纲1、控制系统的基本组成和数学模型掌握:控制系统的组成;控制系统的主要类型;线性连续时间系统的概念,微分方程模型,传递函数模型;方块图及其等效变换;信号流图;方块图化简;Mason增益公式;2、控制系统的时域分析方法掌握:典型输入信号;一阶、二阶系统的动态响应;控制系统动态响应的质量指标;控制系统的劳斯稳定判据;给定和扰动稳态误差分析;了解:高阶系统的响应及主导极点;PID控制方法对系统控制质量的影响;4、频率特性分析法掌握:系统频率特性的定义;典型环节的频率响应;系统频率特性的极坐标图;对数坐标图;非最小相位系统;Nyquist稳定性判据;控制系统的稳定裕度;基于开环频率响应的控制系统频率特性分析;了解:频率特性设计方法;5、根轨迹分析方法掌握:根轨迹的基本概念;绘制根轨迹的基本条件和规则;控制系统的根轨迹分析;广义根轨迹;了解:基于根轨迹方法的控制系统设计;6、采样控制系统掌握:采样过程及采样定理;零阶保持器;Z变换;采样系统的脉冲传递函数;连续模型的离散化;采样系统的数学模型及求解;采样系统的稳定性与稳态偏差分析;了解:数字PID控制器;最小拍采样控制系统的设计;7、状态空间方法掌握:系统状态空间描述,及其与传递函数之间的相互转化;状态转移矩阵的求取及性质,状态运动分析(状态方程的解);能控性、能观性的定义与判别;单入单出系统的能控、能观标准型;按能控性或能观性结构分解;状态反馈设计与极点配置;全维状态观测器设计;带状态观测器的状态反馈;了解:最小阶状态观测器设计;规范分解(同时按能控与能观进行分解);8、非线性系统分析掌握:典型非线性环节;描述函数分析法,及自激振荡(极限环)的参数求取与稳定性分析;相平面分析法;Laypunov稳定性基本定义和基本理论;了解:典型非线性环节的描述函数计算;线性系统的Lyapunov稳定性分析;。
浙江大学04年自动控制原理考研题及答案

则沿任一轨迹,V(x)对时间的导数
是负定的,这说明V(x)沿任一轨迹连续地减小,因此,V(x)是一个李亚普诺夫函数。根据李亚普诺夫稳定性定理,该系统渐近稳定。
又由于V(x)随x偏离平衡状态趋于无穷而变为无穷,即当 时,
故系统是大范围一致渐近稳定的。
十三、(10分/150分)已知系统的状态空间表达式: , ,试设计观测器,使其极点为: -1.8+j2.4,-1.8-j2.4。
S10.25-0.25
S00.25
六.(10分/150分)某系统的单位阶跃响应为 ,试求系统的频率特性。
解:
因为: ;所以:
系统的频率特性为
七.(5分/150分)某系统的传递函数是 ,问:若要求系统为完全能控能观,应如何选择b?
解:对于单变量系统,系统的完全能控能观意味着不存在传递函数的零极点相消
因为
解:(1)设系统开环特征多项式为
(2)因为经状态反馈后闭环系统的特征多项式为
(3)而期望的闭环特征多项式为:
(4)上两式应该相等,故易知:
(5)原系统的能控标准形: ,
十二、(10分/150分)--该题为二选一题,另一题是关于观测器的。研究由方程
描述的系统的稳定性。
解:命 ,可求得系统的平衡状态为原点,即
解:(1)判别可观性: ;系统可观
(2)观测器期望方程:
状态观测器的闭环特征多项式:
上两式应当相等,所以 ;即观测器:L=[29.63.6]
图4
解:
由终值定理:
五.(20分/150分)系统如图5所示,绘制以 为可变参数的根轨迹,并指出系统稳定条件下的 值取值范围,以及系统阶跃响应无超调时 的取值范围
图5
控制科学与工程考研试题

控制科学与工程考研试题一、试卷整体说明这是一份控制科学与工程考研试题试卷,满分100分哦。
试卷最后一页会附上答案和解析,这样大家做完题就能马上对答案,清楚自己的问题在哪啦。
二、题型分布与分值1. 选择题(30分)选择题可是很考验大家基础知识的掌握程度呢。
比如说会有关于控制理论基础概念的题目,像经典控制理论里的反馈控制原理相关的选项,这部分占10分。
还有现代控制理论中的状态空间表达式相关的选择题,这也占10分。
另外10分就是关于控制系统的性能指标相关的内容啦,像稳态误差、超调量这些概念在选项里出现,让大家去判断对错。
2. 填空题(20分)填空题就需要大家把知识掌握得很扎实啦。
可能会让你填一些控制算法的关键参数,例如PID控制算法里比例系数、积分时间常数、微分时间常数的作用或者计算式之类的内容,这部分占8分。
还有像线性系统的传递函数的一些关键要素填空,这占6分。
再有就是控制系统的稳定性判据相关的填空,占6分。
3. 简答题(30分)简答题呢,就是要大家能把知识点有条理地写出来。
比如让你简述控制系统的设计步骤,这大概占10分。
还有可能让你解释一下自适应控制的原理和应用场景,这也占10分。
另外,像鲁棒控制的概念和它在实际工程中的重要性,这部分简答题占10分。
4. 计算题(20分)计算题就有点考验大家的计算能力和对知识的运用能力啦。
可能会出一道关于控制系统的传递函数化简并且求系统响应的题目,这占10分。
还有可能是根据给定的状态空间方程求系统的特征值之类的计算,这占10分。
三、答案与解析1. 选择题答案与解析关于经典控制理论反馈控制原理那题,如果选对了,那是因为你知道反馈控制就是通过测量输出量,然后与给定值比较,再利用偏差进行控制的基本原理。
如果选错了,那可能是对反馈控制中偏差的作用理解不到位哦。
现代控制理论状态空间表达式那题,答案是根据状态变量的定义和状态方程的构建规则来的。
要是做错了,可能是在状态变量的选取或者状态方程的矩阵运算上出了问题。
浙江大学控制科学与工程系自控原理05-95考研初试题(一)-数学模型
浙江大学控制系自动控制原理近年考研题分章集锦(一)(第一、二章: 基本概念及数学模型――连续部分)浙江大学二〇〇五年攻读硕士学位研究生入学考试试题考试科目编号注意:答案必须写在答题纸上,写在试卷或草稿纸上均无效。
2005年1.(10分)电冰箱制冷系统原理见图1。
继电器的输出电压u R 为压缩机上的工作电压。
绘制控制系统框图,简述工作原理。
若出现压缩机频繁起动,请提出相应的改进措施。
答:系统框图:当冰箱温度u2高于设定值,放大器输出Δu ,继电器动作输出u R 。
压缩机运行,从蒸发器吸入低温低压气体。
输出高温高压气态制冷剂至冷凝器;冷凝器送出高压常温液态制冷剂至蒸发器,制冷剂在蒸发器内气化,吸收制冷。
改进措施:调小放大器放大倍数,或选用灵敏度较小的继电器,或者两者兼而用之。
2.(10分)系统框图见图2-1,要求将系统等效变换成图2-2,图2-3框图结构,并求H(S),G(S)表达式。
图2-1 图2-2 图2-3 解:H(S)= 1+2() KG SG(S) =2004年一.(20分/150分)如图1所示,U1(t),U2(t)分别是输入电压和输出电压。
X3,X2分别是输入位移和输出位移,X1则是C点位移。
f1, f2是粘滞阻尼系数,k1, k2是弹性系数。
求两系统的传递函数,并分析两系统变量间的相似关系。
图 1解:1)(1)(1111)()(212211221212211221212211112212+++++++=++++=S C R C R C R S C C R R S C R C R S C C R R S C R SC R S C R SC R s U s U 1)111(11)11(1)()(2122112212122112212132+++++++=S K f K f K f S K K f f S K f K f S K K f f S X S X两相似系统变量间对应关系:电压U---------------------------位移X电阻R---------------------------粘滞阻尼系数f 电容C---------------------------弹性系数的倒数K1二.(10分/150分)用方块图化简法,求图2所示系统的闭环传递函数图 2解:321341431131213213414311311)()(G G G G G G G G G G G G G G G G G G G G G G G G G G S R S Y +++--+++++--=∴2003年1.(10分/150分)求理想运算放大器的传递函数)()(s Ui s Uo ,结构图如下:解:理想运放∞→λZ ,流入运放电流0,0→→B U i)()()()()()()()()()(:)(0)()()()()()()()()()()()()()(414243324232142321s Z s Z s Z s Z s Z s Z s Z s Z s U s U s U U s Z s U s Z s U s U s Z s U s U s Z s U s U s Z s U s U i i i i i i O F B F F B O F F B B i ++==⎪⎪⎩⎪⎪⎨⎧--=--=-+=-=∴得消去即:2003年第1题示意图2.(10分/150分)求右图的传递函数)()()(s U s y s G =解:)()()(1)()()()()(1)(1)()()(1)()(21121221122*12s G s G s G s G s G s G s G s G s G s G s G s G s G s G +--=-+=+=∴2002年 1.(10分/100分)R-L-C 网络如图所示,信号源内阻为零,U r (t)为输入变量,U 0(t)为输入变量,试求电网络的状态变量表达式。
浙江大学控制理论2003-2009真题答案
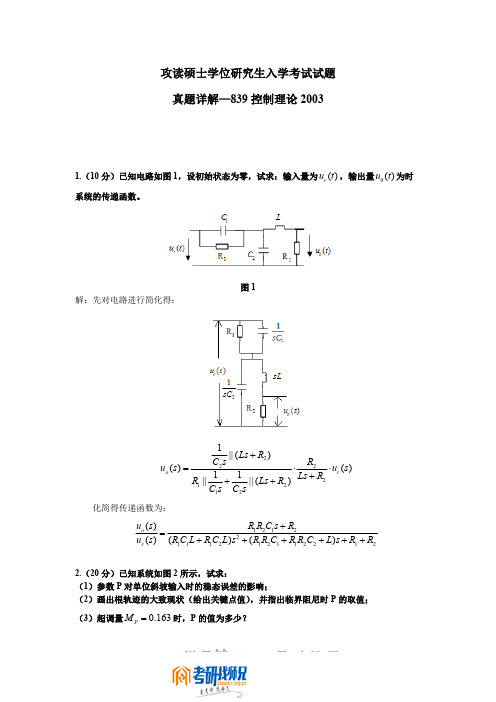
1.(10 分)已知电路如图 1,设初始状态为零,试求:输入量为 ur (t ) ,输出量 u0 (t ) 为时 系统的传递函数。
图1 解:先对电路进行简化得:
1 || ( Ls R2 ) C2 s R2 uo ( s ) ur ( s ) 1 1 Ls R 2 R1 || || ( Ls R2 ) C1s C2 s
(2)相轨迹为
(3)由相轨迹图可知,系统的稳态误差为零。
7.(15 分)有系统 平衡状态及其稳定性。
& x 1 kx2 (k 为大于 0 的常数) ,应用 Lyapunov 第二法分析系统的 & x 2 x1
& 0 xe 0 为系统的平衡状态。 解:由 x
0 k & x x 1 0
(2)系统特征方程为 z 4.95 z 0.368 0 ,
2
令z
r 1 ,上式化简后,得 r 1
6.32r 2 1.264r 3.584 0
劳斯表中第一列有一次符号变化,所以有一根位于右半平面,即对应有一个根位于平面 单位圆之外,系统不稳定。 6.(15 分)已知带有库仑摩擦的随动系统如图 5 所示,设输入信号为零,初始条件为:
& & Qe
& de &de & de de & e dt de dt de
& de & 2e 1 0, e & 0 e de & de & 2e 1 0, e & 0 e amp; 0 (e ) 2 c, e 2 2 2 & e 1 & 0 (e ) 2 c, e 2 2
考研控制工程试题真题及答案

考研控制工程试题真题及答案# 考研控制工程试题真题及答案## 一、选择题1. 题目:在控制系统中,开环传递函数为\[ G(s) =\frac{10}{s(s+10)} \],问该系统是否稳定?答案:是。
因为开环传递函数的极点s=0和s=-10都位于左半平面。
2. 题目:状态空间表示法中,状态变量的选取具有什么性质?答案:状态变量的选取具有任意性,但一般选择能反映系统动态特性的变量。
3. 题目:PID控制器中的I代表什么?答案:I代表积分(Integral),用于消除系统的稳态误差。
4. 题目:在控制系统设计中,Bode图的主要用途是什么?答案:Bode图主要用于分析系统的频率响应特性,帮助设计系统以满足性能要求。
5. 题目:线性时不变系统(LTI)的数学模型是什么?答案:线性时不变系统(LTI)的数学模型通常为线性微分方程或差分方程。
## 二、简答题1. 题目:简述控制系统的稳定性条件。
答案:控制系统的稳定性条件主要取决于系统开环传递函数的极点位置。
如果所有极点都位于复平面的左半部分,则系统是稳定的。
2. 题目:什么是根轨迹法?答案:根轨迹法是一种控制系统设计方法,通过分析系统开环传递函数的极点随参数变化的轨迹,来设计闭环系统的性能。
3. 题目:控制系统的频率响应特性有哪些?答案:控制系统的频率响应特性包括幅频特性和相频特性,它们描述了系统对不同频率信号的响应能力。
## 三、计算题1. 题目:给定一个二阶系统,其开环传递函数为\[ G(s) =\frac{\omega_n^2}{s^2 + 2\zeta\omega_ns + \omega_n^2} \],其中\[ \omega_n = 10 \] rad/s,\[ \zeta = 0.5 \]。
求系统的单位阶跃响应。
答案:首先确定系统的自然频率\[ \omega_n \]和阻尼比\[ \zeta \]。
然后使用二阶系统的时间响应公式计算单位阶跃响应的表达式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010 年硕士研究生试题答案
1、(10 分)系统的微分方程模型如下:
e(t) = k1[r(t)− y(t)]; &x&(t) = Td2e&&(t) + Td1e&(t) + e(t); y&(t) = k2[n(t) + x(t)]
式中, r 、 n 、 y 分别是输入、干扰和输出, k1 、 k2 、Td1 、Td 2 为常数,试建立系统方框
当 T2
=
T1
时,
Re[G
(
jω
)]
=
1
− 10 + ω 2T12
,
Im[G( jω)]=
0
当T2 > T1 时, Re[G( jω)]< 0, Im[G( jω)]< 0
7、 (15 分)列写如图 7 所示系统的状态空间表达式,并判断该系统是否能控?是否能观? 解:1. 列写状态方程
⎡− 8 x& = ⎢⎢10
k p = [- 49.5 - 392 - 5]
3.系统稳定性: 系统开环不稳定。但状态反馈后的闭环系统是稳定的。
4、状态观测器的设计
系统的不能观,故不能设计状态观测器。
11、(5 分)请用李亚普诺夫方法研究如下系统。给出系统在平衡点稳定时参数 a 需满足的 条件。
x&1 = −x2 + ax13
x&2 = x1 + ax23
G(s)
=
( G1G6 G2G4
+
G3G5
G1G6
)(H 4 −
(G2G4 H3)+
+ G3G5 ) (1 + G1H1
)(1
+
G4 H 2
+
G5 H 2
)
( ) 3、 (10 分)已知二阶系统的单位阶跃响应为: y(t ) = 10 −12.5e−1.2t sin 1.6t + 53.1o
试求:系统的超调量σ % 、峰值时间 t p 和调节时间 ts 。
( ( )( ) ) ( )( ) =
− 10 × 1 + ω 2T1T2 1 + T12ω 2 1 + T22ω 2
+
j
10 ⋅ ω(T1 − T2 )
1 + T12ω 2 1 + T22ω 2
显然, ω = 0 时,G(0) = −10
ω = ∞ 时,G( j∞) = 0
当T2 < T1 时, Re[G( jω)]< 0, Im[G( jω)] > 0
图 8 某采样控制系统示意图
解:
C(z) = R(z) + G1(z)E(z) + F (z)z −1 = R(z) + G1(z)G2 R(z) − G1(z)H 2 H1R(z) + F (z)z −1 1+ H 2 H1G1(z)
该系统不存在 C(z)/R(z)。
9、(15 分)一采样控制系统结构见图 9,采样周期 T=1s, H(0 s)为零阶保持器。试确定使 系统稳定时的 K 值范围。注:图 9 中 D(k): e(2 k)= e(2 k − 1)+ 10[e(1 k)− 0.5e(1 k − 1)] 。
[ Gopen = c[sI − A]−1b = 1 0
⎡ s−3
⎢
0]⎢⎢
s2
−
2s *
−
5
⎢*
⎢⎣
0 * *
2⎤
s2
−
2s *
*
−
5 ⎥⎥⎥ ⎢⎢⎡02⎥⎥⎤ ⎥⎥⎦ ⎢⎣1⎥⎦
=
2(s − 2) s2 − 2s − 5
2、设计状态反馈控制器
因为系统是三阶的,选择主导极点满足期望的性能指标,另选择第三个远极点。
y = [1 0 0]x
要求:1)推导该系统的开环传递函数 Gopen; 2)设计状态反馈控制器,使得闭环系统
满足阻尼比 ζ = 0.707 ,调节时间 ts = 2s(±2%) ;3)分别判断开环系统稳定性与闭环系
统稳定性;4)请对该系统设计状态观测器,使得状态观测器的闭环极点均为:s=-5。 解:1、推导系统的开环传递函数
解:1)可以求得系统的平衡点为原点,即: x1 = 0; x2 = 0 。
2)计算李亚普诺夫函数
令: V (x) = x12 + x22 ,显然V (x) > 0 计算:V& (x) = 2x1 x&1 + 2x2 x&2 = 2a(x14 + x24 ) 3)讨论V& (x) 的负定性 由V& (x) 的表达式,显然,当 a < 0 时,V& (x) < 0 ;所以V (x) 是李亚普诺夫函数。 由V (x) > 0 和V& (x) < 0 ,可以判定原点是渐近稳定性。又当 x → ∞ ,V (x) → ∞ ,
R(s)
e(1 k)
e(2 k)
D(k)
T
T
H(0 s)
K s +1
Y(s)
图 9 采样控制系统示意图
解:在 0< K <0.289 范围内,系统是稳定的。 10、(25 分)设一被控对象由以下状态空间代表式描述
⎡−1 0 2⎤ ⎡2⎤
x&
=
⎢ ⎢
0
− 2 1⎥⎥x + ⎢⎢0⎥⎥u
⎢⎣ 1 0 3⎥⎦ ⎢⎣1⎥⎦
结构图。 解:
N (s )
R(s)
−
E(s)
K1
Td2S 2 + Td1S +1 X (s)
S2
K2
1 Y (s)
S
2、
(15
分)系统结构如图
2
所示,试用方框图等效变换法求传递函数 G(s)
=
Y (s) R(s)
H3
R(s)
E(s)
−−
G1
H1
G2
− G4
H2
G3
− G5
G6
Y (s)
H4
图2 解:
⎢⎣ 0
−5 8 1
0 ⎤⎡ x1 ⎤ ⎡ 1
−
1⎥⎥
⎢ ⎢x2⎥Fra bibliotek⎥+
⎢⎢−
2
0 ⎥⎦⎢⎣x3 ⎥⎦ ⎢⎣ 0
0⎤
1⎥⎥ 0⎥⎦
⎡u1 ⎢⎣u2
⎤ ⎥ ⎦
⎡ ⎢ ⎣
y1 y2
⎤ ⎥ ⎦
=
⎡5 ⎢⎣− 10
5 − 10
0⎤ 1⎥⎦
⎡ ⎢ ⎢ ⎢⎣
x1 x2 x3
⎤ ⎥ ⎥ ⎥⎦
+
⎡0 ⎢⎣2
0⎤⎡u1 ⎤
( ) ( ) 【提示:15e−1.2t sin 1.6t + 53.1o − 20e−1.2t cos 1.6t + 53.1o = 25e−1.2t sin1.6t 】
解:
⎩⎨⎧ξω 0=
=2 0.6
− ξπ
σ % = e 1−ξ 2 = 9.5% ;
t p = ω0
π 1−ξ2
= 1.96 ; ts
1 + τS
图5
Gk (s) =
4τS S2 + 4
=
4τ
(S
+
S
j2)(S
−
j2)
6、(15
分)系统开环传递函数为 G(s) =
(T1S
10
+ 1)(T2S
− 1)
,试绘制 T2
<
T1 ,T2
=
T1 ,
T2 > T1 三种情况下的奈奎斯特图。
解: G(s )
=
(
jT1ω
+
10
1)( jT2ω
−
1)
0⎥⎦
⎢⎣u2
⎥ ⎦
u1
+
—
1
x1 +
y1 5
s+3
+
2. 判断系统是否能控、能观 能控矩阵:
故系统能控。 系统能观。
u2 +
2
1 x2 — s+2
1 x3 + y2 s+
8、(10 分)某采样系统如图 8 所示, 请给出 C(z)和 C(z)/R(z)表达式。
图 7 系统方块图
F(s) e-Ts
C(s)
由调节时间为 ts = 2s(±2%) ,ζ = 0.707 ,
故主导极点为: s1,2 = −2 ± j2 ;选择非主导极点: s3 = −100
期望的特征方程:
Δ* = (s + 2 + j2)(s + 2 − j2)(s + 100) = s3 + 104s2 + 408s + 800 = 0
=3 ξω0
= 2.5
4、(15
( ) 分)单位负反馈系统的开环传递函数为:G s =
K S2
(τS (TS
+ 1) + 1)
;K
>
0 、τ
>
0、
( ) ( ) T > 0 ,输入 r t = t 2 。试求系统稳态误差 ess ∞ < 0.1时,系统应满足的条件。
解: ess (∞) =
2 K
<
0.1, K
>
⎧τ 20 ;因此,系统参数应满足: ⎩⎨K
>T > 20
5、(15 分)系统结构如图 5 所示。使闭环极点为 S = −1 ± j 3 ,试确定 K 、τ 值,以计 算出的 K 值为基准,绘制以τ 为参变量的根轨迹。
