第1章-自然坐标系
合集下载
自然坐标系

t)
-
et
(t)
当: t 0 , 0
et
t
t
O Δ P2
s
et t
有 det et d d
P1
方向
det
et
d et d
d t dt
即en方向
en
et
t
t
et
et
t
4
d ds
at
dv dt
c
an
v2 R
(b ct)2 R
(2) at an
解得 t b R cc
12
§1-3 相对运动
一 时间与空间
在两个作相对运动的参考系中,时间 的测量是绝对的,空间的测量也是绝对的, 与参考系无关.
时间和长度的的绝对性是经典力学或 牛顿力学的基础.
13
二 相对运动
o
at
0.4
M at
a
x
11
例5 一质点沿半径为R的圆周运动,其路程s随时
间t 的变化规律为 s bt 1 ct 2,式中b,c为大于
零的常数,且 b2 Rc 。求(2 1)质点的切向加速
度和法向加速度。(2)经过多长时间,切向加速
度等于法向加速度。
解: (1)
v ds b ct dt
解: 按题意作矢量图
y
v v0 v
v v0 tan 60 10 tan 60m s1
17.3 m s1
y´ x´
v0
v
速度:
v
大学物理第一章

加速度与速度的夹角 为钝角
an
a
A
at
a
an
at A
加速度的方向:总是指向轨道曲线凹的一侧。
§1-2 圆周运动和一般曲线运动
用位置矢量、位移、速度、加速度等描述质点圆 周运动的方法,称为线量描述法;在圆周运动中,由 于质点与圆心的距离不变,常用角位置、角位移、角 速度、角加速度来描述,称为角量描述法。
选作参考的物体。
花草相对于地面是静止的。
行星相对于太阳或地球的运动是不同的。
花草相对于小车是运动的。
参考系和坐标系
4.坐标系
直角坐标系、极坐标系、球坐标系、圆柱坐标系等。
为了精确地、定量地描述物体的运动,我们在参考系上建立一个坐标系,用物体所在位 置的坐标表示物体的位置,用坐标的变化来描述物体位置的变化(即表示物体的运动)。
x
dx dt
y
dy dt
z
dz dt
大小
2 x
2 y
2 z
速度
4.速率(标量)
t0时,平均速率的极限。
lim lim S
t 0
t0 t
dS
dt ds dr
dS dr , 或
dt dt
瞬时速率与瞬时速度大小相等。
§1-1 质点运动的描述
八、加速度 描述质点速度的大小和方向随时间变化快慢的物理量。
位移和路程
2.路程 (标量):质点运动所经过的路径z
的长度。S
通常 S AB r r S
o
A
S
B
Δr
rA
rB
y
其中 r rB rA
lim r lim S
t 0
t 0
dr dS
1-3 坐标系的运用

ω
r r
r
ω
r
r
υ
r
ω
r
r r υ = ω×r
d ω d 2θ 角加速度: 角加速度: β = = 2 dt dt
r
P
3、 角加速度 (Angular Acceleration ) 、
14
1.3 坐标系的运用
圆周运动的角量与线量的关系: 圆周运动的角量与线量的关系: 的关系
第1章 质点运动学
ds r dθ υ= = = rω dt dt dυ dω aτ = =r = rβ dt dt
8
1.3 坐标系的运用
曲线运动的 加速度小结: 加速度小结:
第1章 质点运动学
2
r dυ υ ˆ ˆ ˆ a = aττ + ann = n τˆ + dt ρ
r υ2 法向加速度: 法向加速度: a = ˆ n n
大小: 大小:
切向加速度: r 切向加速度:a = dυ τ ˆ τ dt dυ 大小: 大小: aτ = dt
1.3 坐标系的运用
第1章 质点运动学
1.3 坐标系的运用
1
1.3 坐标系的运用
一、自然坐标系
第1章 质点运动学 S为弧坐标。 为弧坐标。
在已知运动轨道上任取一参照点 O,由质点 已知运动轨道上任取一参照点 , 来表示质点的位置 质点的位置。 与参考点之间轨迹的长度 s 来表示质点的位置。 速度方向为切向坐标方向;指向曲率中心的 速度方向为切向坐标方向; 切向坐标方向 方向为法向坐标方向 与速度的方向垂直) 法向坐标方向( 方向为法向坐标方向(与速度的方向垂直)。
ds = v0 − bt 解:1) v = ) dt dv = −b 2) at = ) dt 2 2 v (v0 − bt ) an = = R R
r r
r
ω
r
r
υ
r
ω
r
r r υ = ω×r
d ω d 2θ 角加速度: 角加速度: β = = 2 dt dt
r
P
3、 角加速度 (Angular Acceleration ) 、
14
1.3 坐标系的运用
圆周运动的角量与线量的关系: 圆周运动的角量与线量的关系: 的关系
第1章 质点运动学
ds r dθ υ= = = rω dt dt dυ dω aτ = =r = rβ dt dt
8
1.3 坐标系的运用
曲线运动的 加速度小结: 加速度小结:
第1章 质点运动学
2
r dυ υ ˆ ˆ ˆ a = aττ + ann = n τˆ + dt ρ
r υ2 法向加速度: 法向加速度: a = ˆ n n
大小: 大小:
切向加速度: r 切向加速度:a = dυ τ ˆ τ dt dυ 大小: 大小: aτ = dt
1.3 坐标系的运用
第1章 质点运动学
1.3 坐标系的运用
1
1.3 坐标系的运用
一、自然坐标系
第1章 质点运动学 S为弧坐标。 为弧坐标。
在已知运动轨道上任取一参照点 O,由质点 已知运动轨道上任取一参照点 , 来表示质点的位置 质点的位置。 与参考点之间轨迹的长度 s 来表示质点的位置。 速度方向为切向坐标方向;指向曲率中心的 速度方向为切向坐标方向; 切向坐标方向 方向为法向坐标方向 与速度的方向垂直) 法向坐标方向( 方向为法向坐标方向(与速度的方向垂直)。
ds = v0 − bt 解:1) v = ) dt dv = −b 2) at = ) dt 2 2 v (v0 − bt ) an = = R R
自然坐标系

r
t
t 0
AB .
t R
ern
v2 R
en
法向加速度
a
an
v2 R
vB
B vA
R
O
A
大小,方向,作用
2. 一般圆周运动的
切向加速度和法向加速度 分析方法
vB r
v vB vA vrn vr v
vrn 表示速度方向改变量 vr 表示速度大小改变量
lim lim vr
t 0
rr t
t 0
s t
er
ds dt
er
ds dt
三、 自然坐标系下的加速度
1. 匀速圆周运动, 法向加速度
v vB
vA
v vB
vA
Δv vB vA ,
AB R
lim lim ar
t 0
则:a an2 a 2 (1.88)2 (1.2)2 2.23(m / s2 )
tg an
a
12233'
总结解题策略:
(1)分析问题特点,建立恰当的坐标系 (2)由运动方程求解速度随时间变化的表达式 (3)分别计算出切向加速度与法向加速度,再 求解合加速度的大小和方向
解:根据加速度的定义:
ar
anern
a er
v2 R
ern
dv dt
er
a an2 a 2
v
ds dt
2
R
a
d
dt
1.2t
1-2自然坐标系

加速度
速度、
2、题设加速度关于时间(坐标)的函数
积分
速度、
运动学方程。需注意积分常量和积分上下限。
2015/3/16
DUT 常葆荣
6
例题
一质点运动轨迹为抛物线
x t 2 y t 4 2t 2
z0
求:x = - 4 m 时(t >0) 的位移、速度、速率、加速度。
2 4 2 解 r t x t i y t j z t k t i t 2t
10
圆周运动 速度
v R j
2 v an R 2 R
沿切线方向
法向加速度
沿半径方向指向圆心
切向加速度
dv a R dt
沿切线方向
2015/3/16
DUT 常葆荣
11
三、自然坐标系
速度:
r r s v lim lim ( ) t 0 t t 0 s t r s r ds ( lim )( lim ) ( lim ) t 0 s t 0 t t 0 s d t
j
r 4i 8 j m
x = -4 t= 2
dr v 2ti 4t 3 4t j d t 1 1 2 2 v 4i 24 j ms v 4 24 4 37 ms
a 2i 12t 4 j
2
a 2 i 4 4 j m s 2
所以
的方向 τ / / n 法线方向指向圆心 d( R ) ds v dτ d n n n n dτ d n Rdt Rdt R dt dt
dv v a n dt R
速度、
2、题设加速度关于时间(坐标)的函数
积分
速度、
运动学方程。需注意积分常量和积分上下限。
2015/3/16
DUT 常葆荣
6
例题
一质点运动轨迹为抛物线
x t 2 y t 4 2t 2
z0
求:x = - 4 m 时(t >0) 的位移、速度、速率、加速度。
2 4 2 解 r t x t i y t j z t k t i t 2t
10
圆周运动 速度
v R j
2 v an R 2 R
沿切线方向
法向加速度
沿半径方向指向圆心
切向加速度
dv a R dt
沿切线方向
2015/3/16
DUT 常葆荣
11
三、自然坐标系
速度:
r r s v lim lim ( ) t 0 t t 0 s t r s r ds ( lim )( lim ) ( lim ) t 0 s t 0 t t 0 s d t
j
r 4i 8 j m
x = -4 t= 2
dr v 2ti 4t 3 4t j d t 1 1 2 2 v 4i 24 j ms v 4 24 4 37 ms
a 2i 12t 4 j
2
a 2 i 4 4 j m s 2
所以
的方向 τ / / n 法线方向指向圆心 d( R ) ds v dτ d n n n n dτ d n Rdt Rdt R dt dt
dv v a n dt R
自然坐标系

自然坐标系
作者:Michaelexe
自然坐标系中的速度和加速度
在质点的平面曲线运动中,当运动轨迹已知时,常用自然坐标系表述质点的位置、路程、速度和加速度。
如图所示,在某质点运动的轨迹线上任取一点O为自然坐标原点,以质点所在位置P点与O点间轨迹的长度s来确定质点的位置,则称s为质点的自然坐标,即
当质点经Δt从P点达Q点时,Δt内质点运动的路程为
设t时刻质点处于P点,在质点上做相互垂直的两个坐标轴,一个轴沿轨道切向指向质点前进方向,其单位矢量用表示;另一轴沿轨道法向指向轨道凹侧,其单位矢量用表示。
由于切向和法向坐标轴随
质点沿轨道的运动自然变换位置和方向,通常称这种坐标系为自然坐标系。
当质点沿平面曲线运动时,其速度矢量的大小(速率)可以写为
考虑其速度方向为轨道的切向,则速度矢量可表示为
下面我们讨论质点的加速度
为质点的切向加速度,它只改变速度的大小,所以
为质点的法向加速度,它只改变速度方向,所以
,其中为轨道曲线在该点的曲率半径(因为始终指向轨道内侧,故ρ始终大于0,所以ρ也可以定义为)
所以,
现在来求平面曲线y=f(x)的曲率和曲率半径
曲率的定义:
曲率半径的定义:
下面来求k和ρ的公式所以,。
自然坐标系
dv a dt
v 2 (t ) an R
ˆ v v(t )
3 一般平面曲线运动
dv v 2 a n dt
曲线变化缓慢大 曲线变化急大
详细推导
ˆ v v
ˆ dv dv d ˆ a v dt dt dt
ˆ d的大小为 d 1
• 随质点一起运动,自然变换位置和方向。
举例:圆周运动 1 匀速圆周运动 速度 大小:v=衡量
ˆ n
ˆ
方向:切向
ˆ v v
v ˆ ˆ a an n n R
2
a 加速度 大小: n v / R
2
方向:指向圆心
2 变速率圆周运动 速度 加速度
ˆ ˆ a a an a an n
dv a dt 2 v an
a
a a
a 2 an 2
2 2 2
dv v dt
a tg an
加速度总是指向曲线的凹侧,因为正是加速 度的法向分量改变了质点的运动方向。
1.3 角量描述
v2 B v1
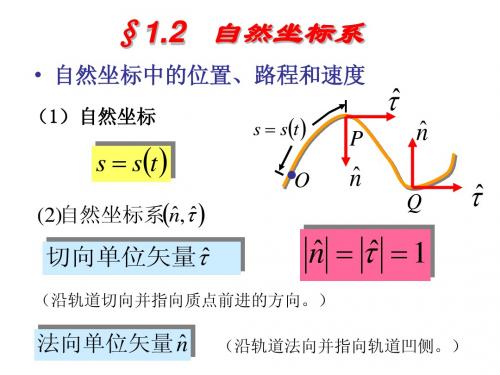
§1.2 自然坐标系
• 自然坐标中的位置、路程和速度
(1)自然坐标
s st
ˆ
s st
ˆ ˆ (2) 自然坐标系n,
P
ˆ n
Q
O
ˆ n
ˆ
ˆ 切向单位矢量
ˆ ˆ n 1
(沿轨道法向并指向轨道凹侧。)
(沿轨道切向并指向质点前进的方向。)
ˆ 法向单位矢量 n
自然坐标的特点
ˆ 方向为n
dˆ d d dr v ˆ ˆ ˆ ˆ n n n n dt dt dt dt
v 2 (t ) an R
ˆ v v(t )
3 一般平面曲线运动
dv v 2 a n dt
曲线变化缓慢大 曲线变化急大
详细推导
ˆ v v
ˆ dv dv d ˆ a v dt dt dt
ˆ d的大小为 d 1
• 随质点一起运动,自然变换位置和方向。
举例:圆周运动 1 匀速圆周运动 速度 大小:v=衡量
ˆ n
ˆ
方向:切向
ˆ v v
v ˆ ˆ a an n n R
2
a 加速度 大小: n v / R
2
方向:指向圆心
2 变速率圆周运动 速度 加速度
ˆ ˆ a a an a an n
dv a dt 2 v an
a
a a
a 2 an 2
2 2 2
dv v dt
a tg an
加速度总是指向曲线的凹侧,因为正是加速 度的法向分量改变了质点的运动方向。
1.3 角量描述
v2 B v1
§1.2 自然坐标系
• 自然坐标中的位置、路程和速度
(1)自然坐标
s st
ˆ
s st
ˆ ˆ (2) 自然坐标系n,
P
ˆ n
Q
O
ˆ n
ˆ
ˆ 切向单位矢量
ˆ ˆ n 1
(沿轨道法向并指向轨道凹侧。)
(沿轨道切向并指向质点前进的方向。)
ˆ 法向单位矢量 n
自然坐标的特点
ˆ 方向为n
dˆ d d dr v ˆ ˆ ˆ ˆ n n n n dt dt dt dt
1-4 自然坐标系中质点运动描述

v2 R
nv
三 变速圆周运动中的加速度
Δv vB vA Δvv Δvvn Δvv
Δvn 反映速度方向变化。
Δvv 反映速度大小变化。
av lim vv lim vvn lim vv t0 t t0 t t0 t
an
lim vn t0 t
av avn av
av
lim vv t0 t
vB
B vA
Δ r Δθ
oR A
Δv vB
Δ
vv
Δvn vA
Δθ
o
a反n 映出质点速度方向的变化,称为法向加速度。
avn
lim
t 0
vvn t
= lim t 0
|
Δvvn|nv= v 2 Δt R
2
(2)根据加速度的定义
an
v2 R
(v 0
bt)2 R
at
dv dt
b
a
at2 an2
b2
(v 0
bt)4 R2
a 1 R
R2b2 (v0 bt)4
由
a 1 R
R2b2 (v0 bt)4 b
解得 t v0 b
这时质点运行的圈数为
n
s 2R
v
0
(v 0 b
) 1 b(v0 2b
2πR
)
2
v02 4πRb
解题思路 自然坐标中质点运动学问题也分为两类问题。 1. 第一类问题:已知自然坐标中运动方程s(t),求质点运动 的速度、切向加速度、法向加速度,用求导法。 2. 第二类问题:已知质点运动的速度或切向加速度及初始条 件,求运动方程,用积分法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-2-5 自然坐标系:
把坐标建立在运动轨迹上的坐标系统。 s
P
et en
s
Q
O
en
规定:
• 切向 • 法向
et
et 坐标轴沿质点前进方向的切向为正,单位矢量为 坐标轴沿轨迹的法向凹侧为正,单位矢量为 en
1
s
P
s en
et
Q
O
et
v
质点位置: s st 路程:
运动的速度
o
xx'
t t
15
ut o '
yy'
r r ' D 或 r r 'ut
速度变换
位移关系
P P'
oo'
*
r r ' u t t v v'u
y
P
y' u Q
r
D
P'
t 0
xx'
r '
an r 2 0.2(2 1 4) 2 m s 2 0.8 m s
2
v 2
an
o
M
a a a 0.89 m s
2 t 2 n
at
x
11
an 0.8 arctan arctan 63.4 at 0.4
a
例5 一质点沿半径为R的圆周运动,其路程s随时 间t 的变化规律为 s bt 1 ct 2,式中b,c为大于 2 1)质点的切向加速 零的常数,且 b 2 Rc 。求( 度和法向加速度。(2)经过多长时间,切向加速 度等于法向加速度。 解: (1)
角位移: 质点从A到B矢径转过的角度 。
规定: 逆时针转向为正 顺时针转向为负
y
B
角速度: 角加速度:
d lim dt t 0 t
R
s
A
O
x
7
d lim dt t 0 t
角量表示匀加速圆周运动的基本公式:
0 t
ds v b ct dt 2 2 dv v (b ct ) at c an dt R R
(2 )
a t an
解得
b R t c c
12
§1-3 相对运动
一 时间与空间
在两个作相对运动的参考系中,时间 的测量是绝对的,空间的测量也是绝对的, 与参考系无关. 时间和长度的的绝对性是经典力学或 牛顿力学的基础.
1
例4 半径为r = 0.2 m的飞轮,可绕 O 轴转动。已知 轮缘上一点M的运动方程为 = -t2+4t ,求在1秒时 刻M点的速度和加速度。 d d 解: 2 2t 4 dt dt
1
at r (2) 0.2 m s 2 0.4 m s 2
et
et t t
et t
4
d
ds
O
et t t
P2 Δ
d et ds en dt ρdt v en ρ
2 det v v en dt ρ
s
P 1
et t
沿法线方向 2 d e v t en 法向加速度: an v dt ρ
5
综上所述:
Байду номын сангаас
dv v 2 a at an et en dt
加速度的大小:
a a a
2 n
2 t
加速度的方向(以与切线方向的夹角表示):
an arctan at
例:抛体运动
an
at
g
6
1-2-6 圆周运动及其角量描述
角位置 :
质点所在的矢径与x 轴的夹角。
s sQ sP
ds 速度: v vet et dt
2
质点的加速度: de t dv d( ve t ) dv et v a dt dt dt dt dv et : dt
速度大小的变化率,其方向指向曲线的切线方向
切向加速度:
dv d s at et 2 et dt dt
1 2 0 0 t t 2 2 02 2 0
角量和线量的关系:
s R
v R at R 2 an R
ds d R dt dt dv d R dt dt 2 v an R R
2
8
可以把角速度看成是矢量 !
3
2
讨论
d et dt
O
Δ
et et (t t ) - et (t )
当: t 0 , 0 有 方向
d et et d d
et t t
s
P 1
P2
et t
det et 即en方向
d et d en dt dt
o
xx'
t t
16
ut o '
v v u
伽利略速度变换
绝对速度
相对速度
dr v dt
a r ω v r R 方向沿着运动的切线方向。 为切向加速度 r y 即 at r
ω
R
v
ω v
方向指向圆心 为法向加速度
r
O
x
10
即 an ω v
z
v r r (2t 4) 0.2 (2 1 4) m s 0.4 m s
13
二 相对运动
物体运动的轨迹依赖于观察者所处的参考系
14
质点在相对作匀速
yy'
P P'
直线运动的两个坐标系 中的位移
S系 (Oxyz ) 基本参考系 S'系 (O' x' y ' z ' ) 运动参考系
oo'
*
y
P
y' u Q
r
D
P'
t 0
xx'
r '
u 是S’系相对S系
方向由右手螺旋法则确定 。
右手的四指循着质点的转动方向弯曲,拇指 的指向即为角速度矢量的方向。 y 线速度与角速度的关系: ω
v r
dv dω dr r ω dt dt dt
O
R
v
r
x
9
z
v 2 v v R
把坐标建立在运动轨迹上的坐标系统。 s
P
et en
s
Q
O
en
规定:
• 切向 • 法向
et
et 坐标轴沿质点前进方向的切向为正,单位矢量为 坐标轴沿轨迹的法向凹侧为正,单位矢量为 en
1
s
P
s en
et
Q
O
et
v
质点位置: s st 路程:
运动的速度
o
xx'
t t
15
ut o '
yy'
r r ' D 或 r r 'ut
速度变换
位移关系
P P'
oo'
*
r r ' u t t v v'u
y
P
y' u Q
r
D
P'
t 0
xx'
r '
an r 2 0.2(2 1 4) 2 m s 2 0.8 m s
2
v 2
an
o
M
a a a 0.89 m s
2 t 2 n
at
x
11
an 0.8 arctan arctan 63.4 at 0.4
a
例5 一质点沿半径为R的圆周运动,其路程s随时 间t 的变化规律为 s bt 1 ct 2,式中b,c为大于 2 1)质点的切向加速 零的常数,且 b 2 Rc 。求( 度和法向加速度。(2)经过多长时间,切向加速 度等于法向加速度。 解: (1)
角位移: 质点从A到B矢径转过的角度 。
规定: 逆时针转向为正 顺时针转向为负
y
B
角速度: 角加速度:
d lim dt t 0 t
R
s
A
O
x
7
d lim dt t 0 t
角量表示匀加速圆周运动的基本公式:
0 t
ds v b ct dt 2 2 dv v (b ct ) at c an dt R R
(2 )
a t an
解得
b R t c c
12
§1-3 相对运动
一 时间与空间
在两个作相对运动的参考系中,时间 的测量是绝对的,空间的测量也是绝对的, 与参考系无关. 时间和长度的的绝对性是经典力学或 牛顿力学的基础.
1
例4 半径为r = 0.2 m的飞轮,可绕 O 轴转动。已知 轮缘上一点M的运动方程为 = -t2+4t ,求在1秒时 刻M点的速度和加速度。 d d 解: 2 2t 4 dt dt
1
at r (2) 0.2 m s 2 0.4 m s 2
et
et t t
et t
4
d
ds
O
et t t
P2 Δ
d et ds en dt ρdt v en ρ
2 det v v en dt ρ
s
P 1
et t
沿法线方向 2 d e v t en 法向加速度: an v dt ρ
5
综上所述:
Байду номын сангаас
dv v 2 a at an et en dt
加速度的大小:
a a a
2 n
2 t
加速度的方向(以与切线方向的夹角表示):
an arctan at
例:抛体运动
an
at
g
6
1-2-6 圆周运动及其角量描述
角位置 :
质点所在的矢径与x 轴的夹角。
s sQ sP
ds 速度: v vet et dt
2
质点的加速度: de t dv d( ve t ) dv et v a dt dt dt dt dv et : dt
速度大小的变化率,其方向指向曲线的切线方向
切向加速度:
dv d s at et 2 et dt dt
1 2 0 0 t t 2 2 02 2 0
角量和线量的关系:
s R
v R at R 2 an R
ds d R dt dt dv d R dt dt 2 v an R R
2
8
可以把角速度看成是矢量 !
3
2
讨论
d et dt
O
Δ
et et (t t ) - et (t )
当: t 0 , 0 有 方向
d et et d d
et t t
s
P 1
P2
et t
det et 即en方向
d et d en dt dt
o
xx'
t t
16
ut o '
v v u
伽利略速度变换
绝对速度
相对速度
dr v dt
a r ω v r R 方向沿着运动的切线方向。 为切向加速度 r y 即 at r
ω
R
v
ω v
方向指向圆心 为法向加速度
r
O
x
10
即 an ω v
z
v r r (2t 4) 0.2 (2 1 4) m s 0.4 m s
13
二 相对运动
物体运动的轨迹依赖于观察者所处的参考系
14
质点在相对作匀速
yy'
P P'
直线运动的两个坐标系 中的位移
S系 (Oxyz ) 基本参考系 S'系 (O' x' y ' z ' ) 运动参考系
oo'
*
y
P
y' u Q
r
D
P'
t 0
xx'
r '
u 是S’系相对S系
方向由右手螺旋法则确定 。
右手的四指循着质点的转动方向弯曲,拇指 的指向即为角速度矢量的方向。 y 线速度与角速度的关系: ω
v r
dv dω dr r ω dt dt dt
O
R
v
r
x
9
z
v 2 v v R
