自动控制理论复习资料
自动控制原理复习资料

一、单选题(共20题,40分)1、在伯德图中反映系统抗高频干扰能力的是( )(2.0)A、低频段B、中频段C、高频段D、无法反应正确答案: C2、设单位负反馈控制系统的开环传递函数G(s)=,其中K>0,a>0,则闭环控制系统的稳定性与()o(2.0)A、K值的大小有关B、a值的大小有关C、a和K值的大小有关D、a和K值的大小无关正确答案: D3、关于线性系统稳态误差,正确的说法是:( )(2.0)A、一型系统在跟踪斜坡输入信号时无误差B、C、增大系统开环增益K可以减小稳态误差D、增加积分环节可以消除稳态误差,而且不会影响系统稳定性正确答案: C4、传递函数定义线性定常系统在零初始状态下系统输出拉氏变换与输入拉氏变换之()。
(2.0)A、积B、比C、和D、差正确答案: B5、下列系统中属于不稳定的系统是( )。
(2.0)A、闭环极点为的系统B、闭环特征方程为的系统C、阶跃响应为的系统D、脉冲响应为的系统正确答案: D6、系统开环对数幅频特性L(ω)中频段主要参数的大小对系统的()性能无影响。
(2.0)A、动态B、稳态C、相对稳定性D、响应的快速性正确答案: D7、设控制系统的开环传递函数为,该系统为( )(2.0)A、 0型系统B、Ⅰ型系统C、Ⅱ型系统D、Ⅲ型系统正确答案: B8、确定系统根轨迹的充要条件是()。
(2.0)A、根轨迹的模方程B、根轨迹的相方程C、根轨迹增益D、根轨迹方程的阶次正确答案: C9、高阶系统的主导闭环极点越靠近虚轴,则系统的 ( )(2.0)A、准确度越高B、准确度越低C、响应速度越快D、响应速度越慢正确答案: D10、闭环系统的动态性能主要取决于开环对数幅频特性的( )(2.0)A、低频段B、开环增益C、高频段D、中频段正确答案: D11、Z变换中复变量z的物理含义是什么?(2.0)A、滞后一个采样周期。
B、超前一个采样周期。
C、跟复变量s一样。
D、没有什么物理含义,就是为了计算方便。
自动控制原理总复习

3.化简结构图求传递函数 ①结构图化简的方法有:
第二章
1、串联方框的简化 2、并联方框的简化 3、反馈连接方框的简化 4、比较点的移动 5、引出点移动
结构图化简原则
❖多个方框串联原则:总传递函数等于各方框传递函数之积。 ❖多个方框并联原则:总传递函数等于各方框传递函数之代数和。
有源校 正装置
无相移校正装置 相位超前校正装置 相位滞后校正装置 相位滞后—超前校正装置
4. 常用校正装置的特性
无源校正网络:电阻电容元件电路 有源校正网络:电阻电容元件电路+线性集成运算放大器
5. 串联校正的分类
1.串联超前校正:
利用超前网络的相角超前特性进行校正
2.串联滞后校正:
利用滞后网络的高频衰减特性进行校正
3.串联超前—滞后校正
第七章
1.为了从采样信号中不失真地复现原连续信号,采样周期T与频率
分量ωm的关系是:
2
T
2m
2.闭环系统脉冲传递函数形式的证明
闭环脉冲传递函数是闭环离散系统输出信号的Z变换与输入信
号的Z变换之比,即
(z) C(z) R(z)
P.276表7-3列出了典型的闭环离散系统及其输出的Z变换函数
G(s) 2(s 2) (s 1)(s 4)
G(s) (0.5s 1) (s 1)(0.25s 1)
第二章
2.传递函数的相关内容
③ 模态与闭环特征根的关系:e pit
④ 根据给定的零初条件下的系统阶跃响应形式,求得系统的 单位脉冲响应 第一步:根据给定的零初条件下的系统阶跃响应形式,写出闭 环传递函数的表达式; 第二步:得到系统输出s域的表达式; 第三步:对系统输出进行拉式反变换。
自动控制理论复习资料

课程名称: 自动控制理论一、填空题(每空 1 分,共15分) 1、反馈控制又称偏差控制,其控制作用是通过 与反馈量的差值进行的。
2、复合控制有两种基本形式:即按 的前馈复合控制和按 的前馈复合控制。
3、两个传递函数分别为G 1(s)与G 2(s)的环节,以并联方式连接,其等效传递函数为()G s ,则G(s)为 (用G 1(s)与G 2(s) 表示)。
4、典型二阶系统极点分布如图1所示,则无阻尼自然频率=n ω ,阻尼比=ξ ,该系统的特征方程为 ,该系统的单位阶跃响应曲线为 。
5、若某系统的单位脉冲响应为0.20.5()105t t g t e e --=+,则该系统的传递函数G(s)为 。
7、设某最小相位系统的相频特性为101()()90()tg tg T ϕωτωω--=--,则该系统的开环传递函数为 。
8、PI 控制器的输入-输出关系的时域表达式是 , 其相应的传递函数为 ,由于积分环节的引入,可以改善系统的 性能。
二、选择题(每题 2 分,共20分)1、采用负反馈形式连接后,则 ( )A 、一定能使闭环系统稳定;B 、系统动态性能一定会提高;C 、一定能使干扰引起的误差逐渐减小,最后完全消除;D 、需要调整系统的结构参数,才能改善系统性能。
2、下列哪种措施对提高系统的稳定性没有效果 ( A )。
A 、增加开环极点;B 、在积分环节外加单位负反馈;C 、增加开环零点;D 、引入串联超前校正装置。
3、系统特征方程为 0632)(23=+++=s s s s D ,则系统 ( C )A 、稳定;B 、单位阶跃响应曲线为单调指数上升;C 、临界稳定;D 、右半平面闭环极点数2=Z 。
4、系统在2)(t t r =作用下的稳态误差∞=ss e ,说明 ( )A 、 型别2<v ;B 、系统不稳定;C 、 输入幅值过大;D 、闭环传递函数中有一个积分环节。
5、对于以下情况应绘制0°根轨迹的是( )A 、主反馈口符号为“-” ;B 、除r K 外的其他参数变化时;C 、非单位反馈系统;D 、根轨迹方程(标准形式)为1)()(+=s H s G 。
自动控制理论复习提纲(1-5章)

自动控制理论复习提纲(第1章)1.什么是自动控制?2.什么是自动控制理论?包括那三大部分?3.经典理论和现代理论的特点是什么?4.什么是自动控制系统?5.什么是反馈控制原理?6.三种基本控制方式是什么?7.按输入量的变化规律,控制系统可以分为哪几类?8.对控制系统的基本要求是什么?9.典型输入信号包括哪几种?自动控制理论复习提纲(第2章)1.什么是数学模型?2.经典理论常用数学模型包括哪几种?3.什么是控制系统的运动模态?有什么决定?4.什么是传递函数?5.传递函数的三种表达式形式分别是什么?6.动态结构图的四种基本组成单元是什么?7.结构图的基本连接方式包括哪三种?8.结构图的化简规则有哪些?9.信号流图的组成单元包括哪两种?10.什么是梅逊公式?学会应用梅逊公式求闭环传递函数。
11.典型结构的几个闭环传递函数:Фr(s), Фn(s),Фer(s),Фen(s)自动控制理论复习提纲(第3章)1.什么是时域分析法?2.时域性能指标的定义。
3.二阶系统的数学模型:结构图、开环传递函数、闭环传递函数、五种阻尼状态及其响应特征。
4.欠阻尼二阶系统的单位阶跃响应:特征根表达式、响应表达式、性能指标关系式。
5.二阶系统的两种性能改善措施:结构、传函、特点。
6.什么是主导极点和偶极子?7.高阶系统的降阶方法。
8.什么是控制系统的稳定性?9.控制系统稳定的充分必要条件是什么?10.劳斯判据:充分必要条件、劳斯表的构造方法、两种特殊情况的处理方法。
11.劳斯判据的四种应用:判稳、求取不稳定根的个数、确定待定参会素的稳定范围、判断系统的相对稳定程度。
12.什么是误差和稳态误差?稳态误差的定义式。
13.稳态误差的一般计算式和简化计算式。
14.减小或消除稳态误差的三种措施是什么?自动控制理论复习提纲(第4章)1.什么是根轨迹?2.三种根轨迹方程分别是什么?3.8条根轨迹法则分别是什么?4.学会绘制四阶以下(含)系统根轨迹。
《自动控制原理》复习提纲

《自动控制原理》复习提纲自动控制原理复习提纲第一章:自动控制系统基础1.1自动控制的基本概念1.2自动控制系统的组成1.3自动控制系统的性能指标1.4自动控制系统的数学建模第二章:系统传递函数与频率响应2.1一阶惯性系统传递函数及特性2.2二阶惯性系统传递函数及特性2.3高阶惯性系统传递函数及特性2.4惯性环节与纯时延环节的传递函数2.5开环传递函数与闭环传递函数2.6频率响应曲线及其特性第三章:传递函数的绘制和分析3.1 Bode图的绘制3.2 Bode图的分析方法3.3 Nyquist图的绘制和分析3.4极坐标图的应用3.5稳定性分析方法第四章:闭环控制系统及稳定性分析4.1闭环控制系统4.2稳定性的概念和判据4.3 Nyquist稳定性判据4.4 Bode稳定性判据4.5系统的稳态误差分析第五章:比例、积分和微分控制器5.1比例控制器的原理和特性5.2积分控制器的原理和特性5.3微分控制器的原理和特性5.4比例积分(P)控制系统5.5比例积分微分(PID)控制系统第六章:根轨迹法6.1根轨迹的概念和基本性质6.2根轨迹的绘制方法6.3根轨迹法的稳定性判据6.4根轨迹设计法则6.5根轨迹法的应用案例第七章:频域设计方法7.1频域设计基本思想7.2平衡点反馈控制法7.3频域设计法的应用案例7.4系统频率响应的优化设计7.5频域方法的灵敏度设计第八章:状态空间分析和设计8.1状态空间模型的建立8.2状态空间的矩阵表示8.3状态空间系统的特性8.4状态空间系统的稳定性分析8.5状态空间设计方法和案例第九章:模糊控制系统9.1模糊控制的基本概念9.2模糊控制系统的结构9.3模糊控制器设计方法9.4模糊控制系统的应用案例第十章:遗传算法与控制系统优化10.1遗传算法的基本原理10.2遗传算法在控制系统优化中的应用10.3遗传算法设计方法和案例第十一章:神经网络及其应用11.1神经网络的基本概念和结构11.2神经网络训练算法11.3神经网络在控制系统中的应用11.4神经网络控制系统设计和优化方法第十二章:自适应控制系统12.1自适应控制的基本概念12.2自适应控制系统的结构12.3自适应控制器设计方法12.4自适应控制系统的应用案例第十三章:系统辨识与模型预测控制13.1系统辨识的基本概念13.2建模方法及其应用13.3模型预测控制的原理13.4模型预测控制系统设计和优化方法第十四章:多变量控制系统14.1多变量控制系统的基本概念14.2多变量系统建模方法14.3多变量系统稳定性分析14.4多变量系统控制器设计14.5多变量系统优化控制方法以上是《自动控制原理》的复习提纲,内容覆盖了自动控制系统的基本概念、传递函数与频率响应、传递函数的绘制和分析、闭环控制系统及稳定性分析、比例、积分和微分控制器、根轨迹法、频域设计方法、状态空间分析和设计、模糊控制系统、遗传算法与控制系统优化、神经网络及其应用、自适应控制系统、系统辨识与模型预测控制、多变量控制系统等知识点。
自动控制原理复习资料
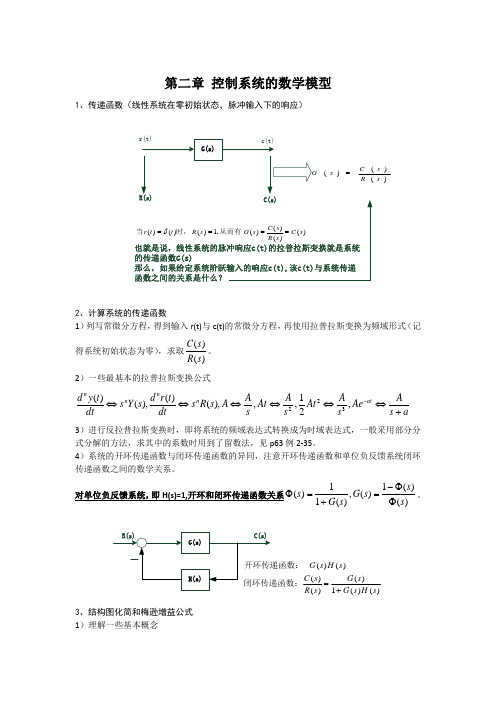
第二章 控制系统的数学模型1、传递函数(线性系统在零初始状态,脉冲输入下的响应)2、计算系统的传递函数1)列写常微分方程,得到输入r(t)与c(t)的常微分方程,再使用拉普拉斯变换为频域形式(记得系统初始状态为零),求取)()(s R s C 。
2)一些最基本的拉普拉斯变换公式as A Ae s A At s A At sA A s R s dtt r d s Y s dtt y d atnnnn+⇔⇔⇔⇔⇔⇔-,21,,),()(),()(322 3)进行反拉普拉斯变换时,即将系统的频域表达式转换成为时域表达式,一般采用部分分式分解的方法,求其中的系数时用到了留数法,见p63例2-35。
4)系统的开环传递函数与闭环传递函数的异同,注意开环传递函数和单位负反馈系统闭环传递函数之间的数学关系。
对单位负反馈系统,即H(s)=1,开环和闭环传递函数关系)()(1)(,)(11)(s s s G s G s ΦΦ-=+=Φ。
3、结构图化简和梅逊增益公式 1)理解一些基本概念比较点,引出点,前向通路,回路2)结构图化简的基本原则:保持前向通路传递函数不变,保持回路传递函数不变3)化简规则包括:引出点的前(后)移动,比较点的前(后)移动,并联相加,串联相减,回路等效(见下图)。
4)根据信号流图使用梅逊增益公式计算传递函数步骤:(a )找出所有回路,并列写回路传递函数i L ;(b)找出所有前向通路,并列写前向通路的传递函数k P ;(c )判断是否存在互不接触的独立回路,并根据公式 (11)-⎪⎪⎭⎫⎝⎛+-=∆∑∑=≠ni n j i j i i L L L 计算分母∆,其中第i 个和第j 个回路互不接触;(d )利用相同的原理计算(a )中与第k 条前向通路不接触的回路的k ∆;(e )根据梅逊增益公式∆∆∑=mk kkP 1计算系统输入到输出的传递函数)()(s R s C 。
第二章 典型习题答案课本的以下典型例题,要认真看一下,最好能试做一下。
自动控制原理复习1资料

(1)一、填空(每空1分,共18分)1.自动控制系统的数学模型有 微分方程 、 传递函数 、 频率特性 、 结构图 共4种。
2.连续控制系统稳定的充分必要条件是 闭环极点位于S 平面左侧 。
离散控制系统稳定的充分必要条件是 系统的特性方程的根都在Z 平面上以原点为圆心的单位圆内。
。
3.某统控制系统的微分方程为:dtt dc )(+0.5C(t)=2r(t)。
则该系统的闭环传递函数 Φ(s)= ;该系统超调σ%= ;调节时间t s (Δ=2%)= 。
4.某单位反馈系统G(s)=)402.0)(21.0()5(1002+++s s s s ,则该系统是 4 阶二 型系统;其开环放大系数K= 62.5 。
5.已知自动控制系统L(ω)曲线为:则该系统开环传递函数G(s)= ;ωC = 。
6.相位滞后校正装置又称为 调节器,其校正作用是 。
7.采样器的作用是 ,某离散控制系统)()1()1()(10210TT e Z Z e Z G -----=(单位反馈T=0.1)当输入r(t)=t 时.该系统稳态误差为 。
二. 1.求图示控制系统的传递函数.求:)()(S R S C (10分)R(s)2.求图示系统输出C (Z )的表达式。
(4分)三、 计算1、 已知t Te tf 11)(--=求F (s )(4分)2、 已知)5(1)(2+=s s s F 。
求原函数f (t )(6分)3.已知系统如图示,求使系统稳定时a 的取值范围。
(10分)R (s )四.反馈校正系统如图所示(12分)求:(1)K f=0时,系统的ξ,ωn和在单位斜坡输入下的稳态误差e ss.(2)若使系统ξ=0.707,k f应取何值?单位斜坡输入下e ss.=?五.已知某系统L(ω)曲线,(12分)(1)写出系统开环传递函数G(s)(2)求其相位裕度γ(3)欲使该系统成为三阶最佳系统.求其K=?,γmax=?(1) (2) (3)六、已知控制系统开环频率特性曲线如图示。
自动控制基础知识复习

自动控制基础知识复习目录一、自动控制基本概念 (3)1.1 自动控制的基本原理 (4)1.2 自动控制系统的组成 (4)1.3 自动控制系统的分类 (6)二、自动控制系统的数学模型 (7)2.1 线性系统的数学模型 (9)2.1.1 微分方程 (10)2.1.2 积分方程 (11)2.1.3 非线性系统的数学模型 (13)2.2 传递函数 (14)2.3 状态空间表达式 (15)三、自动控制系统的时域分析 (16)3.1 典型输入信号 (18)3.2 系统的稳定性分析 (19)3.3 系统的稳态误差分析 (20)四、自动控制系统的频域分析 (22)4.1 频率特性 (23)4.2 相频特性 (24)4.3 系统的频域性能分析 (26)五、自动控制系统的校正与设计 (27)5.1 校正装置的选择 (28)5.2 串联校正 (30)5.3 并联校正 (31)5.4 反馈控制系统的设计 (32)六、自动控制系统的工程应用 (34)6.1 工业自动化系统 (35)6.2 交通运输系统 (36)6.3 生物医学控制系统 (37)七、智能控制基础 (38)7.1 智能控制的基本概念 (40)7.2 智能控制系统的类型 (41)7.3 智能控制算法简介 (42)八、自动控制系统的仿真与实验 (43)8.1 计算机仿真的基本概念 (45)8.2 自动控制系统的仿真方法 (46)8.3 实验技能与实验指导 (48)九、自动控制技术的发展趋势 (49)9.1 控制理论的发展 (51)9.2 控制设备的智能化 (52)9.3 控制系统的绿色化 (53)一、自动控制基本概念自动控制定义:自动控制是指通过某种装置或系统,使得某一过程或设备能够自动地按照预定的规律或程序运行,而无需人为的干预和调整。
在自动控制系统里,输入信号会激发反馈机制,系统会根据反馈调整其输出以达到预期目标。
系统组成:一个基本的自动控制系统通常由控制器、被控对象、执行器和传感器等部分组成。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自动控制理论复习资料一.单项选择题最小相位系统闭环稳定的充要条件是( A )A .奈氏曲线不包围0点;B .曲线包围0点;C .曲线顺时针包围0点; D .曲线逆时针包围0点系统的传递函数完全决定于系统的 ( C )。
A .输入信号 B.输出信号 C.结构和参数 D.扰动信号 一般来说,系统增加积分环节,系统的稳定性将(B )。
A .变好 B.变坏 C.不变 D.可能变好也可能变坏 控制系统的相位稳定裕量反咉了系统的 ( A )。
A .稳定性 B.稳态性能 C.快速性 D.动态性能 系统闭环传递函数为 )()(1)()(s H s G s G s G B +=,则开环传递函数应为 ( C )。
A .G(s) B.1+G(s)H(s) C.G(s)H(s) D.)()(1s H s G系统闭环极点在S 平面的分布如图示。
那么,可以判断该系统是 ( B )。
A .稳定的 B.不稳定的 C .临界稳定的 D.无法判定稳定性一阶系统开环传递函数为11+TS ,误差5=∆%,则调节时间为( A )。
A.3TB.2.2TC.TD.4T闭环系统开环传递函数为 G s s s s s ()()()()=+++83232,则该系统为( C )。
A .0型系统,开环增益为8 B. I 型系统,开环增益为8 C .I 型系统,开环增益为4 D. 0型系统,开环增益为4系统特征方程为0632)(23=+++=s s s s D ,则系统 ( B )A. 稳定;B. 临界稳定;C. 不稳定;D. 型别1=v已知校正装置对数幅频特性如图示。
判断该环节的相位特性是(C )。
A .相位超前 B .相位滞后 C . 相位滞后-相位超前 D .相位超前-相位滞后二. 填空题两个传递函数分别为G 1(s )与G 2(s )的环节,以并联方式连接,其等效传递函数G (s )为 G 1(s )+G 2(s ) ;若以串联方式连接,则()G s 为 G 1(s ) G 2(s ) 。
(用G 1(s )与G 2(s ) 表示)。
惯性环节的传递函数为11τ+s 。
衡量系统稳态性能的主要指标是 稳态误差 。
连续线性定常系统稳定的充分必要条件为:闭环系统特征方程的所有根位于S 平面的 左 半平面。
根轨迹起始于开环 极点 ,终止于开环 零点 。
三.计算分析题1. 求下图所示系统方框图的传递函数解:2211221211)(H G GH G G G P s k kk ++=∆∆=Φ∑=2. 二阶系统方框图如图所示已知条件为:由单位斜坡函数输入所引起的稳态误差为0.25; 系统的暂态调节时间3=s t 秒(%5±误差带)。
试求出:(1)二阶系统闭环传递函数;(2)峰值时间p t和超调量%σ的值。
解:由单位斜坡函数输入所引起的稳态误差为25.0得425.012)2(lim 20===+*=→ξωξωωn n n s v s s s K由系统的暂态调节时间3=s t 秒%)5(±得33=nξω得⎪⎩⎪⎨⎧====8.22235.0221nωξ所以二阶系统闭环传函为 (1)8282)(1)()(2222++=++=+=Φs s s s s G s G s n n n ωξωω (2)%30%%2.135.012212122===-=-=--ξπξσπξωπe s t n p3. 设二阶控制系统的单位阶跃响应曲线如图所示。
如果该系统为单位负反馈控制系统,试确定其开环传递函数及闭环传递函数。
11.2)(t c解:可以从上图直接得出0020=p M 和s t p 1.0=。
由%20%100%21=⨯=--ζζπeM ps t n p 1.012=-=ξωπ ,可以解得:456.0=ξ ,则 s rad t p n /3.3512=-=ξπω所以系统开环传递函数为:)2.32(1.1246)2()(2+=+=s s s s s G n n ξωω1.12462.321.12462)(2222++=++=s s s s s Φn n n ωξωω 4. 设系统的特征方程式分别为:1.05432234=++++s s s s2.022332345=+++++s s s s s试用劳斯稳定判据判断系统的稳定性。
解:(1)列劳斯表如下s 4 1 3 5 s 3 2 4 s 2 1 5 s 1 -6s 0 5 所以系统不稳定。
(2)列劳斯表如下s 5 1 3 2 s 4 1 3 2 s 3 4 6 s 2 3/2 2 s 1 2/3s 0 2可解得系统有两对共轭虚根s 1,2=±j ,s 3,4=±j 2,因而系统处于临界稳定状态。
5. 已知系统开环传递函数为:)()(s H s G =)125.0)(1(++s s s K,(1)绘制系统的根轨迹;(2)确定系统临界稳定的开环增益值K 。
解:(1)绘制系统的根轨迹(2)根轨迹与虚轴的交点: 045023=+++K s s s 令 ωj s =, 得 04)(5)(023=+++K j j j ωωω即: ⎩⎨⎧=±=⇒⎩⎨⎧=-=-2020504023K K ωωωω 系统临界稳定的开环增益值为 54==K K 。
6.试: (1)写出该系统的开环传递函数;(2)求该系统的剪切频率c ω和相位裕量γ。
解:)101.0()12.0(100)1()1()()(2221++=++=s s s s T s s T K sH s G 令0)(=c L ω,1151002≈⨯⨯c cωω 可求得: 20=c ω。
7. 某系统开环传递函数:)5)(1()()(1++=s s s K s H s G试求:试绘制K 1=10时的伯德图(幅值曲线和相位曲线) 解:03.1153.11761802001.0202.0180)(-=-+-=⨯-⨯+-=ωϕarctg arctg c00007.643.115180)(180=-=ωϕ+=γc由于 0>γ,所以闭环系统是稳定的。
8. 某系统开环传递函数:试求:(1)试绘制K 1=10时的伯德图(幅值曲线和相位曲线); (2)求相位裕量γ及幅值裕量)(g g L K 或;并判定稳定性。
则伯德图如图所示:令0)(=c L ω,即1)(=c A ω,可求得c ω: 22≈cω, 414.12=≈c ω000005.1608.157.54902.090)(-=---=---=c c c arctg arctg ωωωϕ 00005.195.160180)(180=-=+=c ωϕγ令180)(-=g ωϕ,可求得gω :01802.090)(-=---=g g g arctg arctg ωωωϕ ,2902.012.12.0=-=+ggg g arctgarctg arctg ωωωω 所以2.012=-g ω, 即24.25==g ω321)5(1)1()(122=++==ggg g g A K ωωωωL g =20lg3=9.5由于 0>γ及1>g K ,所以闭环系统是稳定的。
9. 分别判断下列3个系统的稳定性 ,并说出S 右半平面根的个数。
(1)05432234=++++s s s s(2) P=1 (3) P=0解: (1)不稳定Z=2(2) 不稳定Z=3 (3)稳定Z=0)5)(1()()(1++=s s s K s H sG10.已知单位负反馈系统的开环传递函数为)4)(1()(0++=s s s K s G(1)粗略绘制系统的根轨迹;(2)求出根轨迹渐进线与实轴的交点及夹角;(3)求出根轨迹与虚轴的交点以及使得系统临界稳定的K 值。
解:改写系统开环传递函数 )()(s H s G =)4)(1(0++s s s K(1)绘制系统根轨迹的概图:(2)渐近线:夹角60、-60、-180; 交点:35-根轨迹与虚轴的交点: 用劳斯判据:045023=+++K s s s 2j s ±= (3)系统临界稳定的开环增益值为K 0=20 11. 求下图所示系统的闭环传递函数并画出信号流程图。
解:221122111)(H G G H G G G P s k kk ++=∆∆=Φ=。
