理论力学习题解答第七章
理论力学习题册答案
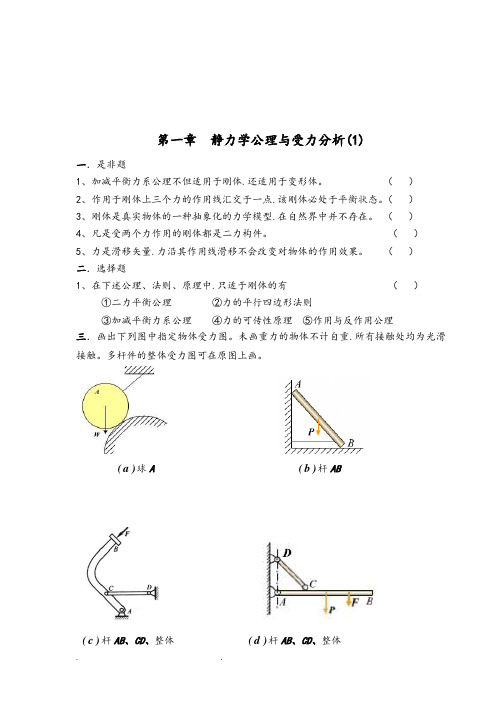
第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体.还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点.该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型.在自然界中并不存在。
()4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量.力沿其作用线滑移不会改变对物体的作用效果。
()二.选择题1、在下述公理、法则、原理中.只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重.所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
b(杆ABa(球A ))d(杆AB、CD、整体)c(杆AB、CD、整体))e(杆AC、CB、整体)f(杆AC、CD、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重.所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A、球B、整体)b(杆BC、杆AC、整体第一章 静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重.所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WADB CE Original FigureAD B CEWWFAxF AyF BFBD of the entire frame)a (杆AB 、BC 、整体)b (杆AB 、BC 、轮E 、整体)c (杆AB 、CD 、整体 )d (杆BC 带铰、杆AC 、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体第二章平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F= - F’.所以力偶的合力等于零。
()2、用解析法求平面汇交力系的合力时.若选用不同的直角坐标系.则所求得的合力不同。
()3、力偶矩就是力偶。
()二.电动机重P=500N.放在水平梁AC的中央.如图所示。
理论力学习题册答案
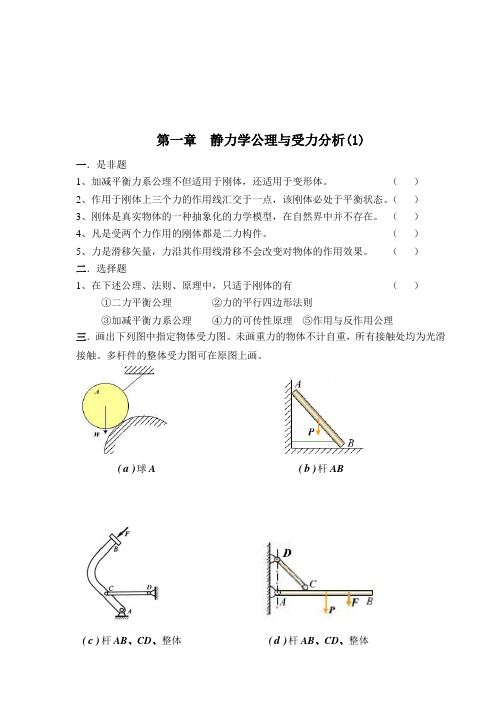
第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体,还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
()4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
()二.选择题1、在下述公理、法则、原理中,只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A )b(杆ABd(杆AB、CD、整体)c(杆AB、CD、整体)-2 -)e (杆AC 、CB 、整体)f (杆AC 、CD 、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a (球A 、球B 、整体)b (杆BC 、杆AC 、整体班级姓名学号- 3 -第一章静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WA DBCEOriginal FigureADBCEWWF AxF Ay F BFBD of the entire frame )a(杆AB、BC、整体)b(杆AB、BC、轮E、整体)c(杆AB、CD、整体)d(杆BC带铰、杆AC、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体- 4 -班级姓名学号- 5 -第二章平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F= - F’,所以力偶的合力等于零。
()2、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。
(彩色版第七版)理论力学哈工大课后题答案
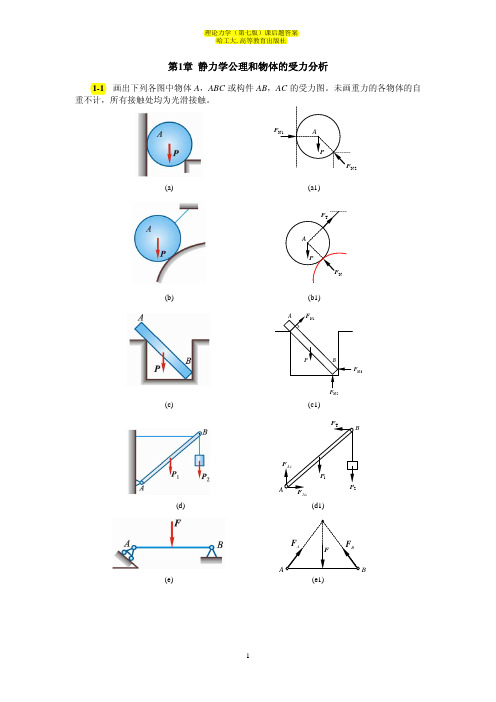
第1章 静力学公理和物体的受力分析1-1 画出下列各图中物体A ,ABC 或构件AB ,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
2F(a)(a1)(b) (b1)2N F 3N(c) (c1)Ax(d) (d1)B(e) (e1)Bq(f) (f1)(g)1F 2(h)(h1)Ax(i)(i1)(j)(j1)F(k) (k1)BA F FF ′ (l) (l2) (l3)图1-11-2画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所有接触处均为光滑接触。
22N(a1)2AxFAx(a2)3N(b)(b1)N3′(b2) (b3)1N2AxF(c)(c1)1N2N2Ax(c2)(c3)(d) (d1)CDy(d2)(d3)CxBxByF By′(e) (e1)(e2) (e3)ByBxAx(f) (f1)AxBx F′(f2)(f3)FB(g) (g1)BCx′F(g3)(h)(h1)FFAxC(i) (i1) (i2)F(i3)(i4)AyFFFCy (j) (j1)(j2) 2TFDx3TEyFCyEx′(j3) (j4) (j5)BBDECyF(k)(k1)BBCx (k2) (k3) DEA1F(l) (l1) (l2)A C E(l3) (l4)或CDxFEyFEy(l2)’(l3)’ (l4)’F′(m)(m1)EADFH2FAD′(m2) (m3)BN(n)q3N(n2)G(o)(o1)BADB(o2) (o3) (o4)图1-2第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心A ,B 和C 处受3个力作用,如图2-1a 所示。
N 1001=F ,沿铅直方向;N 503=F ,沿水平方向,并通过点A ;N 502=F ,力的作用线也通过点A ,尺寸如图。
求此力系的合力。
(a)(b)图2-1解 (1) 几何法作力多边形abcd ,其封闭边ad 即确定了合力F R 的大小和方向。
14理论力学讲义-第十四讲第七章习题

B
v0
A
θ
退出
O
7-1: v0=1m/s, : ,
R=8cm;杆A点的 ; 点的 运动方程和t=4s时 运动方程和 时 速度和加速度。 速度和加速度。
y
y B
B
v
v0
R A
θ
vr ve
v0
x
ve
R
Aa
θ
O O’
θ
O
va
vr
x
取坐标系O’xy 解: (1)取坐标系 取坐标系
y = R − (v0t ) & & vy = y a y = v y = && y
理 论 力 学
第七章习题7-2,3,7
第二部分 运动学
2 2
第七章
点的运动
点的运动方程、速度、加速度数学描述
第九章
点(刚体上)的运动合成 刚体上)
相对运动、绝对运动、 相对运动、绝对运动、牵连运动的速度合成
退出
第七章习题
3 3
7-1: 凸轮机构中的凸轮外形为半圆形,顶杆 沿垂 : 凸轮机构中的凸轮外形为半圆形,顶杆AB沿垂
三种运动:绝对运动、 一般针对滑块、 三种运动:绝对运动、相对运动 1. 一般针对滑块、套筒问题
、牵连运动
动点、动系的选取原则: 2. 动点、动系的选取原则:动 三个速度:绝对速度、 三个速度:绝对速度、相对速度 点通常是两构件的不变接触 、牵连速度 点,动点与动系一定在两个 构件上, 构件上,动点与动系之间有 点的运动合成的解体思路步骤: 点的运动合成的解体思路步骤: 相对运动, 相对运动,而且相对运动关 系明确。 系明确。动系相对静系有运 1. 机构组成分析 动;
理论力学(刘又文 彭献)答案第7章

maCτ aCn
maCn
(a) 思考 7-2 图
②可运用思考 7-1 的解答结果而得之,也可从图 b 所示,先向质心 C 简化, 再向 A 点简化而得到。可见在一般情形下
231
M A ( − maC ) + JCα ≠ J Aα
JCα α
A
aC
C maC
JCα A M A (−maC )
maC C
A
C1
D C
C
C2
2maC
E
B
m
aτ C1C
J α C1
α
C1 D
maC
aC
C
A
J C2α maCτ 2B
maB
C2 Eα
B
aB
(a)
(b)
图 7.7
答:不对。对于可变的刚体系统,其惯性力应分别加于各个刚体上,如图 b
所示。这样,才便于求各运动量及各刚体之间的相互作用力。
10.如图 7.8 所示,两杆质量均为 m,质心在铰 C,则惯性力主矢,应加在
d dt
(ri′×
mi
vi
)
−
dri′ dt
×
mi
⎤ vi′ ⎥
⎥⎦
∑ ∑ = − d dt
(ri′× mi vi ) +
[(vA − vi ) × mi vi ]
=
dLA′ dt
− vA
×
P
可见,质点系的惯性力向任一运动点简化的结果并不简洁,因此通常向质心
简化。
思考 7-2
① 若定轴转动刚体无质量对称面,或转动刚体有质量对称面但转轴不垂直
而主矩与简化中心有关。只有惯性力偶系的简化与简化中心无关。
理论力学第7章答案

x′
a
n A
sin
θ
−
aAτ
cosθ= NhomakorabeaaBx
cos
θ
−
aBy
sin
θ
aAτ
=
−aBx
+
(a
n A
+ aBy )tgθ
=
−1cm/s 2
α OA
=
a
τ A
/ OA
=
−(1/ 40)rad/s2
7.13 滚压机构的滚子沿水平面作纯滚动如图示 曲柄 OA 长 r 连杆 AB 长 l 滚子 半径为 R 若曲柄以匀角速度 ω 绕固定轴 O 转动 计算连杆 AB 和滚子的角加速度
向
v A
垂直于
OA
杆
因此瞬心为 C
不难看出 C 点相对
AB 杆和定系的位置可分别以 (2r, ϕ) 和 (r,2ϕ) 表示 则动 定瞬心迹线分别是半径为 2r 和 r 的圆
7.9 图示反平行四边形机构中 AB = CD = 2a AC = BD = 2c a > c 求杆 BD
的动瞬心轨迹和定瞬心轨迹
b
杆速度瞬心在 点 vC = 0
∴ ωBC = vB / a = ω ωCD = 0
基点
aCτ = aBn + aCτ B + aCnB
x′ acτ cos θ = −aBn − aCnB
Q cos θ = sin ϕ = 7 / 4
aBn = ω2a
aCnB = ω2a
∴ aCτ = −8ω2a / 7
上二式中消去 ψ 得 (ρsin ϕ)2 + (2c − ρ cos ϕ)2 = (2a − ρ)2
理论力学课后习题答案 第7章 质点动力学

习题7-2图习题7-3图习题7-1图(a) g m NF s F a(b)θs F N F gm a 第7章 质点动力学7-1 图示滑水运动员刚接触跳台斜面时,具有平行于斜面方向的速度40.2km/h ,忽略摩擦,并假设他一经接触跳台后,牵引绳就不再对运动员有作用力。
试求滑水运动员从飞离斜面到再落水时的水平长度。
解:接触跳台时 171136001024030..v =⨯=m/s 设运动员在斜面上无机械能损失7688442892171122020....gh v v =⨯⨯-=-=m/s 1418.cos v v x ==θm/s, 2563.sin v v y ==θm/s 5410221.g v h y ==m 33201.gv t y ==s 220121)(gt h h =+780.08.9)44.2541.0(2)(2012=+=+=g h h t s112.121=+=t t t s0591*******...t v x x =⨯==m7-2 图示消防人员为了扑灭高21m 仓库屋顶平台上的火灾,把水龙头置于离仓库墙基15m 、距地面高1m 处,如图所示。
水柱的初速度250=υm/s ,若欲使水柱正好能越过屋顶边缘到达屋顶平台,且不计空气阻力,试问水龙头的仰角α应为多少?水柱射到屋顶平台上的水平距离s 为多少? 解:(1) αcos v t 0115=(1) 2021sin 2110=-⋅gt t v α (2) (1)代入(2),得01.44cos sin 375cos 5002=+-ααα ααα22cos 1cos 3751.44cos 500-=+ 081.1944cos 96525cos 39062524=+-αα 22497.0cos 2=α, ︒=685.61α(2) gv t αsin 02=(到最高点所经过时间) 26.232)15cos (20=⨯-⋅=t v S αm7-3 图示三角形物块置于光滑水平面上,并以水平等加速度a 向右运动。
理论力学 第六版部分习题答案 第七章
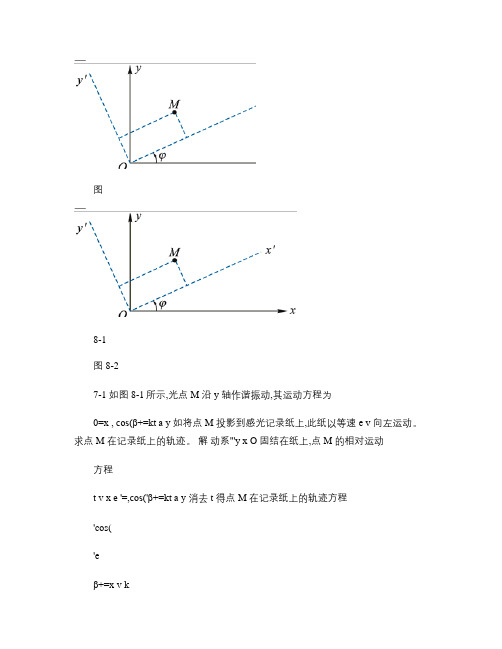
图8-1图8-27-1 如图8-1所示,光点M 沿y 轴作谐振动,其运动方程为0=x , cos(β+=kt a y 如将点M 投影到感光记录纸上,此纸以等速e v 向左运动。
求点M 在记录纸上的轨迹。
解动系'''y x O 固结在纸上,点M 的相对运动方程t v x e '=,cos('β+=kt a y 消去t 得点M 在记录纸上的轨迹方程'cos('eβ+=x v ka y 7-2 如图8-2所示,点M 在平面''y Ox 中运动,运动方程为cos 1(40't x −=,t y sin 40'= 式中t 以s 计,'x 和'y 以mm 计。
平面''y Ox 又绕垂直于该平面的轴O 转动,转动方程为rad t =ϕ,式中角ϕ为动系的'x 轴与定系的x 轴间的交角。
求点M 的相对轨迹和绝对轨迹。
解由点M 的相对运动方程可改写为t yt x sin 40cos 140''=−=⎟⎟⎠⎞⎜⎜⎝⎛−上2式两边平方后相加,得点M 的相对轨迹方程 1600'40'(22=+−y x 由题得点M 的坐标变换关系式ϕϕsin 'cos 'y x x −= ϕϕcos 'sin 'y x y +=将t =ϕ和相对运动方程代入,消去t 得点M 的绝对轨迹方程160040(22=++y x7-3 水流在水轮机工作轮入口处的绝对速度m/s 15a =v ,并与直径成°=60β角,如图8-3a 所示,工作轮的半径m 2=R ,转速r/min 30=n 。
为避免水流与工作轮叶片相冲击,叶片应恰当地安装,以使水流对工作轮的相对速度与叶片相切。
求在工作轮外缘处水流对工作轮的相对速度的大小方向。
′′v(a (b图8-3解水轮机工作轮入口处的1滴水为动点M ,动系固结于工作轮,定系固结于机架/地面(一般定系可不别说明,默认为固结于机架,下同;牵连运动为定轴转动,相对运动与叶片曲面相切,速度分析如图8-3b 所示,设θ为r v 与'x 轴的夹角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7-1. 在图示机构中,曲柄OA上作用一力偶,其矩为M,另在滑块D上作用水平力F。
机构尺寸如图所示。
求当机构平衡时,力F与力偶矩M的关系。
7-2. 图示桁架中,已知AD=DB=6m,CD=3m,节点D处载荷为P。
试用虚位移原理求杆3的内力。
7-3. 组合梁由铰链C 铰接AC 和CE 而成,载荷分布如图所示。
已知跨度l=8m ,P=4900N ,均布力q=2450N/m ,力偶矩M=4900N ⋅m ;求支座反力。
N 2450N 14700N 2450==-=E B A F F F ,,7-4 组合梁由水平梁AC 、CD 组成,如图所。
已知:F 1= 20kN ,F 2 = 12kN ,q = 4kN/m ,M = 2kN ·m 。
不计梁自重,试求:固定端A 和支座B 处的约束力。
组合梁由水平梁AC 、CD 组成,如图12-16a 所。
已知:F 1= 20kN ,F 2 = 12kN ,q = 4kN/m ,M = 2kN ·m 。
不计梁自重,试求:固定端A 和支座B 处的约束力。
2(a)(b)22(d )(e)图12-16 例题12-5图解:组合梁为静定结构,其自由度为零,不可能发生虚位移。
为能应用虚位移原理确定A 、B 二处的约束力,可逐次解除一个约束,代之以作用力,使系统具有一个自由度,并解除约束处的正应力视为主动力;分析系统各主动力作用点的虚位移以及相应的虚功,应用虚位移原理建立求解约束力的方程。
为方便计算,可事先算出分布载荷合力大小及作用点。
对于本例:22δrkN 41=⨯==q F F K H各作用点如图12-16b 所示,且HC = CK = 0.5m 。
1.计算支座B 处的约束力解除支座B ,代之以作用力F N B ,并将其视为主动力。
此时,梁CD 绕点C 转动,系统具有一个自由度。
设梁CD 的虚位移为ϕδ,则各主动力作用点的虚位移如图12-16b 所示。
应用虚位移原理,有0δ=∑F W ,0δ30sin δδδ2N =︒+--D B B K K r F M r F r F ϕ (a )图12-16b 中的几何关系,ϕϕϕδ2δ;δδ;δ5.0δ===D B K r r r将上述各式代入虚位移原理表达式(a ),有0δ)5.0(2N =+--ϕF M F F B K (b )因为0δ≠ϕ,于是,由式(b )求得支座B 的约束力为kN 125.02N =-+=M F F F K B (c )2.求固定端A 处的约束力偶解除A 端的转动约束,使之成为允许转动的固定铰支座,并代之以约束力偶M A , 将M A 视为主动力偶(图12-16c )。
这时,梁AC 和CD 可分别绕点A 、B 转动,系统具有一个自由度。
设梁AC 有一虚位移δβ,则梁AC 、CD 上各主动力作用点相应的虚位移如图12-16c 所示。
根据虚位移原理0δ=∑F W ,可得下述方程δ60cos δδδδδ21=-︒+---γβM r F r F r F r F M D K K H H E A(d )根据图12-6c 中所示之几何关系,各主动力作用点的虚位移分别为βγβγβγββδ2δδ,δδ5.0δδ2δ,δ5.1δ,δ5.0δ=======D K H E r r r r代入式(d ),得到0δ)25.15.0(21=-+---βM F F F F M K H A (e )由于 δβ≠0 ,所以m kN 1225.15.021⋅=+-++=M F F F F M K H A (逆时针转向)(f )3.求固定端A 处的水平约束力解除A 端的水平约束,使之变为只能水平移动、而不能铅直移动和自由转动的新约束(图12-16d ),视水平约束力F Ax 为主动力。
这时系统具有一个自由度,使梁AC 和CD 只能沿水平方向平动,设A 点有一水平虚位移δx A ,则其他主动力作用点,将产生如图12-16d 所示的虚位移。
应用虚位移原理,写出060sin δδ2=︒-D A Ax r F x F (g )由于系统水平平动,所以δx A =δ r D ,故上式为0δ)60sin (2=︒-A Ax x F F (h )因为 δx A ≠0,所以kN 3660sin 2=︒=F F Ax (i )4.求固定端A 处的铅垂约束力解除A 端的铅直约束,使之变成只能铅直移动,而不能水平移动和自由转动的新约束(图12-16e ),并视铅垂约束力F Ay 为主动力。
这时,梁AB 平动,梁CD 绕点B 转动,系统具有一个自由度。
设点A 有一铅垂虚位移δy A ,其余各主动力作用点及梁CD 的虚位移如图12-16e 所示。
应用虚位移原理,有0δδ30sin δδδδ21=-︒+---θM r F r F r F r F y F D K K H H E A Ay (j )由于梁AC 铅垂平动,梁CD 绕点B 转动,于是,由图12-16e 得到:ACA K AC H E y CBr y r y r r r δδδ,δ5.0δδδδδ======θ 将上述各式代入式(j ),得0δ)30sin 5.0(21=-︒+---A K H Ay y M F F F F F (k )因为 0δ≠A y ,故有kN 225.05.021=+-++=M F F F F F K H Ay7-5. 试求图示梁-桁架组合结构中1、2两杆的内力。
已知kN 41=F ,kN52=F 。
1.求杆1内力,给图(a )虚位移,虚功表达式为0cos δcos δδδ1N1N 21='++--ϕϕG F E D r F r F y F y F 因为θδ3δ=D y ,θδ2δ=Ey , θδ5δ=F r ,θδ5δ=G r所以053δ553δ5δ2δ31N1N 21=⋅⋅'+⋅⋅+⋅-⋅-θθθθF F F F 211N 236F F F +=31132211N =+=F F F kN (受拉)A2.求杆2内力,给图(b )虚位移,则θδ4δ=H r ,θδ3δ=D r θδ2δ=E r ,θδ5δ=G rF r δ,G r δ在FG 方向投影响相等,即ϕϕcos δcos δG F r r =G F r r δδ= 虚功式0sin δδδδN222N 1='----ϕF E H D r F r F r F r F即 054524δ3N222N 1=⋅δ⋅-δ⋅-δ⋅-⋅-θF θF θF θF 2223821N2-=--=F F F kN4112N -=F kNA7-6. 在图示结构中,已知F = 4kN ,q = 3kN/m ,M = 2kN · m ,BD = CD ,AC = CB = 4m ,θ = 30º。
试求固定端A 处的约束力偶MA 与铅垂方向的约束力F Ay 。
解:解除A 处约束力偶,系统的虚位移如图(a )。
0δsin δ2δ=-+D A r F r q M θϕ(1)其中:ϕδ1δ⋅=r ;ϕδ4δδδ⋅===B D C r r r代入式(1)得:B0δ)sin 42(=-+ϕθF q M A m kN 22sin 4⋅=-=q F M A θ解除A 处铅垂方向位移的 约束,系统的虚位移如图(b )。
应用虚位移原理:0δδ2cos δ=+-BC D A Ay M r F r F ϕθ (2)其中:BC C A r r ϕθδcos 4δδ==;BC D r ϕδ2δ=代入式(2)得:0δ)22cos cos 4(=+⋅-⋅BC Ay M F F ϕθθ;kN 577.030cos 41=︒-⋅=M F F Ay7-7. 图示结构由三个刚体组成,已知F = 3kN ,M = 1kN · m ,l = 1m 。
试求支座B 处的约束力。
r E(a )解:解除B 处约束,系统的虚位移如图(a )。
应用虚位移原理:δδsin δ=+--F CE B B r F M r F θϕ(1) 其中:101sin =ϕ;CEF E l r r θδ4δ2δ==;CE C l r θδ23δ=;CE C B lr l r θδ23δ10δ== 代入式(1)得:0δ)2(=⋅+--CE B l F M l F θ;kN 52=⋅+-=l F M F B7-8. 在图示刚架中,已知F = 18kN ,M = 4.5kN · m ,l1 = 9m ,l2 = 12m ,自重不计。
试求支座B 处的约束力。
解:解除B虚位移如图(a )。
应用虚位移原理:0δδ=+F Bx Bx r F r F(1)其中:D B D B Bx l OB r θθδ2δδ2=⋅=;DB D OD r θδδ⋅=;DB DF l l ADr r θδδδ22=⋅=代入式(1)得:0δ)2(22=⋅+⋅D B Bx l F l F θδ(a )kN 92-=-=FF Bx 解除B 处铅垂方向位移的约束,系统的 虚位移如图(b )。
应用虚位移原理:0δδδ=+-CE F By By M r F r F θ(2)其中:D B D B By l AB r θθδ2δδ1=⋅=;DB D OD r θδδ⋅=;DB DF l l ADr r θδδδ22=⋅=CE D B E OE AE r θθδδδ⋅=⋅=;DB CE OEAEθθδδ⋅=且:15l AE =;125l OE =;则:DB CE θθδ2δ=代入式(2)得:0δ)22(21=+⋅-⋅D B By M l F l F θ;kN 5.112212=-=l MFl F By。
