直线中点Bresenham算法
中点bresenham算法过程

中点Bresenham算法是一种用于计算在直线上的格点的算法。
它是由Bresenham在1965年提出的,是一种高效的计算机图形学算法,通常用于直线、圆、椭圆等形状的绘制。
通过这篇文章,我们将详细介绍中点Bresenham算法的过程。
1. 背景知识在计算机图形学中,我们经常需要在屏幕上绘制直线、圆、椭圆等形状。
而计算机屏幕上的图像是由像素组成的,因此我们需要一种算法来计算出这些形状上的像素坐标,从而进行绘制。
中点Bresenham算法就是用来解决这个问题的。
2. 中点Bresenham算法的原理中点Bresenham算法的原理是通过巧妙的数学推导,找到离直线最近的像素点,从而确定需要绘制的像素坐标。
该算法通过利用误差项来判断下一个像素点的位置,具有高效、简洁的特点。
3. 中点Bresenham算法的过程中点Bresenham算法的过程可以分为以下几个步骤:3.1 初始化变量:首先需要确定直线的起点和终点,并初始化相关变量,如起点坐标(x0, y0)、终点坐标(x1, y1)、误差项d和增量变化量dx、dy等。
3.2 计算斜率k和误差项初始值:通过计算直线的斜率k,并根据斜率确定误差项的初始值。
3.3 循环计算像素点的坐标:根据误差项的大小,确定下一个像素点的位置,并更新误差项的值,直到绘制完整条直线。
4. 中点Bresenham算法的优势* 算法简洁高效:中点Bresenham算法通过简单的数学计算,即可确定直线上的像素坐标,避免了直接计算斜率导致的浮点数运算,因此在计算速度上具有较大优势。
* 适用范围广泛:中点Bresenham算法不仅适用于直线,还可以用于绘制圆、椭圆等图形,具有良好的通用性。
5. 中点Bresenham算法的应用中点Bresenham算法广泛应用于计算机图形学中的直线、圆、椭圆等图形的绘制。
其高效、简洁的特点使得它成为了计算机图形学中不可或缺的算法之一。
中点Bresenham算法是计算机图形学中的重要算法之一,通过巧妙的数学计算,实现了高效、简洁的直线绘制。
生成直线的bresenham算法

生成直线的bresenham算法
Bresenham算法是由Jack E. Bresenham在1962年提出的一种用于生成直线图形的算法。
它可以根据两个点的坐标来计算出中间所有点的位置,即通过这两个端点可以确定出整条直线的像素点。
Bresenham算法的核心思想是,沿着已知的两个点之间的点,从起点开始向终点靠近,沿途计算斜率的误差,依据误差大小判断是选择水平方向或者垂直方向上的点,从而确定最终的直线图形。
具体步骤如下:
(1)根据两个点坐标计算出斜率dx和dy;
(2)令x0=x1, y0=y1;
(3)计算当前点处斜率误差p,公式为:p=2dy-dx;
(4)根据p的大小,决定下一步是沿水平方向还是垂直方向:
(a)p>0时,下一步沿垂直方向前进,即y++;
(b)p<=0时,下一步沿水平方向前进,即x++;
(5)重复步骤3、4,直到到达终点。
直线的Bresenham算法
生成直线的B resenham算法从上面介绍的DDA算法可以看到,由于在循环中涉及实型数据的加减运算,因此直线的生成速度较慢。
在生成直线的算法中,B resenham算法是最有效的算法之一。
B resenham算法是一种基于误差判别式来生成直线的方法。
一、直线Bresenham算法描述:它也是采用递推步进的办法,令每次最大变化方向的坐标步进一个象素,同时另一个方向的坐标依据误差判别式的符号来决定是否也要步进一个象素。
我们首先讨论m=△y/△x,当0≤m≤1且x1<x2时的B resenham算法。
从DDA直线算法可知这些条件成立时,公式(2-2)、(2-3)可写成:x i+1=x i+△x(2-2)y i+1=y i+△y(2-3)x i+1=x i+1 (2-6)y i+1=y i+m(2-7)有两种B resenham算法思想,它们各自从不同角度介绍了B resenham算法思想,得出的误差判别式都是一样的。
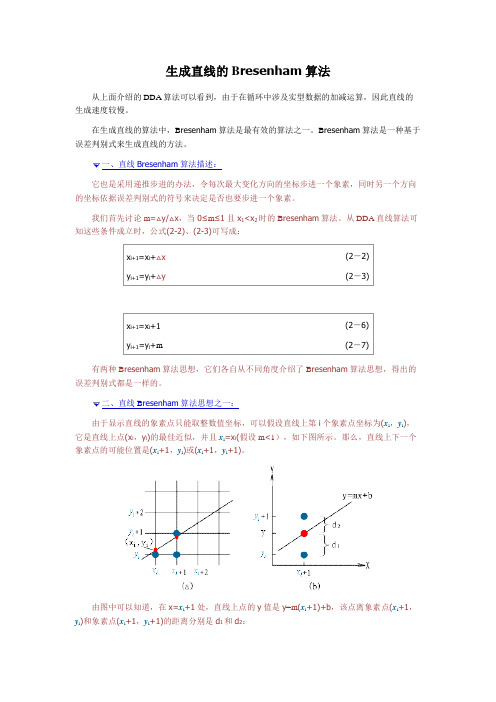
二、直线B resenham算法思想之一:由于显示直线的象素点只能取整数值坐标,可以假设直线上第i个象素点坐标为(x i,y i),它是直线上点(x i,y i)的最佳近似,并且x i=x i(假设m<1),如下图所示。
那么,直线上下一个象素点的可能位置是(x i+1,y i)或(x i+1,y i+1)。
由图中可以知道,在x=x i+1处,直线上点的y值是y=m(x i+1)+b,该点离象素点(x i+1,y i)和象素点(x i+1,y i+1)的距离分别是d1和d2:这两个距离差是我们来分析公式(2-10):(1)当此值为正时,d1>d2,说明直线上理论点离(x i+1,y i+1)象素较近,下一个象素点应取(x i+1,y i+1)。
(2)当此值为负时,d1<d2,说明直线上理论点离(x i+1,y i)象素较近,则下一个象素点应取(x i+1,y i)。
案例2直线中点Bresenham算法

总结
主教材《计算机图形学基础教程(Visual C++版)》中仅 介绍了斜率0≤k≤1直线段的中点Bresenham扫描转换算法。
本案例基于该算法实现的CLine类的成员函数类似于CDC
类的MoveTo()函数和LineTo()函数,可以使用鼠标绘制任意斜 率的直线段。
案例描述
在窗口客户区内按下鼠标左键选择直线
的起点,移动鼠标指针到直线终点,弹起鼠
标左键绘制任意斜率的直线段。
效果图
图2-1 效果图
原理算法
MFC提供的CDC类的成员函数MoveTo()和LineTo()函
数用于绘制任意斜率的直线段,直线段的颜色由所选用的 画笔指定。MoveTo()函数移动当前点到参数(x,y)所指定 的点,不画线;LineTo()函数从当前点画一直线段到参数( x,y)所指定的点,但不包括(x,y)点。
计算机图形学实践教程(VisualC++版)(第2版)
案例2 直线中点Bresenham算法
孔令德 太原工业学院计算机工程系 2017.1.10
知识点
斜率0≤k≤1直线的中点Bresenham算法。
任意斜率直线段绘制算法。 颜色类的定义与调用方法。 直线类的定义与调用方法。 鼠标按键消息映射方法。
原理算法
图2-2 直线段的斜率对称性
程序代码
d=0.5-k; for(p=P0;p.x<P1.x;p.x++) { pDC->SetPixelV(Round(p.x),Round(p.y), RGB(clr.red*255,clr.green*255,clr.blue*255)); if(d<0) { p.y++; d+=1-k; } else d-=k; } }
第4讲 中点Bresanham算法

15
0≤k≤1 0≤k≤1 0≤k≤1时Bresenham算法的算法步骤 算法步骤为: 算法步骤 1.输入直线的两端点P0(x0,y0)和P1(x1,y1). 2.计算初始值△x,△y,d=0.5-k,x=x0,y=y0; 3.绘制点(x,y).判断d的符号; 若d<0,则(x,y)更新为(x+1,y+1),d更新为d+1-k; 否则(x,y)更新为(x+1,y),d更新为d-k. 4.当直线没有画完时,重复步骤3.否则结束. 参见程序brsham0.c 参见程序
判别式: 判别式
1≤k 1≤k
d = F ( xM , yM ) = F ( xi + 0.5, yi + 1) = yi + 1 k ( xi + 0.5) b
则有:
x x= x + 1
( d < 0) ( d ≥ 0)
Q P (x i +1,yi +1) u M
i
P(xi ,yi )
2010-7-27 信息科学与工程学院 23
2010-7-27 信息科学与工程学院 2
5.1.1 数值微分法 DDA法) 数值微分法(
直线的微分方程:设两端点为P(x0,y0), P(x1,y1)
dy y y1 y0 = = =k dx x x1 x0
DDA算法原理: DDA算法原理: 算法原理
由于直线的一阶导数是连续的,而且对于△x和△y 是成比例的,因此,可通过在当前位置(xi,yi )上分 别加上2个小增量ε△x和ε△y(ε为无穷小的正数)来 求出下一点的坐标(xi+1,yi+1) ,如图所示:
2010-7-27 信息科学与工程学院 16
Bresenham算法-直线光栅化算法

Bresenham算法是计算机图形学典型的直线光栅化算法。
∙从另一个角度看直线光栅化显示算法的原理o由直线的斜率确定选择在x方向或y方向上每次递增(减)1个单位,另一变量的递增(减)量为0或1,它取决于实际直线与最近光栅网格点的距离,这个距离的最大误差为0.5。
∙1)Bresenham的基本原理o假定直线斜率k在0~1之间。
此时,只需考虑x方向每次递增1个单位,决定y方向每次递增0或1。
设直线当前点为(xi,y)直线当前光栅点为(xi,yi)则下一个直线的点应为(xi+1,y+k)下一个直线的光栅点或为右光栅点(xi+1,yi)(y方向递增量0)或为右上光栅点(xi+1,yi+1)(y方向递增量1)记直线与它垂直方向最近的下光栅点的误差为d,有:d=(y+k)–yi,且0≤d≤1当d<0.5:下一个象素应取右光栅点(xi+1,yi)当d≥0.5:下一个象素应取右上光栅点(xi+1,yi+1)如果直线的(起)端点在整数点上,误差项d的初值:d0=0,x坐标每增加1,d的值相应递增直线的斜率值k,即:d=d + k。
一旦d≥1,就把它减去1,保证d的相对性,且在0-1之间。
令e=d-0.5,关于d的判别式和初值可简化成:e的初值e0= -0.5,增量亦为k;e<0时,取当前象素(xi,yi)的右方象素(xi+1,yi);e>0时,取当前象素(xi,yi)的右上方象素(xi+1,yi+1);e=0时,可任取上、下光栅点显示。
Bresenham算法的构思巧妙:它引入动态误差e,当x方向每次递增1个单位,可根据e 的符号决定y方向每次递增 0 或 1。
e<0,y方向不递增e>0,y方向递增1x方向每次递增1个单位,e = e + k因为e是相对量,所以当e>0时,表明e的计值将进入下一个参考点(上升一个光栅点),此时须:e = e - 1∙2)Bresenham算法的实施——Rogers 版o通过(0,0)的所求直线的斜率大于0.5,它与x=1直线的交点离y=1直线较近,离y=0直线较远,因此取光栅点(1,1)比(1,0)更逼近直线;o如果斜率小于0.5,则反之;o当斜率等于0.5,没有确定的选择标准,但本算法选择(1,1)(程序)▪//Bresenham's line resterization algorithm for the first octal.▪//The line end points are (xs,ys) and (xe,ye) assumed not equal.▪// Round is the integer function.▪// x,y, ∆x, ∆y are the integer, Error is the real.▪//initialize variables▪x=xs▪y=ys▪∆x = xe -xs▪∆y = ye -ys▪//initialize e to compensate for a nonzero intercept▪Error =∆y/∆x-0.5▪//begin the main loop▪for i=1 to ∆x▪ WritePixel (x, y, value)▪if (Error ≥0) then▪ y=y+1▪ Error = Error -1▪ end if▪ x=x+1▪ Error = Error +∆y/∆x▪next i▪finish∙3)整数Bresenham算法o上述Bresenham算法在计算直线斜率和误差项时要用到浮点运算和除法,采用整数算术运算和避免除法可以加快算法的速度。
DDA法,中点法,Bresenham法画直线

实验名称 DDA 法,中点法,Bresenham 法画直线一、实验目的学会用DDA 法,中点法,Bresenham 法这三种思想画直线,同时,对画直线的操作有一定的了解。
二、实验原理及内容1. DDA 法的基本思想如下:已知过端点P0(x0,y0) , P1(x1,y1)的直线段L :y=kx+b ,直线斜率为k=(y1-y0)/x1-x0 ,从x 的左端点x0开始,向x 右端点步进。
步长=1(个象素),计算相应的y 坐标y=kx+b ;取象素点(x, round(y))作为当前点的坐标。
2. 中点法的基本思想如下:当前象素点为(xp, yp) 。
下一个象素点为P1 或P2 。
设M=(xp+1, yp+0.5),为p1与p2之中点,Q 为理想直线与x=xp+1垂线的交点。
将Q 与M 的y 坐标进行比 较。
当M 在Q 的下方,则P2 应为下一个象素点;M 在Q 的上方,应取P1为下一点。
构造判别式:d=F(M)=F(xp+1,yp+0.5)=a(xp+1)+b(yp+0.5)+c ,其中a=y0-y1, b=x1-x0, c=x0y1-x1y0当d<0,M 在L(Q 点)下方,取右上方P2为下一个象素;当d>0,M 在L(Q 点)上方,取右方P1为下一个象素;当d=0,选P1或P2均可,约定取P1为下一个象素;但这样做,每一个象素的计算量是4个加法,两个乘法。
采用增量算法改进如下:d 是xp, yp 的线性函数,因此可采用增量计算,提高运算效率。
若当前象素处于d 0情况,则取正右方象素P1 (xp+1, yp), 要判下一个象素位置,应计算d1=F(xp+2, yp+0.5)=a(xp+2)+b(yp+0.5)+c=d+a ; 增量为a ,若d<0时,则取右上方象素P2 (xp+1, yp+1)。
要判断再下一象素,则要计算d2= F(xp+2, yp+1.5)=a(xp+2)+b(yp+1.5)+c=d+a+b ;增量为a +b画线从(x0, y0)开始,d 的初值d0=F(x0+1, y0+0.5)=F(x0, y0)+a+0.5b =a+0.5b 。
布雷森汉姆直线算法

布雷森汉姆直线算法布雷森汉姆直线算法(Bresenham's Line Algorithm)是一种计算机图形学中常用的直线绘制算法,其通过在离散的像素格上选择最接近实际直线路径的点来实现高效绘制直线的目的。
该算法由Jack Elton Bresenham在1962年首次提出,被广泛应用于图形显示、打印机及数码扫描仪等领域。
布雷森汉姆直线算法的核心思想是利用整数运算来代替浮点运算,从而提高计算效率。
该算法通过仅使用加法、减法和位移等基本运算,不需要乘法运算和浮点数运算,从而适用于资源有限的嵌入式系统和低成本的图形设备。
算法的基本步骤如下:1. 根据起点P1(x1,y1)和终点P2(x2,y2)确定直线斜率k。
2. 如果|k|≤1,则沿x轴方向递增遍历起点P1到终点P2,并在每个像素上绘制。
若k>1,则沿y轴方向递增遍历P1到P2,绘制每个像素。
3. 对于每一步,根据递增的方向选择相应的像素。
4. 根据斜率k来决定误差累积量,调整绘制位置,保证直线的连续性。
该算法的优势在于其简单而高效的原理,使得绘制直线的速度非常快。
与传统的基于浮点运算的算法相比,布雷森汉姆直线算法的计算开销较小,而且能够得到非常接近实际直线路径的结果,几乎没有明显的视觉差异。
这使得该算法在计算资源有限的场景下非常有用,例如在嵌入式系统中,可以利用该算法绘制图形界面的边界、线条等。
然而,布雷森汉姆直线算法也存在一些局限性。
由于只考虑了整数坐标,因此绘制出来的直线可能会有些锯齿状,这在一些高精度要求的场景下可能会表现出明显的视觉噪点。
此外,该算法仅适用于绘制直线,并不能直接应用于曲线、圆等其他形状的绘制。
总之,布雷森汉姆直线算法是一种非常经典和实用的绘制直线的算法。
它通过巧妙地利用整数计算来取代浮点计算,以提高效率和减少计算资源开销。
虽然存在一些局限性,但在大多数场景下,它仍然是一种高效且精确的绘制直线的选择,对于计算机图形学的发展和应用有着重要的指导意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
}
void CTestView::Mbline(double x0, double y0,double x1,double y1) //直线中点Bresenham函数
{
CClientDC dc(this);
rgb=RGB(255,0,0); //定义直线颜色为红色
double x,y,d,k;
void CTestView::OnMENUMbline()//菜单函数
{
InputDlg dlg;
if(dlg.DoModal()==IDOK)
{
AfxGetMainWnd()->SetWindowText(":直线中点Bresenham算法");
RedrawWindow();
Mbline(dlg.m_x0,dlg.m_y0,dlg.m_x1,dlg.m_y1);
5.如果当前点x小于x1,重复步骤4,否则结束。
源程序:
1)// TestView.h
#include "InputDlg.h"//对话框头文件
#define ROUND(a) int(a+0.5)
class CTestView : public CView
{
…..
}
2)//TestView.cpp
实验一基本图形生成算法
实验目的:
掌握中点Bresenham绘制直线的原理
设计中点Bresenham算法
编程实现中点Bresenham算法
实验描述:
使用中点Bresenham算法绘制斜率为0≤k≤1的直线。
算法设计:
直线中点Bresenham算法
1.输入直线的起点坐标P0(x0,y0)和终点坐标P1(x1,y1)。
x=x0;y=y0;k=(y1-y0)/(x1-x0);d=0.5-k;
for(x=x0;x<=x1;x++)
{
dc.SetPixel(ROUND(x),ROUND(y),rgb);
if(d<0)
{
y++;
d+=1-k;
}
else
d-=k;
}
}
运行结果:
2.定义直线当前点坐标x,y、定义中点偏差判别式d、定义直线斜率k、定义像素点颜色rgb。
3.x=x0,y=y0,计算d=0.5-k,k=(y1-y0)/(x1-x0),rgb=RGB(0,0,255)。
4.绘制点(x,y),判断d的符号。若d<0,则(x,y)更新为(x+1,y+1),d更新为d+1-k;否则(x,y)更新为(x+1,y),d更新为d-k。
