交叉耦合吸收滤波器的设计
实验一交叉耦合滤波器设计与仿真设计

实验一交叉耦合滤波器设计与仿真、实验目的1. 设计一个交叉耦合滤波器2. 查看并分析该交叉耦合滤波器的 S 参数 、实验设备装有HFSS 13.0软件的笔记本电脑一台 三、实验原理具有带外有限传输零点的滤波器,常常采用谐振腔多耦合的形式实现。
这种形式的特点是在谐振腔级联的基础上,非相邻腔之间可以相互耦合即“交叉耦合” ,甚至可以采用源与负载也向多腔耦合,以及源与负载之间的耦合。
交叉耦合带通滤波器的等效电路如下图所示。
在等效电路模型中, el 表示激励电压源,R1、R2分别为电源内阻和负载电阻, ik(k=1,2,3,…,N )表示各谐振腔的回路电流,Mij 表示第i 个谐振腔与第k 个谐振腔之间的互耦合系数(i,j=1,2,…,N ,且i 丰j) o 在这里取3 0=1,即各谐振回路的电感L 和电容C 均取单位值。
Mkk ( k=1,2,3,…,N )表示各谐振腔的自耦合系数。
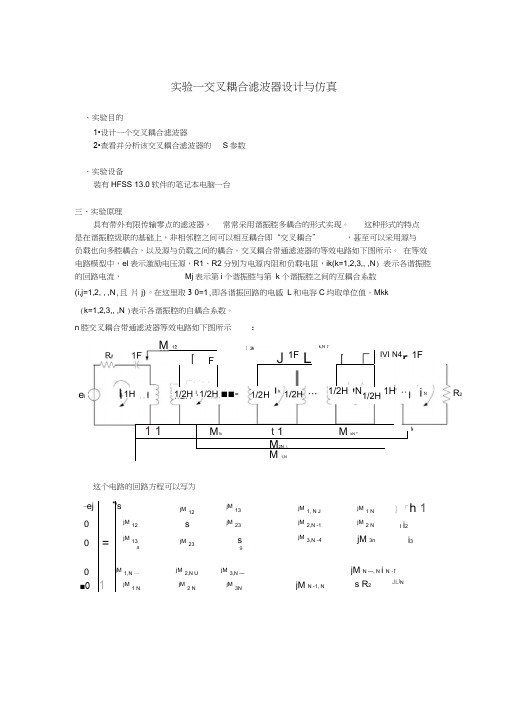
n 腔交叉耦合带通滤波器等效电路如下图所示:这个电路的回路方程可以写为e 1 R 1sjM 12 jM 13 jM 1, N 1 jM 1 N i 1 0 jM 12sjM 23jM2,N 1jM 2 Ni 2 0 jM 13jM 23sjM 3 ,N 1 jM 3ni 30 jM 1 ,N 1 jM 2, N 1 jM 3 ,N 1s jM N 1 , N i N 1 0jM 1 NjM 2 NjM 3NjM N 1,Ns R 2i Ne 1M121F1M2k1FMk,N 1.1F1,N1F1 1皿恢rMkN 'M 2,N 1或者写成矩阵方程的形式:E ZI (sU ° jM R)lR 1k1,N其中,s一般来讲,频率都归一成1,即0=1,则jM ij j M j j 0M ij其中E为电压矩阵,1为电流矩阵,Z为阻抗矩阵,Z sU o jM0 RU0是NX N阶单位矩阵。
M是耦合矩阵,它是一个NX N阶方阵,形式如下:0M 12M 13M 1, N 1M 1 NM 120M 23M 2,N 1M 2 NM 13M M 230M 3, N 1M 3 NM 1, N 1M 2, N 1M 3 , N 10M N 1, NM 1 N M 2 N M 3N M N 1, N0其中对角线上的兀素代表每一个谐振腔回路的自耦合,表示每一个谐振腔的谐振频率fi与中心频率f0之间的偏差。
实验一交叉耦合滤波器设计与仿真
实验一交叉耦合滤波器设计与仿真、实验目的1•设计一个交叉耦合滤波器2•查看并分析该交叉耦合滤波器的S参数、实验设备装有HFSS 13.0软件的笔记本电脑一台三、实验原理具有带外有限传输零点的滤波器,常常采用谐振腔多耦合的形式实现。
这种形式的特点是在谐振腔级联的基础上,非相邻腔之间可以相互耦合即“交叉耦合”,甚至可以采用源与负载也向多腔耦合,以及源与负载之间的耦合。
交叉耦合带通滤波器的等效电路如下图所示。
在等效电路模型中,el表示激励电压源,R1、R2分别为电源内阻和负载电阻,ik(k=1,2,3,, ,N) 表示各谐振腔的回路电流,Mj表示第i个谐振腔与第k个谐振腔之间的互耦合系数(i,j=1,2, , ,N,且片j)。
在这里取3 0=1,即各谐振回路的电感L和电容C均取单位值。
Mkk(k=1,2,3,, ,N )表示各谐振腔的自耦合系数。
n腔交叉耦合带通滤波器等效电路如下图所示:l i 1H丄F J 1F L丨「IVI N4r 1F y1 ----广、'、、L f A1 1M1k t 1M kN *'iM2N人M 1,N_ej■'s jM12jM130jM12s jM23 0=jM13a jM23s9 0jM1,N 一jM2,N U jM3,N —■0 一11jM1 NjM2 NjM3NjM1, N JjM1 NjM2,N -1jM2 NjM3,N -4jM 3njM N —, N i N -1jM N -1, N s R2 JL|N MR i e ik,N 11/2H 'N1/2H 1H1/2H i21/2H ■■-R2这个电路的回路方程可以写为〕「h 1I i2i3或者写成矩阵方程的形式:E = ZI二(sU0• jM R)I般来讲,频率都归一成 1,即0=1,则jM ij j M 厂 j 0M ij其中E 为电压矩阵,I 为电流矩阵,Z 为阻抗矩阵,U0是N X N 阶单位矩阵。
交叉耦合滤波器设计正文

第一章滤波器简介和设计思想1、滤波器概念和简介滤波器是通信工程中常用的重要器件,它对信号具有频率选择性,在通信系统中通过或阻断、分开或合成某些频率的信号。
虽然滤波器的物理实现形式多种多样,但其等效电路网络的拓扑结构是相同的。
显然,滤波器的设计要根据各种因素综合考虑。
通常的,滤波器设计中考虑的主要因素有:●体积和重量●品质因数Q●带宽●调谐范围●耦合结构●功率容量●造价根据不同的波段和应用,各种形式的滤波器可以简单的列表见表1.1,其滤波器实物见图1.1。
表1.1 滤波器工程应用频段UHF L/S C X/Ku Ka工艺SAW螺旋介质梳状平面波导梳状SAW介质平面高温超导波导介质波导高温超导平面梳状介质波导平面波导介质平面应用移动通信卫星通信PCS卫星通信MMDS卫星通信卫星通信链接LMDS卫星图1.1 不同形式的滤波器实物照片2、综合,还是优化传统的滤波器设计,采用网络综合的方法。
所谓网络综合,是预先规定元器件特性而用网络去实现的一个过程。
它大致包括三个步骤:提出目标,即理想响应;选用可能的函数去逼近理想响应;设法实现具有逼近函数特性的网络。
由于采用的逼近函数不同,一般有Butterworth综合、Chebyshev综合、椭圆函数综合等滤波器设计方法。
计算机技术的不断发展为滤波器优化设计提供了可能。
是采用综合的方法,还是采用优化的方法完成滤波器设计呢?它们各自的特点见表1.2。
表1.2 综合与优化设计方法的比较综合优化明确的数学和物理意义可能是最优的有效的需要特定的函数有时是困难和耗时的理论较少,更实际公式简单适应市场需要非特定规划的可能是低效率、耗时和非唯一的近年来,随着计算机计算能力的急剧提高和全波电磁仿真软件(如Ansoft)的大力发展,优化的方法好像越来越有效和简单。
但是,无论计算能力多么巨大,仿真软件如何优秀,单纯地依赖优化的方法仍然有其固有的局限性。
首先,优化的方法需要确定优化的变量和代价函数,通常代价函数可以采用实际响应和理想响应的差距,而优化变量的确定就复杂得多,实际中常常是已确定网络的拓扑,优化元件值;或者已确定基本的结构优化物理尺寸等等。
交叉耦合腔体滤波器的设计与实现

系求解 传输零 点的方法 设计 阻带 任 意幅度 特性 的滤波 器 , 需要求解 一系 列的非线性 方 程组 , 当传 输零 点 个数 多 于 且 2 个时 , 较为繁琐 口。文献[] 已给 定的滤 波器 设计 计算 ] 2在
指标 的基础上 , 根据 带 内反 射 和带外 衰减 之 和 的关 系可 以 达到确定 滤波 器零点位 置 的 目的 , 求解 过程 中所需 的判 但 断范 围具 有一定 的随意 性 。 本 文 结合 以上 2种方 法 , 利用 带 内反 射 和带 外 衰减
Kewo d :g n r l e y h v ta s s in z rs o pi ti ;r s—o pig f tr y rs e e a b s e ;rn miso eo ;c u l marx co sc u l i es Ch g n n l
O 引
言
素 。在通常 的设计 中 , 传输 零 点 的位置 往往 是根 据 经验或 反复 实验来 进 行 人 为 的确 定 。采 用 由广 义 C e yh v函 hbse
微波滤波 器是 雷 达 系统 、 信 系统 、 量 系 统等 系统 通 测
中最 常见的元器 件之 一 , 性 能 的优劣 往往 直 接影 响 到整 其
个系 统的质 量 。广义 切 比雪 夫 滤 波 器在 通 带 内产生 等 波
数 的极 值特性 推 导 出传 输 极值 点 频 率与 传 输 零点 的 关 系
方法 ; 基于提出的分析模 型, A sf HF S建立同轴腔体滤 波器 , 用 n ot S 对谐振 腔的本征频率 、 合系数 、 耦 抽头位 置进行仿 真计算。通过 90 6 MHz 交叉耦合滤波器实例设计验证 了该综合方法 的有效性 。 关键词 :广义 c e yh v 传输零点 ; 合矩 阵; h b se ; 耦 交叉耦合 滤波器
ku波段微带交叉耦合带通滤波器的结构与设计

微带交叉耦合滤波器的结构及设计
微带交叉耦合滤波器是一种金属剩余波段滤波器,可用于宽带信号过
滤和多波段分频。
它具有良好的带宽和相邻频段泄漏特性。
该过滤器
可以用于装备移动通信系统中信号分离和信号过滤的作用,能够提供
低阻抗和低损耗的优良特性,专业用于移动电话和交流通信领域。
沙坑式的微带交叉耦合滤波器由沙坑状的3D加减结构构成,是使用双阈值材料或多层次局部片加制成的微带结构。
该滤波器的阻尼相关特
性依赖于局部片的体积空间分布,其带宽与耦合系数有很大的相关性。
微带交叉耦合滤波器的设计参数有耦合率(CG)、匹配环节带宽(BW)、插入损耗(IL)、输出不平衡(IOI)、通带截止损耗
(C2L)、抑制条件(SC)等。
而在进行设计时,还需考虑其他一些
参数,例如材料的元件尺寸、表面贴装技术等。
微带交叉耦合滤波器设计要充分考虑以上参数,保证设计满足要求,
并保证设备质量,便于量产质量表现。
微带交叉耦合滤波器通常采用
物理设计与电子装配相结合的设计方案,进口物理设计,并采用平高
压双面玻璃板精确玻璃图解画出其形状,完成布线方案,至于电子装配,则需要采用品牌IC、品牌元件、抗干扰技术、高精度的装配技术,这样才能保证微带交叉耦合滤波器的品质和性能,并最大程度满足客
户的要求。
一种新型交叉耦合微带滤波器的设计

一种新型交叉耦合微带滤波器的设计
一种新型交叉耦合微带滤波器的设计
曹锐;孙振鹏
【摘要】文章通过对当前一种先进微带滤波器进行等效电路分析,并进行多方位的仿真和拟合计算,最终设计出6阶高选择性微带滤波器,理论分析和全波仿真结果近似一致;该滤波器不仅尺寸小,而且通带性能好,带外抑制度高;可广泛应用于平面电路中,在MMIC、超导技术等先进电路中也有很高的使用价值.
【期刊名称】《合肥工业大学学报(自然科学版)》
【年(卷),期】2006(029)004
【总页数】4页(P444-447)
【关键词】微带滤波器;开环谐振器;耦合系数
【作者】曹锐;孙振鹏
【作者单位】华东电子工程研究所,安徽,合肥,230031;合肥工业大学,电气与自动化工程学院,安徽,合肥,230009;华东电子工程研究所,安徽,合肥,230031
【正文语种】中文
【中图分类】工业技术
第 29 卷第 4 期 2006 年 4 月合肥工业大学学报(自然科学版)JOURNAL OF HEFEi UNIVERSITY OF TECHNOLOGY Vol.29No.4Apr.2006 一种新型交叉搞合微带滤波器的设计曹锐J,2 ,孙振鹏1(1.华东电子工段研究所.安徽合肥 230031 : 2.合肥工业大学电气与自动化工程学院.安徽合肥230009)摘要:文章通过对当前一种先进微带滤波器进行等效电路分析,并进行多方位的仿真和拟合计算,敲终。
交叉耦合滤波器的综合设计

构造一组满秩基 rank(T)=N
T1k T2k T1,N 1 T1N
T
TNk TNk TN ,N 1 TNN
保持 T 的首尾行不变!对这组基进行正交变换,就能得到一组标准正交基,即正交矩
阵 T。
最后由 M T T t 求出耦合矩阵。
以上求解的是源阻抗和负载归一化后的耦合矩阵,去归一化的方法为:
同理,在奇阶情况下
§从短路导纳参数提取耦合矩阵
Ref. Richard J. Cameron “General Coupling Matrix Synthesis Methods for Chebyshev Filtering Functions”
============================================================
定义网络传输函数 S 21 s ,反射系数 S11 s ,特征函数 CN s ,三者满足:
CN
S11 S21
-----①
----②
双端口无损网络能量守恒
----③
由①②③看出,3 种网络参数都可以表示成 2 个多项式的比值。
其中
特征函数应具有 N 阶切比雪夫特性: 1 时 CN 1, 1时 CN 1, 1 时 CN 1
将 N 阶交叉耦合滤波器器视为一个二端口网络(上上图),并对源阻抗和负载进行归一 化(上图),得到系统导纳矩阵:
“交叉耦合网络模型”一节中讨论过 N 阶谐振网络的环路方程组 计算该双端口网络的短路导纳参数
由于 M 是实对称矩阵,有以下结论: 1. M 的特征值均为实数,
2. 对应于两个不同的特征值的两个特征向量是正交的 存在 N×N 阶正交矩阵 T,满足
---------------------------------------------------------------------------------------------------------------------端口电压电流(V1 V2 I1 I2) → 入射/反射波电压(a1 b1 a2 b2) → 散射矩阵参数(S11 S21) Ref. Jia-Sheng Hong “Microstrip Filters for RF Microwave Applications” 2.1&2.2 ----------------------------------------------------------------------------------------------------------------------
波导腔体与交叉耦合滤波器的设计的开题报告

波导腔体与交叉耦合滤波器的设计的开题报告一、研究背景现代通信技术发展迅速,高速传输和数据处理技术得到了广泛的应用和推广,大大提高了通信网络的数据传输速率和质量。
而波导技术作为一种传输高频电磁波的技术,在通信领域中也得到了广泛的应用。
波导腔体是一种常见的波导导体结构,是由几何形状不同的导体构成的空腔,可以用于实现滤波、功率分配等功能。
交叉耦合滤波器在波导腔体中实现,可以实现高品质因子、低插入损耗和高功率处理能力的滤波器。
二、研究内容本文研究波导腔体与交叉耦合滤波器的设计,主要包括以下几个方面:1. 波导腔体的设计:选择合适的材料和尺寸,设计波导腔体的几何形状,以实现所需的滤波功能。
2. 交叉耦合结构的设计:通过调节交叉结构的材料、尺寸和形状等参数,实现波导腔体中的交叉耦合效应,达到所需的滤波性能。
3. 仿真分析:通过ANSYS等仿真工具对所设计的波导腔体和交叉耦合滤波器进行仿真分析,验证其滤波性能和工作特点。
4. 实验验证:通过实验验证设计的波导腔体和交叉耦合滤波器的性能和可行性,优化设计和改进实验结果。
三、研究意义与价值波导技术和交叉耦合滤波器的研究与应用,具有重要的意义和价值:1. 提高通信网络的传输速率和质量,促进通讯技术的发展。
2. 提升滤波器的工作性能和能力,提高其市场竞争力。
3. 促进波导技术的应用和推广,推动相关科研领域的发展。
4. 对于电子制造、机械制造等相关领域的发展,也会有积极的推动作用。
四、研究方法和技术路线本文主要采用“理论分析-电磁仿真-实验验证”的研究方法和技术路线。
理论分析阶段,我们将从实际应用出发,分别分析波导腔体和交叉耦合滤波器的基本原理和工作原理,以及设计所需的材料、尺寸和形状等参数。
在这个阶段,我们将推导出基本公式,并建立数学模型。
电磁仿真阶段,我们将使用ANSYS等工具对所设计的波导腔体和交叉耦合滤波器进行电磁场仿真分析,验证所设计的数学模型的正确性以及工作特点,设计优化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
交叉耦合吸收滤波器的设计
微波滤波器一般将电磁(EM)波从负载反射回信号源。
但在有些情况下,例如要将反射波从输入中分离出来,以便保护信号源免受过高的功率。
基于这个原因,已经开发出吸收滤波器以尽量减少反射。
图1表示了吸收滤波器的基本结构。
这种类型的滤波器非常有用,其不仅是一个吸收滤波器,还是功率合成器或双工器。
当仅有一个信号输入(端口1)时,端口2是吸收端口,而端口3是隔离端口。
端口4是输出端口。
当不同的输入信号作用于端口1和端口3时,该结构也可以作为一个信号合成器。
最近,在微波和毫米波系统的波导应用中已经提出了基片集成波导(SIW)技术2,3。
SIW由基片上的各种金属阵列组成。
采用标准印制电路板(PCB)或低温共烧陶瓷(LTCC)基片来制造SIW器件。
SIW技术具有一定的优势,例如高品质因数(Q)、低插入损耗、减小了体积、降低了成本,并易于与平面电路进行集成。
因此,SIW 技术广泛地应用于各种不同的滤波器以及双工器的设计。
在本文中,已经研制成功一种基于SIW技术的新型交叉耦合吸收滤波器。
其具有锐选择性和高Q值,并易于与平面电路进行集成。
本文中研发的3-dB两步混合耦合器与先前已出版的著作不同。
这一3-dB混合耦合器具有良好的功率分配性能。
该吸收滤波器采用标准PCB板进行制作,并且将实测数据与仿真结果进行比较后表明二者相差很小。
很明显,以空气填充波导管变换的SIW与SIW-微带波导管变换相比可以提高功率并减小插入损耗。
例如,吸收滤波器常常用于将反射EM波从输入信号端口分离出来,从而保护该端口免于信号过载。
吸收滤波器的结构(图1)也可用于其他应用。
图1中的两个滤波器是一致的。
原则上,当EM波输入端口I(图2)时,在端口III只有输出信号。
端口II和端口IV与端口I是隔离的。
当信号由滤波器反射时,其都集中在端口II(图3),而端口II的输入和反射信号是隔离的。
Atia和Williams首次开发出用于对称滤波器响应的通用切比雪夫滤波器耦合矩阵合成法。
Amari开发出基于梯度的优化方法来合成通用切比雪夫滤波器的耦合矩阵。
此处提出的滤波器耦合矩阵是通过基于梯度的方法进行提取的。
三阶滤波器具有11,900MHz的中心频率以及22dB的回波损耗。
带宽为220MHz。
有限传输零点的位置在11,800MHz处。
耦合矩阵和频率响应如图所示。
在某些情况下,耦合矩阵出现负耦合。
Rosenberg提出该负耦合可以通过采用具有H平面耦合窗口的高阶共振腔模式的变换特性(例如,TE102)来实现。
根据公式1矩阵中所示的归一化耦合矩阵,可以通过仿真获得耦合窗的尺寸。
注意到谐振频率是不一样的,这是因为非对称频率响应。
公式2为通过仿真得到耦合系数的计算公式。
其中:f0i=没有耦合窗的谐振器的谐振频率;f pi=有耦合窗的谐振器的谐振频率,i=1,2。
采用仿真软件来决定滤波器的最初尺寸,并且根据参考文献14的TE101主模式,由对应的谐振频率来决定SIW腔的尺寸:
其中:w eff=SIW腔的等效宽度,而l eff=SIW腔的等效长度。
其表达式为:
其中:w=SIW腔的实际宽度;l=SIW腔的实际长度;d=金属通孔的直径;p=相邻金属孔之间的距离;c=光在自由空间的速度;m r=基片的相对磁导率;e r=基片的相对介电常数。
TE102模式下腔的长度是TE101模式下的两倍。
公式(4)也可用于计算TE101模式下腔的有效长度和宽度。
通过将两个相同滤波器和两个相同的3dB混合耦合器相结合来设计吸收滤波器。
图5是其中一个3-dB混合耦合器的频率响应。
从10.8到11.8GHz,端口1和端口2的回波损耗优于22dB。
图6是其中一个3-dB混合耦合器的尺寸。
直接集成单个滤波器和混合耦合器所需过程进行优化以获得优良的性能。
仿真优化过程中,金属孔的半径并没有变化。
只是两个金属孔中心之间的距离发生了改变。
首先,当利用等效基片波导并且不采用金属孔来制作吸收滤波器时,利用由目前研究小组所开发的模式匹配方法来对吸收滤波器进行优化。
然后,采用公式4中的长度和宽度进行变换后,利用Ansoft公司的高频结构仿真器(HFSS)EM软件对有金属孔的整体结构进行优化,以此消除金属孔的影响。
图6给出了经过优化之后所提出的交叉耦合SIW吸收滤波器的结构及其物理参数。
0.5mm 的金属孔直径没有任何变化。
两个金属孔边缘之间的最小距离是0.8mm。
所有尺寸指的是金属孔中心之间的距离。
采用标准PCB工艺来生产交叉耦合SIW吸收滤波器。
其特点是无需进一步的调整。
它采用Rogers公司的RT/Duroid5880基片材料(图7)。
基片的相对介电常数为2.2,其厚度是0.254,损耗角正切(δ)为0.0009。
采用回波损耗优于20dB的宽频响应来设计SIW-微带锥形变换。
图6表示了SIW-微带结构的尺寸。
图8是仿真和实测结果的比较,两组数据之间具有良好的一致性。
通带回波损耗的值都优于20dB。
端口1反射信号的吸收水平在10.80到11.65GHz之间小于17dB。
通带插入损耗约为5.8dB。
与传统滤波器相比,插入损耗似乎欠佳,这是由于它是许多滤波器的两倍,并且有来自其他端口的损耗。
SMA和SIW-微带变换的损耗也包括在总合中。
上述阻带表现出锐频率选择性。
空气填充矩形波导SIW变换可用于减少插入损耗,并在SIW-微带变换中提高功率。
本文提出的交叉耦合SIW吸收滤波器具有交叉耦合滤波器的锐选择性,该滤波器具有体积小、成本低以及与SIW设计有关的高Q值。
按照这里提出的设计准则,使构建具有类似优点的定制过滤器成为可能。
