Id-Vd仿真的例子
集成电路设计仿真验证分享案例

3.关注新兴领域的发展动态,如量子计算、新型存储技术等,为集成电路设计带来新的创新点。
4.加强产学研合作,培养高素质的专业人才,以应对行业快速发展的人才需求。
5.开展跨学科研究,结合材料科学、生物学等领域的新进展,开拓集成电路设计的新方向。
-关键因素:市场需求的快速变化导致设计风险增加,产品上市时间成为竞争的关键。
-问题剖析:如何在不牺牲产品质量的前提下,缩短设计周期,降低开发成本。
3.人才与教育层面的挑战:集成电路设计是高技术含量的领域,对人才的专业知识和技能要求极高。
-主要挑战:行业内高端人才短缺,人才培养周期长,教育与实践之间存在较大差距。
-竞争激烈,企业间在技术、产品、服务等方面展开全方位竞争。
-市场趋势分析:未来市场将继续向高性能、低功耗、智能化方向发展,同时,物联网、人工智能等新兴领域将为集成电路设计带来新的增长点。
七、发展趋势与未来展望
集成电路设计领域在未来将持续引领科技创新,其发展趋势和前景充满机遇与挑战。
发展趋势:
1.技术微型化:随着摩尔定律的持续演进,集成电路的工艺节点将不断缩小,向3纳米甚至更先进的工艺发展。这将极大提升集成电路的性能,降低功耗,但同时也带来了一系列技术挑战,如量子效应、热管理等问题。
回顾集成电路设计领域的发展历程,从20世纪70年代的CMOS技术取代双极型晶体管,到90年代的深亚微米工艺,再到21世纪初的纳米级工艺,设计规模不断扩大,设计复杂度不断上升。当前,集成电路设计已进入16/14纳米甚至更先进的工艺节点,设计方法学也在不断演变,如基于IP核的设计、系统级设计等。
在社会中的实际应用方面,集成电路设计已深入人们生活的方方面面。以智能手机为例,其内部集成了大量的集成电路,用于实现通信、计算、摄影等功能。此外,在人工智能、物联网、大数据等新兴领域,集成电路设计的地位更是至关重要。
《电力电子技术》单相半波可控整流电路MATLAB仿真实验

《电力电子技术》单相半波可控整流电路MATLAB仿真实验一、实验目的:(1) 单相半波可控整流电路(电阻性负载)电路的工作原理电路设计与仿真。
(2) 单相半波可控整流电路(阻-感性负载)电路的工作原理电路设计与仿真。
(3) 单相半波可控整流电路(阻-感性负载加续流二极管)电路的工作原理电路设计与仿真。
(4)了解三种不同负载电路的工作原理及波形。
二、电阻性负载电路1、电路及其工作原理图1.1单向半波可控整流电路(电阻性负载)如图1.1所示,单向半波可控制整流电路原理图,晶闸管作为开关,变压器T起到变换电压与隔离的作用。
其工作原理:(1)在电源电压正半波(0~π区间),晶闸管承受正向电压,脉冲uG在ωt=α处触发晶闸管,晶闸管开始导通,形成负载电流id,负载上有输出电压和电流。
(2)在ωt=π时刻,u2=0,电源电压自然过零,晶闸管电流小于维持电流而关断,负载电流为零。
(3)在电源电压负半波(π~2π区间),晶闸管承受反向电压而处于关断状态,负载上没有输出电压,负载电流为零。
(4)直到电源电压u2的下一周期的正半波,脉冲uG 在ωt=2π+α处又触发晶闸管,晶闸管再次被触发导通,输出电压和电流又加在负载上,如此不断重复。
2、MATLAB下的模型建立2.1 适当连接后,可得仿真电路。
如图所示:2.2 仿真结果与波形分析下列所示波形图中,波形图分别代表了晶体管VT上的电流、晶体管VT 上的电压、电阻加电感上的电压。
设置触发脉冲α分别为30°、60°、90°、120°时的波形变化。
α=30°α=60°α=90°α=120°分析:与电阻性负载相比,负载电感的存在,使得晶闸管的导通角增大,在电源电压由正到负的过零点也不会关断,输出电压出现了负波形,输出电压和电流平均值减小;大电感负载时输出电压正负面积趋于相等,输出电压平均值趋于零。
西工大CMOS实验课8全差分运放的仿真方法

西工大CMOS实验课8全差分运放的仿真方法一.Gm-Id 曲线仿真1.给定NMOS的宽长W=10um,L=0.5um,采用cis018.l库中model,仿真得到NMOS管的gm-Id曲线。
衬底电位0.仿真图如下:gm-Id曲线2.给定PMOS的宽长W=10um,L=0.5um,采用cis018.l库中model,仿真得到PMOS管的gm-Id曲线。
衬底电位3.3V。
仿真图如下:gm-Id曲线二.如图所示电路,采用cis018.l 库中model 设计 A VDD=1.65V ,A VSS=-1.65V VDDM=0,IDMP1=500uA IDMN1=IDMN2=50uA 问题:限制条件:Cin ≥5pF 1、写出正确的网表。
2、如何确定静态工作点?3、此电路如何实现将电流信号转换成电压信号?如何保证电路正常工作?4、仿真开环增益解:NOMS 的过驱动电压取0.3V ,PMOS 的过驱动电压取0.4V ,阈值电压均取0.7V ,因为()2n 21TH GS ox D V V L W C I -??=μ 50uA500uA 583.3,434.19-9e 9.314-e 85.8DMN2DMN1DMP1r o ro ===-=-=====I I I e C e C t t C ox P ox n ox oxox μμεεεε解得3.161633.91,29.8210321=?=??? ??=???=??? ??=??? ??=?MP MP MN MN MN MN L W L W L W L W L W L W ,1、网表如下:MP2 1 VB1 A VDD A VDD PCH3 L=1E-6 W=16.3E-6MN1 1 VB1 2 0 NCH3 L=1E-6 W=8.29E-6MP1 2 IN VDDM A VDD PCH3 L=1E-6 W=163E-6 M=40MN0 2 VB2 A VSS 0 NCH3 L=1E-6 W=91E-6MN2 A VDD 1 OUT 0 NCH3 L=1E-6 W=8.29E-6MN3 OUT VB3 A VSS 0 NCH3 L=1E-6 W=8.29E-6Cin如下:maximum nodal capacitance= 2.111E-11 on node0:vddmnodal capacitance tablenode = cap node =cap node=cap+0:1 = 95.3783f 0:2 = 5.6510p 0:avdd =14.5071p+0:avss = 509.1362f0:in=19.2273p 0:out=25.1917f+0:vb1 = 108.7357f 0:vb2= 390.2403f 0:vb3 = 34.5431f+0:vddm = 21.1067p2、确定静态工作点:通过改变Vin,观察V out的变化element 0:mp1 0:mn1 0:mn0 0:mp2 0:mn2 0:mn3 model 0:pch3.3 0:nch3.7 0:nch3.3 0:pch3.3 0:nch3.7 0:nch3.7 region Saturati Saturati Saturati Linear Saturati Saturatiid -482.1061u 72.3275u 554.4338u -72.6294u 86.6833u 86.6833u ibs 2.9120f -14.9024a -8.93E-20 8.78E-21 -14.9024a -1.50E-20 ibd 30.7536p -301.8432n -140.2780a 21.1317a -476.3502p -82.6879p vgs -1.5 1.2387 1.04 -1.65 1.6363 1.1 vds -1.239 2.7881 411.2525m -100.6906m 1.737 1.563vbs 1.65 -411.2525m 0 0 -1.563 0vth -1.38 997.1848m 823.4621m -706.0486m 1.3736 821.4963m vdsat -145.3641m 213.8544m 187.6576m -721.3657m 247.5361m 225.6300m vod -120.2468m 241.5627m 216.5379m -943.9514m 262.7101m 278.5037m beta 51.6352m 2.6402m 27.0295m 896.2115u 2.5508m 2.6651m gam eff 653.5583m 1.0839 1.0797 772.6100m 1.1167 1.0687 gm 5.7594m 488.1844u 4.1722m 68.2283u 532.9764u 517.9321u gds 6.1575u2.1537u 75.1740u 667.9622u3.0704u 1.7918u gmb 2.0017m 185.4162u 1.9434m 45.4014u 143.6472u 238.8658u cdtot 1.1392p4.1679f 51.4698f 36.6034f 4.1499f 4.5961f cgtot5.3266p 9.9288f 100.0161f 25.9245f 9.8013f 10.0505f cstot6.3843p 13.3144f 141.6930f 35.8585f 12.0378f 14.3840f cbtot 3.1052p 9.8270f 116.9513f 26.8457f 8.3305f 11.3597f cgs 4.7420p7.4805f 74.7973f 14.9395f 7.5125f 7.5479f cgd 387.1155f 1.4315f 14.5701f 11.8539f 1.4226f 1.4347f3、通过改变从端口VDDM输入的电流值,可以改变流过MN1中的电流,从而改变MN2的栅极电压,实现了改变输出电压的目的。
四 Multisim仿真实例
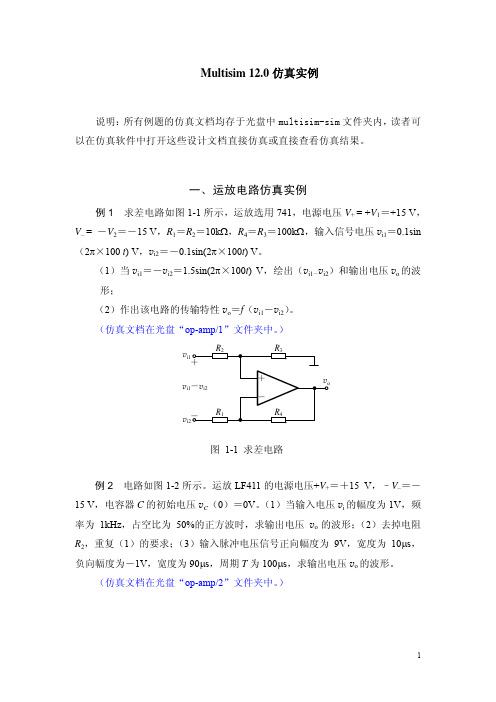
R0kΩ
Rc2 10kΩ
T1
T2
Rb2 1kΩ
Io
190μA
T3
Rc3 5kΩ
图 7-1
+15V
T4 VO
Re4 -15V
例 2 电路如图 7-2 所示。求电路的闭环电压增益 Avf、输入电阻 Rif ,并与 手算闭环电压增益结果比较。
(仿真文档在光盘“feedback/ 2”文件夹中。)
例 3 电路如图 4-1(a)所示。设 BJT 的型号为 2N3904,β=50,rbb′=100Ω,
4
其他参数与例 1 相同。试分析 Ce 在 1μF 到 100μF 之间变化时,下限频率 fL 的变 化范围(Ce 为与 Re 并联的电容)。
(仿真文档在光盘“BJT/3”文件夹中。)
五、差分式放大电路仿真实例
IR
R
IO(IL)
+
+ VR −
IZ
+
VI
DZ
VO
RL
−
−
图 2-3
三、MOSFET 放大电路仿真实例
例 1 电路如图 3-1 所示。设 NMOS 管 T 的参数为 VT = 0.8V,Kn = 1mA/V2。 电路其他参数为 V DD= V SS= 5V,I = 0.5mA,R d = 7kΩ,R g = 200kΩ,Cs = 47μF, 输入信号采用振幅为 10mV,频率为 1kHz 的正弦波。试画出输出电压的波形。
(仿真文档在光盘“actual op-amp/1”文件夹中。)
+VCC
vi
R1
R
-
Rf
C1
vp
A +
R
C2
MOS管相关仿真实验报告

MOS管相关仿真实验报告
一.MOS管共源放大电路仿真(基本要求)
电路如右图所示,
注意:1)设置静态工作点时,调整电位器Rp,使Vd为5~6V.
2)仿真时输出端必须接负载,否则会报错(可以将阻值设为很大的值来仿真开路情况)
放大电路仿真验证设计与仿真要求
(1)电路图
(2)静态工作点:ID、VGs、Vs
得ID=1.34862mA,VGs=2.16362V,Vs=1.41740V
(3)输入、输出电压波形,并计算电压增益A
即得电压增益为Av=45.4773
(4)幅频响应曲线:db((vo)(vs:+),测中频增益、上限频率fH和下限频率fL
如图,由图可知,测得中频增益为45.5854,上限频率fH=797.844kHz,下限频率fL=33.4688Hz (5)相频响应曲线:Vp(Vo)-p(vs:+)或p(V(vo)/Vvs:+))
(6)输入电阻的频率响应:Ri—V(v(i))/I(Vs)
(7)输出电阻的频率响应:Ro—V(V(o))/I(Vs)
(8)非线性失真现象
1)将Rp调整为最大值,做静态分析和瞬态分析,记录静态工作点和波形。
静态分析如下
瞬态分析如下
2)将Rp调整为最小值(不能为0,0是非法值),再做静态分析和瞬态分析,记录静态工作点和波形。
(如果发现没有失真,可以增大输入信号幅值。
)
静态分析如下
瞬态分析如下
由于此时失真不明显,故将输入振幅调至9V得到波形如下
得到明显失真图像。
选做部分
二.MOS管特性曲线仿真任务一:MOSFET输出特性曲线仿真
任务二:MOSFET转移特性曲线仿真。
光伏发电并网仿真实验报告
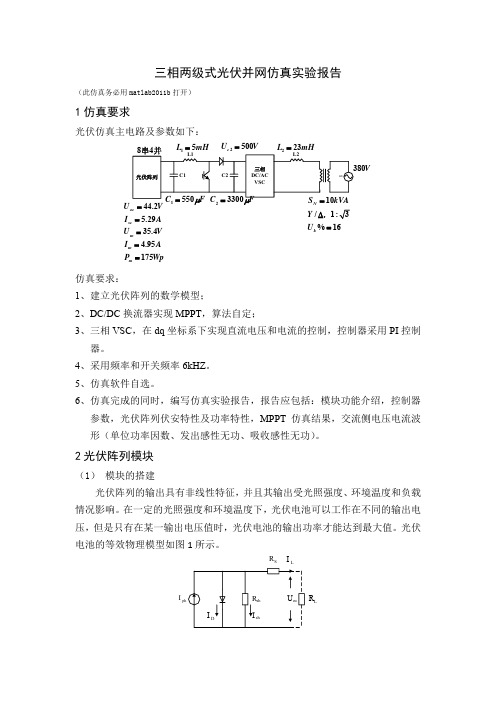
图 7 实现 MPPT 的 P-t 曲线
图 8 实现 MPPT 的 U-t 曲线
图 9 Udc 的输出波形
6 控制系统
光伏并网发电系统的核心是并网逆变器, 其控制系统的好坏直接影响整个系 统的性能, 本仿真中逆变器采用电压外环和电流内环的双环控制策略,其中电压 外环用于控制逆变器的输出电压,电流内环实现网侧电流的波形和相位控制,电 流内环的动态性能直接影响电压外环的控制性能和稳定性。 调制时需要将电网侧 的电流、电压由静止的 abc 坐标系下变换到同步旋转的 dq 坐标系下。外环 PI 的 参数 Kp=10,Ki=20;Kp=1,Ki=2;内环 PI 的参数 Kp=5,Ki=50。 交流侧电压方程:
1单位功率因数时图11单位功率因数交流侧a相电压电流波形图12单位功率因数交流侧a相电压与逆变器输出电流波形2发出感性无功时图13发出感性无功交流侧a相电压电流波形3吸收感性无功时图14吸收感性无功交流侧a相电压电流波形结论光伏电池仿真结果很理想dcdc的mppt功能能够实现逆变器也能够实现直流到交流的转换作用但是逆变器并网的控制效果不好调节电流内环的pi参数可以使交流侧电压电流波形的相位一致但同时又导致dc输出的电压不能达到500v为了是两者尽量都达到预期于是设置了上述参数但导致相位仍有偏差于是对于吸收和发出感性无功的波形不能看出明显的相位的变化
DV DT Rs DI
DT T Tref
T T tc R
式中 tc 为太阳电池模块的温度系数; Rref、Tref 分别为太阳日照强度和太阳能电池温度 参考值;α:在参考日照下,电流变化温度系数(Amps/℃);β:在参考日照下,电压变化温 度系数(V/℃);Rs:光伏模块的串联电阻。 基于上述的数学模型,利用 Simulink 工具建立光伏阵列仿真模型,如图所示,可以获 得任意太阳辐射,环境温度下的光伏电池的电压和电流。
数字PID的仿真实验例子-PPT精品文档26页

G0(z) (1z1)Z s82 0.s16s0 .1560
z
1 z
8Tz (z1)2
0.16z z1
0.16z z e50T
G(z)
z
z
1
(
8Tz z 1)
2
0.16 z z 1
0.16 z z e50T
G0(s)s2
54 18s1
输入信号是脉宽20s、周期50s的脉冲信号。假
设常规PID控制器为:
D(s)0.51 1 2s 3.5s
采用微分先行PID控制器,并设其中的 r0.5
系统采用两种控制器的原理图如下:
系统采用两种控制器的输出响应波形如下:
四、 试凑法
试凑法试一种凭借经验整定参数的方法,
利用增量式PID,采用脚本编程实现对上面对象
的控制,并整定PID参数
被控对象为 G0(s)s240500s
采用零阶保持器离散化,采样时间取0.001s,离 散化得:
400 1 e Ts 400 G 0 (z) ZO s2 H 5s0 s s2 5s0
G 0 (z ) ( 1 z 1 )s (s 2 4 5 0 s ) 0 0 ( 1 z 1 )s 2 ( 4 s 5 0 )0 0
0.9754
)
0.0001968 z 0.0001936 z 2 1.9512 z 0.9512
0.0001968 z 1 0.0001936 z 2 1 1.9512 z 1 0.9512 z 2
G(z)Y(z) U(z)
0.00019z6180.00019z32 6 11.951z210.951z22
SPICE基础仿真实例
Frequency (Hz)
集成电路专业
黑龙江大学
《数模混合集成电路设计》
卜
丹
14
推挽反相器仿真
Vdd=2.5V, PMOS栅极与输入相连 请写出该电路的网表,并仿真其Vout-Vin的DC特性 Vd
0
Vdd
W=2u, L=1u
*Push-pull Inverter .lib 'mix025_1.l' tt Vd vdd 0 2.5V
*NMOS transistor .lib 'mix025_1.l' tt m1 1 2 0 0 nch W=1u L=2u Vd 1 0 1V Vg 2 0 1V .dc Vd 0V 2.5V 0.01 .print gmo(m1) gdso(m1) gbso(m1) .end
集成电路专业 黑龙江大学 《数模混合集成电路设计》 卜 丹 7
• n1 n2 ... 外界调用子电路的端口的名称 • 一般子电路内部的节点都是“局域”(LOCAL)的,也就是说,和外界调用子 电路的电路的节点没有关系,外界不能调用子电路内部的节点. •节点0(地)是“全局”(global)的,对每个子电路都相同
• 调用子电路: Xname n1 <n2 n3 …> subname 必须以X开头
集成电路专业 黑龙江大学 《数模混合集成电路设计》 卜 丹 22
子电路:
*Subckt buffer 两个反相器组成的缓冲器(buffer) .lib 'mix025_1.l' tt Vd vdd 0 2.5V Vin in 0 SIN 1.25 1.25 100MegHz 4/0.2 10/0.2 x1 in 1 vdd inv1 5 5 x2 1 out vdd inv2 C1 out 0 2p 2/0.2 5 5/0.2 5 .subckt inv1 in out vdd Mp1 out in vdd vdd pch W=4u L=0.25u Mn1 out in 0 0 nch W=2u L=0.25u .ends .subckt inv2 in out vdd Mp1 out in vdd vdd pch W=10u L=0.25u Mn1 out in 0 0 nch W=5u L=0.25u .ends .tran 0.01n 100n .print tran v(x2.out) v(x1.in) .end
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
}
* The curve Id(Vg) at Vd=0.1V is traced after dosetime s of irradiation [1s,dosetime s]
* Vd is decreased to 0.1V [dosetime s,dosetime+1 s] and Vg is ramped [dosetime+1 s,dosetime+4 s]
CurrentPlot(Time=(Range=(0 1) Intervals=40))
}
}
可以运行但出来的图像没有曲线的形状,调整了漏段的电压,将Vd由0.2v增大为1v,仍旧是没有曲线,电流随栅电压的增大没有变化。
陈树鹏师兄的65nm辐照特性的仿真例子
File {
Grid = "@grid@"
Doping = "@doping@"
# Parameter = "@parameter@"
Output = "@log@"
Plot = "@dat@"
Current = "@plot@"
}
Physics {
EffectiveIntrinsicDensity( Nobandgapnarrowing )
Recombination( SRH )
}
Math {
Derivatives
RelErrControl
Digits=4
ErRef(electron)=1.e8
ErRef(hole)=1.e8
Notdamped=50
Iterations=40
Newdiscretization
DirectCurrent
ConstRefPot
RhsMin=1e-20
没有在其它的区域内制定复合模型,默认的是没有载流子的产生-复合模型
}
Physics(Material=Silicon){
EffectiveIntrinsicDensity(OldSlotboom NoFermi)
Mobility (DopingDep HighFieldSat Enormal)
Recombination(SRH(DopingDep))
Radiation(DoseRate=2000 DoseTime=(1,@<dosetime>@) doseTsigma=0.2)
}
Physics (Material=Silicon) {
Mobility( DopingDependent HighFieldsat Enormal )
EffectiveIntrinsicDensity( OldSlotboom NoFermi )
#TrapDLN=15
}
Math(Electrode="gate") {
Digits(NonLocal)=3
EnergyResolution(NonLocal)=0.001
Nonlocal(Length=5e-7)
}
Solve {
#-initial solution:
Coupled ( Iterations=100 LineSearchDamping=0.01 ) {Poisson}
50
Iterations=40
Newdiscretization
DirectCurrent
ConstRefPot
RhsMin=1e-20
#TrapDLN=15
}
Solve {
Set(Trapfilling=Empty)
Coupled ( Iterations=100 LineSearchDamping=0.01 ) { Poisson }
Temperature=300
}
Physics(RegionInterface="sub/gatox") {
Recombination(eBarrierTunneling(PeltierHeat))
}
Physics(Electrode="gate"){
Recombination(eBarrierTunneling hBarrierTunneling)
Goal {Name="drain" Voltage=1.0}
) {
Coupled { Poisson Electron Hole }
CurrentPlot(Time=(Range=(0 1) Intervals=40))
}
}
自己编写的例子
File {* input files:
Grid = "@grid@"
Recombination( SRH(DopingDep) )
Temperature=300
}
* Yield function is calculated using VMODEL of theis example
* Trap definition for the Gate Oxide
Physics (Region=gatox) {
Electrode {
{ Name="source" Voltage=0 }
{ Name="drain" Voltage=0 }
{ Name="gate" Voltage=0 }
{ Name="sub_con" Voltage=0 }
}
File {
Grid = "@grid@"
Doping = "@doping@"
Coupled { Poisson Electron Hole }
Unset(Trapfilling)没有这两个Set、Unset则无法仿真出Id-Vg曲线
Plot(FilePrefix="int")
Quasistationary (InitialStep=0.1 Minstep=1e-5 MaxStep=0.2
{ name="source" Voltage=0.0 }
经过对outputfile文件的显示的数据的分析,随着time的增加,已知节点之间的voltage随着t的增加而呈现出线性变化.
Vg(v)0 7e-4 1.68e-3 3.052e-0.3牛顿迭代法计算得到的时间点,根据error控制的步长确定.
Electrode {
{ name="gate" Voltage=( 0.0 at 0 , 0.0 at @<dosetime>@,
0.0 at @<dosetime+0.999>@,
0.0 at @<dosetime+1>@ , 1.5 at @<dosetime+4>@) }
{ name="box_10" Voltage=0.0 }
Traps(hNeutral Conc=5e17 EnergyMid=-0.5 FromMidBandGap
eXsection=5.0e-14 hXsection=5.10e-14 eJfactor=0 hJFactor=0 )
}
Physics(Electrode="gate"){
Recombination(eBarrierTunneling hBarrierTunneling)
Doping = "@doping@"
Parameter="@parameter@"
* output files:
Plot = "@dat@"
Current = "@plot@"
Output = "@log@"
}
Electrode {
{ Name="source" Voltage=0.0 }
{ Name="drain" Voltage=0.2 }
{ Name="gate" Voltage=0.0 }
{ Name="box_10" Voltage=0.0 }
}
Physics {
EffectiveIntrinsicDensity (NobandGapNarrowing)
Radiation(DoseRate=2000 DoseTime=(10,30) doseTsigma=0.2)
}
Physics (Material=Silicon) {
Mobility( DopingDependent HighFieldsat Enormal )
EffectiveIntrinsicDensity( OldSlotboom NoFermi )
Recombination( SRH(DopingDep) )
}
Physics(RegionInterface="sub/gatox") {
Recombination(eBarrierTunneling(PeltierHeat))
}
Plot {
ElectrostaticPotential
eTrappedCharge hTrappedCharge
eDensity hDensity
}
Plot {
eDensity hDensity eCurrent hCurrent
Potential SpaceCharge ElectricField
eMobility hMobility eVelocity hVelocity
