有理数加法应用题
有理数加减法练习题难点

一、有理数加法1. 计算:2 + 32. 计算:5 + (8)3. 计算:7 + (4)4. 计算:6 + 5 + 25. 计算:3 + 2 + (1) + 46. 计算:7 + (2) + 5 + (3)7. 计算:4 + (1) + 3 + (6)8. 计算:2 + 5 + (3) + 49. 计算:6 + (4) + 2 + (1)10. 计算:3 + 2 + (5) + 4二、有理数减法1. 计算:5 32. 计算:8 (2)3. 计算:7 (4)4. 计算:6 55. 计算:3 2 16. 计算:7 (2) 57. 计算:4 1 + 38. 计算:2 + 5 39. 计算:6 4 + 210. 计算:3 2 + 5三、有理数加减混合运算1. 计算:2 + 3 52. 计算:5 8 + 23. 计算:7 (4) + 14. 计算:6 + 5 25. 计算:3 + 2 1 + 46. 计算:7 (2) + 5 37. 计算:4 1 + 3 68. 计算:2 + 5 3 + 49. 计算:6 4 + 2 110. 计算:3 2 + 5 4四、有理数加减法应用题1. 甲数比乙数大5,乙数比丙数大3,求甲数比丙数大多少?2. 一支铅笔比一支钢笔贵1元,一支钢笔比一支圆珠笔贵2元,一支圆珠笔比一支水笔贵3元,求一支铅笔比一支水笔贵多少元?3. 一个班级有男生40人,女生比男生少10人,求这个班级女生有多少人?4. 一辆汽车行驶了300千米,比原计划少行驶了20千米,求原计划行驶的千米数。
5. 一本书原价100元,打八折后售价为80元,求这本书的折扣率。
五、有理数加减法综合题1. 计算:3 + 4 2 + 5 12. 计算:7 (3) + 2 5 + 63. 计算:8 + (4) 3 + 2 (1)4. 计算:5 (2) + 3 4 + (1)5. 计算:6 + 7 3 + 4 (2)6. 计算:5 (3) + 2 1 + 57. 计算:4 + 6 (2) + 3 48. 计算:2 5 + 4 (3) + 19. 计算:7 + 3 (2) + 5 610. 计算:6 (4) + 2 3 + 1六、有理数加减法应用题1. 一辆自行车以每小时15千米的速度行驶,行驶了3小时后,又以每小时10千米的速度行驶了2小时,求这辆自行车总共行驶了多少千米?2. 一个长方形的长是10厘米,宽是6厘米,求这个长方形的面积。
初中数学 有理数的加法和减法运算的解题应用题是什么

初中数学有理数的加法和减法运算的解题应用题是什么解题应用题1:题目:小明去超市买东西,他花费了50元。
如果他支付了30元,还欠15元,那么他以多少元的有理数借了钱?解题步骤:1. 设小明借的钱为x元。
2. 根据题意,我们可以写出方程:30 + x = 50 - 15。
3. 化简方程:x = 50 - 15 - 30。
4. 计算:x = 5元。
答案:小明以5元的有理数借了钱。
解题应用题2:题目:在一场比赛中,小红的得分是-15,小明的得分是10。
他们的总得分是多少?解题步骤:1. 小红的得分是-15,小明的得分是10。
2. 计算总得分:-15 + 10 = -5。
答案:他们的总得分是-5。
解题应用题3:题目:小明家的温度计显示-8摄氏度,他把温度计放在阳台上,经过一段时间后,温度显示变为了3摄氏度。
温度的变化是多少摄氏度?解题步骤:1. 温度计的初始温度是-8摄氏度,变化后的温度是3摄氏度。
2. 计算温度的变化:3 - (-8) = 3 + 8 = 11摄氏度。
答案:温度的变化是11摄氏度。
解题应用题4:题目:小明在一家书店买了一本书,原价是50元,打折后的价格是-40元。
小明支付了-30元,他实际上还要支付多少钱?解题步骤:1. 书的原价是50元,打折后的价格是-40元。
2. 计算小明还要支付的钱:-40 - (-30) = -40 + 30 = -10元。
答案:小明还要支付-10元。
解题应用题5:题目:小明的银行账户里有100元,他取出了-50元,还款给朋友借的钱。
他账户里还剩下多少钱?解题步骤:1. 小明的账户里有100元,取出了-50元。
2. 计算账户剩下的钱:100 + (-50) = 100 - 50 = 50元。
答案:小明账户里还剩下50元。
通过这些解题应用题,我们可以更好地理解有理数的加法和减法运算在实际生活中的应用。
这些应用题能够帮助我们将数学的知识与实际问题相结合,提高解决实际问题的能力。
(完整版)有理数加法应用题
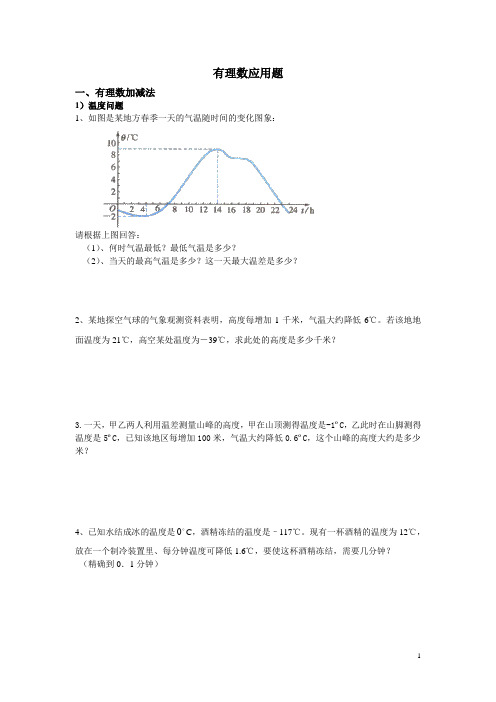
有理数应用题一、有理数加减法1)温度问题1、如图是某地方春季一天的气温随时间的变化图象:请根据上图回答:(1)、何时气温最低?最低气温是多少?(2)、当天的最高气温是多少?这一天最大温差是多少?2、某地探空气球的气象观测资料表明,高度每增加1千米,气温大约降低6℃。
若该地地面温度为21℃,高空某处温度为-39℃,求此处的高度是多少千米?3.一天,甲乙两人利用温差测量山峰的高度,甲在山顶测得温度是-1ºC,乙此时在山脚测得温度是5ºC,已知该地区每增加100米,气温大约降低0.6ºC,这个山峰的高度大约是多少米?4、已知水结成冰的温度是 0C,酒精冻结的温度是–117℃。
现有一杯酒精的温度为12℃,放在一个制冷装置里、每分钟温度可降低1.6℃,要使这杯酒精冻结,需要几分钟?(精确到0.1分钟)2)时差问题1.下表列出了国外几个大城市与北京的时差(带正号的数表示同一时刻比北京时间早的时数)(1)如果现在是北京时间上午8:00,那么东京时间是多少?(2)如果小强在北京时间下午15:00打电话给远在纽约的姑姑,你认为合适吗?试说明你的理由。
3)路程问题1.柳州出租车司机小李,一天下午以白沙客站为出发点,在南北走向的跃进路上营运,如果规定向北为正,向南为负,他这天下午行车里程(单位:千米)如下:+15,-2,+5,-13, +10,-7,-8,+12,+4,-5,+6(1)将最后一名乘客送到目的地时,小李距下午出车时的出发白沙客站多远? 在白沙客站的什么方向?(2)若每千米的价格为3.5元,这天下午小李的营业额是多少?2. 某一出租车一天下午以鼓楼为出发地在东西方向营运,向东为正,向西为负,行车里程(单位:km)依先后次序记录如下:+9、-3、-5、+4、-8、+6、-3、-6、-4、+10。
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?3.李老师在学校西面的南北路上从某点A出发来回检查学生的植树情况,设定向南的路程记为正数.向北的路程记为负数,那么李老师所行路程依次为(单位:百米):+12,-l0,+10,-8,-6,-5,-3.(1)求李老师最后是否回到出发点A?(2)李老师离开出发点A最远时有多少千米? (3)李老师共走了多少千米?4.在一条东西走向的马路旁,有青少年宫、党校、商场、医院四家公共场所.已知青少年宫在学校东300m处,商场在学校西200m处,医院在学校东500m处,若将马路近似地看作一条直线,以学校为原点,向东为正方向,用1个单位长度表示100m.(1)在数轴上表示四家公共场所的位置.(2)列式计算青少年宫与商场之间的距离.5.检修组乘汽车,沿公路检修线路,约定向东为正.向西为负,某天自A出发,到收工时,行走记录为(单位:千米):+8、-9、+4、+7、-2、-10、+18、-3、+7、+5 回答下列问题:(1)收工时在A地的哪边?距A地多少千米?(2)若每千米耗油0.3升,问从A地出发到收工时,共耗油多少升?6. 某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行-+-++--驶为负,一天中七次行驶纪录如下。
初一有理数计算试题及答案

初一有理数计算试题及答案试题一:有理数的加减法1. 计算:(-3) + (-5)2. 计算:7 + (-2)3. 计算:(-4) + 6试题二:有理数的乘除法1. 计算:(-2) × (-3)2. 计算:(-4) ÷ (-2)3. 计算:(-6) × 0试题三:有理数的混合运算1. 计算:[(-3) + 4] - 22. 计算:(-5) × 2 - 33. 计算:(-2) ÷ (-4) + 3试题四:有理数的比较大小1. 比较大小:-7 和 -32. 比较大小:-2 和 03. 比较大小:-5 和 -9试题五:有理数的应用题1. 一个数是 -8,另一个数比它大 3,求另一个数。
2. 一个数是 5,另一个数是它的相反数,求另一个数。
3. 一个数的一半是 -4,求这个数。
答案:试题一:1. (-3) + (-5) = -82. 7 + (-2) = 53. (-4) + 6 = 2试题二:1. (-2) × (-3) = 62. (-4) ÷ (-2) = 23. (-6) × 0 = 0试题三:1. [(-3) + 4] - 2 = 1 - 2 = -12. (-5) × 2 - 3 = -10 - 3 = -133. (-2) ÷ (-4) + 3 = 0.5 + 3 = 3.5试题四:1. -7 < -32. -2 < 03. -9 < -5试题五:1. -8 + 3 = -52. 5 的相反数是 -53. -4 × 2 = -8结束语:通过这些有理数的计算试题,同学们可以加深对有理数概念的理解,掌握加减乘除等基本运算规则,以及如何比较有理数的大小。
希望同学们能够通过练习,不断提高自己的计算能力。
七年级数学有理数加减混合运算应用题

七年级数学有理数加减混合运算应用题
以下是一些七年级数学有理数加减混合运算应用题的例子:
1.小明从A地出发,向北走20米到达B地,然后向东走30米到达C地,最
后再向南走40米到达D地。
请问他最终离出发点A地有多远?
解答:小明从A地出发,先向北走20米到B地,再向东走30米到C地,最后向南走40米到D地。
因为北和南是相反的方向,所以20米和40米会相互抵消,只剩下向东的30米。
因此,他最终离A地30米。
2.一个书架上有10本图书,第一天借出了4本,第二天归还了2本。
请问两
天后书架上还剩多少本书?
解答:开始时有10本书,第一天借出了4本,所以剩下10 - 4 = 6本。
第二天归还了2本,所以6 + 2 = 8本。
因此,两天后书架上还剩8本书。
3.小华和小明一起从学校出发去图书馆。
小华先走了20分钟,然后小明开始
追赶他。
如果小明的速度是每小时6公里,而小华的速度是每小时4公里,请问小明需要多长时间才能追上小华?
解答:因为小华先走了20分钟,所以他已经走了4×20/60 = 1.33公里。
小明每小时比小华快6 - 4 = 2公里,所以他需要追赶1.33公里。
因此,所需时间为1.33/2 = 0.665小时,也就是40分钟。
含有理数原理的实际应用题

含有理数原理的实际应用题题目一:购物计算假设你去超市购物,购买了以下商品:•牛奶:14元•面包:6元•鸡蛋:12元请计算你购买这些商品的总价格。
解答:不难发现,购物的总价格等于各种商品的价格之和。
我们可以用数学中的加法来表示这个关系。
所以,购物的总价格 = 牛奶的价格 + 面包的价格 + 鸡蛋的价格将每个商品的价格代入公式:购物的总价格 = 14元 + 6元 + 12元 = 32元所以,购买这些商品的总价格是32元。
题目二:温度转换假设现在的室外温度是摄氏30度,要将它转换为华氏温度,请计算。
解答:温度的转换关系有一个转换公式,我们可以使用这个公式来计算。
华氏温度 = 摄氏温度 × 1.8 + 32将摄氏30度代入公式进行计算:华氏温度 = 30 × 1.8 + 32 = 86所以,将摄氏30度转换为华氏温度是86度。
题目三:速度计算假设一辆汽车以每小时60公里的速度行驶,经过3个小时,它行驶了多远?请计算。
解答:速度的计算公式是:距离 = 速度 × 时间将题目中给出的速度和时间代入公式进行计算:距离 = 60公里/小时 × 3小时 = 180公里所以,经过3个小时,汽车行驶了180公里。
题目四:货币兑换假设你去国外旅行,想要将100美元兑换为人民币,汇率是1美元兑换为6.5人民币,请计算你可以得到多少人民币。
解答:货币兑换的计算公式是:兑换获得的货币 = 要兑换的货币 × 汇率将题目中给出的数据代入公式进行计算:兑换获得的人民币 = 100美元 × 6.5人民币/美元 = 650人民币所以,你可以得到650人民币。
题目五:面积计算假设一个正方形的边长是5米,求其面积。
请计算。
解答:正方形的面积计算公式是:面积 = 边长²将题目中给出的边长代入公式进行计算:面积 = 5米 × 5米 = 25平方米所以,这个正方形的面积是25平方米。
初中数学 有理数的加法和减法运算的应用题是什么

初中数学有理数的加法和减法运算的应用题是什么以下是一些初中数学中关于有理数加法和减法运算的应用题:1. 问题解决:a) 一个温度计上的温度为-5摄氏度,经过3小时后温度上升了7摄氏度,求现在的温度是多少摄氏度?b) 一辆汽车从一个城市出发,行驶了120公里后向左转行驶了80公里,最后又向右转行驶了100公里,求汽车最后所在的位置离出发点的距离是多少公里?2. 债务问题:a) 小明向小红借了20元钱,小红又向小明借了15元钱,最后小明又向小红借了8元钱,求小明最后欠小红多少元钱?b) 爸爸从银行取了200元钱,妈妈又从银行取了150元钱,然后他们一起去商场购物,最后付款时他们还剩下350元钱,求他们在商场上花了多少钱?3. 海拔问题:a) 一个城市的海拔为-100米,另一个城市的海拔为150米,求这两个城市的海拔差是多少米?b) 一个滑雪场的海拔为2400米,一个登山基地的海拔为3800米,求这两个地点的海拔差是多少米?4. 温度变化问题:a) 早晨气温为-3摄氏度,中午气温上升了8摄氏度,晚上气温下降了5摄氏度,求晚上的气温是多少摄氏度?b) 一天中的最高气温为30摄氏度,最低气温为15摄氏度,求一天的温差是多少摄氏度?5. 账户余额问题:a) 小明的银行账户里有300元钱,他向账户存入了120元钱,然后又从账户取出了80元钱,最后账户里还剩多少钱?b) 爸爸的信用卡欠款为-500元钱,他向信用卡还款了200元钱,然后又向信用卡借款了100元钱,最后信用卡欠款是多少元钱?这些应用题涉及到有理数加法和减法在实际问题中的应用。
通过解决这些问题,学生可以将数学知识与现实生活相结合,提高解决实际问题的能力。
建议学生在解决问题时,先分析问题,提取关键信息,然后应用有理数加法和减法的规则进行计算。
希望这些应用题能够帮助学生更好地理解有理数运算的实际应用,并提高数学解题的能力。
有理数和除法竖式练习题

有理数和除法竖式练习题一、有理数的加减法1. 计算:3 + (2)2. 计算:4 (5)3. 计算:7 + 9 34. 计算:8 + 15 65. 计算:12 18 + 24二、有理数的乘除法1. 计算:3 × 42. 计算:5 × (6)3. 计算:7 ÷ 24. 计算:8 ÷ (4)5. 计算:9 × (10)三、混合运算1. 计算:(3 + 5) × (2)2. 计算:4 (6 8) × 33. 计算:7 × (3) + 9 ÷ 34. 计算:5 × (4 2) 6 ÷ (3)5. 计算:8 + 15 ÷ (3) × 2四、除法竖式计算1. 计算:24 ÷ 32. 计算:56 ÷ 73. 计算:81 ÷ 94. 计算:100 ÷ 255. 计算:144 ÷ 12五、应用题1. 小明有5个苹果,他吃掉了2个,然后又得到了3个,现在他有几个苹果?2. 小红买了4本书,每本书的价格是8元,她一共花了多少钱?3. 一个长方形的长是8厘米,宽是4厘米,求这个长方形的面积。
4. 一辆汽车行驶了120公里,平均速度为40公里/小时,求汽车行驶的时间。
5. 一个班级有40人,其中男生占全班人数的50%,求这个班级女生的人数。
六、有理数的比较1. 比较:5 和 3 的大小。
2. 比较:2 和 7 的大小。
3. 比较:4.5 和 4.5 的大小。
4. 比较:0 和 0.01 的大小。
5. 比较:100 和 99 的大小。
七、有理数的化简1. 化简:2 + 2 22. 化简:3 (3) + 33. 化简:4 × (4) ÷ 44. 化简:5 ÷ (5) × (5)5. 化简:6 + 6 6 + 6八、有理数的乘方1. 计算:(2)^32. 计算:3^43. 计算:(5)^24. 计算:4^3 ÷ 2^35. 计算:(3)^3 × (3)^2九、除法竖式计算(带余数)1. 计算:17 ÷ 52. 计算:23 ÷ 43. 计算:38 ÷ 74. 计算:51 ÷ 95. 计算:65 ÷ 11十、综合应用题1. 一个数加上它的相反数等于0,这个数是多少?2. 一个数的2倍减去4等于这个数,求这个数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 有一批食品罐头,标准质量为每听454 克。现抽取10听样品进行检测,结果如下 表(单位:千克)
2 3 4 5 听号 1 质量 444 459 454 459 454 7 8 9 10 听号 6 质量 454 449 454 459 464
你能根据差值表求出这10听罐头的总 质量吗00千克记作0,称重如下: +4,-3,+5,+1,+3,0,+3,+2, +1,-7,问这10袋小麦的总重量是 多少?
有一个农民家库存了10袋小麦, 称重如下:(单位:千克)104, 97,105, 101,103,99, 100, 102, 101,93,问这10袋小麦的 总重量是多少?
某自行车厂一周生产任务为1050辆自行 车,计划平均每天生产150辆,由于各种 原因实际每天生产量与计划量相比有出 入.下表是某周的生产情况(超产为正、 减产为负): 星期 一 二 三 四 五 六 日
增减
+5
﹣2 ﹣4 +13 ﹣10 +16 ﹣9
若该厂工人工资实行计件工资制,每生 产一辆车50元,每超产一辆奖10元,每 少生产一辆扣10元,那么该厂工人这一 周的工资总额是多少?
7、某水泥仓库6天内进出水泥的吨数如 下(“+”表示进库,“﹣”表示出库): +20、﹣25、﹣13、+28、﹣29、﹣16. (1)经过这6天,仓库里的水泥是增多 还是减少了?增多或减少了多少吨? (2)经过这6天,仓库管理员结算发现 库里还存200吨水泥,那么6天前,仓库 里存有水泥多少吨? (3)如果进出仓库的水泥装卸费都是每 吨5元,那么这6天要付多少元装卸费?
3、为创建国家级卫生城,某天“创城
办”人员乘车沿东西公路巡回指导,早 晨从A地出发,傍晚到达B地结束,若 规定向西为正方向,当天的行驶记录 如下(单位:千米):+8,﹣9,+7, ﹣4,+5,﹣6,﹣8,问B地在A地的 何方,相距多少千米?如果汽车行驶 每千米耗油a升,求该天共耗油多少升?
4、为体现社会对教师的尊重,教师 节这一天上午,出租车司机小王在东 西向的公路上免费接送老师.如果规 定向东为正,向西为负,出租车的行 程如下(单位:千米):+5,﹣4, +3,﹣10,+3,﹣9 (1)最后一名老师送到目的地时, 小王距出租车出发地的距离是多少千 米? (2)若汽车耗油量为0.4升/千米,这 天下午汽车共耗油多少升?
2.某一出租车一天下午以一中为出发 地在东西方向运营,向东走为正,向 西走为负,行车里程(单位:km)依 先后次序记录如下:+9,-3,-5,+4, -8,+6,-3,-6,-4,+10. (1)将最后一名乘客送到目的地,出 租车离一中出发点多远?在一中的什 么方向? (2)若每千米的价格为1元,司机一 个下午的营业额是多少?
5、检修小组从A地点出发,在东西走 向的路上检修线,如果规定向东为正, 向西为负,一天中行驶记录如下(单位: 千米);﹣4,+7,﹣9,+8,+6,﹣4, ﹣ 3. (1)收工时距A地多远? (2)距A地最远的是哪一次? (3)若每千米耗油0.3升,从出发到收 工共耗油多少升?
6、某司机在东西路上开车接送乘客, 他早晨从A地出发,(取向东的方向为 正方向)到晚上送走最后一位客人为止, 他一天行驶里程记录如下(单位:km): +10,﹣5,﹣15,+30,﹣20,﹣16, +14 (1)若该车毎百公里耗油8L,则这车 今天共耗油多少升? (2)据记录的情况,你能否知道该车 送完最后一个乘客时,他在A地的什么 方向?距A地多远?
这10听罐头的总质量是多少?
如果把上题中超过标准质量的克数用正数表 示,不足的用负数表示,请同学们填出10听 罐头与标准质量的差值表(单位:克):
2 3 4 5 听号 1 459 0 454 +5 459 0 454 质量 444 -10 +5 差值 7 8 9 10 听号 6 0 -5 差值 449 0 454 +5 459 +10 464 质量 454
某铁矿码头将运进铁矿石记为正,运出铁矿石 记为负.某天的记录如下:(单位:t) +100,﹣80,+300,+160,﹣200,﹣180, +80,﹣160. (1)当天铁矿石库存是增加了还是减少了? 增加或减少了多少吨? (2)码头用载重量为20t的大卡车运送铁矿石, 每次运费100元,问这一天共需运费多少元?
某食品厂从生产的袋装食品中抽出样品20袋, 检测每袋的质量是否符合标准,超出或不足 的部分分别用正、负数来表示,记录如下表:
与标准质量的差 ﹣4 值(单位:克) 3 袋 数 ﹣2 4 0 3 2 4 3 5 5 1
这样样品的平均质量比标准质量多几克?如 果标准质量为400克,则抽样样品的总质量 是多少?
中江县城南北干道上有一位城管在巡逻,如果 规定向北为正,向南为负,他从出发地开始巡 逻的路程为: +3,﹣8,﹣1.5,+2,+5,﹣1,﹣2.5.(单 位:千米) (1)当城管车巡逻到最后一站时,城管如何 向队长描述他的位置? (2)如果队长命令他马上返回出发地,问这 次巡逻(含返回)共耗油多少升?(已知每千 米耗油0.10升)
某自行车厂一周计划生产1400辆自行车,平均每 天生产200辆,由于各种原因实际每天生产量与计 划量相比有出入.下表是某周的生产情况(超产 为正、减产为负):
星期 增减 一 +4 二 ﹣2 三 ﹣5 四 +13 五 ﹣11 六 +17 日 ﹣9
(1)根据记录可知前三天共生产 _________ 辆; (2)产量最多的一天比产量最少的一天多生产 _________ 辆; (3)该厂实行每周计件工资制,每生产一辆车可 得 60 元,若超额完成任务,则超过部分每辆另奖 15 元;少生产一辆扣 15 元,那么该厂工人这一 周的工资总额是多少?
