矩阵位移法练习题
矩阵位移法题目及答案
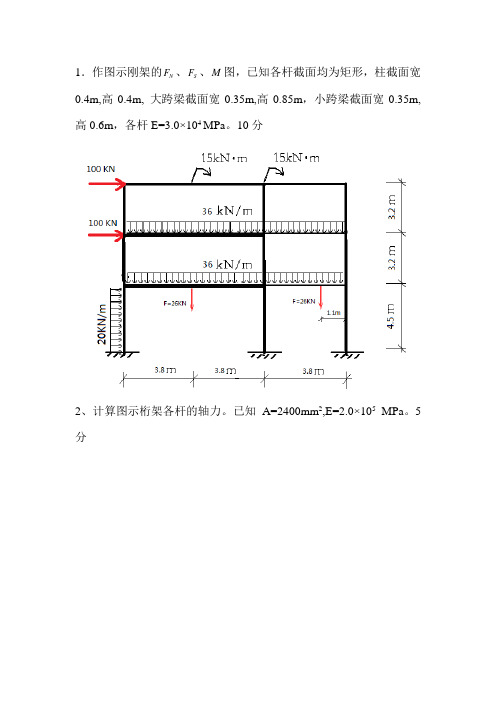
1.作图示刚架的F、S F、M图,已知各杆截面均为矩形,柱截面宽N0.4m,高0.4m, 大跨梁截面宽0.35m,高0.85m,小跨梁截面宽0.35m,高0.6m,各杆E=3.0×104 MPa。
10分2、计算图示桁架各杆的轴力。
已知A=2400mm2,E=2.0×105MPa。
5分3.作图示连续梁的F、M图,已知各梁截面面积A=6.52m,惯性矩SI=5.504m,各杆E=3.45×104MPa。
5分答案1******************************************************************** ** 1 composite beam 2012.10.17 ** ********************************************************************3E10 16 13 9 11 2 0.2975 17.912E-32 3 0.2975 17.912E-33 4 0.21 6.3E-31 5 0.16 2.133E-33 6 0.16 2.133E-34 7 0.16 2.133E-35 6 0.2975 17.912E-36 7 0.21 6.3E-35 8 0.16 2.133E-36 9 0.16 2.133E-37 10 0.16 2.133E-38 9 0.2975 17.912E-39 10 0.21 6.3E-38 11 0.16 2.133E-39 12 0.16 2.133E-310 13 0.16 2.133E-3 0 10.93.8 10.97.6 10.911.4 10.90 7.77.6 7.711.4 7.70 4.57.6 4.511.4 4.50 07.6 011.4 0111 0112 0113 0121 0122 0123 0131 0132 0133 041 100E3 0 02 0 0 -15E33 0 0 -15E35 100E3 0 0712 2 -26E3 3.813 2 -26E3 2.77 4 -36E3 7.68 4 -36E3 3.812 4 -36E3 7.613 4 -36E3 3.814 3 20E3 4.5第一题结果******************************************************************* * * * 1 composite beam 2012.10.17 * * * *******************************************************************The Input DataThe General InformationE NM NJ NS NLC3.000E+10 16 13 9 1The Information of Membersmember start end A I1 12 2.975000E-01 1.791200E-022 23 2.975000E-01 1.791200E-023 34 2.100000E-01 6.300000E-034 15 1.600000E-01 2.133000E-035 36 1.600000E-01 2.133000E-036 47 1.600000E-01 2.133000E-037 5 6 2.975000E-01 1.791200E-028 6 7 2.100000E-01 6.300000E-039 5 8 1.600000E-01 2.133000E-0310 6 9 1.600000E-01 2.133000E-0311 7 10 1.600000E-01 2.133000E-0312 8 9 2.975000E-01 1.791200E-0213 9 10 2.100000E-01 6.300000E-0314 8 11 1.600000E-01 2.133000E-0315 9 12 1.600000E-01 2.133000E-0316 10 13 1.600000E-01 2.133000E-03The Joint Coordinatesjoint X Y1 .000000 10.9000002 3.800000 10.9000003 7.600000 10.9000004 11.400000 10.9000005 .000000 7.7000006 7.600000 7.7000007 11.400000 7.7000008 .000000 4.5000009 7.600000 4.50000010 11.400000 4.50000011 .000000 .00000012 7.600000 .00000013 11.400000 .000000The Information of SupportsIS VS111 .000000112 .000000113 .000000121 .000000122 .000000123 .000000131 .000000132 .000000133 .000000( NA= 357 )( NW= 1167 )Loading Case 1The Loadings at JointsNLJ= 4ILJ PX PY PM1 100000.0000 .0000 .000002 .0000 .0000 -15000.000003 .0000 .0000 -15000.00000 5 100000.0000 .0000 .00000The Loadings at MembersNLM= 7ILM ITL PV DST12 2 -26000.0000 3.80000013 2 -26000.0000 2.7000007 4 -36000.0000 7.6000008 4 -36000.0000 3.80000012 4 -36000.0000 7.60000013 4 -36000.0000 3.80000014 3 20000.0000 4.500000The Results of CalculationThe Joint Displacementsjoint u v phi1 1.845349E-02 -1.982711E-04 -1.263100E-042 1.841771E-02 -3.424398E-04 -8.180773E-063 1.838193E-02 -5.043591E-04 -1.356524E-044 1.836317E-02 -3.892198E-04 -1.683554E-045 1.608566E-02 -2.069957E-04 -9.278065E-046 1.601139E-02 -5.147233E-04 6.593305E-057 1.599555E-02 -3.701310E-04 -4.819689E-048 1.132049E-02 -1.535800E-04 -1.283845E-039 1.131820E-02 -3.849935E-04 3.869225E-0510 1.130585E-02 -2.796765E-04 -9.193725E-0411 7.105234E-18 -1.638186E-17 -1.781240E-1712 9.610834E-18 -4.106598E-17 -2.156936E-1713 7.783932E-18 -2.983216E-17 -1.882119E-17The Terminal Forcesmember N(st) Q(st) M(st) N(en) Q(en) M(en)1 84035.890 -13086.980 -41569.990 -84035.890 13086.980 -8160.5532 84035.890 -13086.980 -6839.447 -84035.890 13086.980 -42891.1003 31099.080 -28633.300 -52776.720 -31099.080 28633.300 -56029.8104 -13086.980 15964.110 41569.990 13086.980 -15964.110 9515.1395 -15546.320 52936.810 80667.820 15546.320 -52936.810 88729.9806 28633.300 31099.080 56029.810 -28633.300 -31099.080 43487.2307 87221.910 93210.620 -62622.290 -87221.910 180389.400 -268657.0008 26256.560 29751.550 -2861.126 -26256.560 107048.500 -144003.0009 80123.640 28742.190 53107.150 -80123.640 -28742.190 38867.85010 194594.600 113902.200 182788.200-194594.600-113902.200 181698.70011 135681.800 57355.640 100515.700-135681.800 -57355.640 83022.30012 2689.851 83695.000 -146729.300 -2689.851 215905.000 -355668.70013 20483.680 160.171 -42824.000 -20483.680 162639.800 -245087.30014 163818.600 26052.340 107861.500-163818.600-116052.300 211874.00015 410659.800 96108.340 216794.000-410659.800 -96108.340 215693.50016 298321.600 77839.320 162065.000-298321.600 -77839.320 188211.900( NA= 357 )单位(N m)( NW= 1195 )第二题答案******************************************************************* * * * 2 composite beam 2012.10.17 * * * ******************************************************************* 2E11 14 9 4 11 2 2.4E-3 1E-102 3 2.4E-3 1E-103 4 2.4E-3 1E-104 5 2.4E-3 1E-101 8 2.4E-3 1E-101 6 2.4E-3 1E-102 6 2.4E-3 1E-103 6 2.4E-3 1E-103 7 2.4E-3 1E-104 7 2.4E-3 1E-105 7 2.4E-3 1E-105 9 2.4E-3 1E-106 8 2.4E-3 1E-107 9 2.4E-3 1E-100 62 64 66 68 62 36 30 08 081 082 091 092 051 0 -50E3 02 0 -50E3 03 0 -50E3 04 0 -50E3 05 -10E3 -50E3 0第二题结果******************************************************************* * * * 2 composite beam 2012.10.17 * * * *******************************************************************The Input DataThe General InformationE NM NJ NS NLC2.000E+11 14 9 4 1The Information of Membersmember start end A I1 12 2.400000E-03 1.000000E-102 23 2.400000E-03 1.000000E-103 34 2.400000E-03 1.000000E-104 45 2.400000E-03 1.000000E-105 1 8 2.400000E-03 1.000000E-106 1 6 2.400000E-03 1.000000E-107 2 6 2.400000E-03 1.000000E-108 3 6 2.400000E-03 1.000000E-109 3 7 2.400000E-03 1.000000E-1010 4 7 2.400000E-03 1.000000E-1011 5 7 2.400000E-03 1.000000E-1012 5 9 2.400000E-03 1.000000E-1013 6 8 2.400000E-03 1.000000E-1014 7 9 2.400000E-03 1.000000E-10The Joint Coordinatesjoint X Y1 .000000 6.0000002 2.000000 6.0000003 4.000000 6.0000004 6.000000 6.0000005 8.000000 6.0000006 2.000000 3.0000007 6.000000 3.0000008 .000000 .0000009 8.000000 .000000The Information of SupportsIS VS81 .00000082 .00000091 .00000092 .000000( NA= 270 )( NW= 907 )Loading Case 1The Loadings at JointsNLJ= 5ILJ PX PY PM1 .0000 -50000.0000 .000002 .0000 -50000.0000 .000003 .0000 -50000.0000 .000004 .0000 -50000.0000 .000005 -10000.0000 -50000.0000 .00000The Loadings at MembersNLM= 0The Results of CalculationThe Joint Displacementsjoint u v phi1 -1.052370E-04 -9.375000E-04 -7.026900E-052 -1.746814E-04 -1.193735E-03 1.087907E-043 -2.441259E-04 -8.137530E-04 -3.230397E-054 -3.552370E-04 -1.302888E-03 -1.022944E-045 -4.663480E-04 -9.375000E-04 1.412285E-046 3.860367E-04 -8.812350E-04 1.226822E-047 -7.938921E-04 -9.903881E-04 -6.211760E-058 -3.833334E-18 -1.325000E-17 -2.257494E-049 2.833334E-18 -1.175000E-17 3.510750E-04The Terminal Forcesmember N(st) Q(st) M(st) N(en) Q(en) M(en)1 16666.660 .009 .007 -16666.660 -.009 .0112 16666.660 -.009 -.008 -16666.660 .009 -.0113 26666.660 .011 .011 -26666.660 -.011 .0104 26666.660 -.010 -.012 -26666.660 .010 -.0075 75000.000 -.001 -.003 -75000.000 .001 -.0046 -30046.240 -.002 -.004 30046.240 .002 -.0027 49999.980 -.002 -.003 -49999.980 .002 -.0038 39060.150 -.002 -.005 -39060.150 .002 -.0039 21032.390 .002 .004 -21032.390 -.002 .00310 49999.980 .002 .002 -49999.980 -.002 .00311 -30046.240 .002 .005 30046.240 -.002 .00212 75000.000 .001 .003 -75000.000 -.001 .00413 69106.410 .003 .008 -69106.410 -.003 .00414 51078.650 -.004 -.009 -51078.650 .004 -.004( NA= 270 )( NW= 907 )第三题答案******************************************************************** ** 3 composite beam 2012.10.17 ** ******************************************************************** 3.45E10 4 5 6 11 2 6.5 5.52 3 6.5 5.53 4 6.5 5.54 5 6.5 5.50 040 060 080 0120 011 012 013 022 042 052 013 0 -320E3 -100E341 4 -10.5E3 402 4 -10.5E3 203 4 -10.5E3 204 4 -10.5E3 40第三题结果******************************************************************* * * * 3 composite beam 2012.10.17 * * * *******************************************************************The Input DataThe General InformationE NM NJ NS NLC3.450E+10 4 5 6 1The Information of Membersmember start end A I1 12 6.500000E+00 5.500000E+002 23 6.500000E+00 5.500000E+003 34 6.500000E+00 5.500000E+004 45 6.500000E+00 5.500000E+00The Joint Coordinatesjoint X Y1 .000000 .0000002 40.000000 .0000003 60.000000 .0000004 80.000000 .0000005 120.000000 .000000The Information of SupportsIS VS11 .00000012 .00000013 .00000022 .00000042 .00000052 .000000( NA= 66 )( NW= 299 )Loading Case 1The Loadings at JointsNLJ= 1ILJ PX PY PM3 .0000 -320000.0000 -100000.00000The Loadings at MembersNLM= 4ILM ITL PV DST1 4 -10500.0000 40.0000002 4 -10500.0000 20.0000003 4 -10500.0000 20.0000004 4 -10500.0000 40.000000The Results of CalculationThe Joint Displacementsjoint u v phi1 0.000000E+00 3.713943E-18 4.951923E-172 0.000000E+00 -2.916827E-17 -5.219418E-053 0.000000E+00 -1.405865E-03 1.038816E-064 0.000000E+00 -3.431731E-17 4.276883E-055 0.000000E+00 6.771635E-18 5.239688E-05The Terminal Forcesmember N(st) Q(st) M(st) N(en) Q(en) M(en)1 .000 172860.600 904807.700 .000 247139.400-2390385.0002 .000 359543.300 2390385.000 .000-149543.300 2700481.0003 .000-170456.700-2800481.000 .000 380456.700-2708654.0004 .000 277716.300 2708654.000 .000 142283.700 .000( NA= 66 )( NW= 315 )。
矩阵位移法大作业
①
1
2
ql
②
2
3
③
4
q
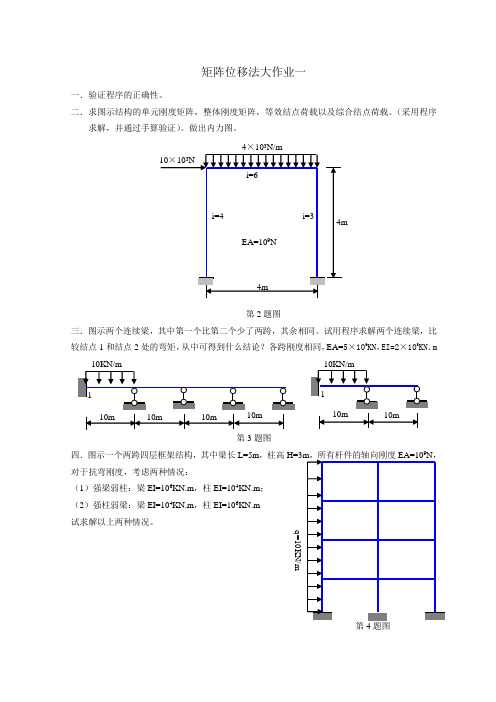
1① 2 ② 3 ③
4
y M, x
(a)
(b)
第 3 题图
各 杆 EI 、l 相 同,杆长也相同,具体数值可自己给定。
四.采用程序计算图示结构
i
跨长 l(m)
层高 h(m)
集中力(KN)
1
6
7
30
2
10
4
100
3
8
3
50
其他:
柱刚度:EA=105KN,EI=1.5×104KN.m2 梁刚度:EA=106KN,EI=1.0×104KN.m2 支座沉降 C=0.01m
四.采用程序计算图示结构,并作出弯矩图。 已知各杆 E=3.0×106KN/m2,A1=0.16m2,I1=0.012m4,I2=2I1, A2=2A1,I3=3I1,A3=3A1
第 3 题图
20KN
40KN.m
I1,A1 50KN
40KN
15KN/m I3,A3
25KN
I2,A2 40KN.m
4m
4m
3m
3m
五.编写一段程序,实现“将已知支座位移转化为等效节点荷载”。 六.采用程序计算图示结构,并作出最后内力图。已知各杆 E=3.2×106KN/m2,A=0.16m2,I=0.012m4。
36KN
8KN/m
12KN/m
36KN 54KN.m 3m
3m
q=10KN/m
6KN/m
36KN
3m
3m
六.不修改源程序,计算图示结构。
10KN
35KN
6m
15KN
自测题9 矩阵位移法答案

整体(结构)坐标系、局部(单元)坐标系
转换:
定位:
名称和意义:各矩阵、列阵(向量)、
第十章矩阵位移法
答案
一、1 O 2 X 3 X4X
二、1 A2 B 3 B4 C5 B
6 C7 D
三、
1、1、2EA/L
2、b
3、
四、
(7分)
五、
(10分)
六、
(7分)
七、
(7分)
八、
( 7分)
九、
(7分)
十、
(4分);
(2分)
(3分)
M图(3分)
本章小结
编码:
整体(结构)编码:
单元码①②③…
结点码ABCD…(1234…)
结点位移(力)码=总码1234…
局部(单元)编码:
杆端码1 2
(局部坐标系)杆端位移(力)码=局部码
(整体坐标系)杆端位移(力)码=局部码
不同结点:固定端、铰支端、自由端、中间铰、
中间滑动
不同结构:刚架、忽略轴向变形矩形刚架、来自、连续梁、桁架、组合结构
单元:
刚架单元 、梁单元 、连续梁单元 、桁架单元
第9章 矩阵位移法 例题

第9章 矩阵位移法习 题9-1:请给图示结构编号(同时用先处理法和后处理法)及建立坐标。
题9-1图 9-2:求图示连续梁的整体刚度矩阵。
题9-2图9-3:求图示刚架的整体刚度矩阵。
(c )(e )题9-3图9-4:求图示组合结构的整体刚度矩阵。
题9-4图9-5:求图示桁架结构的整体刚度矩阵,所有杆件的EA 均相同。
题9-5图9-6:求图示排架结构的整体刚度矩阵。
题9-6图 9-7:求图示结构的等效结点荷载,请利用结构的对称性。
1kN/m题9-7图9-8:求图示结构的等效结点荷载,请利用结构的对称性。
题9-8图9-9:求图示结构的等效结点荷载。
题9-9图9-10:求出图示结构的荷载列阵。
题9-10图9-11:求出图示结构的荷载列阵,请分别用先处理法和后处理法进行编号。
qq题9-11图9-12:求图示结构的荷载列阵,考虑轴向变形。
题9-12图9-13:求图示结构的荷载列阵。
题9-13图9-14:图示连续梁中间支座发生了下向的移动a ,请求出其整体刚度方程。
题9-14图10kN/mq9-15:请求出图示连续梁的整体刚度方程。
题9-15图9-16:求图示连续梁的整体刚度矩阵。
题9-16图9-17:图示结构温度发生了变化,请求出整体刚度方程。
杆件的EI 、EA 相同。
题9-17图9-18:图示结构温度发生了变化,请求出整体刚度方程。
题9-18图9-19:图示结构发生了支座移动,请画出结构的内力图。
00题9-19图9-20:已知图示梁B 点的B v 、B ϕ和C 点的C ϕ,请求出单元杆端力的列阵。
题9-20图9-21:求题9-3图示刚架的整体刚度矩阵,忽略轴向变形。
9-22:求题9-10图示结构的整体刚度矩阵,用后处理法编号。
9-23:求出梁的整体刚度方程,弹簧的刚度系数为k 。
题9-23图9-24:求出图示结构的整体刚度方程,忽略轴向变形,弹簧刚度系数为k 。
题9-24图L。
矩阵位移法例题1

50 3 10 15 57 . 5
3 . 891 50 6 . 228 15 79 . 625 57 . 5
2 . 2387 10 6 m 7 2 . 6993 10 m 4 . 2905 10 6 rad
矩 阵 位 移 法(例题)
结构刚度方程为
F K
即
50 202 . 667 3 8 10 15 10 57 . 794 57 . 5 14 . 425 57 . 794 129 . 422 12 . 948 14 . 425 1 12 . 948 2 127 . 306 3
1 (0,0,0)
5m
y
(2)
(1 )
( 2 )
o
x
5m
(0,0,0) 3
2.5m
矩 阵 位 移 法(例题)
单元(1)
0
168 0 0 8 10 168 0 0
0
0 8 . 064 20 . 16 0 8 . 064 20 . 16
(2)
k
(2)
矩 阵 位 移 法(例题)
结构刚度矩阵
168 34 . 667 8 K 10 57 . 794 14 . 425 202 . 667 8 10 57 . 794 14 . 425 57 . 794 8 . 064 121 . 358 20 . 16 7 . 212 20 . 16 7 . 212 67 . 2 60 . 106 14 . 425
《结构力学习题集》-矩阵位移法习题及答案

第八章 矩阵位移法 – 老八校一、判断题:1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。
2、单元刚度矩阵均具有对称性和奇异性。
3、局部坐标系与整体坐标系之间的坐标变换矩阵T 是正交矩阵。
4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。
5、结构刚度方程矩阵形式为:[]{}{}K P ∆=,它是整个结构所应满足的变形条件。
6、图示结构用矩阵位移法计算时(计轴向变形)未知量数目为8个。
7、在直接刚度法的先处理法中,定位向量的物理意义是变形连续条件和位移边界条件。
8、等效结点荷载数值等于汇交于该结点所有固端力的代数和。
9、矩阵位移法中,等效结点荷载的“等效原则”是指与非结点荷载的结点位移相等。
10、矩阵位移法既能计算超静定结构,也能计算静定结构。
11、已知图示刚架各杆EI = 常数,当只考虑弯曲变形,且各杆单元类型相同时,采用先处理法进行结点位移编号,其正确编号是:(0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.2134123412341234( )二、计算题:12、用先处理法计算图示结构刚度矩阵的元素133322,,K K K 。
123ll4l5EI2EIEA(0,0,0)(0,0,1)(0,2,3)(0,0,0)(0,2,4)(0,0,0)EI13、用先处理法计算图示刚架结构刚度矩阵的元素153422,,K K K 。
EI ,EA 均为常数。
l14、计算图示结构整体刚度矩阵的元素665544,,K K K 。
E 为常数。
ll1342A , I AA /222A I , 2A15、写出图示结构以子矩阵形式表达的结构原始刚度矩阵的子矩阵[][]K K 2224,。
[][]k k 1112 [][]k k 2122 []k =ii iii单刚分块形式为 :16、已知平面桁架单元在整体坐标系中的单元刚度矩阵,计算图示桁架结构原始刚度矩阵[]K 中的元素,,7877K K EA =常数。
矩阵位移法例题
0
2 1 2
0
0
4 1 3
00 2 00 3
0
0
K③
41
3
0
0
0
00 3 000
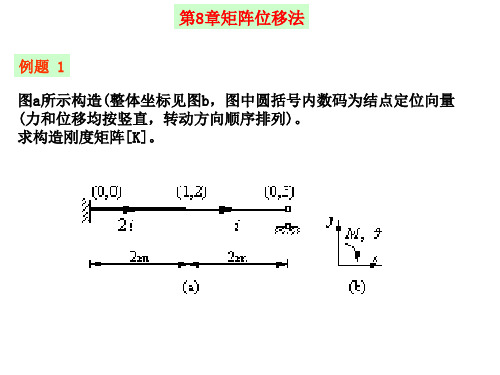
5 集成总刚度矩阵
第8章矩阵位移法
4 2 2 2
0 1 8 4 0
K 2 2 4 2 4 1
21
2
4
12
2
0
2 1 4 1 4 1 3 0 2 8
1
2
3
6 形成荷载向量
P 60 190 62.5T
2 结点位移编号矩阵 3 各单元旳定位向量
0 0 0 C 0 0 1
0 0 2 0 0 0
2 3T
U1 0 0 0 0 0 1 U2 0 0 1 0 0 2 U3 0 0 2 0 0 0
-90 250
-250 187.5 -112.5
1
2
3
4
第8章矩阵位移法
4 各单元旳刚度矩阵
单元旳刚度矩阵与解法一相同
2 12i 2 BCx l2 Cy
12i (B l2 )CxC y
2 12i 2
BC Y
2 l
Cx
6i l Cy 6i l Cx
2 12i 2 BCx 2 C y
l 12i (B 2 )CxC y l
12i (B 2 )CxC y
l 2 12i 2 BCy 2 Cx
l
6i l Cy 6i l Cx
(e)
K
6i
4i
l Cy
6i l Cx
2i
2 12i 2 BCx 2 C y
l
12i (B 2 )CxC y
l
6i
习题课1 矩阵位移法(含答案作业)_518706462

4
5
6
7
8
k
i = 2,3 (1) 54
+ k
i = 2,3 (1) 55
(2) (3) (3) (3) k16 k15 k16 k14 0 (2) (3) (3) (3) k26 k25 k26 k24 0 (2) (3) (3) (3) k36 k34 k35 k36 0
+ k
+
(i ) 33
k
3EIa 2 a 3 + b3
A
3EIab a 3 + b3
B A
3EIab a 3 + b3
3EIb 2 a 3 + b3
B
3EIa a 3 + b3
e θA =1
−3EIa a 3 + b3
3EIb a 3 + b3
e θB =1
−3EIb a 3 + b3
[k ]
e
=
a2 ab
ab b2
e
3EI a 3 + b3
{F }
u2
v2 θ 2 θ 3 ]
−M 0 ]
[0 M 0
0 0 2M 0
T
4
3
3
4
5
0
0
6
2 2 2 2 2 2 k12 k13 k14 k15 k16 k11
2 2 2 2 2 2 k22 k24 k25 k21 k23 k26 2 2 2 2 2 2 k32 k34 k35 k31 k33 k36 2 2 2 2 2 2 k42 k45 k44 k41 k46 k43
y
x
解: T 用位移法求解,未知量为 {∆} = [θ 2 v3 ] 。 1) 杆端弯矩表达式
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结构力学自测题(第八单元)矩阵位移法姓名 学号一、是 非 题(将 判 断 结 果 填 入 括 弧 :以 O 表 示 正 确 ,以 X 表 示 错 误 )1、用 矩 阵 位 移 法 计 算 连 续 梁 时 无 需 对 单 元 刚 度 矩 阵作 坐 标 变 换。
()2、结 构 刚 度 矩 阵 是 对 称 矩 阵 ,即 有K ij = K ji ,这 可 由位 移 互 等 定 理 得 到 证 明 。
() 3、图 示 梁 结 构 刚 度 矩 阵 的 元 素 K EI l 11324=/ 。
()EI llEI 212xy M , θ附:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--------l EI l EI l EI l EI lEI l EI l EI l EI l EAl EA l EI lEI l EI l EI l EI l EI l EI l EI lEA l EA 4602606120612000002604606120612000002223232223234、在 任 意 荷 载 作 用 下 ,刚 架 中 任 一 单 元 由 于 杆 端 位移 所 引 起 的 杆 端 力 计 算 公 式 为 :{}[][]{}FT K eee=δ 。
()二、选 择 题 ( 将 选 中 答 案 的 字 母 填 入 括 弧 内 )1、已 知 图 示 刚 架 各杆 EI = 常 数,当 只 考 虑 弯 曲 变 形 ,且各 杆 单 元 类 型 相 同 时 ,采 用 先 处 理 法 进 行 结 点 位 移 编 号 ,其 正 确 编 号 是 :(0,1,2) (0,0,0) (0,0,0) (0,1,3) (0,0,0) (1,2,0) (0,0,0) (0,0,3)(1,0,2)(0,0,0) (0,0,0) (1,0,3) (0,0,0)(0,1,2)(0,0,0) (0,3,4)A.B.C.D.2134 123 4 12 34 1 2 3 4 xyM , θ ( ) 2、平 面 杆 件 结 构 一 般 情 况 下 的 单 元 刚 度 矩 阵 []k 66⨯,就 其 性 质 而 言 ,是 :()A .非 对 称 、奇 异 矩 阵 ;B .对 称 、奇 异 矩 阵 ;C .对 称 、非 奇 异 矩 阵 ;D .非 对 称 、非 奇 异 矩 阵 。
3、单 元 i j 在 图 示 两 种 坐 标 系 中 的 刚 度 矩 阵 相 比 :A . 完 全 相 同 ;B . 第 2、3、5、6 行 (列 ) 等 值 异 号 ;C . 第 2、5 行 (列 )等 值 异 号 ;D . 第 3、6 行 (列 ) 等 值 异 号 。
()ijyxijyx M , θM , θ4、矩 阵 位 移 法 中 ,结 构 的 原 始 刚 度 方 程 是 表 示 下 列两 组 量 值 之 间 的 相 互 关 系 :()A .杆 端 力 与 结 点 位 移 ;B .杆 端 力 与 结 点 力 ;C .结 点 力 与 结 点 位 移 ;D .结 点 位 移 与 杆 端 力 。
5、单 元 刚 度 矩 阵 中 元 素 k ij 的 物 理 意 义 是 :A .当 且 仅 当 δi =1 时 引 起 的 与 δj 相 应 的 杆 端 力 ;B .当 且 仅 当 δj =1时 引 起 的 与 δi 相 应 的 杆 端 力 ;C .当 δj =1时 引 起 的 δi 相 应 的 杆 端 力 ;D .当 δi =1时 引 起 的 与 δj 相 应 的 杆 端 力。
() 6、用 矩 阵 位 移 法 解 图 示 连 续 梁 时 ,结 点 3 的 综 合 结点 荷 载 是 :A .[]-ql ql 2 12T132; B .[]ql ql 213212T-;C .[]--ql ql 2112 12T; D .[]ql ql 211212T。
()123l /2ll ql2q4qll /2xyM , θ7、用 矩 阵 位 移 法 解 图 示 结 构 时 ,已 求 得 1 端 由 杆 端位 移 引 起 的 杆 端 力 为 {}[]TF 461--=,则 结 点 1 处 的 竖向 反 力Y 1 等 于 :A .6-;B .-10;C .10 ;D .14 。
()2m4m123M 1Y 20kN/m1xyM , θ三、填 充 题 ( 将 答 案 写 在 空 格 内)1、图 示 桁 架 结 构 刚 度 矩 阵 有 个 元 素 ,其 数 值等 于。
2m3m3m ABC DEAEAEAxyM , θ2、图 示 刚 架 用 两 种 方 式 进 行 结 点 编 号 ,结 构 刚 度 矩 阵最 大 带 宽 较 小 的 是 图。
35641271234567(a)(b)3、图 示 梁 结 构 刚 度 矩 阵 的 主 元 素K K 1122== , 。
ll2EI EI 12xy M , θ四、图 a 、b 所 示 两 结 构 ,各 杆 EI 、l 相 同 ,不 计 轴 向 变 形 ,已 求 得 图 b 所 示 结 构 的 结 点 位 移 列 阵 为{}∆=-⎡⎣⎢⎤⎦⎥ql EI ql REI ql EI 34396192192 T。
试 求 图 a 所 示 结 构 中 单 元 ① 的 杆 端 力 列 阵。
q1234(a)ql2②③①1234(b)② ③① xyM , θ五、图 a 所 示 结 构 (整 体 坐 标 见 图 b ),图 中 圆 括 号 内 数码 为 结 点 定 位 向 量 (力 和 位 移 均 按 水 平 、竖 直 、转 动方 向 顺 序 排 列 )。
求 结 构 刚 度 矩 阵 []K 。
(不 考 虑 轴 向 变 形 )6m(0,0,0)(1,0,3)(1,0,2)6m(a)i ix yM , θ①② (b)六、求 图 示 结 构 的 自 由 结 点 荷载 列 阵 {}P 。
llqMxyM , θ七、图 a 所 示 结 构 ,整 体 坐 标 见 图 b ,图 中 圆 括 号 内 数码 为 结 点 定 位 向 量 (力 和 位 移 均 按 水 平 、竖 直 、转 动方 向 顺 序 排 列 )。
求 等 效 结 点 荷 载 列 阵 {}P E 。
( 不 考 虑 轴 向 变 形 )kN m 384kN(1,0,3)m /m 14m36(1,0,2)(b)(a)xy M , θ①②八、已 知 图 示 连 续 梁 结 点 位 移 列 阵 {}θ如 下 所 示 ,试用 矩 阵 位 移 法 求 出 杆 件 23 的 杆 端 弯 矩 并 画 出 连 续 梁的 弯 矩 图 。
设 q = 20kN/m ,23 杆 的 i =⨯⋅10106.kN cm 。
{}θ=--⎧⎨⎪⎪⎩⎪⎪⎫⎬⎪⎪⎭⎪⎪⨯-365714572286104....rad1234q i 6m3m3m xy M , θ九、已 知 图 示 桁 架 的 结 点 位 移 列 阵 为{}[]∆=--01726504007 0 2.5677 0.0415 1.0415 1.3673 1.6092 1.6408 0 1.2084 T.. ,EA =1kN 。
试 求 杆 14 的 轴 力 。
1m1kN1m1m135246xy M , θ1kN十、试 用 矩 阵 位 移 法 解 图 示 连 续 梁,绘 弯 矩 图 。
EI =已 知 常 数 。
A BC EI 2D 10 k N/m50 20 k N kN . m6 m4 m2 mEI xyM , θ自测题(第八单元)矩阵位移法答案一、 1 O 2 X 3 X 4 X 二、 1 A 2 B 3 B 4 C 5 B6 C7 D三、1、 1 、 2EA/L2、 b3、 i EI lK i K i === , , 1122124 四、{}{}∆∆a ql EI ql EI ql EI =-=--⎡⎣⎢⎤⎦⎥1281616343T{}F ql ql ql ql a①=---⎡⎣⎢⎤⎦⎥341434222 T(7分 )五、[]K i =--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥ 1 0 1 8 2 0 2 413/ (10分 )六、{}[]T/ql +m -/ql -P 12202= (7分 )七、{}[] 2 3422142E T1P =-- (7分 )八、M M 233242885140⎧⎨⎩⎫⎬⎭=-⎧⎨⎩⎫⎬⎭.. 42.8851.4090(kN m).M( 7分)九、N 1400587=-.kN (7分 )十、⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡408021213721θθEI EI EI EI ( 4 分 ); ⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧6448121EI θθ ( 2 分 ) ()()⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧--=⎭⎬⎫⎩⎨⎧40163462221121M M M M ( 3 分 )6216 40 3445kN m.MM 图 ( 3 分 )本章小结编码:整体(结构)编码: 单元码①②③…结点码ABCD…(1234…)结点位移(力)码=总码1234… 局部(单元)编码: 杆端码 1 2(局部坐标系)杆端位移(力)码=局部码)6)...(2)(1((整体坐标系)杆端位移(力)码=局部码)6)...(2)(1(不同结点:固定端、铰支端、自由端、中间铰、 中间滑动不同结构:刚架、忽略轴向变形矩形刚架、梁、 连续梁、桁架、组合结构[]{}{}P K =∆{}[]{}eeF T F ={}[]{}{}e PeeeF k F +∆={}[]{}{}eP e e e F k F +∆={}[]{}eeT ∆=∆{}{}{}ee∆⇓∆λ{}[]{}P K 1-=∆{}⇒eF 内力图[][][][]T k T k e T e ={}{}=e PF {}{}{}J E P P P +={}[]{}eP TeP F T F ={}[]{}e E Te E P T P ={}{}eP eEF P -={}{}e Pe E F P -={}{}{}E eeE P P λ⇓[]{}[]K k eeλ⇓ 前处理法公式汇总:[][]=ek单元: 刚架单元[]66⨯k、梁单元[]44⨯k 、连续梁单元[]22⨯k 、桁架单元[]44⨯k坐标系:整体(结构)坐标系、局部(单元)坐标系转换:定位:名称和意义:各矩阵、列阵(向量)、ij ij ij K k k。
