兰州文理学院2018-2019学年第二学期 期末考试《数学分析Ⅱ》(A)卷
兰州2018-2019第二学期七年级数学期末考试试卷

兰州08—09 第二学期七年级数学期末考试试卷本卷满分120 分,考试用时120 分钟.一、选择题( 本题共10 个小题,每小题 3 分,共计30 分.在每小题给出的 4 个选项中,只有一项是符合题目要求的) 1.下列计算中,正确的是( )A.a a2 a3 a B.(3 1) 32 2 2(a b) a bC.(2a b)2 4a2 2ab b2 D. 2( 2a 3)(2a 3) 9 4a 2.在长分别为1,2,3,4,5 的五条线段中,任取三条线段,能围成几种不同的三角形( )A.1 种B.2 种C.3 种D.4 种3.如图,若∠1=46°,a∥b,则∠2 的度数是A .134°B .46°C.44°D.100°4.天安门广场的面积是44 万米当于( )2,那么它的百万分之一相A.一间教室地面B.教室内的黑板C.一本教学课本D.一张讲桌5.下列说法中合理的是( )A.天气预报员说今天某地区下雨的概率是90%,由此可以断定今天该地区一定要下雨B.小莹在10 次抛图钉的试验中发现 3 次钉尖朝上,据此他说钉尖朝上的概率一定是30%C.某种福利彩票的中奖概率是1%,买一张这样的彩票不一定中奖,而买100 张这样的彩票一定会中奖D.抛掷一枚硬币落地后正面朝上的概率为 12就是正面朝上的可能性是50%6.下列语句正确的是( )A.近似数0.003 精确到了百分位B.近似数600 精确到个位,有一个有效数字C.近似数23.8 万精确到千位,有三个有效数字D.近似数3.620 108 精确到千分位7.小丽从兰州给远在天津的奶奶打电话,电话费随着时间的变化而变化,在这个问题中,因变量是( )A.小丽 B .时间C .奶奶 D .电话费8.如图,已知AB=AC,E 是角平分线AD上任意一点,则图中全等三角形有( )A .4对B.3对C.2对D.1对9.给出具备下列特征的△ABC:①∠A=∠B;②∠A=45°,∠C=90°;③∠A=72°,∠B=36o ;④AB=AC=B.C是轴对称图形的个数是( )A.4 个B.3 个C.2 个D.1 个10.如图,在△ABC 中,∠A=52°,∠ABC与∠ACB的角平分线交于点D,1 ABD 与1ACD1的角平分线交于点D,依次类推,2 ABD 与4ACD 的角平分线交于点4 D ,则5BD C 的度数5是( )A .60°B.56°C.94°D.68°二、填空题( 本题有10 小题,每小题 3 分,共30 分) 11.请你写出一个只含有字母x,y 的单项式,使它的系数为5,次数为3,________.12.把标有号码1,2,3,⋯⋯,10 的10 个乒乓球放在一个箱子中,摇匀后,从中任意取一个,号码为小于7 的奇数的概率是________.13.如图1,已知∠ABC=∠DCB,现要说明△ABC≌△DCB,则还要补加一个条件为________.14.某公路急转弯处设立了一面大镜子,从镜子中看到汽车的车牌号码如图 2 所示,则该汽车的号码是________.15.若整式 24m p 1是完全平方式,请你写一个满足条件的单项式p 是________.16.如图3,△ABC中,∠ACB=90°,CD⊥AB于D,则图中所有与∠A互余的角是________.17.光在真空中的速度大约为310 千米/ 秒,太阳系以外的5距离地球最近的恒星是比邻星,它发出光到达地球大约需要 4.22 年,一年以73 10 秒计算,比邻星与地球的距离约为________千米( 保留三个有效数字)18.小明拿 5 元钱去邮局买面值为0.80 元的邮票,买邮票所剩钱数y( 元) 与买邮票的枚数x( 枚) 的关系式为________,最多可以买________枚.19.探照灯、锅形天线、汽车灯以及其它很多灯具都可以反射光线.如图所示是一探照灯灯碗,侧面看上去,从位于O点的灯泡发出的两束光线OB、OC经灯碗反射以后平行射出.如果图中∠ABO=34°,∠DCO=66°,则∠BOC的度数为________.20.图(1) 是一个三角形,分别连接这个三角形三边中点得到图(2) ,再分别连接图(2) 中间的小三角形的中点得到图(3) ,按此方法继续下去,图(n) 中的三角形的个数是________.三、解答题( 本大题共8道题,共计60 分,解答时写出必要的文字说明、证明过程或演算步骤)21.(6 分) 已知x2 2x 2 ,将下式先化简,再求值:( x 1)2 ( x 3)(x 3) ( x 3)(x 1).22.(6 分) 下面是数学课堂的一个学习片断.阅读后,请回答下面的问题:学习等腰三角形有关内容后,张老师请同学们交流讨论这样一个问题:“已知等腰△A BC的∠A 等于30°,请你求出其余两角.”:“其同学们经片刻的思考与交流后,李明同学举手讲余两角是30°和120°;王华同学说:”其余两角是75°和75°.还有一些同学也提示了不同的看法⋯⋯(1) 假如你也在课堂中,你的意见如何,为什么?(2) 通过上面数学问题的讨论,你有什么感觉?(用一句话表示)23.(6分)某小商店开展购物摸奖活动,声明:购物时每消费2元可获得一次摸奖机会,每次摸奖时,购物者从标有数字1,2,3,4,5的5个小球(小球之间只有号码不同)中摸出一球,若号码是2就中奖,奖品为一张精美图片.(1)摸奖一次时,得到一张精美图片的概率是多少?得不到精美图片的概率是多少?(2)一次,小聪购买了10元钱的物品,前4次摸奖都没有摸中,他想:“第5次摸奖我一定能摸中”,你同意他的想法吗?说说你的想法.24.(6 分) 如图4 是小明用棋子摆成的字母“T”,它的主要特点是轴对称图形.请你再用棋子摆出两个轴对称图形的字母( 用○代表棋子) .25.(8 分) 推理填空.如图5,已知AB∥CD,AB=CD,要得到AD∥BC,小强的推理过程如下,请你补充完整.因为AB∥CD,所以________,(________)又因为AB=CD,AC=CA,所以△ADC≌________.所以∠DAC=∠BCA,(____________________) .所以AD∥BC.(____________________) .26.(9 分) 司机小王开车从A地出发去B地送信,其行驶若路程s 与行驶时间t 之间的关系如图所示,当汽车行驶C地时,汽车发生了故障,需停车检修,理干小时到达了几小时后,为了按时赶到 B 地,汽车加快了速度,结果下列问题:正好按时赶到,根据题意结合图回答①上述问题中反映的是哪两个变量之间的关系?指出自变量和因变量.②汽车从A地到C地用了几小时?平均每小时行驶多少千米?③汽车停车检修了多长时间?车修好后每小时走多少千米?27.(9 分) 如图,MN,EF是两面互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,则∠1=∠2(1) 用尺规作图作出的光线BC经镜面EF反射后的反射光线CD(不写作法,但保留作图痕迹) ;(2) 试判断AB与CD的位置关系,并说明理由.28.(10 分) 如图,已知∠B=∠C=90°,M是BC的中点,DM 平分∠ADC,试说明:∠1=∠2.。
兰州2018-2019第二学期新初一数学期末考试试题答卷

兰州08—09第二学期七年级数学期末考试试卷本卷满分120分,考试用时120分钟.一、选择题(本题共10个小题,每小题3分,共计30分.在每小题给出的4个选项中,只有一项是符合题目要求的)1.下列计算中,正确的是()A.23()+=+a b a ba a a a B.222--=--(31)3C.222(222A.13A.134100°4AC5ABC.而D50%6.下列语句正确的是()A.近似数0.003精确到了百分位B.近似数600精确到个位,有一个有效数字C.近似数23.8万精确到千位,有三个有效数字D.近似数8⨯精确到千分位3.620107.小丽从兰州给远在天津的奶奶打电话,电话费随着时间的变化而变化,在这个问题中,因变量是()A.小丽B.时间C.奶奶D.电话费8.如图,已知AB=AC ,E 是角平分线AD 上任意一点,则图中全等三角形有()A .4对B .3对C .2对D .1对9.给出具备下列特征的△ABC :①∠A=∠B ;②∠A=45°,∠C=90°;③∠A=72°,∠B=36o ;④AB=AC=BC .是轴对称图形的个数是()A .4个B .3个C .2个D .1个10.如图,在△ABC 中,∠A=52°,∠ABC 与∠ACB 的角平分线交于点1D ,1ABD ∠与1ACD ∠的角平分线交于点2D ,依次类推,4ABD ∠与4ACD ∠的角平分线交于点5D ,则5BD C ∠A .60° 11.3,121314图15p 是16A 互177秒计18.小明拿5元钱去邮局买面值为0.80元的邮票,买邮票所剩钱数y(元)与买邮票的枚数x(枚)的关系式为________,最多可以买________枚.19.探照灯、锅形天线、汽车灯以及其它很多灯具都可以反射光线.如图所示是一探照灯灯碗,侧面看上去,从位于O 点的灯泡发出的两束光线OB 、OC 经灯碗反射以后平行射出.如果图中∠ABO=34°,∠DCO=66°,则∠BOC 的度数为________.20.图(1)是一个三角形,分别连接这个三角形三边中点得到图(2),再分别连接图(2)中间的小三角形的中点得到图(3),按此方法继续下去,图(n)中的三角形的个数是________.三、解答题(本大题共8道题,共计60分,解答时写出必要的文字说明、证明过程或演算步骤)21.(6分)已知222-=,将下式先化简,再求值:x x2(1)(3)(3)(3)(1)-++-+--.x x x x x22.(6分)下面是数学课堂的一个学习片断.阅读后,请回答下面的问题:学习等腰三角形有关内容后,张老师请同学们交流讨论这样一个问题:“已知等腰△ABC的∠A等于30°,请你求出其余两角.”同学们经片刻的思考与交流后,李明同学举手讲:“其余两角是30°和120°;王华同学说:”其余两角是75°和75°.还有一些同学也提示(1)(2)23.(65个小球((1)(2)“第524.(6分)如图4是小明用棋子摆成的字母“T”,它的主要特点是轴对称图形.请你再用棋子摆出两个轴对称图形的字母(用○代表棋子).25.(8分)推理填空.如图5,已知AB∥CD,AB=CD,要得到AD∥BC,小强的推理过程如下,请你补充完整.因为AB∥CD,所以________,(________)又因为AB=CD,AC=CA,所以△ADC≌________.所以∠DAC=∠BCA,(____________________).所以26.(9间t量.27.(9分)如图,MN,EF是两面互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,则∠1=∠2(1)用尺规作图作出的光线BC经镜面EF反射后的反射光线CD(不写作法,但保留作图痕迹);(2)试判断AB与CD的位置关系,并说明理由.28.(10分)如图,已知∠B=∠C=90°,M是BC的中点,DM平分∠ADC,试说明:∠1=∠2。
高等数学AⅡ2019年试卷期末复习题及答案

2018级第2学期高等数学考试试题一、填空题(本题20分,每小题4分)1、螺旋线⎪⎩⎪⎨⎧===θθθb z a y a x sin cos 在xoy 面上的投影曲线方程为 .2、设)(),(x y g y x xy f z +=,其中g f ,均可微,则=∂∂xz. 3、设)cos sin (21x C x C e y x +=(21,C C 为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为 了 . 4、二次积分=⎰⎰xxdy yydx sin 10 . 5、设L 为逆时针取向的圆周)0(222>=+R R y x ,则=+-⎰Lyx xdyydx 22 . 二、(10分)设平面π是过直线⎩⎨⎧=+--=+-0620223:z y x y x L 的平面,且点)1,2,1(M 到平面π的距离为1,求平面π的方程.三、(10分)设函数⎪⎩⎪⎨⎧=+≠+++++=0 ,00 ,1sin )(),(22222222y x y x y x y x y x y x f ,(1)问),(y x f 在原点)0,0(处是否连续? (2)问),(y x f 在原点)0,0(的偏导数是否存在? (3)问),(y x f 在原点)0,0(处是否可微? 四、(10分)设Ω是由22y x z +=及1=z 所围成的立体,计算⎰⎰⎰Ω++=dv yxzI 221.五、(共16分,每小题8分)(1)求函数z y x u 32+-=在条件632222=++z y x 下的极大值与极小值; (2)求圆锥面222y x z +=被柱面x y x 222=+截下有限限部分的面积. 六、(10分)计算⎰⎰∑++=dxdy r z dzdx r y dydz rx I 333,222z y x r ++=,其中∑取曲面2222a z y x =++的外侧)0(>a .七、(共14分,其中第1小题7分,第2小题7分)(1)计算⎰Γ--dz yz xzdy ydx 23,其中Γ为曲面z y x 222=+与平面2=z 的交线,从z 轴正向看逆时针方向.(2)求方程0)d 3(d )3(2323=-+-y y x y x xy x 的通解. 八、(10分)设)(r f u =,222z y x r ++=,)0(>r ,且函数u 满足方程0222222=∂∂+∂∂+∂∂zuy u x u ,求函数)(r f 的表达式.2018级第2学期高等数学考试试题参考答案一、1. ⎩⎨⎧==+0222z a y x ; 2. g x yf y yf x z '-+=∂∂2211; 3. 022=+'-''y y y ; 4. 1sin 1-;5. π2-.二、利用平面束方程,可得01022=-++z y x 或01634=-+z y . 三、(1))0,0(0),(lim 0f y x f y x ==→→,所以),(y x f 在原点)0,0(处连续;(2)1)1sin 1(lim 1sinlim )0,0()0,(lim)0,0(202200=+=+=-=→→→x x xx x x xf x f f x x x x ,同理,1)0,0(=y f ,所以),(y x f 在原点)0,0(的偏导数存在; (3)ρyf x f f y x y x ∆-∆-∆→∆→∆)0,0()0,0(lim22222200)()()()(1sin ])()[(limy x y x y x y x y x y x ∆+∆∆-∆-∆+∆∆+∆+∆+∆=→∆→∆所以),(y x f 在原点)0,0(处可微.四、解法1(利用柱坐标)πθ20,10,1:≤≤≤≤≤≤Ωr z r ,⎰⎰⎰Ω+=dz rdrd r z I θ21⎰⎰⎰+=1102201r zdz dr r r d πθ⎰⎰+-=1102211r zdz rdr r r π)12ln 2(2-=π. 解法2(先二后一)222:,10:z y x D z z ≤+≤≤Ω,⎰⎰⎰++=zD dxdy y x zdz I 22111⎰⎰⎰+=zdr r r d zdz 022011πθ⎰+=102)1ln(dz z z π)12ln 2(2-=π. 五、(1)令)632(32),,,(222-++++-=z y x z y x z y x L λλ,令⎪⎪⎩⎪⎪⎨⎧=-++==+==+-==+=0632063042021222z y x L z L y L x L z y xλλλλ,解方程组得驻点)1,1,1(),1,1,1(21---M M ,且6)(1-=M u ,6)(2=M u .由于函数z y x u 32+-=在椭球面632222=++z y x 上连续,故函数z y x u 32+-=在点1M 取得极小值6-,在点2M 取得极大值6.(2)记221:y x z +=∑,222:y x z +-=∑,曲面在xOy 上的投影区域为x y x D xy ≤+22:,22y x x xz +=∂∂,22y x y yz +=∂∂,dxdy dxdy yzx z dS 2)()(122=∂∂+∂∂+=, 由对称性可得,π2222)()(12211122==∂∂+∂∂+==⎰⎰⎰⎰⎰⎰∑∑∑dxdy dxdy y zx z dS S . 六、记曲面∑围成的立体为Ω,由于2222a z y x =++,所以⎰⎰⎰⎰∑∑++=++++=yx z x z y z y x a z y x yx z x z y z y x I d d d d d d 1)(d d d d d d 323222ππ4343d d 3d 1333=⋅⋅==⎰⎰⎰Ωa a z y x a . 七、(1)解法1(利用Stokes 公式)取2:=∑z ,上侧,其法向量为}1,0,0{=n.⎰⎰⎰⎰⎰⎰⎰∑∑∑Γ--=--=--∂∂∂∂∂∂=--dS dS z dS yzxz y z y x dz yz xzdy ydx )32()3(3100322ππ20455-=⋅⋅-=-=⎰⎰∑dS .解法2(利用参数方程直接计算)Γ的参数方程为⎪⎩⎪⎨⎧===2sin 2cos 2z t y t x ,π20→由t ,………………………(2)因为xQxy y P ∂∂=-=∂∂6,所以所给方程为全微分方程. ⎰-+-=),()0,0(2323)d 3(d )3(),(y x y y x y x xy x y x u224402303234141)d 3(d y x y x y y x y x x yx-+=-+=⎰⎰, 故所求通解为C y x y x =-+22446. 八、r x r f x r r f x u ⋅'=∂∂⋅'=∂∂)()(,3222222)()(r x r r f r x r f x u -⋅'+⋅''=∂∂,由对称性得 3222222)()(ry r r f r y r f y u -⋅'+⋅''=∂∂,3222222)()(r z r r f r z r f z u -⋅'+⋅''=∂∂,代入已知条件中得,0)(2)(='+''r f rr f ,02)()(=+'''r r f r f ,22ln ln )(ln c r r f '=+', 22)(r c r f '='∴,从而12)(c r c r f +'-=,令22c c '-=,r c c r f 21)(+=∴.。
2018-2019学度甘肃兰州高二上年末数学试卷(文科)含解析解析.doc.doc

2018-2019学度甘肃兰州高二上年末数学试卷(文科)含解析解析注意事项:认真阅读理解,结合历年的真题,总结经验,查找不足!重在审题,多思考,多理解!无论是单选、多选还是论述题,最重要的就是看清题意。
在论述题中,问题大多具有委婉性,尤其是历年真题部分,在给考生较大发挥空间的同时也大大增加了考试难度。
考生要认真阅读题目中提供的有限材料,明确考察要点,最大限度的挖掘材料中的有效信息,建议考生答题时用笔将重点勾画出来,方便反复细读。
只有经过仔细推敲,揣摩命题老师的意图,积极联想知识点,分析答题角度,才能够将考点锁定,明确题意。
【一】单项选择题〔每题5分〕1、〔5分〕在数列1,2,,…中,2是这个数列的〔〕A、第16项B、第24项C、第26项D、第28项2、〔5分〕在△ABC中,假设2cosB•sinA=sinC,那么△ABC的形状一定是〔〕A、等腰直角三角形B、直角三角形C、等腰三角形D、等边三角形3、〔5分〕设变量x,y满足约束条件,那么z=x﹣y的取值范围为〔〕A、【2,6】B、〔﹣∞,10】C、【2,10】D、〔﹣∞,6】4、〔5分〕等差数列{an }的公差为2,假设a1,a3,a4成等比数列,那么a2等于〔〕A、﹣4B、﹣6C、﹣8D、﹣105、〔5分〕假设a《b《0,以下不等式成立的是〔〕A、a2《b2B、a2《abC、D、6、〔5分〕不等式ax2+bx+2》0的解集是〔﹣,〕,那么a+b的值是〔〕A、10B、﹣14C、14D、﹣107、〔5分〕抛物线y=2x2的焦点到准线的距离为〔〕A、B、C、D、4A、∀n∈N,n2》2nB、∃n∈N,n2≤2nC、∀n∈N,n2≤2nD、∃n∈N,n2=2n9、〔5分〕向量=〔1,m﹣1〕,=〔m,2〕,那么“m=2”是“与共线”的〔〕A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件10、〔5分〕函数f〔x〕的导函数f′〔x〕的图象如下图,那么函数f〔x〕的图象最有可能的是〔〕A、B、C、D、11、〔5分〕x,y》0,且,那么x+2y的最小值为〔〕A、B、C、D、12、〔5分〕椭圆〔a》b》0〕的两个焦点分别为F1,F2,假设椭圆上不存在点P,使得∠F1PF2是钝角,那么椭圆离心率的取值范围是〔〕A、B、C、D、【二】填空题〔每题5分〕13、〔5分〕假设当x》2时,不等式恒成立,那么a的取值范围是、14、〔5分〕曲线y=x3﹣2x+1在点〔1,0〕处的切线方程为、15、〔5分〕在△ABC中,角A,B,C的对边分别为a,b,C、假设〔a2+c2﹣b2〕tanB=ac,那么角B的值为、16、〔5分〕F1,F2为椭圆的两个焦点,过F1的直线交椭圆于A、B两点,假设|F2A|+|F2B|=12,那么|AB|=、【三】解答题17、〔10分〕在等差数列{an }中,a2=4,a4+a7=15、〔1〕求数列{an}的通项公式;〔2〕设,求b1+b2+b3+…+b10的值、18、〔12分〕在△ABC中,角A,B,C所对的边分别为a,b,c,a=2,c=5,cosB=、〔1〕求b的值;〔2〕求sinC的值、19、〔12分〕p:“∀x∈【1,2】,x2﹣a≥0”,q:“∃x∈R,x2+2ax+2﹣a=0”、假设命题p∧q是真命题,求a的取值范围、20、〔12分〕函数f〔x〕=x3+bx2+cx+d的图象经过点P〔0,2〕,且在点M〔﹣1,f〔﹣1〕〕处的切线方程为6x﹣y+7=0、〔Ⅰ〕求函数y=f〔x〕的解析式;〔Ⅱ〕求函数y=f〔x〕的单调区间、21、〔12分〕动点M〔x,y〕到定点A〔1,0〕的距离与M到直线l:x=4的距离之比为、①求点M的轨迹C的方程;②过点N〔﹣1,1〕的直线与曲线C交于P,Q两点,且N为线段PQ中点,求直线PQ的方程、22、〔12分〕椭圆C:+=1〔a》b》0〕的两个焦点分别为F1〔﹣,0〕,F2〔,0〕,以椭圆短轴为直径的圆经过点M〔1,0〕、〔1〕求椭圆C的方程;〔2〕过点M的直线l与椭圆C相交于A、B两点,设点N〔3,2〕,记直线AN,BN的斜率分别为k1,k2,问:k1+k2是否为定值?并证明你的结论、2017-2018学年兰州高二〔上〕期末数学试卷〔文科〕参考答案与试题解析【一】单项选择题〔每题5分〕1、〔5分〕在数列1,2,,…中,2是这个数列的〔〕A、第16项B、第24项C、第26项D、第28项【解答】解:数列1,2,,…就是数列,,,,,…,==,∴an∴=2=,∴n=26,故2是这个数列的第26项,应选:C、2、〔5分〕在△ABC中,假设2cosB•sinA=sinC,那么△ABC的形状一定是〔〕A、等腰直角三角形B、直角三角形C、等腰三角形D、等边三角形【解答】解析:∵2cosB•sinA=sinC=sin〔A+B〕⇒sin〔A﹣B〕=0,又B、A为三角形的内角,∴A=B、答案:C3、〔5分〕设变量x,y满足约束条件,那么z=x﹣y的取值范围为〔〕A、【2,6】B、〔﹣∞,10】C、【2,10】D、〔﹣∞,6】【解答】解:根据变量x,y满足约束条件画出可行域,由⇒A〔3,﹣3〕,由图得当z=x﹣y过点A〔3,﹣3〕时,Z最大为6、故所求z=x﹣y的取值范围是〔﹣∞,6】应选:D、4、〔5分〕等差数列{an }的公差为2,假设a1,a3,a4成等比数列,那么a2等于〔〕A、﹣4B、﹣6C、﹣8D、﹣10【解答】解:∵等差数列{an }的公差为2,a1,a3,a4成等比数列,∴〔a1+4〕2=a1〔a1+6〕,∴a1=﹣8,∴a2=﹣6、应选:B、5、〔5分〕假设a《b《0,以下不等式成立的是〔〕A、a2《b2B、a2《abC、D、【解答】解:方法一:假设a《b《0,不妨设a=﹣2,b=﹣1代入各个选项,错误的选项是A、B、D,应选C、方法二:∵a《b《0∴a2﹣b2=〔a﹣b〕〔a+b〕》0即a2》b2,应选项A不正确;∵a《b《0∴a2﹣ab=a〔a﹣b〕》0即a2》ab,应选项B不正确;∵a《b《0∴﹣1=《0即《1,应选项C正确;∵a《b《0∴》0即,应选项D不正确;应选C6、〔5分〕不等式ax2+bx+2》0的解集是〔﹣,〕,那么a+b的值是〔〕A、10B、﹣14C、14D、﹣10【解答】解:不等式ax2+bx+2》0的解集是〔﹣,〕,∴﹣,是方程ax2+bx+2=0的两个实数根,且a《0,∴﹣=﹣+,=﹣×,解得a=﹣12,b=﹣2,∴a+b=﹣14应选:B7、〔5分〕抛物线y=2x2的焦点到准线的距离为〔〕A、B、C、D、4【解答】解:根据题意,抛物线的方程为y=2x2,其标准方程为x2=y,其中p=,那么抛物线的焦点到准线的距离p=,应选:C、8、〔5分〕设命题p:∃n∈N,n2》2n,那么¬p为〔〕A、∀n∈N,n2》2nB、∃n∈N,n2≤2nC、∀n∈N,n2≤2nD、∃n∈N,n2=2n 【解答】解:命题的否定是:∀n∈N,n2≤2n,应选:C、9、〔5分〕向量=〔1,m﹣1〕,=〔m,2〕,那么“m=2”是“与共线”的〔〕A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件【解答】解:假设与共线,那么1×2﹣m〔m﹣1〕=0,即m2﹣m﹣2=0,得m=2或m=﹣1,那么“m=2”是“与共线”的充分不必要条件,应选:A10、〔5分〕函数f〔x〕的导函数f′〔x〕的图象如下图,那么函数f〔x〕的图象最有可能的是〔〕A、B、C、D、【解答】解:由导函数图象可知,f〔x〕在〔﹣∞,﹣2〕,〔0,+∞〕上单调递减,在〔﹣2,0〕上单调递增,应选A、11、〔5分〕x,y》0,且,那么x+2y的最小值为〔〕A、B、C、D、【解答】解:由得,,∴,当且仅当x=y=时取等号、应选:D、12、〔5分〕椭圆〔a》b》0〕的两个焦点分别为F1,F2,假设椭圆上不存在点P,使得∠F1PF2是钝角,那么椭圆离心率的取值范围是〔〕A、B、C、D、【解答】解:∵点P取端轴的一个端点时,使得∠F1PF2是最大角、椭圆上不存在点P,使得∠F1PF2是钝角,∴b≥c,可得a2﹣c2≥c2,可得:a、∴、应选:A、【二】填空题〔每题5分〕13、〔5分〕假设当x》2时,不等式恒成立,那么a的取值范围是〔﹣∞,2+2】、【解答】解:当x》2时,不等式恒成立,即求解x+的最小值,x+=x﹣2++2=2+2,当且仅当x=2+时,等号成立、所以a的取值范围是:〔﹣∞,2+2】、故答案为:〔﹣∞,2+2】、14、〔5分〕曲线y=x3﹣2x+1在点〔1,0〕处的切线方程为x﹣y﹣1=0、【解答】解:由y=x3﹣2x+1,得y′=3x2﹣2、∴y′|x=1=1、∴曲线y=x3﹣2x+1在点〔1,0〕处的切线方程为y﹣0=1×〔x﹣1〕、即x﹣y﹣1=0、故答案为:x﹣y﹣1=0、15、〔5分〕在△ABC中,角A,B,C的对边分别为a,b,C、假设〔a2+c2﹣b2〕tanB=ac,那么角B的值为或、【解答】解:∵,∴cosB×tanB=sinB=∴B=或应选B、16、〔5分〕F1,F2为椭圆的两个焦点,过F1的直线交椭圆于A、B两点,假设|F2A|+|F2B|=12,那么|AB|=8、【解答】解:根据题意,椭圆的方程为,那么a=5,由椭圆的定义得,|AF1|+|AF2|=|BF1|+|BF2|=2a=10,两式相加得|AB|+|AF2|+|BF2|=20,又由|F2A|+|F2B|=12,那么|AB|=8,故答案为:8、【三】解答题17、〔10分〕在等差数列{an }中,a2=4,a4+a7=15、〔1〕求数列{an}的通项公式;〔2〕设,求b1+b2+b3+…+b10的值、【解答】解:〔1〕设等差数列{an}的公差为d,由得解得…〔4分〕∴an =3+〔n﹣1〕×1,即an=n+2…〔6分〕〔2〕由〔1〕知,b 1+b2+b3+…+b10=21+22+…+210=…〔10分〕=2046…〔12分〕18、〔12分〕在△ABC中,角A,B,C所对的边分别为a,b,c,a=2,c=5,cosB=、〔1〕求b的值;〔2〕求sinC的值、【解答】解:〔1〕由余弦定理b2=a2+c2﹣2accosB,代入数据可得b2=4+25﹣2×2×5×=17,∴b=;〔2〕∵cosB=,∴sinB==由正弦定理=,即=,解得sinC=19、〔12分〕p:“∀x∈【1,2】,x2﹣a≥0”,q:“∃x∈R,x2+2ax+2﹣a=0”、假设命题p∧q是真命题,求a的取值范围、【解答】解:p:∀x∈【1,2】,x2﹣a≥0,只要〔x2﹣a〕min≥0,x∈【1,2】,又y=x2﹣a,x∈【1,2】的最小值为1﹣a,所以1﹣a≥0,a≤1、q:∃x∈R,x2+2ax+2﹣a=0,所以△=4a2﹣4〔2﹣a〕≥0,a≤﹣2或a≥1,由p且q为真可知p和q为均真,所以a≤﹣2或a=1,∴a的取值范围是{a|a≤﹣2或a=1}、20、〔12分〕函数f〔x〕=x3+bx2+cx+d的图象经过点P〔0,2〕,且在点M〔﹣1,f〔﹣1〕〕处的切线方程为6x﹣y+7=0、〔Ⅰ〕求函数y=f〔x〕的解析式;〔Ⅱ〕求函数y=f〔x〕的单调区间、【解答】解:〔Ⅰ〕由y=f〔x〕的图象经过点P〔0,2〕,知d=2,∴f〔x〕=x3+bx2+cx+2,f'〔x〕=3x2+2bx﹣C、由在点M〔﹣1,f〔﹣1〕〕处的切线方程为6x﹣y+7=0,知﹣6﹣f〔﹣1〕+7=0,即f〔﹣1〕=1,又f'〔﹣1〕=6、解得b=c=﹣3、故所求的解析式是f〔x〕=x3﹣3x2﹣3x+2、〔Ⅱ〕f'〔x〕=3x2﹣6x﹣3、令f'〔x〕》0,得或;令f'〔x〕《0,得、故f〔x〕=x3﹣3x2﹣3x+2的单调递增区间为和,单调递减区间为、21、〔12分〕动点M〔x,y〕到定点A〔1,0〕的距离与M到直线l:x=4的距离之比为、①求点M的轨迹C的方程;②过点N〔﹣1,1〕的直线与曲线C交于P,Q两点,且N为线段PQ中点,求直线PQ的方程、【解答】解:①由题意动点M〔x,y〕到定点A〔1,0〕的距离与它到定直线l:x=4的距离之比为,得=,化简并整理,得+=1、所以动点M〔x,y〕的轨迹C的方程为椭圆+=1、②设P,Q的坐标为〔x1,y1〕,〔x2,y2〕,∴3x12+4y12=12,3x22+4y22=12,两式相减可得3〔x1+x2〕〔x1﹣x2〕+4〔y1+y2〕〔y1﹣y2〕=0,∵x1+x2=﹣2,y1+y2=2,∴﹣6〔x1﹣x2〕+8〔y1﹣y2〕=0,∴k==,∴直线PQ的方程为y﹣1=〔x+1〕,即为3x﹣4y+7=0、22、〔12分〕椭圆C:+=1〔a》b》0〕的两个焦点分别为F1〔﹣,0〕,F2〔,0〕,以椭圆短轴为直径的圆经过点M〔1,0〕、〔1〕求椭圆C的方程;〔2〕过点M的直线l与椭圆C相交于A、B两点,设点N〔3,2〕,记直线AN,BN的斜率分别为k1,k2,问:k1+k2是否为定值?并证明你的结论、【解答】解:〔1〕∵椭圆C:+=1〔a》b》0〕的两个焦点分别为F1〔﹣,0〕,F2〔,0〕,以椭圆短轴为直径的圆经过点M〔1,0〕,∴,解得,b=1,∴椭圆C的方程为=1、〔2〕k1+k2是定值、证明如下:设过M的直线:y=k〔x﹣1〕=kx﹣k或者x=1①x=1时,代入椭圆,y=±,∴令A〔1,〕,B〔1,﹣〕,k 1=,k2=,∴k1+k2=2、②y=kx﹣k代入椭圆,〔3k2+1〕x2﹣6k2x+〔3k2﹣3〕=0设A〔x1,y1〕,B〔x2,y2〕、那么x1+x2=,x1x2=,y 1+y2=﹣2k=,y 1y2=k2x1x2﹣k2〔x1+x2〕+k2=﹣,k 1=,k2=,∴k1+k2==2、。
2018-2019学年甘肃省兰州一中高二下学期期末考试数学(文)试题Word版含解析

兰州一中2018--2019--2高二期末考试文科数学试卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给的四个选项中,只有一项是符合题目要求的。
1.已知集合{}|5213, M x x x R =-≤-≤∈, (){}|80, N x x x x Z =-≤∈,则M N ⋂=( )A .()0,2B .[]0,2 C .{}0,2 D .{}0,1,22.已知两向量AB →=(4,-3),CD →=(-5,-12),则AB →在CD →方向上的投影为( )A .(-1,-15)B .(-20,36)C .1613D .1653.已知2log 7a =,3log 8b =,0.20.3c =,则,,a b c 的大小关系为 ( )A. c b a <<B. a b c <<C. b c a <<D. c a b <<4设函数f (x )=cos x +b sin x (b 为常数),则“b =0”是“f (x )为偶函数”的( ) A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件D. 既不充分也不必要条件5.在同一直角坐标系中,函数11,log (02a x y y x a a ⎛⎫==+> ⎪⎝⎭且0)a ≠的图象可能是( )A. B.C. D.6.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为( )A.0.5 B.0.6 C.0.7 D.0.87.执行如图所示的程序框图,输出的s值为()A. 1B. 2C. 3D.4(第7题) (第8题)8.如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M 是线段ED的中点,则( )A.BM=EN,且直线BM、EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM、EN是异面直线D.BM≠EN,且直线BM,EN是异面直线9.若实数,x y满足约束条件340340x yx yx y-+≥⎧⎪--≤⎨⎪+≥⎩,则32z x y=+的最大值是()A. 1-B. 1C. 10D. 1210.在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足212152–lg E m m E =,其中星等为m 1的星的亮度为E 2(k =1,2).已知太阳的星等是–26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的比值为 ( ) A. 1010.1B. 10.1C. lg10.1D. 10.110-11.知点A ,B ,C ,D 均在球O 上,AB =BC =3,AC =3,若三棱锥D -ABC 体积的最大值为334,则球O 的表面积为( )A .36πB .16πC .12πD .163π12.数学中有许多形状优美、寓意美好的曲线,曲线C :y x y x +=+122就是其中之一(如图).给出下列三个结论:①曲线C 恰好经过6个整点(即横、纵坐标均为整数的点); ②曲线C 上任意一点到原点的距离都不超过2;③曲线C 所围成的“心形”区域的面积小于3.其中,所正确结论的序号是 ( ) A.①B. ②C. ①②D . ①②③二、填空题:本题共4小题,每小题5分,共20分。
甘肃省2018-2019学年高二下学期期末考试数学试卷及参考答案解析
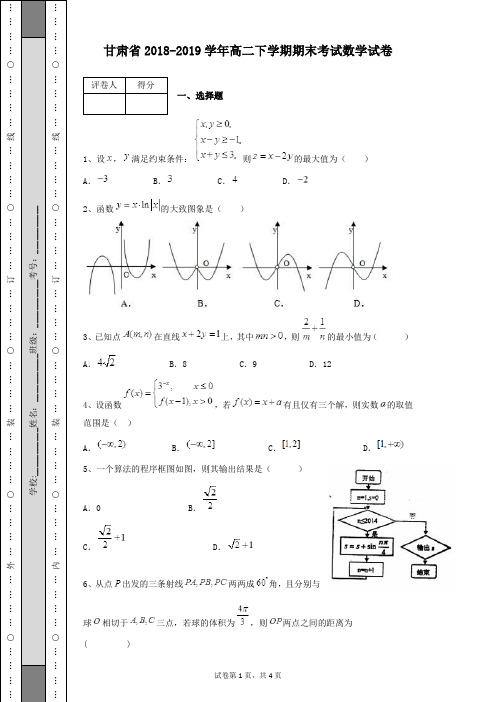
甘肃省2018-2019学年高二下学期期末考试数学试卷一、选择题1、设,满足约束条件:则的最大值为( )A .B .C .D .2、函数的大致图象是( )3、已知点在直线上,其中,则的最小值为( )A .B .8C .9D .124、设函数,若有且仅有三个解,则实数的取值范围是( ) A .B .C .D .5、一个算法的程序框图如图,则其输出结果是( )A .0B .C .D .6、从点出发的三条射线两两成角,且分别与球相切于三点,若球的体积为,则两点之间的距离为( )A .B .C .1.5D .27、一个几何体的三视图如上图所示,则该几何体的体积为 ( )A .B .C .D .8、已知、取值如下表:从散点图可知:与线性相关,且,则当x=10时,的预测值为( )A. 10.8B. 10.95C. 11.15D. 11.39、已知为锐角,且,,则的值为( )A .B .C .D .10、在中,已知向量,,,则=( )A .B .C .D . 11、若a,b,c 是是实数,则下列选项正确的是( )A .若,则B .若,则C .若,则D .若,则12、已知集合,集合,则( )。
A .B .C .D .二、填空题13、设平面向量,定义以轴非负半轴为始边,逆时针方向为正方向,为终边的角称为向量的幅角.若是向量的模,是向量的模,的幅角是,的幅角是,定义的结果仍是向量,它的模为,它的幅角为+.给出.试用、的坐标表示的坐标,结果为_______。
14、在区间上随机取一个数X ,则的概率为______________。
15、已知函数的图象经过点,则不等式的解为_________。
16、已知为等差数列,为其前项和.若,,则=__________。
三、解答题17、如图,在直角坐标系中,圆与轴负半轴交于点,过点的直线,分别与圆交于,两点。
(Ⅰ)若,,求的面积;(Ⅱ)若直线过点,证明:为定值,并求此定值。
18、从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间,,内的频率之比为。
甘肃省兰州市2018-2019学年高一上学期第二片区丙组期末联考数学试题(精校Word版含答案)

2018-2019学年度第一学期第二片区丙组期末联考高一数学试卷注意事项:1.本试卷共150分,考试时间120分钟2.作答时,将答案写在答题卡上,写在试卷上无效.3.考试结束后,将答题卡交回,试卷自己保留.一、选择题(本大题共12小题,每小题5分,共60分) 1.已知直线l 的方程为1y x =+,则该直线l 的倾斜角为( )A 、30B 、45C 、60D 、135 2.直线2x-y=7与直线3x+2y-7=0的交点是( ) A 、(3,-1) B 、(-1, 3) C 、(-3,-1) D 、(3,1)3.长方体的三个面的面积分别是632、、,则长方体的体积是( ).A 、23B 、32C 、6D 、64.边长为a 的正四面体的表面积是 ( )A 3B 3C 2D 2 5.对于直线:360l x y -+=的截距,下列说法正确的是 ( )A 、在y 轴上的截距是6B 、在x 轴上的截距是6C 、在x 轴上的截距是3D 、在y 轴上的截距是3-6.已知,a b αα⊂//,则直线a 与直线b 的位置关系是 ( )A 、平行B 、相交或异面C 、异面D 、平行或异面7.两条不平行的直线,其平行投影不可能是 ( )A 、两条平行直线B 、一点和一条直线C 、两条相交直线D 、两个点8.若某空间几何体的三视图如图所示,则该几何体的体积是( )1A 、2B 、1C 、23D 、139.下列叙述中,正确的是( )A 、因为,P Q αα∈∈,所以PQ ∈αB 、因为P α∈,Q β∈,所以αβ⋂=PQC 、因为AB α⊂,C ∈AB ,D ∈AB ,所以CD ∈αD 、因为AB α⊂,AB β⊂,所以()A αβ∈⋂且()B αβ∈⋂10.长方体的一个顶点上的三条棱长分别为3、4、5,且它的8个顶点都在同一个球面上,则这个球的表面积是( )A 、25πB 、50πC 、125πD 、都不对11.在空间四边形ABCD 中,,,,E F G H 分别是,,,AB BC CD DA 的中点.若AC BD a ==,且AC 与BD 所成的角为60,则四边形EFGH 的面积为 ( )A 2B 2C 2aD 2 12.已知点)3,2(-A 、)2,3(--B 直线l 过点)1,1(P ,且与线段AB 相交,则直线l 的斜率的取值k 范围是 ( )A 、34k ≥或4k ≤-B 、34k ≥或14k ≤-C 、434≤≤-kD 、443≤≤k第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)13.底面直径和高都是4cm 的圆柱的侧面积为 cm 2. 14.两平行直线0962043=-+=-+y x y x 与间的距是 . 15.过点(1,2),且在两坐标轴上截距相等的直线方程 .16.如果对任何实数k ,直线(3+k)x +(1-2k)y +1+5k=0都过一个定点A ,那么点A 的坐标是 .三、解答题:(本大题共6小题,其中17小题10分,其余每小题12分,共70分,解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分10分)求经过M (-1,2),且满足下列条件的直线方程 (1)与直线2x + y + 5 = 0平行; (2)与直线2x + y + 5 = 0垂直.18.(本小题满分12分)已知ABC 的三个顶点是()()()4,0,6,7,0,8A B C (1) 求BC 边上的高所在直线的方程; (2) 求BC 边上的中线所在直线的方程.19. (本小题满分12分)如图所示,在四棱锥P ABCD -中,四边形ABCD 是平行四边形,,M N 分别是,AB PC 的中点. 求证:MN PAD //平面 .20.(本小题满分12分)如图,已知正四棱锥V -ABCD 中AC BD M VM 与交于点,是棱锥的高,若6cm AC =,5cm VC =,求正四棱锥V -ABCD 的体积.21.(本小题满分12分)如图所示,在三棱锥A BCD -中,,O E 分别是,BD BC 的中点,2CA CB CD BD ====,.AB (1) 求证:AO ⊥平面BCD ;(2) 求异面直线AB 与CD 所成角的余弦值;22.(本小题满分12分)如图所示,在正方体ABCD -A 1B 1C 1D 1中,已知E 为棱CC 1上的动BCAD MNPEC点.(1)求证:A 1E ⊥BD ;(2)是否存在这样的E 点,使得平面A1BD ⊥平面EBD ? 若存在,请找出这样的E 点;若不存在,请说明理由.高一数学答题卡班级:______________姓名:________________ 考场:______________座号:________________一、 选择题(每小题5分,共计60分)二、填空题(每小题5分,共计20分)13. ____________________________;14. ;. 15. ____________________________; 16. 。
2018~2019学年度第二学期高二期末考试文科数学试题(含答案)

2018~2019学年度第⼆学期⾼⼆期末考试⽂科数学试题(含答案)绝密★启⽤前2018~2019学年度第⼆学期⾼⼆期末考试⽂科数学试题注意事项:1.答卷前,考⽣务必将⾃⼰的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每⼩题答案后,⽤铅笔把答题卡对应题⽬的答案标号涂⿊。
如需改动,⽤橡⽪擦⼲净后,再选涂其它答案标号。
回答⾮选择题时,将答案写在答题卡上。
写在本试卷上⽆效。
⼀、选择题:本题共12⼩题,每⼩题5分,共60分。
在每⼩题给的四个选项中,只有⼀项是符合题⽬要求的。
1.复平⾯内表⽰复数z=i(-2+i)的点位于()A. 第⼀象限B. 第⼆象限C. 第三象限D. 第四象限2.观察下列各式:a+b=1,+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,……,则a9+b9=A. 28B. 76C. 123D. 1993.执⾏如图所⽰的程序框图,输出的S值为()A. 2B.C.D.4.直线(t为参数)的倾斜⾓为()A. B. C. D.5.极坐标⽅程ρ=2cosθ表⽰的圆的半径是()A. B. C. 2 D. 16.设复数z满⾜(1+i)z=2i,则|z|=()A. B. C. D. 27.不等式|x+3|<1的解集是()A. B.C. D. 或8.下列命题中,正确的是()A. 若,,则B. 若,则C. 若,则D. 若,,则9.则对的回归直线⽅程必过点()A. B. C. D.10.在研究吸烟与患肺癌的关系中,通过收集数据,整理、分析数据得出“吸烟与患肺癌有关”的结论,并有99%的把握认为这个结论是成⽴的,下列说法中正确的是()A. 吸烟⼈患肺癌的概率为B. 认为“吸烟与患肺癌有关”犯错误的概率不超过C. 吸烟的⼈⼀定会患肺癌D. 100个吸烟⼈⼤约有99个⼈患有肺癌11.在直⾓坐标系中,点P坐标是(-3,3),以原点为极点,x轴正半轴为极轴建⽴的极坐标系中,点P的极坐标是()A. B. C. D.12.⾼考⽂科综合由政治、历史、地理三个科⽬组成,满分300分,每个科⽬各100分,若规定每个科⽬60分为合格,总分180分为⽂科综合合格.某班⾼考⽂科综合各则该班政治、历史、地理三个科⽬都合格的⼈数最多有()A. 13⼈B. 15⼈C. 17⼈D. 20⼈⼆、填空题:本题共4⼩题,每⼩题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、判断题(每题1分,共8分)
11. 函数)
(x
f在[a,b]上可积的必要条件是连续. ( )
12. 函数项级数一致收敛的必要条件是通项收敛. ( )
13. 若)
(x
f在[a,b]上可积,则|)
(x
f|在[a,b]上必可积. ( ) 14. dx
x
f
a⎰
+∞
)
(收敛,则0
)
(
lim=
∞
→
x
f
x
. ( )
15.
n
n
n
1
)1
(
1
∑+∞
=
-收敛,∑+∞
=1
1
n
n
也收敛. ( )
16. 在收敛级数的项中任意加括号,既不改变级数的收敛性,也不改变它的和.( )
17. 设级数∑n u与∑n v都发散,则∑+)
(
n
n
v
u也一定发散. ( )
18.
3
1
1
x
+
的幂级数展开式为∑+∞
=0
3
n
n
x. ( )
三、选择题(每题2分,共12分)
19. 设x
e
x
f-
=
)
(,则:=
⎰dx
x
x
f)
(ln
( )
A c
x
+
1
B c
x+
ln C c
x
+
-
1
D c
x+
-ln
20. 设)
(x
f是[a,b]上可积的奇函数,则dt
t
f x⎰0)(是( )
A 连续的奇函数
B 连续的偶函数
C 未必连续的奇函数
D 未必连续的偶函数
21.n
n
x
n
)1
(
1
1
-
∑+∞
=
的收敛域为( )
A (-1,1)
B [-1,1)
C (0,2]
D [0,2)
22. 下列说法错误的是 ( )
A 函数列{
f
n
}收敛的全体收敛点集合,称为函数列{
f
n
}的收敛域
B 若函数列{
f
n
}在区间I 上一致收敛且每项都连续,则其极限函数在I 上也连续
C 若连续函数列{
f
n
}在区间I 上内闭一致收敛,则极限函数在I 上连续
D 一致收敛性是极限运算与求导运算的交换的充要条件
23. x
e x
f =)(在[0,1]上绕x 旋转一周生成体的体积是 ( ) A
22
e π
B
e 2
π
C
)1(2
2-e π
D 12-e
24. ∑=
3sin )(n nx
x f 在),(+∞-∞上 ( )
A f 连续但f '不连续
B f 连续且f '连续
C f 不连续
D f 不可导
四、计算题(每题10分,共20分)
25. 计算 1) 6
20
sin lim
x dt t x
x ⎰→(5分) 2) dx e e x
x ⎰+-1
(5分).
26. 求由摆线]2,0[)
cos 1()sin (π∈⎩⎨
⎧-=-=t t a y t t a x 与x 轴围成的平面图形的面积.
五、证明题(每题10分,共20分)
27. 证明:若正项级数
∑+∞
=1
n n
a
收敛,且数列n a 单调,则n n na 0
lim →=0.
41
.
10分,共20分)
. 30. 将x x f =)(在[0,2]上展开成余弦级数,并由此推出
++++
=2
222
71
513118
π.。
