结构力学§5-6_温度变化时的位移计算
合集下载
第六章 结构位移计算

同,截面的I、A均为常数。
解:(1)虚拟状态如图b,各杆内力为
AB段: M x , FN 0, FS 1 BC段: M l , FN 1, FS 0
(2)实际状态中,各杆内力为
AB段:
MP
qx2 2
,
FNP 0,
FSP qx
BC段:
MP
ql 2 2
,
FNP ql,
FSP 0
(3)代入位移计算公式
三、计算位移的有关假定
1、结构材料服从“虎克定律”,即应力、应变成线形关系。
2、小变形假设。变形前后荷载作用位置不变。
3、结构各部分之间为理想联结,不计摩擦阻力。
4、当杆件同时承受轴力与横向力作用时, 不考虑由于杆 弯曲所引起的杆端轴力对弯矩及弯曲变形的影响。
P
A
B
P
满足以上要求的体系为“线变形体系”。因位移与荷载 为线形关系,故求位移时可用叠加原理。
第6章
求图a所示桁架AB杆的角位移。
在位移微小的前提下,桁架杆件的 角位移=其两端在垂直于杆轴方向上的 相对线位移除以杆长,如图b。
AB杆的角位移
AB
ΔA
d
ΔB
荷载所做的虚功
1 d
ΔA
1 d
ΔB
ΔA
d
ΔB
AB
第6章
计算对象:线弹性结构,位移与荷载成正比,应力与应变符合
胡克定律。
求图a所示结构K点的竖向位
A —截面A的角位移(顺时针方向) B —截面B的角位移(逆时针方向) AB A B —截面A、B的相对角位移
ΔC —C点水平线位移(向右) ΔD —D点水平线位移(向左) ΔCD ΔC ΔD —C、D两点的水平相对线位移
解:(1)虚拟状态如图b,各杆内力为
AB段: M x , FN 0, FS 1 BC段: M l , FN 1, FS 0
(2)实际状态中,各杆内力为
AB段:
MP
qx2 2
,
FNP 0,
FSP qx
BC段:
MP
ql 2 2
,
FNP ql,
FSP 0
(3)代入位移计算公式
三、计算位移的有关假定
1、结构材料服从“虎克定律”,即应力、应变成线形关系。
2、小变形假设。变形前后荷载作用位置不变。
3、结构各部分之间为理想联结,不计摩擦阻力。
4、当杆件同时承受轴力与横向力作用时, 不考虑由于杆 弯曲所引起的杆端轴力对弯矩及弯曲变形的影响。
P
A
B
P
满足以上要求的体系为“线变形体系”。因位移与荷载 为线形关系,故求位移时可用叠加原理。
第6章
求图a所示桁架AB杆的角位移。
在位移微小的前提下,桁架杆件的 角位移=其两端在垂直于杆轴方向上的 相对线位移除以杆长,如图b。
AB杆的角位移
AB
ΔA
d
ΔB
荷载所做的虚功
1 d
ΔA
1 d
ΔB
ΔA
d
ΔB
AB
第6章
计算对象:线弹性结构,位移与荷载成正比,应力与应变符合
胡克定律。
求图a所示结构K点的竖向位
A —截面A的角位移(顺时针方向) B —截面B的角位移(逆时针方向) AB A B —截面A、B的相对角位移
ΔC —C点水平线位移(向右) ΔD —D点水平线位移(向左) ΔCD ΔC ΔD —C、D两点的水平相对线位移
结构力学第六章-5(温度、位移)
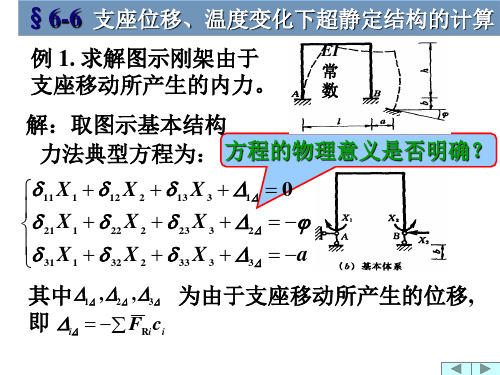
例2. 试求图示两端固定单跨梁在下属情 况下的M图。 (a) A端逆时针转动单位转角。 (b) A端竖向向上移动了单位位移。 (c) A、B两端均逆时针转动单位转角。 (d) A、B两端相对转动单位转角。 P (e) A端竖向向上、BF 端竖向向下移动了单 位位移。
A
EI
B
例 3. 求图示刚架由于温度变X3X1Fra bibliotekX2b a
1 l b 2 a 3
用几 何法 与公 式法 相对 比。
基本体系3
11 X 1 12 X 2 13 X 3 1 0 21 X 1 22 X 2 23 X 3 2 0 X X X 0 31 1 32 2 33 3 3
§6-6 支座位移、温度变化下超静定结构的计算
例 1. 求解图示刚架由于 支座移动所产生的内力。
EI 常 数
解:取图示基本结构 力法典型方程为: 方程的物理意义是否明确?
11 X 1 12 X 2 13 X 3 1 0 21 X 1 22 X 2 23 X 3 2 X X X a 31 1 32 2 33 3 3
其中 1 , 2 , 3 为由于支座移动所产生的位移, 即 i FRi ci
单位基本未知力引起的弯矩图和反力
b b b b ( Δ) , 2Δ ( ) , 3 0 、Δ 等于多少? δ 由自乘、互乘求 1 2Δ 3 1Δ 、 Δ, ij与荷载作用时一样 l l l l
简 化
例 4. 求作弯矩图(同例3)。 10 EI ( k ) EI常数 l
3
解:选取基本体系 建立典型方程
结构力学 虚功原理与结构位移计算

FP
B
C
c
cu
cv
B
C
M
FP 1
M
FN
A
FR 2
FN
A
FR1
FQ ds FQ
给定位移、变形
虚设平衡力系
18
2. 位移计算一般公式 外力虚功 W 1 CV FRK CK
K
内虚功
Wi ( M FQ 0 FN )ds
K
所求位移 1 CV ( M FQ 0 FN )ds FRK CK
l
( 1 2 )
25
三、广义位移的计算
ΔAH
求图a)结构A、B截面相对水平位移 AB AH BH。
A κ,γ0 , ε q
a) 给定位移
B
ΔBH
1 A
M , FQ , FN
b)
B 1
1 A
B
A
1 B
=
M 1 , FQ1 , FN 1
+
M 2 , FQ 2 , FN 2
1. 截面位移
FP
FP
B
Bu
B
C
c
cu
BV
cv
A
C
桁架受荷载作用
2
A
刚架受荷载作用
A
C
cv
cu
C'
t1 c t 2
B
A
C
t2 t1
C' c
cv
B
温度变化
支座B下沉
2. 广义位移 通常把两个截面的相对水平位移、相对竖向 位移以及相对转角叫做广义位移。
B
C
c
cu
cv
B
C
M
FP 1
M
FN
A
FR 2
FN
A
FR1
FQ ds FQ
给定位移、变形
虚设平衡力系
18
2. 位移计算一般公式 外力虚功 W 1 CV FRK CK
K
内虚功
Wi ( M FQ 0 FN )ds
K
所求位移 1 CV ( M FQ 0 FN )ds FRK CK
l
( 1 2 )
25
三、广义位移的计算
ΔAH
求图a)结构A、B截面相对水平位移 AB AH BH。
A κ,γ0 , ε q
a) 给定位移
B
ΔBH
1 A
M , FQ , FN
b)
B 1
1 A
B
A
1 B
=
M 1 , FQ1 , FN 1
+
M 2 , FQ 2 , FN 2
1. 截面位移
FP
FP
B
Bu
B
C
c
cu
BV
cv
A
C
桁架受荷载作用
2
A
刚架受荷载作用
A
C
cv
cu
C'
t1 c t 2
B
A
C
t2 t1
C' c
cv
B
温度变化
支座B下沉
2. 广义位移 通常把两个截面的相对水平位移、相对竖向 位移以及相对转角叫做广义位移。
结构力学5-6静定结构在非荷载因素作用下的位移计算
F
N
图
⑵作单位荷载作用下的轴力图和弯矩图。 ⑶求D点竖向位移。
yD
10
2
2
20
2a 10
1 2 a a 2
1 2
a
20 0 .1 5 a
0 .1 5 a
1 2
a
2
M 图
2 5 a ( )
Kt
t0 A
F
N
பைடு நூலகம்
t
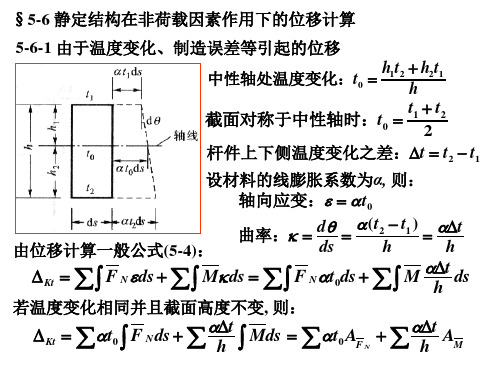
§5-6 静定结构在非荷载因素作用下的位移计算
5-6-1 由于温度变化、制造误差等引起的位移
中 性 轴 处 温 度 变 化 : t0 h1 t 2 h 2 t 1 h
截 面 对 称 于 中 性 轴 时 : t0
t1 t 2 2
杆 件 上 下 侧 温 度 变 化 之 差 : t t 2 t1
F P i ii
§5-7 线性弹性体的互等定理 5-7-1 功的互等定理 5-7-2 位移互等定理
F Pi
ij
F Pj
ji
ji
ij
1
ij
1
ji
5-7-3 反力互等定理
r ji r ij
rii 0 r ji 1 rij 1 r jj 0
§5-7 线性弹性体的互等定理 5-7-1 功的互等定理 5-7-2 位移互等定理
F Pi
ij
F Pj
ji
ji
ij
5-7-3 反力互等定理 5-7-4 反力与位移互等定理
r ji r ij r ji ij
r ji 1 1 ij 0
N
图
⑵作单位荷载作用下的轴力图和弯矩图。 ⑶求D点竖向位移。
yD
10
2
2
20
2a 10
1 2 a a 2
1 2
a
20 0 .1 5 a
0 .1 5 a
1 2
a
2
M 图
2 5 a ( )
Kt
t0 A
F
N
பைடு நூலகம்
t
§5-6 静定结构在非荷载因素作用下的位移计算
5-6-1 由于温度变化、制造误差等引起的位移
中 性 轴 处 温 度 变 化 : t0 h1 t 2 h 2 t 1 h
截 面 对 称 于 中 性 轴 时 : t0
t1 t 2 2
杆 件 上 下 侧 温 度 变 化 之 差 : t t 2 t1
F P i ii
§5-7 线性弹性体的互等定理 5-7-1 功的互等定理 5-7-2 位移互等定理
F Pi
ij
F Pj
ji
ji
ij
1
ij
1
ji
5-7-3 反力互等定理
r ji r ij
rii 0 r ji 1 rij 1 r jj 0
§5-7 线性弹性体的互等定理 5-7-1 功的互等定理 5-7-2 位移互等定理
F Pi
ij
F Pj
ji
ji
ij
5-7-3 反力互等定理 5-7-4 反力与位移互等定理
r ji r ij r ji ij
r ji 1 1 ij 0
建筑力学结构位移计算

退出 返回
中南大学
14:46
§6-1 概述
C'
CV CDV DV
结构力学
C D
D'
截面C、D 的相对竖向 线位移为 :
A
B
CDV CV DV
截面C、D 的相对角位移为:
C' D'
C
D
C
D
Δ CD C D
A B
中南大学
退出
返回
14:46
§6-1 概述
退出 返回
中南大学
14:46
§6-2 变形体系的虚功原理
2.杆系结构虚功方程
Wi FN d FSd Md
s s s
结构力学
We Wi
以上结论与材料物理性质及具体结构无关,因 此,虚功原理虚功方程既适用于一切线性结构,也 适用于一切非线性结构。 希望能很好理解,尽可能达到掌握!
中南大学
退出
返回
14:46
§6-1 概述
三、 本章位移计算的假定 (1) 线弹性 (Linear Elastic), (2) 小变形 (Small Deformation), (3)理想联结 (Ideal Constraint)。
结构力学
叠加原理适用(principle of superposition)
静定结构在荷载作用下的位移计算 图乘法 静定结构温度变化时的位移计算 静定结构支座移动时的位移计算 线弹性结构的互等定理
退出 返回
中南大学
14:46
§6-1 概述
结构力学
一、结构的位移 (Displacement of Structures)
1. 结构的位移是指结构上的某一截面在荷载或其它 因素作用下由某一位置移动到另一位置,这个移动 的量就称为该截面的位移(线位移和角位移)。
中南大学
14:46
§6-1 概述
C'
CV CDV DV
结构力学
C D
D'
截面C、D 的相对竖向 线位移为 :
A
B
CDV CV DV
截面C、D 的相对角位移为:
C' D'
C
D
C
D
Δ CD C D
A B
中南大学
退出
返回
14:46
§6-1 概述
退出 返回
中南大学
14:46
§6-2 变形体系的虚功原理
2.杆系结构虚功方程
Wi FN d FSd Md
s s s
结构力学
We Wi
以上结论与材料物理性质及具体结构无关,因 此,虚功原理虚功方程既适用于一切线性结构,也 适用于一切非线性结构。 希望能很好理解,尽可能达到掌握!
中南大学
退出
返回
14:46
§6-1 概述
三、 本章位移计算的假定 (1) 线弹性 (Linear Elastic), (2) 小变形 (Small Deformation), (3)理想联结 (Ideal Constraint)。
结构力学
叠加原理适用(principle of superposition)
静定结构在荷载作用下的位移计算 图乘法 静定结构温度变化时的位移计算 静定结构支座移动时的位移计算 线弹性结构的互等定理
退出 返回
中南大学
14:46
§6-1 概述
结构力学
一、结构的位移 (Displacement of Structures)
1. 结构的位移是指结构上的某一截面在荷载或其它 因素作用下由某一位置移动到另一位置,这个移动 的量就称为该截面的位移(线位移和角位移)。
建筑结构力学位移计算

2019/2/27 建筑结构力学 14
位移计算公式也是变形体虚功原理的一种表达式。
( M N Q ) ds R c k k
c2
K
K
ds
t1
1
R1
t2
c1
ds d ds ds ds
R2
ds
d
d
Q N 外虚功:W 内虚功:W 1 R c M N Q d e k k i
(2)由上面的内力计算应变,其表达式由材料力学知
M P
EI
N P
1.2
EA
Q kP
10 9
GA
A A1
k--为截面形状系数 (3) 荷载作用下的位移计算公式
M M N N k Q Q P P P ds ds ds EI EA GA
2019/2/27
建筑结构力学
20
。 例1. 试计算悬臂梁A点的竖向位移 ,EI C AV P=1 q x A x C C B A AV
B
l 2
1)列出两种状态
l 2
(a) 实际状态
l 2
l 2
(b) 虚设状态
N 0 M x Q 1
的内力方程:
l 0 x AC段 2
实功恒为正。
虚功是力在其它原因产生的位移上作的功。如T12, 如力与位移同向,虚功为正,反向时,虚功为负。 产生位移的原因 位移发生的位置
ΔKj
2、虚功原理
虚力原理:在给定的位移状态与虚设的力状态之间应用虚
3、虚功原理
功原理,这种虚功原理的形式称为虚力原理。 虚位移原理:在给定的力状态与虚设的位移状态之间应用
位移计算公式也是变形体虚功原理的一种表达式。
( M N Q ) ds R c k k
c2
K
K
ds
t1
1
R1
t2
c1
ds d ds ds ds
R2
ds
d
d
Q N 外虚功:W 内虚功:W 1 R c M N Q d e k k i
(2)由上面的内力计算应变,其表达式由材料力学知
M P
EI
N P
1.2
EA
Q kP
10 9
GA
A A1
k--为截面形状系数 (3) 荷载作用下的位移计算公式
M M N N k Q Q P P P ds ds ds EI EA GA
2019/2/27
建筑结构力学
20
。 例1. 试计算悬臂梁A点的竖向位移 ,EI C AV P=1 q x A x C C B A AV
B
l 2
1)列出两种状态
l 2
(a) 实际状态
l 2
l 2
(b) 虚设状态
N 0 M x Q 1
的内力方程:
l 0 x AC段 2
实功恒为正。
虚功是力在其它原因产生的位移上作的功。如T12, 如力与位移同向,虚功为正,反向时,虚功为负。 产生位移的原因 位移发生的位置
ΔKj
2、虚功原理
虚力原理:在给定的位移状态与虚设的力状态之间应用虚
3、虚功原理
功原理,这种虚功原理的形式称为虚力原理。 虚位移原理:在给定的力状态与虚设的位移状态之间应用
结构力学I-第五章 虚功原理与结构位移计算(温度位移、虚功、互等)

温度改变时的位移计算
结构位移计算的一般公式
普遍性
Δ = ∑ ∫ ( Mκ + FNε + FQγ0 ) ds- ∑FRK·cK
⑵ 变形因素:荷载、温度改变或支座移动引起的位移;
温度改变的位移计算公式
应用背景
Page 10
14:26
LOGO
温度改变时的位移计算
温度改变的位移计算公式
基本假设
FQ FN
dFN
pdx
0
dFQ qdx 0
dM FQdx 0
• 集M M 0 0
M
FQ FN
M
Page 22
q
FQ+ dFQ
p
FN+ dFN
O
x
M+ dM dx
y
dx
M0 O
Fx
Fy y
FQ+ ΔFQ FN+ ΔFN x
M+ ΔM
14:26
D 1
α=1×10-5,求D点的竖向位移ΔDV。
2m 2m
解:⑴ 在D点作用一向上的单位力F=1,
4m
作弯矩图 M 和轴力图 F N;
⑵ 由于各杆 α,t0,Δt,h 相同,
故可先计算
+1
1
M ds
1 2
4
4
4
4
24(m2
)
M
FN
F Nds 1 2 1 4 2(m)
Page 15
14:26
LOGO
结构力学I
第五章 虚功原理与 结构位移计算
2021年4月15日
LOGO
3-12(g)
指出弯矩图错误并改正;
作业点评
第6章 位移计算

2 0
钢筋混凝土结构G≈0.4E,矩形截面,k=1.2,I/A=h2/12
FQ M EI 1h k GAr 2 4 r
h <1 r 10 FQ 1 < M 400 FN
2
FN I 1 h 2 M Ar 12 r
2
如
M
D
E
3c
d
C B
c
A
P 3 3 b 3b ctg X 2 2 2c 4c 3 b 0 (3)解方程求X X X P X 2 2c
b
x x X
3b X P 4c
小结:1)虚功原理(这里是用虚位移原理)的特点是用几 何方法解决平衡问题。 2)求解问题直接,不涉及约束力。
a qa
2a qa2
D
a
C
FQC
2a
B
a
A
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
FQC
0.25
0.5
虚功方程为: +qa×0.25 -qa2×0.25/a -q×(1×2a/2+0.5 ×a/2 )=0 FQC×1
FQC=1.25qa
1
0.25/a
作功的两方面因素:力、位移。
广义力 单个力 单个力偶 等值反向共线的一对力
真实 位移 状态
注:(1)EI、EA、GA是杆件截面刚度; k是截面形状系数k矩=1.2, k圆=10/9。 (2)FNP、FQP、MP实际荷载引起的内力, 是产生位移的原因;虚设单位荷载 引起的内力是 F N , F Q , M
F N FNP F Q FQP MM P iP k ds EA GA EI
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5章 虚功原理与结构位移计算
§5-1 刚体体系的虚功原理与位移计算 §5-2 结构位移计算的一般公式 §5-3 荷载作用下的位移计算
§5-4 荷载作用下的位移计算举例
§5-5 图乘法 §5-6 温度变化时的位移计算 §5-7 互等定理
▲静定结构位移的类型 支座移动产生的位移——刚体位移 制造误差产生的位移——刚体位移 荷载作用产生的位移——变形体位移 温度改变产生的位移——变形体位移
结 束
下面内容: 互等定理
d 原因不同,变形 d 的表达式也不同。
d
d 、 d 的表达式。 现在要讨论温度变化时, d 、
d (温度变化不会产生剪切变形 d ) 2. 温度变化引起的 d 、
假定 t2 t1 α——线胀系数 1)微段发生的轴向变形
h
αt1 ds
h1
h2 +t1 +t0 dθ αt0ds αt2ds
t1 t2 d t0 ds ds 2
2)微段发生的弯曲变形
+t2 ds
(微段的温度变形图)
d
其中:
t2 ds t1ds
h
tds
h
t
t t2 t1 — 杆件上下边缘的温度差值
t1 t2 0 — 杆件轴线处的温度变化值 2
N
t
h
ds
N、M图 面积
若t0 、Δt和h沿每一杆长为常数,则上式可写成:
t0 F ds
N
t
h
Mds t
0
N
t
h
M
正负号的规定:虚力状态中的变形与温度改变产生的 变形方向一致时,取正号,反之取负号。
4.举例 图示刚架ABC,试求C点竖向位移。设各杆截面为矩形,高 度为60cm,a=6m, =0.00001。
3. 温度引起的位移公式 t2 ds t1ds tds t1 t2 ds 和 d 将 d t0 ds h h 2 代入一般公式 1 [ 得到:
l
0
Md F Q d F N d ]
0 0
l
l
F t0 ds M
0 0 0 10 C 0 C 解: t 0 t 10 C 5 C 0 2 10 3 2 t 5 a a C t0 N M h 2 h 3a 5 a 0.93cm 1 h
用刚体体系的 虚力原理计算
用变形体系的 虚力原理计算
§5-6 温度变化时公式的回顾: (不考虑支座移动)
1 [ Md F Q d F N d ]
0 0 0
l
l
l
(弯曲)
(剪切)
(轴向)
说明: 荷载 此公式适用于 温度变化 诸因素引起的位移。
§5-1 刚体体系的虚功原理与位移计算 §5-2 结构位移计算的一般公式 §5-3 荷载作用下的位移计算
§5-4 荷载作用下的位移计算举例
§5-5 图乘法 §5-6 温度变化时的位移计算 §5-7 互等定理
▲静定结构位移的类型 支座移动产生的位移——刚体位移 制造误差产生的位移——刚体位移 荷载作用产生的位移——变形体位移 温度改变产生的位移——变形体位移
结 束
下面内容: 互等定理
d 原因不同,变形 d 的表达式也不同。
d
d 、 d 的表达式。 现在要讨论温度变化时, d 、
d (温度变化不会产生剪切变形 d ) 2. 温度变化引起的 d 、
假定 t2 t1 α——线胀系数 1)微段发生的轴向变形
h
αt1 ds
h1
h2 +t1 +t0 dθ αt0ds αt2ds
t1 t2 d t0 ds ds 2
2)微段发生的弯曲变形
+t2 ds
(微段的温度变形图)
d
其中:
t2 ds t1ds
h
tds
h
t
t t2 t1 — 杆件上下边缘的温度差值
t1 t2 0 — 杆件轴线处的温度变化值 2
N
t
h
ds
N、M图 面积
若t0 、Δt和h沿每一杆长为常数,则上式可写成:
t0 F ds
N
t
h
Mds t
0
N
t
h
M
正负号的规定:虚力状态中的变形与温度改变产生的 变形方向一致时,取正号,反之取负号。
4.举例 图示刚架ABC,试求C点竖向位移。设各杆截面为矩形,高 度为60cm,a=6m, =0.00001。
3. 温度引起的位移公式 t2 ds t1ds tds t1 t2 ds 和 d 将 d t0 ds h h 2 代入一般公式 1 [ 得到:
l
0
Md F Q d F N d ]
0 0
l
l
F t0 ds M
0 0 0 10 C 0 C 解: t 0 t 10 C 5 C 0 2 10 3 2 t 5 a a C t0 N M h 2 h 3a 5 a 0.93cm 1 h
用刚体体系的 虚力原理计算
用变形体系的 虚力原理计算
§5-6 温度变化时公式的回顾: (不考虑支座移动)
1 [ Md F Q d F N d ]
0 0 0
l
l
l
(弯曲)
(剪切)
(轴向)
说明: 荷载 此公式适用于 温度变化 诸因素引起的位移。
