重庆大学2016-2017材料力学期末试题
材料力学I期末考试题及答案

材料力学I期末考试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是基本假设?A. 均匀性假设B. 连续性假设C. 各向同性假设D. 各向异性假设答案:D2. 在拉伸试验中,材料的屈服强度是指:A. 弹性极限B. 屈服极限C. 强度极限D. 断裂强度答案:B3. 影响材料弹性模量的因素不包括:A. 材料种类B. 温度C. 材料的几何形状D. 加载速度答案:C4. 梁的弯曲应力公式为:A. σ = My/IB. σ = Mx/IC. σ = VQ/ID. σ = Vx/I答案:A5. 材料力学中,下列哪一项不是应力状态的描述?A. 正应力B. 剪应力C. 应力集中D. 应力梯度答案:D6. 材料的疲劳破坏通常发生在:A. 最大应力处B. 最小应力处C. 应力集中处D. 应力均匀处答案:C7. 根据材料力学理论,下列哪一项不是材料的强度理论?A. 最大正应力理论B. 最大剪应力理论C. 最大应变理论D. 能量理论答案:D8. 梁的弯曲变形公式为:A. v = (Mx/EI)(1 - x^2/L^2)B. v = (Mx/EI)(1 - x^3/L^3)C. v = (Mx/EI)(1 - x/L)D. v = (Mx/EI)(1 - x^2/L^3)答案:B9. 材料的塑性变形是指:A. 弹性变形B. 永久变形C. 可逆变形D. 弹性和塑性变形的总和答案:B10. 在拉伸试验中,材料的弹性模量可以通过下列哪一项来确定?A. 弹性阶段的斜率B. 屈服阶段的斜率C. 断裂阶段的斜率D. 塑性变形阶段的斜率答案:A二、填空题(每题2分,共20分)1. 材料力学中,__________是指材料在外力作用下发生形变,但当外力移除后,形变能够完全恢复的性质。
答案:弹性2. 当材料受到拉伸时,其内部产生的__________应力称为正应力。
答案:垂直3. 材料力学中,__________是指材料在外力作用下发生形变,但当外力移除后,形变不能完全恢复的性质。
重庆大学材料力学本科试卷

重庆大学材料力学课程试题(A 卷)一、作简支梁的内力图。
(20 分)题 1 图解:1. 计算支座反力.将梁上的载荷向梁的中点简化,简化结果为一集中力偶:m = 32KN ⋅m (逆时针)支座反力:RA 2. 作内力图=32=4KN(↑),R8 B=32= 4KN (↓)8根据支座反力及载荷作剪力图及弯矩图。
Q (KN)M (KN•m)二、简支梁AB 和悬臂梁DH 用直杆CH 相联。
C 点和H 点均为铰接,H 点承受垂直载荷P 的作用。
已知梁AB 和DH 的抗弯刚度为EI,杆CH 的抗拉刚度为EA,试求杆CH 的轴力及点H 的垂直位移。
(20 分)1 3解:1. 静不定次数确定 题 2 图m = 3, n = 2, r = 6结构的自由度 2. 分析计算D = 3m - 2n - r = 3⨯ 3 - 2 ⨯ 2 - 6 = -1 1 次静不定结构 去掉二力杆 CH ,即可得到基本结构,设 CH 杆轴向拉力为 N ,梁的挠度δ C 、 δ H 以向下为正,则变形集合条件为: δ H - δ C = ⊗l CH (1)δ= (P - N )a 3 H 3EI = N (2a )3 C 48EI , ⊗l C H =NaEA代入式(1),得:(P - N )a 3 -N (2a )3= Na3EI 由此式解出: 48EI N =EA2Pa 2 A3(2I + a 2 A )代入δ H ,即得 H 点的垂直位移为:δ =Pa 3 6I + a 2 AH 9EI ( 2I + a 2A )三、 直径为 20mm 的圆截面平面折杆ADBC 在C 点受竖向力P 的作用,∠ABC =90 度,杆的弹性模量E=200Gpa ,泊松比μ=0.3,现由实验测得D 点截面处的顶部表面的主应变ε =508×10-6, ε =-288×10-6,试确定外力P 及BC 段的长度a 的大小。
已知l =314mm 。
重庆大学材料力学复习试题

------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------
(2)定性地绘出 A , B , C 三点的应力圆。 (3)在各点的单元体上,大致画出主应力单元体图。 (4)试根据第一强度理论,说明(画图表示)梁破坏时裂缝在 B , C 两点处的走向。
图2 解: (1)中间段是纯弯曲,故切应力为零。点 C 在中性层上,所以正应力为零。单元体受力如 图 2.1 所示。
直 径 d = 80mm 的 圆 截 面 钢 杆 制 成 的 钢 架 , 在 自 由 端 C 处 受 到 集 中 力 F = 1kN 作用,钢杆的弹性模量为 E = 200GPa , R = 0.8m , h = 2.4m ,不计剪力 和轴力的影响, 试求自由端 c 处的水平位移。 (提示: 可采用莫尔积分方法求解)
∆l p =
l pDl (σ x , p − µσ τ , p ) = (1 − 2µ ) > 0 E 4δ E
在约束力 FR 作用下,筒体的轴向变形则为
∆ l FR =
( − FR ) l FR l =− EA Eπ Dδ
利用叠加法,得到筒体的总轴向变形为
∆l = ∆l p + ∆lFR =
FR l pDl (1 − 2µ ) − 4δ E Eπ Dδ
直径 d=10cm 的等截面圆轴的受力情况如图所示。试验中在轴向拉力和扭转力 偶矩共同作用下,测得轴表面 K 点处沿轴线方向的线应变 =300×10-6,沿与 轴 线 成 45 ° 方向的 线 应变 45 ° =- 140×10-6 。 已知 轴 材料 的弹性模量 = 200GPa,泊松比 =0.29, 许用应力[σ]=120 MPa,试求: 1、 扭矩 M 和轴 力T 。 2、 用第 四强度理 论 校核 轴的 强 度。 (17 分) 2 2 (提示: σ 1,3= (σ x + σ y ) / 2 ± (σ x − σ y ) / 4 + τ xy )
《材料力学》期末考试试卷及答案

***学院期末考试试卷一、填空题(总分20分,每题2分)1、杆件在外力作用下,其内部各部分间产生的 ,称为内力。
2、杆件在轴向拉压时强度条件的表达式是 。
3、低碳钢拉伸时,其应力与应变曲线的四个特征阶段为 阶段, 阶段, 阶段, 阶段。
4、线应变指的是 的改变,而切应变指的是 的改变。
5.梁截面上弯矩正负号规定,当截面上的弯矩使其所在的微段梁凹向下时为 。
6.梁必须满足强度和刚度条件。
在建筑中,起控制做用的一般是 条件。
7、第一和第二强度理论适用于 材料,第三和第四强度理论适用于 材料。
8、求解组合变形的基本方法是 。
9、力作用于杆端方式的不同,只会使与杆端距离在较小的范围内受到影响,该原理被称为 。
10、欧拉公式是用来计算拉(压)杆的 ,它只适用于 杆。
二、 单项选择(总分20分,每题2分)1、用截面法可求出图示轴向拉压杆a-a 截面的内力12N P P =-,下面说法正确的是( ) A. N 其实是应力 B. N 是拉力C. N 是压力D. N 的作用线与杆件轴线重合2、构件的强度是指( )A. 在外力作用下构件抵抗变形的能力B. 在外力作用下构件保持原有平衡态的能力C. 在外力作用下构件抵抗破坏的能力D. 在外力作用下构件保持原有平稳态的能力 3、现有钢、铸铁两种杆材,其直径相同。
从承载能力与经济效益两个方面考虑,图示结构中两种合理选择方案是( )A. 1杆为钢,2杆为铸铁B. 1杆为铸铁,2杆为钢C. 2杆均为钢D. 2杆均为铸铁4、从拉压杆轴向伸长(缩短)量的计算公式EANll =∆可以看出,E 和A 值越大,l ∆越小,故( )。
A. E 为杆的抗拉(压)刚度。
B. 乘积EA 表示材料抵抗拉伸(压缩)变形的能力。
C. 乘积EA 为杆的抗拉(压)刚度D. 以上说法都不正确。
5、空心圆轴的外径为D ,内径为d ,α=d /D 。
其抗扭截面系数为( )。
A )1(163απ-=D W P B )1(1623απ-=D W PC )1(1633απ-=D W P D )1(1643απ-=D W P6、在没有荷载作用的一段梁上,( )A. 剪力图为一水平直线B.剪力图为一斜直线 C .没有内力 D.内力不确定7、在平行移轴公式21Z Z I I a A =+中,其中Z 轴和轴1Z 轴互相平行,则( )。
(完整版)《材料力学》期末考试试卷(A卷)

石河子大学函授大专班工业与民用建筑《材料力学》期末考试试卷(A卷)班级:姓名:得分;一、判断题(2×10=20分)()1、若平面汇交力系的力多边形自行闭合,则该平面汇交力系一定平衡。
()2、剪力以对所取的隔离体有顺时针趋势为正。
()3、过一点总有三个主应力。
()4、与最大主应力对应的方位角总在剪应力Z X指向的象限内。
()5、平面弯曲梁的上下边缘有最大正应力。
()6、平面弯曲梁横截面上剪力对应着一种应力,即剪应力。
()7、在弹性范围内,杆件的正应力和正应变成正比。
()8、若某平面上有剪应力,则在与该平面相垂直的平面上一定有剪应力存在,且该平面上的剪应力方向与原剪应力共同指向或背离两平面交线。
()9、若某点三个主应力分别是б1=6MPa,б2=0,б3=-2MPa,则该点的最大剪应力是4MPa。
()10、第一强度理论适用于各种类型的破坏。
二、名词解释(3×5=15分)1、平衡:2.刚体3、约束力:4、轴力图:5、面积矩三、简答题(10分)如何提高梁刚度的措施?五、绘制下图所示求梁的剪力图及弯矩图。
(15分)四、计算题分别计算下图所示的F1、F2对O点的力矩(10分)。
六、一矩形截面的简支木梁,梁上作用有均布荷载,已知:l =5m ,b=140mm ,h=210mm ,q=4kN/m ,弯曲时木材的容许正应力〔σ〕=10MPa 。
试校核该梁的强度。
(15分)七、图示一正方形截面的阶形砖柱,柱顶受轴向压力P 作用。
上段柱重为G 1,下段柱重为G 2已知:P =10kN ,G 1=15kN ,G 2=10 KN ,l =3m ,求上、下段柱的底截面1-1和2-2上的应力。
(15分)石河子大学函授大专班土木工程专业《材料力学》期末考试试卷(A卷)答案班级:姓名:得分;一、判断题1、若平面汇交力系的力多边形自行闭合,则该平面汇交力系一定平衡。
(√ )2、剪力以对所取的隔离体有顺时针趋势为正。
材料力学期末考试试试题库

材料力学期末考试试试题库材料力学复习题(答案在最终面)绪论1.各向同性假设以为,材料内部各点的()是相同的。
(A)力学性质;(B)外力;(C)变形;(D)位移。
2.依照小变形条件,能够以为 ( )。
(A)构件别变形;(B)构件别变形;(C)构件仅发生弹性变形;(D)构件的变形远小于其原始尺寸。
3.在一截面的任意点处,正应力σ与切应力τ的夹角( )。
(A)α=900;(B)α=450;(C)α=00;(D)α为任意角。
4.依照材料的要紧性能作如下三个基本假设___________、___________、___________。
5.材料在使用过程中提出三个方面的性能要求,即___________、___________、___________。
6.构件的强度、刚度和稳定性()。
(A)只与材料的力学性质有关;(B)只与构件的形状尺寸关(C)与二者都有关;(D)与二者都无关。
7.用截面法求一水平杆某截面的内力时,是对( )建立平衡方程求解的。
(A) 该截面左段; (B) 该截面右段;(C) 该截面左段或右段; (D) 整个杆。
8.如图所示,设虚线表示单元体变形后的形状,则该单元体的剪应变为( )。
(A)α; (B) π/2-α; (C) 2α; (D) π/2-2α。
答案1(A)2(D)3(A)4 均匀性假设,延续性假设及各向同性假设。
5 强度、刚度和稳定性。
6(A)7(C)8(C)拉压1. 轴向拉伸杆,正应力最大的截面和切应力最大的截面()。
(A)分不是横截面、45°歪截面;(B)基本上横截面,(C)分不是45°歪截面、横截面;(D)基本上45°歪截面。
2. 轴向拉压杆,在与其轴线平行的纵向截面上()。
(A)正应力为零,切应力别为零;(B)正应力别为零,切应力为零;(C)正应力和切应力均别为零;(D)正应力和切应力均为零。
3. 应力-应变曲线的纵、横坐标分不为σ=F N /A,ε=△L / L,其中()。
重庆大学材料力学本科期末真题试卷3
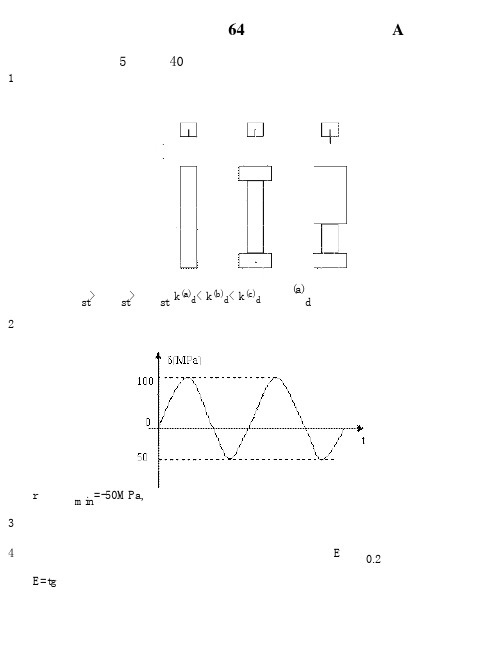
重庆大学材料力学(64学时类)课程试题(A)说明:开卷考试,可本人携带、但不得相互借用计算机和任何参考书一、简答(每没题5分,共40分)1、三根材料相同的圆杆,受到高度相等、重量相同的自由落体冲击,如果不考虑应力集中因素,哪一杆中的最大动应力σd最小?解:∵Δ(a)st >Δ(b)st>Δ(c)stk(a)d< k(b)d< k(c)d∴σ(a)d最小2、有一构件内某一点处的交变应力随时间变化的曲线如图,则该交点应变力的循环特征、最大应力、最小应力和平均应力分别是多少?解:r=1/2,σmin =-50MPa,σm=25MPa3、材料力学用到了哪些假设或模型?枚举两例、扼要解释之。
解:梁在纯弯曲时的平面假设,梁的纵向纤维间无挤压应力的假设等。
4、画出高碳钢静态拉力试验得到的应力应变曲线。
要表示出E和σ0.2,并说明其意义。
解:E=tgα,σ0.2名义屈服极限,将产生0.2%塑性应变的应力作为名义屈服极限σ0.25、直径和长度相同但材料的剪切模量不同的轴,在相同扭矩作用下最大切应力和扭转角是否相同?为什么?解:最大切应力τmax相同,最大扭转角φmax 不同; τmax=T/wt, φmax=T l/GIP6、对于均匀材料,什么情况下用T形截面梁是合理的?为什么?解:材料力学的抗拉能力与抗压能力不相同十采用T形截面梁。
7、试指出下列概念的区别:纯弯曲与平面弯曲;中性轴与形心轴;截面的抗弯刚度和抗弯模数。
解:略8、试从研究内容、目的合方法三方面叙述你对材料力学的认识。
解:略二、(10分)图示简易的承重架,P=60kN。
AC模型为刚性直杆。
试由抗拉强度确定受拉板条BC的截面积,由剪切强度确定铰B和C处销钉的直径。
已知板条BC的抗拉许用应力[σ]=100MPa,,销钉材料的许用剪应力[τ]=50MPa。
解:1、计算BC杆的横截面积Asinα=,设BC杆的轴力为N,由有平衡方程,解得: N= , p=60kN,2、计算B、C处销钉直径d1及d2.销钉BQ1 Q22、销钉C三、(10分)等截面实心传动轴的转速为n=191r/min,轮A为主动轮,输入功率为N A=8kW,轮B、C和D为从动轮。
重庆大学材料力学试题一

重庆大学材料力学(II )课程试题A 卷一、 问答题(20分,每小题5分)1、在推导材料力学的某些基本理论和方法时,需要作一些必要的假设。
试列举其中的三个假设。
答:略;2、对于低碳钢,何谓 P σ? 答:比例极限;3、工程中经常使用工字梁,从力学的角度看,工字梁的优点是什么? 答:与矩形梁和圆形截面相比,工字梁的高,能充分利用材料。
A W z /4、图示为材料相同、长度相等的等截面圆杆和变截面圆杆,试问哪一种杆件承受冲击的能力强?简述理由。
(a ) (b )答:不好定性判别。
因为a 杆的动载系数小于b 杆的动载系数,但a 杆的静应力大于b 杆的静应力。
二、 图示为内外直径比值2/1=α的空心圆轴,其转速度n 为每分钟300转,主动轮输入的功率N 1=500马力,三个从动轮输出的功率分别为N 2=150马力, N 3=150马力, N 4=200马力。
已知材料参数:G =80Gpa ,[]MPa 40=τ;单位长度杆的允许扭转角[]m /3.0o =ϕ。
试按照强度条件和刚度条件选择轴的外径。
(15)提示:)(7024m N nNm ⋅=,N 的单位为马力。
解: 计算作用于各轮上的外力偶矩:m N n N m .1117003005007024702411=×==; m N nN m m .35127024232===; m N m .468030020070244=×= 作扭矩图:可见: m N .7024max =τ 由强度条件: ][)1(1643maxmax max ταπτ≤−==D T W T t得: m T D 0984.01040)5.01(702416])[1(1636434max =××−××=−≥πταπ 由刚度条件: ][180max max ϕπϕ≤×=p GI T 得: m G T D 1162.0])[1(18032442max =−×≥ϕαπ 取轴得直径为: D =120mm三、 一矩形截面梁如图所示,已知kN P 10=,m a 2.1=;材料的许用应力MPa 10][=σ.设梁的高宽比2/=b h 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模拟题
一、选择题(3x5=15分):
1. 有A、B、C三种材料,其拉伸应力-应变实验曲线如图1所示,曲线()材料的弹性模量E最大,曲线()材料的强度高,曲线()材料的塑性好。
2.轴向拉伸杆,正应力最大的截面和剪应力最大的截()。
A分别是横截面、45°斜截面;B都是横截面;
C 分别是45°斜截面、横截面;D都是45°斜截面。
3. 设计某一主轴,发现原方案刚度不足,将进行修改设计,有效的措施是()。
A轴材料改用优质高强钢;B减小轴的长度;C加大轴径;D把轴挖空
4. 等截面直梁在弯曲变形时,挠曲线的曲率最大发生在()处。
A挠度最大;B转角最大;C剪力最大;D弯矩最大
5. 压杆柔度大小与压杆的哪个参数无关()。
A 压杆的长度;
B 压杆所受的外力;
C 压杆的约束条件;D压杆的截面形状和尺寸。
二、计算题
1. 题图所示结构,AB为刚体,载荷P可在其上任意移动。
试求使CD杆重量最轻时,夹角α应取何值?
题图1
2. 一阶梯形圆轴如题图2所示。
已知轮B 输入的功率B
N =45kW ,轮A 和轮C 输出的功率分别为A N =30Kw, C N =15kW ;轴的转速n=240r/min, 1d =60mm, 2d =40mm;许用扭转角[]θ=2
()/m ︒,材料的[]τ=50Mpa,G=80Gpa.试校核轴的强度和刚度。
3. 图示外伸梁在外伸段受均布载荷q 作用,全梁EI 为常数。
试用莫尔积分计算梁在C 截面的挠度C y 。
q
4. 空心圆杆AB和CD杆焊接成整体结构,受力如图。
AB杆的外径D=140mm,内、外径之比α= d/D=0.8,材料的许用应力[ ]=160MPa。
试用第三强度理论校核AB杆的强度。
5.图示结构,杆1和杆2的横截面均为圆形,d 1=30mm ,两杆材料的弹性模量E =200GPa, a =304MPa ,b =1.12MPa ,p λ=100, s λ=60,稳定安全系数取3=st n ,求:压杆AB 允许的许可载荷P 。
