平行四边形题型和辅助线(完美打印版)
人教版初二数学8年级下册 第18章(平行四边形)含辅助线证明题训练(含答案)

人教版数学八年级下期第十八章平行四边形含辅助线证明题训练1.已知边长为2的正方形ABCD中,P是对角线AC上的一个动点(与点A,C不重合),过点P作PE⊥PB,PE交DC于点E,过点E作EF⊥AC,垂足为点F.(1)求证:PB=PE;(2)在点P的运动过程中,PF的长度是否发生变化?若不变,求出这个不变的值;若变化,试说明理由.2.在▱ABCD中,BE平分∠ABC交AD于点E.(1)如图1,若∠D=30°,AB=6,求△ABE的面积;(2)如图2,过点A作AF⊥DC,交DC的延长线于点F,分别交BE,BC于点G,H,且AB=AF.求证:ED-AG=FC.3.如图,在平行四边形ABCD中,AC,BD交于点O,且AO=BO,∠ADB的平分线DE交AB于点E.(1)求证:四边形ABCD是矩形.(2)若AB=8,OC=5,求AE的长.4.如图,在正方形ABCD中,E是边AB上一动点(不与点A,B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E 作EH⊥DE交DG的延长线于点H,连接BH.(1)求证:GF=GC;(2)用等式表示线段BH与AE的数量关系,并证明.5.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC,CF为邻边作平行四边形ECFG.(1)证明平行四边形ECFG是菱形;(2)若∠ABC=120°,连接BG,CG,DG,①求证:△DGC≌△BGE;②求∠BDG的度数;(3)若∠ABC=90°,AB=8,AD=14,M是EF的中点,求DM的长.6.已知正方形ABCD如图所示,连接其对角线AC,∠BCA的平分线CF交AB于点F,过点B作BM⊥CF于点N,交AC于点M,过点C作CP⊥CF,交AD延长线于点P.(1)求证:DP=BF;(2)若正方形ABCD的边长为4,求DP的长;(3)求证:CP=BM+2FN.7.如图,四边形ABCD是菱形,E是AB的中点,AC的垂线EF交AD于点M,交CD的延长线于点F.(1)求证:AM=AE;(2)连接CM,DF=2.①求菱形ABCD的周长;②若∠ADC=2∠MCF,求ME的长.8.在菱形ABCD中,AB=4,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点.且CF=AE,连接BE、EF.(1)如图1,若E是线段AC的中点,求EF的长;(2)如图2.若E是线段AC延长线上的任意一点,求证:BE=EF.AC,将菱形ABCD绕着点B (3)如图3,若E是线段AC延长线上的一点,CE=12顺时针旋转α°(0≤α≤360),请直接写出在旋转过程中DE的最大值.9.如图所示,在边长为1的菱形ABCD中,∠DAB=60°,M是AD上不同于A,D两点的一动点,N是CD上一动点,且AM+CN=1.(1)证明:无论M,N怎样移动,△BMN总是等边三角形;(2)求△BMN面积的最小值.10.如图,正方形ABCD中,F在CD上,AE平分∠BAF,E为BC的中点.求证:AF=BC+CF.11.已知:如图(1),点E、F分别为正方形ABCD的边BC、DC上的点,线段AE和AF分别交BD于点M和点N,连接MF,MF⊥AE于点M.(1)求证:∠EAF=45°;(2)如图(2),连接EF,当AD=5,DF=1时,求线段EF的长度;BD.(3)如图(3),作FR⊥BD于R.求证:RM=12BC,CE⊥AB于点E,F是AD的中点,连接12.如图,在平行四边形ABCD中,AB=12EF,CF.求证:(1)EF=CF;(2)∠EFD=3∠AEF.13.如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF.(1)求∠EAF的度数;(2)如图2,连接FC交BD于M,交AD于N.求证:BD=AF+2DM.14.已知:如图,G为平行四边形ABCD中BC边的中点,点E在AD边上,且∠1=∠2.(1)求证:E是AD的中点;(2)若F为CD延长线上一点,连接BF,得∠3=∠2,求证:CD=BF+DF.15.如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.(1)若ED⊥EF,求证:ED=EF:(2)在(1)的条件下,若DC的延长线与FB交于点P,试判断四边形ACPE是否为平行四边形.并证明你的结论(请先补全图形,再解答):(3)若ED=EF,则ED与EF垂直吗?若垂直给出证明,若不垂直说明理由.16.在▱ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F。
数学初三平行四边形中常做的辅助线

数学初三平行四边形中常做的辅助线一、平行四边形的对角线平行四边形有两条对角线,我们可以通过引入对角线来研究平行四边形的性质。
首先,我们可以证明平行四边形的对角线互相平分。
具体证明如下:设平行四边形ABCD的对角线AC和BD相交于点O,连接OA、OB、OC 和OD。
由于平行四边形的两对边分别平行且相等,所以可以得到AO=CO,BO=DO。
又由于AO=CO,BO=DO,所以AOBO和CODA都是菱形。
因为菱形的对角线互相平分,所以AC和BD互相平分。
利用对角线平分的性质,我们可以得到平行四边形中很多有用的结论。
例如,当平行四边形的两对角线相等时,它是一个矩形;当平行四边形的两对角线垂直且相等时,它是一个正方形。
二、平行四边形的中位线平行四边形的中位线是连接相邻两边中点的线段。
通过引入中位线,我们可以研究平行四边形的对应边的关系。
具体来说,我们可以得到以下结论:1. 平行四边形的中位线互相平行且相等;2. 平行四边形的中位线平分平行四边形的面积;3. 平行四边形的中位线长度等于对应边长度的平均值。
三、平行四边形的高线平行四边形的高线是从一个顶点到与对立边垂直相交的线段。
通过引入高线,我们可以研究平行四边形的高度和底边的关系。
具体来说,我们可以得到以下结论:1. 平行四边形的高线互相平行;2. 平行四边形的高线长度相等;3. 平行四边形的高线长度等于底边长度乘以对应高度的比值。
四、平行四边形的角平分线平行四边形的角平分线是从一个内角的顶点到对立边上的一点并且与对立边相交的线段。
通过引入角平分线,我们可以研究平行四边形的内角之间的关系。
具体来说,我们可以得到以下结论:1. 平行四边形的角平分线互相平行;2. 平行四边形的角平分线平分对立角,即对立内角的两个角平分线相交于对立边上的一点。
五、平行四边形的中心连线平行四边形的中心连线是连接两对对边中点的线段。
通过引入中心连线,我们可以研究平行四边形的对角线之间的关系。
与平行四边形有关的常用辅助线作法归类

与平行四边形有关的常用辅助线作法归类解析第一类:连结对角线,把平行四边形转化成两个全等三角形。
例1如左下图1,在平行四边形ABCD 中,点F E ,在对角线AC 上,且CF AE =,请你以F 为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的某一条线段相等(只需证明一条线段即可)⑴连结BF ⑵DE BF =⑶证明:连结DF DB ,,设AC DB ,交于点O∵四边形ABCD 为平行四边形 ∴OB DO OC AO ==, ∵FC AE = ∴FC OC AE AO -=- 即OF OE = ∴四边形EBFD 为平行四边形 ∴DE BF =图2图1ECAAB第二类:平移对角线,把平行四边形转化为梯形。
例2如右图2,在平行四边形ABCD 中,对角线AC 和BD 相交于点O ,如果12=AC , 10=BD ,m AB =,那么m 的取值范围是( )A 111<<mB 222<<mC 1210<<mD 65<<m解:将线段DB 沿DC 方向平移,使得CE DB =,BE DC =,则有四边形CDBE 为平行四边形,∵在ACE ∆中, 12=AC ,10==BD CE ,m AB AE 22==∴101221012+<<-m ,即2222<<m 解得111<<m 故选A第三类:过一边两端点作对边的垂线,把平行四边形转化为矩形和直角三角形问题。
例3已知:如左下图3,四边形ABCD 为平行四边形求证:222222DA CD BC AB BD AC +++=+证明:过D A ,分别作BC AE ⊥于点E ,BC DF ⊥的延长线于点F∴BC BE BC AB BE BC BE AB CE AE AC ⋅-+=-+-=+=2)(22222222 CF BC BC CD CF BC CF CD BF DF BD ⋅++=++-=+=2)()(22222222 则BE BC CF BC DA CD BC AB BD AC ⋅-⋅++++=+22222222∵四边形ABCD 为平行四边形 ∴AB ∥CD 且CD AB =,BC AD =∴DCF ABC ∠=∠ ∵090=∠=∠DFC AEB∴DCF ABE ∆≅∆ ∴CF BE = ∴222222DA CD BC AB BD AC +++=+图4图3KDCFBB第四类:延长一边中点与顶点连线,把平行四边形转化为三角形。
中考数学几何辅助线大全及常考题型解析

中考数学几何辅助线大全及常考题型解析中考数学几何辅助线作法及常考题型解析第一部分常见辅助线做法等腰三角形:1.作底边上的高,构成两个全等的直角三角形2.作一腰上的高; 3.过底边的一个端点作底边的垂线,与另一腰的延长线相交,构成直角三角形。
梯形1.垂直于平行边2.垂直于下底,延长上底作一腰的平行线3.平行于两条斜边4.作两条垂直于下底的垂线5.延长两条斜边做成一个三角形菱形1.连接两对角2.做高平行四边形1.垂直于平行边2.作对角线——把一个平行四边形分成两个三角形3.做高——形内形外都要注意矩形1.对角线2.作垂线很简单。
无论什么题目,第一位应该考虑到题目要求,比如AB=AC+BD....这类的就是想办法作出另一条AB等长的线段,再证全等说明AC+BD=另一条AB,就好了。
还有一些关于平方的考虑勾股,A字形等。
三角形图中有角平分线,可向两边作垂线(垂线段相等)。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
解几何题时如何画辅助线①见中点引中位线,见中线延长一倍在几何题中,如果给出中点或中线,可以考虑过中点作中位线或把中线延长一倍来解决相关问题。
②在比例线段证明中,常作平行线。
③对于梯形问题,常用的添加辅助线的方法有1、过上底的两端点向下底作垂线2、过上底的一个端点作一腰的平行线3、过上底的一个端点作一对角线的平行线4、过一腰的中点作另一腰的平行线5、过上底一端点和一腰中点的直线与下底的延长线相交6、作梯形的中位线7、延长两腰使之相交四边形平行四边形出现,对称中心等分点。
梯形里面作高线,平移一腰试试看。
平行移动对角线,补成三角形常见。
证相似,比线段,添线平行成习惯。
等积式子比例换,寻找线段很关键。
直接证明有困难,等量代换少麻烦。
(完整版)平行四边形有关的常用辅助线(20201019185928)

PART A 知识讲解六类与平行四边形有关的常见辅助线,供借鉴:第一类:连结对角线,把平行四边形转化成两个全等三角形。
例1如左下图1,在平行四边形 ABCD 中,点E,F 在对角线AC 上,且AE CF ,请你以F 为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已 有的某一条线段相等(只需证明一条线段即可)⑴连结BF⑵BF DE⑶证明:连结 DB,DF ,设DB,AC 交于点0第二类:平移对角线,把平行四边形转化为梯形。
例2如右图2,在平行四边形 ABCD 中,对角线AC 和BD 相交于点O,如果AC 12,BD 10, AB m ,那么m 的取值范围是()A 1 m 11B 2 m 22C 10 m 12D 5 m 6解:将线段 DB 沿DC 方向平移,使得 DB CE ,DC BE ,则有四边形CDBE 为平 行四边形「••在ACE 中,AC 12,CE BD 10, AE 2AB 2m• 12 10 2m 12 10,即 2 2m 22 解得 1 m 11故选 A第三类:过一边两端点作对边的垂线,把平行四边形转化为矩形和直角三角形问题。
例3已知:如左下图3,四边形ABCD 为平行四边形求证:2 2 2 2 2 2AC BD AB BC CD DA证明:过A,D 分别作AE BC 于点E , DF BC 的延长线于点FAB 2 BE 2 (BC BE)2 AB 2 BC 2 2BE BC BD 2DF 2 BF 2 (CD 2 CF 2) (BC CF)22 2CD 2BC 2 2BC CF则AC 2BD 2 AB 2 BC 2 CD 2 DA 2 2BC CF 2BC BE••四边形 ABCD 为平行四边形 • AB // CD 且AB CD , AD BC•••四边形 ABCD 为平行四边形••• AE •••四边形FC • AO AE EBFD 为平行四边形• AO OC,DO OBOC FC 即 OE OF• BF DE••• AC 2 AE 2 CE 2 C图1图2ABC DCF AEB DFC 900ABEDCF••• BE CFAC 22 2BD AB 2 2 2BC CDDA第四类:延长一边中点与顶点连线,把平行四边形转化为三角形。
北师大版八年级下册数学第六章平行四边形含辅助线证明题—截长补短类 训练
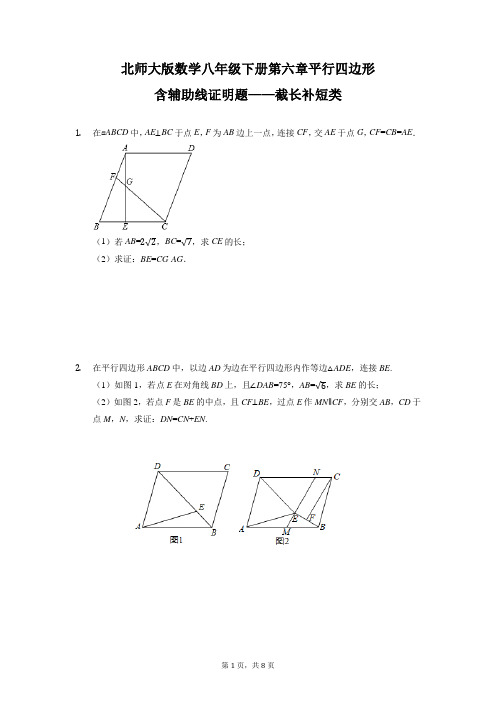
北师大版数学八年级下册第六章平行四边形含辅助线证明题——截长补短类1.在▱ABCD中,AE⊥BC于点E,F为AB边上一点,连接CF,交AE于点G,CF=CB=AE.(1)若AB=2√2,BC=√7,求CE的长;(2)求证:BE=CG-AG.2.在平行四边形ABCD中,以边AD为边在平行四边形内作等边△ADE,连接BE.(1)如图1,若点E在对角线BD上,且∠DAB=75°,AB=√6,求BE的长;(2)如图2,若点F是BE的中点,且CF⊥BE,过点E作MN∥CF,分别交AB,CD于点M,N,求证:DN=CN+EN.3.如图,在▱ABCD中,AE⊥BC,垂足为E,AE=CE.BF⊥AC,垂足为F,分别与AE,AD交于点G,H.(1)若AG=GE=BE=1,求▱ABCD的面积;(2)若CH平分∠BCD,求证:BC=AG+CH.4.已知在▱ABCD中,AE⊥CD,且AB=AE,F为AE上一点,且BF平分∠ABC,(1)若∠ABC=60°,AB=√3,求EF的长;(2)求证:AF+DE=BC.5.在平行四边形ABCD中,E为对角线AC上任意一点,连接BE(1)如图①所示,若AB=BE,AC=BC,∠BAC=75°,AB=2√2,求平行四边形ABCD的面积;(2)如图②所示,延长BE至F,使得EF=EB,连接CF,FD,求证:CE=AE+FD.6.在平行四边形ABCD中,连接BD,过点B作BE⊥BD于点B交DA的延长线于点E,过点B作BG⊥CD于点G.(1)如图1,若∠C=60°,∠BDC=75°,BD=6√2,求AE的长度;(2)如图2,点F为AB边上一点,连接EF,过点F作FH⊥FE于点F交GB的延长线于点H,在△ABE的异侧,以BE为斜边作Rt△BEQ,其中∠Q=90°,若∠QEB=∠BDC,EF=FH,求证:BF+BH=BQ.7.在平行四边形ABCD中,以AB为边作等边△ABE,点E在CD上,以BC为边作等边△BCF,点F在AE上,点G在BA延长线上且FG=FB.(1)若CD=6,AF=3,求△ABF的面积;(2)求证:BE=AG+CE.8.如图,在▱ABCD中,点F是对角线BD上一点,且满足AB=AF,过点F作EG交AD于E,交BC于G,作AH⊥BC于点H,交BD于M.(1)若F为MD中点,AF=2,AM=√3,求BC的长度;(2)若∠ABH=∠AFE,求证:BH+FG=HG.9.如图,平行四边形ABCD中,AB∥CD,AD∥BC,点G是线段BC的中点,点E是线段AD上的一点,点F是线段AB延长线上一点,连接DF,且∠ABE=∠CDG=∠FDG.(1)∠A=45°,∠ADF=75°,CD=3+√3,求线段BC的长;(2)求证:AB=BF+DF.10.如图,△ABC的高AD与中线BE相交于点F,过点C作BE的平行线,过点F作AB的平行线,两平行线相交于点G,连接BG,FG.(1)若AE=2.5,CD=3,BD=2,求AB的长;(2)若∠CBE=30°,求证:CG=AD+EF.11.如图,在□ABCD中,E为BC边的中点,连接AE,F为CD边上一点,且满足∠DFA=2∠BAE.(1)若∠D=100°,∠DAF=30°,求∠FAE的大小;(2)求证:AF=CD+CF.12.已知在平行四边形ABCD中,过点D作DE⊥BC于点E,且AD=DE.连接AC交DE于点F,作DG⊥AC于点G.(1)如图1,若EFDF =12,AF=√13,求DG的长;(2)如图2,作EM⊥AC于点M,连接DM,求证:AM-EM=2DG.13.如图,在平行四边形ABCD中,AE⊥BC于点E,AE=AD,EG⊥AB于点G,延长GE、DC交于点F,连接AF.(1)若BE=2EC,AB=√13,求AD的长;(2)请猜想线段EG、BG、FC之间的等量关系并证明.14.如图,已知平行四边形ABCD中,DE⊥BC于点E,DH⊥AB于点H,AF平分∠BAD,分别交DC、DE、DH于点F、G、M,且DE=AD,CE=3,AB=5.(1)求线段CF的长度;(2)求证:AB=DG+CE.15.如图所示,在平行四边形ABCD中,∠DAC=60°,点E是BC边上一点,连接AE,AE=AB,点F是对角线AC边上一动点,连接EF.(1)如图1,若点F与对角线交点O重合,已知BE=4,OC:EC=5:3,求AC的长度;(2)如图2,若EC=FC,点G是AC边上一点,连接BG、EG,已知∠AEG=60°,∠AGB+∠BCD=180°,求证:BG+EG=DC.16.如图所示,平行四边形ABCD和平行四边形CDEF有公共边CD,边AB和EF在同一条直线上,AC⊥CD且AC=AF,过点A作AH⊥BC交CF于点G,交BC于点H,连接EG.(1)若AE=2,CD=5,求△BCF的周长;(2)求证:BC=AG+EG.。
人教版初二数学8年级下册 第18章(平行四边形)含辅助线证明 专项训练(含答案)

人教版数学八年级下册第十八章平行四边形含辅助线证明训练一1.如图,□ABCD中,AC⊥AB,点E在线段AC上,AE=AB,BE的延长线交边AD于点F,AG⊥BC,且AG=AF,AG交BF于点O.(1)若AD=13,AC=12,求BE的长;(2)若点O恰好是线段AG的中点,连接GE,求证:AF=GE.2.已知正方形ABCD如图所示,连接其对角线AC,∠DAC的平分线AE交CD于点E,过点D作DM⊥AE于F,交AC于点M,共过点A作AN⊥AE交CB延长线于点N.(1)若AD=3,求△CAN的面积;(2)求证:AN=DM+2EF.3.如图1,已知正方形ABCD中,点E在BC上,连接AE,过点B作BF⊥AE于点G,交CD于点F.图1 图2(1)如图1,连接AF,若AB=4,BE=1,求AF的长;(2)如图2,连接BD,交AE于点N,连接AC,分别交BD、BF于点O、M,连接GO,求证:AG-BG=2GO4.如图,平行四边形ABCD中,BF⊥DC交DC于点F,且BF=AB,E点是BC边上一点,连接AE交BF于G;(1)若AE平分∠DAB,∠C=60∘,BE=3,求BG的长;(2)若AD=BG+FC,求证:AE平分∠DAB.5.如图,在□ABCD中,AD上有一点E,连接BE,AH⊥BC于H,AH、BE交于点G,连接CG并延长交AB于F,且GC=CD,∠GCD=90∘.(1) 若GC=6,∠BAG=30∘,求四边形AGCD的面积;(2) 求证:DE=2BG.6.如图,▱ABCD中,点E为BC边上一点,过点E作EF⊥AB于F,已知∠D=2∠AEF.(1)若∠BAE=70°,求∠BEA的度数;(2)连接AC,过点E作EG⊥AC于G,延长EG交AD于点H,若∠ACB=45°,求AC.证:AH=AF+227.如图,▱ABCD中,DF平分∠ADC交AC于点H,G为DH的中点.(1)如图①,若M为AD的中点,AB⊥AC,AC=9,CF=8,CG=25,求GM;(2)如图②,M为线段AB上一点,连接MF,满足∠MCD=∠BCG,∠MFB=∠BAC.求证:MC=2CG.8.如图,在▱ABCD中,连结BD,点E在BD上,且DE=DC,连结CE并延长它与AD交于点F,过点C作CG⊥BD垂足为G,交AD于点H.(1)若DG=3,CG=23,求△CDE的面积;(2)若∠DFC=45°,求证:EF+2FH=CF.9.如图所示,在正方形ABCD的边CB的延长线上取点F,连结AF,在AF上取点G,使得AG=AD,连结DG,过点A作AE⊥AF,交DG于点E.(1)若正方形ABCD的边长为4,且AB=2FB,求FG的长;(2)求证:AE+BF=AF.10.如图,▱ABCD中,E为平行四边形内部一点,连接AE,BE,CE.(1)如图1,AE⊥BC交BC于点F,已知∠EBC=45°,∠BAF=∠ECF,AB=5,EF=1,求AD的长;(2)如图2,AE⊥CD交CD于点F,AE=CF且∠BEC=90°,G为AB上一点,作GP⊥BE 且GP=CE,并以BG为斜边作等腰Rt△BGH,连接EP、EH.求证:EP=2EH.11.如图1,在等腰△ABO中,AB=AO,分别延长AO、BO至点C、点D,使得CO=AO、BO=BO,连接AD、BC.(1)如图1,求证:AD=BC;(2)如图2,分别取边AD、CO、BO的中点E、F、H,猜想△EFH的形状,并说明理由.12.已知,如图,▱ABCD的对角线AC、BD相交于点O,(1)如图1,若AC=AD过点A作AE⊥BC于点E,若AE=3,BC=5,求AB边的长;(2)如图2,过点A作BD的垂线,垂足为F,且AF=BF,过点B作BC的垂线,两条垂线相交于点G,若∠BAG=∠BFC,连接DG.求证:GF=4FO13.已知,在平行四边形ABCD中,AB⊥BD,E为射线BC上一点,连接AE交BD于点F,AB=BD.(1)如图1,若点E与点C重合,且AF=25,求AD的长;(2)如图2,若点E在BC边上时,过点D作DG⊥AE于G,延长DG交BC于H,连接FH.求证:AF=DH+FH;(3)如图3,当点E在射线BC上运动时,过点D作DG⊥AE于G,M为AG的中点,点N在BC边上且BN=1,已知AB=42,请直接写出MN的最小值。
专题04 平行四边形几何辅助线(专题详解)(解析版)

专题04 平行四边形几何辅助线专题详解专题04 平行四边形几何辅助线专题详解 (1)1 平行四边形 (3)知识框架 (3)方法1 分类讨论思想 (3)一、动态讨论 (3)(1)1个点的移动 (3)(2)2个点的移动 (3)二、高的位置的讨论 (5)(1)过点作下(上)侧边的高 (5)(2)过点右(左)侧边的高 (5)三、求平行四边形第4点坐标 (7)方法2 平行四边形的面积 (8)一、利用面积解决问题 (8)二、方程思想 (8)方法3 构造中位线 (9)一、连接法 (9)(1)连接两中点 (9)(2)知一中点,取另一中点 (10)(3)知两中点,构双中位线 (11)二、倍长法 (12)(1)倍长垂直于角平分线的线段 (12)(2)倍长线段 (14)2 特殊的平行四边形 (16)知识框架 (16)方法1 矩形的折叠问题 (16)方法2 构造斜边上的中线 (17)一、连中点 (18)二、取中点 (20)方法3 60°的菱形模型 (21)方法4 利用菱形的对称性解题 (23)方法5 正方形的典型模型 (24)一、a=2b型 (24)二、a=√2b型 (25)三、a±b=c型 (27)四、a±b=√2c型 (28)方法6 构造正方形 (30)一、利用45°角构造正方形 (30)二、利用四边形构造正方形 (31)三、利用直角三角形构造正方形 (31)方法7 运用正方形的性质求坐标 (32)方法8 动点问题的研究 (33)1 平行四边形知识框架{分类讨论思想{动态讨论{1个点的移动2个点的移动高的位置的讨论{过点作下(上)侧边的高过点作右(左)侧边的高求平行四边形第4个点的坐标平行四边形的面积{利用面积解决问题方程思想构造中位线{连接法{连接两中点知一中点,取另一中点知两中点,构双中位线倍长法{倍长垂直于角平分线的线段倍长线段 方法1 分类讨论思想分类讨论思想{动态讨论{1个点的移动2个点的移动高的位置的讨论{过点作下(上)侧边的高过点作右(左)侧边的高求平行四边形第4点坐标一、动态讨论解题技巧:点在线段的不同位置,也会造成不同的结果 (1)1个点的移动如下图,1个点C 在直线AB 上移动,会出现3种情况:①在线段AB 左侧;②在线段AB 当中;③在线段AB 右侧,具体见例1.(2)2个点的移动如下图,2个点C 、D 在线段AB 上移动(C 、D 两点在AB 中),会出现2种情况:①点C 在点D 的左侧;②点C 在点D 的右侧,具体见例2.例1.▱ABCD的内角∠BCD的平分线CE交射线DA于点E,若AE=3,DE=4,求▱ABCD的周长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、平行四边形的性质:
四边形ABCD 是平行四边形 ⎪⎪⎪⎩⎪⎪⎪⎨⎧.
54321)邻角互补()对角线互相平分;()两组对角分别相等;()两组对边分别相等;()两组对边分别平行;( 二、平行四边形判定方法的选择
三、平行四边形方法、考点归纳总结: 平行四边形常见考法:
(1)利用平行四边形的性质,求角度、线段长、周长; (2)求平行四边形某边的取值范围; (3)考查一些综合计算问题;
(4)利用平行四边形性质证明角相等、线段相等和直线平行; (5)利用判定定理证明四边形是平行四边形。
平行四边形中常用辅助线的添法 1、连对角线或平移对角线
2、过顶点作对边的垂线构造直角三角形
3、连接对角线交点与一边中点,或过对角线交点作一边的平行线,构造线段平行或中位线
4、连接顶点与对边上一点的线段或延长这条线段,构造三角形相似或等积三角形。
5、过顶点作对角线的垂线,构成线段平行或三角形全等。
平行四边形(包括矩形、正方形、菱形)的两组对边、对角和对角线都具有某些相同性质,所以在添辅助线方法上也有共同之处,目的都是造就线段的平行、垂直,构成三角形的全等、相似,把平行四边形问题转化成常见的三角形、正方形等问题处理。
A
B
D
O
C
性质
判定
一、连对角线或平移对角线:
例1 如图1,E 是平行四边形ABCD 中AB 延长线上一点,ED 交BC 于F ,求证:。
例2 如图2,在平行四边形ABCD 中,对角线AC 和BD 相交于点O ,如果12=AC , 10=BD ,m AB =,求m 的取值范围。
二、过顶点作对边的垂线构造直角三角形 例3 如图3,平行四边形ABCD 中,∠DBC=
,DE ⊥DB 交BC 的延长线于E ,AD=a ,DE=b ,求。
例4 如图4,平行四边形ABCD 的周长为40,∠ABC=,E 、F 是BD 上的三等分点,AE 的延长线交BC 于M ,MF 的延长线交AD 于N ,设
,
,试求y 与x 的函数关系。
三、连接对角线交点与一边中点,或过对角线交点作一边的平行线,构造线段平行或中位线 例5 如图5,平行四边形ABCD 中,N 是AB 中点,BE=
31BC ,NE 与BD 交于F ,求BD
BF 的值。
例6 如图6,平行四边形ABCD 中,O 是对角线交点,F 是AB 延长线上一点,OF 交BC 于E ,AB=a ,BC=b ,BF=c 。
求BE 长。
四、连接顶点与对边上一点的线段或延长这条线段,构造三角形相似或等积三角形。
例7 如图7,正方形ABCD中,E、F分别为CD、DA的中点,BE、CF交于P,求证AP=AB。
例8 如图8,平行四边形ABCD中,E、F分别是DC、DA上一点,AE=CF,AE与CF交于P,求证PB平分∠APC。
五、过顶点作对角线的垂线,构成线段平行或三角形全等
例9 如图9,E是平行四边形ABCD对角线BD上一点,EF⊥BC,EG⊥BA,垂足分别为F、G,求证:。
例10 如图10,ABCD是正方形,BE∥AC,AE=AC,CF∥AE,求证:∠AEB=2∠BCF。
六、利用一组对边平行且相等构造平行四边形
例11 如图,已知点O是平行四边形ABCD的对角线AC的中点,四边形OCDE是平行四边形.
求证: OE与AD互相平分.
说明:当已知条件中涉及到平行,且要求
证的结论中和平行四边形的性质有关,可
试通过添加辅助线构造平行四边形.
七、利用两组对边平行构造平行四边形
例12 如图,在△ABC 中,E 、F 为AB 上两点,AE=BF ,ED//AC ,FG//AC 交BC 分别为D ,G. 求证: ED+FG=AC.
八、利用对角线互相平分构造平行四边形
例13 如图,已知AD 是△ABC 的中线,BE 交AC 于E ,交AD 于F ,且AE=EF.求证BF=AC.
说明:当图形中涉及到一组对边平行时,可通过作平行线构造另一组对边平行,得
到平行四边形解决问题. 说明:本题通过利用对角线互相平分构造平行四边形,实际上是采用了平移法构造平行四边形.当已知中点或中线应思考这种方法.。
