四阶幻方解法
四阶幻方的解法

四阶幻方的解法
四阶幻方是一种古老的数学游戏,在互联网时代仍然颇受欢迎。
说到四阶幻方,就必须先说到它最核心的解题方式--穷举空间搜索。
该方法按照一定的顺序解决问题,从数个选项中寻找正确答案。
穷举空间搜索的方法是由计算机科学家Saul Amarel提出的,于1962年发表
于卡皮罗国际学术期刊。
该方法以“搜索与发现”为核心策略,有效地解决约束形式求解问题,即四阶幻方。
例如:每行和每列的和相等、每个三角形的和为34等。
四阶幻方的解题步骤基本为三步:第一步采用在线推理,基于当前已有数字,
筛选出可行方案;第二步就是穷举空间搜索,按照一定顺序枚举多种可行方案,进行模拟测试;第三步是选取最优解,从测试结果最优的方案中挑选出最优解。
此外,四阶幻方也可以采用人工智能技术。
典型的人工智能技术有:机器学习、神经网络和进化计算。
这些技术可以帮助四阶幻方在秒内进行快速解算,让用户几分钟就能完成游戏,可谓是一种精旨体验。
结论:四阶幻方的解题方式主要有穷举空间搜索和人工智能两种。
穷举空间搜
索具有速度快、效率高的优势,对每行、每列和每个三角形的求和都进行约束计算;而人工智能技术则可以借助机器学习、神经网络和进化计算等技术,将复杂过程变得简单、快捷,解决四阶幻方问题。
四阶幻方解法
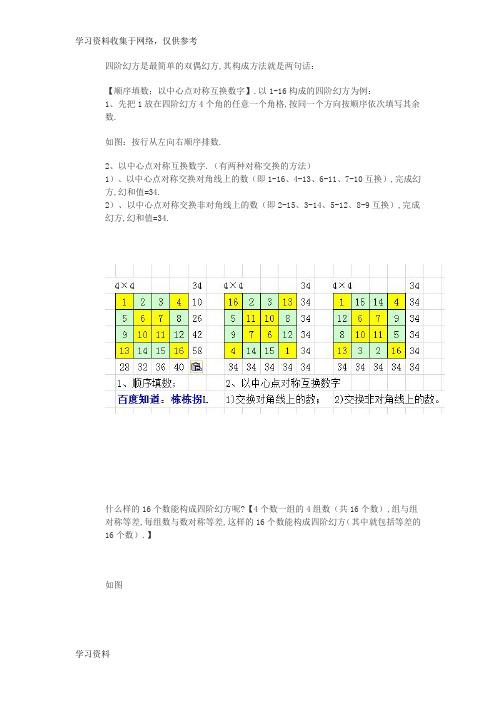
四阶幻方是最简单的双偶幻方,其构成方法就是两句话:
【顺序填数;以中心点对称互换数字】.以1-16构成的四阶幻方为例:
1、先把1放在四阶幻方4个角的任意一个角格,按同一个方向按顺序依次填写其余数.
如图:按行从左向右顺序排数.
2、以中心点对称互换数字.(有两种对称交换的方法)
1)、以中心点对称交换对角线上的数(即1-16、4-13、6-11、7-10互换),完成幻方,幻和值=34.
2)、以中心点对称交换非对角线上的数(即2-15、3-14、5-12、8-9互换),完成幻方,幻和值=34.
什么样的16个数能构成四阶幻方呢?【4个数一组的4组数(共16个数),组与组对称等差,每组数与数对称等差,这样的16个数能构成四阶幻方(其中就包括等差的16个数).】
如图
上图,每组数与数以2-3-2对称等差,组与组以10-20-10对称等差.
下图,每组数与数以1-2-1对称等差,组与组以10-20-10对称等差. 再如:
上图,每组数与数等差为1,组与组等差为5.
中图,每组数与数等差为1,组与组以5-10-5对称等差.
下图,每组数与数以2-3-2对称等差,组与组以5-10-5对称等差.
【四阶幻方的特点:】
1、互换对称的行(列),幻方成立.
2、互换一侧的行(或列),再互换另一侧的行(或列),幻方亦成立.
3、互换不对称的行(或列),再互换另外不对称的行(或列),幻方亦成立.
4、平移互换对角的行或列、平移互换对角,幻方成立.
另,每16个能构成四阶幻方的数,幻方的填法有880种.。
幻方解法

幻方解法
幻方,就是对于一个n×n的方阵,将1—n²这n²个数填入其中,使每行每列以及对角线上的数字之和都相等的方阵。
幻方分为奇数阶幻方(n=2k+1)、单偶数幻方
(n=4k+2)、双偶数幻方(n=4k)三种,每种幻方解法不同,但都有其固定的解。
下面我来具体介绍下幻方的解法:
1.奇数阶幻方
①将1填入第一行中间位置
②向右上方向依次填入
③如果上方出格了,则将其填入最后一行与其同列的位置
④如果右方出格了,则将其填入第一列与其同行的位置
⑤如果右上都出格,则将其填入第一列最后一格
⑥如果将要填入的方格已有数字,则填入上一个数字的下方
这里已三阶幻方为例:
2.双偶数阶幻方(n=4k):
①先将1,2,3……n²依次填入方阵中
②拟出方阵对角线
③对角线上数字不动,将其余所有数字移至与其中心对称的位置
这里以四阶幻方为例
↓
↓ 3.单偶数阶幻方(n=4k+2):
①先将1,2,3……n平方依次填入方阵中
②拟出对角线,将对角线上所有数字移至与其中心对称的位置。
③从方阵左半部分的每一列数字中抽出一对上下对称的数字互换位置(每一列抽出一对)
④从方阵上半部分的每一行数字中抽出一对左对称的数字互换位置(每一行抽出一对)
注:已经移动过或换过位置的数字不能再移动或换位
这里以六阶幻方为例:
↓
↓②↓
↓
↓③↓
↓
↓④↓。
幻方题目解题思路

幻方题目解题思路幻方这玩意儿挺有趣的呢!咱来唠唠解题思路哈。
一、啥是幻方首先得知道幻方是个正方形的格子阵,就像九宫格那种(当然也有其他规格的,像四阶幻方啥的)。
每一行、每一列还有对角线上的数字加起来都得等于同一个数,这个数就叫幻和。
二、三阶幻方(九宫格)的基本思路1. 确定幻和- 对于三阶幻方(3×3的格子),因为1 + 2+3+4+5+6+7+8+9 = 45,这9个数要平均分配到三行(或者三列),所以幻和就是45÷3 = 15。
2. 找中心数- 在三阶幻方里,中心数特别重要。
因为它会在四条线上(一行、一列和两条对角线)参与求和。
- 假设中心数是x,那么它在四条线上相加的总和就是4x。
其他八个数两两组合成四组,每组和都等于幻和 - x。
- 经过计算就会发现中心数是5(你可以自己试着推导一下哦,挺好玩的)。
3. 填角上的数- 角上的数也很关键。
一般先从和5能凑成15的数开始考虑,像1、9,2、8,3、7,4、6这几组。
- 先试着把1放在左上角(只是个例子,放哪儿都行开始),那它对角就得是9,这样才能保证对角线的和是15。
然后再根据每行每列的和是15慢慢填其他的数。
1. 连续自然数幻方- 对于四阶幻方,1到16这16个数的和是136。
因为要四行(或四列),所以幻和是136÷4 = 34。
- 有一种方法叫“对称交换法”。
先把1到16按顺序填到四阶方阵里,就像从左上角开始横着填。
- 然后把对角线上的数保留,其他的数关于中心对称交换位置。
这样就得到了四阶幻方。
- 更高阶的幻方也有一些类似的方法,不过会更复杂一些。
2. 不是连续自然数的幻方- 如果不是1、2、3……这样连续的数,那首先得算出这些数的总和,然后确定幻和(总和除以阶数)。
- 然后可以先找一个和这些数相近的连续自然数幻方,再通过调整数字的大小来得到想要的幻方。
总之呢,幻方就像一个数字谜题,要根据幻和、数字的规律还有一些特殊位置(像中心数、角上数)的特点来慢慢拼凑出答案,多试几次就会找到感觉啦!。
幻方解题技巧

六阶幻方
幻和是:6×(62+1)÷2=111
构 成
三阶幻方构成方法之一
九子斜排 上下对易 左右更替 四维挺出
三阶幻方构成方法之二
画格辅助 九子斜排 送子回家 清除辅助
1
4 7
8 9
2
5
6
3
9
3
1
7
这种方法适用于所有的 奇阶幻方
1
6
11 24 7
2 20 3 4 5 10
16 4
21 22
偶阶幻方 都可以照这样的方法去填
如;八阶幻方
十阶幻方 十二阶幻方
神 奇
四阶幻方
幻和
是34
16+13+1+4
5+2+12+15 3+8+9+14
16+2+11+5 9+7+4+14 3+13+8+10 6+12+1+15
左右对开并交换, 也是一个四阶幻方
上下对开并交换 仍是一个四阶幻方
纵向切开,交换后再接起来
横切一刀,交换后再接起来
距 离 幻 方 中 心 41 的 任 何 中 心 对 称 位 置 上 两 数 和 都 为 82
九阶幻方
将 幻 方 按 图 中 粗 线 分 成 九 块 , 即 为 九 个 三 阶 幻 方
若把上述九个三阶幻方的每个幻方的“幻和”值写在九宫格中,又构成一个新的三阶幻方
分类 构成 神奇
分 类
按照纵横各有数字的个数,可以分为: 三阶幻方、 四阶幻方、 五阶幻方、 六阶幻方… … 按照纵横数字数量奇偶的不同,可以分为: 奇阶幻方 偶阶幻方
四阶幻方代数推理

四阶幻方代数推理引言幻方是一种众所周知的数学奇观,它是一种排列在正方形格子中的数字集合,使得每一行、每一列和对角线上的数字和都相等。
四阶幻方是其中的一种特殊情况,它是一个4×4的正方形格子,被填满了1到16的数字,使得每一行、每一列和对角线上的数字和都相等。
在本文中,我们将展示如何通过代数推理来构建四阶幻方。
我们将使用数学原理和方法来解释如何填充幻方,使得它满足特定的条件。
我们将展示如何利用代数运算和数学推理来构建四阶幻方,并给出详细的步骤和例子。
通过本文的阐述,读者可以了解代数推理在构建幻方中的重要作用,同时也能够对代数推理有更深入的理解。
第一部分:基本原理为了构建四阶幻方,我们首先需要了解一些基本原理。
幻方的构建是基于一种特殊的数学规律,这个规律被称为幻方的特性。
幻方的特性可以用代数推理来解释和证明,这将为我们的构建过程提供基础和指导。
首先,我们需要了解四阶幻方的特性。
根据幻方的定义,每一行、每一列和对角线上的数字和都相等。
对于四阶幻方来说,这个数字和可以表示为S=4×(4×4+1)/2=34。
这个数字34称为幻方的常数,它是幻方中每一行、每一列和对角线上数字和的总和。
了解了这个特性之后,我们就可以通过代数推理来构建四阶幻方了。
第二部分:代数推理接下来,我们将介绍如何通过代数推理来构建四阶幻方。
我们将按照以下步骤来进行推理和构建:步骤一:确定幻方的常数首先,我们需要确定四阶幻方的常数。
根据前面的讨论,我们知道四阶幻方的常数为34。
这个常数将会成为我们构建幻方的重要依据,我们需要保证每一行、每一列和对角线上的数字和都等于34。
步骤二:填充幻方的中心数字接下来,我们将填充幻方的中心数字。
四阶幻方的中心数字是16,我们可以将它填充在幻方的中心位置。
这样一来,幻方的第一步就完成了。
步骤三:确定幻方的边界数字然后,我们需要确定幻方的四个边界数字。
四阶幻方的数字范围是1到16,我们需要将这些数字填充在幻方的边界位置。
求四阶的素数幻方

求四阶的素数幻方。
即在一个4X4 的矩阵中,每一个格填入一个数字,使每一行、每一列和两条对角线上的4 个数字所组成的四位数,均为可逆素数。
*问题分析与算法设计有了前面的基础,本题应当说是不困难的。
最简单的算法是:采用穷举法,设定4X4矩阵中每一个元素的值后,判断每一行、每一列和两条对角线上的4个数字组成的四位数是否都是可逆素数,若是则求出了满足题意的一个解。
这种算法在原理是对的,也一定可以求出满足题意的全部解。
但是,按照这一思路编出的程序效率很低,在微机上几个小时也不会运行结束。
这一算法致命的缺陷是:要穷举和判断的情况过多。
充分利用题目中的“每一个四位数都是可逆素数”这一条件,可以放弃对矩阵中每个元素进行的穷举的算法,先求出全部的四位可逆素数(204个),以矩阵的行为单位,在四位可逆素数的范围内进行穷举,然后将穷举的四位整数分解为数字后,再进行列和对角线方向的条件判断,改进的算法与最初的算法相比,大大地减少了穷举的次数。
考虑矩阵的第一行和最后一行数字,它们分别是列方向四位数的第一个数字和最后一个数字,由于这些四位数也必须是可逆素数,所以矩阵的每一行和最后一行中的各个数字都不能为偶数或5。
这样穷举矩阵的第一行和最后一行时,它们的取值范围是:所有位的数字均不是偶数或5的四位可逆数。
由于符合这一条件的四位可逆素数很少,所以这一范围限制又一次减少了穷举的次数。
对算法的进一步研究会发现:当设定了第一和第二行的值后,就已经可以判断出当前的这种组合是否一定是错误的(尚不能肯定该组合一定是正确的)。
若按列方向上的四个两位数与四位可逆数的前两位矛盾(不是其中的一种组合),则第一、二行的取值一定是错误的。
幻方的技巧和解题思路

幻方的技巧和解题思路
幻方是一个矩阵,其中每行、每列和对角线上的元素之和都相等。
解题和构建幻方的方法有很多,以下是一些常用的技巧和解题思路:
1.奇阶幻方的构建:
o3阶幻方:可以使用"Siamese(托马斯维尔纳·托马斯纳格尔)方法"来构建。
o5阶幻方:可以使用"Burr(亨利·伯尔)方法"来构建。
o对于其他奇数阶的幻方,可以使用"La Hire(菲利普·莱尔)方法"来构建。
2.偶阶幻方的构建:
o4阶幻方:可以使用"De la Loubère(安德烈·纳诺·德拉卢贝尔)方法"来构建。
o6阶幻方:可以使用"J. R. Hendricks(乔布·亨德里克斯)方法"来构建。
o对于其他偶数阶的幻方,可以使用"Siamese(托马斯维尔纳·托马斯纳格尔)方法"或其他类似的方法来构
建。
3.递推法:可以使用递推法构建幻方,即通过给定的幻方来
构建更大阶数的幻方。
这种方法可以应用于各种阶数的幻
方。
4.数学公式:还有一些数学公式可以用来生成特定阶数的幻
方。
例如,Ramanujan公式可以用来生成8阶幻方,而Strachey公式可以用来生成12阶幻方。
5.对称性和规则性:在构建幻方时,利用对称性和规则性可
以更容易地确定某些元素的值,从而简化构建过程。
这些是一些常用的技巧和解题思路,但构建幻方是一个复杂的数学问题,需要深入的数学知识和技巧。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
创作编号:
GB8878185555334563BT9125XW
创作者:凤呜大王*
四阶幻方是最简单的双偶幻方,其构成方法就是两句话:
【顺序填数;以中心点对称互换数字】.以1-16构成的四阶幻方为例:
1、先把1放在四阶幻方4个角的任意一个角格,按同一个方向按顺序依次填
写其余数.
如图:按行从左向右顺序排数.
2、以中心点对称互换数字.(有两种对称交换的方法)
1)、以中心点对称交换对角线上的数(即1-16、4-13、6-11、7-10互换),完成幻方,幻和值=34.
2)、以中心点对称交换非对角线上的数(即2-15、3-14、5-12、8-9互换),完成幻方,幻和值=34.
什么样的16个数能构成四阶幻方呢?【4个数一组的4组数(共16个数),
组与组对称等差,每组数与数对称等差,这样的16个数能构成四阶幻方(其中就包括等差的16个数).】
如图
上图,每组数与数以2-3-2对称等差,组与组以10-20-10对称等差. 下图,每组数与数以1-2-1对称等差,组与组以10-20-10对称等差. 再如:
上图,每组数与数等差为1,组与组等差为5.
中图,每组数与数等差为1,组与组以5-10-5对称等差.
下图,每组数与数以2-3-2对称等差,组与组以5-10-5对称等差.
【四阶幻方的特点:】
1、互换对称的行(列),幻方成立.
2、互换一侧的行(或列),再互换另一侧的行(或列),幻方亦成立.
3、互换不对称的行(或列),再互换另外不对称的行(或列),幻方亦成立.
4、平移互换对角的行或列、平移互换对角,幻方成立.
另,每16个能构成四阶幻方的数,幻方的填法有880种.
创作编号:
GB8878185555334563BT9125XW
创作者:凤呜大王*。
