《信号与系统》_系统的时域分析
第二章 信号与系统的时域分析

二 卷积积分(The convolution integral) 若 (t ) h(t ) 则 (t ) h(t ) = h (t )
x t x h t
x(t ) x( ) (t )d y(t ) x( )h (t )d
则 y(t ) ak yk (t )
k
4
信号与系统的时域分析:
一般的信号都可以表示为延迟冲激的线性组合。
结合系统的叠加性和时不变性,就能够用LTI的单位
冲激响应来完全表征任何一个LTI系统的特性。这样
一种表示在离散情况下称为卷积和;在连续时间情
况下称为卷积积分。
5
分析方法:
对信号分解可在时域进行,也可在频域或变换域 进行,相应地产生了对LTI系统的时域分析法、频 域分析法和变换域分析法。
h( n n kk n h ) uu (n k )k
1
1
k
0
...
0
k
n
12
运算过程:
k k) ,再随参变量 为 h(
点值累加,得到
将一个信号 xk 不动,另一个信号反转后成为
下,将 xk 与 hn k 对应点相乘,再把乘积的各
n
移位.在每个 n 值的情况
x( [ n] y x x[ (n n] )* [ (n) h2 (n n)] x ) y( n n) (h h1 ) 1 n h2 h (n ) h( n) h2 x(t ) 11 y(t ) x(t ) [h1 (t ) h2 (t )] h1 (t ) h2 (t )
0
16
对一般信号 x(t ) ,可以分成很多 宽度的区段, 用一个阶梯信号 x (t ) 近似表示 x(t ) .当 0 时,
《信号与系统》第三章 离散系统的时域分析

h(k) = h1(k) – h1(k – 2) =[(1/3)(– 1)k + (2/3)(2)k]ε(k) – [(1/3)(– 1)k –2 + (2/3)(2)k–2]ε(k – 2)
f (i)h(k i) ai (i)bki (k i)
i
i
当i < 0,ε(i) = 0;当i > k时,ε(k - i) = 0
1
a
k
1
yzs
(k
)
k i0
aibk
i
(k
)
bk
k i0
a b
i
(k
)
bk
bk
b 1 a
b (k 1)
注:ε(k)*ε(k) = (k+1)ε(k)
当ik时ki0???????????????iikiiikbiaikhif?????????????????????????????????????????????????bakbbabababkbabkbakykkkkiikkiikizs111100??注
《信号与系统》 第三章 离散系统的时域分析
λ n + an-1λn– 1 + … + a0 = 0 其根λi( i = 1,2,…,n)称为差分方程的特征根。 齐次解的形式取决于特征根。
参看教材第87页 表3-1。
2. 特解yp(k): 特解的函数形式与激励的函数形式有关
信号与系统教案第2章
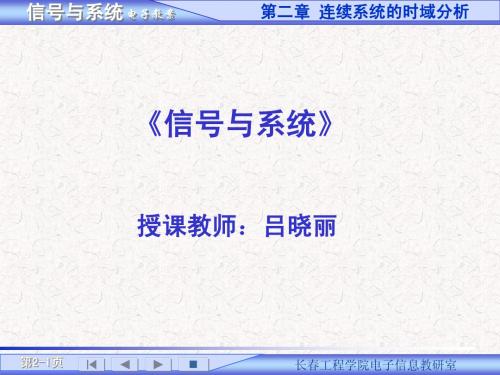
bm f
( m)
(t ) bm1 f
( m1)
ai 、 bj为常数。
2.1 LTI连续系统的响应
经典时域分析方法 y(t ) yh (t ) yp (t ) 卷积法
y(t) = yzi (t) + yzs (t)
一、经典时域分析方法(微分方程经典解)
微分方程的全解即系统的完全响应, 由齐次解 yh(t)和特解yp(t)组成
信号与系统 电子教案
2.2 冲激响应和阶跃响应
2.2
冲激响应和阶跃响应
一、冲激响应
由单位冲激函数δ(t)所引起的零状态响应称为 单位冲激响应,简称冲激响应,记为h(t)。 h(t)=T[{0},δ(t)]
t
h t T 0 , t
def
h t
t
信号与系统 电子教案
第二章 连续系统的时域分析
《信号与系统》
授课教师:吕晓丽
第2-1页
■
长春工程学院电子信息教研室
信号与系统 电子教案
第二节总结
总
结
1、LTI系统的判定方法 线性性质 时不变性质 2、 LTI系统的分类 因果系统 稳定系统 3、系统的描述 系统框图与系统方程
第2-2页
■
长春工程学院电子信息教研室
[例] 已知某二阶线性时不变连续时间系统的动态方程
y" (t ) 6 y' (t ) 8 y(t ) f (t ), t 0
初始条件y(0)=1, y '(0)=2, 输入信号f (t)=et ε(t),求 系统的完全响应y(t)。
解:
(3) 求方程的全解
y (t ) yh (t ) yp (t ) C1e
信号与系统分析第二章 连续时间系统的时域分析

第二章 连续时间系统的时域分析
2.1.1
对系统进行分析时, 首先要建立系统的数学模型。 对于电的系统, 只要利用理想的电路元件, 根据基尔霍 夫定律, 就可以列出一个或一组描述电路特征的线性 微分方程。 现举例来说明微分方程的建立方法。
第二章 连续时间系统的时域分析
例2.1 图2.1所示为RLC串联电路, 求电路中电流i(t) 与激励e(t)之间的关系。
第二章 连续时间系统的时域分析
(3)
y(t) C 1 e t C 2 e 6 t5 2c 0 1o 2 t)s 5 3 (s0i2 n t) (
D(p)y(t)=N(p)f(t)
y(t) N(p) f (t) D(P)
式(2.15)中的 N ( p ) 定义为转移算子, 用H(p)表示,
D (P)
(2.14) (2.15)
H (p ) N D ( (P p ) ) b a m n p p m n a b n m 1 1 p p n m 1 1 a b 1 1 p p a b 0 0 (2.16)
t0
解 (1) 齐次解。 由例2.4 yh (t)=C1e-t+C2e-6t
第二章 连续时间系统的时域分析
(2) 特解。 查表2.2, yp(t)=B1cos (2t)+B2sin(2t)
-14B1+2B2-6=0 2B1+14B2=0
于是,
B15201,
B2530
yp(t)5 20 c 1o2ts) (530 si2 nt)(
第二章 连续时间系统的时域分析
3. 用算子符号表示微分方程, 不仅书写简便, 而且在建 立系统的数学模型时也很方便。 把电路中的基本元件R、 L、 C的伏安关系用微分算子形式来表示, 可以得到相应 的算子模型, 如表2.1所示。
信号与系统分析第六章 离散时间信号与系统的时域分析

应用上述性质, 可以将任意离散信号f(k)表示为单位序
列的延时加权和,
f ( k ) f ( 1 ) ( k 1 ) f ( 0 ) ( k ) f ( 1 ) ( k 1 )
f (n)(k n) n
同样, 根据单位序列δ(k)的特点,
(6.5)
f(k)(k) f(0)
第六章 离散时间信号与系统的时域分析
2. 单位阶跃序列ε(k) 单位阶跃序列ε(k)
(k) 10
k 0 k 0
(6.8)
ε(k)的波形如图6.3所示。 单位阶跃序列ε(k)类似于
连续时间系统的单位阶跃信号ε(t), 但应注意, ε(t)在t=0点
处发生跳变, 在此处不定义或定义为 定义为1。
, 而1 ε(k)在k=0处 2
实际处理时, 常把信号存放在处理器的存储单元 中, 随时取用, 也可以先记录数据后分析或短时间内存 入, 数据在较长时间内完成处理过程。 考虑到上述因 素, 离散时间信号f(kTs)可以不必以kTs为变量, 而可以 直接用f(k)表示离散信号, k为信号出现的序号。 用f(k) 表示离散信号不仅简便而且具有更为普遍的意义, 即 离散变量k可以不限于代表时间。 通常, 离散时间信 号也称为序列, 可以把它看成是一组序列值的集合。
可以看出, 任意信号与单位序列δ(k)相乘得到的仍然是 一个δ(k)序列, 只不过序列的幅度不再为1而是被f(0)加 权,δ(k)的这个性质称之为“加权性”, 或“取样性”。 推广后可以得到, 对于任意延时的单位序列δ(k-n),
f(k)δ(k-n)=f(n)δ(k-n) (6.4)
第六章 离散时间信号与系统的时域分析
k 0 k 0
(6.1)
第六章 离散时间信号与系统的时域分析
信号与系统引论 课件 郑君里 第2章 连续时间系统的时域分析

网络拓扑约束:由网络结构决定的电压电流约束关系,
KCL,KVL。
例2-1
电阻 电感 电容
求并联电路的端电压v(t)与激励is(t)间的关系。
1 iR iR t v t R i s t R L 1 t i L t v d L d v t iC t C 元件特性约束 dt
E (常数)
B(常数)
B1t p B2 t p1 B p t B p1
tp e t
cos t sin t
Be t
B1 cos t B2 sin t
t p e t sin t B1t p B2 t p 1 B p t B p 1 e t cos t
2.2 系统数学模型(微分方程)的建立
对于电路系统,主要是根据元件特性约束和网络拓扑
约束列写系统的微分方程。
对于其他物理系统,根据实际系统的物理特性列写系 统的微分方程。 元件特性约束:表征元件特性的关系式。例如二端元
件电阻、电容、电感各自的电压与电流的关系以及
四端元件互感的初、次级电压与电流的关系等等。
等式两端各对应幂次的系数应相等,于是有
3 B1 1 4 B1 3 B2 2 2 B 2 B 3 B 0 2 3 1
联解得到
1 2 10 B1 , B2 , B3 3 9 27
所以,特解为
1 2 2 10 rp t t t 3 9 27
i L (0 ) i L (0 )
例2-6 如图示出RC一阶电路,电路中无储能,起始电
压和电流都为零,激励信号e(t)=u(t),求t >0系统的响
应——电阻两端电压vR(t)。
信号与系统重点概念公式总结

信号与系统重点概念公式总结一、信号的基本概念:1.离散信号:在离散时间点上取值的信号,用x[n]表示。
2.连续信号:在连续时间上取值的信号,用x(t)表示。
3.周期信号:在一定时间内重复出现的信号。
4.能量信号:能量信号的能量有限,用E表示。
5.功率信号:功率信号的能量无限,用P表示。
二、时域分析:1. 时域表示:x(t) = X(t)eiωt,其中X(t)是振幅函数,ω是角频率。
2.常用信号的时域表示:- 矩形脉冲信号:rect(t/T)- 三角函数信号:acos(ωt + φ)-单位跳跃信号:u(t)-单位斜坡信号:r(t)3.信号的分解与合成:线性时不变系统能够将一个信号分解为若干个基础信号的线性组合。
4.性质:-时域平移性:如果x(t)的拉普拉斯变换是X(s),那么x(t-t0)的拉普拉斯变换是e^(-t0s)X(s)。
-线性性:设输入信号的拉普拉斯变换为X(s),系统的拉普拉斯变换表达式为H(s),那么输出为Y(s)=X(s)H(s)。
-倍乘性:设输入信号拉普拉斯变换为X(s),输出信号的拉普拉斯变换为Y(s),那么输出信号的拉普拉斯变换为cX(s),即输出信号的幅度放大为c倍。
-时间反转性:x(-t)的拉普拉斯变换是X(-s)。
-时间抽取性:设输入信号的拉普拉斯变换为X(s),那么调整时间尺度为t/T的信号的拉普拉斯变换为X(s/T)。
三、频域分析:1.傅里叶级数:将周期信号表示为一系列谐波的和。
2.离散傅里叶变换(DFT):将离散信号从时域变换到频域的过程。
3.傅里叶变换:将连续信号从时域变换到频域的过程。
4.频域表示:- 矩形函数:sinc(ωt) = sin(πωt)/(πωt)- 高斯函数:ft(x) = e^(-πx^2)5.频域滤波:系统的传输函数是H(ω),那么输出信号的频率表示为Y(ω)=X(ω)H(ω)。
四、信号与系统的系统分析:1.系统稳定性:-意义:系统稳定指的是当输入有界时,输出有界。
郑君里《信号与系统》(第3版)(上册)(课后习题 连续时间系统的时域分析)【圣才出品】
圣才电子书
十万种考研考证电子书、题库视频学习平 台
解:对汽车底盘进行受力分析。
图 2-4
图 2-5
设汽车底盘运动速度为 v(t) ,方向向上; Fk 为弹簧对汽车底盘的拉力,方向向下; Ff 为减震器阻尼力,方向向下。
汽车底盘的加速度:
a(t)
dv(t) dt
d dt
[ dy(t)] dt
d
2 y(t) dt 2
①
因弹簧的位移量为 x(t) y(t) ,所以拉力: Fk (t) k[ y(t) x(t)]
②
减震器对汽车底盘的作用力: Ff
(t)
f
d [ y(t) x(t)] dt
③
由牛顿第二定律知: Fk (t) Ff (t) ma(t)
将式①②③代入上式,可得微分方程
2-6 给定系统微分方程
若激励信号和起始状态为: 试求它的完全响应,并指出其零输入响应、零状态响应,自由响应、强迫响应各分量。
解:方程的特征方程为
特征根为
(1)设零输入响应
①
6 / 36
圣才电子书
由已知条件可得
十万种考研考证电子书、题库视频学习平 台
rzi (0 ) rzi (0 ) r(0 ) 1
台
(2)
d dt
r
t
2r
t
3
d dt
et
,r
0
0,et
ut
。
试判断在起始点是否发生跳变,据此对(1)(2)分别写出其 r0 值。
解:当微分方程右端包含 (t) 及其各阶导数时,系统从 0 状态到 0 状态发生跳变。
(1)将 e(t) u(t) 代入原方程得:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)
将式(2)(3)代入式(1)得
[a (t) b (t) cu(t)] 3[a (t) bu(t)] 3 (t)
解得 a 3, b 9, c 9 所以有 r(0 ) r(0) b 9 r(0 ) r(0) 9
练习 P86 2-5
信号与系统
第二部分 连续时间系统的时域分析
$$ 微分方程的建立与经典求解 $$ 起始点的跳变
$$ 连续时间LTI系统的响应 零输入响应
零状态响应 $$ 连续时间系统的冲激响应 $$ 卷积积分及其性质 $$ 用算子符号表示微分方程
(2.2-2.3) (2.4) (2.5)
(2.6) (2.7-2.9) (2.10)
6
t
C i(t)dt
f
(t)
0+电路方程 5i(0+)+i′(0+)+vC(0+)=0
iL(0+)=iL(0-)=1A, vC(0+)= vC(0-)=10V
5+i′(0+) +10=0 解得标准初始条件为 i(0+)=1 A 及 i′(0+)=-15 A/s
ih(t)=K1e-2t+K2e-3t t>0
时变 q(0 ) q(0 ), (0 ) (0 )
② 冲激匹配(平衡)法
信号与系统
例2 已知电路如图所示,且iL(0-)=1A,vC(0-)=10V, 求ih(t)。
解:由电路有
R= 5 L= 1H iL(0-) +
di(t) 1 t
Ri(t) L i(t)dt f (t) dt C
零输入响应 yzi (t) K1e2t K2e3t
信号与系统
由初始状态为y(0-) = 1,y’(0-) = 3,有
yzi (0 ) K1 K2 1 yzi (0 ) 2K1 3K2 3
解得 K1 6, K2 5
零输入响应 yzi (t) 6e2t 5e3t
K1 K2 2K1
112
12 13
所以 ih(t)=12e-2t+13e-3t t>0
信号与系统
冲激平衡法 问题:当系统已经用微分方程表示时,如何由系统 的0-状态求0+状态?
系统的0-状态→0+状态是否有跳变?
取决于微分方程右端是否包含δ(t)及其各阶导数
信号与系统
例1 已知某线性时不变系统的动态方程式为:
y(t) 5 y(t) 6 y(t) 4 f (t), t 0
系统的初始状态为y(0-) = 1,y’(0-) = 3,求 系统的零输入响应yzi(t)。 解 零输入响应,即f(t)=0
微分方程变为齐次方程 y(t) 5y(t) 6y(t) 0 特征方程为 2 5 6 0 特征根为 1 2, 2 3
一、系统的零输入响应 系统的零输入响应 是输入信号为零,仅由系统的 初始状态单独作用而产生的输出响应。 * 数学模型:
y(n) (t) an1 y(n1) (t) a1 y(t) a0 y(t) 0
* 求解方法: ①根据微分方程的特征根确定零输入响应的形式; ②再由初始条件确定待定系数。 类似经典法的齐次解求解方法
ul
(t)
l
dil (t) dt
,
1 il (t) l
t
ul ( )d
* 耦合电感V-I关系
信号与系统
耦合电路中的V-I关系
信号与系统
例1 对下图所示电路,分别列写出电压v0(t)的微分 方程表示式。(P86 2-1)
信号与系统
解:
对图中所示电路列写网孔电流方程,得
2i1(t)
三者之间的关系:r(k)(0+) = rzs(k)(0+) + r(k)(0-)
信号与系统
2.初始条件的确定
①
ic
(t
)
c
duc (t dt
)
换 路
ul
(t)
l
dil (t) dt
若电容电流有界 若电感电压有界
定 律
时不变 vc (0 ) vc (0 ), il (0 ) il (0 )
2)若输入信号不变,初始条件y(0)=0, y '(0)=1, 则系统的完全响应 y(t) = ?
经典 若微分方程右边激励项较复杂,则难以处理。 法不 • 若激励信号发生变化,则须重新求解。 足之 • 若初始条件发生变化,则须重新求解。 处 • 这种方法是一种纯数学方法,无法突出系统
响应的物理概念。
①不含δ(t)及其各阶导数,0-→0+状态无跳变: r(0+) =r(0-)
②含δ(t)及其各阶导数,0-→0+状态有跳变:
r(0 ) r(0 ), r(0 ) r(0 )
信号与系统
如 系统用微分方程 dr(t) 3r(t) 3 (t) 描述,已知
dt
系统的起始状态r(0-),求r(0+)。
③特征根是成对共轭复根 Si=σi±jωi,i=n/2
yh (t) e1t (K1 cos1t K2 sin1t) eit (Kn1 cosit Kn sinit)
信号与系统 常用激励信号对应的特解形式(P51 表2-3)
Ci、Di的求解为yp(t)代入方程, 两边系数匹配求得
1 y(0) K1 K2 3 1
y(0)
2K1
4K2
1 3
2
解得
K1
5 2
,
K2
11 6
全解 y(t) 5 e2t 11 e4t 1 et , t 0
2
6
3
通解(自由响应) 特解(强迫响应)
信号与系统
思考:1)若初始条件不变,输入信号 f(t) = sin t u(t), 则系统的完全响应 y(t) =?
di1(t) dt
t
i1( )d
t
i2 ( )d
e(t)
t
[i2 (
)
i1(
)]d
i2 (t)
v0 (t)
又
v0
(t
)
2
di2 (t dt
)
整理得
2
d
3v0 (t) dt3
5
d
2v0 (t dt 2
)
6
d dt
v0
(t)
3v0
(t)
+
f (t)
i(t)
-
1 6
F
C(0-)
5i(t) di(t) 6 t i(t)dt f (t)
dt
-
d 2i(t) dt 2
5
di(t) dt
6i(t)
df (t) dt
解得 ih(t)=K1e-2t+K2e-3t t>0
信号与系统
v (t) 5i(t)
di(t) dt
特解yp(t)的形式由方程右边激励信号的形式确定
信号与系统
齐次解yh(t)的形式 ①特征根是不等实根 S1,S2,S3,…,Sn
yh (t) K1es1t K 2es2t K nesnt
②特征根是相等实根 S1=S2=S3= … =Sn=S yh (t) K1est K2test Knt n1est
卷积法
信号与系统
$$ 起始点的跳变 0- 0+ (2.4) 1.系统的状态:系统在 t=t0 时刻的状态是一组必 须知道的最少量数据,利用这组数据和系统模型 以及t>t0的激励信号,就能够完全确定t0以后任何 时刻的响应。
以0-表示激励接入之前的瞬时 以0+表示激励接入之后的瞬时
信号与系统
① 起始状态r(k)(0-):它决定了yzi在激励接入之前的 瞬时t=0- 系统的状态,它总结了计算未来响应所需 要的过去的全部信息。 ② 初始状态rzs(k)(0+):跳变量,它决定了yzs在激励 接入之后的瞬时t=0+系统的状态。 ③ 初始条件r(k)(0+):它决定了完全响应。
①待定系数确定的时间不同: 齐次解——求出全响应之后再求系数; 零输入响应——求出零输入响应后立刻求。
②待定系数确定的条件不同: 齐次解——初始条件y(0-) ; 零输入响应——起始状态y(0+) 。
信号与系统
例1 已知某二阶线性时不变连续时间系统的动态方程 y(t) 6y(t) 8y(t) f (t),t 0 ,初始条件y(0)=1, y '(0)=2, 输入信号f (t)=et u(t),求系统的完全响应y(t)。
解 1)求齐次方程 y(t) 6y(t) 的8y齐(t)次解0 yh(t) 特征方程为 2 6 8 0 特征根为 1 2, 2 4 齐次解yh(t) yh (t) K1e2t K2e4t
信号与系统
$$ 连续时间LTI系统响应的时域求解 (2.5)
√经典时域分析方法:齐次解+特解 √卷积法
系统完全响应 = 零输入响应 + 零状态响应 y(t)=yzi(t)+yzs(t)=yzi(t)+f(t)*h(t)
& 零输入响应求解 :求解齐次微分方程 & 零状态响应求解 :卷积积分
信号与系统
2
d dt
e(t)
信号与系统
练习 P86 2-1 2-2
