博弈论知识地图
博弈论基础-A-xjh(共48张PPT)

例如:
—— 出门:带伞 或 不带伞 —— 打牌:出牌
信息(information)指局中人在博弈中的知识,特别是有 关其他局中人(竞争者或对手)的特征和行动的知识。
一般地,信息是以信息集(information set)的概念来模型 化的。可以将局中人的信息集看成是其在特定时点对于不同变 量的取值的了解程度。
评论2:在重复博弈中,以往的经历或做法通常就确局定了中聚人点的B位置。
通零俗和地 博说弈,指博在弈博结弈果中总一和组为局零中的人博所弈得称到为的零支左和付博(弈或。收益)恰好是另右一组局中人的损失。
——对产品的了解
(三)划分博弈的主要概上念
2, 1
完 全 信 息——如“石头、剪刀、布”游戏
0, 0
局中人A 完 备 信 息——“石头、剪刀、布”游戏中,你知道对方40%出石头,30%出布,30%出剪刀
林自由大学、比勒菲尔特大学和波恩大学。其主要贡献 是在博弈论中引入了动态分析。
1920年Harsanyi出生于匈牙利,1947年获布达佩斯大学博士 学位,后到 ,1954年获斯坦福大学博士学位,曾先后任教于澳 大利亚国立大学、加州伯克利分校。于2000年去世。他的贡献是 将不完全信息引入了博弈论的研究。
S4=。可以选择的花的品种为3种。
不同的花在不同的气候条件下的收成为:
天气
S1
S2
S3
S4
品种
A1
12
10
9
0
A2
8
8
4
4
A3
161232概率0.2
例如:
出门 ——对天气的判断
打牌
——对其他人的判断 装修
——对产品的了解
第28章博弈论1

Game Theory
博弈论
• 博弈论是对策略互动进行一般分析的理 论。
• 博弈论的英文名称为game theory,是研 究决策主体的行为发生直接相互作用的 失衡的决策以及这种决策的均衡问题的。
博弈论的应用
• 经济学:市场往往是不完全的,参与者的行为 相互影响,因此,个人决策时必须考虑到对方 的反应
谁先选择?
• 在前面的两个例子中,参与者都是同时 采取行动的。
• 这种博弈称为同时博弈 (simultaneous play games).
• 但是某些博弈是某个参与者首先采取行 动,其他参与者后采取行动。
• 这类博弈称为序贯博弈(sequential play games)。
• 首先行动的参与者是领导者,第二个行 动的参与者是跟随者。
纳什均衡
• 如果存在一个策略组合,其中每一个参 与者的选择都是他的最优选择,此时的 策略组合就是一个纳什均衡 (Nash equilibrium)组合。
• 我们的例子中有两个纳什均衡策略组合 (U,L)和(D,R)。
例子
Player B LR
U (3,9) (1,8)
Player A
D (0,0) (2,1)
序贯博弈举例
• 有时博弈不止一个纳什均衡结果,此时 很难看出哪一种结果可能发生。
• 此时如果博弈行动有先后,那么我们就 有可能判断出哪一种结果更可能出现。
Player B LR
U (3,9) (1,8)
Player A
D (0,0) (2,1)
当同时行动时,(U,L) 、(D,R) 都是纳什均衡 的策略组合,我们无法判断哪一种组合结果 出现的可能性更大。
Clyde
博弈论基础知识.ppt

The theory of rational choice
–
The action chosen by a decision-maker is at least as good, according to her preferences, as every other available action.
第一讲( 第一讲(续) 博弈论基础知识
The theory of rational choice
Actions Preferences and payoff functions
epresents a decision-maker’s preferences if, for any actions a in A and b in A, u(a)>u(b) if and only if the decision-maker prefers a to b. – A decision-maker’s preferences convey only ordinal information.
Conditional probability and Bayes’s rule
– –
Conditional probability and Bayes’s rule
条件概率: P ( B | A) = P ( AB ) P ( A)
全概率公式:设试验 E的样本空间为 S, A为 E的事件, B1, B2, Bn为 S的一个划分, P ( Bi ) > ( i = 1, 2,⋯ , n), 0 则: P ( A) = P ( A | B1 ) P ( B1 ) + P ( A | B2 ) P ( B2 ) + ⋯ + P ( A | Bn ) P ( Bn ) 贝叶斯公式: P ( Bi | A) = P ( A | Bi ) P ( Bi )
博弈论入门PPT课件

基于对其他参与 者信息的了 解程度
完全信息博 弈
不完全信息 博弈
负和博弈
根据结果
零和博弈
正和博弈
特征 合作中如何分配利益,使大家都满意。 只考虑自己的利益,不考虑对方的利益。 做出策略虽然有先后,但每一方都不知
道对方的策略。 做出策略虽然有先后,但参与者对对方
做出的策略是知道。(例如下象棋) 博弈中对其他参与者的各方面信息、可
最理想的结局:双赢
一、正和博弈各方本着相互合作,公平公 正,互利互惠的原则分配利益,让每一 个人参与者都满意的博弈。
案例:鳄鱼鸟与鳄鱼和谐相处,生存搭档 的典型。凶恶的鳄鱼可以容忍鳄鱼鸟清 理它牙缝里的残肉,因为这样可以避免 滋生细菌,它的牙就不会生虫了。
二、博弈中发生冲突的时候,充公了解对 方、取长补短,各取所需,往往会使双 方走出负和博弈和零和博弈的误区,实 现合作共赢。
一年轻人在酒吧喝酒,中途去厕所。一美女尾随 他打劫,对他说:将钱和手机都交出来,否则 我说你非礼我。年轻人转念一想,计上心来, 用手指自己的嘴和耳朵。美女误以为他是聋哑 人,想放弃。年轻人掏出一支笔和一张纸在上 面写上:你说什么呀?
美女见状拿过笔来也在纸上写了:将钱和手机都 交出来,否则我说你非礼我。这时年轻人一把 抓住美女的手,大声喊道:我要送你去派出所 。
最坏的结果:两败俱伤
战争是典型的负和博弈:二战共有61个国 家卷入,涉及人口20亿以上。二战中军 民伤亡1.9亿,其中死亡6000万,受伤 1.3亿。其中死亡的平民有2730万。盟 军中苏联军队伤亡最为惨重,死亡890 万,中国军队死亡148万,英国与美国 各死亡38万。法西斯德国军队伤亡人数 1170万,军队死亡600万,日本军队伤 亡216万。
博弈论最全完整ppt-讲解

施锡铨编著,《博弈论》上海财大出版社,2000年版。
谢识予编著,《经济博弈论》,复旦大学出版社, 2002年版。
谢识予主编,《经济博弈论习题指南》,复旦大学出 版社,2003年版。
2021/3/11
34
课程主要内容
第一章 完全信息静态博弈 第二章 完全信息动态博弈 第三章 不完全信息静态博弈 第四章 不完全信息动态博弈 第五章 委托-代理理论 第六章 逆向选择与信号传递
通过几次严打来获得“冷面杀手”的声 誉
2021/3/11
11
导论
博弈均衡与一般均衡 博弈论与诺贝尔经济学奖获得者
博弈论的基本概念与类型 主要参考文献
2021/3/11
12
导论
一、博弈均衡与一般均衡
2021/3/11
13
案例:囚犯困境
支付
嫌疑 人B
嫌疑人A
抵赖
坦白
抵赖 -1,-1 0,-9
坦白 -9,0 -6,-6
了解自己行动的限制和约束,然后以精心策划的方式 选择自己的行为,按照自己的标准做到最好。 • 博弈论对理性的行为又从新的角度赋予其新的含义— —与其他同样具有理性的决策者进行相互作用。 • 博弈论是关于相互作用情况下的理性行为的科学。
2021/3/11
4
如何在博弈中获胜?
…… 真的能在博弈中(总是)获 胜吗?
托马斯·谢林
24
导论
三、博弈论的基本类型
2021/3/11
25
合作博弈与非合作博弈
合作博弈(cooperative game)
达成有约束力的协议(binding agreement),强调团体理性,强调效 率、公正、公平
非合作博弈(non-cooperative game)
博弈论最全完整ppt 讲解

完全信息
纳什均衡(NE)
子博弈完美纳什 均衡(SPNE)
不完全信息
贝氏纳什均衡 (BNE)
完美贝氏纳什均衡 (PBNE)及序贯均 衡(SE)
静态博弈与动态博弈
(static games and dynamic games)
同时决策或者同时行动的博弈属于静态 博弈;先后或序贯决策或者行动的博弈, 属于动态博弈
如果一个博弈在所有各种对局下全体参 与人之得益总和总是保持为一个常数, 这个博弈就叫常和博弈;
相反,如果一个博弈在所有各种对局下 全体参与人之得益总和不总是保持为一 个常数,这个博弈就叫非常和博弈。
常和博弈也是利益对抗程度最高的博弈。 非常和(变和)博弈蕴含双赢或多赢。
导论
四、主要参考文献
博弈论为众多学科提供了分析的概念和方 法:经济学和商学,政治科学,生物学, 心 理学和哲学。
如何在“博弈”中获胜?
日常生活中的博弈(“游戏”)往往指的是 诸如赌博和运动这样的东西: 赌抛硬币 百米赛跑 打网球/橄榄球
How can you win such games? 许多博弈都包含着运气、技术和策略。 策略是为了获胜所需要的一种智力的技巧。
威廉·维克瑞, 1914-1996, 生于美国
詹姆斯·莫里斯 1936年生于英国
2001年诺贝尔经济学奖获得者
三位美国学者乔治-阿克尔洛夫(George A. Akerlof)、迈克尔-斯彭斯(A. Michael Spence)和约瑟夫-斯蒂格利茨(Joseph E. Stiglitz)
获奖理由:在“对充满不对称信息市场进 行分析”领域做出了重要贡献。
即使决策或行动有先后,但只要局中人 在决策时都还不知道对手的决策或者行 动是什么,也算是静态博弈
第十章博弈论初步(可编辑修改word版)
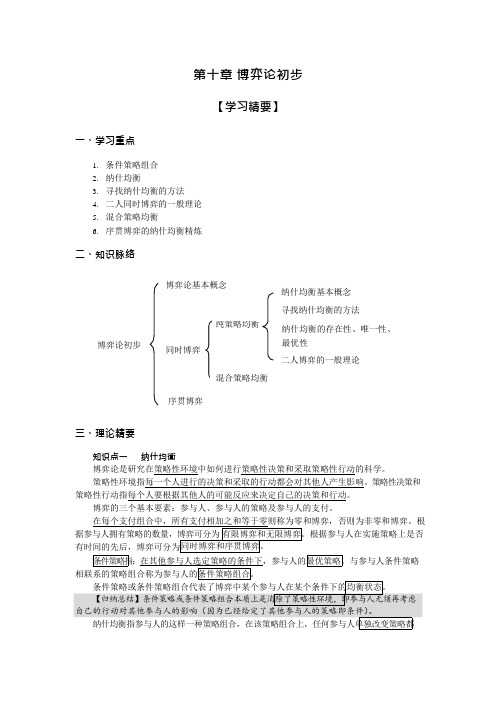
第十章 博弈论初步【学习精要】一、学习重点1. 条件策略组合2. 纳什均衡3. 寻找纳什均衡的方法4. 二人同时博弈的一般理论5. 混合策略均衡6. 序贯博弈的纳什均衡精炼二、知识脉络博弈论基本概念 纳什均衡基本概念博弈论初步 同时博弈 序贯博弈 寻找纳什均衡的方法纳什均衡的存在性、唯一性、最优性 二人博弈的一般理论三、理论精要知识点一 纳什均衡博弈论是研究在策略性环境中如何进行策略性决策和采取策略性行动的科学。
策略性环境指每一个人进行的决策和采取的行动都会对其他人产生影响。
策略性决策和策略性行动指每个人要根据其他人的可能反应来决定自己的决策和行动。
博弈的三个基本要素:参与人、参与人的策略及参与人的支付。
不会得到好处。
知识点二寻找纳什均衡的方法寻找纳什均衡的方法:条件策略下划线法。
根据纳什均衡定义和条件策略组合的定义可得:纳什均衡是所有参与人的条件策略组合的公约数,即纳什均衡是每一个参与人的条件策略组合。
条件策略下划线法:在支付矩阵中每一个参与人的条件策略所对应的支付下面划线,如果支付组合中都有划线,则该支付组合代表的策略组合即为纳什均衡。
知识点三纳什均衡的存在性、唯一性和最优性在同时博弈中,(纯策略的)纳什均衡既可能存在,也可能不存在。
在纳什均衡存在的条件下,它既可能是唯一的,也可能不唯一。
知识点四二人同时博弈的一般理论二人同时博弈(二个策略)每个参与人有9 种可能的支付矩阵,整个博弈有81 种可能的支付矩阵。
全部纳什均衡可分为五种类型:第一种:四个均衡;第二种:三个均衡;第三种:二个均衡;第四种:一个均衡;第五种:零个均衡。
知识点五混合策略均衡混合策略指赋予纯策略的概率向量。
纯策略可以是有限的,由于概率取值的无限性,以有限的纯策略为基础的混合策略一定是无限的。
混合策略组合:((p1, p2),(q1, q2)。
期望支付是指对于每一个混合策略组合,参与人都有一个期望支付即支付的期望值。
条件混合策略: 在其他参与人选择既定的混合策略条件下,参与人所选择的可以使其期望支付最大的混合策略。
3博弈论知识要点

博弈论与信息经济学
一、完全信息静态博弈
博弈矩阵:
1、占优博弈均衡唯一解表28.1
2、多解图(性别战)表28.2
3、无解图(发接球)表28.3
4、无效率解表28.4
5、重复博弈28.5(有限与无限次重复博弈、针锋相对)、
6、合作博弈的协调29.3
(表29.5保证博弈、表29.3性别战、表29.6斗鸡博弈、表29.4囚徒困境)
二、完全信息动态博弈
扩展式博弈树28.7:
反向归纳法表28.5,图28.1
关键是理解“威胁”是否可信,
三、反应曲线29.1
四、混合策略解29.2(性别大战)与竞争博弈29.4(接发球博弈)
五、共存博弈29.5与例子:承诺博弈29.6,青蛙-蝎子;绑匪;智
猪博弈;储蓄与社保;敲竹杠;
六、讨价还价29。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
纯战略纳什均衡-重复剔除的占优均衡智猪博弈
1完全信息静态博弈--纳什均衡任何有限博
弈都至少存
在一个纳什
均衡
是合作共
赢,而不是
斗争到底什均衡
混合战略纳
什均衡
有两个纯策
略,且都帕
累托有效
均衡筛选
非合作博弈类型秩序与产权
非合作博弈
类型
2完全信息
动态博弈--
子博弈精炼
纳什均衡
SPNE
理
还价与耐心砝码与谈判能力
誉
3不完全信
息(信息不
对称)静态
博弈--贝叶
斯纳什均衡
BNE
衡的应用举
例
书/349
设计与收入分配公共产品偏好
克服信息不对称的方法。
