第11章 作业
机械原理作业参考答案-第11章-孙桓-第8版-Appt课件

5
可编辑课件PPT机械原理》(第8版)--孙
桓等主编,高等教育出版社机械原理》 (第8版)--孙桓等主编,高等教育出版
6
可编辑课件PPT机械原理》(第8版)--孙
桓等主编,高等教育出版社机械原理》 (第8版)--孙桓等主编,高等教育出版
7
此课件下载可自行编辑修改,此课件供参考! 部分内容来源于网络,如有侵权请与我联系删除!感谢你的观看!
第11章作业:11-11, 11-14, 11-15, 11-17, 11-19,11-20
可编辑课件PPT机械原理》(第8版)--孙桓等主编,高等教育出版社
机械原理》(第8版)--孙桓等主编,高等教育出版社
1
可编辑课件PPT机械原理》(第8版)--孙
桓等主编,高等教育出版社机械原理》 (第8版)--孙桓等主编,高等教育出版
2
可编辑课件PPT机械原理》(第8版)--孙
桓等主编,高等教育出版社机械原理》 (第8版)--孙桓等主编,高等教育出版
3
可编辑课件PPT机械原理》(第8版)--孙
桓等主编,高等教育出版社机械原理》 (第8版)--孙桓等主编,高等教育出版
4
可编辑课件PPT机械原理》(第8版)--孙
桓等主编,高等教育出版社机械原理》 (第8版)--孙桓等主编,高等教育出版
八年级数学 第11章 数的开方 11.1 平方根与立方根 1平方根作业数学

12/9/2021
第二十二页,共二十二页。
第十七页,共二十二页。
19.用计算器计算,不难得到 2≈1.414, 200≈14.14, 20 000≈ 141.4, 0.02≈0.141 4, 0.000 2≈0.014 14. (1)你发现什么规律? (2)利用(1)中的规律,解决下面的问题:已知 7≈2.646, 70≈8.367, 直接写出 700, 7 000, 70 000, 700 000, 0.7, 0.07, 0.007,
0.000 7的近似值.
第十八页,共二十二页。
解:(1)规律:被开方数的小数点向右(或向左)每移动两位,它的算 术平方根的小数点向右(或向左)移动一位. (2) 700≈26.46, 7 000≈83.67, 70 000≈264.6, 700 000≈836.7,
0.7≈0.836 7, 0.07≈0.264 6, 0.007≈0.083 67, 0.000 7≈0.026 46
第六页,共二十二页。
知识点 2:算术平方根 6.(2016·杭州) 9=( B ) A.2 B.3 C.4 D.5 7.下列说法中正确的是( B ) A.25 是 5 的算术平方根 B.5 是 25 的算术平方根 C.5 是 25的算术平方根 D. 25是 5 的算术平方根
第七页,共二十二页。
8. 16的算术平方根是( B ) A.±2 B.2 C.±4 D.4 9.如果 x 是 9 的算术平方根,那么 x 的算术平方根是( C ) A.3 B.1 C. 3 D.±3
第十二页,共二十二页。
第十三页,共二十二页。
14.(2016·怀化)(-2)2 的平方根是( C ) A.2 B.-2 C.±2 D. 2 15.一个正数的正的平方根是 m,那么比这个正数大 1 的数的平 方根是( D ) A.m2+1 B.± m+1 C. m2+1 D.± m2+1
第11章作业1

B2 0 I 2 /(2R)
⊙
×
导体管电流产生的磁场
B3 0 I1 /[2(d R)]
I2
B B1 B2 B3
0 I 2 ( R d )(1 ) RI1
2 R( R d )
I1
O R d I2
⊙
11-19 一根同轴线由半径为 R1 的长导线和套在它外面的内半径
R
b R2 R1
R2 ln 2 R1
NIb
(2)同样在环外 (r R , r R ) 作圆形回路 1 2
由于
I
i
0
B 2r 0
N
所以 B = 0
b R2 R1
11-17 边长为 l 0.1m B 1T 的均匀磁场中,线圈平面与磁场方向平行.如图所示,使线圈 通以电流 I 10 A ,求: (1)线圈每边所受的安培力; 轴的磁力矩大小。 (2)对 OO 解: (1)
(B) 回路L内的I不变, L上各点的B改变
(C) 回路L内的I改变, L上各点的B不变 (D) 回路L内的I改变, L上各点的B改变 11-6若某空间存在两无限长直载流导线, 空间的磁场就不 存在简单的对称性. 此时该磁场的分布[D (A) 可以直接用安培环路定理来计算; ]
(B) 只能用安培环路定理来计算;
(A) 仅在象限Ⅰ. (B) 仅在象限Ⅱ. (C) 仅在象限Ⅰ,Ⅲ. (D) 仅在象限Ⅰ,Ⅳ. (E) 仅在象限Ⅱ,Ⅳ. [ E ]
Ⅱ Ⅲ i
Ⅰ
Ⅳ i
11-5取一闭合积分回路L, 使三根载流导线穿过L所围成的面.
现改变三根导线之间的相互间隔, 但不越出积分回路, 则[B (A) 回路L内的I不变, L上各点的B不变 ]
第11章-作业及习题参考答案

第11章(8分)将下面程序划分为基本块,并画出其基本块程序流图。
(1) if a<b goto (3)(2) halt(3) if c<d goto (5)(4) goto (8)(5) t1:=y+z(6) x :=t1(7) goto (1)(8) t2:=y-z(9) x :=t2(10) goto (1)11.1答:所谓代码优化即对代码进行等价变换,使得变换后的代码与变换前代码运行结果相同,而运行速度加快或占用存储空间少,或两者兼有。
进行优化的基础是中间或目标代码生成,以及基本块的识别、控制流分析和数据流分析。
2答:根据不同的阶段,分为中间代码优化和目标代码的优化。
根据优化所涉及的程序范围,又可分为局部优化、循环优化和全局优化。
3答:最常用的代码优化技术有:(1)删除多余运算(2)代码外提(3)强度削弱(4)变换循环控制条件(5)合并已知量和复写传播(6)删除无用赋值4 图11.23是图11.22的C代码的部分四元式代码序列(1) 请将图11.23的四元式代码序列划分为基本块并做出其流图?(2) 将每个基本块的公共子表达式删除?(3) 找出流图中的循环,将循环不变量计算移出循环外?(4) 找出每个循环中的归纳变量,并且在可能的地方删除它们图11.22void quicksort(m,n)int m,n;1 / 10{ int i,j;int v,x; if (n<=m) return;/* fragment begins here */ i = m-1;j = n;v = a[n];while(1) {do i = i+1;while (a[i]<v);do j = j-1; while (a[j]>v);if (i>=j) break;x = a[i];a[i] = a[j];a[j] = x;}x = a[i];a[i] = a[n];a[n] = x;/* fragment ends here */ quicksort (m,j);quicksort(i+1,n);}图11.23(1) i:=m-1(2)j:=n(3) t1:=4*n(4) v:=a[t1](5) i:=i+1(6) t2:=4*i(7) t3:=a[t2](8) if t3< v goto (5)(9) j:=j-1(10)t4:=4*j(11)t5:=a[t4](12)if t5> v goto (9)(13)if i >= j goto (23)(14)t6:=4*i(15)x:=a[t6] (16) t7:=4*i(17) t8:=4*j(18) t9:=a[t8](19) a[t7]:=t9(20) t10:=4*j(21) a[t10]:=x(22) goto (5)(23) t11:=4*i(24) x:=a[t11](25) t12:=4*i(26) t13:=4*n(27) t14:=a[t13](28) a[t12]:=t14(29) t15:=4*n(30) a[t15]:=x答:(1)1-4为第1块,5-8为第2块,9-12为第3块,13句为第4块,14-22为第5块,23-30句为第6块。
MBA公司理财第11章和12章作业
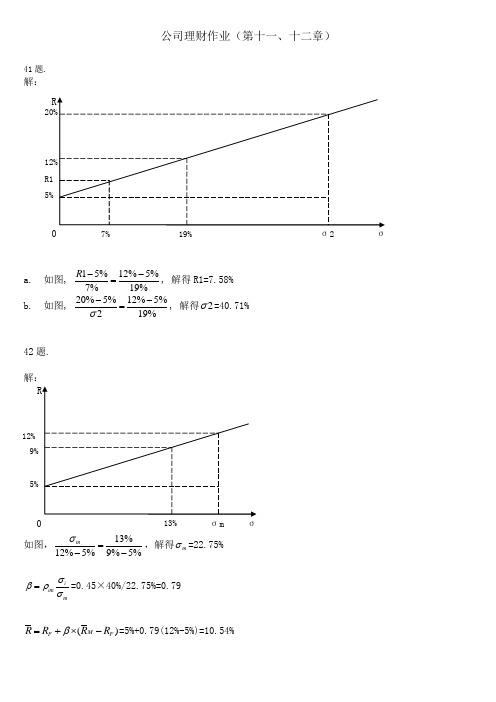
公司理财作业(第十一、十二章)41题.解:a. 如图,15%12%5%7%19%R --=, 解得R1=7.58% b. 如图, 20%5%12%5%219%σ--=, 解得2σ=40.71%42题. 解:如图,13%12%5%9%5%mσ=--,解得m σ=22.75%iimmσβρσ==0.45×40%/22.75%=0.79 ()M F F R R R R β=+⨯-=5%+0.79(12%-5%)=10.54%19%7%2 σ13%12%σm 011()M F F R R R R β=+⨯-,即32.25%=4%+β1×7.5%,解得β1=3.77 同理15.3%=4%+β2×7.5%,解得β2=1.51由于标准差1<标准差2,可得股票1的总风险<股票2的总风险 由于β1>β2,可得股票1的系统风险>股票2的系统风险 而由于总风险=系统风险+非系统风险 因此股票1的非系统风险<股票2的非系统风险由于股票1的期望收益大于股票2的期望收益,也就是相对无风险利率的风险溢价更大,因此股票1的风险更大。
47题.b.()M F F R R R R β=+⨯-15.1%=()MF A F R R R β+⨯-=F A R β+⨯风险溢价 ① 13.4%=(0.25)F A R β+-⨯风险溢价 ②联立以上两个式子,①-② 解得,风险溢价=0.068AA Ammσβρσ==0.8×14.1%/18%=0.627 BB Bmmσβρσ==0.25×34%/18%=0.472 因为股票B 的期望收益13%>股票A 的期望收益8.8%,而系统性风险B A ββ< 因此投资者更喜欢股票B b.0.7,0.3,14.1%,34%,0.48A B A B AB σσρX =X ====组合期望收益= p A B A B R R R =X +X =70%×8.8%+30%×13%=10.06%组合的标准差=P σ==c.组合贝塔系数=p A A B B βββ=X +X =70%×0.627+30%×0.472=0.58第十二章: 18题.根据单只股票收益的方差:222211()()()()(1)i i i i i Var R Var F Var Var F N Nεεεβεβσρσ=+=++- 1()i Var R =22()i i Var F εεβρσ+可得投资组合收益的方差:22()()(,)()(,)P i j i j i j Var R Var F Cov Var F εεβεεβσσρεε=+=+10%F σ=,()Var F =(10%)2=0.01a.1122(,)(,)i j i j ρεερεε==0,1β=1.5,2β=0.5,112220%i j i j εεεεσσσσ====2111()()()i i Var R Var F Var βε=+2111111()()(,)P i j i j Var R Var F εεβσσρεε=+221.50.01(20%)0=⨯+⨯= 0.0225同理,2222222()()(,)P i j i j Var R Var F εεβσσρεε=+220.50.01(20%)0=⨯+⨯= 0.0025因为两个市场的总体期望收益相同(同为10%),而12()()P P Var R Var R >,也就是第二个市场的投资组合风险更小,而因此选择投资风险更小的第二个市场。
九年级物理第十一章第三节作业

九年级物理第十一章第三节作业班级姓名1.物体有吸引的___ ___性质,就说该物体带了电。
2.自然界只存在______种电荷,用毛皮摩擦过的橡胶棒带的是______电,与另一个带负电的物体将相互______。
3.验电器带电时,两金属箔片张开的原因是______。
4.有A、B两个带电体,若A与B能相互吸引,而A又能与带正电物体C相吸,那么B一定是带______电,B与C一定能相互______。
5.下面说法正确的是 [ ]A.能够吸引轻小物体,是带电体具有的一种性质B.与橡胶棒摩擦过的毛皮带负电C.正电荷一定比负电荷的电量多D.要使物体带电,只有用摩擦的方法6.一个物体接触带正电的验电器的金属球时,若验电器的金属箔先合拢后又逐渐张开,则可判断,该物体是[ ] A.带负电 B.带正电 C.不带电 D.带正、负电都可能7、判断a.绝对不能导电的物体叫绝缘体。
()b.绝缘体不导电的原因是绝缘体内部没有电荷。
()c.绝缘体不容易导电是因为绝缘体内部正、负电荷束缚得很紧,一般情况下不能分离。
()d.半导体导电性能随外界条件变化而明显变化。
()e.人体是导体,所以在日常生活中要防止触电。
()1.原子的中心是______,带______电,核外有绕核运动的______,带______电。
在通常情况下,原子对外呈____。
2.摩擦起电并不是创造了电,只是______从一个物体上移到了另一个物体上。
3.1C电量等于______个电子所带的电量。
4.用毛皮摩擦橡胶棒,橡胶棒带负电,这时是电子从______转移到了______上。
5.两个带等量异种电荷的物体互相接触,这两个物体都没有多余的______,也不缺少______,这种现象叫做______。
6.用丝绸摩擦过的玻璃棒接触一只原来不带电的验电器,金属箔张开,在这过程中 [ ]A.玻璃棒上的质子转移到金属箔上B.玻璃棒上的电子转移到金属箔上C.金属箔上的质子转移到玻璃棒上D.金属箔上的电子转移到玻璃棒上7.把两个原来都不带电的绝缘物体相互摩擦,可能出现的情况是 [ ]A.两个物体带等量的正电荷B.两个物体带等量的负电荷C.一个带电,另一个不带电D.两个物体带等量的异种电荷8.铜棒、油、干燥的木条、塑料棒、人体、大地、碳棒、干燥空气中属导体的有______,属绝缘体的有______。
仪器分析作业第十一章(16)

专业:生物工程姓名:潘红波学号:1025004350 1、何谓瑞利散射、拉曼散射、斯托克斯散射、反斯托克斯散射?答:瑞利散射:散射光的频率与入射光相同的散射现象。
拉曼散射:光通过介质时由于入射光与分子运动相互作用而引起的频率发生变化的散射。
斯托克斯散射:处于振动基态的分子,被入射光激发到虚拟态,然后回到振动激发态,产生能量为h(v0-v1)拉曼散射。
这种散射光的能量比入射光的能量低此过程称为斯托克斯散射。
反斯托克斯散射:处于振动激发态的分子,被入射光激发到虚拟态后跃迁会振动基态,产生能量为h(v0+v1)的拉曼散射,称为反斯托克斯散射。
2、何为拉曼位移,它的物理意义是什么?答:拉曼位移是以激发光波数作为零并处于图的最右边且略去反斯托克斯线的谱带。
它表示散射光与入射光频率的差值。
3、何谓共振拉曼效应,它有哪些特点?答:激发光等于或接近于待测分子中生色团的电子吸收频率时,入射激光与生色基团的电子耦合而处于共振状态,即产生共振拉曼效应。
特点:灵敏度高,选择性高,可以判别细菌等物种属性和体内研究活细胞的膜组成和物种代谢。
5、激光为什么是拉曼光谱的理想光源?答:(1)激光亮度极强,可得到较强的拉曼射线。
(2)激光的单色性极好,有利于得到高质量的拉曼光谱图。
(3)激光的准直性可使激光束汇聚到试样的微小部位以得到该部位的拉曼信息。
(4)激光几乎完全是线偏振光,简化了去偏振度的测量。
7、为什么提到拉曼光谱时,总要联想到红外光谱?答:因为拉曼光谱与红外光谱同源与分子振动光谱。
但拉曼光谱是散射光谱,拉曼活性取决于振动中极化率是否变化。
红外光谱是吸收光谱,只有产生偶极距变化的振动才是红外活性的。
8、为什么讲拉曼光谱能提供较多的分子结构信息?答:对于一定基团,其拉曼频率的变化反映了与基团相连的分子其余部分和结构。
拉曼光谱具有较宽的测定范围,且可从同一仪器,同一试样室中测得,可在较短的时间内获得更多的信息。
第11章作业题

11-8 在双缝干涉实验中,两缝间距为0.30 mm ,用单色光垂直照射双缝,在离缝1.20m 的屏上测得中央明纹一侧第5条暗纹与另一侧第5条暗纹间的距离为22.78 mm .问所用光的波长为多少,是什么颜色的光?分析与解 在双缝干涉中,屏上暗纹位置由()212λ+'=k d d x 决定,式中d ′为双缝到屏的距离,d 为双缝间距.所谓第5 条暗纹是指对应k =4 的那一级暗纹.由于条纹对称,该暗纹到中央明纹中心的距离mm 27822.=x ,那么由暗纹公式即可求得波长λ.此外,因双缝干涉是等间距的,故也可用条纹间距公式λdd x '=∆求入射光波长.应注意两个第5 条暗纹之间所包含的相邻条纹间隔数为9(不是10,为什么?),故mm 97822.=∆x 。
解1 屏上暗纹的位置()212λ+'=k d d x ,把m 102782243-⨯==.,x k 以及d 、d ′值代入,可得λ=632.8 nm ,为红光.解2 屏上相邻暗纹(或明纹)间距'd x dλ∆=,把322.7810m 9x -∆=⨯,以及d 、d ′值代入,可得λ=632.8 nm .11-9 在双缝干涉实验中,用波长λ=546.1 nm 的单色光照射,双缝与屏的距离d ′=300mm .测得中央明纹两侧的两个第五级明条纹的间距为12.2mm ,求双缝间的距离.分析 双缝干涉在屏上形成的条纹是上下对称且等间隔的.如果设两明纹间隔为Δx ,则由中央明纹两侧第五级明纹间距x 5 -x -5 =10Δx 可求出Δx .再由公式Δx =d ′λ/d 即可求出双缝间距d .解 根据分析:Δx =(x 5 -x -5)/10 =1.22×10-3 m双缝间距: d =d ′λ/Δx =1.34 ×10-4 m11-10 一个微波发射器置于岸上,离水面高度为d ,对岸在离水面h 高度处放置一接收器,水面宽度为D ,且,D d D h ,如图所示.发射器向对面发射波长为λ的微波,且λ>d ,求接收器测到极大值时,至少离地多高?分析 由发射器直接发射的微波与经水面反射后的微波相遇可互相干涉,这种干涉与劳埃德镜实验完全相同.形成的干涉结果与缝距为2d ,缝屏间距为D 的双缝干涉相似,如图(b )所示,但要注意的是和劳埃德镜实验一样,由于从水面上反射的光存在半波损失,使得两束光在屏上相遇产生的光程差为2/sin 2λθd +,而不是θd sin 2.题11-10 图解 由分析可知,接收到的信号为极大值时,应满足(),...2,12/sin 2==+k λk λθd()d k D D D h 412sin tan /-=≈≈λθθ取k =1 时,得d D h 4min /λ=.11-11 如图所示,由光源S 发出的λ=600 nm 的单色光,自空气射入折射率n =1.23的一层透明物质,再射入空气.若透明物质的厚度为d =1.0 cm ,入射角θ =30°,且SA =BC =5.0cm ,求:(1) 折射角θ1 为多少? (2) 此单色光在这层透明物质里的频率、速度和波长各为多少? (3) S 到C 的几何路程为多少?光程又为多少?解 (1) 由折射定律n =1sin sin θθ可得 o o 124231sin30arcsin sin arcsin =⎪⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=.n θθ (2) 单色光在透明介质中的速度v n ,波长λn 和频率ν 分别为Hz 100.5nm 488m 1088.4s m 1044.214718⨯===⨯==⋅⨯==--n c nλλnc n n v v (3) S 到C 的几何路程为m 1110cos 1.=++=++=BC d SA BC AB SA SC θ S 到C 的光程为m 114011.=⨯+⨯+⨯=∑BC n AB SA D n ii题11-11 图11-12 一双缝装置的一个缝被折射率为1.40的薄玻璃片所遮盖,另一个缝被折射率为1.70 的薄玻璃片所遮盖.在玻璃片插入以后,屏上原来中央极大的所在点,现变为第五级明纹.假定λ=480nm ,且两玻璃片厚度均为d ,求d 值.题11-12图分析 本题是干涉现象在工程测量中的一个具体应用,它可以用来测量透明介质薄片的微小厚度或折射率.在不加介质片之前,两相干光均在空气中传播,它们到达屏上任一点P 的光程差由其几何路程差决定,对于点O ,光程差Δ=0,故点O 处为中央明纹,其余条纹相对点O 对称分布.而在插入介质片后,虽然两相干光在两介质薄片中的几何路程相同,但光程却不同,对于点O ,Δ≠0,故点O 不再是中央明纹,整个条纹发生平移.这时,干涉条纹空间分布的变化完全取决于光程差的变化.因此,对于屏上某点P (明纹或暗纹位置),只要计算出插入介质片前后光程差的变化,即可知道其干涉条纹的变化情况.插入介质前的光程差Δ1 =r 1 -r 2 =k 1 λ(对应k 1 级明纹),插入介质后的光程差Δ2 =[(n 1-1)d +r 1 ]-[(n 2 -1)d +r 2 ]=k 2 λ(对应k 2 级明纹).光程差的变化量为Δ2 -Δ1 =(n 2 -n 1 )d =(k 2 -k 1 )λ式中(k 2 -k 1 )可以理解为移过点P 的条纹数(本题为5).因此,对于这类问题,求解光程差的变化量是解题的关键.解 由上述分析可知,两介质片插入前后,对于原中央明纹所在点O ,有()λ51212=-=∆-∆d n n将有关数据代入可得μm 08512.=-=n n d λ 11-13 白光垂直照射到空气中一厚度为380 nm 的肥皂膜上.设肥皂的折射率为1.32.试问该膜的正面呈现什么颜色? 背面呈现什么颜色?分析 这是薄膜干涉问题,求正面呈现的颜色就是在反射光中求因干涉增强光的波长(在可见光范围),求背面呈现的颜色就是在透射光中求干涉增强(即反射减弱)光的波长.解 根据分析对反射光加强,有(),...,/2122==+k k ne λλ()124-=k ne /λ在可见光范围,k =2 时,nm 8668.=λ(红光)k =3 时,nm 3401.=λ(紫光)故正面呈红紫色.同理,对透射光加强,有2ne =kλ (k =1,2,…)在可见光范围仅有k =2 时,λ=501.6 nm (绿光).即背面呈绿色.11-14 在折射率n 3 =1.52 的照相机镜头表面涂有一层折射率n 2 =1.38的MgF 2 增透膜,若此膜仅适用于波长λ=550nm 的光,则此膜的最小厚度为多少?分析 在薄膜干涉中,膜的材料及厚度都将对两反射光(或两透射光)的光程差产生影响,从而可使某些波长的光在反射(或透射)中得到加强或减弱,这种选择性使薄膜干涉在工程技术上有很多应用.本题所述的增透膜,就是希望波长λ=550nm 的光在透射中得到加强,从而得到所希望的照相效果(因感光底片对此波长附近的光最为敏感).具体求解时应注意在d >0的前提下,k 取最小的允许值.解1 因干涉的互补性,波长为550nm 的光在透射中得到加强,则在反射中一定减弱,两反射光的光程差Δ2 =2n 2 d ,由干涉相消条件()2122λ+=∆k ,得()2412n k d λ+=取k =0,则d min =99.6nm . 解2 由于空气的折射率n 1 =1,且有n 1 <n 2 <n 3 ,则对透射光而言,两相干光的光程差2221λ+=∆d n ,由干涉加强条件Δ1 =kλ,得()2412n k d λ+=取k =1,则膜的最小厚度d min =99.6nm .11-15 利用空气劈尖测细丝直径.如图所示,已知λ=589.3 nm ,L =2.888 ×10-2m ,测得30 条条纹的总宽度为4.259 ×10-3 m ,求细丝直径d .分析 在应用劈尖干涉公式L nb d 2λ= 时,应注意相邻条纹的间距b 是N 条条纹的宽度Δx 除以(N -1).对空气劈尖n =1.解 由分析知,相邻条纹间距1-∆=N x b ,则细丝直径为 ()m 107552125-⨯=∆-==.xn N L nb d λλ题11-15 图11-17 如图(a )所示,将符合标准的轴承钢珠a 、b 和待测钢珠c 一起放在两块平板玻璃之间,若垂直入射光的波长λ=580 nm ,问钢珠c 的直径比标准小多少? 如果距离d 不同,对检测结果有何影响?分析 很显然,如钢珠c 与标准件a 、b 相同,则呈现厚度相同的薄膜干涉;如钢珠与标准件不同,则为劈尖干涉.后者有等厚干涉条纹出现,a 与c 之间的条纹分布如图(b )所示.由于相邻条纹的厚度差Δd =λ/2n .而空气的折射率n ≈1,则两钢珠之间的直径差2λN x =∆,式中N 为a 与c 之间的条纹间隔数目(注:条纹数目较多时,也可用条纹数目作近似计算),由图(a )知N 约为416. 改变钢珠间的距离d ,将钢珠c 移至c′处,如图(c )所示,a 与c′之间条纹数并未改变,但由于相邻条纹间距变小,从而影响观测.题11-17 图解 钢珠c 和a 、b 的直径不同,则两平板玻璃形成空气劈.由分析得,钢珠c 的直径与标准件直径相差m 1081126-⨯==∆.λN x当距离d 稍微改变时,a 、b 与c 之间条纹数目未变,故不影响检验结果.11-18 折射率为1.60 的两块标准平面玻璃板之间形成一个劈形膜(劈尖角θ 很小).用波长λ=600nm 的单色光垂直入射,产生等厚干涉条纹.假如在劈形膜内充满n =1.40 的液体时的相邻明纹间距比劈形膜内是空气时的间距缩小Δl =0.5 mm ,那么劈尖角θ 应是多少?分析 劈尖干涉中相邻条纹的间距l ≈λ/2nθ,其中θ 为劈尖角,n 是劈尖内介质折射率.由于前后两次劈形膜内介质不同,因而l 不同.则利用l ≈λ/2nθ和题给条件可求出θ.解 劈形膜内为空气时,θλ2/=空l劈形膜内为液体时,θλn l 2/=液则由θλθλn l l l 2//-=-=∆液空,得()rad 107112114-⨯=∆-=./l n λθ11-21 在牛顿环实验中,当透镜与玻璃之间充以某种液体时,第10 个亮环的直径由1.40×10-2 m 变为1.27 ×10-2 m ,试求这种液体的折射率.分析 当透镜与平板玻璃间充满某种液体(n 2 >1),且满足n 1 >n 2 ,n 2 <n 3或n 1 <n 2 ,n 2 >n 3 时,在厚度为d 的地方,两相干光的光程差为222λ+=∆d n .由此可推导出牛顿环暗环半径2n kR r λ=和明环半径221n R k r λ⎪⎭⎫ ⎝⎛-=,这里明、暗环半径和充入的介质折射率n 2 有关.有兴趣的读者可自行推导.必须指出,在牛顿环中,若介质不均匀或分析的是透射光而不是反射光,那么关于暗环、明环半径的公式与教材中的公式是不同的,不能随意套用.解 当透镜与玻璃之间为空气时,k 级明纹的直径为λR k r d k k ⎪⎭⎫ ⎝⎛-==2122 当透镜与玻璃之间为液体时,k 级明纹的直径为22122λR k r d k k ⎪⎭⎫ ⎝⎛-='=' 解上述两式得22122.=⎪⎪⎭⎫ ⎝⎛'=k k d d n11-23 把折射率n =1.40 的薄膜放入迈克耳孙干涉仪的一臂,如果由此产生了7.0 条条纹的移动,求膜厚.设入射光的波长为589 nm .分析 迈克耳孙干涉仪中的干涉现象可以等效为薄膜干涉(两平面镜相互垂直)和劈尖干涉(两平面镜不垂直)两种情况,本题属于后一种情况.在干涉仪一臂中插入介质片后,两束相干光的光程差改变了,相当于在观察者视野内的空气劈尖的厚度改变了,从而引起干涉条纹的移动.解 插入厚度为d 的介质片后,两相干光光程差的改变量为2(n -1)d ,从而引起N 条条纹的移动,根据劈尖干涉加强的条件,有2(n -1)d =Nλ,得d = Nλ()m 101545126-⨯=-=.n N d λ 11-24 如图所示,狭缝的宽度b =0.60 mm ,透镜焦距f =0.40m ,有一与狭缝平行的屏放置在透镜焦平面处.若以单色平行光垂直照射狭缝,则在屏上离点O 为x =1.4 mm 处的点P ,看到的是衍射明条纹.试求:(1) 该入射光的波长;(2) 点P 条纹的级数;(3) 从点P 看来对该光波而言,狭缝处的波阵面可作半波带的数目.分析 单缝衍射中的明纹条件为()212sin λϕ+±=k b ,在观察点P 确定(即φ确定)后,由于k 只能取整数值,故满足上式的λ只可取若干不连续的值,对照可见光的波长范围可确定入射光波长的取值.此外,如点P 处的明纹级次为k ,则狭缝处的波阵面可以划分的半波带数目为(2k +1),它们都与观察点P 有关,φ越大,可以划分的半波带数目也越大.解 (1) 透镜到屏的距离为d ,由于d >>b ,对点P 而言,有dx ≈ϕsin .根据单缝衍射明纹条件()212sin λϕ+=k b ,有()212λ+=k d bx 将b 、d (d ≈f )、x 的值代入,并考虑可见光波长的上、下限值,有272nm 760754nm 400max max max min .,.,====k k 时时λλ 因k 只能取整数值,故在可见光范围内只允许有k =4 和k =3,它们所对应的入 射光波长分别为λ2 =466.7 nm 和λ1 =600 nm .(2) 点P 的条纹级次随入射光波长而异,当λ1 =600 nm 时,k =3;当λ2 =466.7 nm 时,k =4.(3) 当λ1 =600 nm 时,k =3,半波带数目为(2k +1) =7;当λ2 =466.7 nm 时,k =4,半波带数目为9.题11-24 图11-25 单缝的宽度b =0.40 mm ,以波长λ=589 nm 的单色光垂直照射,设透镜的焦距f =1.0 m .求:(1) 第一级暗纹距中心的距离;(2) 第二级明纹距中心的距离;*(3) 如单色光以入射角i =30°斜射到单缝上,则上述结果有何变动.题11-25图分析 对于问题(3)单色光倾斜入射单缝的情况,在入射光到达单缝时,其上下两列边界光线之间已存在光程差i b sin (若为光栅,则为i d sin ),对应等光程的中央主极大将移至点O ′(此时φ=i =30°),屏上衍射条纹原有的对称性受到一定的破坏.如图所示,对于点O ′上方的条纹(此时入射光与衍射光位于法线两侧,且φ>i ),满足()()()()⎩⎨⎧-+-=-暗条纹明条纹212sin sin λλϕk k i b / 如令1sin =ϕ,可求得最大条纹级次k m1 .对于点O 下方的条纹(此时入射光与衍射光位于法线同侧),满足()()()()⎩⎨⎧+=+暗条纹明条纹212sin sin λλϕk k i b / 如令1sin =ϕ,可求得另一侧的最大条纹级次k m2 .对于点O ′与O 之间的条纹(此时入射光与衍射光位于法线两侧,但φ<i ),满足()()()()⎩⎨⎧+=-暗条纹明条纹212sin sin λλϕk k i b / 需要说明的是,点O ′与O 之间的条纹与点O 下方的条纹属于中央主极大同一侧的各级条纹,不同的是前者k 值较小,后者k 值较大,且k 值在点O 附近连续变化.解 (1) 由单缝衍射的暗纹条件λϕk b =1sin ,得bk λϕϕ=≈11sin ,则第一级(k =1)暗纹距中心的距离为 m 101.47tan -3111⨯=≈=ϕϕf f x(2) 由明纹条件()212sin 2λϕ+=k b ,得()b k 212sin 22λϕϕ+=≈,则第二级(k =2)明纹距中心的距离为 m 10683tan -3222⨯=≈=.ϕϕf f x在上述计算中,由于k 取值较小,即φ较小,故ϕϕϕtan sin ≈≈.如k 取值较大,则应严格计算.*(3) 斜入射时,中央主极大移至点O ′,先计算点O ′上方条纹的位置:对于第 一级暗纹,有()50sin sin sin3011o .+='-='-b b λϕλϕ,,该暗纹距中心的距离m 580050arcsin tan tan 11..=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+='='b f f x λϕ 对于第二级明纹,有()5025sin 25sin sin3022o .+='-='-bb λϕλϕ,,该明纹距中心的距离 m 58305025arcsin tan tan 22..=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+='='b f f x λϕ 再计算O ′点下方条纹的位置(由于所求k 值较小,其条纹应在O ′与O 之间):对于第一级暗纹,有()λϕλϕb b -=''=''-50sin sin sin3011o .,,该暗纹距中心的距离m 57550arcsin tan tan 11=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=''=''b f f x λϕ. 对于第二级明纹,有()bb 2550sin 25sin sin3022o λϕλϕ-=''=''-.,,该明纹距中心的距离 m 57205025arcsin tan tan 22..=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+=''=''b f f x λϕ 讨论 斜入射时,中央主极大移至点O ′(此时φ=i =30°),它距中心点O 的距离为m 5770tan30o 0.==f x ,由上述计算数据可知,此时衍射条纹不但相对点O 不对称,而且相对中央主极大的点O ′也不再严格对称了.11-26 一单色平行光垂直照射于一单缝,若其第三条明纹位置正好和波长为600 nm 的单色光垂直入射时的第二级明纹的位置一样,求前一种单色光的波长.分析 采用比较法来确定波长.对应于同一观察点,两次衍射的光程差相同,由于衍射明纹条件()212sin λϕ+=k b ,故有()()22111212λλ+=+k k ,在两明纹级次和其中一种波长已知的情况下,即可求出另一种未知波长.解 根据分析,将32nm 600122===k k ,,λ代入(()()22111212λλ+=+k k ,得()nm 642812121221.=++=k k λλ 11-28 迎面而来的一辆汽车的两车头灯相距为1.0 m ,问在汽车离人多远时,它们刚能为人眼所分辨? 设瞳孔直径为3.0 m m ,光在空气中的波长λ=500 nm .分析 两物体能否被分辨,取决于两物对光学仪器通光孔(包括人眼)的张角θ 和光学仪器的最小分辨角θ0 的关系.当θ≥θ0 时能分辨,其中θ=θ0 为恰能分辨.在本题中D λθ2210.=为一定值,而dl ≈θ,式中l 为两灯间距,d 为人与车之间的距离.d 越大或l 越小,θ 就越小,当θ <θ0 时两灯就不能被分辨,这与我们的生活经验相符合.解 当θ =θ0时, Dd l λ221.=,此时,人与车之间的距离为 m 4918221==λ.Dl d11-30 一束平行光垂直入射到某个光栅上,该光束中包含有两种波长的光:λ1 =440 nm 和λ2 =660 nm .实验发现,两种波长的谱线(不计中央明纹)第二次重合于衍射角φ=60°的方向上,求此光栅的光栅常数.分析 根据光栅衍射方程λϕk d ±=sin ,两种不同波长的谱线,除k =0 中央明纹外,同级明纹在屏上位置是不同的,如果重合,应是它们对应不同级次的明纹在相同衍射角方向上重合.故由d sin φ=k λ1 =k ′λ2 可求解本题.解 由分析可知 21sin λλϕk k d '==得 2312///=='λλk k上式表明第一次重合是λ1 的第3 级明纹与λ2 的第2级明纹重合,第二次重合是λ1 的第6 级明纹与λ2 的第4级明纹重合.此时,k =6,k ′=4,φ=60°,则光栅常数μm 053m 10053/sin 61..=⨯==-ϕλk d11-31 用一个1.0mm 内有500 条刻痕的平面透射光栅观察钠光谱(λ=589nm ),设透镜焦距f =1.00 m .问:(1) 光线垂直入射时,最多能看到第几级光谱;*(2) 光线以入射角30°入射时,最多能看到第几级光谱;(3) 若用白光垂直照射光栅,求第一级光谱的线宽度. 分析 (1) 首先确定光栅常数m 103Nd -=,式中N 为刻痕数,然后由光线垂直照射光栅时的衍射条件,即可解得结果.(2) 如同光线倾斜入射单缝一样, 此时光栅衍射的明纹条件改变为()λϕk i d ±=±sin sin (详见题11-25 的分析),由于两侧条纹不再对称,令1sin =ϕ,可求得k m1 和k m2 两个值,其中一个比垂直入射时的k m 值小,另一个比k m 值大,因而,在其他条件不变的情况下,倾斜入射时可以观察到较高级次的条纹.(3) 用白光照射光栅,除中央明纹仍为白光外,其余处出现一系列光谱带,称为光栅光谱.每个光谱带是由同一级次不同波长的明纹依次排列而成.所谓第一级光谱的线宽度是指入射光中最小波长(取nm 400min =λ)和最大波长(取nm 760max =λ)的第一级明纹在屏上的间距,其余波长的第一级明纹均出现在此范围内.需要指出的是,对于较高级次的光谱会出现相邻光谱间的交错重叠的现象.解 (1) 光波垂直入射时, 光栅衍射明纹的条件为λϕk d ±=sin ,令1sin =ϕ,可得393m .±=±=λdk取整数k m =3,即最多能看到第3级光谱.(2) 倾斜入射时,光栅明纹的条件为()λϕk i d ±=±sin sin令1sin =ϕ,可求得位于中央主极大两侧,能观察到条纹的最大k m 值分别为k m1 =5和k m2 =1(已取整数值).故在法线两侧能观察到的最大级次分别为五级和一级.(3) 白光的波长范围为400 nm ~760 nm ,用白光垂直照射时,由λϕk d =sin 可得第一级(k =1)光谱在屏上的位置.对应于λ1 =400 nm 和λ2 =760 nm 的明纹的衍射角为d d 2211arcsin arcsin λϕλϕ==;,利用fx =ϕtan 可得明纹的位置为 m 410tan m,20tan 2211..====ϕϕf x f x则第一级光谱的线宽度为m 21012.=-=∆x x x11-32 波长为600 nm 的单色光垂直入射在一光栅上,第二级主极大出现在200sin .=ϕ处,第四级缺级.试问(1) 光栅上相邻两缝的间距是多少?(2) 光栅上狭缝的宽度有多大? (3) 在-90°<φ<90°范围内,实际呈现的全部级数.分析 (1) 利用光栅方程()λϕϕk b b d ±='+=sin sin ,即可由题给条件求出光栅常数d (即两相邻缝的间距).(2) 光栅衍射是多缝干涉的结果,也可看成是光透过许多平行的单缝衍射的结果.缺级就是按光栅方程计算屏上某些应出现明纹的位置,按各个单缝衍射计算恰是出现暗纹的位置.因此可以利用光栅方程()λϕϕk b b d ='+=sin sin 和单缝衍射暗纹公式'sin b k ϕλ=计算缝宽和屏上缺级的情况,从而求出屏上条纹总数.解 (1) 由题已知k =2 时,200sin .=ϕ,则由分析可得光栅常数:μm 6m 106sin 6=⨯==-ϕk λλd(2) 由分析知缺级条件()()()⎩⎨⎧±=''=±=='+,...,,...,10sin 10sin k k b k k b b λϕλϕ 则(b +b ′)/b =k /k ′=m ,k =m k ′,即m k ′级明纹缺级.由题意k =4 缺级,即(b +b ′)/b =4/k ′当k ′=1 时,m =4,⎩⎨⎧==μm54μm 51..b b ,即±4, ±8, ±12,…级缺级.(符合题意)当k ′=2 时,m =2,第±2, ±4, ±6,…级缺级.(第二级已存在,不符合题意,舍 去)当k ′=3 时,⎩⎨⎧===μm51μm 5434..,b b m ,第±4, ±8, ±12,…级缺级.(符合题意) 当k ′=4 时,m =1,第±1, ±2, ±3, ±4,…级全部缺级.(不符合题意,舍去) 因此,狭缝宽度b 为1.5 μm 或者4.5μm ,而缺级只发生在±4, ±8, ±12,…级.(3) 由光栅方程()λϕk b b ±='+s i n ,可知屏上呈现条纹最高级次应满足()10='+<λ/b b k ,故考虑到缺级,实际屏上呈现的级数为:0, ±1, ±2, ±3,±5, ±6, ±7, ±9,共15 条.11-33 以波长为0.11 nm 的X 射线照射岩盐晶体,实验测得X 射线与晶面夹角为11.5°时获得第一级反射极大.(1) 岩盐晶体原子平面之间的间距d 为多大? (2) 如以另一束待测X 射线照射,测得X 射线与晶面夹角为17.5°时获得第一级反射光极大,求该X 射线的波长.分析 X 射线入射到晶体上时,干涉加强条件为2d sin θ =k λ(k =0,1,2,…)式中d 为晶格常数,即晶体内原子平面之间的间距(如图).解 (1) 由布拉格公式(),...,,210sin 2==k k d λθ第一级反射极大,即k =1.因此,得 nm 2760/sin 11.==θλd(2) 同理,由2d sin θ2 =kλ2 ,取k =1,得nm 1660sin 22.=θd题11-33图11-34 测得一池静水的表面反射出来的太阳光是线偏振光,求此时太阳处在地平线的多大仰角处? (水的折射率为1.33)题11-34 图分析 设太阳光(自然光)以入射角i 入射到水面,则所求仰角i θ-=2π.当反射光起偏时,根据布儒斯特定律,有120arctann n i i ==(其中n 1 为空气的折射率,n 2 为水的折射率).解 根据以上分析,有 120arctan 2πn n θi i =-== 则 o 12936arctan 2.=-=n n πθ 11-35 使自然光通过两个偏振化方向相交60°的偏振片,透射光强为I 1 ,今在这两个偏振片之间插入另一偏振片,它的方向与前两个偏振片均成30°角,则透射光强为多少?分析 设入射自然光强为I 0 ,偏振片I 对入射的自然光起起偏作用,透射的偏振光光强恒为02I ,而偏振片Ⅱ对入射的偏振光起检偏作用,此时透射与入射的偏振光强满足马吕斯定律.若偏振片Ⅲ插入两块偏振片之间,则偏振片Ⅱ、Ⅲ均起检偏作用,故透射光强必须两次应用马吕斯定律方能求出.解 根据以上分析,入射光通过偏振片Ⅰ和Ⅱ后,透射光强为o 20160cos 21⎪⎭⎫ ⎝⎛=I I 插入偏振片Ⅲ后,其透射光强为o 2o 20230cos 30cos 21⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛=I I 两式相比可得 12252I I .=11-36 一束光是自然光和线偏振光的混合,当它通过一偏振片时,发现透射光的强度取决于偏振片的取向,其强度可以变化5 倍,求入射光中两种光的强度各占总入射光强度的几分之几.分析 偏振片的旋转,仅对入射的混合光中的线偏振光部分有影响,在偏振片旋转一周的过程中,当偏振光的振动方向平行于偏振片的偏振化方向时,透射光强最大;而相互垂直时,透射光强最小.分别计算最大透射光强I max 和最小透射光强I min ,按题意用相比的方法即能求解.解 设入射混合光强为I ,其中线偏振光强为xI ,自然光强为(1-x )I .按题意旋转偏振片,则有最大透射光强 ()I x x I ⎥⎦⎤⎢⎣⎡+-=121max 最小透射光强 ()I x I ⎥⎦⎤⎢⎣⎡-=121min 按题意5min max =I I /,则有 ()()x x x -⨯=+-1215121 解得 x =2/3即线偏振光占总入射光强的2/3,自然光占1/3.*11-37 试分别计算用方解石晶体制成的对波长为λ1 =589.3nm 的钠黄光和波长为λ2 =546.1nm 的汞灯绿光的1/4波片的最小厚度为多少?解 1/4 波片的最小厚度d 应满足40/λ=-d n n e ,而方解石晶体中o 光和e 光的折射率分别为n 0 =1.658 和n e =1.486.故对λ1 和λ2 的1/4波片的最小厚度分别为 nm,7944nm,8574022011=-==-=e e n n d n n d λλ11-19 如图所示的干涉膨胀仪,已知样品的平均高度为3.0 ×10-2m ,用λ=589.3 nm 的单色光垂直照射.当温度由17 ℃上升至30 ℃时,看到有20 条条纹移过,问样品的热膨胀系数为多少?题11-19 图分析 温度升高ΔT =T 2 -T 1 后,样品因受热膨胀,其高度l 的增加量Δl =lαΔT .由于样品表面上移,使在倾角θ 不变的情况下,样品与平板玻璃间的空气劈的整体厚度减小.根据等厚干涉原理,干涉条纹将整体向棱边平移,则原k 级条纹从a 移至a′处,如图(b )所示,移过某一固定观察点的条纹数目N 与Δl 的关系为2λNl =∆,由上述关系可得出热膨胀系数α.解 由题意知,移动的条纹数N =20,从分析可得 T l N ∆=αλ2则热膨胀系数5105112-⨯=∆=.Tl Nλα 11 -20 在利用牛顿环测未知单色光波长的实验中,当用已知波长为589.3 nm 的钠黄光垂直照射时,测得第一和第四暗环的距离为Δr =4.00 ×10-3 m ;当用波长未知的单色光垂直照射时,测得第一和第四暗环的距离为Δr ′=3.85 ×10-3 m ,求该单色光的波长.分析 牛顿环装置产生的干涉暗环半径λkR r =,其中k =0,1,2…,k =0,对应牛顿环中心的暗斑,k =1 和k =4 则对应第一和第四暗环,由它们之间的间距λR r r r =-=∆14,可知λ∝∆r ,据此可按题中的测量方法求出未知波长λ′.解 根据分析有λλ'=∆'∆r r故未知光波长 λ′=546 nm11-27 已知单缝宽度b =1.0 ×10-4 m ,透镜焦距f =0.5 m ,用λ1 =400 nm 和λ2 =760 nm 的单色平行光分别垂直照射,求这两种光的第一级明纹离屏中心的距离,以及这两条明纹之间的距离.若用每厘米刻有1000条刻线的光栅代替这个单缝,则这两种单色光的第一级明纹分别距屏中心多远? 这两条明纹之间的距离又是多少?分析 用含有两种不同波长的混合光照射单缝或光栅,每种波长可在屏上独立地产生自己的一组衍射条纹,屏上最终显示出两组衍射条纹的混合图样.因而本题可根据单缝(或光栅)衍射公式分别计算两种波长的k 级条纹的位置x 1和x 2 ,并算出其条纹间距Δx =x 2 -x 1 .通过计算可以发现,使用光栅后,条纹将远离屏中心,条纹间距也变大,这是光栅的特点之一.解 (1) 当光垂直照射单缝时,屏上第k 级明纹的位置()f b k x 212λ+=当λ1 =400 nm 和k =1 时, x 1 =3.0 ×10-3 m当λ2 =760 nm 和k =1 时, x 2 =5.7 ×10-3 m其条纹间距 Δx =x 2 -x 1 =2.7 ×10-3 m(2) 当光垂直照射光栅时,屏上第k 级明纹的位置为f dk x λ=' 而光栅常数 m 10m 1010532--==d 当λ1 =400 nm 和k =1 时, x 1 =2.0 ×10-3 m当λ2 =760 nm 和k =1 时, x 2 =3.8 ×10-3 m其条纹间距 m 1081212-⨯='-'='∆.x x x11-29 老鹰眼睛的瞳孔直径约为6 mm ,问其最多飞翔多高时可看清地面上身长为5cm 的小鼠? 设光在空气中的波长为600 nm .解 根据上题的分析:θ0 =1.22λ/D .这里D 是鹰的瞳孔直径.而θ =L /h ,其中L 为小鼠的身长, h 为老鹰飞翔的高度.恰好看清时θ =θ0, 则由L /h =1.22λ/D ,得飞翔高度:h =LD /(1.22λ) =409.8 m .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第11章作业
(1)下列指令对标志寄存器内容产生影响,但不会改变参与其执行过程的其它寄存器内容的是______。
A、loop s
B、cmp cx,0
C、jcxz s
D、div cx
(2)对于Intel8086cpu标志寄存器的说法正确的是_____。
A、cpu执行每一条指令都有可能改变标志寄存器的内容。
B、无符号数运算的进位或借位情况由cf标志位记录,有符号数运算的溢出情况由of标志位记录。
C、当前指令对标志寄存器的影响为此指令的执行提供了所需的依据,对后续指令没有任何指导作用。
D、所有的条件转移指令都要参考标志寄存器中的相关标志位。
(3)sub ax,ax
mov ax,5
add ax,-3
以上程序执行完后,CF,OF的值是_____
A、0,0
B、0,1
C、1,0
D、1,1
(4)mov ax,8 mov bx,3 cmp ax,bx
上面指令执行前ZF,PF的值是0,0,执行后ZF,PF的值是_____ 。
A、 0,1
B、0,0
C、1,0
D、1,1
(5)下面程序执行后ax的值是____。
mov ax,0
push ax
popf
mov ax,0fff0h
add ax,0010h
pushf
pop ax
and al,11000101B
and ah,00001000B
A、845H
B、8C5H
C、45H
D、C5H。
