梁坤京理论力学第十二章动量矩定理课后答案
动量矩定理
分离变量
d (Jω) = −M , M = kω dt
上式积分
J dω = −kdt ω
ωo
∫2
ω0
J
dω ω
=
∫
t 0
−
kdt
解得
t = J 1n2
k
再对式(1)积分,将等式左边积分上限改为ω ,得
ω
∫ ω0 J
dω ω
=
∫
t 0
−
kdt
解得
ω
=
ω
0
e
−k J
t
即
dθ dt
−k t
= ω0e J
∫ θ =
FT1 = FT′1
FT2 = FT′2
以顺时针转向为正,分别应用两轮对其转动轴的转动微分方程有
J1α1 = M − (FT1 − FT2 )R1
J 2α 2
=
( FT1′
−
FT
′
2
)R2
−M′
α1 : α 2 = R2 : R1
(1)
(2) (3)
159
理论力学(第七版)课后题答案 哈工大.高等教育出版社
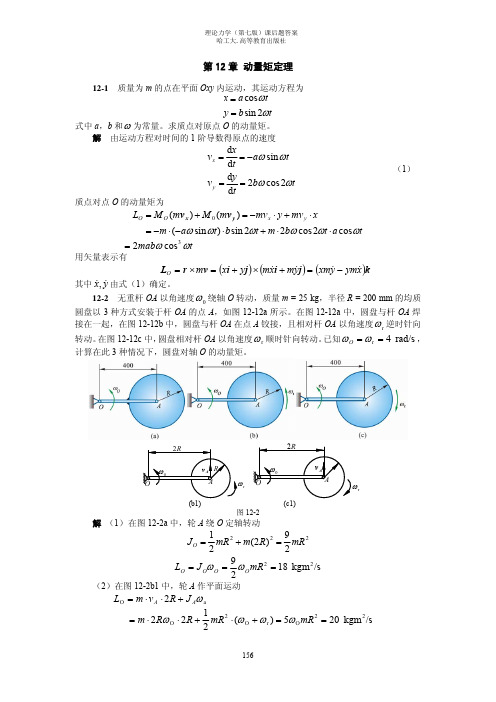
计算在此 3 种情况下,圆盘对轴 O 的动量矩。
2R
2R
ω0 O
vA R A
ω0 ωr O
vA A ωr
(b1)
(c1)
图 12-2
解 (1)在图 12-2a 中,轮 A 绕 O 定轴转动
JO
=
1 2
mR 2
+
m(2R)2
=
9 2
mR 2
LO
=
J OωO
=
9 2
ω
O
动量矩定理

J z = J zC + md 2
要求记住三个简单几何体转动惯量
mR2 (1) 均质圆盘对盘心轴的转动惯量 ) 2 (2) 均质薄圆环对中心轴的转动惯量 mR2 )
(3) 均质细直杆对一端的转动惯量 )
均质细直杆对中心轴的转动惯量
ml 2 3
ml 2 12
4.组合法
例13-5 已知杆长为 l 质量为 m,圆盘直径为 d 1 质量为 m2.
J 求: O .
解:
JO = JO杆 + JO盘
1 2 JO杆 = ml 3
1 d 2 d 2 JO盘 = m2 ( ) + m2 (l + ) 2 2 2 3 2 2 = m2 ( d + l + ld ) 8 1 2 3 2 2 JO = m l + m2 ( d + l + ld ) 1 3 8
应用时一般用投影式:
maCx = ∑Fx ( e) maCy = ∑Fy ( e) JCα = ∑MC (F )
( e)
( e) n maC = ∑F n ( e) JCα = ∑MC (F ) ma = ∑F t
t C
( e)
以上各组均称为刚体平面运动微分方程. 以上各组均称为刚体平面运动微分方程
2 r 2 + ρC M ≤ fsmg r
例12-7 均质细杆AB长2l,质量为m,B端搁在光滑水平地板上, A端靠在光滑墙壁上,A,B均在垂直于墙壁的同一铅直平面内. 初瞬时,杆与墙壁的夹角为θ0,杆由静止开始运动,求杆的角加 速度,角速度及墙壁和地面的反力,(表示为θ 的函数). 解:以杆为研究对象,其受力图如 图示,列平面运动方程
mC = F A x
12第十二章 动量矩定理

1质点系对某轴的动量矩等于质点系中各质点的动量对同一轴之矩的代数和。
( ) 2刚体的质量是刚体平动时惯性大小的度量,刚体对某轴的转动惯量则是刚体绕该轴转动时惯性大小的度量。
( ) 3刚体对某轴的回转半径等于其质心到该轴的距离。
( ) 4如果作用于质点系上的所有外力对固定点O 的主矩不为零,那么,质点系的动量矩一定不守恒。
( ) 5如果质点系所受的力对某点(或轴)的矩恒为零,则质点系对该点(或轴)的动量矩不变。
( ) 6图中所示已知两个均质圆柱,半径均为R ,质量分别为2m 和3m ,重物的质量为1m 。
重物向下运动的速度为V ,圆柱C 在斜面上只滚不滑,圆柱O 与绳子之间无引对滑动,则系统对O 轴的动量矩为vR m R m vR m H o 12232++=ω。
( )7图中已知均质圆轮的半径为R ,质量为m ,在水平面上作纯滚动,质心速度为C v,则轮子对速度瞬心I 的动量矩为R mv H c I =。
( )1已知刚体质心C 到相互平行的z z 、'轴的距离分别为b a 、,刚体的质量为m ,对z 轴的转动惯量为z J ,则'z J 的计算公式为__________________。
A .2)(b a m z z ++='J J ;B .)(22b a m z z -+='J J ; C.)(22b a m z z --='J J 。
2两匀质圆盘A 、B ,质量相等,半径相同,放在光滑水平面上,分别受到F 和'F 的作用,由静止开始运动,若'F F =,则任一瞬间两圆盘的动量相比较是_____________________。
A.B A p p >; B.B A p p <; C.B A p p =。
3在一重W 的车轮的轮轴上绕有软绳,绳的一端作用一水平力P ,已知车轮的半径为R ,轮轴的半径为r ,车轮及轮轴对中心O 的回转半径为ρ,以及车轮与地面间的滑动摩擦系数为f ,绳重和滚阻皆不计。
第12章动量矩定理

又, a (h C 2R h A ) 0.5 7783km
c VC hC 2R hA
c a ( R h A ) 973km b a 2 c 2 7722km vB R hA v A 7.14km / s b
例二. 质量为m 的小球 悬挂在一绳索下端且以匀速率在水平面内作圆周运动. 试分析小球对O, A 两点的动量矩及其守恒问题. A
解 : 卫星在轨道运行中只受 地球的
VB b C a O′ O
B
V F VA A
引力作用, 故卫星对地心 点的 O 动量矩守恒. (R h A ) v A (R hC ) vC vC 6371 439 8.1 6.3km / s 6371 2384 ( R h A ) v A v B b
r
T
m
R O
v
mg
结论: 动量矩是否守恒, 与矩心的选择有关.
§12 – 3 刚体绕定轴转动的微分方 程
对绕定轴(不妨设为z轴)转动的刚体而言 对转轴的动量矩定理可 , 写为
n d ( J z ) M z ( F i ) dt i 1
去掉微分符号即是 J z M z ( Fi )
LO r i m i V i (r C r'i ) m i V i
Vi
r
n
n
Vi
mi
i 1 n
i 1
VC VC
C
r 'i
r C m i V i LC r C m i V i LC
i 1 i 1
n
r C MV C L C
rc
M O (m v )
12动量矩定理

图12.7 钟摆
第12章 动量矩定理
12.1 转 动 惯 量
【例12.5】 匀质圆盘与匀质杆组成的钟摆如图12.7所示。已知圆盘质量m1, 直径d,杆的质量m2,长l,试求钟摆对悬挂轴O的转动惯量J0。
解:钟摆由匀质杆和匀质盘组成,所以有 = JO JO杆 + JO
其中
JO
=J c
+
m1
l
+
d 2
平方的乘积,即
12.7
J=z J zc + md 2
(12.7)
第12章 动量矩定理
12.1 转 动 惯 量
证明:如图12.5所示,设刚体总的质量为m,轴zc通过质心C,z与zc平行且 相距为d。不失一般性,可令y与yc重合,在刚体内任取一质量为mi的质点Mi,它 至zc轴和z轴的距离分别为ric和ri。刚体对于z、zc轴的转动惯量分别为
12.9
第12章 动量矩定理
12.1 转 动 惯 量
【例12.4】 质量为m,长为l的匀质杆如图12.6所示,求杆对yc的转动惯量。
解:由例12.1知
Jy
=
1 ml2 3
,根据平行轴定理式(12.7)有
J yc
=J y
−
md 2
=1 ml2 3
−
m
l
2
2
=1 12
ml 2
12.10
图12.6 匀质杆
在工程问题上,计算刚体的转动惯量时,常应用下面公式
12.3
第12章 动量矩定理
12.1 转 动 惯 量
Jz
=
mρ
2 z
(12.2)
ρ 其中m为整个刚体的质量, z 为刚体对z轴的回转半径,它具有长
理论力学(哈工大版)第十二章动量矩定理(全面版)资料

理论力学(哈工大版)第十二章动量矩定理(全面版)资料第八章 动量矩定理8-1 质点系的动量矩(待强化) 一.动量矩的概念质点对点O 的动量矩:v m r v m m O ⨯=)( 质点对轴 z 的动量矩:)()(xy O z v m m v m m = 对着轴看:顺时针为负 逆时针为正质点对点O 的动量矩与对轴z 的动量矩之间的关系:[])( )(v m m v m m z z O = kg·m2/s 。
二.质点系的动量矩 质系对点O 动量矩:i i i i i OO v m r v m mL ⨯==∑∑)(质系对轴z 动量矩:[]z Oii zz L v m m L)(==∑三.质点系的动量矩的计算c c c mv r L L ⨯+=0质点系对任意定点O 的动量矩,等于质点系对质心的动量矩,与将质点系的动量集中于质心对于O 点动量矩的矢量和。
质点系对质心的绝对运动动量矩,等于质点系对随质心平动的参考系的相对运动动量矩。
结论:在计算质点系对于质心的动量矩时,用质点相对于惯性参考系的绝对速度vi ,或用质点相对于固结在质心上的平动参考系的相对速度vi `,所得结果是一样的。
四、刚体的动量矩 1.平动刚体C C C O O v m r v m m L ⨯==)( )(C z z v m m L =2.定轴转动刚体ωZ z J L =3.平面运动刚体C C C C C O m m L v O C L v r L +⨯=+⨯= ω⋅+=C C z z J v m m L )(平面运动刚体对垂直于质量对称平面的固定轴的动量矩,等于刚体随同质心作平动时质心的动量对该轴的动量矩与绕质心轴作转动时的动量矩之和。
8-2 动量矩定理(待强化) 一.质点的动量矩定理)()]([ , )(F m v m F r v r O O m dtdm dt d =⨯=⨯ 质点对任一固定点的动量矩对时间的导数,等于作用在质点上的力对同一点之矩。
理论力学_12.动量矩定理

故:
d dt
(r m v ) r F ,
d dt
[ m O ( m v )] m O ( F )
质点对任一固定点的动量矩对时间的导数,等于作用在质 点上的力对同一点之矩。这就是质点对固定点的动量矩定理。
例3 单摆 已知m,l,t =0时= 0,从静止 开始释放。 求单摆的运动规律。 解:将小球视为质点。 受力分析;受力图如图示。
r
i
i
m iv
C
ri ) m i v
i
rC m i v i
ri m i v i
i
rC m v C
ri m i v
其中 L C ri m i v i 为质点系相对质心C的动量矩。 (注意:vi为质点的绝对速度。) 即 质点系对任意定点O的动量矩,等于质点系对质心的动量矩, 与将质点系的动量集中于质心对于O点动量矩的矢量和。
L z J z m 2 vr 1 2 ( m1r
2
J ,z
1
m1r ;
2
v r
m 2 vr
1 2
m 1 m 2 ) rv
系统所受外力对转轴z的矩为
M z ( Fi
(e)
) M
(e)
O
Fr M
O
f m 2gr
dL dt
z
M z (Fi
)
d 1 ( m m 2 ) rv M 2 1 dt
例如:试计算圆盘对轴O的 动量矩。质点的质量均为m。
O1 B C
vr vr
vr
L O L O 1 rO 1 m v O 1 3 mv r R l 3 m l 0 3m (vr R l 0 )
理论力学第12章-动量矩定理

z
M ,底圆半径为 R ,高为 h 。
r
h z dz
解:把圆锥体分成许多厚度为 d z
的薄圆片,该薄圆片的质量为
d m r2d z
O
y
R
x
为圆锥体的密度,r为薄圆片的半径。
圆锥体的质量
M 1R2h
3
薄圆片对自身直径的转动惯量
由几何关系知: r R h z
h 薄圆片对 y 轴转动惯量 d J y 为:
x
x yi
J z mi ri2
mi
xi2
yi
d
2
mi xi2 yi2 2 yid d 2
J z mi xi2 yi2 2d mi yi mi d 2
mi xi2 yi2 JzC
mid 2 Md 2
由质心坐标公式 :
因为
yC0
mi yi M yC
速度 a 。
解:小车与鼓轮组成质点系对 O 轴的动量矩为 :
LO J O m2 v R
作用于质点系的外力除M ,G 1 和 G 2 外,尚有轴承 O 的反力 Fo x 和 Fo y ,轨道对车的约束力FN 。其中G 1 , FO x ,Fo y 对 O 轴力矩为零。将 G 2 分解为 Gτ和 G n ,
(12-10)
l 为任意轴上的单位矢量。
动量矩的单位是牛·米·秒 ( N ·m ·s )。
12.2.3 定轴转动刚体的动量矩 设刚体绕固定轴 z 转动,某瞬时刚体
的角速度。对于刚体内任一质点 M i ,
其质量为 m i ,转动半径为 r i ,动量 m i v i 。 于是质点 M i 对轴的动量矩为:
LO MO mv r mv (12-8)
质点系对各坐标轴动量矩
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动量矩定理12-1 质量为m 的点在平面Oxy 内运动,其运动方程为: x a cos t y bsin2 t 式中a 、b 和 为常量。
求质点对原点 O 的动量矩。
解:由运动方程对时间的一阶导数得原点的速度V xdxsin t dt aV y dy 2b cos2 t 质点对点 O 的动量矩为L O M o (mV x ) M 0(mV y )mv x y mv y x m ( a sin t) bsin2 t m 2b cos2 t acos t 2mab cos 3 t 12-3 如图所示,质量为m 的偏心轮在水平面上作平面运动。
轮子轴心为A,质心为C, AC = e ;轮子半径为 R,对轴心A 的转动惯量为J A ; C 、A 、B 三点在同一铅直线上。
(1 )当轮子只 滚不滑时,若 V A 已知,求轮子的动量和对地面上 B 点的动量矩。
(2)当轮子又滚又滑时, 若V A 、 已知,求轮子的动量和对地面上 B 点的动量矩。
解:(1)当轮子只滚不滑时 B 点为速度瞬心。
轮子角速度V A R质心C 的速度V CBCR e轮子的动量p mv Cmv A (方向水平向右)R对B 点动量矩L B J B2 2 2由于 J B J C m (R e) J A me m (R e) 故 L B J A me 2 m (R e )2食 (2)当轮子又滚又滑时由基点法求得 C 点速度。
V C V A V CA V A e 轮子动量 p mv C m(v A e) (方向向右) 对B 点动量矩L B mv C BC J Cm(v A 2e) (R e) (J A me) mv A (R e) (J A mRe) 12-13 如图所示,有一轮子,轴的直径为 50 mm 无初速地沿倾角 20的轨道滚下,设 只滚不滑,5秒内轮心滚动的距离为 s =3m 。
试求轮子对轮心的惯性半径。
解:取轮子为研究对象,轮子受力如图( a )所示,根据刚体平面运动微分方程有 ma C mgsi n F ( 1) J C = Fr ( 2)因轮子只滚不滑,所以有 a c = r ( 3) ® 12将式(3)代入式(1)、(2)消去F 得到mr sinm?g上式对时间两次积分,并注意到 t = 0时 0, 0,则 mgrt 2 sin mgrt 2s in 2(J C mr 2) 2(m 2 mr 2) 把 r = 0.025 m 及 t = 5 s 时,s 'grt 2sin f gt 2sin-r r「s r 1grt 2sin 2( 2 r 2) r 3 m 代入上式得0.0259.8 52si n202 30.09 m 90 mm12-17 图示均质杆 AB 长为I ,放在铅直平面内,杆的一端 A 靠在光滑铅直墙上,另一端 B 放在光滑的水平地板上,并与水平面成 °角。
此后,令杆由静止状态倒下。
求(1)杆在任 意位置时的角加速度和角速度; (2)当杆脱离墙时,此杆与水平面所夹的角。
解:(1)取均质杆为研究对象,受力分析及建立坐标系 Oxy 如图(a ),杆AB 作平面运动,质心在C 点。
mx c F NA (1)my c F NB mg ⑵J c匚l 匚l • F NB 2cos F N A 2 sin(3)由于 1 l . X c cos , y c sin 2 2将其对间 t 求两次导数,且注意到 J ?刚体平面运动微分方程为 得到y c-(sin 2-(cos 22cos ) 2sin )将式 再将 J c(4 )、( 5)代入式 F NA , F N B 的表达式代入式ml 2 ( 4 ml 2(1 )、(2)中,得mlNA —( sinmlN B ~2~ ( cos3)中,得(4) (5)2cos2 .sin cos mgl 24 l 2代入上式得12 d dt分离变量并积分得)mg2・sin )cos mgl cos2止(sin4cos塑cos2IH 12 17 [?]2cos )sin{^(sin o sin )(2)当杆脱离墙时F NA = 0 ,设此时 1则 F NAml( sin 1 2cos 1) 0 22将和表达式代入上式解得sin 1—sin 0 321 arcsin(-sin 0)312-19 均质实心圆柱体 A 和薄铁环B 的质量均为 m 半径都等于r ,两者用杆 AB 铰接,无 滑动地沿斜面滚下,斜面与水平面的夹角为 ,如图所示如杆的质量忽略不计,求杆 AB 的(2)若在圆柱体 A 上作用一逆时针转向,矩为 M 的力偶,试问在什么条件下圆柱体 B 的质a )、(b )所示,A 和B 均作平 面运动,杆AB 作平动,由题意知AB,a A a Ba, F TF T。
对圆柱A 有ma mgsi n F T F 1(1) Rr J A(2)对薄铁环B 有ma T mgsi nF 2⑶F 2r J B(4)滚不滑条件得到的 a = r 代入,解得(4),并将 J A mr 2, J2 1 . F T F Tmg sin 2mr , F T F T ,以及根据只4(压力)及 a gsin712-21 图示均质圆柱体的质量为 m 半径为r ,放在倾角为60的斜面上。
一细绳缠绕在圆 柱体上,其一端固定于点 A ,此绳与A 相连部分与斜面平行。
若圆柱体与斜面间的摩擦系数1为f,试求其中心沿斜面落下的加速度as3解:取均质圆柱为研究对象,其受力如图( a )所示,圆柱作平面运动,则其平面运动微分方程为J (F T F )r (1) 0 F N mgcos60(2)ma C mgs in 60 F T F (3)而F = fF N( 4)圆柱沿斜面向下滑动,可看作沿AD 绳向下滚动,且只滚不滑, 所以有 a c = r1把上式及f —代入式(3)、(4)解方程(1)至(4),得3a =(方向沿斜面向下)12-23 均质圆柱体 A 和B 的质量均为 m 半径为r ,一绳缠在绕固定轴 O 转动的圆柱A 上, 绳的另一端绕在圆柱 B 上,如图所示。
摩擦不计。
求: (1)圆柱体B 下落时质心的加速度; 加速度和杆的内力。
解:分别取圆柱 A 和薄铁环B 为研究对象,其受力分析如图( 联立求解式( 1)、 (2)、 (3)、US 12証圉心加速度将向上。
解:(1 )分别取轮A 和B 研究,其受力如图(a )、(b )所示,轮A 定轴转动,轮B 作平面运 动。
对轮A 运用刚体绕定轴转动微分方程J A A F T r( 1)对轮B 运用刚体平面运动微分方程有mg F T ma B ⑵J B BF T r(3)再以C 为基点分析B 点加速度,有a B a C a BCA rB r( 4)联立求解式(1)、( 2)、( 3 )、( 4),并将M 2mgr故当转矩M 2mgr 时轮B 的质心将上升。
B 固定。
圆柱体沿绳子解开的而降落, 其初速为零。
求当圆柱体的轴降落了高度 h 时圆柱体中心A 的速度力F T 。
解:法1 :图(a )ma A mg F T (1) 」a F T 「 (2)a Ar a (3)J A 1 2 mr 2解得 F T 1 3 mg (拉)a A ■|g (常量)3 (4)由运动学 V A , 2a A h 3 .3gh (J)法2:由于动瞬心与轮的质心距离保持不变,故可对瞬心 量矩定理:J C mgr (5)J C . 2彳2 J A mr mr2又 a A ra A Z 3g (同式(4))再由 ma A mg F T9-8图示圆柱体A 的质量为m 在其中部绕以细绳, 绳的一端 u 和绳子的拉C 用动(a)F TF T 及 J B JA 予2代入,解得4 a B -g52 )若在A 轮上作用一逆时针转矩 动微分方程有J A以C 点为基点分析 M 则轮A 将作逆时针转动,对 A 运用刚体绕定轴转A M F T r( 5)B 点加速度,根据题意,在临界状态有a Ba C a BCA rBr 0(6)联立求解式(5)、 (6 )和(2 )、( 3)并将 T T 及 J B J A予2代入,得K 7 12 - 23 I*]得 F T 3mg (拉)V A j2a A h |,/3gh (J)3 9- 10图示重物A 的质量为 绳子跨过不计质量的定滑轮 C 沿水平轨道滚动而不滑动。
子C 的半径为r ,二者总质量为 m m 当其下降时,借无重且不可伸长的绳使滚子 D 并绕在滑轮B 上。
滑轮B 与滚子C 固结为一体。
已知滑轮 B 的半径为R,滚,其对与图面垂直的轴 0的回转半径为 。
求:重物A 的加速度。
解:法1:对轮: J O TR Fr ma o对A : ma A (1) (2) mg (3) 又: a A 以0为基点: t a Hta H aH 绳 na H t 3HO a O a oa A (R r) 由上四式联立,得 a H n a HO R ta HO (R r) (J)(注意到mg(R r)2(4) aA m ( 2 r 2) m(R r)2g nz 口 m (R r)2啲 E (a)11* 1 法2:对瞬心 J E ma A 又a A J E E 用动量矩定理T(R r) mg T (R J 0 r) 可解得:a A 2 / 2 m r m ( g m ( 2 r 2) 1矿 i m (R r)2(本题质心瞬心之距离为常数) r 2) 9- 11图示匀质圆柱体质量为 ,求圆柱中心 a on a Hin a HO(b) t a H 4 t a HO常数,滚动阻碍系数为 解:J D M fF N M M f 半径为r ,在力偶作用下沿水平面作纯滚动。
若力偶的力偶矩 M 为 0的加速度及其与地面的静滑动摩擦力。
(1) 代入(1), F N mg 3 2mr 2 a r 得2(M mg)3mr习题9- 11图(a)又:ma FF 2(M mg)3r 9- 12跨过定滑轮 上,如图所示。
已知圆柱 的加速度以及绳索的拉力。
解:对轮C : J C D 的细绳,一端缠绕在均质圆柱体 A 上,另一端系在光滑水平面上的物体 A 的半径为r ,质量为 滑轮 F T 「 m ;物块B 的质量为 D 和细绳的质量以及轴承摩擦忽略不计。
B m 2。
试求物块 B 和圆柱质心 C F T F TAm i a c mg F T 对物块B:m2a B F T且:a。
a B r ;J c 1 mr 22解得:aa Bm ig ;a cm i2m23m2g m 3m2m iF T mmg m i 3m2。
