理论力学课后答案(范钦珊)
材料力学_范钦珊_习题参考解答
OB
B F P 60kN
Ea
1 .2 m
A
FP
x
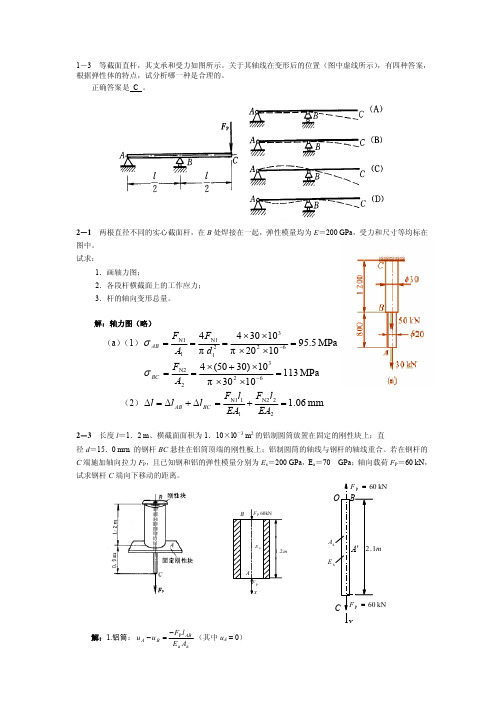
解：1.铝筒： u A − u B
=
−FPl AB Ea Aa
（其中 uA = 0）
As
A' 2.1m
Es
C FP = 60 kN
x
uB
=
60 ×103 ×1.2 ×103 70 ×103 ×1.10 ×10−3 ×106
= 0.935 mm
Mx1＝ Mx2 2．确定轴和薄壁管横截面上的最大剪应力 设轴受 T = 73.6N·m 时，相对扭转角为 ϕ0 ，于是，有
dφ0 = M x = T dx GIp1 GIp1
（a）
焊接后卸载，管承受扭转，其相对扭转角为 ϕ 2 ，轴上没有恢复的相对扭转角为 ϕ1 = ϕ0 − ϕ2 ，即
其中
ϕ1 + ϕ2 = ϕ0
×103 × 10 −6
= 95.5 MPa
σ BC
=
FN2 A2
=
4 × (50 + 30) ×103 π × 302 ×10−6
= 113 MPa
（2） ∆l = ∆l AB
+ ∆lBC
=
FN1l1 EA1
+ FN2l2 EA2
= 1.06 mm
2－3 长度 l＝1．2 m、横截面面积为 1．10×l0－3 m2 的铝制圆筒放置在固定的刚性块上；直 径 d＝15．0 mrn 的钢杆 BC 悬挂在铝筒顶端的刚性板上；铝制圆筒的轴线与钢杆的轴线重合。若在钢杆的 C 端施加轴向拉力 FP，且已知钢和铝的弹性模量分别为 Es＝200 GPa，Ea＝70 GPa；轴向载荷 FP＝60 kN， 试求钢杆 C 端向下移动的距离。
工程力学课后习题答案_范钦珊(合订版)
(a)
(b)
习题 1－1 图
解：图（a）： F = F cosα i1 + F sinα j1 分力： Fx1 = F cosα i1 ， Fy1 = F sinα j1
投影： Fx1 = F cosα ， Fy1 = F sinα
讨论： ϕ = 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
∴ ϕ2 = 29°51′ 由 A 平衡： FNA = 1⋅ cosϕ1 = 0.092N
由 B 平衡： FNB = 2 ⋅ cosϕ 2 = 1.73N
（4） （5）
返回总目录 下一章
11
eBook
工程力学
（静力学与材料力学）
习题详细解答
（教师用书） (第 2 章)
范钦珊 唐静静
2006-12-18
y
FTA
FR
α
FTB
x
FTC
习题 2－3 图
习题 2－3 解图
解：（1）由题意知 FTA = FTB = FTC = 5kN 。
由习题2－3解图，作用于大船上的合力在x、y轴上的投影的大小分别为：
FAx
A
C FC' x
FAy
FC' y
习题 1－5b 解 3 图
FC C
FB'
B
D FD' FD
FAx
A
D
FE FE'
E
E
B
FAy
FB
习题 1－5c 解图
1—6 图示刚性构件 ABC 由销钉 A 和拉杆 D 所悬挂，在构件的 C 点作用有一水力 F。 如果将力 F 沿其作用线移至 D 点或 E 点处（如图示），请问是否会改变销钉 A 和 D 杆的受 力？
工程力学 第二版 (范钦珊 唐静静 著) 高等教育出版社 课后答案 第11章 压杆的稳定性问题
角钢(连结成一整体)。试确定梁与柱的工作安全因 数。
解：1．查型钢表得
习题 11－12 图
No.16aI：Iz = 1130cm4，Wz = 141cm3 2No. 63×63×5： A = 2 × 6.143 = 12.286 cm2
i y = 1.94cm I y = 2 × 23.17 = 46.34 cm
采用，欧拉公式计算临界力
FPcr = σ cr A =
轴的工作安全因数
2 π E
λ2
=
所以，轴不安全。
11－11 图示正方形桁架结构，由五根圆截面钢杆组成，
连接处均为铰链，各杆直径均为 d＝40 mm，a＝1 m。材料 均为 Q235 钢，E＝200 GPa，[n]st＝1.8。试；
网
ww w
.k hd 案
μ =1
co
界力。
m
11－5
图示 a、b、c、d 四桁架的几何尺寸、圆杆的横截面直径、材料、加力点及加力
方向均相同。关于四桁架所能承受的最大外力 FPmax 有如下四种结论，试判断哪一种是正确 的。 （A）FPmax(a)=FPmax(c)<FPmax(b)=FPmax(d)； （B）FPmax(a)=FPmax(c)=FPmax(b)=FPmax(d)； （C）FPmax(a)=FPmax(d)<FPmax(b)=FPmax(c)；
案
对于 A3 钢， λ P = 102,
λs = 61.6 。因此，第一杆为大柔度杆，第二杆为中柔度杆，
网
i μl λ2 = 2 i μl λ3 = 3 i
λ1 =
=
ww w
FPcr = ( a − bλ ) A = (304 − 1.12 × 62.5) × 10 3 ×
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第8章 弯曲刚度
课
后 答
案
网
解：由挠度表查得：
FP al 180° × 3 EI π Wal 180° = ⋅ 3 EI π 20000 × 1 × 2 × 64 180° = ⋅ 3 × 200 × 109 × π d 4 π ≤ 0 .5 ° d ≥ 0.1117 m，取 d = 112mm。
θB =
ww w
6 ( 246 + 48) ×10 × 200 ×10 × π × 32 × 10−12
2
co
m
8—3 具有中间铰的梁受力如图所示。试画出挠度曲线的大致形状，并说明需要分几段 建立微分方程，积分常数有几个，确定积分常数的条件是什么？（不要求详细解答）
习题 8－3 图
后 答
案
网
习题 8－4 图
课
习题 8－4a 解图
解： (a)题 1.
wA = wA1 + wA 2
wA1 =
⎛l⎞ q⎜ ⎟ ⎝2⎠
87图示承受集中力的细长简支梁在弯矩最大截面上沿加载方向开一小孔若不考虑应力集中影响时关于小孔对梁强度和刚度的影响有如下论述试判断哪一种是正确的
eBook
工程力学
（静力学与材料力学）
习题详细解答
(第 8 章) 范钦珊 唐静静
课
后 答
案
网
2006-12-18
ww w
1
.k hd
aw .
co
m
（教师用书）
−3 9 4
(
.k hd
解：由挠度表查得 F ba 2 wC = P l − a 2 − b2 6lEI
(
)
习题 8－9 图
8
aw .
)
范钦珊版材料力学习题全解 第5章 梁的弯曲问题(1)-剪力图与弯矩图
M A = ql 2
| FQ | max = 5 ql 4
| M | max = ql 2
题（c）
∑ F y = 0 ， FRA = ql （↑）
9
∑ M A = 0 ， M A = ql 2
∑ M D = 0 ， ql 2 + ql ⋅ l − ql ⋅ − M D = 0
3 2 ql 2 | FQ | max = ql MD =
C
4000 4000
B
FB
习题 5－8 载荷图之二
5－9 试作图示刚架的剪力图和弯矩图，并确定 FQ
max
、 M
max
12
习题 5－9 图
解：题（a） ：
∑M A = 0
FRB ⋅ 2l − FP ⋅ l − FP ⋅ l = 0
FRB = FP （↑）
∑ F y = 0 ， F Ay = FP （↓）
∑ Fx = 0 ， FAx = FP （←）
C
2
1
B
C
－
B
1
D
M(FPl)
1 +
D
FQ(FP)
A
A
习题 5－9a 的弯矩图
剪力图和弯矩图如图所示，其中 | M | max = 2 FP l ， 位于刚节点 C 截面；
| FQ |max = FP
题（b） ： ∑ F y = 0 ， F Ay = ql （↑）
8
习题 5－6c、e 解图
习题 5－6d、f 解图
题（b）
∑ M A = 0 − ql 2 − ql ⋅ l + ql ⋅ l + FRB ⋅ 2l = 0
2
FRB
材料力学高教第二版范钦珊第6章习题答案要点
材料力学_高教第二版_范钦珊_第6章习题答案第6章杆件横截面的位移分析6－1 直径d = 36mm的钢杆ABC与铜杆CD在C处连接，杆受力如图所示。
若不考虑杆的自重，试： 1．求C、D二截面的铅垂位移；Fl2．令FP1 = 0，设AC段长度为l1，杆全长为l，杆的总伸长，写出E的表达式。
EA习题6-1图(a) (F)l(F)l解：（1）πdπdEsEs2332(FN)CDlCDπdEc4（2）EAEsAEcAEEsEclEcEs令FP6－2 承受自重和集中载荷作用的柱如图所示，其横截面积沿高度方向按材料的比重。
试作下列量的变化曲线： 1．轴力FNx(x)； 2．应力； 3．位移u(x)。
解：（1），(FN变化，其中为FPFN(x)-FPx习题6-2图(a)FPFPA0FP（2）A(x)A0eFPFP— 89 —（3）A0，当。
∴，则EA0EA0EA06－3 图示连接件由两片宽20mm、厚6mm的铜片与一片同样宽厚的钢片在B处连接而成。
已知钢与铜的弹性模量分别为Es = 200GPa，Ec =105GPa，钢片与铜片之间的摩擦忽略不计。
试求E和B处的位移。
F习题6-3图解：6－4 长为1.2m、横截面面积为的铝制筒放置在固定刚块上，直径为15.0mm的钢杆BC悬挂在铝筒顶端的刚性板上，若二者轴线重合、载荷作用线与轴线一致，且已知钢和铝的弹性模量分别为kNEs = 200Gpa，Ea = 70GPa，FP = 60kN。
试求钢杆上C处位移。
Am EkN(a) 习题6-4图 (b)解：（其中uA = 0） EaAa ∴钢杆6－5 变截面圆锥杆下端B处固定，上端A处承受外力偶矩T作用，如图所示，试证明A端扭转角表达式为解：Mx = T习题6-5图6－6 试比较图示二梁的受力、内力（弯矩）、变形和位移，总结从中所得到的结论。
(a) 解：(b) wmaxFPl3 48EIFlEI— 90 —两者弯矩相同，挠曲线曲率相同，但（b）梁的最大挠度比（a）梁要大，即不相等。
清华大学材料力学习题详解(范钦珊) 第13章
eBook材料力学习题详细解答教师用书(第13章)2006-01-18范 钦 珊 教 育 教 学 工 作 室FAN Qin-Shan’s Education & Teaching Studio习题13－1 习题13－2 习题13－3 习题13－4 习题13－5 习题13－6 习题13－7 习题13－8第13章 动载荷与疲劳强度概述13－1 图示的No.20a 普通热轧槽钢以等减速度下降，若在0.2s 时间内速度由1.8m/s 降至0.6m/s ，已知l =6m ，b =1m 。
试求槽钢中最大的弯曲正应力。
解：No.20a 槽钢的线密度63.22=ρkg/m槽钢的加速度62.08.16.0−=−=a m/s 2 由自重引起的均布载荷集度：g q ρ=1(↓)由惯性力引起的均布载荷集度： a q ρ=2(↓) (加速度↑)总的均布载荷集度：)(21a g q q q +=+=ρ由总载荷（动载荷＋静载荷）引起的弯矩：)(4432824max a g q q q M M C +=×=××+××−==ρ=4×22.63(9.8+6)=1430 N ·m于是，槽钢横截面上的最大正应力MPa 1591022414306min dmax ..=×==−W M C σ13－2 钢制圆轴AB 上装有一开孔的匀质圆盘如图所示。
圆盘厚度为δ，孔直径300mm 。
圆盘和轴一起以匀角速度ω转动。
若已知：δ=30mm ，a =1000mm ，e =300mm；轴习题13－1图习题13－2图直径d =120mm ，ω=40rad/s ；圆盘材料密度33m kg 108.7×=ρ。
试求由于开孔引起的轴内最大弯曲正应力（提示：可以将圆盘上的孔作为一负质量（-m ），计算由这一负质量引起的惯性力）。
解：将圆盘上的孔作为一负质量（-m ），计算由这一负质量引起的惯性力：222I π4F me D e ==××××ωρδω由此引起的附加动约束力：2IF F F B A == 动载荷引起的附加最大动弯矩发生在C 截面，其值为：a F a F M A I max 21== 于是，最大附加弯曲动应力：22dmax dmax 3π24672MPa π32.a D e M d W⋅⋅===ρδωσ13－3 质量为m 的匀质矩形平板用两根平行且等长的轻杆悬挂着，如图所示。
高教范钦珊材料力学习题集有答案
材料力学习题集第1章引论1－1图示矩形截面直杆，右端固定，左端在杆的对称平面内作用有集中力偶，数值为M。
关于固定端处横截面A－A上的内力分布，有四种答案，根据弹性体的特点，试分析哪一种答案比较合理。
，A－Ad(b-1)(a-2) (b-2)(c) (d)(c-2) (d-2)(e) (f)(e-1) (f-1)(e-2) (a) (b)(c) (d)(a-1)(c-1) (d-1)(f-2)ql F B 41R =（↑） 0=∑y F ，ql F A 41R =（↓）， 2R 4141ql l ql l F M B C =⋅=⋅=（＋） 2ql M A =（c ）0=∑y F ，ql F A =R （↑） 0=∑A M ，2ql M A =0=∑D M ，022=-⋅-⋅+D M lql l ql ql（d ）0=∑B Mql F A 45R =（↑） 0=∑y F ，ql F B 43R =（↑）0=∑B M ，22l qM B =0=∑D M ，23225ql M D = （e ）0=∑y F ，F R C = 00=∑C M ，0223=+⋅+⋅-C M lql l ql0=∑B M ，221ql M B =0=∑y F ，ql F B =Q2max ||ql M =（f ）0=∑A M ，ql F B 21R =（↑）0=∑y F ，ql F A 21R =（↓）0=∑y F ，021Q =-+-B F ql ql0=∑D M ，042221=+⋅-⋅D M ll q l ql281ql M E =∴ ql F 21||max Q =2－5 试作图示刚架的弯矩图，并确定max ||M 。
解：图（a ）：0=∑A M ，02P P R =⋅-⋅-⋅l F l F l F B P R F F B =（↑）0=∑y F ，P F F Ay =（↓） 0=∑x F ，P F F Ax =（←）弯距图如图（a-1），其中l F M P max 2||=，位于刚节点C 截面。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
C(a-2)DR(a-3)(b-1)DR第1篇 工程静力学基础第1章 受力分析概述1－1 图a 、b 所示，Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一力F 分别对两坐标系进行分解和投影，并比较分力与力的投影。
习题1－1图解：（a ）图（c ）：11 s i n c o s j i F ααF F +=分力：11 cos i F αF x = ， 11 s i n j F αF y =投影：αcos 1F F x = ， αs i n 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
（b ）图（d ）： 分力：22)cot sin cos (i F ϕααF F x -= ，22sin sin j F ϕαF y = 投影：αcos 2F F x = ， )cos(2αϕ-=F F y讨论：ϕ≠90°时，投影与分量的模不等。
1－2 试画出图a 和b习题1－2图比较：图（a-1）与图（b-1）不同，因两者之F R D 值大小也不同。
（c ） 22x（d ）1－3 试画出图示各物体的受力图。
习题1－3图B或(a-2)B(a-1)(b-1)F(c-1) 或(b-2)(e-1)F(a)1－4 图a 所示为三角架结构。
荷载F 1作用在铰B 上。
杆AB 不计自重，杆BC 自重为W 。
试画出b 、c 、d 所示的隔离体的受力图，并加以讨论。
习题1－4图1－5 图示刚性构件ABC 由销钉A 和拉杆D 支撑，在构件C 点作用有一水平力F 。
试问如果将力F 沿其作用线移至D 或E （如图示），是否会改为销钉A 的受力状况。
解：由受力图1－5a ，1－5b 和1－5c 分析可知，F 从C 移至E ，A 端受力不变，这是因为力F 在自身刚体ABC 上滑移；而F 从C 移至D，则A 端受力改变，因为HG 与ABC 为不同的刚体。
1(f-1)'A(f-2)1O(f-3)F F'F 1(d-2)F yB 21(c-1)F A B1B FDx y(b-2)1(b-3)F yB 2 A A B1B F习题1－5图AxF(b-3)E D(a-3)B(b-2)(b-1)F 'CBC(c)AxF1－6 试画出图示连续梁中的AC 和CD 梁的受力图。
习题1－6图1－7 画出下列每个标注字符的物体的受力图，各题的整体受力图未画重力的物体的自重均不计，所有接触面均为光滑面接触。
(b)F H(c)F Dx(b)'F(a)1-7d1-7e 1-7f 1-7g2N2CyDRDR CyFByBxAxFF'FFFFCy2TTFDxTF'3TFEyFCyEx'1-7h1-7i1-7jAyBxByFCyBx'BF C RDR GRFHR FFAyBRFFAy第2章 力系的等效与简化2－1试求图示中力F 对O 点的矩。
解：（a ）l F F M F M F M M y O y O x O O ⋅==+=αsin )()()()(F （b ）l F M O ⋅=αsin )(F（c ）)(sin cos )()()(312l l Fl F F M F M M y O x O O +--=+=ααF （d ）2221sin )()()()(l l F F M F M F M M y O y O x O O +==+=αF2－2 图示正方体的边长a =0.5m ，其上作用的力F =100N ，求力F 对O 点的矩及对x 轴的力矩。
解：)(2)()(j i k i Fr F M +-⨯+=⨯=Fa A O m kN )(36.35)(2⋅+--=+--=k j i k j i Fam kN 36.35)(⋅-=F x M2－3 曲拐手柄如图所示，已知作用于手柄上的力F =100N ，AB=100mm ，BC =400mm ，CD =200mm ，α = 30°。
试求力F 对x 、y 、z 轴之矩。
解：)cos cos sin (sin )4.03.0()(2k j i k j F r F M αααα--⨯-=⨯=F D Ak j i αααα22sin 30sin 40)sin 4.03.0(cos 100--+-=力F 对x 、y 、z 轴之矩为：m N 3.43)2.03.0(350)sin 4.03.0(cos 100)(⋅-=+-=+-=ααF x M m N 10sin 40)(2⋅-=-=αF y Mm N 5.7sin 30)(2⋅-=-=αF z M2—4 正三棱柱的底面为等腰三角形，已知OA=OB =a ，在平面ABED 内沿对角线AE 有一个力F ， 图中θ =30°，试求此力对各坐标轴之矩。
习题2-1图A r A习题2-2图（a ）习题2-3图ABr(a)解：)sin 45sin cos 45cos cos ()(k j i i F r F M θθθ+︒+︒-⨯=⨯=F a A O )45sin cos sin (k j ︒+-=θθaF 力F 对x 、y 、z 轴之矩为：0)(=F x M230sin )(aF aF M y -=︒-==F Fa aF M z 4645sin 30cos )(=︒︒=F2－5 如图所示，试求力F 对A 点之矩及对x 、y 、z 轴之矩。
解：F r F M ⨯=AB A )(5354F F d d d-k j i = =)743(51k j i -+-Fd)34(5)(j i j F M +⨯=Fd O力F 对x 、y 、z 轴之矩为：0)(=F x M ；0)(=F y M ；Fd M z 54)(-=F2—6面。
求这四个力偶的合力偶。
解：4321M M M M M+++=k j i )53()54(43241M M M M M +--+-=m N 8.1284.14⋅---=k j i2－7 已知一平面力系对A （3,0），B A B = 0，M C =–10kN ·m 。
试求该力系合力的大小、方向和作用线。
解：由已知M B = 0知合力F R 过B 点； 由M A = 20kN ·m ，M C = -10kN ·m 知F R 位于A 、C 间，且CD AG 2=（图a ）在图（a ）中，设 OF = d ，则 θc o t 4=dCD AG d 2)sin 3(==+θ （1）θθs i n )25.4(s i n dCE CD -== （2）即 θθs i n )25.4(2s i n )3(dd -=+ d d -=+93， 3=dF 点的坐标为（-3, 0） 合力方向如图（a ），作用线如图过B 、F 点；习题2－4图习题2－5图习题2－6图 （a ） 43 M 1M 2 M 3M 4习题2－7图34tan =θ 8.4546sin 6=⨯==θAG8.4R R ⨯=⨯=F AG F M AkN 6258.420R ==F 即 )k N 310,25(R =F作用线方程：434+=x y讨论：本题由于已知数值的特殊性，实际G 点与E 点重合。
2－8 已知F 1 = 150N ，F 2 = 200N ，F 3 = 300N ，F =F '= 200N 。
求力系向点O 的简化结果，并求力系合力的大小及其与原点O 的距d 。
80200100131121FFF'解：N .64375210145cos 321-=--︒-=∑F F F F xN .61615110345sin 321-=+-︒-=∑F F F F ym N 44.2108.02.0511.045sin )(31⋅=-⨯+⨯︒=∑F F F M O F向O 点简化的结果如图（b ）；合力如图（c ），图中N 5.466)()(22'R =∑+∑=y x F F F ，m N 44.21⋅=O M合力N 5.466'R R ==F F ，mm 96.45R==F M d O2－9 图示平面任意力系中F 1 = 402N ，F 2 = 80N ，F 3 = 40N ，F 4 = 110M ，M = 2000 N ·mm 。
各力作用位置如图所示，图中尺寸的单位为mm 。
求（1）力系向O 点简化的结果；（2）力系的合力的大小、方向及合力作用线方程。
FFFF (0,30)(20,20)(20,-30)(-50,0)45解：N 15045cos 421R -=--︒=∑=F F F F F x x045sin 31R =-︒=∑=F F F F y yR(a)习题2－8图习题2－9图N 150)()(22'R =∑+∑=y x F F Fm m N 900305030)(432⋅-=--+=∑=M F F F M M O O F向O 点简化结果如图（b ）；合力如图（c ），其大小与方向为N 150'R R i F F -==设合力作用线上一点坐标为（y x ,），则x y O O yF xF M M R R R )(-==F将O M 、'R y F 和'R x F 值代入此式，即得合力作用线方程为：mm 6-=y2－10 图示等边三角形板ABC ，边长a ，今沿其边缘作用大小均为F P 的力，方向如图（a ）所示，求三力的合成结果。
若三力的方向改变成如图（b ）所示，其合成结果如何？解（a ）0'R =∑=i F Fa F a F M A P P 2323=⋅=（逆） 合成结果为一合力偶a F M P 23=（逆） （b ）向A 点简化i F P 'R 2F -=（←）a F M A P 23=（逆） 再向'A 点简化，a F M d A 43'R==合力i F P R 2F A -=（←）2－11 图示力系F 1 = 25kN ，F 2 = 35kN ，F 3 = 20kN ，力偶矩m = 50kN ·m 。
各力作用点坐标如图。
试计算（1）力系向O 点简化的结果；（2）力系的合力。
解（1）向O 点简化 kN 10'R k F F =∑=i)(F M M O O ∑=mkN )10580(200 002 3- 35- 0 00 2 2 250 00 2- 3 50⋅+-=+++=j i kj i k j i k j i j（2）合力kN 10R k F =设合力作用线过点)0,,(y x ，则F F FF F F 习题2－10图 F F FF F A 习题2－11图j i M kj i 10580100 00 +-==O x y 5.10-=x ，0.8-=y ，0=z合力作用线过点（-10.5，-8.0，0）。