高中数学交集并集教案新人教版必修1
交集、并集五 新课标 人教版 必修一 教案

交集、并集五教学目标(1)进一步掌握交集、并集的概念,交集及并集有关性质,能运用性质解决一些简单问题; (2)进一步提高学生的思维能力,开发学生的创新精神,鼓励学生勤于思考; (3)理解区间的表示法. 教学重点集合的交、并运算. 教学难点正确理解集合的内涵从而找准元素. 教学过程 一、复习回顾1.集合的交集、并集的定义、符号表示. 2.填空 AA = A ∅= AB B AA A = A ∅= AB B AA B B A A B B A B若A B A =,则A 与B 的关系为 ,若A B A =,则A 与B 的关系为 .二、数学运用 1.例题:例1.学校举办了排球赛,某班45名同学中有12名同学参赛,后来又举办了田径赛,这个班有20名同学参赛.已知两项都参赛的有6名同学,两项比赛中,这个班共有多少同学没有参赛?分析:(一)用文恩图求解; (二)立方程组求解.例2.设U={1,2,3,4,5,6,7,8},A ={3,4,5},B ={4,7,8},求 U C A 、U C B 、 (U C A )∩(U C B )、(U C A )∪(U C B ).例3.已知集合2{|0}A x x px q =--=,2{|0}B x x qx p =+-=,且{1}A B =,求A B .例4.设2{|320}A x x x =-+=,2{|20}B x x ax =-+=,若AB A =,求实数a 的取值的组成的集合.例5.已知集合{|45}P x x =≤<,{|121}Q x k x k =+<≤-,求PQ φ≠时实数k 的取值范围.2.设,a b R ∈,且a b <,规定:[,]{|}a b x a x b =≤≤, (,){|}a b x a x b =<< [,){|}a b x a x b =≤< (,]{|}a b x a x b =<≤(,){|}a x x a +∞=>, (,){|}b x x b -∞=< (,)R -∞+∞=3.练习:(1)设(2,3],[1,4)A B =-=,求A B ,A B ;(2)课本第13页第7题.五、回顾小结:1.集合的交、并运算的方法及性质的应用;2.区间概念的认识.六、课外作业:课本第13页习题1.3 第3、4、8、10题、第17页第6、7题. 补充:1.设2{,21,9},{1,5,9}M a a P a a =--=--,已知{9}MP =,求a 的值;2.设2{|20}A x x px q =-+=,2{|6(2)50}B x x p x q =++++=,若1{}2AB =,求A B .。
高中数学人教版(新教材)必修1教学设计4:1.3 第1课时 并集与交集

1.3 第1课时并集与交集教学目标1.理解并集、交集的概念.2.会用符号、Venn图和数轴表示并集、交集.3.会求简单集合的并集和交集.教学知识梳理知识点一并集(1)定义:一般地,由所有属于集合A或属于集合B的元素组成的集合,称为集合A与B的并集,记作A∪B(读作“A并B”).(2)并集的符号语言表示为A∪B={x|x∈A,或x∈B}.(3)图形语言:、.阴影部分为A∪B.(4)性质:A∪B=B∪A,A∪A=A,A∪∅=A,A∪B=A⇔B⊆A,A⊆A∪B.知识点二交集(1)定义:一般地,由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集,记作A∩B(读作“A交B”).(2)交集的符号语言表示为A∩B={x|x∈A,且x∈B}.(3)图形语言:,阴影部分为A∩B.(4)性质:A∩B=B∩A,A∩A=A,A∩∅=∅,A∩B=A⇔A⊆B,A∩B⊆A∪B,A∩B⊆A,A∩B⊆B. 题型探究题型一并集及其运算例1(1)设集合A={1,2,3},B={2,3,4},则A∪B等于()A.{1,2,3,4}B.{1,2,3}C.{2,3,4}D.{1,3,4}『答案』A『解析』∵A={1,2,3},B={2,3,4},∴A∪B={1,2,3,4}.故选A.(2)A={x|-1<x<2},B={x|1<x<3},求A∪B.解如图:由图知A∪B={x|-1<x<3}.反思感悟有限集求并集就是把两个集合中的元素合并,重复的保留一个;用不等式表示的,常借助数轴求并集.由于A∪B中的元素至少属于A,B之一,所以从数轴上看,至少被一道横线覆盖的数均属于并集.跟踪训练1 (1)A ={-2,0,2},B ={x |x 2-x -2=0},求A ∪B .解 B ={-1,2},∴A ∪B ={-2,-1,0,2}.(2)A ={x |-1<x <2},B ={x |x ≤1或x >3},求A ∪B .解 如图:由图知A ∪B ={x |x <2或x >3}.题型二 交集及其运算例2 (1)已知集合A ={1,2,3},B ={x |(x +1)(x -2)=0},则A ∩B 等于( )A.{1}B.{2}C.{-1,2}D.{1,2,3}『答案』B『解析』B ={}-1,2,∴A ∩B ={}2.(2)若集合A ={x |-5<x <2},B ={x |-3<x <3},则A ∩B 等于( )A.{x |-3<x <2}B.{x |-5<x <2}C.{x |-3<x <3}D.{x |-5<x <3}『答案』A『解析』在数轴上将集合A ,B 表示出来,如图所示,由交集的定义可得A ∩B 为图中阴影部分,即A ∩B ={x |-3<x <2},故选A.(3)已知集合M ={(x ,y )|x +y =2},N ={(x ,y )|x -y =4},那么M ∩N 为( )A.x =3,y =-1B.(3,-1)C.{3,-1}D.{(3,-1)}『答案』D『解析』解方程组⎩⎪⎨⎪⎧ x +y =2,x -y =4,得⎩⎪⎨⎪⎧x =3,y =-1.∴M ∩N ={(3,-1)}. 反思感悟 求集合A ∩B 的步骤(1)首先要搞清集合A ,B 的代表元素是什么;(2)把所求交集的集合用集合符号表示出来,写成“A ∩B ”的形式;(3)把化简后的集合A ,B 的所有公共元素都写出来即可.跟踪训练2 (1)设集合A ={x |x ∈N ,x ≤4},B ={x |x ∈N ,x >1},则A ∩B =________.(2)集合A ={x |x ≥2或-2<x ≤0},B ={x |0<x ≤2或x ≥5},则A ∩B =________.(3)集合A ={(x ,y )|y =x +2},B ={(x ,y )|y =x +3},则A ∩B =________.『答案』(1){2,3,4} (2){x |x ≥5或x =2} (3)∅『解析』(1)因为A ={x |x ∈N ,x ≤4}={0,1,2,3,4},B ={x |x ∈N ,x >1},所以A ∩B ={2,3,4}.(2)易知A ∩B ={x |x ≥5或x =2}.题型三 利用集合并集、交集性质求参数例3 已知A ={x |2a ≤x ≤a +3},B ={x |x <-1或x >5},若A ∪B =B ,求a 的取值范围. 解 A ∪B =B ⇔A ⊆B .当2a >a +3,即a >3时,A =∅,满足A ⊆B .当2a =a +3,即a =3时,A ={6},满足A ⊆B .当2a <a +3,即a <3时,要使A ⊆B ,需⎩⎪⎨⎪⎧ a <3,a +3<-1或⎩⎪⎨⎪⎧a <3,2a >5, 解得a <-4或52<a <3. 综上,a 的取值范围是{a |a >3}∪{a |a =3}∪⎩⎨⎧⎭⎬⎫a ⎪⎪ a <-4或52<a <3 =⎩⎨⎧⎭⎬⎫a ⎪⎪a <-4或a >52. 反思感悟 (1)在利用交集、并集的性质解题时,常常会遇到A ∩B =A ,A ∪B =B 这类问题,解答时常借助于交、并集的定义及上节学习的集合间的关系去分析,如A ∩B =A ⇔A ⊆B ,A ∪B =B ⇔A ⊆B 等.(2)当集合B ⊆A 时,如果集合A 是一个确定的集合,而集合B 不确定,运算时要考虑B =∅的情况,切不可漏掉.(3)在这里理解运算对象,掌握运算法则,探究运算思路,求得运算结果,充分体现了数学运算的数学核心素养.课堂小结1.在解决有关集合运算的题目时,关键是准确理解题目中符号语言的含义,善于将其转化为文字语言.2.集合的运算可以用Venn 图帮助思考,实数集合的交集、并集运算可借助数轴求解,体现了数形结合思想的应用.3.对于给出集合是否为空集,集合中的元素个数是否确定,都是常见的讨论点,解题时要注意分类讨论思想的应用.达标检测1.设集合M ={x |x 2+2x =0,x ∈R },N ={x |x 2-2x =0,x ∈R },则M ∪N 等于( )A.{0}B.{0,2}C.{-2,0}D.{-2,0,2}『答案』D『解析』M={x|x2+2x=0,x∈R}={0,-2},N={x|x2-2x=0,x∈R}={0,2},故M∪N ={-2,0,2},故选D.2.已知集合A={0,1,2,3,4,6,7},集合B={1,2,4,8,0},则A∩B等于()A.{1,2,4,0}B.{2,4,8}C.{1,2,8}D.{1,2,0}『答案』A3.已知集合A={x|x2-2x=0},B={0,1,2},则A∩B等于()A.{0}B.{0,1}C.{0,2}D.{0,1,2}『答案』C4.若集合A={x|-2≤x≤3},B={x|x<-1或x>4},则A∩B=________.『答案』{x|-2≤x<-1}5.已知集合A={-1}且A∪B={-1,3},则所有满足条件的集合B=________.『答案』{3}或{-1,3}『解析』因为集合A={-1},A∪B={-1,3},所以B至少含有元素3,集合B的所有可能情况为{3}或{-1,3}.。
人教版数学高一-交集与并集 导学案

1.1.3集合的基本运算(并集、交集)导学案课前预习学案一、预习目标:了解交集、并集的概念及其性质,并会计算一些简单集合的交集并集。
二、预习内容:1、交集:一般地,由所有属于A又属于B的元素所组成的集合,叫做A,B 的.记作 ,即2、并集:一般地,对于给定的两个集合A,B把它们所有的元素并在一起所组成的集合,叫做A,B的.记作,即3、用韦恩图表示两个集合的交集与并集。
提出疑惑同学们,通过你的自主学习,你还有那些疑惑,请填在下面的表格中疑惑点疑惑内容课内探究学案(一)学习目标:1、熟练掌握交集、并集的概念及其性质。
2、注意用数轴、韦恩图来解决交集、并集问题。
3、体会数学语言的简洁性与明确性,发展运用数学语言交流问题的能力。
学习重难点:会求两个集合的交集与并集。
(二)自主学习1.设A={x|x是等腰三角形},B={x|x是直角三角形},求A∩B.2.设A={x|x是锐角三角形},B={x|x是钝角三角形},求A∪B.(三)合作探究:思考交集与并集的性质有哪些?(四)精讲精练例1、已知集合M={(x,y)|x+y=2},N={(x,y)|x-y=4},那么集合M∩N为( )A.x=3,y=-1B.(3,-1)C.{3,-1}D.{(3,-1)}变式训练1:已知集合M={x|x+y=2},N={y|y= x2},那么M∩N为例2.设A={x|-1<x<2},B={x|1<x<3},求A∪B.变式训练2:已知A={x|x2-px+15=0},B={x|x2-ax-b=0},且A∪B={2,3,5},A∩B={3},求p,a,b的值。
三、课后练习与提高1、选择题(1)设M={0,1,2,4,5,7},N={1,4,6,8,9},P={4,7,9},则(M∩N)∪(M∩P)=()A.{1,4}B.{1,7}C.{4,7}D.{1,4,7}(2)已知A={y|y=x2-4x+3,x∈R},B={y|y=x-1,x∈R},则A∩B=()A.{y|y=-1或0}B.{x|x=0或1}C.{(0,-1),(1,0)}D.{y|y≥-1}(3)已知集合M={x|x-a=0},N={x|ax-1=0},若M∩N=M,则实数a=()A.1B.-1C.1或-1D.1或-1或02、填空题(4).若集合A、B满足A∪B=A∩B,则集合A,B的关系是_________________________________.(5)设},32|{2R x x x y y A ∈--==,},132|{2R x x x y y B ∈++-==,则B A =________。
新教材高中数学第1章集合与常用逻辑术语1.3集合的基本运算第1课时并集与交集教学案新人教A版必修第一册
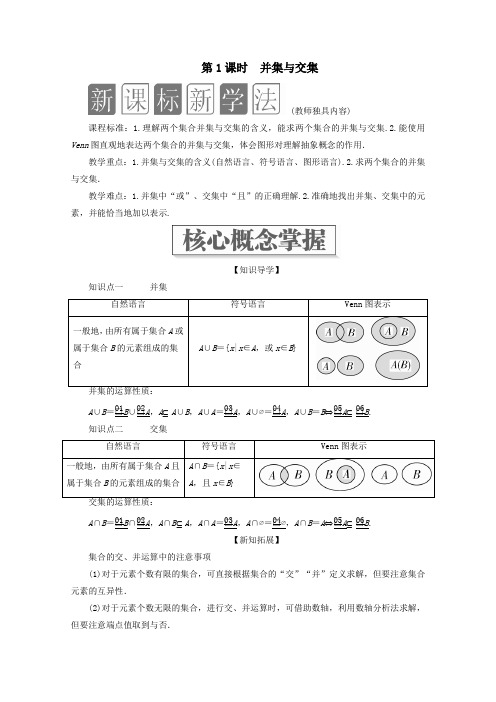
第1课时并集与交集(教师独具内容) 课程标准:1.理解两个集合并集与交集的含义,能求两个集合的并集与交集.2.能使用Venn图直观地表达两个集合的并集与交集,体会图形对理解抽象概念的作用.教学重点:1.并集与交集的含义(自然语言、符号语言、图形语言).2.求两个集合的并集与交集.教学难点:1.并集中“或”、交集中“且”的正确理解.2.准确地找出并集、交集中的元素,并能恰当地加以表示.【知识导学】知识点一并集自然语言符号语言Venn图表示一般地,由所有属于集合A或属于集合B的元素组成的集合A∪B={x|x∈A,或x∈B}A∪B=□01B∪□02A,A⊆A∪B,A∪A=□03A,A∪∅=□04A,A∪B=B⇔□05A⊆□06B.知识点二交集自然语言符号语言Venn图表示一般地,由所有属于集合A且属于集合B的元素组成的集合A∩B={x|x∈A,且x∈B}A∩B=□01B∩□02A,A∩B⊆A,A∩A=□03A,A∩∅=□04∅,A∩B=A⇔□05A⊆□06B.【新知拓展】集合的交、并运算中的注意事项(1)对于元素个数有限的集合,可直接根据集合的“交”“并”定义求解,但要注意集合元素的互异性.(2)对于元素个数无限的集合,进行交、并运算时,可借助数轴,利用数轴分析法求解,但要注意端点值取到与否.1.判一判(正确的打“√”,错误的打“×”)(1)若A∩B=∅,则A,B至少有一个是∅.( )(2)若A∪B=∅,则A,B都是∅.( )(3)对于任意集合A,B,下列式子总成立:A∩B⊆A⊆A∪B.( )(4)对于任意集合A,B,下列式子总成立:A∪B=B⇔A⊆B⇔A∩B=A.( )(5)对于两个非空的有限集合A,B,A∪B中的元素一定多于A中的元素.( )答案(1)×(2)√(3)√(4)√(5)×2.做一做(1)已知集合A={x|x=3n+2,n∈N},B={6,8,10,12,14},则集合A∩B中元素的个数为( )A.5 B.4C.3 D.2(2)已知集合A={x|-1<x<2},B={x|0<x<3},则A∪B=( )A.{x|-1<x<3} B.{x|-1<x<0}C.{x|0<x<2} D.{x|2<x<3}(3)已知集合A={1,2,x2},B={2,x},若A∪B=A,则x=________.答案(1)D (2)A (3)0题型一求两个集合的交集与并集例1 已知集合A={x|-1<x≤2},B={x|-2≤x<1},求A∩B,A∪B.[解] 把集合A与B在数轴上表示出来,如图所示.由上图可得,A∩B={x|-1<x<1},A∪B={x|-2≤x≤2}.金版点睛集合A与B的“交”“并”运算,实质上就是对集合A与B中元素的“求同”“合并”:(1)A∩B中的元素是“所有”属于集合A且属于集合B的元素,而不是部分,特别地,当集合A和集合B没有公共元素时,不能说A与B没有交集,而是A∩B=∅.(2)对于并集,要注意其中“或”的意义,“或”与通常所说的“非此即彼”有原则性的区别,它们是“相容”的.“x ∈A 或x ∈B ”这一条件,包括下列三种情况:x ∈A 但x ∉B ;x ∈B 但x ∉A ;x ∈A 且x ∈B .因此,A ∪B 是由所有至少属于A ,B 两者之一的元素组成的集合.[跟踪训练1] 已知集合A ={y |y =x 2-1},B ={x |-2≤x <0},求A ∩B ,A ∪B . 解 A ∩B ={x |-1≤x <0},A ∪B ={x |x ≥-2}.题型二 简单的含参问题例2 已知集合A ={0,1},B ={x |(x -1)(x -a )=0}.求A ∩B ,A ∪B .[解] 集合B 是方程(x -1)(x -a )=0的解集,它可能只有一个元素1(a =1),也可能有两个元素1,a (a ≠1).(1)当a =1时,A ∩B ={1},A ∪B ={0,1}; (2)当a =0时,A ∩B ={0,1},A ∪B ={0,1}; (3)当a ≠0且a ≠1时,A ∩B ={1},A ∪B ={0,1,a }. 金版点睛由于参数a 的变化,集合B 中的元素也在变化,即集合B 是变化的集合,因此需要分类讨论;特别注意,不能把集合B 写成{1,a }(因为当a =1时,不满足元素的互异性);对于两集合的“交”“并”运算,应当首先弄清两集合中的元素是什么,之后再根据集合“交”“并”运算的概念求解.[跟踪训练2] 已知集合A ={x |2a -2<x <a },B ={x |x ≤1或x ≥2},且A ∩B =A ,求a 的取值范围.解 ∵A ∩B =A ,∴A ⊆B , ∴分A =∅和A ≠∅两种情况讨论. ①若A =∅,此时有2a -2≥a ,∴a ≥2. ②若A ≠∅,则有⎩⎪⎨⎪⎧2a -2<a ,a ≤1或⎩⎪⎨⎪⎧2a -2<a ,2a -2≥2.∴a ≤1.综上所述,a ≤1或a ≥2.题型三 类似于“交”“并”运算的一些新定义型问题例3 设M ,P 是两个非空集合,规定M -P ={x |x ∈M ,且x ∉P },根据这一规定,M -(M-P)等于( )A.M B.PC.M∪P D.M∩P[解析] 当M∩P≠∅时,由图可知M-P为图中的阴影部分,则M-(M-P)显然是M∩P;当M∩P=∅时,M-P=M,此时M-(M-P)=M-M={x|x∈M,且x∉M}=∅=M∩P,故选D.[答案] D金版点睛题目给出了两个集合的一种运算“M-P”,其运算法则是:M-P是由所有属于M且不属于P的元素组成的集合,弄清法则便可以进行运算,特别是借助Venn图,使问题简捷明了.[跟踪训练3]设A,B是两个非空集合,规定A*B={x|x∈A∪B,且x∉A∩B}.若A={0,1,2,4},B={1,2,3},求A*B.解∵A∪B={0,1,2,3,4},A∩B={1,2},∴A*B={0,3,4}.1.已知集合A={x|x是不大于8的正奇数},B={x|x是9的正因数},则A∩B=________,A∪B=________.答案{1,3} {1,3,5,7,9}解析由题意,知A={1,3,5,7},B={1,3,9},所以A∩B={1,3},A∪B={1,3,5,7,9}.2.已知集合A={x|x是菱形},B={x|x是矩形},则A∩B=________.答案{x|x是正方形}解析菱形的四条边相等,矩形的四个角均为90°,四条边相等并且四个角均为90°的四边形为正方形,所以A∩B={x|x既是菱形,又是矩形}={x|x是正方形}.3.已知集合A ={(x ,y )|x +y =4},B ={(x ,y )|x -y =2},则A ∩B =________. 答案 {(3,1)}解析 由题意,知A ∩B ={(x ,y )|x +y =4且x -y =2}={|(x ,y )⎩⎪⎨⎪⎧x +y =4,x -y =2,解⎩⎪⎨⎪⎧x +y =4,x -y =2,得⎩⎪⎨⎪⎧x =3,y =1,故A ∩B ={(3,1)}.4.已知A ={x |-4<x ≤2},B ={x |-2≤x ≤3},则A ∩B =________,A ∪B =________. 答案 {x |-2≤x ≤2} {x |-4<x ≤3}解析 把集合A 与B 在数轴上表示出来,如图所示.由上图可知,A ∩B ={x |-2≤x ≤2},A ∪B ={x |-4<x ≤3}.5.已知A ={x |x >a },B ={x |-1≤x ≤1},若A ∪B =A ,则a 的取值范围是________. 答案 a <-1解析 A ∪B =A ⇔B ⊆A ,则a <-1,故a 的取值范围是a <-1.。
必修高中数学交集并集教案

诚西郊市崇武区沿街学校交集、并集教学目的:理解交集、并集、全集、补集的概念,掌握集合的运算性质,能利用数轴或者者文氏图进展集合的运算,进一步掌握集合问题的常规处理方法.教学重点:交集、并集、补集的求法,集合语言、集合思想的运用.教学过程:〔一〕主要知识:1.交集、并集、全集、补集的概念;2.A B A A B=⇔⊆,A B A A B=⇔⊇;3.()U U UC A C B C A B=,()U U UC A C B C A B=.〔二〕主要方法:1.求交集、并集、补集,要充分发挥数轴或者者文氏图的作用;2.含参数的问题,要有讨论的意识,分类讨论时要防止在空集上出问题;3.集合的化简是施行运算的前提,等价转化常是顺利解题的关键.〔三〕例题分析:1.A={x|-1<x<3},A∩B=∅,A∪B=R,求B.分析:问题解决主要靠有关概念的正确运用,有关式子的正确利用.解:由A∩B=∅及A∪B=R知全集为R,RA=B故B=RA={x|x≤-1或者者x≥3},B集合可由数形结合找准其元素.2.全集I={-4,-3,-2,-1,0,1,2,3,4},A={-3,a2,a+1},B={a-3,2a-1,a2+1},其中a∈R,假设A∩B={-3},求I(A∪B).分析:问题解决关键在于求A∪B中元素,元素的特征运用很重要.解:由题I={-4,-3,-2,-1,0,1,2,3,4},A={-3,a2,a+1},B={a-3,2a-1,a2+1},其中a∈R,由于A∩B={-3},因a2+1≥1,那么a-3=-3或者者2a-1=-3,即a=0或者者a=-1那么A={-3,0,1},B={-4,-3,2},A∪B={-4,-3,0,1,2}I(A∪B)={-2,-1,3,4}3.设A={x|x2+ax+b=0},B={x|x2+cx+15=0},又AB={3,5},A∩B={3},务实数a,b,c的值.解:∵A∩B={3},∴3∈B,∴32+3c+15=0,∴c=-8.由方程x2-8x+15=0解得x=3或者者x=5,∴B={3,5}.由A ⊆〔AB={3,5}知,3∈A,5∉A〔否那么5∈A∩B,与A∩B={3}矛盾〕故必有A={3},∴方程x2+ax+b=0有两一样的根3,由韦达定理得3+3=-a,3⨯3=b,即a=-6,b=9,c=-8.4.设A={x|x2+4x=0},B={x|x2+2〔a+1〕x+a2-1=0}.〔1〕假设A∩B=B,求a的值;〔2〕假设A∪B=B,求a的值.方法引导:什么情况下有A∩B=B什么情况下有A∪B=B弄清它们的含义,问题就可以解决了.解:A={-4,0},〔1〕∵A∩B=B,∴B⊆A.①假设0∈B,那么a2-1=0,a=±1.当a=1时,B=A;当a=-1时,B={0}.②假设-4∈B,那么a2-8a+7=0,a=7或者者a=1.当a=7时,B={-12,-4},B A.③假设B=∅,那么Δ=4〔a+1〕2-4〔a2-1〕<0,a<-1.由①②③得a=1或者者a≤-1.〔2〕∵A∪B=B,∴A⊆B.∵A={-4,0},又∵B至多有两个元素,∴A=B.由〔1〕知a=1.方法技巧:1.有些数学问题很难从整体入手,需要分割处理,把整体科学合理地划分为假设干个局部独立问题解决,以到达整体问题的解决,这种重要的数学思想方法就是分类讨论的方法,要学会这种思维的方法.2.B=∅也是B⊆A的一种情况,不能遗漏,要注意结果的检验.5.非空集合A={x|2a+1≤x≤3a-5},B={x|3≤x≤22},那么能使A ⊆(A∩B)成立的所有a值的集合是什么?解:由题有:A ⊆A∩B,即A⊆B,A非空,用数轴表示为,那么⎪⎩⎪⎨⎧≤-≥+-≤+22533125312aaaa由方程表示为:6≤a≤9评述:要使A A∩B,需A ⊆A且A⊆B,又A⊆A恒成立,故A⊆B,由数轴得不等式.注意A是非空.假设去掉这一条件效果如何.求解过程及结果是否会变化.请考虑.6.集合A={x|x2-〔p+2〕x+1=0,x∈R|,设B={正实数},且A B=φ,务实数p的取值范围.解析:AB=φ,即方程x2-〔p+2〕x+1=0没有正实根.由AB=φ,∴A=φ或者者A≠φ〔此时A中无正根〕.当A=φ时,即方程x2-〔p+2〕x+1=0无实根,△=〔p+2〕2-4<0,解得-4<p<0.当A≠φ时,即方程x2-〔p+2〕x+1=0无正根,那么⎩⎨⎧≤≥,+,-+24)2(2pp解得p≤-4.综上,知p<0.点评:注意此题不要丢掉无实根这一情况,最后p的取值范围是对两种情况求并集.进步题:1.在100种食物中,含维生素A的有53种,含维生素C的有72种,那么同时含有维生素A与维生素C的食物可能取数的最小值是多少?解析:画韦氏图.设同时含有维生素A与维生素C的食物的种数为x,不含有维生素A与维生素C的食物的种数为y,那么0≤y≤28,y∈N,所以〔53-x〕+〔72-x〕+x+y=100,解得x=25+y,当y=0时,x取最小值25.答案:25.α、β,方程x2-bx+c=0的两根为γ、δ,其中α、β、γ、δ互不2.方程x2-ax+b=0的两根为α、β、γ、δ},且集合S={x|x=u+υ,u∈M,υ∈M,u≠υ},P={x|x=uυ,相等,设集合M={u∈M,υ∈M,u≠υ},假设S={5,7,8,9,10,12},P={6,10,14,15,21,35},求a,b,c.αβ∈P,b=γ+δ∈S,解析:∵b=∈p S={10},故b=10.∴bα+β,α+γ,α+δ,β+γ,β+δ,γ+δ,它们的和是因为S的元素是α+β+γ+δ〕=5+7+8+9+10+12=51由韦达定理,得3〔α+β=a,γ+δ=b,∴a+b=17.∵b=10,∴a=7.αβ,αγ,αδ,βγ,βδ,γδ,它们的和是αβ+〔γ+δ〕〔α+β〕+因为P的元素是γδ=6+10+14+15+21+35由韦达定理,得b+ac+c=101.∵b=10,a=7,∴c=21.答案:a=7,b=10,c=21.3.开运动会时,高一某班28名同学参加比赛,有15人参加游泳比赛,有8人参加田径比赛,有14人参加球类比赛,同时参加游泳径比赛的3人,同时参加游泳和球类比赛的有3人,没有同时参加三项比赛的人,问同时参加田径和球类比赛的有多少人,只有参加游泳一项比赛的有多少人?思路:此题涉及到元素个数问题,可用公式:card〔ABC〕=cardA+cardB+cardC-card〔AB〕-card〔BC〕-card〔AC〕+card〔AC〕+card〔ABC〕,或者者利用文氏图.设同时参加田径和球类比赛的一一共有x人,参加游泳为A,那么cardA=15,参加田径为B,cardB=8,参加球类为C,cardC=14,由条件card〔AB〕=3,card〔AC〕=3,ABC=φ,故有15+8+14-3-3-x=28,解得x=3,因此,同时参加田径和球类比赛的一一共有3人,同时只参加游泳的有15-3-3=9人.4.设集合M={a,b},N={c,d},定义M与N的一个运算“〞为:M N={x|x=mn,其中m∈M,n∈N}.〔1〕试举出两组集合M、N,分别计算M N;〔2〕对上述集合M、N,计算N M,由此你可以得到什么一般性的结论〔3〕举例说明〔A B〕C与A〔B C〕之间的关系.思路分析:此题是一道开放型的信息迁移题,解题时必须紧扣新定义,用好新信息.解:〔1〕不妨设M={1,2},N={3,4},那么M N={3,4,6,8};或者者设M={-1,1},N={3,-3},那么M N={-3,3}等.〔2〕对M={1,2},N={3,4},那么N M={3,6,4,8};对M={-1,1},N={3,-3},那么N M={-3,3}.由〔1〕知,N M=M N,由此猜测,对任意集合M={a,b},N={c,d},总有M N=N M.证明如下:对任意x∈M N,有x=mn,其中m∈M,n∈N;又x=mn=nm,那么x∈N M.于是M N⊆N M.对任意x∈N M,有x=nm,其中n∈N,m∈M;又x=nm=mn,那么x∈N M.于是N M⊆M N.因此M N=N M.〔3〕设A={-1,1},B={3,-3},C={2,4},那么A B={-3,3},于是〔A B〕C={-6,6,-12,12};又B C={6,12,-6,-12},于是A〔B C〕={-6,-12,6,12}.因此〔A B〕C=A〔B C〕.。
高中数学 第一讲 集合的概念与运算教案(教师版) 新人教版

第一讲 集合的概念与运算教学目的: 理解集合、子集、交集、并集、补集的概念。
了解空集和全集的意义,了解属于、包含、相等关系的意义,能正确进行“集合语言”、“数学语言”“图形语言”的相互转化.教学重点: 交集、并集、补集的定义与运算.教学难点: 交集、并集、补集的定义及集合的应用.【知识概要】新课标教学目标: 1.集合的含义与表示(1)通过实例,了解集合的含义,体会元素与集合的“属于”关系;(2)能选择自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题,感受集合语言的意义和作用; 2.集合间的基本关系(1)理解集合之间包含与相等的含义,能识别给定集合的子集; (2)在具体情境中,了解全集与空集的含义; 3.集合的基本运算(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集; (2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集;(3)能使用Venn 图表达集合的关系及运算,体会直观图示对理解抽象概念的作用. 知识点1 集合某些指定的对象集在一起就成为一个集合。
集合中每个对象叫做这个集合的元素 点评:(1)集合是数学中不加定义的基本概念.构成集合的元素除了常见的数、式、点等数学对象之外,还可以是其他任何对象. (2)集合里元素的特性确定性:集合的元素,必须是确定的.任何一个对象都能明确判断出它是或者不是某个集合的元素.互异性:集合中任意两个元素都是不相同的,也就是同一个元素在集合中不能重复出现. 无序性:集合与组成它的元素顺序无关.如集合{a, b, c}与{c, a, b}是同一集合. (3)元素与集合的关系如果a 是集合A 的元素,就说a 属于集合A ,记作a ∈A ;如果a 不是集合A 的元素,就说a 不属于集合A ,记作a ∉A (或a ∈A ).(4)集合的分类集合的种类通常可分为有限集、无限集、空集(用记号φ表示).有限集:含有有限个元素的集合(单元素集:只有一个元素的集合叫做单元素集。
人教A版高中数学必修一第一章教案交集与并集(1)

第七教时教材:交集与并集(2)目的:通过复习及对交集与并集性质的剖析,使学生对概念有更深刻的理解 过程:一、复习:交集、并集的定义、符号提问(板演):(P 13 例8 )设全集 U = {1,2,3,4,5,6,7,8},A = {3,4,5} B = {4,7,8} 求:(C U A )∩(C U B), (C U A)∪(C U B), C U (A ∪B), C U (A ∩B)解:C U A = {1,2,6,7,8} C U B = {1,2,3,5,6}(C U A)∩(C U B) = {1,2,6}(C U A)∪(C U B) = {1,2,3,5,6,7,8}A ∪B = {3,4,5,7,8} A ∩B = {4}∴ C U (A ∪B) = {1,2,6}C U (A ∩B) = {1,2,3,5,6,7,8,}结合图 说明:我们有一个公式:(C U A)∩( C U B) = C U (A ∪B)(C U A)∪( C U B) = C U (A ∩B)二、另外几个性质:A ∩A = A, A ∩φ= φ, A ∩B = B ∩A,A ∪A = A, A ∪φ= A , A ∪B = B ∪A.(注意与实数性质类比)例6 ( P 12 ) 略进而讨论 (x,y) 可以看作直线上的点的坐标A ∩B 是两直线交点或二元一次方程组的解同样设 A = {x | x 2-x -6 = 0} B = {x | x 2+x -12 = 0}则 (x 2-x -6)(x 2+x -12) = 0 的解相当于 A ∪B即:A = {3,-2} B = {-4,3} 则A∪B = {-4,-2,3} 三、关于奇数集、偶数集的概念略见P12例7 (P12 )略练习P13四、关于集合中元素的个数规定:集合A 的元素个数记作:card (A)观察、分析得:作图card (A∪B) = card (A) +card (B) -card (A∩B)五、(机动):《课课练》P8 课时5 “基础训练”、“例题推荐”六、作业:课本P14 6、7、8《课课练》P8—9 课时5中选部分。
人教版高一数学必修一教案(优秀4篇)

人教版高一数学必修一教案(优秀4篇)人教版高一数学必修一教案篇一教学目的:(1)理解两个集合的并集与交集的的含义,会求两个简单集合的并集与交集;(2)能用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用。
课型:新授课教学重点:集合的交集与并集的概念;教学难点:集合的交集与并集“是什么”,“为什么”,“怎样做”;教学过程:一、引入课题我们两个实数除了可以比较大小外,还可以进行加法运算,类比实数的加法运算,两个集合是否也可以“相加”呢?思考(P9思考题),引入并集概念。
二、新课教学1、并集一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集(Union)记作:A∪B 读作:“A并B”即:A∪B={x|x∪A,或x∪B}Venn图表示:说明:两个集合求并集,结果还是一个集合,是由集合A与B的所有元素组成的集合(重复元素只看成一个元素)。
例题1求集合A与B的并集① A={6,8,10,12} B={3,6,9,12}② A={x|-1≤x≤2} B={x|0≤x≤3}(过度)问题:在上图中我们除了研究集合A与B的并集外,它们的公共部分(即问号部分)还应是我们所关心的,我们称其为集合A与B的交集。
2、交集一般地,由属于集合A且属于集合B的元素所组成的集合,叫做集合A与B的交集(intersection)。
记作:A∩B 读作:“A交B”即:A∩B={x|∪A,且x∪B}交集的Venn图表示说明:两个集合求交集,结果还是一个集合,是由集合A与B的公共元素组成的集合。
例题2求集合A与B的交集③ A={6,8,10,12} B={3,6,9,12}④ A={x|-1≤x≤2} B={x|0≤x≤3}拓展:求下列各图中集合A与B的并集与交集(用彩笔图出)说明:当两个集合没有公共元素时,两个集合的交集是空集,而不能说两个集合没有交集3、例题讲解例3(P12例1):理解所给集合的含义,可借助venn图分析例4 P12例2):先“化简”所给集合,搞清楚各自所含元素后,再进行运算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学交集并集教案新人教版必修1
一、教学目标
1.交集
2.并集
二、考点、典型例题
1.交集
际上“A⋂B”是由所有集合A和集合B的公共元素所组成的集合,用集合的方法,可以表示为:x
x
对A⋂φ=φ证明如下:假设存在元素),
(φ
⋂
∈A
x则由交集定义,得,φ
∈
x与空集中的定义矛盾,所此外,还容易证明A⋂B= B与B A
⊆等价,这个结论在解题时会用到.
x
x x
x
x
x
x
x
2 并集
(1)并集的定义
由所有
..属于集合A或.属于集合B的元素所组成的集合,叫做集合A与B的并集,用符号“"
B
A⋃表示,实际上“B
A⋃”是由集合A和集合B中所有元素组成的集合,但集合A与集合B中的公共元素在B
A⋃中只能出现一次。
用集合的写法,可以表示为{}
B
x
A
x
x
B
A∈
∈
=
⋃或
,.
应注意:这里“B
x
A
x∈
∈或
,”中“或”的意义包含三种情况:①;
,B
x
A
x∉
∈但②;
,B
x
A
x∈
∉但
))y y x x x x 例7.已知集合{}{}
A B B A mx x x B c x x x A ,,06,06=⋃=++==++=且B ⋂={}2,求实数b,c,m 例9. 若用n (A)表示有限集A 的元素个数。
x x x x x x x x 5.设全集U=R ,集合{}{}0)()
(,0)(,0)(=====x g x f x g x N x f x M 则方程的解集是( ).
6.设全集为U ,非空集合A ,B 满足A ⊂B ⊂U ,则( ).
C.A ⋂( ⋃B)=φ
D.( ⋃A)⋂( ⋃ B)=φ
-x 0x x x x x ( S A )⋂B={},9S (A ⋃B )={},7,5 则A=___________,B=_____________.
11.已知集合A={},0=-x x x B={},042=+-x ax x 且A ⋂B=B ,求实数a 的取值范围。
求实数a 的取值范围. 14.已知A ={},01)1(2=+--ax x a x B={},01272=+-x x x C={
)2)(1(--x x x },0)3(=-x 若A ⋂B=,φA ⋃C =C ,求实数a 的值.。
