《概率论与随机过程》第1章习题答案汇编

合集下载

《概率论与随机过程》第1章习题答案

《概率论与随机过程》第一章习题答案1. 写出下列随机试验的样本空间。

（1）记录一个小班一次数学考试的平均分数（设以百分制记分）。

解： ⎭⎬⎫⎩⎨⎧⨯=n n nn S 100,,1,0 ，其中n 为小班人数。

（2）同时掷三颗骰子，记录三颗骰子点数之和。

解：{}18,,4,3 =S 。

（3） 10只产品中有3只是次品，每次从其中取一只（取出后不放回），直到将3只次品都取出，记录抽取的次数。

解： {}10,,4,3 =S 。

（4）生产产品直到得到10件正品，记录生产产品的总件数。

解： {} ,11,10=S 。

（5）一个小组有A ，B ，C ，D ，E5个人，要选正副小组长各一人（一个人不能兼二个职务），观察选举的结果。

解： {}ED EC EB EA DE DC DB DA CE CD CB CA BE BD BC BA AE AD AC AB S ,,,,,,,,,,,,,,,,,,,=其中，AB 表示A 为正组长，B 为副组长，余类推。

（6）甲乙二人下棋一局，观察棋赛的结果。

解： {}210,,e e e S =其中，0e 为和棋，1e 为甲胜，2e 为乙胜。

（7）一口袋中有许多红色、白色、蓝色乒乓球，在其中任意取4只，观察它们具有哪几种颜色。

解： {}rwb wb rb rw b w r S ,,,,,,=其中，,,,b w r 分别表示红色、白色、蓝色。

（8）对某工厂出厂的产品进行检查，合格的盖上“正品”，不合格的盖上“次品”，如连续查出二个次品就停止检查，或检查4个产品就停止检查，记录检查的结果。

解： {}1111,1110,1101,0111,1011,1010,1100,0110,0101,0100,100,00=S 其中，0为次品，1为正品。

（9）有A ，B ，C 三只盒子，a ，b ，c 三只球，将三只球装入三只盒子中，使每只盒子装一只球，观察装球的情况。

概率论与数理统计第一章习题解答

《概率论与数量统计》第一章习题解答1、写出下列随机试验的样本空间：（1）记录一个班一次数学考试的平均分数（设以百分制记分）。

（2）生产产品直到有10件正品为止，记录生产产品的总件数。

（3）对某工厂出厂的产品进行检查，合格的产品记上“正品”，不合格的记上“次品”，如连续查出了2件次品就停止检查，或检查了4件产品就停止检查，记录检查的结果。

（4）在单位圆内任意取一点，记录它的坐标。

解：（1）设该班有n人，则该班总成绩的可能值是0，1，2，……，100n。

故随机试验的样本空间S=｛i/n|i=0,1,2,……,100n｝。

（2）随机试验的样本空间S=｛10,11,12,……｝。

（3）以0表示检查到一个次品，1表示检查到一个正品，则随机试验的样本空间S=｛00，0100，0101，0110，0111，100，1010，1011，1100，1101，1110，1111｝。

（4）随机试验的样本空间S=｛（x,y）|x2+y2<1｝。

2、设A，B，C为三个事件，用A，B，C的运算关系表示下列各事件：（1）A发生，B 与C都不发生。

（2）A与B都发生，而C不发生。

（3）A，B，C中至少有一个发生。

（4）A，B，C都发生。

（5）A，B，C都不发生。

（6）A，B，C中不多于一个发生。

（7）A，B，C中不多于两个发生。

（8）A，B，C中至少有两个发生。

解：（1）A B C（2）AB C（3）A∪B∪C （4）ABC（5）A B C（6）A B C∪A B C∪A B C∪A B C（7）S-ABC （8）ABC∪AB C∪A B C∪A BC3、（1）设A，B，C为三个事件，且P（A）=P（B）=P（C）=1/4，P（AB）=P（BC）=0，P（AC）=1/8，求A，B，C至少有一个发生的概率。

（2）已知P（A）=1/2，P（B）=1/3，P（C）=1/5，P（AB）=1/10，P（AC）=1/15，P（BC）=1/20，P（ABC）=1/30，求A∪B，A B，A∪B∪C，A B C，A B C，A B∪C的概率。

概率论~第一章习题参考答案与提示

第一章随机事件与概率习题参考答案与提示1．设为三个事件，试用表示下列事件，并指出其中哪两个事件是互逆事件：C B A 、、C B A 、、（1）仅有一个事件发生；（2）至少有两个事件发生；（3）三个事件都发生；（4）至多有两个事件发生；（5）三个事件都不发生；（6）恰好两个事件发生。

分析：依题意，即利用事件之间的运算关系，将所给事件通过事件表示出来。

C B A 、、解：（1）仅有一个事件发生相当于事件C B A C B A C B A 、、有一个发生，即可表示成C B A C B A C B A ∪∪；类似地其余事件可分别表为（2）或AC BC AB ∪∪ABC B A BC A C AB ∪∪∪；（3）；（4）ABC ABC 或C B A ∪∪；（5）C B A ；（6）B A BC A C AB ∪∪或。

ABC AC BC AB −∪∪ 由上讨论知，（3）与（4）所表示的事件是互逆的。

2．如果表示一个沿着数轴随机运动的质点位置，试说明下列事件的包含、互不相容等关系：x {}20|≤=x x A {}3|>=x x B {}9|<=x x C{}5|−<=x x D{}9|≥=x x E 解：（1）包含关系：、 A C D ⊂⊂B E ⊂ 。

（2）互不相容关系：C 与E （也互逆）、B 与、D E 与。

D 3．写出下列随机事件的样本空间：（1）将一枚硬币掷三次，观察出现H （正面）和T （反面）的情况；（2）连续掷三颗骰子，直到6点出现时停止, 记录掷骰子的次数；（3）连续掷三颗骰子，记录三颗骰子点数之和；（4）生产产品直到有10件正品时停止，记录生产产品的总数。

提示与答案：（1）；{}TTT TTH THT HTT THH HTH HHT HHH ,,,,,,,=Ω（2）； {,2,1=Ω}（3）；{}18,,4,3 =Ω（4）。

{} ,11,10=Ω4．设对于事件有C B A 、、=)(A P 4/1)()(==C P B P , ，8/1)(=AC P0)()(==BC P AB P ，求至少出现一个的概率。

《随机过程》课后习题解答

6、证函数 f (t ) 解（1）
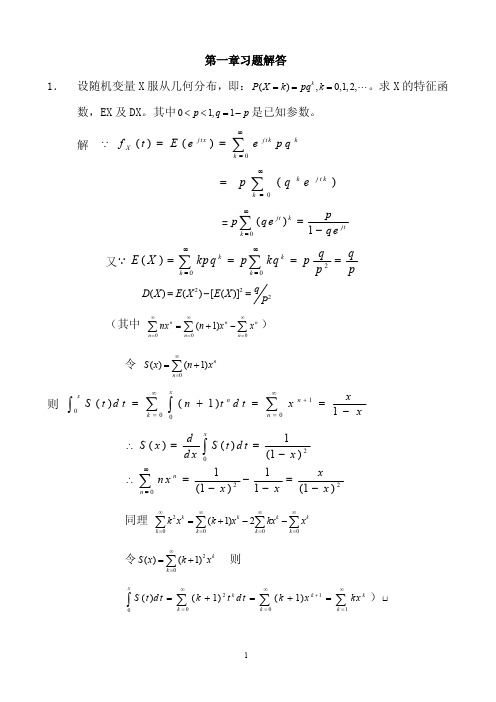
（ k 0, 2, n ）
1 为一特征函数，并求它所对应的随机变量的分布。 1 t2
n n i
f (t
i 1 k 1
tk )i k
5
=
i 1 k 1
n
n
i k
1 (ti tk )
2

i 1 k 1
n
n
e jti e jti e jti {1 ( jtk )(1 jtk )} n n e jtk e e i k jti = i 1 k 1 e n(1 jtk ) e
1 n n n j ( ti tk ) l ] i k = [e n i 1 k 1 l 1
（2）（3）
其期望和方差；证明对具有相同的参数的 b 的分布，关于参数 p 具有可加性。
解（1）设 X 服从 ( p , b ) 分布，则
f X (t ) e jtx
0
b p p 1 bx x e dx ( p )
bp ( p)

x
0
p 1 ( jt b ) x
i k
1 M 2
0
ti t k } ）（ M 1max{ i , j n
且 f (t ) 连续 f (0) 1 （2） f (t )

f (t ) 为特征函数
1 1 1 1 1 [ ] 2 2 1 t 1 ( jt ) 2 1 jt 1 jt

3
fZ(k)() t (1 )kk! jk (1 jt)(k1)
E (Z k ) 1 (k ) f Z (0) ( 1) k k ! k j
n

随机过程第一章习题答案

似水年华轻轻一瞥，年华似水轻描淡写
随机过程第一章习题答案
1.方法一： F (t ; x) P{ X (t ) x} P{ X sin t x} 当t k 时，P{ X (t ) 0} 1,其中k为整数，
k 当t 时，
x x sin t （i）若 sin t 0, F (t ; x) P{ X } ( x) dx sin t x 1 1 1 1 x 2 f (t ; x) ( ) exp{ ( )} sin t sin t sin t 2 2 sin t x x x sin t (ii )若 sin t 0, F (t ; x) P{ X } 1 P{ X } 1 ( x)dx sin t sin t 1 1 1 x 2 f (t ; x) Fx' (t ; x) exp{ ( )} sin t 2 2 sin t 1 1 x 2 f (t ; x) exp{ ( ) }, k 为整数。 2 sin t 2 sin t

时，k为整数，有 X
一维分布密度为：f (t ; x) 当t= k

时，k为整数，有P{ X (t ) 0} 1
1 1 Xt x}=P{e } e Xt x 1 1 1 =P{Xt ln }=P{Xt ln x}=P{X ln x}=1-P{X ln x} x t t 1 11 1 1 f (t ; x) Fx' (t ; x) f ( ln x)( ) f ( ln x) t t x tx t 2.F(t;x)=P{X(t) x}=P{e Xt x}=P{
方法二： X N(0,1) EX=0,EX 2 =DX=1 EX(t)=E(Xsin t)=sin tEX 0 k N(0 , sin 2 t) 1 1 x 2 exp{ ( ) }, x 2 sin t 2 sin t DX (t ) D(Xsin t) (sin t) 2 DX sin 2 t 当t

概率论与数理统计答案第一章

概率论第一章习题解答习题1.11．写出下列随机试验的样本空间Ω及指定的事件：（1）袋中有3个红球和2个白球，现从袋中任取一个球，观察其颜色；（2）掷一枚硬币，设H 表示“出现正面”，T 表示“出现反面”．现将一枚硬币连掷两次，观察出现正、反面的情况，并用样本点表示事件A =“恰有一次出现正面”；（3）对某一目标进行射击，直到击中目标为止，观察其射击次数，并用样本点表示事件A =“射击次数不超过5次”；（4）生产某产品直到5件正品为止，观察记录生产该产品的总件数；（5）从编号a 、b 、c 、d 的四人中，随机抽取正式和列席代表各一人去参加一个会议，观察选举结果，并用样本点表示事件A =“编号为a 的人当选”．解：（1）Ω = {红色, 白色}；（2）Ω = {(H , H ), (H , T ), (T , H ), (T , T )}，A = {(H , T ), (T , H )}；（3）Ω = {1, 2, 3, …, n , …}，A = {1, 2, 3, 4, 5}；（4）Ω = {5, 6, 7, …, n , …}；（5）Ω = {(a , b ), (a , c ), (a , d ), (b , a ), (b , c ), (b , d ), (c , a ), (c , b ), (c , d ), (d , a ), (d , b ), (d , c )}，A = {(a , b ), (a , c ), (a , d ), (b , a ), (c , a ), (d , a )}．2．某射手射击目标4次，记事件A =“4次射击中至少有一次击中”，B =“4次射击中击中次数大于2”．试用文字描述事件A 与B ．解：A 表示4次射击都没有击中，B 表示4次射击中击中次数不超过2．3．设A , B , C 为三个事件，试用事件的运算关系表示下列事件：（1）A , B , C 都发生；（2）A , B , C 都不发生；（3）A , B , C 中至少有一个发生；（4）A , B , C 中最多有一个发生；（5）A , B , C 中至少有两个发生；（6）A , B , C 中最多有两个发生．解：（1）ABC ；（2）C B A ；（3）A ∪B ∪C ；（4）C B A C B A C B A C B A U U U ；（5）ABC BC A AB U U U ；（6）ABC ．4．在一段时间内，某电话交换台接到呼唤的次数可能是0次，1次，2次，…．记事件A n =“接到的呼唤次数小于n ”（n = 1, 2, …），试用事件的运算关系表示下列事件：（1）呼唤次数大于2；（2）呼唤次数在5到10次范围内；（3）呼唤次数与8的偏差大于2．解：（1）3A ；（2）A 11 − A 5；（3）116A A U ．5．证明：（1）Ω=−A B A AB U U )(；（2）AB B A B A B A =))()((U U U ．证：（1）Ω==Ω===−A A B A A AB B A AB U U U U U U U U )()(；（2）U U U U U U A B A B B A B A B A B A ())(())()((==∅AB AB A A B A A B A ===U U U )())(．习题1.21．设P (A ) = P (B ) = P (C ) = 1/4，P (AB ) = P (BC ) = 0，P (AC ) = 1/8，求A 、B 、C 三个事件至少有一个发生的概率．解：因P (AB ) = P (BC ) = 0，且ABC ⊂ AB ，有P (ABC ) = 0，则8581414141)()()()()()()()(=−++=+−−−++=ABC P BC P AC P AB P C P B P A P C B A P U U ． 2．设P (A ) = 0.4，P (B ) = 0.5，P (A ∪B ) = 0.7，求P (A − B )及P (B − A )．解：因P (AB ) = P (A ) + P (B ) − P (A ∪B ) = 0.4 + 0.5 − 0.7 = 0.2，则P (A − B ) = P (A ) − P (AB ) = 0.4 − 0.2 = 0.2，P (B − A ) = P (B ) − P (AB ) = 0.5 − 0.2 = 0.3．3．某市有A , B , C 三种报纸发行．已知该市某一年龄段的市民中，有45%的人喜欢读A 报，34%的人喜欢读B 报，20%的人喜欢读C 报，10%的人同时喜欢读A 报和B 报，6%的人同时喜欢读A 报和C 报，4%的人同时喜欢读B 报和C 报，1%的人A , B , C 三种报纸都喜欢读．从该市这一年龄段的市民中任选一人，求下列事件的概率：（1）至少喜欢读一种报纸；（2）三种报纸都不喜欢；（3）只喜欢读A 报；（4）只喜欢读一种报纸．解：分别设A , B , C 表示此人喜欢读A , B , C 报，有P (A ) = 0.45，P (B ) = 0.34，P (C ) = 0.2，P (AB ) = 0.1，P (AC ) = 0.06，P (BC ) = 0.04，P (ABC ) = 0.01，（1）P (A ∪B ∪C ) = P (A ) + P (B ) + P (C ) − P (AB ) − P (AC ) − P (BC ) + P (ABC ) = 0.8；（2）2.0)(1)((=−==C B A P C B A P P U U U U ；（3）3.0)()()()()()()(=+−−=−=ABC P AC P AB P A P B A P B A P C B A P ；（4）因21.0)()()()()()()(=+−−=−=ABC P BC P AB P B P P B P B P ，11.0)()()()()()()(=+−−=−=ABC P BC P AC P C P BC A P C A P C B A P ，故62.0)()()()(=++=++C B A P C B A P C B A P C B A C B A C B A P ．4．连续抛掷一枚硬币3次，求既有正面又有反面出现的概率．解：样本点总数n = 2 3 = 8，事件A 中样本点数62313=+=C C k A ，则75.043)(===n k A P A ． 5．在分别写有2, 4, 6, 7, 8, 11, 12, 13的8张卡片中任取两张，把卡片上的两个数字组成一个分数，求所得分数为既约分数的概率．解：样本点总数2828==C n ，事件A 中样本点数18231315=+=C C C k A ，则6429.0149)(===n k A P A ． 6．一部5卷文集任意地排列在书架上，问卷号自左向右或自右向左恰好为1, 2, 3, 4, 5顺序的概率等于多少？解：样本点总数12055==A n ，事件A 中样本点数k A = 2，则0167.0601)(===n k A P A ． 7． 10把钥匙中有3把能打开某一门锁，今任取两把，求能打开某该门锁的概率．解：样本点总数45210==C n ，事件A 中样本点数24231317=+=C C C k A ，则5333.0158)(===n k A P A ． 8．一副扑克牌有52张，进行不放回抽样，每次一张，连续抽取4张，计算下列事件的概率：（1）四张花色各异；（2）四张中只有两种花色．解：样本点总数270725452==C n ，（1）事件A 1中样本点数285611131131131131==C C C C k A ，则1055.0208252197)(11===n k A P A ；（2）事件A 2表示两种花色各两张，或者一种1张一种3张，样本点数81120)2(113313213213242=+=C C C C C k A ，则2996.041651248)(22===n k A P A ． 9．口袋内装有2个伍分、3个贰分、5个壹分的硬币共10枚，从中任取5枚，求总值超过壹角的概率．解：样本点总数252510==C n ，事件A 分三种情形：①两枚5分，三枚其它，②一枚5分，三枚2分，一枚1分，③一枚5分，两枚2分，两枚1分，样本点数1262523121533123822=++=C C C C C C C C k A ，则5.021)(===n k A P A ．方法二：10枚硬币总额2角1分，任取5枚若超过1角，那么剩下的5枚将不超过1角，可见事件A 中的样本点与A 中的样本点一一对应，即A k k =，则5.0)()(==A P A P ．10．在10个数字0, 1, 2, …, 9中任取4个（不重复），能排成一个4位偶数的概率是多少（最好是更正为：排在一起，恰好排成一个4位偶数的概率是多少）？解：样本点总数5040410==A n ，事件A 的限制条件是个位是偶数，首位不是0，样本点数2296281814281911=+=A A A A A A k A ，则4556.09041)(===n k A P A ． 11．一个教室中有100名学生，求其中至少有一人的生日是在元旦的概率（设一年以365天计算）．解：样本点总数n = 365 100，A 的对立事件A 表示所有学生生日都不在元旦，100364=A k ，则2399.036536411(1)(100=⎟⎠⎞⎜⎝⎛−=−=−=n k A P A P A ．12．在 [0, 1] 区间内任取两个数，求两数乘积小于1/4的概率．解：设所取得两个数为x , y ，Ω = {(x , y ) | 0 < x < 1, 0 < y < 1}，}1,10,10|),{(<<<<=y x y x A 有m (Ω) = 1，4034.042ln 23)41ln 4141(1)ln 41(411()(141141=−=−−=−=−=∫x x dx x A m 则5966.042ln 21)()(1(1)(=+=Ω−=−=m A m P A P ．习题1.31．一只盒子有3只坏晶体管和7只好晶体管，在其中取二次，每次随机地取一只，作不放回抽样，发现第一只是好的，问另一只也是好的概率是多少？解：设A 表示第一只是好的，B 表示第二只是好的，当第一只是好的时，第二次抽取前有3只是坏的，6只是好的，则6667.03296)|(===A B P ． 2．某商场从生产同类产品的甲、乙两厂分别进货100件、150件，其中：甲厂的100件中有次品4件，乙厂的150件中有次品1件．现从这250件产品中任取一件，从产品标识上看它是甲厂生产的，求它是次品的概率．解：设A 表示甲厂产品，B 表示次品，故04.01004)|(==A B P ． 3．根据抽样调查资料，2000年某地城市职工家庭和农村居民家庭收入按人均收入划分的户数如下：户数 6000元以下 6000 ~ 12000元 12000元以上合计城市职工 25 125 50 200 农村居民 120 132 48 300 合计 145 257 98 500 现从被调查的家庭中任选一户，已知其人均收入在6000元以下，试问这是一个城市职工家庭的概率是多少？解：设A 表示人均收入在6000元以下，B 表示城市职工家庭，故1724.014525)|(==A B P ． 4．某单位有92%的职工订阅报纸，93%的职工订阅杂志，在不订阅报纸的职工中仍有85%的职工订阅杂志，从单位中任找一名职工，求下列事件的概率：（1）该职工至少订阅报纸或杂志中一种；（2）该职工不订阅杂志，但是订阅报纸．解：设A 表示订阅报纸，B 表示订阅杂志，有P (A ) = 0.92，P (B ) = 0.93，85.0|(=A B P ，则068.085.008.0)|()()(=×==A B P A P B A P ，862.0068.093.0)()()(=−=−=B A P B P AB P ，（1）P (A ∪B ) = P (A ) + P (B ) − P (AB ) = 0.92 + 0.93 − 0.068 = 0.988；（2）P (A − B ) = P (A ) − P (AB ) = 0.92 − 0.862 = 0.058．5．某工厂有甲、乙、丙三个车间生产同一种产品，各个车间的产量分别占全厂产量的25%、35%、40%，各车间产品的次品率分别为5%、4%、2%．（1）求全厂产品的次品率；（2）如果从全厂产品中抽取一件产品，恰好是次品，问这件次品是甲、乙、丙车间生产的概率分别是多少？解：（1）任取一件产品，设A 1, A 2, A 3分别表示甲、乙、丙车间产品，B 表示次品，则P (B ) = P (A 1) P (B | A 1) + P (A 2) P (B | A 2) + P (A 3) P (B | A 3)= 0.25 × 0.05 + 0.35 × 0.04 + 0.4 × 0.02 = 0.0345；（2）3623.069250345.005.025.0)()|()()()()|(1111==×===B P A B P A P B P B A P B A P ， 4058.069280345.004.035.0)()|()()()()|(2222==×===B P A B P A P B P B A P B A P ， 2319.069160345.002.04.0)()|()()()()|(3333==×===B P A B P A P B P B A P B A P ． 6．有三个形状相同的罐，在第一罐中有两个白球和一个黑球；在第二个罐中有三个白球和一个黑球；在第三个罐中有两个白球和两个黑球．某人随机地取一罐，再从该罐中任取一球，试问这球是白球的概率有多少？解：设321,,A A A 分别表示第一、二、三罐，B 表示白球，则6389.03623423143313231)|()()|()()|()()(332211==×+×+×=++=A B P A P A B P A P A B P A P B P ． 7．三部自动的机器生产同样的汽车零件，其中机器A 生产的占40%，机器B 生产的占25%，机器C 生产的占35%，平均说来，机器A 生产的零件有10%不合格，对于机器B 和C ，相应的百分数分别为5%和1%，如果从总产品中随机地抽取一个零件，发现为不合格，试问：（1）它是由机器A 生产出来的概率是多少？（2）它是由哪一部机器生产的可能性最大？解：设A 1, A 2, A 3分别表示机器A , B , C 生产的零件，D 表示不合格的零件，（1）)|()()|()()|()()|()()()()|(3322111111A D P A P A D P A P A D P A P A D P A P D P D A P D A P ++== 7143.075056.004.001.035.005.025.01.04.01.04.0===×+×+××=；（2）2232.011225056.00125.0056.005.025.0)()()|(22===×==D P D A P D A P ，0625.01127056.00035.0056.001.035.0)()()|(33===×==D P D A P D A P ，则由机器A 生产的概率最大．8．设P (A ) > 0，试证：)()(1)|(A P B P A B P −≥．证：)()(1)()(11)(1)()()()()()()()()|(A P B P A P B P A P B P A P A P B A P B P A P A P AB P A B P −=−−=−+≥−+==U ．习题1.41．一个工人看管三台机床，在一小时内机床不需要工人看管的概率分别为0.9、0.8、0.7，求在一小时内3台机床中最多有一台需要工人看管的概率．解：设A 1, A 2, A 3分别表示一小时内第一、二、三台机床不需要工人照管，可以认为A 1, A 2, A 3相互独立，则概率为)()()()()(321321321321321321321321A A A P A A A P A A A P A A A P A A A A A A A A A A A A P +++=U U U)()()()()()()()()()()()(321321321321A P A P A P A P A P A P A P A P A P A P A P A P +++== 0.9 × 0.8 × 0.7 + 0.9 × 0.8 × 0.3 + 0.9 × 0.2 × 0.7 + 0.1 × 0.8 × 0.7 = 0.902．2．电路由电池A 与两个并联的电池B 及C 串联而成，设电池A , B ,电路发生断电的概率．解：设A , B , C 分别表示电池A , B , C 损坏，电路断电为事件A ∪BC ，则概率为P (A ∪BC ) = P (A ) + P (BC ) − P (ABC ) = P (A ) + P (B ) P (C ) − P (A ) P (B ) P (C ) = 0.3 + 0.2 × 0.2 − 0.3 × 0.2 × 0.2 = 0.328．方法二：设A , B , C 分别表示电池A , B , C 正常工作，系统正常工作为事件A (B ∪C ) = AB ∪AC ，则概率为1 − P (AB ∪AC ) = 1 − P (AB ) − P (AC ) + P (ABC )= 1 − P (A ) P (B ) − P (A ) P (C ) + P (A ) P (B ) P (C )= 1 − 0.7 × 0.8 − 0.7 × 0.8 + 0.7 × 0.8 × 0.8 = 0.328．3．加工某一零件共需经过四道工序．设第一、二、三、四道工序的次品率分别为2%, 3%, 5%, 3%，假定各道工序是互不影响的，求加工出来的零件的次品率．解：设A 1, A 2, A 3, A 4分别表示第一、二、三、四道工序加工出合格品，有A 1, A 2, A 3, A 4相互独立，则概率为1 − P (A 1A 2A 3A 4) = 1 − P (A 1) P (A 2) P (A 3) P (A 4) = 1 − 0.98 × 0.97 × 0.95 × 0.97 = 0.1240．4．抛掷一枚质地不均匀的硬币8次，设正面出现的概率为0.6，求下列事件的概率：（1）正好出现3次正面；（2）至多出现2次正面；（3）至少出现2次正面．解：将每次掷硬币看作一次试验，出现正面A ，反面A ；独立；P (A ) = 0.6．伯努利概型，n = 8，p = 0.6．（1）1239.04.06.0)3(53388=××=C P ；（2）0498.04.06.04.06.04.06.0)2()1()0(622871188008888=××+××+××=++C C C P P P ；（3）9915.04.06.04.06.01)1()0(17118800888=××−××−=−−C C P P ．5．设每次射击时命中率为0.2，问至少必须进行多少次独立射击才能使至少击中一次的概率不小于0.9？解：将每次射击看作一次试验，击中A ，没击中A ；独立；P (A ) = 0.2．伯努利概型，n 次试验，p = 0.2，则9.08.018.02.01)0(100≥−=××−=−n n n n C P ，即0.8 n ≤ 0.1，故32.108.0lg 1.0lg =≥n ，取n = 11．6．一大批产品的优质品率为60%，从中任取10件，求下列事件的概率：（1）取到的10件产品中恰有5件优质品；（2）取到的10件产品中至少有5件优质品；（3）取到的10件产品中优质品的件数不少于4件且不多于8件．解：将取每件产品看作一次试验，优质品A ，非优质品A ；独立；P (A ) = 0.6．伯努利概型，n = 10，p = 0.6．（1）2007.04.06.0)5(5551010=××=C P ；（2）P 10 (5) + P 10 (6) + P 10 (7) + P 10 (8) + P 10 (9) + P 10 (10)288103771046610555104.06.04.06.04.06.04.06.0××+××+××+××=C C C C8338.04.06.04.06.0010101019910=××+××+C C ；（3）P 10 (4) + P 10 (5) + P 10 (6) + P 10 (7) + P 10 (8)28810377104661055510644104.06.04.06.04.06.04.06.04.06.0××+××+××+××+××=C C C C C= 0.8989；7．证明：若)|()|(B A P B A P =，则事件A 与B 独立．证：因)(1)()()(1)()()()|()()()|(B P AB P A P B P B A P P B A P B A P B P AB P B A P −−=−−====，则P (AB )[1 − P (B )] = P (B )[P (A ) − P (AB )]，即P (AB ) − P (AB ) P (B ) = P (B ) P (A ) − P (B ) P (AB )，故P (AB ) = P (A ) P (B )，A 与B 相互独立．复习题一1．设P (A ) = 0.5，P (B ) = 0.6，问：（1）什么条件下P (AB )可以取最大值，其值是多少？（2）什么条件下P (AB )可以取得最小值，其值是多少？解：（1）当A ⊂ B 时P (AB ) 最大，P (AB ) = P (A ) = 0.5；（2）当A ∪B = Ω 时P (AB ) 最小，P (AB ) = P (A ) + P (B ) − P (A ∪B ) = 0.5 + 0.6 − 1 = 0.1．2．一电梯开始上升时载有5名乘客，且这5人等可能地在8层楼的任何一层出电梯，求：（1）每层至多一人离开的概率；（2）至少有两人在同一层离开的概率；（3）只有一层有两人离开的概率．解：样本点总数是8取5次的可重排列，即n = 8 5 = 32768，（1）事件A 1中样本点数6720581==A k A ，则2051.0512105)(11===nk A P A ；（2）事件A 2是A 1的对立事件，则7949.0512407)(1)(12==−=A P A P ；（3）事件A 3表示有两人在同一层离开，而另外三人分别在3个不同楼层或者都在同一层离开，样本点数17360)(33173725183=+=C A A C A k A ，则5298.020481085)(33===n k A P A ． 3．从5副不同的手套中任取4只手套，求其中至少有两只手套配成一副的概率．解：样本点总数210410==C n ，A 的对立事件表示4只手套都不配套，801212121245==C C C C C k A ，则6190.021131(1)(==−=−=n k A P A P A ． 4．从1, 2, …, n 中任取两数，求所取两数之和为偶数的概率．解：样本点总数为)1(212−=n n C n ，事件A 表示取得两个偶数或两个奇数，当n 为偶数时，共有2n 个偶数和2n 个奇数，样本点数)2(41)12(22222−=−=+=n n n n C C k n n A ，则)1(22)(2−−==n n C k A P n A ；当n 为偶数时，共有21−n 个偶数和21+n 个奇数，样本点数2221221)1(41212121232121−=−⋅+⋅+−⋅−⋅=+=+−n n n n n C C k n n A ，则n n C k A P nA 21)(2−==． 5．在中国象棋的棋盘上任意地放上一只红“车”及一只黑“车”，求它们正好可以一只吃掉另一只的概率．解：样本点总数4005290==C n ，事件A 中样本点数7652911021019=+=C C C C k A ，则1910.08917)(===n k A P A ． 6．某货运码头仅能容一船卸货，而甲、乙两船在码头卸货时间分别为1小时和2小时．设甲、乙两船在24小时内随时可能到达，求它们中任何一船都不需等待码头空出的概率．解：Ω = {(x , y ) | 0 ≤ x < 24, 0 ≤ y < 24}，A = {(x , y ) | 0 ≤ x < 24, 0 ≤ y < 24, x − y > 2或y − x > 1}，有m (Ω) = 24 2 = 576，5.50622212321)(22=×+×=A m ，则8793.05765.506)()()(==Ω=m A m A P ． 7．从区间 [0, 1] 中任取三个数，求三数和不大于1的概率．解：Ω = {(x , y , z ) | 0 ≤ x , y , z ≤ 1}，A = {(x , y , z ) | 0 ≤ x , y , z ≤ 1, x + y + z ≤ 1}，有m (Ω) = 1，A 是一个三棱锥，6112131)(=××=A m ，则1667.061)()()(==Ω=m A m A P ． 8．已知5%的男人和0.25%的女人是色盲，现随机地挑选一人，此人恰为色盲，问此人是男人的概率是多少？（假设男人和女人各占人数的一半．）解：设A 1, A 2分别表示男人和女人，B 表示色盲，则9524.021200025.05.005.05.005.05.0)|()()|()()|()()()()|(22111111==×+××=+==A B P A P A B P A P A B P A P B P B A P B A P ． 9．发报台分别以0.7和0.3的概率发出信号0和1（例如：分别用低电频和高电频表示）．由于随机干扰的影响，当发出信号0时，接收台不一定收到0，而是以概率0.8和0.2收到信号0和1；同样地，当发报台发出信号1时，接收台以概率0.9和0.1收到信号1和0．试求：（1）接收台收到信号0的概率；（2）当接收台收到信号0时，发报台确是发出信号0的概率．解：设A 0, A 1分别表示发出信号0, 1，B 0, B 1表示收到信号0, 1，（1）P (B 0) = P (A 0) P (B 0 | A 0) + P (A 1) P (B 0 | A 1) = 0.7 × 0.8 + 0.3 × 0.1 = 0.59；（2）9492.0595659.08.07.0)()|()()()()|(000000000==×===B P A B P A P B P B A P B A P ． 10．设A , B 独立，AB ⊂ D ，D B A ⊂，证明P (AD ) ≥ P (A ) P (D )．证：因AB ⊂ D ，有AB ⊂ AD ，则P (AD ) − P(AB ) = P (AD − AB )，B D ΩA因B A ⊂=U ，有D ⊂ A ∪B ，D − B ⊂ A ∪B − B ⊂ A ，则AD − AB = A (D − B ) = D − B ，故P (AD ) − P (AB ) = P (AD − AB ) = P (D − B ) ≥ P (A ) P (D − B ) ≥ P (A ) [P (D ) − P (B )]，由于A , B 独立，有P (AB ) = P (A ) P (B )，故P (AD ) ≥ P (A ) P (D )．11．甲、乙、丙三人同时向一架飞机射击，他们击中目标的概率分别为0.4, 0.5, 0.7．假设飞机只有一人击中时，坠毁的概率为0.2，若2人击中，飞机坠毁的概率为0.6，而飞机被3人击中时一定坠毁．现在如果发现飞机已被击中坠毁，计算它是由三人同时击中的概率．解：结果：设B 表示目标被击毁，原因：设A 0, A 1, A 2, A 3分别表示无人、1人、2人、3人击中目标，则)|()()|()()|()()|()()|()()()()|(332211003333A B P A P A B P A P A B P A P A B P A P A B P A P B P B A P B A P +++==，且有P (B | A 0) = 0，P (B | A 1) = 0.2，P (B | A 2) = 0.6，P (B | A 3) = 1，又设C 1, C 2, C 3分别表示甲、乙、丙击中目标，则09.03.05.06.0)()()()()(3213210=××===C P C P C P C C C P A P ，)()(3213213211C C C C C C C C C P A P U U =)()()()()()()()()(321321321C P P P P C P P P P C P ++== 0.4 × 0.5 × 0.3 + 0.6 × 0.5 × 0.3 + 0.6 × 0.5 × 0.7 = 0.36，)()(3213213212C C C C C C C C C P A P U U =)()()()()()()()()(321321321C P C P P C P P C P P C P C P ++== 0.4 × 0.5 × 0.3 + 0.4 × 0.5 × 0.7 + 0.6 × 0.5 × 0.7 = 0.41，P (A 3) = P (C 1C 2C 3) = P (C 1) P (C 2) P (C 3) = 0.4 × 0.5 × 0.7 = 0.14，故3057.0458.014.0114.06.041.02.036.0009.0114.0)|(3==×+×+×+××=B A P ． 12．已知某种疾病患者的痊愈率为25%，为试验一种新药是否有效，把它给10个病人服用，且规定若10个病人中至少有4人治好则认为这种药有效，反之则认为无效．试求：（1）虽然新药有效，且把痊愈率提高到35%，但通过试验被否定的概率；（2）新药完全无效，但通过试验被认为有效的概率．解：将每人服药看作一次试验，痊愈A ，没有痊愈A ；独立；（1）新药有效，痊愈率为0.35，即P (A ) = 0.35，伯努利概型，n = 10，p = 0.35，故概率为P 10 (0) + P 10 (1) + P 10 (2) + P 10 (3) 5138.065.035.065.035.065.035.065.035.0733108221091110100010=××+××+××+××=C C C C ．（2）新药完全无效，痊愈率为0.25，即P (A ) = 0.25，伯努利概型，n = 10，p = 0.25，故所求概率为1 − P 10 (0) − P 10 (1) − P 10 (2) − P 10 (3)2241.075.025.075.025.075.025.075.025.01733108221091110100010=××−××−××−××−=C C C C ．。

(整理)概率论第一章习题解答

00第一章随机事件与概率I 教学基本要求1、了解随机现象与随机试验，了解样本空间的概念，理解随机事件的概念，掌握事件之间的关系与运算；2、了解概率的统计定义、古典定义、几何定义和公理化定义，会计算简单的古典概率和几何概率，理解概率的基本性质；3、了解条件概率，理解概率的乘法公式、全概率公式、贝叶斯公式，会用它们解决较简单的问题；4、理解事件的独立性概念.II 习题解答A 组1、写出下列随机试验的样本空间(1) 抛掷两颗骰子，观察两次点数之和； (2) 连续抛掷一枚硬币，直至出现正面为止； (3) 某路口一天通过的机动车车辆数； (4) 某城市一天的用电量.解：(1) {2,3,,12}Ω=；(2) 记抛掷出现反面为“0”，出现正面为“1”，则{(1),(0,1),(0,0,1),}Ω=；(3) {0,1,2,}Ω=；(4) {|0}t t Ω=≥.2、设A 、B 、C 为三个事件，试表示下列事件： (1) A 、B 、C 都发生或都不发生； (2) A 、B 、C 中至少有一个发生； (3) A 、B 、C 中不多于两个发生.解：(1) ()()ABC ABC ；(2) AB C ；(3) ABC 或ABC .3、在一次射击中，记事件A 为“命中2至4环”、B 为“命中3至5环”、C 为“命中5至7环”，写出下列事件：(1) AB ；(2) AB ；(3) ()A BC ；(4) ABC .解：(1) AB 为“命中5环”； (2) A B 为“命中0至1环或3至10环”；(3) ()A B C 为“命中0至2环或5至10环”；(4) ABC 为“命中2至4环”.4、任取两正整数，求它们的和为偶数的概率？解：记取出偶数为“0”，取出奇数为“1”，则其出现的可能性相同，于是任取两个整数的样本空间为{(0,0),(0,1),(1,0),(1,1)}Ω=.设A 为“取出的两个正整数之和为偶数”，则{(0,0),(1,1)}A =，从而1()2p A =. 5、从一副52张的扑克中任取4张，求下列事件的概率：(1) 全是黑桃；(2) 同花；(3) 没有两张同一花色；(4) 同色？解：从52张扑克中任取4张，有452C 种等可能取法.(1) 设A 为“全是黑桃”，则A 有413C 种取法，于是413452()C p A C =；(2) 设B 为“同花”，则B 有4134C 种取法，于是4134524()C p B C =；(3) 设C 为“没有两张同一花色”，则C 有413种取法，于是445213()p C C =；(4) 设D 为“同色”，则D 有4262C 种取法，于是4264522()C p D C =.6、把12枚硬币任意投入三个盒中，求第一只盒子中没有硬币的概率？解：把12枚硬币任意投入三个盒中，有123种等可能结果，记A 为“第一个盒中没有硬币”，则A 有122种结果，于是122()()3p A =.7、甲袋中有5个白球和3个黑球，乙袋中有4个白球和6个黑球，从两个袋中各任取一球，求取到的两个球同色的概率？解：从两个袋中各任取一球，有11810C C ⨯种等可能取法，记A 为“取到的两个球同色”，则A 有11115436C C C C⨯+⨯种取法，于是111154361181019()40C C C C p A C C ⨯+⨯==⨯. 8、把10本书任意放在书架上，求其中指定的三本书放在一起的概率？解：把10本书任意放在书架上，有10!种等可能放法，记A 为“指定的三本书放在一起”，则A 有3!8!⨯种放法，于是3!8!1()10!15p A ⨯==. 9、5个人在第一层进入十一层楼的电梯，假若每个人以相同的概率走出任一层(从第二层开始)，求5个人在不同楼层走出的概率？解：5个人从第二层开始走出电梯，有510种等可能结果，记A 为“5个人在不同楼层走出”，则A 有510P 种结果，于是5105()10P p A =.10、n 个人随机地围一圆桌而坐，求甲乙两人相邻而坐的概率？解：设甲已坐好，只考虑乙的坐法，则乙有1n -种坐法，记A 为“甲乙两人相邻而坐”，则A 有2种坐法，于是2()1p A n =-. 11、甲乙两艘轮船驶向一个不能同时停泊两艘轮船的码头，它们在一昼夜内到达的时间是可能的，若甲船的停泊时间为一小时，乙船的停泊时间为两小时，求它们中任何一艘都不需要等候码头空出的概率？解：设x 、y 分别为甲、乙两艘轮船到达码头的时间，则{(,)|0,24}x y x y Ω=≤≤，其面积224S Ω=，记A 为“它们中任何一艘都不需要等候码头空出”，于是{(,)|12}A x y y x x y =-≥-≥或，其面积221(2322)2A S =+，从而2222322()0.879224A S p A S Ω+===⨯.12、在区间(0,1)中随机地取两个数，求事件“两数之和小于6/5”的概率？解：设x 、y 分别为取出的两个数，则{(,)|0,1}x y x y Ω=≤≤，其面积1S Ω=，记A 为“两数之和小于6/5”，于是6{(,)|}5A x y x y =+<，其面积2141()25A S =-，从而17()0.6825A S p A S Ω===. 13、设0a >，有任意两数x 、y ，且0,x y a <<.试求24a xy <的概率？解：由题意知{(,)|0,}x y x y a Ω=<<，其面积2S a Ω=，记2{(,)|}4a A x y xy =<，则其面积244422223ln 4()()(1)444a a axa aaA a S a dy dx a a dx a x =-=--=-+⎰⎰⎰从而3ln 4()10.596644A S p A S Ω==-+=. 14、从0、1、2、…、9这十个数字中任选三个不同的数字，试求下列事件的概率：(1) 1A 为“三个数字中不含０和５”； (2) 2A 为“三个数字中不含０或５”； (3) 3A 为“三个数字中含０但不含５”？解：记A 为“三个数字不含０”、B 为“三个数字不含５”，则393107()10C p A C ==、393107()10C p B C ==、383107()15C p AB C ==于是有(1) 17()()15p A p AB ==； (2) 27714()()()()()2101515p A p AB p A p B p AB ==+-=⨯-=； (3) 3777()()()()101530p A p AB p B p AB ==-=-=. 15、某工厂的一个车间有男工7人、女工4人，现要选出3个代表，求选出的3个代表中至少有1个女工的概率？解：设A 为“选出的3个代表中至少有1个女工”，则373117()33C p A C ==726()1()13333p A p A ⇒=-=-=. 16、从数字1、2、…、9中重复地取n 次，求n 次所取数字的乘积能被10整除的概率？解：记A 为“至少取到一次５”、B 为“至少取到一次偶数”，则8()9n n p A =、5()9n n p B =、4()9nn p AB =于是，所求概率为854()1()1()()()1999n n nn n n p AB p AB p A p B p AB =-=--+=--+.17、已知事件A 、B 满足()()p AB p AB =，记()p A p =，求()p B ？解：由()()()1()1()()()p AB p AB p AB p A B p A p B p AB ===-=--+1()()0p A p B ⇒--= ()1()1p B p A p ⇒=-=-.18、已知()0.7p A =，()0.3p AB =－，求()p AB ？解：由()()()0.3p A B p A p AB =-=－和()0.7p A =()0.4p AB ⇒=()1()0.6p AB p AB ⇒=-=.19、设1()()2p A p B ==，试证：()()p AB p AB =. 证明：由1()()2p A p B ==()1()1()()()()p AB p AB p A p B p AB p AB ⇒=-=--+=.20、某班级在一次考试中数学不及格的学生占15％，英语不及格的学生占5％，这两门课都不及格的学生占3％.(1) 已知一个学生数学不及格，他英语也不及格的概率是多少； (2) 已知一个学生英语不及格，他数学也不及格的概率是多少？解：记A 为“数学不及格”、B 为“英语不及格”，则()0.15p A =、()0.05p B =、()0.03p AB =(1) ()0.03(|)0.2()0.15p AB p B A p A ===； (2) ()0.03(|)0.6()0.05p AB p A B p B ===. 21、掷两颗骰子，以A 记事件“两颗点数之和为10”，以B 记事件“第一颗点数小于第二颗点数”，求(|)p A B 和(|)p B A ？解：掷两颗骰子的样本空间为(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)⎧⎫⎪⎪⎪⎪⎪⎪Ω=⎨⎬⎪⎪⎪⎪⎪⎪⎩⎭由于{(4,6),(5A =、(1,2)(1,3)(1,4)(1,5)(1,6)(2,3)(2,4)(2,5)(2,6)(3,4)(3,5)(3,6)(4,5)(4,6)(5,6)B ⎧⎫⎪⎪=⎨⎬⎪⎪⎩⎭、{(4,6)}AB =，于是3()36p A =、15()36p B =、1()36p AB =()1(|)()15p AB p A B p B ⇒==、()1(|)()3p AB p B A p A ⇒==. 22、设10件产品中有4件不合格品，从中任取二件，已知其中一件是不合格品，求另一件也是不合格的概率？解：记i A 为“第i 次取出不合格品”(1,2)i =，B 为“有一件不合格品”，C 为“另一件也是不合格品”，则121212()()()B A A A A A A =，于是1212124664432()()()()1091091093p B p A A p A A p A A ⨯⨯⨯=++=++=⨯⨯⨯ 432()10915p BC ⨯==⨯ ()1(|)()5p BC p C B p B ⇒==. 23、已知()0.3p A =、()0.4p B =、()0.5p AB =，求(|)p B AB ？解：由()0.3p A =、()0.4p B =、()0.5p AB =()()()()0.70.60.50.8p A B p A p B p AB ⇒=+-=+-=再由()()()0.7()0.5p AB p A p AB p AB =-=-=()0.2p AB ⇒= 从而(())()0.21(|)()()0.84p B A B p AB p B AB p A B p A B ====.24、两台车床加工固焊零件，第一台出次品的概率是0.03，第二台出次品的概率为0.06，加工出来的零件放在一起且已知第一台加工的零件比第二台加工的零件多一倍.(1) 求任取一个零件是合格品的概率；(2) 如果取出的零件是不合格品，求它是由第二台车床加工的概率？解：记A 为“取到第一台车床加工的零件”、B 为“取到合格品”，则2()3p A =、(|)0.97p B A =、(|)0.94p B A = (1) 21()()(|)()(|)0.970.940.9633p B p A p B A p A p B A =+=⨯+⨯=；(2) 10.06()()(|)13(|)()1()0.042p AB p A p B A p A B p B p B ⨯====-. 25、已知男人中有5％是色盲患者，女人中有0.25％是色盲患者，现从男女人数相等的人群中随机挑选一人，发现恰好是色盲患者，问此人是男人的概率是多少？解：记A 为“选到色盲患者”、B 为“选到男人”，则1()2p B =、(|)5%p A B =、(|)0.25%p A B = 于是，所求概率为()(|)0.50.05(|)0.9524()(|)()(|)0.50.050.50.0025p B p A B p B A p B p A B p B p A B ⨯===+⨯+⨯.26、证明：()(|)1()p B p B A p A ≥-，其中()0p A >. 证明：由于()()()()()()1()()p AB p A p B p AB p A p B p A p B =+-≥+-=-()()()()(|)1()()()p AB p A p B p B p B A p A p A p A -=≥=-. 27、设A 、B 为任意两个事件，且A B ⊂、()0p B >，证明：()(|)p A p A B ≤.证明：由A B ⊂得()()(|)()()()p AB p A p A B p A p B p B ==≥. 28、甲乙两人独立地对同一目标射击一次，其命中率分别为0.6和0.7，已知目标被击中，求它是甲击中的概率？解：记A 为“目标被击中”、1B 为“甲击中目标”、2B 为“乙击中目标”，则121212()()()()()0.60.70.60.70.88p A p B B p B p B p B B ==+-=+-⨯=再由1B A ⊂可得所求概率为111()()0.6(|)0.682()()0.88p B A p B p B A p A p A ====.29、设电路由A 、B 、C 三个元件组成，若元件A 、B 、C 发生故障的概率分别是0.3、0.2、0.2，各元件独立工作，求下列三种情况下电路发生故障的概率.(1) A 、B 、C 三个元件串连； (2) A 、B 、C 三个元件并联； (3) B 与C 并联后再与A 串联？解：记A 、B 、C 分别表示元件A 、B 、C 发生故障. (1) 所求概率为()1()1()()()10.70.80.80.552p A B C p ABC p A p B p C =-=-=-⨯⨯=；(2) 所求概率为()()()()0.30.20.20.012p ABC p A p B p C ==⨯⨯=；(3) 所求概率为(())()()()()()()()()()p A BC p A p BC p ABC p A p B p C p A p B p C =+-=+-0.30.20.20.30.20.20.328=+⨯-⨯⨯=.30、若()0.4p A =、()0.7p AB =，在下列情况下求()p B .(1) A 、B 不相容； (2) A 、B 独立； (3) A B ⊂？解：(1) 由于A 、B 不相容，从而()()()p AB p A p B =+，于是()()()0.70.40.3p B p A B p A =-=-=；(2) 由于A 、B 独立，从而()()()()()p AB p A p B p A p B =+-，于是0.70.4()0.4()p B p B =+- ()0.5p B ⇒=；(3) 由于A B ⊂，从而AB B =，于是()()0.7p B p A B ==.B 组1、一个书架上有6本数学书和4本物理书，求指定的3本数学书放在一起的概率？解：6本数学书和4本物理书在书架上有10!种等可能放法，记A 为“指定的3本数学书放在一起”，则A 有3!8!⨯种放法，于是3!8!1()10!15p A ⨯==. 2、设有n 个人，每个人都等可能地被分配到N 个房间中的任一间去住()n N ≤，求下列事件的概率.(1) 指定的n 间房间里各有一个住； (2) 恰有n 间房各住一人？解：将n 个人分配到N 个房间中去住，有nN 种等可能分法.(1) 记A 为“指定的n 间房间里各有一个住”，则A 有!n 种分法，于是!()nn p A N =； (2) 记B 为“恰有n 间房各住一人”，则B 有!nNC n 种分法，于是!()n N nC n p B N =.3、公安人员在某地发现一具尸体，经分析认为凶手还在该地的概率为0.4，乘车外逃的概率为0.5，自首的概率为0.1，现派人追捕，在该地抓到凶手的概率为0.9，若外逃则抓到凶手的概率为0.5，问此次凶手在该地或外逃被抓到的概率是多少？解：记1A 为“凶手还在该地”、2A 为“凶手已乘车外逃”、B 为“凶手被抓到”，则1()0.4p A =、2()0.5p A =、1(|)0.9p B A =、2(|)0.5p B A =，于是所求概率为12121122(()())()()()(|)()(|)p A B A B p A B p A B p A p B A p A p B A =+=+0.40.90.50.50.61=⨯+⨯=.4、有两箱零件，第一箱装50件，其中10件是一等品；第二箱装30件，其中18件是一等品，现从两箱中任取一箱，然后从该箱中先后取出两个零件，试求在第一次取到一等品的条件下，第二次取出的零件仍是一等品的概率？解：记i A 为“第i 次取到一等品”、B 为“取到第一箱”，则111110118()()(|)()(|)0.4250230p A p B p A B p B p A B =+=⨯+⨯= 121212()()(()|)()(()|)p A A p B p A A B p B p A A B =+1109118170.194232504923029⨯⨯=⨯+⨯=⨯⨯ 于是12211()0.19423(|)0.4856()0.4p A A p A A p A ===.5、掷均匀硬币n m +次，已知至少出现一次正面，求第一次正面出现在第n 次实验的概率？解：记A 为“至少出现一次正面”、B 为“第一次正面出现在第n 次实验”，则0()1()1(0.5)1(0.5)n m n m n m p A p A C +++=-=-=- 1()0.5(0.5)(0.5)n n p B -=⨯=再由B A ⊂可得所求概率为()()(0.5)(|)()()1(0.5)nn m p AB p B p B A p A p A +===-.6、甲、乙、丙三人进行比赛，规定每局两个人比赛，胜者再与第三人比，依次循环，直至有一人连胜二局为止，此人即为冠军，假设每次比赛双方取胜的概率均为0.5，若甲、乙两人先比，求甲得冠军的概率？解：记A 为“甲得冠军”；i A 、i B 、i C 分别为“第i 局中甲、乙、丙获胜”，则121234512345678()[()()()]p A p A A p AC B A A p AC B A C B A A =++++12341234567[()()]p B C A A p B C A B C A A ++25847(0.50.50.5)(0.50.5)=++++++24330.50.5510.510.514=+=--.7、乒乓球单打比赛采用五局三胜制，甲、乙两名运动员在每局比赛中获胜的概率各为0.6和0.4，当比赛进行完二局时，甲以2:0领先，求在以后的比赛中甲获胜的概率？解：记B 为“甲获胜”、i A 为“甲在第i 局比赛中获胜”，由于甲以2:0领先，因而334345()()B A A A A A A =334345()()()()()()()p B p A p A p A p A p A p A ⇒=++20.60.40.60.40.60.936=+⨯+⨯=.8、保险公司把被保险人分为“谨慎”、“一般”、“冒失”三类，统计资料表明上述三种人在一年中发生事故的概率分别是0.05、0.15、0.3；如果“谨慎”的被保险人占20%，“一般”的被保险人占50%，“冒失”的被保险人占30%，现知某保险人在一年内发生了事故，则他是属“谨慎”客户的概率是多少？解：记1A 为“谨慎客户”、2A 为“一般客户”、3A 为“冒失客户”、B 为“保险人在一年内发生事故”，则1()0.2p A =、2()0.5p A =、3()0.3p A =、1(|)0.05p B A =、2(|)0.15p B A =、3(|)0.3p B A =，于是11131()(|)0.20.052(|)0.20.050.50.150.30.335()(|)iii p A p B A p A B p A p B A =⨯===⨯+⨯+⨯∑.。

概率论第一章随机事件及其概率答案

概率论与数理统计练习题系专业班姓名学号第一章随机事件及其概率（一）一．选择题1．对掷一粒骰子的试验，在概率论中将“出现奇数点”称为 [ C ]（A ）不可能事件（B ）必然事件（C ）随机事件（D ）样本事件2．下面各组事件中，互为对立事件的有 [ B ]（A ）1A ={抽到的三个产品全是合格品} 2A ={抽到的三个产品全是废品}（B ）1B ={抽到的三个产品全是合格品} 2B ={抽到的三个产品中至少有一个废品}（C ）1C ={抽到的三个产品中合格品不少于2个} 2C ={抽到的三个产品中废品不多于2个}（D ）1D ={抽到的三个产品中有2个合格品} 2D ={抽到的三个产品中有2个废品}3．下列事件与事件A B -不等价的是 [ C ]（A ）A AB - （B ）()A B B ⋃- （C ）A B （D ）A B4．甲、乙两人进行射击，A 、B 分别表示甲、乙射中目标，则A B ⋃表示 [ C ]（A ）二人都没射中（B ）二人都射中（C ）二人没有都射着（D ）至少一个射中5．以A 表示事件“甲种产品畅销，乙种产品滞销”，则其对应事件A 为. [ D ]（A ）“甲种产品滞销，乙种产品畅销”；（B ）“甲、乙两种产品均畅销”；（C ）“甲种产品滞销”；（D ）“甲种产品滞销或乙种产品畅销6．设{|},{|02},{|13}x x A x x B x x Ω=-∞<<+∞=≤<=≤<，则AB 表示 [ A ]（A ）{|01}x x ≤< （B ）{|01}x x <<（C ）{|12}x x ≤< （D ）{|0}{|1}x x x x -∞<<⋃≤<+∞7．在事件A ，B ，C 中，A 和B 至少有一个发生而C 不发生的事件可表示为 [ A ]（A ）C A Y C B ；（B ）C AB ；（C ）C AB Y C B A Y BC A ；（D ）A Y B Y C .8、设随机事件,A B 满足()0P AB =，则 [ D ]（A ）,A B 互为对立事件 (B) ,A B 互不相容(C) AB 一定为不可能事件 (D) AB 不一定为不可能事件二、填空题1．若事件A ，B 满足AB φ=，则称A 与B 互斥或互不相容。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

《概率论与随机过程》第一章习题答案1. 写出下列随机试验的样本空间。

（1）记录一个小班一次数学考试的平均分数（设以百分制记分）。

解： ⎭⎬⎫⎩⎨⎧⨯=n n nn S 100,,1,0 ，其中n 为小班人数。

（2）同时掷三颗骰子，记录三颗骰子点数之和。

解：{}18,,4,3 =S 。

（3） 10只产品中有3只是次品，每次从其中取一只（取出后不放回），直到将3只次品都取出，记录抽取的次数。

解： {}10,,4,3 =S 。

（4）生产产品直到得到10件正品，记录生产产品的总件数。

解： {} ,11,10=S 。

（5）一个小组有A ，B ，C ，D ，E5个人，要选正副小组长各一人（一个人不能兼二个职务），观察选举的结果。

解： {}ED EC EB EA DE DC DB DA CE CD CB CA BE BD BC BA AE AD AC AB S ,,,,,,,,,,,,,,,,,,,=其中，AB 表示A 为正组长，B 为副组长，余类推。

（6）甲乙二人下棋一局，观察棋赛的结果。

解： {}210,,e e e S =其中，0e 为和棋，1e 为甲胜，2e 为乙胜。

（7）一口袋中有许多红色、白色、蓝色乒乓球，在其中任意取4只，观察它们具有哪几种颜色。

解： {}rwb wb rb rw b w r S ,,,,,,=其中，,,,b w r 分别表示红色、白色、蓝色。

解： {}1111,1110,1101,0111,1011,1010,1100,0110,0101,0100,100,00=S 其中，0为次品，1为正品。

（9）有A ，B ，C 三只盒子，a ，b ，c 三只球，将三只球装入三只盒子中，使每只盒子装一只球，观察装球的情况。

解： {}Ca Bb Ac Cc Ba Ab Cb Bc Aa Cb Ba Ac Ca Bc Ab Cc Bb Aa S ,,;,,;,,;,,;,,;,,=其中，Aa 表示球a 放在盒子A 中，余者类推。

（10）测量一汽车通过给定点的速度。

解：{}0>=v v S（11）将一尺之棰折成三段，观察各段的长度。

解： (){}1,0,0,0,,=++>>>=z y x z y x z y x S 其中，z y x ,,分别表示第一段，第二段，第三段的长度。

#2. 设A ，B ，C 为三事件，用A ，B ，C 的运算关系表示下列事件。

（1） A 发生，B 与C 不发生。

解：C B A （2） A 与B 都发生，而C 不发生。

解： C AB （3） A ，B ，C 都发生。

解： ABC（4） A ，B ，C 中至少有一个发生。

解： C B A ⋃⋃ （5） A ，B ，C 都不发生。

解： C B A（6） A ，B ，C 中至多于一个发生。

解： A C C B B A ⋃⋃ （7） A ，B ，C 中至多于二个发生。

解： C B A ⋃⋃（8） A ，B ，C 中至少有二个发生。

解： CA BC AB ⋃⋃. #3. 设{}10,2,1, =S ,{}4,3,2=A ，{}5,4,3=B ，{}7,6,5=C ，具体写出下列各等式（1）B A 。

解： {}5=B A ；（2）B A ⋃。

解： {}10,9,8,7,6,5,4,3,1=⋃B A ；（3）B A 。

解：{}5,4,3,2=B A ；（4） BC A 。

解： {}10,9,8,7,6,5,1=BC A（5）)(C B A ⋃。

解： {}10,9,8,7,6,5,2,1)(=⋃C B A . #4. 设{}20≤≤=x x S ，⎭⎬⎫⎩⎨⎧≤<=121x x A ，⎭⎬⎫⎩⎨⎧<≤=2341x x B ，具体写出下列各式。

（1）B A ⋃。

解： ⎭⎬⎫⎩⎨⎧≤≤⋃⎭⎬⎫⎩⎨⎧≤≤=⋃223410x xx x B A （2）B A ⋃。

解： ⎭⎬⎫⎩⎨⎧≤≤⋃⎭⎬⎫⎩⎨⎧≤≤⋃⎭⎬⎫⎩⎨⎧<≤=⋃223121410x x x xx x B A （3）B A 。

解： {}φ=B A （4）B A 。

解：⎭⎬⎫⎩⎨⎧≤<⋃⎭⎬⎫⎩⎨⎧≤≤=2312141x x x xB A . #5. 设A ，B ，C 是三事件，且41)()()(===C P B P A P ，0)()(==CB P AB P ，81)(=AC P ，求A ，B ，C 至少有一个发生的概率。

解：由题意可知：0)(=ABC P ，故()()()()85)()()()(=+---++=⋃⋃ABC P AC P BC P AB P C P B P A P C B A P 。

或 φ=⋃⋃B C A )( ，∴()()()()85)()()())((=+-+=+⋃=⋃⋃=⋃⋃B P AC P C P A P B P C A P B C A P C B A P 。

#6. 在1500个产品中有400个次品，1100个正品，任意取200个。

（1）求恰有90个次品的概率。

（2）至少有2个次品的概率。

解：（1）⎪⎪⎭⎫⎝⎛⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛2001500110110090400；（2）设)(k P 表示有k 个次品的概率，故至少有2个次品的概率为：⎪⎪⎭⎫⎝⎛⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=--=∑=200150019911001400200150020011001)1()0(1)(2002P P k P k . #7.（1）在房间里有500个人，问至少有一个人的生日是10月1日的概率是多少（设一年以365天计算）？（2）在房间里有4个人，问至少有二个人的生日在同一个月的概率是多少？解：（1）属“分房问题”，即有n 个人，每个人都以N 1的概率被分在N 间房中的每一间中，某指定房间中至少有一人的概率。

设某指定房间中恰有k 个人的概率为)(k P ，则有()kn k nk n N N N k n N N k n k P --⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛=111)(。

故，某指定房间中至少有一人的概率为： nn k N N P k P ⎪⎭⎫⎝⎛--=-=∑=11)0(1)(1。

所以，500个人中至少有一个人的生日是10月1日的概率为：74634.025366.013653641500=-=⎪⎭⎫⎝⎛-（2）属“分房问题”，即有n 个人，每个人都以N 1的概率被分在N 间房中的每一间中，至少有二个人在同一间房中的概率。

设A 为“每一间房中至多有一个人” 基本事件个数：n N 。

“每一间房中至多有一个人”事件的个数为：!n)(N !N -。

所以，“至少有二个人在同一间房中的概率”等于“至少有二个人的生日在同一个月的概率”。

0.42710.57291124-(12!12114=-=-=--！）n N !n)(N !N 。

#8. 一盒子中有4只次品晶体管，6只正品晶体管，随机地抽取一只测试，直到4只次品管子都找到为止。

求第4只次品管子在下列情况发现的概率。

（1）在第5次测试发现。

（2）在第10次测试发现。

解：（1） 10526789101234634=⨯⨯⨯⨯⨯⨯⨯⨯⎪⎪⎭⎫ ⎝⎛；或1052!6!4!10!3!441034=⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛；（2） 529106634=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛。

#9. 甲、乙位于二个城市，考察这二个城市六月份下雨的情况。

以A ，B 分别表示甲，乙二城市出现雨天这一事件。

根据以往的气象记录已知4.0)()(==B P A P ，28.0)(=AB P ，求)/(B A P ，)/(A B P 及)(B A P ⋃。

解： 7.04.028.0===P(B)P(AB)P(A/B)；7040280...P(A)P(AB)P(B/A)== 5202804040....P(AB)P(B)P(A)B P(A =-+=-+=⋃。

#10. 已知在10只晶体管中有2只次品，在其中取二次，每次随机地取一只，作不放回抽样，求下列事件的概率。

（1）二只都是正品。

（2）二只都是次品。

（3）一只是正品，一只是次品。

（4）第二次取出的是次品。

解： (1) 4528106!2!2!8!821028=⨯⨯⨯⨯=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛！！； (2) 45110!2!821022=⨯=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛！； (3) 451610!2!8282101218=⨯⨯⨯=⎪⎪⎭⎫ ⎝⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛！；或45169810292108=⨯+⨯； (4)4599110292108=⨯+⨯。

#11. 某人忘记了电话号码的最后一个数字，因而随意地拨号，求他拨号不超过三次而接通所需的电话的概率是多少？如果已知最后一个数字是奇数，那么此概率是多少？解：(1) 3.010!7!37!2!!931029=⨯⨯⨯=⎪⎪⎭⎫ ⎝⎪⎪⎭⎫ ⎝⎛！;(2) 6.05!2!32!2!!43524=⨯⨯⨯=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛！。

#12. 某工厂中，机器321,,B B B 分别生产产品总数的25%，35%和40%。

它们生产的产品中分别有5%，4%，2%的次品，将这些产品混在一起，今随机地取一只产品，发现是次品。

问这一次品是机器321,,B B B 生产的概率分别是多少？解：设A 为“次品”，已知：25.0)(1=B P ，35.0)(2=B P ，40.0)(3=B P ；05.0)/(1=B A P ，04.0)/(2=B A P ，02.0)/(3=B A P ，0345.040.002.035.004.025.005.0)()/()(31=⨯+⨯+⨯==∑=j jjB P B A P A P 。

故由，)()()/()/(A P B P B A P A B P i i i =可得：36232.069250345.025.005.0)()()/()/(111≈=⨯==A PB P B A P A B P ；40580.069280345.035.004.0)()()/()/(222≈=⨯==A P B P B A P A B P ；23188.069160345.040.002.0)()()/()/(333≈=⨯==A PB P B A P A B P 。

《概率论与随机过程》第1章习题答案汇编