1. 10 勾股定理的应用 课件(华东师大八年级上)
合集下载
华东师大版八年级上册14.反证法课件(共23张)
王戎是怎样知道李子是苦的呢？他运用了
怎样的推理方法？
王戎的推理方法是:
假设李子不苦 则因树在“道”边,李子早就被别人采摘, 这与“多子”产生矛盾. 所以假设不成立，李为苦李.
生活实例: 妈妈:小华，听说邻居小芳全家这几天在外 地旅游. 小华:不可能，我上午还在学校碰到了她和 她妈妈呢!
上述对话中，小华要告知妈妈的命题是什么？
课后作业
1、已知：一个整数的平方能被2整除.
求证：这个数是偶数.
2、已知a≠0，证明x的方程ax=b有且只有一个根.
3、已知x＞0，y＞0，x+y＞2.
求证：1+x y
，1+y x
中至少有一个小于2.
4、求证： 2 是无理数.
5、求证：在三角形的内角中，至少有一个角大于 或等于60º. 6、证明：等腰三角形的两底角必定是锐角. 7、证明：两直线平行，同旁内角互补. 8、如图，已知AB∥CD，
当∠B是_钝__角__时，则_∠__B_+__∠__C_＞__1_8_0_°
这与__三__角__形__的__三__个__内__角__和__等__于__1_8_0_°_矛盾； 综上所述,假设不成立. ∴∠B一定是锐角.
强调 用反证法证题时,应注意的事项 : （1）周密考察原命题结论的否定事项， 防止否定不当或有所遗漏； （2）推理过程必须完整，否则不能说 明命题的真伪性； （3）在推理过程中，要充分使用已知条 件，否则推不出矛盾，或者不能断 定推出的结果是错误的。
P
a
证明： 假设c与b不相交，
则c∥b.
b c
∵ a∥b，
∴ a∥c，
这与“c、a相交于点P”矛盾， ∴ 假设不成立，故c与b相交.
变式练习
怎样的推理方法？
王戎的推理方法是:
假设李子不苦 则因树在“道”边,李子早就被别人采摘, 这与“多子”产生矛盾. 所以假设不成立，李为苦李.
生活实例: 妈妈:小华，听说邻居小芳全家这几天在外 地旅游. 小华:不可能，我上午还在学校碰到了她和 她妈妈呢!
上述对话中，小华要告知妈妈的命题是什么？
课后作业
1、已知：一个整数的平方能被2整除.
求证：这个数是偶数.
2、已知a≠0，证明x的方程ax=b有且只有一个根.
3、已知x＞0，y＞0，x+y＞2.
求证：1+x y
，1+y x
中至少有一个小于2.
4、求证： 2 是无理数.
5、求证：在三角形的内角中，至少有一个角大于 或等于60º. 6、证明：等腰三角形的两底角必定是锐角. 7、证明：两直线平行，同旁内角互补. 8、如图，已知AB∥CD，
当∠B是_钝__角__时，则_∠__B_+__∠__C_＞__1_8_0_°
这与__三__角__形__的__三__个__内__角__和__等__于__1_8_0_°_矛盾； 综上所述,假设不成立. ∴∠B一定是锐角.
强调 用反证法证题时,应注意的事项 : （1）周密考察原命题结论的否定事项， 防止否定不当或有所遗漏； （2）推理过程必须完整，否则不能说 明命题的真伪性； （3）在推理过程中，要充分使用已知条 件，否则推不出矛盾，或者不能断 定推出的结果是错误的。
P
a
证明： 假设c与b不相交，
则c∥b.
b c
∵ a∥b，
∴ a∥c，
这与“c、a相交于点P”矛盾， ∴ 假设不成立，故c与b相交.
变式练习
课件华东师大版八年级数学上册 勾股定理解题的十种常见题型 复习精美PPT课件
第公1交4站章D的勾距股离定相理等，求商店C与公交站D之间的距离．
∴BC ＝AB ，即 华东师大版 八年级2 数学上册 复2习课件 AB＝BC.
3．如图，在等腰直角三角形 ABC 中，AB＝AC，D 是斜边 BC 的中点，E，F 分别为 AB，AC 上的点，且 DE⊥DF. (1)若设 BE＝a，CF＝b，且 a－12＋|b－5|＝ m－2＋ 2－m， 求 BE 及 CF 的长；
解：如图，连接 BD，作 BE⊥AD 于点 E. ∵AB＝AD，∠A＝60°， ∴∠1＝∠ABD＝180°－ 2 60°＝60°. 易得△BAE≌△BDE.∴BD＝AB＝8. 又∠1＋∠2＝150°，则∠2＝90°. 设 BC＝x，则 CD＝16－x，由勾股定理得 x2＝82＋(16－x)2. 解得 x＝10.∴BC＝10，CD＝6.
7．如图，某学校(A点)到公路(直线l)的距离为300 m，到公交站(D点)的距离为500 m．现要在公路边上建一个商店(C点)，使之到学校A及 公交站D的距离相等，求商店C与公交站D之间的距离．
(1)求BC边的长； (2)求证：BE2＋CF2＝EF2.
解：在Rt△ABC中，BC2＝AB2－AC2＝52－32＝16，∴BC＝4 cm. 7．如图，某学校(A点)到公路(直线l)的距离为300 m，到公交站(D点)的距离为500 m．现要在公路边上建一个商店(C点)，使之到学校A及 公交站D的距离相等，求商店C与公交站D之间的距离． ②根据勾股定理写出三边长的平方关系； 解：如图，连接CD1. 解：小明在河边B处取水后是沿南偏东60°方向行走的．理由如下： ②根据勾股定理写出三边长的平方关系； 解：小明在河边B处取水后是沿南偏东60°方向行走的．理由如下：
(3)当△ABP为等腰三角形时，借助图②求t的值．
四川省内江市资中县板栗中心学校八年级数学上册 勾股定理的综合应用课件 华东师大版
22
在Rt△ABC中，
B
Ｄ
C
A D A2 B B2D 6 2 3 22 7 5 .196
∴ S C 1 2 BA C D 1 2 6 5 .1 9 1.5 6 5 1 8.6 5
例2：在等腰△ABC中，AB＝AC＝ 13cm ，BC=10cm,求△ABC的面
积及AC边A上的高。
13
13
15
13
B
14-x
xC
14 D
及时练
如图，盒内长，宽，高分别是30米，24米和18米， 盒内可放的棍子最长是多少米？
18
24
30
及时练
如图，在△ABC中，AB=AC，D点在CB延长线上，求证：
AD2-AB2=BD·CD
A
证明： 过A作AE⊥BC于E
∵AB=AC，∴BE=CE
D
在Rt △ADE中， AD2=AE2+DE2 在Rt △ABE中， AB2=AE2+BE2 ∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
B
AC =6–1=5 ，BC =24× =112，
A
2
由勾股定理得 AB²= AC²+ BC²=169, C
B
∴AB=13(m) .
A
即最短路线AB为13m
如图，边长为1的正方体中，一只蚂 蚁从顶点A出发沿着正方体的外表面爬到 顶点B的最短距离是_____
B
B
B
A
A
A
如图所示，现在已测得长方体木块的 长2，宽1，高3.一只蜘蛛潜伏在木块的一 个顶点A处，一只苍蝇在这个长方体上和 蜘蛛相对的顶点B处。
C
2m
D
如图，现要在此楼梯旁建造无障碍通道，经测量 每格楼梯的高为11.25cm，宽20cm，你能求出通道的 长度吗？
在Rt△ABC中，
B
Ｄ
C
A D A2 B B2D 6 2 3 22 7 5 .196
∴ S C 1 2 BA C D 1 2 6 5 .1 9 1.5 6 5 1 8.6 5
例2：在等腰△ABC中，AB＝AC＝ 13cm ，BC=10cm,求△ABC的面
积及AC边A上的高。
13
13
15
13
B
14-x
xC
14 D
及时练
如图，盒内长，宽，高分别是30米，24米和18米， 盒内可放的棍子最长是多少米？
18
24
30
及时练
如图，在△ABC中，AB=AC，D点在CB延长线上，求证：
AD2-AB2=BD·CD
A
证明： 过A作AE⊥BC于E
∵AB=AC，∴BE=CE
D
在Rt △ADE中， AD2=AE2+DE2 在Rt △ABE中， AB2=AE2+BE2 ∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
B
AC =6–1=5 ，BC =24× =112，
A
2
由勾股定理得 AB²= AC²+ BC²=169, C
B
∴AB=13(m) .
A
即最短路线AB为13m
如图，边长为1的正方体中，一只蚂 蚁从顶点A出发沿着正方体的外表面爬到 顶点B的最短距离是_____
B
B
B
A
A
A
如图所示，现在已测得长方体木块的 长2，宽1，高3.一只蜘蛛潜伏在木块的一 个顶点A处，一只苍蝇在这个长方体上和 蜘蛛相对的顶点B处。
C
2m
D
如图，现要在此楼梯旁建造无障碍通道，经测量 每格楼梯的高为11.25cm，宽20cm，你能求出通道的 长度吗？
1勾股定理(第1课时)(教学PPT课件(华师大版))28张
正方形中小方格的个数，你有什么猜想？
1955年希腊发行的一枚纪念邮票.
讲授新课
知识点一 直角三角形三边的关系
视察正方形瓷砖铺成的地面.
（1）正方形P的面积是
1
（2）正方形Q的面积是
1
平方厘米；
（3）正方形R的面积是
2
平方厘米.
平方厘米；
上面三个正方形的面积之间有什么关系？
等腰直角三角形ABC三边长度之间存在什么关系吗？
程.
b
a
b
a
c
c
b
c
c
a
a
b
讲授新课
证明：大正方形的面积=(a+b)2.
四个个全等的直角三角形和小正方形的面积
1
2
2
之和= 4 ab c 2ab c .
2
b
由题可知(a+b)2=2ab+c2，
a
c
化简可得a2+b2=c2.
我们利用拼图的方法，将形的问题
与数的问题结合起来，再进行整式
A的面积
B的面积
C的面积
左图
4
9
13
右图
16
9
25
结论：以直角三角形两直角边为边长的小正方形的面积的和，等于以斜边为边长的正方形的面积.
SA+SB=SC
讲授新课
猜想:两直角边a、b与斜边 c 之间的关系？
A
a
B b
c
a2+b2=c2
C
讲授新课
概念总结
由上面的探索可以发现：对于任意的直角三角形，如果它的两
数学（华东师大版）
八年级 上册
第14章 勾股定理
1955年希腊发行的一枚纪念邮票.
讲授新课
知识点一 直角三角形三边的关系
视察正方形瓷砖铺成的地面.
（1）正方形P的面积是
1
（2）正方形Q的面积是
1
平方厘米；
（3）正方形R的面积是
2
平方厘米.
平方厘米；
上面三个正方形的面积之间有什么关系？
等腰直角三角形ABC三边长度之间存在什么关系吗？
程.
b
a
b
a
c
c
b
c
c
a
a
b
讲授新课
证明：大正方形的面积=(a+b)2.
四个个全等的直角三角形和小正方形的面积
1
2
2
之和= 4 ab c 2ab c .
2
b
由题可知(a+b)2=2ab+c2，
a
c
化简可得a2+b2=c2.
我们利用拼图的方法，将形的问题
与数的问题结合起来，再进行整式
A的面积
B的面积
C的面积
左图
4
9
13
右图
16
9
25
结论：以直角三角形两直角边为边长的小正方形的面积的和，等于以斜边为边长的正方形的面积.
SA+SB=SC
讲授新课
猜想:两直角边a、b与斜边 c 之间的关系？
A
a
B b
c
a2+b2=c2
C
讲授新课
概念总结
由上面的探索可以发现：对于任意的直角三角形，如果它的两
数学（华东师大版）
八年级 上册
第14章 勾股定理
【华东师大版】数学八年级上册数学：勾股定理
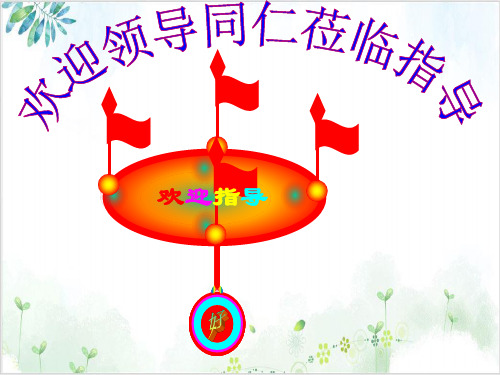
❖ AC2+BC2=AB2 → ∠ACB为直角
❖ AC2+BC2>AB2 → ∠ACB为锐角
C
A
C
A
BC
A B
B
归纳应用方法：
用勾股定理的逆定理判断直角三角形的步骤：
△ABC中
①、确定最大边（最大边c所对的角是最大角）
②、验证：c2与a2+b2是否相等 若 c2 == a2 ++ b2则△ABC是以∠C=90°的直角三角形
BC ＝ 4 ， CD ＝ 12 ， AD ＝ 13, 求 四
边形ABCD的面积?
S C
四边形ABCD=36
B D
A
华东师大版八年级上册数学：勾股定 理-精品 课件pp t(实用 版)
华东师大版八年级上册数学：勾股定 理-精品 课件pp t(实用 版)
2. 已知a，b，c为△ABC的三边,且 满足
练一练
1、 三 角 形 三 边 长 a、 b、 c满 足 条 件 a:b:c= = 9:12:15,则 此 三 角 形 是 ( B )
A、锐角三角形 C、钝角三角形
B、直角三角形 D、等边三角形
2. 满足下列条件△ABC,不是直角三角形的是( D )
A.b2=a2-c2
B. a:b:c=3:4:5
A、锐角三角形
B、直角三角形
C、钝角三角形
D、等边三角形
华东师大版八年级上册数学：勾股定 理-精品 课件pp t(实用 版)
思 维 激 活
华东师大版八年级上册数学：勾股定 理-精品 课件pp t(实用 版)
1、△ABC三边a,b,c为边向外作 正方形，（以三边为直径作半 圆，）若S1+S2=S3成立， 则△ABC 是直角三角形吗？
华东师大版八年级上册数学说课稿《勾股定理的应用》
华东师大版八年级上册数学说课稿《勾股定理的应用》一. 教材分析华东师大版八年级上册数学的《勾股定理的应用》一课，主要让学生了解勾股定理在实际问题中的应用。
教材通过引入实际问题，引导学生运用勾股定理解决问题，培养学生的数学应用能力。
本节课的内容是在学生已经掌握了勾股定理的基础上进行教学的，因此，教材在编写上注重引导学生将理论知识与实际问题相结合，提高学生的解决问题的能力。
二. 学情分析学生在学习本节课之前，已经学习了勾股定理的相关知识，对勾股定理有一定的理解。
但是，学生在实际应用勾股定理解决问题时，可能会遇到一些困难。
因此，在教学过程中，教师需要关注学生的学习情况，针对学生的困难进行有针对性的教学。
三. 说教学目标1.知识与技能目标：使学生掌握勾股定理在实际问题中的应用，提高学生的数学应用能力。
2.过程与方法目标：通过解决实际问题，培养学生运用勾股定理解决问题的能力。
3.情感态度与价值观目标：激发学生学习数学的兴趣，培养学生的团队合作精神。
四. 说教学重难点1.教学重点：引导学生运用勾股定理解决实际问题。
2.教学难点：学生在解决实际问题时，如何灵活运用勾股定理。
五. 说教学方法与手段1.教学方法：采用问题驱动法、案例教学法、小组合作学习法等。
2.教学手段：利用多媒体课件、实物模型等辅助教学。
六. 说教学过程1.导入新课：通过一个实际问题，引导学生回忆勾股定理的内容。
2.讲解新课：讲解勾股定理在实际问题中的应用，引导学生学会运用勾股定理解决问题。
3.案例分析：分析几个典型的实际问题，让学生动手解决，巩固所学知识。
4.小组讨论：让学生分组讨论，分享各自解决问题的方法，培养学生的团队合作精神。
5.总结提升：总结本节课的主要内容，强调勾股定理在实际问题中的应用。
6.课后作业：布置一些实际问题，让学生课后练习，巩固所学知识。
七. 说板书设计板书设计如下：1.勾股定理的应用2.实际问题 -> 勾股定理 -> 解决问题3.案例分析4.小组讨论5.总结提升八. 说教学评价教学评价主要包括以下几个方面：1.学生对勾股定理的理解程度。
14.2 勾股定理的应用 华东师大版数学八年级上册知识考点梳理课件
又 ∵BF=6 cm，∴BG=5+6=11（cm）.
在 Rt△ABG 中，AG= +
= + = （cm）；
14.2 勾股定理的应用
返回目录
方案二：如图 2，当蚂蚁从点 A 出发经过 BF 到点 G
重
难
题 时（将前面和右面展开），
型
∵AB=3 cm，BC=5 cm，
设 B′E=BE=x，则 CE=4-x.
∵S△AEC=
∴
Βιβλιοθήκη CE×AB=
（4-x）×3=
AC×B′E，
×5x，解得 x=
，∴B′E=
.
14.2 勾股定理的应用
返回目录
变式衍生 1
如图，在长方形 ABCD 中，AB=8，BC=4
重
难
题 ，将长方形沿 AC折叠，点 D 落在点 D′处，则重叠部分
突
破 ，BF=6 cm，蚂蚁要沿着怎样的路线爬行，才能最快吃到饼
干渣？ 这时蚂蚁走过的路程是多少？
14.2 勾股定理的应用
返回目录
［答案］解：分以下三种方案讨论：
重
难
方案一：如图 1，当蚂蚁从点 A 出发经过 EF 到点 G
题
型
突 时（将前面和上面展开），
破
∵BC=5 cm，∴FG=BC=5 cm.
对点典例剖析
考
点
典例
如图，一架 2.5 m 长的梯子AB 斜靠在墙 AC 上
清
单
解 ，梯子的顶端 A离地面的高度为 2.4 m，如果梯子的底部 B
读 向外滑出 1.3 m 后停在 DE位置上，则梯子的顶部下滑多少
在 Rt△ABG 中，AG= +
= + = （cm）；
14.2 勾股定理的应用
返回目录
方案二：如图 2，当蚂蚁从点 A 出发经过 BF 到点 G
重
难
题 时（将前面和右面展开），
型
∵AB=3 cm，BC=5 cm，
设 B′E=BE=x，则 CE=4-x.
∵S△AEC=
∴
Βιβλιοθήκη CE×AB=
（4-x）×3=
AC×B′E，
×5x，解得 x=
，∴B′E=
.
14.2 勾股定理的应用
返回目录
变式衍生 1
如图，在长方形 ABCD 中，AB=8，BC=4
重
难
题 ，将长方形沿 AC折叠，点 D 落在点 D′处，则重叠部分
突
破 ，BF=6 cm，蚂蚁要沿着怎样的路线爬行，才能最快吃到饼
干渣？ 这时蚂蚁走过的路程是多少？
14.2 勾股定理的应用
返回目录
［答案］解：分以下三种方案讨论：
重
难
方案一：如图 1，当蚂蚁从点 A 出发经过 EF 到点 G
题
型
突 时（将前面和上面展开），
破
∵BC=5 cm，∴FG=BC=5 cm.
对点典例剖析
考
点
典例
如图，一架 2.5 m 长的梯子AB 斜靠在墙 AC 上
清
单
解 ，梯子的顶端 A离地面的高度为 2.4 m，如果梯子的底部 B
读 向外滑出 1.3 m 后停在 DE位置上，则梯子的顶部下滑多少
八年级数学上册1《勾股定理的应用》课件 2022年北师大版八上数学PPT+
9．一个木工师傅测量了一个等腰三角形木板的腰、底边和高的长，
但他把这三个数据与其他的数据弄混了，请你帮助他找出来为( C )
A．13，12，12
B．12，12，8
C．13，10，12
D．5，8，4
10．如图，王大伯家屋后有一块长12 m，宽8 m的矩形空地，他在以
长边BC为直径的半圆内种菜，他家养的一只羊平时拴A处的一棵树上，
思路探究:除了截短法和延长法外,在等腰三角形中,我们通常作底边的中线或高或顶角平分 线,以便使用等腰三角形的性质(三线合一).
第一章 三角形的证明 复习
回顾 思考1
“原名〞 知多少
公理:公认的真命题称为公理(axiom). 证明:除了公理外,其它真命题的正确性都通过推理的方法证实.
推理的过程称为证明. 定理:经过证明的真命题称为定理(theorem). 推论:由一个公理或定理直接推出的定理,叫做这个公理或定理的推论(corollary).推 论可以当作定理使用.
第8题图
第9题图
15．(8分)在一棵树的10 m高处有两只猴子，其中一只爬下树走向离树 20 m的池塘，而另一只爬向树顶后直扑池塘，如果两只猴子经过的距 离相等，问这棵树有多高？ 解：如图，点B为树顶，D处有两只猴子，那么AD＝10 m，C为池塘， 那么AC＝20 m．设BD的长为x m，那么树的高度为(10＋x) m．因为 AC＋AD＝BD＋BC，所以BC＝20＋10－x＝(30－x)m.在△ACB中， ∠A＝90°，所以AC2＋AB2＝BC2.即202＋(10＋x)2＝(30－x)2，解得 x＝5，所以x＋10＝5＋10＝15，即这棵树高为15 m
结论4: 等腰三角形腰上的高线与底边的夹角等于顶 角的一半.
结论5:等腰三角形底边上的任意一点到两腰的距离 之和等于一腰上的高.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
14.2勾股定理的应用
勾股定理的内容是什么?
A
b c
a2+b2=c2
B a 勾股定理:直角三角形两直角边的平方 和等于斜边的平方． C
如果已知三角形的三边长a、b、c，怎样 判定这个三角形是否为直角三角形？ 如果三角形的三边长a、b、c有 关系：a2+b2=c2，那么这、个三 角形是直角三角形．
B
C
B
A
A
探 索 与 研 究
A
3.6米
D
B
１.２米O
C
A
3米 ３.６米
D
B
O
C
C
A O D B
C
2.3 米
O
H
2米
D
如图,从电杆离地面5米处向地面拉一条7米 长的钢缆,求地面钢缆固定点A到电杆底部B 的距离． C
B
A
一个圆柱形的封闭易拉罐，它的底面半径 为４cm,高为１５cm,问易拉罐内可放的搅 拌棒（直线型）最长可为多长？
一圆柱体的底面周长为２０cm, 高AB为４ cm, BC是上底面的直径 .一只蚂蚁从点A出发， 沿着圆柱的侧面爬行到点C, 试求出爬行的最 短路程．（精确到０.０１cm）
B
C B
C
A
D A
D
一只蜘蛛从长、宽都是3,高是8的长方体 纸箱的A点沿纸箱爬到B点，那么它所爬 行的最短路线的长是多少？
A A1
A2
B
C
应用勾股定理解决实际问题的一般思路： １、立体图形中路线最短的问题，往往是把 立体图形展开，得到平面图形．根据“两点 之间，线段最短” 确定行走路线，根据勾股 定理计算出最短距离．
２、在解决实际问题时，首先要画出适当的 示意图，将实际问题抽象为数学问题，并构 建直角三角形模型，再运用勾股定理解决实 际问题．
勾股定理的内容是什么?
A
b c
a2+b2=c2
B a 勾股定理:直角三角形两直角边的平方 和等于斜边的平方． C
如果已知三角形的三边长a、b、c，怎样 判定这个三角形是否为直角三角形？ 如果三角形的三边长a、b、c有 关系：a2+b2=c2，那么这、个三 角形是直角三角形．
B
C
B
A
A
探 索 与 研 究
A
3.6米
D
B
１.２米O
C
A
3米 ３.６米
D
B
O
C
C
A O D B
C
2.3 米
O
H
2米
D
如图,从电杆离地面5米处向地面拉一条7米 长的钢缆,求地面钢缆固定点A到电杆底部B 的距离． C
B
A
一个圆柱形的封闭易拉罐，它的底面半径 为４cm,高为１５cm,问易拉罐内可放的搅 拌棒（直线型）最长可为多长？
一圆柱体的底面周长为２０cm, 高AB为４ cm, BC是上底面的直径 .一只蚂蚁从点A出发， 沿着圆柱的侧面爬行到点C, 试求出爬行的最 短路程．（精确到０.０１cm）
B
C B
C
A
D A
D
一只蜘蛛从长、宽都是3,高是8的长方体 纸箱的A点沿纸箱爬到B点，那么它所爬 行的最短路线的长是多少？
A A1
A2
B
C
应用勾股定理解决实际问题的一般思路： １、立体图形中路线最短的问题，往往是把 立体图形展开，得到平面图形．根据“两点 之间，线段最短” 确定行走路线，根据勾股 定理计算出最短距离．
２、在解决实际问题时，首先要画出适当的 示意图，将实际问题抽象为数学问题，并构 建直角三角形模型，再运用勾股定理解决实 际问题．