人教版八年级上期末试题归纳
人教版八年级上册语文期末测试题及答案

1综合测试一、积累与运用(28分) (一)基础知识(24分)1、中国书法是我们民族文化的瑰宝,请将下面格言抄写在方格内,要求正确、工整、整洁(32、下列词语中加点字读音有误的一项是( )(2分)A 惟妙惟肖.(xi ào) 绮.丽(q ǐ) 憎.恨(z ēng) 两栖.(q ī)B 销声匿.迹(n ì) 愧怍.(zu ò) 琐屑.(xi â) 追溯.(s ù)C 风雪载.途 (z ài) 蹒跚..(p án sh ān) 褶.皱(zh ě) 震悚.(s ǒng)D 日薄.西山(b ó) 箱箧.(qi â) 殷.红(y ān ) 绥.靖(s úi) 3、请根据具体的语境和拼音写出汉字。
(4分) ①父亲明明该高兴,却露出些g ān g à ( )的笑。
②历史、现实,在雨中融合了——融成一幅悲哀而美丽、真实而荒mi ù( )的画面③一个物种在新的环境中必然遵循物j ìng( )天择的法则 ④有一个信客,年纪不小了,已经长途b ásh â( )了二三十年。
4、下列句子中加点词语使用有误的一项是( )(2分)A 、各级政府应该加大力度,因地制宜....的发展地方农村经济,增加农民收入。
B 、巴勒斯坦的斯瓦特被誉为“东方的瑞士”,但“9.11”事件以后,来这里旅游的人几乎是凤毛麟角....。
C 、玉雕作品“翠玉白菜”因其材质上乘,惟妙惟肖....,富有创意而被誉为我国的国宝。
D 、看着他瘦骨嶙峋....的样子,母亲的眼角湿润了。
5、下列句子中说法错误的一项是( )(2分)A 、记叙文的主要表达方式是叙述和描写,但议论和抒情在记叙文中也经常运用。
B 、说明文是客观的说明事物、阐明事理的一种文体。
常见的说明顺序有三种:时间顺序,空间顺序和逻辑顺序。
C 、说明文的结构一般有两种:总——分式和总——分——总式。
人教版八年级语文上册期末试题及答案(完整)

人教版八年级语文上册期末试题及答案(完整)满分:120 分 考试时间:120 分钟一、语言的积累与运用。
( 35 分)1、下列各组词语中加点字的书写或注音无误的一组是() A .溃退(kuì) .屏息敛声 督战(dū) . 残绝人寰 殚精竭虑 锐不可当 B .颁发(bān ) .眼花瞭乱 遗嘱(zhǔ) . C .仲裁(zhōng )摧枯拉朽 辱没(mò) . . D .娴熟(xián ) . 震聋发聩 悄然(qiāo ) 一丝不苟. 3、下列句子中加点的成语使用正确的一项是() A .托尔斯泰一直都是长相平平,鹤立鸡群,混在人群里找都找不出来。
....B .近二十年来,我们学校的面貌有了很大变化,但与先进学校相比,就黯然失 ... 色了。
.C .这对眼睛不会放过微不足道的细节,同样也能全面揭示广袤无垠的宇宙。
....D .我们只有学会观察生活,善于积累生活素材,写作时才能做到言之有物,言 之有情,不至于粗制滥造。
....4、下列语句没有语病的一句是( )A .当我走到路口时,看到一片热闹的景象。
B .一进屋子,我看到的第一眼是一幅油画。
C .这次比赛的胜利,将决定我们能否进入决赛阶段。
D .从咿呀学语,到走入学校,再到进入社会,学习伴随每个人的一生。
5、下面语句所使用的修辞手法不同于其他三项的一项是( )A .再见了,奥地利50 先令钞票上的弗洛伊德。
再见了,塞尚和你的苹果。
再见 了,阿波罗和亚历山大大帝。
B .森林里的害虫大量繁殖,成群地向树木进攻,吃树叶,咬树根,钻树心。
C .蟋蟀在青草中快乐地弹琴。
D .我思念那洞庭湖,我思念那长江,我思念那东海,那浩浩荡荡的无边无际的 波澜呀!6、给下列句子排序,最恰当的一项是( )①当阳光洒在身上时,它更坚定了心中的信念---要开出:一朵鲜艳的花。
②不久,它从泥土里探出了小脑袋,渐渐地,种子变成了嫩芽。
③从此,它变得沉默,只有它知道,它在努力,它在默默地汲取土壤中的养料。
人教版数学八年级上学期《期末测试题》及答案解析

15.因式分解:
(1) ;(2) .
16.(1)解分式方程: .
(2)如图, 与 中,AC与BD交于点E,且 , ,求证: .
四、解答题(共32分,每题8分)
17.(1)已知 ,求 的值.
(2)化简: ,并从±2,±1,±3中选择一个合适的数求代数式的值.
18.为厉行节能减排,倡导绿色出行,我市推行“共享单车”公益活动.某公司在小区分别投放A、B两种不同款型 共享单车,其中A型车的投放量是B型车的投放量的 倍,B型车的成本单价比A型车高20元,A型、B型单车投放总成本分别为30000元和26400元,求A型共享单车的成本单价是多少元?
例如:
利用这种分组的思想方法解决下列问题:
(1)分解因式 ;
(2) 三边a,b,c满足 判断 的形状,并说明理由.
五、解答题(本题共18分,其中每9分)
21.如图,在 中, ,点 在 内, , ,点 在 外, , .
(1)求 的度数;
(2)判断 形状并加以证明;
(3)连接 ,若 , ,求 的长.
22.阅读下面材料:
①AD是∠BAC 平分线
②∠ADC=60°
③点D在AB的垂直平分线上
④若AD=2dm,则点D到AB的距离是1dm
⑤S△DAC:S△DAB=1:2
A.2B.3C.4D.5
[答案]D
[解析]
[分析]
①根据作图的过程可以判定AD是∠BAC的角平分线;
②利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质来求∠ADC的度数;
(1) ;(2) .
[答案](1) ;(2)
[解析]
[分析]
(1)先提取公因式,然后利用完全平方公式因式分解即可;
人教版八年级上册数学期末考试试卷附答案

人教版八年级上册数学期末考试试题一、单选题1.下列长度的三根木棒能组成三角形的是( )A .2 ,3 ,4B .2 ,2 ,4C .2 ,3 ,6D .1 ,2 ,4 2.若分式224x x +-有意义,则x 的取值范围是( ) A .x≠2 B .x≠ ±2 C .x≠﹣2 D .x ≥﹣23.五边形的外角和等于( )A .180°B .360°C .540°D .720°4.某细菌直径长约0.0000152米,那么该细菌的直径长用科学记数法可表示为( )A .152×105米B .1.52×10﹣5米 C .﹣1.52×105米 D .1.52×10﹣4米 5.若把分式xy x y +的x 和y 都扩大3倍,那么分式xy x y+的值( ) A .扩大3倍 B .扩大9倍 C .扩大4倍 D .不变 6.如果三角形的三个内角的度数比是2:3:4,则它是( )A .锐角三角形B .钝角三角形C .直角三角形D .钝角或直角三角形7.若点A (m ,n )和点B (5,﹣7)关于x 轴对称,则m+n 的值是( )A .2B .﹣2C .12D .﹣128.如图,AD 是△ABC 的中线,点E 是AD 的中点,连接BE 、CE ,若△ABC 的面积是8,则阴影部分的面积为( )A .2B .4C .6D .89.如图,△ABC 中AB 边上的高是( )A .线段ADB .线段AC C .线段CD D .线段BC10.如图,在Rt△ABC 中,△ACB =90°,△A =30°,CD 是斜边AB 上的高,BD =2,那么AD 的长为( )A .2B .4C .6D .8二、填空题11.分解因式:23m m -=________.12.一个正多边形的内角和等于1440°,则此多边形是________边形.13.若a m =3,a n =4,则a m+n =_____.14.已知1112a b -=,则ab b a -的值是_____. 15.如图,已知△ABC△△DCB ,△BDC=35°,△DBC=50°,则△ABD=________.16.如图,若△A =15°,AB =BC =CD =DE =EF ,则△DEF 等于_____.17.如图.已知ABC 中,12AB AC ==厘米,B C ∠=∠,8BC =厘米,D 为AB 的中点.如果点P 在线段BC 上以2厘米/秒的速度由点B 向点C 运动,同时,点Q 在线段CA 上由点C向点A 运动.若点Q 的运动速度为a 厘米/秒,则当BPD △与CQP 全等时,a 的值为______.18.如图,在ABC ∆中,AC 的垂直平分线交BC 于点D ,交AC 于点E ,ABD ∆的周长为12,cm AC 的长为5cm ,那么ABC ∆的周长是___________cm三、解答题19.解方程:312x x =-. 20.先化简,再求值:2229344--⋅+-+x x x x x ,其中x =﹣1 21.已知a ,b ,c 是△ABC 的三边长,且满足a 2+b 2﹣4a ﹣8b+20=0,c=3cm ,求△ABC 的周长.22.如图,在四边形ABCD 中,AD△BC ,E 为CD 的中点,连接AE 、BE ,BE△AE ,延长AE 交BC 的延长线于点F. 已知AD=2cm ,BC=5cm.(1)求证:FC=AD ;(2)求AB 的长.23.某服装店用960元购进一批服装,并以每件46元的价格全部售完.由于服装畅销,服装店又用2220元,再次以比第一次进价多5元的价格购进服装,数量是第一次购进服装的2倍,仍以每件46元的价格出售.()1该服装店第一次购买了此种服装多少件?()2两次出售服装共盈利多少元?24.在直角坐标系中,ABC ∆的三个顶点的位置如图所示.(1)请画出ABC ∆关于y 轴对称的'''A B C ∆(其中',','A B C 分别是,,A B C 的对应点,不写画法);(2)直接写出',','A B C 三点的坐标'A ( ),'B ( ),'C ( ),(3)求出'''A B C 的面积25.从边长为a 的正方形中剪掉一个边长为b 的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).(1)上述操作能验证的等式是 ;(请选择正确的一个)A 、a 2﹣2ab+b 2=(a ﹣b )2B 、a 2﹣b 2=(a+b )(a ﹣b )C 、a 2+ab=a (a+b )(2)应用你从(1)选出的等式,完成下列各题:△已知x 2﹣4y 2=12,x+2y=4,求x ﹣2y 的值.△计算:(1﹣212)(1﹣213)(1﹣214)…(1﹣2119)(1﹣2120).26.如图,△ABC 和△AOD 是等腰直角三角形,AB=AC ,AO=AD ,△BAC=△OAD=90°,点O 是△ABC 内的一点,△BOC=130°.(1)求证:OB=DC ;(2)求△DCO 的大小;(3)设△AOB=α,那么当α为多少度时,△COD 是等腰三角形.27.如图,,ABC AEF ∆∆均为等边三角形,连接BE ,连接并延长CF 交BE 于点D . (1)求证:CAF BAE ∆≅∆;(2)连接AD ,求证DA 平分CDE ∠.参考答案1.A2.B3.B4.B5.A6.A7.C8.B9.C10.Cm m11.(3)12.1013.1214.215.45°.16.60°17.2或3【分析】此题要分两种情况:△当BD=PC时,△BPD与△CQP全等,计算出BP的长,进而可得运动时间,然后再求a;△当BD=CQ时,△BDP△△CQP,计算出BP的长,进而可得运动时间,然后再求a.【详解】解:当BD=PC时,△BPD与△CQP全等,△点D为AB的中点,AB=6cm,△BD=12△BD=PC,△BP=8-6=2(cm),△点P在线段BC上以2厘米/秒的速度由B点向C点运动,△运动时间时1s,△△DBP△△PCQ,△BP=CQ=2cm,△a=2÷1=2;当BD=CQ时,△BDP△△CQP,△BD=6cm,PB=PC,△QC=6cm,△BC=8cm,△BP=4cm,△运动时间为4÷2=2(s),△a=6÷2=3(m/s),故答案为:2或3.【点睛】此题主要考查了全等三角形的判定,关键是要分情况讨论,不要漏解,掌握全等三角形的判定方法:SSS 、SAS 、ASA 、AAS 、HL .18.17.【分析】由DE 是AC 的垂直平分线,可得AD=DC ,由ABD △的周长为12cm ,可得AB+AD+BD=12cm ,再由AD=DC ,可得AB+BC=12cm ,结合AC=5cm 进行计算即可.【详解】解:△ABD △的周长为12cm ,△AB+AD+BD=12cm ,△DE 是AC 的垂直平分线,△AD=DC ,△AB+DC+BD=12cm ,△AB+BC=12cm ,△AC=5cm ,△AB+BC+AC=17cm ,即ABC 的周长是17cm ,故答案为:17.【点睛】本题考查了线段的垂直平分线的性质,正确理解线段的垂直平分线的性质是解题的关键.19.3x =【分析】根据分式方程的一般求解步骤求解即可,最后检验方程的根. 【详解】解:312x x =- 化为整式方程为:3(2)x x -=去括号得:36x x -=移项,合并同类项得:26x =解得:3x =经检验:3x =是原方程的根,所以原方程的解为:3x =【点睛】本题考查了分式方程的解法,熟悉掌握分式方程的解法步骤是解题的关键. 20.32x x --,43【分析】根据分式乘法的运算法则对分式进行化简,然后代入求解即可.【详解】解:2229344--⋅+-+x x x x x 2(3)2)3(3)(2x x x x x -+--⋅+=, 32x x -=-, 将1x =-代入得, 原式134123--==--, 【点睛】此题考查了分式的化简求值,解题的关键是掌握分式的有关运算法则,正确对分式进行化简.21.△ABC 的周长为9.【分析】由a 2+b 2﹣4a ﹣8b+20=0,利用非负数的性质可求得a ,b 的值,然后根据三角形的周长公式进行求解即可得.【详解】△a 2+b 2﹣4a ﹣8b+20=0,△a 2﹣4a+4+b 2﹣8b+16=0,△(a ﹣2)2+(b ﹣4)2=0,又△(a ﹣2)2≥0,(b ﹣4)2≥0,△a ﹣2=0,b ﹣4=0,△a=2,b=4,△△ABC 的周长为a+b+c=2+4+3=9,答:△ABC 的周长为9.【点睛】本题考查了因式分解的应用、非负数的性质等,解题的关键是利用因式分解将所给式子的左边转化成非负数的和的形式.22.(1)证明见解析 ;(2)AB=7cm.【详解】试题分析:(1)根据AD△BC 可知△ADC=△ECF ,再根据E 是CD 的中点可求出△ADE△△FCE ,根据全等三角形的性质即可解答.(2)根据线段垂直平分线的性质判断出AB=BF 即可.试题解析:(1)△AD△BC△△ADC=△ECF ,△E 是CD 的中点,△DE=EC ,△在△ADE与△FCE中,ADC ECFDE ECAED CEF∠=∠⎧⎪=⎨⎪∠=∠⎩,△△ADE△△FCE(ASA) ,△FC=AD ;(2)△△ADE△△FCE,△AE=EF,AD=CF ,△BE△AE ,△BE是线段AF的垂直平分线,△AB=BF=BC+CF,△AD=CF ,△AB=BC+AD=5+2=7(cm).23.(1)该服装店第一次购买了此种服装30件;(2)两次出售服装共盈利960元【分析】(1)设该服装店第一次购买了此种服装x件,则第二次购进2x件,根据单价总价数量结合第二次购进单价比第一次贵5元,即可得出关于x的分式方程,解之经检验后即可得出结论;(2)根据销售单价x销售数量两次进货总价利润,即可求出结论.【详解】解:()1设该服装店第一次购买了此种服装x件,则第二次购进2x件,根据题意得:222096052x x-=,解得:x30=,经检验,x30=是原方程的根,且符合题意.答:该服装店第一次购买了此种服装30件.()()246303029602220960(⨯+⨯--=元).答:两次出售服装共盈利960元.【点睛】本题考查分式方程的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)根据数量间的关系,列式计算.24.(1)所画图形见解析;(2)3,-3 ;-1,-3;0,4 ;(3)11【分析】(1)分别作出各点关于y轴的对称点,再顺次连接各点即可;(2)根据各点在坐标系中的位置写出各点坐标即可;(3)作矩形DB EF ',用矩形的面积减去三个三角形的面积,即可得到A B C S'''.【详解】解:(1)如图所示:(2)由图可知,A '(3,-3),B '(-1,-3),C '(0,4);(3)如图,作矩形DB EF ',则DB EF S S S S S ''''''''''=---△A B C △C DB △C FA △A EB 四边形1117417316411222=⨯-⨯⨯-⨯⨯-⨯⨯=, △11A B C S '''=△.25.(1)B ;(2)△3;△2140. 【分析】(1)根据两个图形中阴影部分的面积相等,即可列出等式;(2)△把x 2﹣4y 2利用(1)的结论写成两个式子相乘的形式,然后把x+2y=4代入即可求解;△利用(1)的结论化成式子相乘的形式即可求解.【详解】(1)第一个图形中阴影部分的面积是a 2﹣b 2,第二个图形的面积是(a+b )(a ﹣b ),则a 2﹣b 2=(a+b )(a ﹣b ).故答案是B ;(2)△△x 2﹣4y 2=(x+2y )(x ﹣2y ),△12=4(x ﹣2y )得:x ﹣2y=3;△原式=(1﹣12)(1+12)(1﹣13)(1+13)(1﹣14)(1+14)…(1﹣119)(1+119)(1﹣120)(1+120) 1324351820192122334419192020=⨯⨯⨯⨯⨯⨯⋯⨯⨯⨯⨯ =12×2120 =2140. 26.(1)证明见解析;(2)40°;(3)当α的度数为115°或85°或145°时,△AOD 是等腰三角形【分析】(1)由已知证明△AOB△△ADC ,根据全等三角形的性质即可证得;(2)由△BOC=130°,根据周角的定义可得△BOA+△AOC=230°,再根据全等三角形的性质继而可得△ADC+△AOC=230°,由△DAO=90°,在四边形AOCD 中,根据四边形的内角和即可求得△DCO 的度数;(3)分三种情况进行讨论即可得.【详解】(1)△△BAC=△OAD=90°,△△BAC ﹣△CAO=△OAD ﹣△CAO ,△△DAC=△OAB ,在△AOB 与△ADC 中,AB AC OAB DAC AO AD =⎧⎪∠=∠⎨⎪=⎩,△△AOB△△ADC ,△OB=DC;(2)△△BOC=130°,△△BOA+△AOC=360°﹣130°=230°,△△AOB△△ADC△AOB=△ADC,△△ADC+△AOC=230°,又△△AOD是等腰直角三角形,△△DAO=90°,△四边形AOCD中,△DCO=360°﹣90°﹣230°=40°;(3)当CD=CO时,△△CDO=△COD=1801804022DCO︒-∠︒-︒==70°,△△AOD是等腰直角三角形,△△ODA=45°,△△CDA=△CDO+△ODA=70°+45°=115°,又△AOB=△ADC=α,△α=115°;当OD=CO时,△△DCO=△CDO=40°,△△CDA=△CDO+△ODA=40°+45°=85°,△α=85°;当CD=OD时,△△DCO=△DOC=40°,△CDO=180°﹣△DCO﹣△DOC=180°﹣40°﹣40°=100°,△△CDA=△CDO+△ODA=100°+45°=145°,△α=145°,综上所述:当α的度数为115°或85°或145°时,△AOD是等腰三角形.27.(1)见解析;(2)详见解析.【分析】(1)利用SAS证明即可;(2)逆用角的平分线性质定理证明.【详解】(1)△△ABC,△AEF 是等边三角形,△AC=AB,AF=AE,△CAB=△EAF,△△CAB -△FAB =△EAF -△FAB,△△CAF=△BAE,△△CAF△△BAE;(2)过点A 分别作AH△CD 于点H,AG△BE,交BE 的延长线于点G, 由(1)知,△CAF△△BAE ,△CF=BE ,CAF BAE S S =, △1122CE AH BE AG ⨯⨯=⨯⨯,△AH=AG ,△DA 平分△CDE.。
人教版数学八年级上册期末考试试卷附答案

人教版数学八年级上册期末考试试题一、选择题(每小题只有一个正确答案。
每小题2分,共12分)1.(2分)下列平面图形中,不是轴对称图形的是()A.B.C.D.2.(2分)计算(﹣2x2y)3的结果是()A.﹣2x5y3B.﹣8x6y3C.﹣2x6y3D.﹣8x5y33.(2分)如果代数式有意义,那么x的取值范围是()A.x≥0B.x≠1C.x>0 D.x≥0且x≠1 4.(2分)一个三角形的三条边长分别为1、2、x,则x的取值范围是()A.1≤x≤3B.1<x≤3C.1≤x<3 D.1<x<35.(2分)如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是()A.180°B.220°C.240°D.300°6.(2分)如图,已知∠1=∠2,∠B=∠C,下列结论:(1)AB=AC;(2)∠BAE=∠CAD;(3)BE=DC;(4)AD=DE.中正确的个数是()A.1 B.2 C.3 D.4二、填空题(每小题3分,共24分)7.(3分)芝麻作为食品和药物,均广泛使用.经测算,一粒芝麻约有0.00000201千克,用科学记数法表示为.8.(3分)因式分解:ax2﹣ay2=.9.(3分)已知等腰三角形两边的长分别是9和4,则它的周长为.10.(3分)如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,需添加一个条件是.(只需添加一个条件即可)11.(3分)如图是某超市一层到二层滚梯示意图.其中AB、CD分别表示超市一层、二层滚梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘滚梯从点B到点C上升的高度h约为米.12.(3分)将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF =90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF=.13.(3分)计算+的结果是.14.(3分)如图,在△ABC中,CD是它的角平分线,DE⊥AC于点E.若BC=6cm,DE =2cm,则△BCD的面积为cm2.三、解答题(每题5分,共20分)15.(5分)计算:(π﹣3.14)0+()﹣1﹣|﹣2|﹣(﹣1)2020.16.(5分)计算:(a+3)(a﹣1)+a(a﹣2)17.(5分)已知一个多边形的内角和与外角和之比为9:2,求它的边数.18.(5分)解分式方程:﹣=1.四、解答题(每小题7分,共28分)19.(7分)如图,在平面直角坐标系中.(1)请画出△ABC关于y轴对称的△AB1C1,并写出B1、C1的坐标;(2)直接写出△ABC的面积:S△ABC=;(3)在x轴上找到一点P,使PA+PC的值最小,请标出点P在坐标轴上的位置.20.(7分)如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.(1)从图中任找两组全等三角形;(2)从(1)中任选一组进行证明.21.(7分)已知:a+b=4,ab=2,求下列式子的值:①a2+b2②(a﹣b)222.(7分)如图所示,在△ABC中,BO,CO分别平分∠ABC和∠ACB;BD、CD分别平分∠ABC和∠ACB的外角.(1)若∠BAC=70°,求:∠BOC的度数;(2)探究∠BDC与∠A的数量关系.(直接写出结论,无需说明理由)五、解答题(每小题8分,共16分)23.(8分)学校在假期内对教室内的黑板进行整修,需在规定日期内完成.如果由甲工程小组做,恰好按期完成;如果由乙工程小组做,则要超过规定日期3天.结果两队合作了2天,余下部分由乙组独做,正好在规定日期内完成,问规定日期是几天?24.(8分)如图1,等边△ABC中,AD是BC边上的中线,E为AD上一点(点E与点A 不重合),以CE为一边且在CE下方作等边△CEF,连接BF.(1)猜想线段AE,BF的数量关系:(不必证明);(2)当点E为AD延长线上一点时,其它条件不变.①请你在图2中补全图形;②(1)中结论成立吗?若成立,请证明;若不成立请说明理由.六、解答题(每小题10分,共20分)25.(10分)如图①所示,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿虚线AB剪开,把剪成的两张纸片拼成如图②所示的等腰梯形.(1)设图①中阴影部分的面积为S1,图②中阴影部分面积为S2,请直接用含a,b的式子表示S1和S2.(2)请写出上述过程中所揭示的乘法公式;(3)用这个乘法公式计算:①(x﹣)(x+)(x2+);②107×93.26.(10分)在△ABC中,AB=AC=2,∠B=40°,D是线段BC上一动点(不与B、C 两点重合),且∠ADE=40°.(1)若∠BDA=115°,则∠CDE=,∠AED=;(2)当DC等于多少时,△ABD≌△DCE?试说明理由;(3)在D点运动过程中,能使△ADE是等腰三角形吗?若能,请求出使△ADE是等腰三角形时的∠ADB的度数;若不能,请说明理由.答案与解析一、单项选择题1.(2分)下列平面图形中,不是轴对称图形的是()A.B.C.D.【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析.【解答】解:A、是轴对称图形,故此选项不合题意;B、是轴对称图形,故此选项不合题意;C、不是轴对称图形,故此选项符合题意;D、是轴对称图形,故此选项不合题意;故选:C.【点评】此题主要考查了轴对称图形,判断轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.2.(2分)计算(﹣2x2y)3的结果是()A.﹣2x5y3B.﹣8x6y3C.﹣2x6y3D.﹣8x5y3【分析】积的乘方法则,把每一个因式分别乘方,再把所得的幂相乘,据此求解即可.【解答】解:(﹣2x2y)3=(﹣2)3(x2)3y3=﹣8x6y3.故选:B.【点评】本题主要考查了幂的乘方与积的乘方,熟记幂的运算法则是解答本题的关键.3.(2分)如果代数式有意义,那么x的取值范围是()A.x≥0B.x≠1C.x>0 D.x≥0且x≠1【分析】代数式有意义的条件为:x﹣1≠0,x≥0.即可求得x的范围.【解答】解:根据题意得:x≥0且x﹣1≠0.解得:x≥0且x≠1.故选:D.【点评】式子必须同时满足分式有意义和二次根式有意义两个条件.分式有意义的条件为:分母≠0;二次根式有意义的条件为:被开方数≥0.此类题的易错点是忽视了二次根式有意义的条件,导致漏解情况.4.(2分)一个三角形的三条边长分别为1、2、x,则x的取值范围是()A.1≤x≤3B.1<x≤3C.1≤x<3 D.1<x<3【分析】已知两边,则第三边的长度应是大于两边的差而小于两边的和,这样就可求出第三边长的范围.【解答】解:根据题意得:2﹣1<x<2+1,即1<x<3.故选:D.【点评】考查了三角形三边关系,本题需要理解的是如何根据已知的两条边求第三边的范围.5.(2分)如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是()A.180°B.220°C.240°D.300°【分析】本题可先根据等边三角形顶角的度数求出两底角的度数和,然后在四边形中根据四边形的内角和为360°,求出∠α+∠β的度数.【解答】解:∵等边三角形的顶角为60°,∴两底角和=180°﹣60°=120°;∴∠α+∠β=360°﹣120°=240°;故选:C.【点评】本题综合考查等边三角形的性质及三角形内角和为180°,四边形的内角和是360°等知识,难度不大,属于基础题6.(2分)如图,已知∠1=∠2,∠B=∠C,下列结论:(1)AB=AC;(2)∠BAE=∠CAD;(3)BE=DC;(4)AD=DE.中正确的个数是()A.1 B.2 C.3 D.4【分析】先证AB=AC,再证△ABE≌△ACD(AAS)得AD=AE,BE=CD,∠BAE =∠CAD,即可得出结论.【解答】解:∵∠B=∠C,∴AB=AC,故(1)正确;在△ABE和△ACD中,,∴△ABE≌△ACD(AAS),∴AD=AE,BE=CD,∠BAE=∠CAD,故(2)(3)正确,(4)错误,正确的个数有3个,故选:C.【点评】本题考查了全等三角形的判定与性质、等腰三角形的判定等知识,熟练掌握全等三角形的判定与性质是本题的关键.二、填空题(每小题3分,共24分)7.(3分)芝麻作为食品和药物,均广泛使用.经测算,一粒芝麻约有0.00000201千克,用科学记数法表示为 2.01×10﹣6.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.00000201=2.01×10﹣6.故答案为:2.01×10﹣6.【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.8.(3分)因式分解:ax2﹣ay2=a(x+y)(x﹣y).【分析】首先提取公因式a,再利用平方差公式分解因式得出答案.【解答】解:ax2﹣ay2=a(x2﹣y2)=a(x+y)(x﹣y).故答案为:a(x+y)(x﹣y).【点评】此题主要考查了提取公因式法以及公式法分解因式,正确应用平方差公式是解题关键.9.(3分)已知等腰三角形两边的长分别是9和4,则它的周长为22.【分析】因为等腰三角形的两边分别为4和9,但没有明确哪是底边,哪是腰,所以有两种情况,需要分类讨论.【解答】解:当4为底时,其它两边都为9,即:9、9、4可以构成三角形,周长为22;当4为腰时,其它两边为9和4,因为4+4=8<9,所以不能构成三角形,故舍去.所以答案只有22.故答案为:22.【点评】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.10.(3分)如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,需添加一个条件是∠D=∠B.(只需添加一个条件即可)【分析】利用全等三角形的判定与性质进而得出当∠D=∠B时,△ADF≌△CBE.【解答】解:当∠D=∠B时,在△ADF和△CBE中∵,∴△ADF≌△CBE(SAS),故答案为:∠D=∠B.(答案不唯一)11.(3分)如图是某超市一层到二层滚梯示意图.其中AB、CD分别表示超市一层、二层滚梯口处地面的水平线,∠ABC=150°,BC的长约为12米,则乘滚梯从点B到点C上升的高度h约为6米.【分析】先过点C作CE⊥AB,交AB的延长线于E,易求∠CBE=30°,在Rt△BCE中可知CE=BC,进而可求CE.【解答】解:过点C作CE⊥AB,交AB的延长线于E,如右图,∵∠ABC=150°,∴∠CBE=30°,在Rt△BCE中,∵BC=12,∠CBE=30°,∴CE=BC=6.故答案是6.【点评】本题考查了含30°角的直角三角形的性质,解题的关键是作辅助线构造直角三角形.12.(3分)将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF =90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF=25°.【分析】由∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,可求得∠ACE的度数,又由三角形外角的性质,可得∠CDF=∠ACE﹣∠F=∠BCE+∠ACB﹣∠F,继而求得答案.【解答】解:∵AB=AC,∠A=90°,∴∠ACB=∠B=45°,∵∠EDF=90°,∠E=30°,∴∠F=90°﹣∠E=60°,∵∠ACE=∠CDF+∠F,∠BCE=40°,∴∠CDF=∠ACE﹣∠F=∠BCE+∠ACB﹣∠F=45°+40°﹣60°=25°.故答案为:25°.13.(3分)计算+的结果是.【分析】利用分式加减法的计算方法进行计算即可.【解答】解:原式=﹣===,故答案为:.14.(3分)如图,在△ABC中,CD是它的角平分线,DE⊥AC于点E.若BC=6cm,DE =2cm,则△BCD的面积为6cm2.【分析】作DF⊥BC于F,根据角平分线的性质求出DF,根据三角形的面积公式计算即可.【解答】解:作DF⊥BC于F,∵CD是它的角平分线,DE⊥AC,DF⊥BC,∴DF=DE=2,∴△BCD的面积=×BC×DF=6(cm2),故答案为:6.【点评】本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.三、解答题(每题5分,共20分)15.(5分)计算:(π﹣3.14)0+()﹣1﹣|﹣2|﹣(﹣1)2020.【分析】先算零指数幂、负整数指数幂、绝对值、乘方,再算加减法即可求解.【解答】解:(π﹣3.14)0+()﹣1﹣|﹣2|﹣(﹣1)2020=1+2﹣2﹣1=0.【点评】考查了实数的运算,解决此类题目的关键是熟练掌握零指数幂、负整数指数幂、绝对值、乘方等知识点的运算.16.(5分)计算:(a+3)(a﹣1)+a(a﹣2)【分析】根据整式混合运算的顺序和法则分别进行计算,再把所得结果合并即可.【解答】解:(a+3)(a﹣1)+a(a﹣2)=a2+2a﹣3+a2﹣2a=2a2﹣3;【点评】此题考查了整式的混合运算,在计算时要注意混合运算的顺序和法则以及运算结果的符号,是一道基础题.17.(5分)已知一个多边形的内角和与外角和之比为9:2,求它的边数.【分析】根据多边形的内角和与外角和之间的关系列出有关边数n的方程求解即可.【解答】解:设该多边形的边数为n则(n﹣2)×180°:360=9:2,解得:n=11.故它的边数为11.【点评】本题考查了多边形的内角与外角,解题的关键是牢记多边形的内角和公式与外角和定理.18.(5分)解分式方程:﹣=1.【分析】先去分母,再解整式方程,一定要验根.【解答】解:﹣=1(x+1)2﹣4=x2﹣1x2+2x+1﹣4=x2﹣1x=1,检验:把x=1代入x2﹣1=1﹣1=0,∴x=1不是原方程的根,原方程无解.【点评】本题考查了解分式方程,掌握分式方程一定要验根是解题的关键.四、解答题(每小题7分,共28分)19.(7分)如图,在平面直角坐标系中.(1)请画出△ABC关于y轴对称的△AB1C1,并写出B1、C1的坐标;(2)直接写出△ABC的面积:S△ABC=5;(3)在x轴上找到一点P,使PA+PC的值最小,请标出点P在坐标轴上的位置.【分析】(1)利用关于y轴对称的点的坐标特征写出B1、C1的坐标,然后描点即可;(2)用一个矩形的面积分别减去三个直角三角形的面积去计算△ABC的面积;(3)作A点关于x轴的对称点A′,然后连接A′C交x轴于P点.【解答】解:(1)如图,△AB1C1为所作,B1(﹣2,﹣4),C1(﹣4,﹣1);(2)S△ABC=3×4﹣×2×2﹣×2×3﹣×4×1=5;故答案为5;(3)如图,点P为所作.【点评】本题考查了作图﹣轴对称变换:几何图形都可看做是由点组成,我们在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的.也考查了最短路径问题.20.(7分)如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.(1)从图中任找两组全等三角形;(2)从(1)中任选一组进行证明.【分析】(1)根据题目所给条件可分析出△ABE≌△CDF,△AFD≌△CEB;(2)根据AB∥CD可得∠1=∠2,根据AF=CE可得AE=FC,然后再证明△ABE≌△CDF即可.【解答】解:(1)△ABE≌△CDF,△AFD≌△CEB;(2)∵AB∥CD,∴∠1=∠2,∵AF=CE,∴AF+EF=CE+EF,即AE=FC,在△ABE和△CDF中,,∴△ABE≌△CDF(AAS).【点评】此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.21.(7分)已知:a+b=4,ab=2,求下列式子的值:②(a﹣b)2.【分析】①根据(a+b)2=a2+2ab+b2,可得a2+b2=(a+b)2﹣2ab,再把a+b=4,ab=2代入计算即可;②根据(a﹣b)2=a2﹣2ab+b2=(a+b)2﹣4ab,再把a+b=4,ab=2代入计算即可.【解答】解:∵a+b=4,ab=2,∴①a2+b2=(a+b)2﹣2ab=42﹣2×2=16﹣4=12;②(a﹣b)2=a2﹣2ab+b2=(a+b)2﹣4ab=42﹣4×2=16﹣8=8.【点评】本题考查完全平方公式的应用,根据题中条件,变换形式即可.22.(7分)如图所示,在△ABC中,BO,CO分别平分∠ABC和∠ACB;BD、CD分别平分∠ABC和∠ACB的外角.(1)若∠BAC=70°,求:∠BOC的度数;(2)探究∠BDC与∠A的数量关系.(直接写出结论,无需说明理由)【分析】(1)根据三角形的角平分线定义和三角形的内角和定理求出∠OBC+∠OCB的度数,再根据三角形的内角和定理即可求出∠BOC的度数;(2)根据三角形外角平分线的性质可得∠BCD=(∠A+∠ABC)、∠DBC=(∠A+∠ACB);根据三角形内角和定理可得∠BDC=90°﹣∠A.【解答】解:(1)∵OB、OC分别是∠ABC和∠ACB的角平分线,∴∠OBC+∠OCB=∠ABC+∠ACB=(∠ABC+∠ACB),∵∠A=70°,∴∠OBC+∠OCB=(180°﹣70°)=55°,∴∠BOC=180°﹣(∠OBC+∠OCB)=125°;(2)∠BDC=90°﹣∠A.理由如下:∵BD、CD为△ABC两外角∠ABC、∠ACB的平分线,∴∠BCD=(∠A+∠ABC)、∠DBC=(∠A+∠ACB),由三角形内角和定理得,∠BDC=180°﹣∠BCD﹣∠DBC,=180°﹣[∠A+(∠A+∠ABC+∠ACB)],=180°﹣(∠A+180°),=90°﹣∠A;【点评】本题考查的是三角形内角和定理,涉及到三角形内角与外角的关系,角平分线的性质,三角形内角和定理,结合图形,灵活运用基本知识解决问题.五、解答题(每小题8分,共16分)23.(8分)学校在假期内对教室内的黑板进行整修,需在规定日期内完成.如果由甲工程小组做,恰好按期完成;如果由乙工程小组做,则要超过规定日期3天.结果两队合作了2天,余下部分由乙组独做,正好在规定日期内完成,问规定日期是几天?【分析】由题意可知甲的工作效率=1÷规定日期,乙的工作效率=1÷(规定日期+3);根据“结果两队合作了2天,余下部分由乙组独做,正好在规定日期内完成”可知甲做两天的工作量+乙做规定日期的工作量=1,由此可列出方程.【解答】解:设规定日期为x天,根据题意,得2(+)+×(x﹣2)=1解这个方程,得x=6经检验,x=6是原方程的解.∴原方程的解是x=6.答:规定日期是6天.【点评】找到关键描述语,找到等量关系是解决问题的关键.本题主要考查的等量关系为:工作时间=工作总量÷工作效率,当题中没有一些必须的量时,为了简便,应设其为1.24.(8分)如图1,等边△ABC中,AD是BC边上的中线,E为AD上一点(点E与点A 不重合),以CE为一边且在CE下方作等边△CEF,连接BF.(1)猜想线段AE,BF的数量关系:AE=BF(不必证明);(2)当点E为AD延长线上一点时,其它条件不变.①请你在图2中补全图形;②(1)中结论成立吗?若成立,请证明;若不成立请说明理由.【分析】(1)利用等边三角形的性质得出AC=BC,CE=CF,∠ACB=∠ECF=60°,进而得出∠ACE=∠BCF,进而判断出△ACE≌△BCF,即可得出结论;(2)①由题意补全图形,即可得出结论;②同(1)的方法,即可得出结论.【解答】解:(1)AE=BF,理由:∵△ABC和△CEF是等边三角形,∴AC=BC,CE=CF,∠ACB=∠ECF=60°,∴∠ACB﹣∠BCE=∠ECF﹣∠BCE,∴∠ACE=∠BCF,在△ACE和△BCF中,,∴△ACE≌△BCF(SAS),∴AE=BF,故答案为:AE=BF;(2)①补全图形如图2所示;②AE=BF仍然成立,理由:∵△ABC和△CEF是等边三角形,∴AC=BC,CE=CF,∠ACB=∠ECF=60°,∴∠ACB+∠BCE=∠ECF+∠BCE,∴∠ACE=∠BCF,在△ACE和△BCF中,,∴△ACE≌△BCF(SAS),∴AE=BF.【点评】此题是三角形综合题,主要考查了等边三角形的性质,全等三角形的判定和性质,判断出△ACE≌△BCF是解本题的关键.六、解答题(每小题10分,共20分)25.(10分)如图①所示,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿虚线AB剪开,把剪成的两张纸片拼成如图②所示的等腰梯形.(1)设图①中阴影部分的面积为S1,图②中阴影部分面积为S2,请直接用含a,b的式子表示S1和S2.(2)请写出上述过程中所揭示的乘法公式;(3)用这个乘法公式计算:①(x﹣)(x+)(x2+);②107×93.【分析】(1)图①中的阴影部分的面积为两个正方形的面积差,图②中的阴影部分是上底为2b,下底为2a,高为a﹣b的梯形,利用梯形面积公式可得答案;(2)图①、图②面积相等可得等式;(3)①连续两次利用平方差公式可求结果;②将107×93转化为(100+7)(100﹣7),即可利用平方差公式求出结果.【解答】解:(1)S1=a2﹣b2,S2=(2a+2b)(a﹣b)=(a+b)(a﹣b);(2)a2﹣b2=(a+b)(a﹣b);(3)①原式=(x2﹣)(x2+)=x4﹣;②107×93=(100+7)(100﹣7)=1002﹣72=10000﹣49=9951.【点评】本题考查平方差公式的几何背景,掌握平方差公式的结构特征是解决问题的关键.26.(10分)在△ABC中,AB=AC=2,∠B=40°,D是线段BC上一动点(不与B、C 两点重合),且∠ADE=40°.(1)若∠BDA=115°,则∠CDE=25°,∠AED=65°;(2)当DC等于多少时,△ABD≌△DCE?试说明理由;(3)在D点运动过程中,能使△ADE是等腰三角形吗?若能,请求出使△ADE是等腰三角形时的∠ADB的度数;若不能,请说明理由.【分析】(1)利用等腰三角形的性质和三角形的外角性质解答即可;(2)先求出∠ADB=∠DEC,再由∠B=∠C,AB=DC=2,即可得出△ABD≌△DCE (AAS);(3)分两种情况讨论即可.【解答】解:(1)∵AB=AC,∴∠B=∠C=∠40°,∵∠BDA=115°,∴∠ADC=180°﹣115°=65°,∴∠CDE=∠ADC﹣∠ADE=65°﹣40°=25°,∴∠AED=∠CDE+∠C=25°+40°=65°,故答案为:25°,65°;(2)当DC=2时,△ABD≌△DCE,理由如下:∵∠C=40°,∴∠DEC+∠EDC=140°,∵∠ADE=40°,∴∠ADB+∠EDC=140°,∴∠ADB=∠DEC,在△ABD和△DCE中,,∴△ABD≌△DCE(AAS);(3)△ADE能成为等腰三角形,理由如下:∵∠ADE=∠C=40°,∠AED>∠C,∴△ADE为等腰三角形时,只能是AD=DE或AE=DE,当AD=DE时,∠DAE=∠DEA=(180°﹣40°)=70°,∴∠EDC=∠AED﹣∠C=70°﹣40°=30°,∴∠ADB=180°﹣40°﹣30°=110°;当EA=ED时,∠ADE=∠DAE=40°,∴∠AED=180°﹣40°﹣40°=100°,∴∠EDC=∠AED﹣∠C=100°﹣40°=60°,∴∠ADB=180°﹣40°﹣60°=80°;综上所述,当∠ADB的度数为110°或80°时,△ADE是等腰三角形.【点评】此题考查了等腰三角形的判定与性质,全等三角形的判定与性质,三角形外角的性质等知识点,此题涉及到的知识点较多,综合性较强.21。
人教版八年级上册数学期末试题及答案
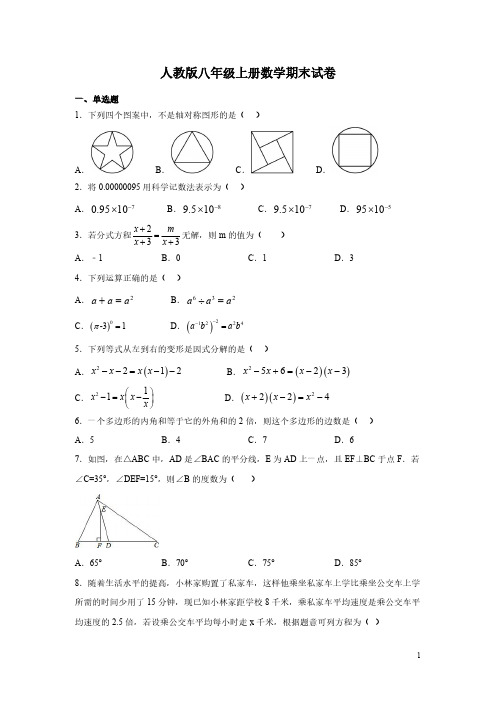
人教版八年级上册数学期末试卷一、单选题1.下列四个图案中,不是轴对称图形的是()A .B .C .D .2.将0.00000095用科学记数法表示为()A .70.9510-⨯B .89.510-⨯C .79.510-⨯D .59510-⨯3.若分式方程233x m x x +=++无解,则m 的值为()A .﹣1B .0C .1D .34.下列运算正确的是()A .2a aa +=B .632a a a ÷=C .()0-31π=D .()21224a b a b --=5.下列等式从左到右的变形是因式分解的是()A .()2212x x x x --=--B .()()25623x x x x -+=--C .211x x x x ⎛⎫-=- ⎪⎝⎭D .()()2224x x x +-=-6.一个多边形的内角和等于它的外角和的2倍,则这个多边形的边数是()A .5B .4C .7D .67.如图,在△ABC 中,AD 是∠BAC 的平分线,E 为AD 上一点,且EF ⊥BC 于点F .若∠C=35°,∠DEF=15°,则∠B 的度数为()A .65°B .70°C .75°D .85°8.随着生活水平的提高,小林家购置了私家车,这样他乘坐私家车上学比乘坐公交车上学所需的时间少用了15分钟,现已知小林家距学校8千米,乘私家车平均速度是乘公交车平均速度的2.5倍,若设乘公交车平均每小时走x 千米,根据题意可列方程为()A .8815 2.5x x+=B .8184 2.5x x +=C .88152.5x x =+D .8812.54x x =+9.如图,在ABC 中,90,30A C PQ ∠=︒∠=︒,垂直平分BC ,与AC 交于点,P 下列结论正确的是()A .2PC PA <B .2PC PA >C .2AB PA <D .2AB PA>10.如图,用尺规作图作已知角平分线,其根据是构造两个三形全等,它所用到的判别方法是()A .SASB .AASC .ASAD .SSS二、填空题11.使分式211x x -+的值为0,这时x=_____.12.计算:22222155ab b a b ab a b+⋅-=______________.13.已知点1(1,5)P a -和点2(2,1)P b -关于x 轴对称,则2016()b a +的值为_____________.14.若m+n=3,则2m 2+4mn+2n 2-6的值为________.15.已知6m x =,3n x =,则2m n x -的值为________.16.多项式x 2+2mx+64是完全平方式,则m =________.17.如图,已知∠AOB=60°,点P 在边OA 上,OP=24,点M ,N 在边OB 上,PM=PN ,若NM=6,则OM=______________.18.如图,等边ABC 的边长为4,AD 是BC 边上的中线,F 是AD 边上的动点,E 是AC 边上一点.若2AE =,当EF CF +取最小值时,ECF ∠的度数为___________度.19.如图,D 是AB 边上的中点,将ABC ∆沿过D 的直线折叠,使点A 落在BC 上F 处,若50B ∠=︒,则BDF ∠=__________度.20.如图,BC=EC ,∠1=∠2,要使△ABC ≌△DEC ,则应添加的一个条件为_____________(答案不唯一,只需填一个)三、解答题21.解分式方程:(1)21322x x x-+=--(2)262393x x x x x -+=+--22.化简求值:(1)()()()322484a b a b ab a bab +-+-÷,其中21a b ==,(2)2234221121x x x x x x ++-÷---+(,其中x 取﹣1,1,﹣2,﹣3中你认为合理的数.23.在△ABC 中,AB=CB ,∠ABC=90°,F 为AB 延长线上一点,点E 在BC 上,且AE=CF .(1)求证:△ABE ≌△CBF ;(2)若∠CAE=30°,求∠ACF 度数.24.如图,在△ABC 中,AB=AC ,点D 、E 、F 分别在BC 、AB 、AC 边上,且BE=CF ,AD+EC=AB .(1)求证:△DEF 是等腰三角形;(2)当∠A=40°时,求∠DEF 的度数;(3)△DEF 可能是等腰直角三角形吗?为什么?(4)请你猜想:当∠A 为多少度时,∠EDF+∠EFD=120°,并请说明理由.25.某公司计划购买A ,B 两种型号的机器人搬运材料.已知A 型机器人比B 型机器人每小时多搬运30kg 材料,且A 型机器人搬运1000kg 材料所用的时间与B 型机器人搬运800kg 材料所用的时间相同.(1)求A ,B 两种型号的机器人每小时分别搬运多少材料;(2)该公司计划采购A ,B 两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg ,则至少购进A 型机器人多少台?26.已知如图,AD 是BAC ∠的角平分线,DE AB ⊥,DF AC ⊥,垂足分别是E ,F .求证:AD 垂直平分EF .27.已知:如图,已知△ABC(1)点A 关于x 轴对称的点A 1的坐标是,点A 关于y 轴对称的点A 2的坐标是;(2)画出与△ABC 关于x 轴对称的△A 1B 1C 1;(3)画出与△ABC 关于y 轴对称的△A 2B 2C 2.28.某农资公司购进甲、乙两种农药,乙种农药的单价是甲种农药单价的3倍,购买250元甲种农药的数量比购买300元乙种农药的数量多15,求两种农药单价各为多少元?参考答案1.C【分析】根据轴对称的概念对各选项分析判断即可求解.【详解】解:A 、是轴对称图形,故本选项不合题意;B 、是轴对称图形,故本选项不合题意;C 、不是轴对称图形,故本选项符合题意;D 、是轴对称图形,故本选项不合题意.故选:C .【点睛】本题主要考查了轴对称图形的概念,判断轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.2.C【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10−n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】解:0.00000095=79.510-⨯故选:C【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10−n ,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.3.A【详解】解:两边同乘以(x+3)得:x+2=m ,x=m-2,∵方程无解∴x+3=0,即m-2+3=0,∴1m =-,故选:A.4.C【分析】根据合并同类项法则、幂运算法则进行计算判断.【详解】A 、2a a a +=,故原计算错误;B 、633a a a ÷=,故原计算错误;C 、()0-31π=,故正确;D 、()21224a b a b ---=,故原计算错误;故选:C .【点睛】本题考查整式的加减乘除运算,熟练掌握运算法则是关键.5.B【分析】根据因式分解是把一个多项式转化成几个整式积的形式,可得答案.【详解】A 、()()2221x x x x --=-+,没有把一个多项式转化为几个整式积的形式,故A 错误;B 、把一个多项式转化为几个整式积的形式,故B 正确;C 、()()21+11x x x -=-,故C 错误;D 、()()2224x x x +-=-,整式的乘法,故D 不是因式分解.故选:B【点睛】本题考查了因式分解的意义,因式分解是把一个多项式转化成几个整式积的形式.6.D【分析】利用多边形内角和公式和外角和定理,列出方程即可解决问题.【详解】解:根据题意,得:(n-2)×180=360×2,解得n=6.故选:D .【点睛】本题考查了多边形内角与外角,解答本题的关键是根据多边形内角和公式和外角和定理,利用方程法求边数.7.A【详解】解:∵EF ⊥BC ,∠DEF=15°,∴∠ADB=90°-15°=75°.∵∠C=35°,∴∠CAD=75°-35°=40°.∵AD 是∠BAC 的平分线,∴∠BAC=2∠CAD=80°,∴∠B=180°-∠BAC-∠C=180°-80°-35°=65°.故选A .8.D【分析】根据乘私家车平均速度是乘公交车平均速度的2.5倍,乘坐私家车上学比乘坐公交车上学所需的时间少用了15分钟,利用时间得出等式方程即可.【详解】解:设乘公交车平均每小时走x 千米,根据题意可列方程为:8812.54x x =+.故选D .【点睛】此题主要考查了由实际问题抽象出分式方程,解题关键是正确找出题目中的相等关系,用代数式表示出相等关系中的各个部分,列出方程即可.9.C【分析】由题意连接BP ,并根据垂直平分线的性质进行分析求解即可.【详解】解:连接BP则130C ∠∠︒==.230∴∠︒=2PC PB PA ∴==.AB PB <,2AB PA ∴<.故选:C.【点睛】本题考查垂直平分线相关,熟练掌握垂直平分线的性质是解题的关键.10.D【分析】根据作图过程可知:OC=OD ,PC=PD ,又OP=OP ,从而利用SSS 判断出△OCP ≌△ODP ,根据全等三角形的对应角相等得出∠COP=∠DOP ,即OP 平分∠AOB ,从而得出答案.【详解】解:由画法得OC=OD ,PC=PD ,而OP=OP ,所以△OCP ≌△ODP (SSS ),所以∠COP=∠DOP ,即OP 平分∠AOB.故答案为:D.【点睛】本题考查了用尺规作图作已知角平分线,三角形全等的判定,用尺规作图作已知角平分线,三角形全等的判定掌握是解题的关键.11.1【详解】由题意得211x x -+=0,所以x 2-1=0且x+1≠0,解之得x=1,故答案为:1.12.3aa b-【分析】先把分子、分母分别分解因式,再约分计算.【详解】原式=()()()22155b a b a b ab a b a b +⋅+-=3a a b-,故填:3a a b-.【点睛】本题考查分式的乘法运算法则,熟练掌握因式分解是关键.13.1【详解】解:∵点()11,5P a -和点()22,1Pb -关于x 轴对称,∴a-1=2,b-1=-5,∴a=3,b=-4,∴()2016a b +=(-1)2016=1,故答案为:1.14.12【详解】解:原式=2(m 2+2mn+n 2)-6=2(m+n )2-6=2×9-6=12故答案为:12.15.12【分析】逆运用同底数幂的乘法公式和幂的乘方公式对原式适当变形,再将值代入计算即可.【详解】解:2222()6312m n m n n m x x x xx -=÷=÷=÷=.故答案为:12.【点睛】本题考查幂的乘方公式的逆运用,同底数幂的乘法逆运用.熟练掌握相关公式是解题关键.16.±8【详解】根据完全平方式的特点,首平方,尾平方,中间是加减首尾积的2倍,因此可知2mx=2×(±8)x,所以m=±8.故答案为±8.【点睛】此题主要考查了完全平方式,解题时,要明确完全平方式的特点:首平方,尾平方,中间是加减首尾积的2倍,关键是确定两个数的平方.17.9【分析】过P作PD⊥OB,交OB于点D,在直角三角形POD中,求出OD的长,再由PM=PN,利用三线合一得到D为MN中点,根据MN求出MD的长,由OD-MD即可求出OM的长.【详解】解:过P作PD⊥OB,交OB于点D,∵∠AOB=60°,∴∠OPD=30°,∴OD=12OP=12.∵PM=PN,PD⊥MN,∴MD=ND=12MN=3,∴OM=OD﹣MD=12﹣3=9.故答案为:9.【点睛】本题考查的是含30度直角三角形的性质,等腰三角形的性质等知识,根据题意添加适当辅助线是解本题的关键.18.30【分析】由等边三角形三线合一,可知:点B 和点C 关于AD 成轴对称,连接BE 交AD 于点F ,此时,EF CF +取得最小值,进而,求出ECF ∠的度数即可.【详解】∵ABC ∆是等边三角形,AD 是BC 边上的中线,∴AD ⊥BC ,AD 平分∠BAC ,∴点B 和点C 关于AD 所在直线成轴对称,连接BE 交AD 于点F ,则BF=CF ,∴EF CF +=EF+BF=BE ,即:此时,EF CF +取得最小值,∵等边ABC ∆的边长为4,2AE =,∴E 是AC 的中点,∴BE 平分∠ABC ,∵点F 是角平分线AD 与BE 的交点,∴CF 平分∠BCA ,即:∠FCA=12∠ACB=12×60°=30°,∴∠ECC=30°.故答案是:30.【点睛】本题主要考查等边三角形中,两线段和最小时,求角的度数,通过轴对称,把两线段和化为两点之间的一条线段的长,是解题的关键.19.80【分析】先根据折叠的性质可得AD DF =,根据等边对等角的性质可得B BFD ∠=∠,再根据三角形的内角和定理列式计算即可求解.【详解】解:DEF 是DEA △沿直线DE 翻折变换而来,AD DF ∴=,D 是AB 边的中点,AD BD ∴=,BD DF ∴=,B BFD ∴∠=∠,50B ∠=︒ ,180180505080BDF B BFD ∴∠=︒-∠-∠=︒-︒-︒=︒.故答案为:80.【点睛】本题考查的是折叠的性质,以及等边对等角、三角形内角和定理,熟知折叠的性质是解答此题的关键.20.AC=DC (答案不唯一)【详解】根据∠1=∠2可得∠BCA=∠ECD ,添加AC=DC 可以利用SAS 来进行判定;添加∠B=∠E 可以利用ASA 来进行判定;添加∠A=∠D 可以利用AAS 来进行判定.故答案为:AC=DC (答案不唯一)21.(1) 1.5x =;(2)无解【分析】(1)两边同乘2x -进行去分母,再求解整式方程,最后检验即可;(2)两边同乘()()33x x +-进行去分母,再求解整式方程,最后检验即可.【详解】(1)21322x x x-+=--解:两边同乘2x -得()2321x x +-=-解得 1.5x =检验:当 1.5x =时,20x -≠,∴ 1.5x =是原分式方程的解,(2)262393x x x x x -+=+--解:两边同乘()()33x x +-得()()()3623x x x x -+=-+解得3x =检验:当3x =时,()()330x x +-=,∴3x =不是原分式方程的解,∴原分式方程无解.【点睛】本题考查解分式方程,熟练掌握分式方程的求解过程并注意检验是解题关键.22.(1)22a ab -,0;(2)11x x -+,2【分析】(1)原式利用平方差公式,以及多项式除以单项式法则计算,去括号合并得到最简结果,把a 与b 的值代入计算即可求出值;(2)首先把括号内的分式的分母分解因式,把除法转化为乘法,进行分式的加减,利用分配律计算,然后根据题意选择合理的数,代入即可.【详解】(1)原式2222a b b ab=-+-22a ab =-,当2a =,1b =时,原式22221=-⨯⨯0=;(2)原式()()()()()()22113411112x x x x x x x x ⎡⎤+-+=-⋅⎢⎥+-+-+⎣⎦()()()212112x x x x x -+=⋅+-+11x x -=+,由题意可知,1x ≠±且2x ≠-∴3x =-,当3x =-时,原式2=.【点睛】本题考查了整式和分式的混合运算,熟练掌握运算法则是解题的关键.23.(1)见解析(2)∠ACF=60°【分析】(1)根据HL 可证明Rt △ABE ≌Rt △CBF ;(2)由全等三角形的性质得出∠BCF =∠BAE =15°,则可得出答案.【详解】(1)证明:∵∠ABC =90°,∴∠CBF =∠ABE =90°,在Rt △ABE 和Rt △CBF 中,AE CFAB BC =⎧⎨=⎩,∴Rt △ABE ≌Rt △CBF (HL );(2)解:∵AB =BC ,∠ABC =90°,∴∠CAB =∠ACB =45°,又∵∠BAE =∠CAB ﹣∠CAE =45°﹣30°=15°,由(1)知:Rt △ABE ≌Rt △CBF ,∴∠BCF =∠BAE =15°,∴∠ACF =∠BCF+∠ACB =15°+45°=60°.【点睛】本题考查了全等三角形的判定与性质,等腰直角三角形的性质,熟练掌握三角形全等的判定方法是解题的关键.24.(1)证明见解析;(2)∠DEF=70°;(3)△DEF 不可能是等腰直角三角形,理由见解析;(4)当∠A=60°时,∠EDF+∠EFD=120°,理由见解析.【分析】(1)首先根据条件证明△DBE ≌△ECF ,根据全等三角形的性质可得DE=FE ,进而可得到△DEF 是等腰三角形;(2)由(1)中的全等得出∠BDE=∠CEF ,再由角之间的转化,从而可求解∠DEF 的大小;(3)由于AB=AC ,可得∠B=∠C≠90°=∠DEF ,从而可确定其不可能是等腰直角三角形;(4)先猜想出∠A 的度数,则可得∠EDF+∠EFD=120°,根据前面的推导过程知∠EDF+∠EFD=120°时,∠DEF=60°,再由∠B=∠DEF 以及等腰三角形的性质继而推得猜想的正确性.【详解】(1)∵AB=AC ,∴∠B=∠C ,∵AD+EC=AB ,AB=AD+BD ,∴BD=CE ,在△BDE 和△CEF 中,BD CE B C BE CF =⎧⎪∠=∠⎨⎪=⎩,∴△BDE ≌△CEF (SAS )∴DE=EF ,∴△DEF 是等腰三角形;(2)∵∠DEC=∠B+∠BDE ,即∠DEF+∠CEF=∠B+∠BDE ,由(1)知△BDE ≌△CEF ,则∠BDE=∠CEF ,∴∠DEF=∠B ,∵∠A=40°,∴∠B=∠C=()1180402⨯︒-︒=70°,∴∠DEF=70°;(3)△DEF 不可能是等腰直角三角形,∵AB=AC ,∴∠B=∠C≠90°,由(2)知∠DEF=∠B ,∴∠DEF=∠B≠90°,∴△DEF 不可能是等腰直角三角形;(4)当∠A=60°时,∠EDF+∠EFD=120°,理由是:当∠EDF+∠EFD=120°时,则∠DEF=180°-120°=60°,∴∠B=∠DEF=60°,∴∠A=180°-∠B-∠C=180°-60°-60°=60°,∴当∠A=60°时,∠EDF+∠EFD=120°.【点睛】本题主要考查了全等三角形的判定及性质以及等腰三角形的判定和性质问题,能够熟练掌握和灵活运用相关质是解题的关键.25.(1)A 型机器人每小时搬运150千克材料,B 型机器人每小时搬运120千克材料;(2)至少购进A 型机器人14台.【分析】(1)设B 型机器人每小时搬运x 千克材料,则A 型机器人每小时搬运(x+30)千克材料,根据A 型机器人搬运1000kg 材料所用的时间与B 型机器人搬运800kg 材料所用的时间相同建立方程求出其解即可得;(2)设购进A 型机器人a 台,根据每小时搬运材料不得少于2800kg 列出不等式进行求解即可得.【详解】(1)设B 型机器人每小时搬运x 千克材料,则A 型机器人每小时搬运(x+30)千克材料,根据题意,得100080030x x=+,解得:x=120,经检验,x=120是所列方程的解,当x=120时,x+30=150,答:A 型机器人每小时搬运150千克材料,B 型机器人每小时搬运120千克材料;(2)设购进A 型机器人a 台,则购进B 型机器人(20﹣a )台,根据题意,得150a+120(20﹣a )≥2800,解得a≥403,∵a 是整数,∴a≥14,答:至少购进A 型机器人14台.【点睛】本题考查了分式方程的应用,一元一次不等式的应用,读懂题意,找到关键描述语句,找准等量关系以及不等关系是解题的关键.26.见解析【分析】根据角平分线的性质可得DE DF =,易证AE AF =,即△AEF 为等腰三角形,根据三线合一可证结论.【详解】证明:∵AD 是BAC ∠的角平分线,DE AB ⊥,DF AC ⊥,∴DE DF =,∴12∠=∠,∵90AED AFD ∠=∠=︒,∴3=4∠∠,∴AE AF =,∵AD 是等腰三角形AEF 的顶角平分线,∴AD 垂直平分EF (三线合一)【点睛】本题考查了角平分线的性质和等腰三角形的性质—“三线合一”的应用,熟练掌握性质是解题的关键.27.(1)(-4,-2),(4,2);(2)图形见解析(3)图形见解析【分析】(1)分别利用关于x 轴以及y 轴对称点的性质得出对应点坐标即可;(2)直接利用关于x轴对称点的性质得出对应点坐标即可;(3)直接利用关于y轴对称点的性质得出对应点坐标即可.【详解】解:(1)(-4,-2),(4,2);(2)如图所示:△A1B1C1,即为所求;(3)如图所示:△A2B2C2,即为所求.28.10元、30元.【分析】设甲农药的单价为x元,乙农药的单价为3x元,根据购买250元甲农药的数量比购买300元乙农药的数量多15件列出方程,求出方程的解即可得到结果;【详解】解:设甲农药的单价为x元,乙农药的单价为3x元,根据题意得,250360-=15x3x,解得x=10,经检验,x=10是所列方程的根,∴3x=3×10=30(元),答:甲、乙两种农药品的单价分别为10元、30元.【点睛】本题主要考查了分式方程的应用,掌握分式方程是解题的关键.。
人教版八年级上册物理《期末考试试卷》(附答案解析)

人教版物理八年级上学期期末测试卷一、选择题1. “估测”是物理学中常用的一种方法.小华同学尝试估测了与自己身体相关的一些物理量,其中不合理的是A. 脉搏跳动约为68次/sB. 质量约为50kgC. 身体的平均密度约为1.0×103kg/m3D. 步行的速度约为1.1m/s2. 关于声现象,下列说法正确的是A. 随着科技进步,物体不振动也能发声B. 声音从空气传入水中,音调、响度以及传播速度都不变C. 用超声波粉碎人体内的结石,说明超声波具有能量D. 考试期间,学校路段禁止汽车鸣笛,这是在传播过程中减弱噪声3. 《中国诗词大会》深受观众喜爱,下列诗词中涉及的物态变化现象解释正确的是A. 风雨送春归,飞雪迎春到——雪是升华形成的B. 不知明镜里,何处得秋霜——霜是凝固形成的C. 露从今夜白,月是故乡明——露是液化形成的D. 岚雾今朝重,江山此地深——雾是汽化形成的4. 人们在生活中遇到的透镜及其组合所成的像是各种各样的,其中只能成实像的是A. 眼睛B. 放大镜C. 望远镜D. 显微镜5. 我们可以把初中物理的密度概念扩大,从一维线密度、二维面密度、三维体密度到四维密度进行深刻理解:描述电线上鸟的疏密程度用一维线密度(个数/长度),描述田野中昆虫的疏密程度用二维面密度(个数/面积),那么我们学习的密度(质量/体积)则可以称为A. 一维线密度B. 二维面密度C. 三维体密度D. 四维密度6. 如图,小明利用玻璃板“探究平面镜成像的特点”,B是蜡烛A的像,则下列说法中()①看到像,是因为B发光进入人眼②在像B的位置放一张白纸,纸上不会出现蜡烛A的像③蜡烛A向玻璃板靠近,像B也会靠近玻璃板④蜡烛A向玻璃板靠近,像B会变大A. 只有①③正确B. 只有②④正确C. 只有①④正确D. 只有②③正确7. 如图所示,甲试管装酒精(酒精沸点为78℃),乙试管装水,同时放入盛水的大烧杯中,对大烧杯加热至使里面的水沸腾一段时间,则下列说法中正确的是()A. 甲试管内的酒精和乙试管内的水都不沸腾B. 甲试管内的酒精和乙试管内的水同时沸腾C. 甲试管内的酒精先沸腾,乙试管内的水后沸腾D. 甲试管内的酒精会沸腾,乙试管内的水不沸腾8. 根据烟囱中冒的烟和甲、乙两小车上小旗飘动的情况,有关甲、乙两小车相对于房子的运动情况,下列说法中正确的是()A.甲、乙两小车一定向左运动B. 甲小车可能运动,乙小车向右运动C. 甲、乙两小车一定向右运动D. 甲小车可能静止,乙小车向左运动9. 某一物体做变速直线运动,总路程为12m,已知它在前一半路程的速度为4m/s,后一半路程的速度为6m/s,那么它在整个路程中的平均速度是()A. 4m/sB. 4.8m/sC. 5m/sD. 6m/s10. 如图,手机扫描二维码,相当于绘二码拍了一张照片,手机摄像头相当于凸透镜,影像传感器相当于光屏,下列说法正确的是A. 物体上的二维码是光源B.扫码时二维码要位于摄像头二倍焦距以外C. 要使屏幕上二维码的像变小,只需将二维码靠近凸透镜D. 影像传感器上成的是正立的实像11. 一刻度均匀但示数不准确的温度计,用它测标准气压下冰水混合物的温度时为5℃,测沸水的温度时为95℃,若用它来测得室内温度为32℃,则室内的实际温度约为A.35℃ B. 30℃ C. 33℃ D. 37℃12. 现有密度分别为a和b的两种液体,a的密度小于b,在甲杯中装满这两种液体,质量各占一半,在乙杯中装满这两种液体,体积各占一半,假设两种液体不发生混合,两个杯子完全相同,则A甲杯中液体质量大 B. 乙杯中液体质量大C. 两杯中质量一样大D. 无法确定质量大小13. 有一光电控制液面高度的仪器,是通过光束在液面上的反射光线打到光电屏上来显示液面高度的,光路图如图所示.当光屏上的光点由S1移到S2时,表示液面()A. 下降B. 上升C. 不变D. 先下降后上升14. 在测量液体密度的实验中,小明利用天平和量杯测量出液体和量杯的总质量m及液体的体积V,得到几组数据并绘出如图所示的m-V图像,下列说法正确的是A. 量杯质量为40gB. 40cm3的该液体质量为40gC. 该液体密度为1.25g/cm3D. 该液体密度为2g/ cm315. 交通部门常用测速仪来检测车速.测速原理是测速仪前后两次发出并接收到被测车反射回的超声波信号,再根据两次信号的时间差,测出车速,如图甲.某次测速中,测速仪发出与接收超声波的情况如图乙所示,x表示超声波与测速仪之间的距离.若超声波的速度为340m/s,且保持不变,则该被测汽车速度是()A. 28.334 m/sB. 13. 602 m/sC. 14. 167 m/sD. 14. 716 m/s二、填空题16. 小立同学不在“中国好声音”现场,通过收音机传来的声音就辨别出是导师李荣浩在唱歌,他是根据声音的________去判断的,收音机音量太大会使耳膜受损,说明声音能够传递________(“信息”或“能量”),为此需要减小声音的________(“音调”、“响度”或“音色”).17. 建国70周年国庆阅兵的一个电视画面.爸爸观看阅兵时告诉小明不要在电视机前站着,影响他看电视,这是因为________的.18. 如图甲所示,检查视力时要求人与视力表的距离是5m,现使用一个平面镜,视力表到平面镜的像距为3m,则人到平面镜的距离应该是_______m.一束光在空气与透明物质的界面处发生了反射和折射现象,入射光线和折射光线如图乙所示,界面MN的右侧是______(填选“空气”或“透明介质”)19. 2019年4月10日,发布了首张黑洞照片,为解开星系演化之谜提供了宝贵资料,照片中的黑洞距离我们5500万光年,它是根据接收到射线(一种特殊的光)经过处理而形成的,高能射线在真空中的传播速度为_________m/s.20. 2019年1月3日,嫦娥四号成功着陆月球表面,如图,遇视器“玉兔二号"正在稳步驶出停稳在月球表面的嫦娥四号,以月球为参照物,嫦娥四号是______ (选填“运动”或“静止”)的.21. 在某次青少年机器人展示活动中,甲、乙、丙三个智能机器人在周长为20米的圆形轨道上进行速度测试活动,它们同时从同一位置出发甲率先跑完5圈此时乙正好落后甲半圈,当乙也跑完5圈时,丙恰好也落后乙半圈,v甲:v乙=_____.假设甲、乙、丙沿圆周轨道运动时速度大小均保持不变,按照大赛的要求3个机器入都要跑完50圈,那么当甲完成任务丙还要跑______m.三、实验探究题22. 小明在实验室里测量一块形状不规则、体积较大的矿石的密度.(1)用调节好的天平测量矿石的质量.当天平平衡时右盘中的砝码及游码的位置如图所示;(2)因矿石的体积较大,放不进量简,因此他利用一只烧杯,按如图所示方法进行测量则矿石的体积是_______cm3;(3)矿石的密度是_______ kg/m3 (结果保留三个有效数字),图A到图B的操作引起的密度测量值比真实值_______(选填“偏大”“偏小”或“不变”).23. 某小组在做“探究水的沸腾”实验时,实验装置如图甲所示.(1)要完成图中实验需要的测量仪器是温度计和_______;在安装器材时,最后安装的是_______(选填“酒精灯”或 “温度计”).(2)通过图乙中b 的现象,可以判定水_____(选填“正在”或“没有”)沸腾.(3)实验结束停止加热后,发现水在高温时散热快,低温时散热慢.查阅资料,同一燃气灶不同火力加热的耗气量和其他信息如下表所示: 火力大小 水的质量M /kg 水的初温0t /℃ 水的末温t /℃ 消耗的燃气V /m 3 大火 4.0 26.0 50.0 0.0453 中火 4.026.050.00.0278综合分析可知:从节能的角度,用燃气灶烧开水的策略为( ) A.先中火后大火 B.先大火后中火 C.一直用大火. D.一直用中火24. 小雨用凸透镜做“探究凸透镜成像规律”的实验.(1)如图甲,将凸透镜正对着太阳光,在透镜下方,平行地放上白纸,测出透镜与白纸间距s 与对应的白纸被烤焦的时间t ,绘出图象,如图乙,则可判断该透镜的焦距f 为_____cm; (2)调整器材高度时,应_______(选填“点燃”或“不点燃”)蜡烛;(3)如图丙,将蜡烛移至45cm 刻度处时,从凸透镜右侧通过凸透镜可以看到烛焰的_____(选填“虚”或“实”)像;(4)小超想利用LED 发光字母来探究凸透镜成像上下左右位置关系,“HFBZ ”的4个字母适合做LED 光源的有______个.四、计算题25. 一小汽车在平直公路上以108 km/h 的速度匀速行驶,司机突然发现前方有紧急情况以后过0. 6 s 开始刹车(这0. 6 s 称为反应时间),刹车后又经过4.4 s 滑行52 m,车停止. (1)在司机的反应时间内,车前进的距离是多少m? (2)从发现情况到车停止,车的平均速度为多少?26. 如图所示,一个空烧杯质量为50g,装满水后质量为2.55kg,把正方体甲浸没在烧杯中,并把溢出的水擦干后,测得正方体甲、剩余水和烧杯的总质量为7.85 kg.把甲取出后,烧杯和剩余水的质量为1. 55 kg.实心正方体乙的边长为0.2m,质量为6kg,33110kg/m 水ρ=⨯.求:(1)正方体乙的密度ρ乙; (2)正方体甲的密度ρ甲;(3)若沿实心正方体乙的上表面向内部挖去一个底面积为0.01 m 2,高为h 的长方体如图所示,并在挖去部分中倒满水,是否可能使乙变化后的总质量与甲的质量相等?若可能,请计算h ;若不可能,请简要说明理由.答案与解析一、选择题1. “估测”是物理学中常用的一种方法.小华同学尝试估测了与自己身体相关的一些物理量,其中不合理的是A. 脉搏跳动约为68次/sB. 质量约为50kgC. 身体的平均密度约为1.0×103kg/m3D. 步行的速度约为1.1m/s【答案】A【解析】【分析】首先对题目中涉及的物理量有个初步的了解,对于选项中的单位,可根据需要进行相应的换算或转换,排除与生活实际相差较远的选项,找出符合生活实际的答案【详解】A. 正常情况下,人的脉搏1min跳动的次数在75次左右,跳动一次的时间接近1s,此选项不符合实际;B. 成年人的质量在65kg左右,中学生的质量比成年人小一些,在50kg左右,此选项符合实际; C. 水的密度是1.0×103kg/m3,人体密度与水的密度差不多,在1.0×103kg/m3左右,此选项合理;D. 正常步行的速度约为1.1m/s,此选项符合实际.故选A.2. 关于声现象,下列说法正确的是A.随着科技进步,物体不振动也能发声B. 声音从空气传入水中,音调、响度以及传播速度都不变C. 用超声波粉碎人体内的结石,说明超声波具有能量D. 考试期间,学校路段禁止汽车鸣笛,这是在传播过程中减弱噪声【答案】C 【解析】【详解】A.声音是由物体振动产生的,故随着科技进步,物体不振动一定不能发声,A说法错误;B.声音在不同介质中的传播速度不同,故声音从空气传入水中,传播速度发生改变,B说法错误;C.声音不仅能够传递能量,而且能够传递信息,故用超声波粉碎人体内的结石,说明超声波具有能量,C 说法正确;D.中考期间,学校路段禁止汽车鸣笛,这是在声源处减弱噪声,D说法错误.3. 《中国诗词大会》深受观众喜爱,下列诗词中涉及的物态变化现象解释正确的是A. 风雨送春归,飞雪迎春到——雪是升华形成的B. 不知明镜里,何处得秋霜——霜是凝固形成的C. 露从今夜白,月是故乡明——露是液化形成的D. 岚雾今朝重,江山此地深——雾是汽化形成的 【答案】C 【解析】【详解】雪和霜是由水蒸气凝华形成;露珠和雾均为小水珠,为液化形成. 【点睛】分清各种状态以及生活中常见的物态变化.4. 人们在生活中遇到的透镜及其组合所成的像是各种各样的,其中只能成实像的是 A. 眼睛 B. 放大镜C. 望远镜D. 显微镜【答案】A 【解析】【详解】A 、眼睛的原理和照相机相似,物体的光经晶状体在视网膜上成倒立、缩小的实像.A 符合题意为答案.B 、放大镜是凸透镜,当u<f 时,放大镜成正立、放大的虚像,B 不符合题意.C 、望远镜的物镜相当于照相机成倒立、缩小的实像,目镜相当于放大镜成正立、放大的虚像.C 不符合题意.D 、显微镜的物镜相当于投影仪成倒立、放大的实像,目镜相当于放大镜成正立、放大的虚像,故D 不符合题意.5. 我们可以把初中物理的密度概念扩大,从一维线密度、二维面密度、三维体密度到四维密度进行深刻理解:描述电线上鸟的疏密程度用一维线密度(个数/长度),描述田野中昆虫的疏密程度用二维面密度(个数/面积),那么我们学习的密度(质量/体积)则可以称为 A. 一维线密度 B. 二维面密度C. 三维体密度D. 四维密度【答案】C 【解析】【详解】密度是指单位体积某种物质的质量,即密度mVρ=,是指三维体密度,故C 正确. 6. 如图,小明利用玻璃板“探究平面镜成像的特点”,B 是蜡烛A 的像,则下列说法中( ) ①看到像,是因为B 发光进入人眼②在像B 的位置放一张白纸,纸上不会出现蜡烛A 的像 ③蜡烛A 向玻璃板靠近,像B 也会靠近玻璃板 ④蜡烛A 向玻璃板靠近,像B 会变大A. 只有①③正确B. 只有②④正确C. 只有①④正确D. 只有②③正确【答案】D【解析】【详解】①B为平面镜所成的虚像,我们能通过玻璃板看到蜡烛B,是因为A发出的光线经过平面镜反射后进入人的眼睛,虚像B本身不会发光,故①错误;②平面镜所成的像是虚像,虚像不能成在光屏上,故在像B的位置放一张白纸,纸上不会出现蜡烛A的像,故②正确;③蜡烛A向玻璃板靠近,由于像到镜面的距离等于物体到镜面的距离,故像B也会靠近玻璃板,故③正确;④蜡烛A向玻璃板靠近,由于像的大小始终和物体的大小相同,物体大小不变,像B不会改变,故④错误.故选D.7. 如图所示,甲试管装酒精(酒精沸点为78℃),乙试管装水,同时放入盛水的大烧杯中,对大烧杯加热至使里面的水沸腾一段时间,则下列说法中正确的是()A. 甲试管内的酒精和乙试管内的水都不沸腾B. 甲试管内的酒精和乙试管内的水同时沸腾C. 甲试管内的酒精先沸腾,乙试管内的水后沸腾D. 甲试管内的酒精会沸腾,乙试管内的水不沸腾【答案】D【解析】【详解】在大烧杯底部加热使烧杯内的水温度升高,由于水的沸点高于酒精的沸点,所以温度首先达到酒精的沸点,由于继续加热,所以甲试管内的酒精会沸腾;而乙试管内的水温度虽然能达到沸点,但不能继续从同温度的大烧杯里的水中吸热,所以试管内的水不能沸腾.故选D.8. 根据烟囱中冒的烟和甲、乙两小车上小旗飘动的情况,有关甲、乙两小车相对于房子的运动情况,下列说法中正确的是()A. 甲、乙两小车一定向左运动B. 甲小车可能运动,乙小车向右运动C. 甲、乙两小车一定向右运动D. 甲小车可能静止,乙小车向左运动 【答案】D 【解析】【详解】由图中的信息可以判断出:因为房子的烟向左飘,所以风是向左吹所以甲车运动状态有三种可能 1、向右运动;2、静止;3、向左运动,但速度小于风速;因为乙车旗向右飘,所以乙车只能向左运动,且速度要大于风的速度.9. 某一物体做变速直线运动,总路程为12m,已知它在前一半路程的速度为4m/s,后一半路程的速度为6m/s,那么它在整个路程中的平均速度是( ) A. 4m/s B. 4.8m/sC. 5m/sD. 6m/s【答案】B 【解析】前一半的时间为6m 4m /s 1.5?s ÷=,后一半的时间为6m 6m /s 1s ÷=,全程的总时间为 2.5s ,所以整个路程中的平均速度为12m4.8m /s 2.5ss v t ===,故应选B 【点睛】平均速度不是速度的平均值,而是总路程与总时间的比值.10. 如图,手机扫描二维码,相当于绘二码拍了一张照片,手机摄像头相当于凸透镜,影像传感器相当于光屏,下列说法正确的是A. 物体上的二维码是光源B. 扫码时二维码要位于摄像头二倍焦距以外C. 要使屏幕上二维码的像变小,只需将二维码靠近凸透镜D. 影像传感器上成的是正立的实像【答案】B【解析】【分析】能发光的物体称为光源.手机摄像头的镜头是凸透镜,其是利用物体在2倍焦距以外,像成在另一侧的1倍焦距和2倍焦距之间,成倒立缩小实像的原理制作的.凸透镜成实像时,物近像远像变大的特点.【详解】A、二维码本身不发光,不是光源,故A错误;B、手机摄像头相当于凸透镜,其是利用物体在2倍焦距以外,像成在另一侧的1倍焦距和2倍焦距之间,成倒立缩小实像的原理制作的,故B正确;C、如果要让像变小一些,凸透镜成实像时,物远像近像变小,应增大物距,应将二维码远离凸透镜,故C 错误.D、手机摄像头相当于凸透镜,影像传感器相当于光屏,影像传感器上成的是倒立缩小实像,故D错误.故选B.11. 一刻度均匀但示数不准确的温度计,用它测标准气压下冰水混合物的温度时为5℃,测沸水的温度时为95℃,若用它来测得室内温度为32℃,则室内的实际温度约为A. 35℃B. 30℃C. 33℃D. 37℃【答案】B【解析】解答:摄氏温度的规定是:标准大气压下水的沸点为100℃,冰水混合物为0℃,100℃和0℃之间有100等份,每一份代表1℃.由题意可知:该温度计下边第五个格的位置代表0℃,第九十五个格的位置代表100℃,即该温度计的95-5=90个小格表示100℃,据此可求出一个格代表的度数:(100℃-0℃)/(95-5)=10/9℃当室内温度为32℃,则室内的实际温度约为10/9℃╳(32-5)=30℃故【答案】B12. 现有密度分别为a和b的两种液体,a的密度小于b,在甲杯中装满这两种液体,质量各占一半,在乙杯中装满这两种液体,体积各占一半,假设两种液体不发生混合,两个杯子完全相同,则A. 甲杯中液体质量大B. 乙杯中液体质量大C. 两杯中质量一样大D. 无法确定质量大小【答案】B【详解】模型1即为甲杯:由于12ρρ<两种液体的质量且各占一半,可得密度1ρ 的液体体积大于密度2ρ的液体,密度1ρ的液体体积用灰色标记,密度2ρ的液体体积用蓝色标记.模型2即为乙杯:两种液体体积相等,密度1ρ的液体体积用灰色标记,密度2ρ的液体体积用蓝色标记;对照组体现体积相等时之间的分界线,对模型1密度1ρ的液体体积进行处理,切割成和模型1中密度1ρ的液体体积相同,即是容器体积的一半(如图所示).对模型2中密度2ρ的液体体积进行处理,切割成和模型1中密度2ρ的液体体积相同(如图所示),经过处理便可以直接从对比处比较甲、乙两杯内液体质量的大小了,答案很明显是对比处是蓝色的乙杯大,即乙杯内液体的质量大.故选B13. 有一光电控制液面高度的仪器,是通过光束在液面上的反射光线打到光电屏上来显示液面高度的,光路图如图所示.当光屏上的光点由S 1移到S 2时,表示液面( )A. 下降B. 上升C. 不变D. 先下降后上升【答案】A【详解】光屏上的光点由S 1移到S 2时,由于入射光线的方向固定不变,那么它的反射光线方向也不变,过S 2作平行线平行于过S 1的反射光线,这条平行线与入射光线交于O 点,O 点在CD 线上,液面CD 相对于液面AB 是下降,如图所示,故选A .14. 在测量液体密度的实验中,小明利用天平和量杯测量出液体和量杯的总质量m 及液体的体积 V ,得到几组数据并绘出 如图所示的 m -V 图像,下列说法正确的是A. 量杯质量为 40gB. 40cm 3 的该液体质量为40gC. 该液体密度为 1.25g/cm 3D. 该液体密度为 2g/ cm 3 【答案】B 【解析】 【分析】与纵轴的交点液体体积为0,此时所对应质量为量杯质量【详解】由图像可解出图像与纵轴交于20g 处,此时液体体积为0,则可知量杯质量为20g ;由图像可知,当液体体积为20cm 3时,总质量为40g ,则液体质量为20g ,密度3320g =1g /cm 20cmm V ρ==,则40cm 3的该液体质量331g /cm 40cm =40g m V ρ==⨯.15. 交通部门常用测速仪来检测车速.测速原理是测速仪前后两次发出并接收到被测车反射回的超声波信号,再根据两次信号的时间差,测出车速,如图甲.某次测速中,测速仪发出与接收超声波的情况如图乙所示,x 表示超声波与测速仪之间的距离.若超声波的速度为340m/s ,且保持不变,则该被测汽车速度是A. 28.334 m/sB. 13. 602 m/sC. 14. 167 m/sD. 14. 716 m/s【答案】C 【解析】【详解】由题图知,超声波第一次从测试仪发出到与汽车相遇的地点,经过的时间为:10.32s 10.16s =2t ⨯=由sv t=得,超声波通过的距离为: 11•340m/s 0.16s 54.4m s v t ==⨯=波波超声波第二次从测试仪发出到与汽车相遇的地点,经过的时间为:210.24s 0.12s 2t =⨯=超声波通过的距离为:22•340m/s 0.12s 40.8m s v t ==⨯=波波汽车行驶的距离为:1254.4m 40.8m 13.6m s s s =-=-=波波测试仪发出的超声波两次间隔时间为1s ,且测试仪第一次发出超声波记为0时刻,则超声波第一次从测试仪发出到与汽车相遇的地点,经过的时间为0.16s ;超声波第二次发出的时间为1s 末,超声波第二次与车相遇的时刻应该是:1s 0.12s 1.12s +=汽车行驶的时间是:1.12s 0.16s 0.96s t =-=所以汽车行驶的速度为:13.6m 14.167m/s 0.96st v s ==≈故选C.二、填空题16. 小立同学不在“中国好声音”现场,通过收音机传来的声音就辨别出是导师李荣浩在唱歌,他是根据声音的________去判断的,收音机音量太大会使耳膜受损,说明声音能够传递________(“信息”或“能量”),为此需要减小声音的________(“音调”、“响度”或“音色”).【答案】(1). 音色(2). 能量(3). 响度【解析】【分析】根据题中“辨别出是导师李荣浩在唱歌”、“收音机音量太大会使耳膜受损”、“声音能够传递”可知,本题考查声音的三个特性、声音的利用,根据它们的规律,运用响度与振幅有关、音调与频率有关、音色与与材料有关、声音能够传递信息与能量,分析推断.【详解】[1]每个人说话的声音都不一样,通过收音机传来的声音就辨别出是导师李荣浩在唱歌,这是根据声音的音色去判断的;[2]收音机音量太大会使耳膜受损,说明声音能够传递能量;[3]音量太大是指声音的振幅大,为此需要减小声音的响度.17. 建国70周年国庆阅兵的一个电视画面.爸爸观看阅兵时告诉小明不要在电视机前站着,影响他看电视,这是因为________的.【答案】光是沿直线传播【解析】【详解】爸爸观看阅兵时告诉小明不要在电视机前站着,是因为光是沿直线传播的,电视发出的光被小明挡住,影响他看电视.18. 如图甲所示,检查视力时要求人与视力表的距离是5m,现使用一个平面镜,视力表到平面镜的像距为3m,则人到平面镜的距离应该是_______m.一束光在空气与透明物质的界面处发生了反射和折射现象,入射光线和折射光线如图乙所示,界面MN的右侧是______(填选“空气”或“透明介质”)【答案】(1). 2 (2). 空气【解析】【详解】[1]视力表距离平面镜3m,根据平面镜成像特点,视力表的像到平面镜的距离是3m,检查视力时眼睛离视力表的像距离是5m,所以人到镜子的距离应该是:-=5m3m2m[2]光在空气与某透明物质的界面处发生了折射,其光路及夹角如图所示,由于空气中的角度总是大的,所以界面右侧为空气.19. 2019年4月10日,发布了首张黑洞照片,为解开星系演化之谜提供了宝贵资料,照片中的黑洞距离我们5500万光年,它是根据接收到射线(一种特殊的光)经过处理而形成的,高能射线在真空中的传播速度为_________m/s.【答案】3.0×108【解析】【详解】高能射线是一种电磁波,其在真空中的传播速度为3×108m/s.20. 2019年1月3日,嫦娥四号成功着陆月球表面,如图,遇视器“玉兔二号"正在稳步驶出停稳在月球表面的嫦娥四号,以月球为参照物,嫦娥四号是______ (选填“运动”或“静止”)的.【答案】静止【解析】【详解】以月球为参照物,嫦娥四号与月球之间位置没有发生变化,所以嫦娥四号是静止的.21. 在某次青少年机器人展示活动中,甲、乙、丙三个智能机器人在周长为20米的圆形轨道上进行速度测试活动,它们同时从同一位置出发甲率先跑完5圈此时乙正好落后甲半圈,当乙也跑完5圈时,丙恰好也落后乙半圈,v甲:v乙=_____.假设甲、乙、丙沿圆周轨道运动时速度大小均保持不变,按照大赛的要求3个机器入都要跑完50圈,那么当甲完成任务丙还要跑______m.【答案】(1). 10:9 (2). 190【解析】【详解】[1] [2]设甲跑完5圈用的时间为t则根据题意可知,。
初二历史人教部编版八年级上学期期末考试试题答案解析

初二历史人教版八年级上学期期末考试试题一、选择题1. 我们要再现林则徐反抗外来侵略、维护民族利益的爱国场景,最好选择()A. 虎门销烟B. 黄海海战C. 收复新疆D. 第二次鸦片战争【答案】A【解析】本题考察学生对林则徐领导的禁烟运动的史实的认识,英国资产阶级为了扭转贸易逆差,竟无耻的向中国走私鸦片,鸦片的输入给中华民族带来了沉重的灾难,也引起一些地主阶级知识分子的警觉,以林则徐魏源为代表主张严禁鸦片,道光帝命令林则徐为钦差大臣到广州去禁烟,林则徐到广州后缉拿烟贩,整顿海防,并把搜集来的鸦片在虎门海滩当面销毁,这就是著名的禁烟运动,禁烟运动显示了中国人民反抗外国侵略的坚强决心和信心,也是中国人民反抗斗争的开始,根据所学知识,本题选A。
【考点】林则徐的禁烟运动【点评】本题难度适中,考察学生对历史知识的理解能力,林则徐的禁烟运动是中华民族反侵略的开始,它大长了中国人民的志气,永远铭记在人民心中,该知识点也是考试命题的重点,希望同学们注意。
2.成语“趁火打劫”用来比喻乘人之危牟取私利。
在第二次鸦片战争中干此勾当,强占中国大片领土的国家是A. 英国B. 法国C. 日本D. 俄国【答案】D【解析】依据所学知识,第二次鸦片战争期间,俄国在英法联军以武力对中国侵略之际,趁火打劫,强迫清政府签订了一系列平等条约,共割占中国东北和西北150多万平方公里领土,是强占中国领土最多的国家。
D项符合题意。
ABC三项不合题意,故选择D。
3.《天朝田亩制度》中绝对平均分配方案无法实施的根本原因是A. 当时军事斗争紧张客观环境不利B. 民族资本主义兴起后使其失去吸引力C. 违背了社会发展的客观规律D. 中外反动势力合流力量对比悬殊【答案】C【解析】结合所学可知,《天朝田亩制度》中绝对平均分配方案违背了农民小生产者、小私有者的本性,具有空想性,违背了社会发展的客观规律,因此无法实现,C符合题意;当时军事斗争紧张客观环境不利、中外反动势力合流力量对比悬殊是《天朝田亩制度》不能实施的原因之一,但不是根本原因;当时没有产生民族资本主义,所以ABD不符合题意,故选择C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 17页(共 8页)第十一章三角形11.1与三角形有关的线段 11.2与三角形有关的角 11.3多边形及其内角和 选择题(2015-2016)1.下列长度的各种线段,可以组成三角形的是 ( )A.123,,B.155,,C.336,,D.351,, 2.一个多边形的内角和是1260°,则这个多边形的边数是 ( )A.9B. 8C.7D.63.如图,在折纸活动中,小明制作了一张△ABC 纸片,点D E 、分别在AB AC 、上,将△ABC 沿DE 折叠压平,A 与'A 重合,若A 75∠=.则12∠+∠=(A.105°B.210°C.150°D.75° 4.如图,在四边形ABCD 中,BA BC =,AC 是DAE ∠,α 的度数是 ( ) A.20° B.30° C.35° D.40° (2016-2017)5.如图,AD 是△ABC 的角平分线,DE AB ⊥于E ,点F G 、分别是ABAC 、上的点,DF DG = , △ADG 与△DEF 的面积分别 是a 和b ()a b >,则△ADF 的面积是 () A.a b - B.a b 2- C.a b3- D. a 2b - (2017-2018)6.一个多边形的内角和是720°,则这个多边形的边数为 ( )A.5B.6C.7D.8 7.将一个四边形截去一个角后,它不可能是 ( )A.六边形B.五边形C.四边形D.三角形 (2018-2019)8.已知等腰三角形的一边长为4,另一边长为8,则这个等腰三角形的周长为( ) A.16 B.20 C.20或16 D.12 9.一个多边形内角和是900°,则这个多边形的边数是( )A.7B.6C.5D.4填空(2015-2016)1.等腰三角形的周长为13cm ,其中一边长为4cm 如图,已知方形格子中是4个相同的正方形,则123∠+∠+∠= .2.如图,直角坐标系中,点()(),,A 22B 01-、,点P 在x 轴上,且△PAB 是等腰三角形,则满足条件的点P 共 个.(2016-2017)3.已知一个多边形的内角和为1080°,则这个多边形的边数为 .如图,在△ABC 中,AC 7cm =,DE 垂直平分AB ,且BD 5cm =,则CD 的长为 cm .(2017-2018) 4.如图,若,,,==∠=∠=AB AC BD CD B 20BDC 120 ,则∠A 等于 度.5.已知⊿ABC 的三条边分别为,,346,在⊿ABC 所在平面内画一条直线,将⊿ABC 分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画 条. (2018-2019). AC 于点D .连 接BD ;若,=CD BC A 32=∠,则C ∠的度数为 .A第 17页(共 8页)解答题(2015-2016)1.如图,线段AD和BC相交于点O,AB∥BC,D55B45∠=∠=,.求AOC∠的度数.2.如图,已知AOB∠,一块30度角的直角三角形(有刻度).请只用这块三角板作出AOB∠的平分线(保留作图痕迹),简要写出作图步骤.3.⑴.已知△ABC中,.A90B 675∠=∠=,,请画出一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,把所有不同的分割方法都画出来,只需画图不必说明理由,但要在图中标出相等两角的度数)⑵.已知钝角△ABC中,C∠是其最小的内角.....,B∠是钝角,过顶点B的一条直线把这个三角形分割成了两个等腰三角形,请探求ABC∠与C∠之间的关系.(2016-2017)4.已知:如图,点A B C D、、、在同一直线上,AB CD=,AE∥CF ,且AE CF=. 求证:EB FD= .5. 如图,在△ABC中,B C,AD BC∠>∠⊥,B70,DAE22∠=∠=;求C∠的度数.(2017-2018)6如图,点B E C F、、、.求证:=AC DE.7.已知等腰三角形一腰上的中线将三角形的周长分成6cm和15cm的两部分,求这个三角形的腰和底边的长度.8.如图,已知⊿ABC.⑴.用直尺和圆规作出⊿ABC的角平分线CD.(不写作法,但保留作图痕迹.)⑵.过点D画出⊿ACD的高DE和⊿BCD的高DF.⑶.量出DE DF、的长度,你有怎样的发现?并把你的发现用文字语言表达出来.(2018-2019).9.如图,点E A C、、共线,,AB CE AC CD==,且AB∥CD.求证:B E∠=∠90,BAC∠备用图⑴备用图⑵备用图⑶备用图⑸备用图⑹备用图⑷第 17页(共 8页) 求证:⑴.BD CD =; ⑵.FG ∥AB .十二章全等三角形 12.1全等三角形12.2三角形全等的判定 12.3角的平分线的性质 选择题(2016-2017)1.如图是两个全等三角形,图中的字母表示三角形的 边长,则1∠的度数是 ( ) A.54° B.60° C.66° D.76°2.如图,等腰直角△ABC 中,BAC 90∠=,AD BC ⊥于D ,ABC ∠的平分线分别交AC AD 、于E F 、两点, M 为EF 的中点,延长AM 交BC 于点N , 连接DM .下列结论:①.AE AF =;②.AM EF ⊥;③.AF DF =;④.DF DN =.其中正确的结论有( )A.1个B.2个C.3个D.4个 解答题(2015-2016)1.雨伞的中截图如图所示,伞背AB AC =,支撑杆,,11OE OF AE AB AF AC 44===,当O 沿AD滑动时,雨伞开闭;问雨伞开闭过程中,BEO ∠与CFO ∠2.如图,在△ABC 中,CD AB ⊥于点D ,BE AC ⊥于点E , CD BE =,BE 与CD 相交于点O .连结OA ,试判断直线OA BC 、的位置关系,并说明理由.(2016-2017)3. 已知:如图,点AB C D 、、、在同一直线上,AB CD =,AE ∥CF ,且AE CF =.求证:EB FD = .4.(本题满分6分)如图,已知ABC 90∠=,D 是直线AB 上的点,AD BC = ;如图,过点A 作AF AB ⊥,并截取AF BD = ,连接DC DF CF 、、 . ⑴.求证:⊿FAD ≌⊿DBC ; ⑵.判断⊿CDF 的形状并证明.5.在解决线段数量关系问题中,如果条件中有角平分线,经常采用下面构造全等三角形的解决思路.如:在图1中,若C 是MON ∠的平分线OP 上一点,点A 在OM 上,此时,在ON 截取OB OA = ,连接BC ,根据三角形全等的判定()SAS ,容易构造出全等三角形⊿OBC 和⊿OAC ,参考上面的方法,解答下列问题:如图2,在非等边⊿ABC 中,B 60∠=,AD CE 、分别是BAC BCA ∠∠、的平分线,且AD CE 、交于点E .求证:AC AE =(2017-2018)6.如图,点B E C F 、、、在同一条直线上,=∠=∠∠=∠BE CF,A D,12.求证:=AC DE . BA 图2O O 图1第 17页(共 8页)7.证明:如果两个三角形有两边和其中一边上的中线分别相等,那么这两个三角形全等.(2018-2019).8.如图,点E A C 、、共线,,AB CE AC CD ==,且AB ∥CD . 求证:B E ∠=∠9.在直角三角形△ABC 中,ACB 90∠=,BAC ∠的角平分线交BC 于D ,CE AB ⊥于点E ,交AD 于点F ,取BG CD =,连接FG . 求证:⑴.BD CD =; ⑵.FG ∥AB .10.如图,平面直角坐标系中,A 点的坐标为(),60,B 点的坐标为(),06,C 是线段OA 表的中点.⑴.P 为坐标轴上一点,且P 到直线AB 的距离等于线段AB 的长,请直接写出P 点的坐标; ⑵.D 为AB 上的一点,且DCA BCO ∠=∠,连接OD CD 、,线段CD OD BC 、、之间存在怎样的数量关系,并给出证明.十三章轴对称 13.1轴对称13.2画轴对称图形 13.3等腰三角形 13.4最短路径问题 选择题(2015-2016)1.在以下永结环保、绿色食品、节能、绿色环保四个标志中,是轴对称图形的是 ( )(2016-2017)2.12月2日是全国交通安全日,你认为下列交通标识不是轴对称图形的是 ( )(2017-2018)3.如图,把长方形纸片ABCD 沿对角线折叠,设重叠部分为⊿EBD ,那么有下列说法:①.⊿EBD 是等腰三角形,=EB ED ;②.折叠后∠ABE 和∠CBD 一定相等;③.折叠后得到的图形是轴对称图形;④.⊿EBA 和⊿EDC 一定是全等三角形.其中正确的是 ( )A.①②③B.①③④C.①②④D.①②③④(2018-2019)4.下列图形是轴对称图形的是 ( )填空题(2016-2017)1.如图,已知△ABC 中。
BAC 145∠=,现将△ABC 进行折叠,A B C D D A C B E CDBA 8题图A C D ECAG FDE B C Ax yC BA O 图(1)x y D C B A O 图(2)第 17页(共 8页)使顶点B C 、 均与顶点A 重合,则DAE ∠ 的度数为 . 已知()+P 2a b,b 与(),-Q 82 关于y 轴对称,则+a b = . (2018-2019)2.将△ABC 沿EF DE 、翻折,顶点A C 、均落在点M 处,且CE 与AE 重合于线段EM ,若线段FMD 145∠=, 则B ∠的度数为 .若()()2x bx c x 5x 3++=+- ,则(),P b c 关于原点对称点的坐标是 . 解答题(2015-2016)1.如图,在平面直角坐标系中,△ABC 的三个顶点的坐标分别为()()(),,,,A 23B 31C 22--,.⑴.请在图中作出△ABC 关于y 轴的轴对称图形△DEF ( A B C 、、的对称点分别是D E F 、、),并直接写出D E F 、、的坐标; ⑵.求△ABC 的面积.(2016-2017)2.如图,已知网格上最小正方形的边长为1. ⑴.作△ABC 关于x 轴对称的图形△111A B C ;(不写作法) ⑵.在y 轴上找一点P 使得PB PC +最小.(2017-2018)3.如图,⑴.画出⊿ABC 关于y 轴对称的⊿111A B C ,并写出⊿A B C 的各顶点坐标;⑵.求⊿111A B C 的面积.(2018-2019)4..如图,在直角坐标系中,A B C D 、、、各点的坐标分别是(),77-、(),71-、(),31-、(),14-.⑴.在结合的图形中,画出四边形ABCD 关于y 轴对称的四边形1111A B C D ;(不写作法) ⑵.点1A 的坐标为 ,点1C 的坐标为 ; ⑶.求四边形1111A B C D 的面积.十四章整式的乘法与因式分解 14.1整式的分解 14.2乘法公式 14.3因式分解 选择题(2015-2016)1.下列计算正确的是( ) A.()222a b a b +=+ B.2a 3b 5ab += C.325a a a ⋅= D.632a a a ÷= 2.下列各式是完全平方式的是( )A.2x 2x 1+-B.22x y +C.2x 2xy 1++D.24x 4x 1++ (2016-2017)3.下列计算正确的是 ( )A.257a a a += B.()3233aa a ÷= C.1111a a a ÷= D..01012518⎛⎫-= ⎪⎝⎭4.若()(),22a b 26a b 6+=-=,则ab 的值是 ( ) A.5 B.5- C.32 D.32- FMECABD xy C B AO y123A yD C B AO第 17页(共 8页) (2017-2018)5.下列运算结果正确的是 ( )A.()=326a2a 8a B.()=235xx C.()÷-=-326xy 2xy 3y D.()-=-2x x y x y6.。
