经典算法例题分析
(整理版)几种常见的算法案例分析

几种常见的算法案例分析算法不仅是数学及其应用的重要的组成局部,也是计算机科学的重要根底,其中算法的重要思想在几种常见的算法例案中得以较好的表达。
本文从几种常见算法案例出发,来探究一下算法的内涵。
一、辗转相除法所谓辗转相除法,就是对于给定的两个数,用较大的数除以较小的数,假设余数不为零,那么将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽,那么这时的较小的数就是原来两个数的最大公约数。
例1. 写出求两个正数,()a b a b >的最大公约数的一个算法。
算法设计:第一步:输入两个正整数,()a b a b >;第二步:把a b ÷的余数赋予r ;第三步:如果0r ≠,那么把b 赋予a ,把r 赋予b ,转到第二步;否那么转到第四步;第四步:输入最大公约数b 。
程序框图下列图所示:用伪代码表示:input “a=,b=〞;a,bdo r=mod(a,b)a=bb=rloop until r=0print bend二、更相减损术所谓更相减术,就是对于给定的两个数,以其中较大的数减去较小的数,然后将差和较小的数构成一对新数,再用较大的数减去较小的数,反复执行此步骤,直到差数和较小的数相等,此时相等的两个数就是原两个数的最大公约数。
在我国古代的<<九章算术>>中有这样的描述“约分术曰:可半者半之,不可半者会置分母分子之数,以少减多,更相损减,求其等也,以等数约之。
〞意思是说如果分母、分子都是偶数,那么先除以2;如果不全是偶数,便将分子与分母互减,以少减多,直到得出最大公约数为止,用最大公约数约分子与分母,便可使分数最简。
如果两个数都是偶数,也不除以2,直接求最大公约数。
这是一种多么奇妙的方法啊,我们古代人在许多方面都比西方先进,这是值得我们自豪的。
以上题为例,算法可以这样来设计:第一步:输入两个正整数,()a b a b >;第二步:假设a 不等于b ,那么执行第三步;否那么执行第五步;第三步:把a b -的差赋予r ;第四步:如果b r >,那么把b 的值赋予a ,否那么把r 的值赋予a ,执行第二步; 第五步:输出最大公约数b 。
c经典算法与分析

卡车更新问题(第二届选拔赛第三题,即设备更新问题)【试题】某人购置了一辆新卡车, 从事个体运输业务. 给定以下各有关数据:R[t], t=1,2,...,k, 表示已使用过 t 年的卡车, 再工作一年所得的运费, 它随 t 的增加而减少, k (k≢20) 年后卡车已无使用价值.U[t], t=1,...,k, 表示已使用过 t 年的卡车, 再工作一年所需的维修费, 它随 t 的增加而增加.C[t], t=1,2,...,k, 表示已使用过 t 年的旧卡车, 卖掉旧车, 买进新车, 所需的净费用, 它随 t 的增加而增加. 以上各数据均为实型, 单位为"万元".设某卡车已使用过 t 年,①如果继续使用, 则第 t+1 年回收额为 R[t]-U[t],②如果卖掉旧车,买进新车, 则第 t+1 年回收额为 R[0]-U[0]-C[t] .该运输户从某年初购车日起,计划工作 N (N<=20) 年, N 年后不论车的状态如何,不再工作. 为使这 N 年的总回收额最大, 应在哪些年更新旧车? 假定在这 N 年内, 运输户每年只用一辆车, 而且以上各种费用均不改变.输入: 用文件输入已知数据, 格式为:第 1 行: N (运输户工作年限)第 2 行: k (卡车最大使用年限, k≢20 )第 3 行: R[0] R[1] ... R[k]第 4 行: U[0] U[1] ... U[k]第 5 行: C[0] C[1] ... C[k]输出: 用文本文件按以下格式输出结果:第 1 行: W ( N 年总回收额 )第 2--N+1 行: 每行输出 3 个数据:年序号 ( 从 1 到 N 按升序输出 );是否更新 ( 当年如果更新,输出 1, 否则输出 0);当年回收额 ( N 年回收总额应等于 W ).例: 设给定以下数据:N=4, k=5,i: 0 1 2 3 4 5R[i]: 8 7 6 5 4 2U[i]: 0.5 1 2 3 4 5C[i]: 0 2 3 5 8 10则正确的输出应该是24.51 0 7.52 1 5.53 1 5.54 0 6.0【分析】这是动态规划的一个典型的例题.由题意可知,用过t年的卡车,继续使用一年的收益为d[t]=R[t]-U[t],更换新车后一年的收益为e[t]=R[0]-U[0]-C[t]. 我们采用倒推分析的方法.F[j,t]表示已经使用了t年的卡车, 在第j年不论继续使用还是更新,到第N年为止,可能得到的最大收益. 规定当j>N时, F[j,t]≡0. 如果在第j年更新,则收益为p=e[t]+F[j+1,1]; 如果仍使用旧车,则收益为 q=d[t]+F[j+1,t+1]. 这里,e[t]或d[t]为第j年的收益, F[j+1,1]或F[j+1,t+1]为从第j+1年到第N年在不同条件下的最大收益.显然,F[j,t]=Max(p,q).这就是所需要的计算公式.在下面的程序中,数组g[j,t]用于记录使用过t年的车,在第j年的选择方案,g[j,t]=1表示更换新车,g[j,t]=0表示仍使用旧车.【参考程序】program tjcoi2_3; { Write By Li Xuewu }type arr20=array[0..20] of real;var rr,uu,cc,d,e:arr20;f:array [0..22,0..21] of real;g:array [0..22,0..21] of integer;i,j,k,k2,n,t:integer;file1:string[20];p,q:real;text2,text3:text;procedure init;var i:integer;beginwriteln('Input filename:');readln(file1);assign(text2,file1); reset(text2);readln(text2,n); readln(text2,k);for i:=0 to k do read(text2,rr[i]); readln(text2);for i:=0 to k do read(text2,uu[i]); readln(text2);for i:=0 to k do read(text2,cc[i]); readln(text2);close(text2);for i:=0 to k dobegin d[i]:=rr[i]-uu[i]; e[i]:=d[0]-cc[i]; end;end;procedure result3;var i:integer;beginwriteln('enter filename for output:');readln(file1);assign(text3,file1); rewrite(text3);writeln(text3,f[1,1]:8:3);writeln(text3,' 1 0', e[0]:8:2); t:=1;for i:=2 to n doif g[i,t]=1 thenbegin writeln(text3,i:2,' 1',e[t]:8:2); t:=1 endelsebegin writeln(text3,i:2,' 0',d[t]:8:2); t:=t+1; end ; writeln(f[1,1]:8:3);writeln(' 1 0',e[0]:8:2); t:=1;for i:=2 to n doif g[i,t]=1 thenbegin writeln(i:2,' 1',e[t]:8:2); t:=1 endelsebegin writeln(i:2,' 0',d[t]:8:2); t:=t+1; end ;close(text3);end;begin {main}init;for i:=0 to n dofor j:=0 to k do g[i,j]:=1;for i:=0 to k do f[n+1,i]:=0;for i:=1 to n+1 do f[i,k+1]:=-100;for j:=n downto 2 dobegink2:=k;if j<k then k2:=j-1;for t:=1 to k2 dobeginp:=e[t]+f[j+1,1]; q:=d[t]+f[j+1,t+1]; f[j,t]:=p; g[j,t]:=1;if q>p thenbegin g[j,t]:=0; f[j,t]:=q; end; end;end;f[1,1]:=d[0]+f[2,1];result3;end.省刻度尺问题program e04_06;label 10;type arr40=array [0..40]of byte;var a,b,c,d:arr40;i,j, k,kz,r,m,t1,t2:byte;done: boolean;procedure result;var file1:string[20];text2:text;i,j,w:integer;beginwriteln('enter filename for output:');readln (file1);assign(text2,file1); rewrite(text2);writeln(k:2);for i:=1 to k do write(a[i]:4);writeln;for i:=1 to m do writeln(i:2, c[i]:4,d[i]:4);writeln(text2,k:2);for i:=1 to k do write(text2,a[i]:4);writeln(text2);for i:=1 to m do writeln(text2,i:2, c[i]:4,d[i]:4);close(text2);done:=true;halt;end;procedure init1;var i:integer;beginfor i:=0 to 40 do b[i]:=0; c:=b; d:=b;for i:=2 to k do a[i]:=0;a[0]:=0; a[k+1]:=m; a[1]:=1;end;procedure find2(r,t1,t2:integer);var i,j,j2,v1,v2,t,t3,t4,temp:integer;begin {1}for i:=t1 to t2 dobegin {2}a[r]:=i;if (r<k) and (i<t2) thenbegin t3:=i+1; find2(r+1,t3,t2); end;if r=k thenbegin{3}if ((kz=1)or(kz=3)) and (k>2) thenbegintemp:=a[2];for j:=2 to k-1 do a[j]:=a[j+1];a[k]:=temp;end;for j:=1 to m do b[j]:=0;for j:=0 to k dofor j2:=j+1 to k+1 dobegint:=a[j2]-a[j];if b[t]=0 thenbeginb[t]:=1; c[t]:=a[j]; d[t]:=a[j2];end;end;done:=true; j:=0;repeat j:=j+1 until (b[j]=0)or(j>m);if j<=m then done:=false;if done then result;end;{3}end; {2}end; {1}begin{main}writeln('inptu L:(L<=40 and L>3)'); readln(m); k:=0;repeat k:=k+1 until ((k+2)*(k+1) div 2) >= m; 10: init1;for kz:=1 to 3 docase kz of1: begin{*}a[2]:=m-2;if k=2then find2(2,a[2],a[2])elsebeginr:=3; t1:=2; t2:=m-3;find2(r,t1,t2);end;end;{*}2: begin{**}a[2]:=2;r:=3; t1:=3; t2:=m-1;if t2<t1 then t2:=t1;find2(r,t1,t2);end;{**}3: begin{***}a[2]:=m-1;r:=3; t1:=2; t2:=m-2;if t2<t1 then t2:=t1;find2(r,t1,t2);end;{***}end;{case}k:=k+1; goto 10;end.排列问题输入整数N(<15),输出1..N的全部不同排列的总数,当N<=6时,还要输出全部排列. int p[30];int pr1(int n){ int i,m,j, t,j1,j2;for (i=n;i>0 && p[i]>=p[i+1];i--);if(i<=0) return 0;for(j=i+1,t=i+1;t<=n && p[i]<p[t];t++)j=t;m=p[i];p[i]=p[j];p[j]=m;for (j1=i+1,j2=n;j1<j2;j1++,j2--)m=p[j1],p[j1]=p[j2],p[j2]=m;return 1;}main() /*n!*/{int j,t,n,m;long num;printf("input n:\n");scanf("%d",&n);for (j=1;j<=n;j++) p[j]=j;t=1; num=0;while (t>0) /***/{if (n<=6){for(j=1;j<=n;j++) printf("%d ",p[j]);printf("\n");}num++;t=pr1(n);}printf("num=%ld\n",num);}取奇数游戏{ 该游戏规则如下: 操作者先输入一个奇数N(<200)表示N个石子. 设计算机为A 方,操作者为B 方, 双方轮流取石子,每次取1-3个. 最后取到石子总数为奇数的一方获胜. 编制程序使计算机有较多的获胜机会,}unit lxw022;typesetab=set of 0..200;varevena,evenb,odda,oddb:setab;i,j,n,na,nb,k,kz,r,t:integer;ab,ll:char;procedure init0(var n:integer);beginclrscr;gotoxy(1,1);writeln('***************************************');writeln(' 取奇数游戏规则如下: ');writeln(' 1.操作者先输入一个奇数N(<200).');writeln(' 2.设计算机为A 方,操作者为B 方,双方轮流取数,每次取1-3个.');writeln(' 3.最后取到奇数的一方为胜方. ');writeln('***************************************');n:=400;while not odd(n)or(n>200) dobegingotoxy(10,7);writeln('输入一个奇数N(<200):');gotoxy(10,8); readln(n);end;end;procedure prt1;begingotoxy(1,17);writeln(' 总计计算机已取得操作手已取得剩余');gotoxy(50,19);writeln(' ');gotoxy(1,19);writeln(' ',n,' ',na,' ',nb,' ',r);end;procedure prt2(var ll:char);begingotoxy(10,21);if odd(na) then writeln('可惜, 你输了!')else writeln ('祝贺你的成功!');gotoxy(10,22);writeln('再玩一次吗? (Y/N)');gotoxy(10,23); readln(ll);end;procedure aget(var r,t,na:integer);var k,kz:integer;beginkz:=0; k:=0;while (k<3)and(kz=0)and(k<r) dobegink:=k+1;if (not odd(na+k))and(r-k in evena) thenbegin kz:=1; t:=k end;if (odd(na+k))and(r-k in odda) thenbegin kz:=1; t:=k end;end;if kz=0 then t:=1;gotoxy(50,14);writeln(' 计算机这次取',t,' 个.');na:=na+t; r:=r-t;end;procedure bget(var r,t,nb,i:integer);begint:=0;while not(t in[1,2,3])or(t>r) dobegingotoxy(30,13); writeln(' ');gotoxy(2,13);writeln('第',i:2,' 轮: 输入你的选择(1/2/3) 并且不得超过',r);gotoxy(5,14); write(' ');gotoxy(5,14); readln(t); gotoxy(20,14);if not(t in[1,2,3])or(t>r)then write('数据错! 请重新输入.')else write(' ');end;nb:=nb+t; r:=r-t;end;begin{main}ll:='y';while (ll='Y')or(ll='y') dobegin{2}init0(n);r:=n;{ 1. 建立获胜策略集EVENA,EVENB,ODDA,ODDB }evena:=[4,5]; evenb:=[0,1,2,3];odda:=[0,1]; oddb:=[2..5];for i:=6 to n dobegin{3}nb:=0;if not odd(i) then nb:=1;kz:=0; k:=0;while (k<3)and(kz=0) dobegink:=k+1;if odd(nb+k)and (i-k in odda) then kz:=1;if (not odd(nb+k))and(i-k in evena) then kz:=1;end;if kz=0then evena:=evena+[i]else evenb:=evenb+[i];nb:=0;if odd(i) then nb:=1;kz:=0; k:=0;while (k<3)and(kz=0) dobegink:=k+1;if odd(nb+k)and (i-k in odda) then kz:=1;if (not odd(nb+k))and(i-k in evena) then kz:=1;end;if kz=0then odda:=odda+[i]else oddb:=oddb+[i];end;{3}{ 2. 开始取数. }na:=0; nb:=0; t:=0; ab:=' ';while not (ab in ['a','b','A','B']) dobegingotoxy(10,9);writeln('输入: "谁先开始(A/B) ?" A: 计算机, B:操作手.');gotoxy(10,10); readln(ab);end;i:=1;if (ab='B')or(ab='b') then bget(r,t,nb,i);repeatif r>0 thenbegin {5}aget(r,t,na);prt1;if r>0 then bget(r,t,nb,i);i:=i+1;end;{5}until r=0;gotoxy(3,16); writeln(' 最后结果:');prt1; prt2(ll);end{2}end.{main}unit Unit1;interfaceusesWindows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs;typeTForm1 = class(TForm)private{ Private declarations }public{ Public declarations }end;varForm1: TForm1;implementation{$R *.DFM}end.取石子游戏任给N堆石子,两人(游戏者与计算机)轮流从任一堆中任取,计算机先取,取最后一颗石子胜.#include <stdio.h>unsigned int a[11];int n;void init1(){int i;printf("input n(2--10):"); scanf("%d",&n);for (i=1;i<=n;i++){printf("input No.%d Number of stone:\n",i);scanf("%d",&a[i]);}}void status(){int i;printf("Now remainder:\n");for (i=1;i<=n;i++) printf(" No.%d rem: %u \n",i,a[i]);}unsigned int sum1(){unsigned int s; int i;s=0;for(i=1;i<=n;i++) s+=a[i];return s;}unsigned int xorall(){unsigned int s; int i;s=0;for (i=1;i<=n;i++) s^=a[i];return s;}main(){unsigned int t;int i,s,e;init1();while (sum1()){if (xorall()==0){for (i=1;i<=n;i++)if(a[i]>0){printf("computer take 1 from No.%d \n",i);a[i]--; goto loop2;}}elsefor (i=1;i<=n;i++){ s=a[i]-(xorall()^a[i]) ;if (s>0){printf("computer take %u from No.%d \n",s,i);a[i]^=xorall();goto loop2;}}loop2:;if(sum1()==0){printf("computer win!"); break;}status();while (1){printf("Input your selection(examp. 1 2 means take 2 from No.1):\n");scanf("%d %u",&e,&t);if ((e>=1)&&(e<=n)&&(a[e]>=t)){a[e]-=t; goto loop1;}elseprintf("data error! re-input...\n");}loop1:;if(sum1()==0){printf("you win!"); break;}}}跳马问题16.(*)( 6_24 p.197 )int map[12][12], status[12][12],kp;int c[8][2]={{2,1},{2,-1},{1,2},{1,-2},{-2,1},{-2,-1},{-1,2},{-1,-2}};void prt(int a[][12]) /* 打印棋盘状态 */{int i,j,i2,j2;printf("\n");for (i=2;i<=9;i++){ for (j=2;j<=9;j++) printf("%4d",a[i][j]);printf("\n");}}void status2(void) /* 计算棋盘各点条件数 */{ int i,j,k,i2,j2,kz;for(i=0;i<12;i++)for(j=0;j<12;j++)status[i][j]=100;for(i=2;i<=9;i++)for(j=2;j<=9;j++){kz=0;for (k=0;k<=7;k++){i2=i+c[k][0];j2=j+c[k][1];if (map[i2][j2]<50) kz++;}status[i][j]=kz;}prt(status);}void sort1(int b1[],int b2[]) /* 对8个可能的方向按条件数排序 */ {int i,j,mini,t; /*b1[]记录状态值(升序),b2[]记录排序后的下标 */ for (i=0;i<7;i++){mini=i;for (j=i+1;j<=7;j++)if (b1[j]<b1[mini]) mini=j;t=b1[i];b1[i]=b1[mini];b1[mini]=t;t=b2[i];b2[i]=b2[mini];b2[mini]=t;}}void init1(void) /* 初始化 */{int i,j,k;for(i=0;i<12;i++)for(j=0;j<12;j++)map[i][j]=100;for(i=2;i<=9;i++)for(j=2;j<=9;j++)map[i][j]=0;status2();}void search(int i2,int j2) /* 利用递归回溯进行搜索 */ {int b1[8],b2[8],i,i3,j3;kp++;if(kp==65){prt(map); exit(0); }for(i=0;i<=7;i++){b2[i]=i;b1[i]=status[i2+c[i][0]][j2+c[i][1]];}sort1(b1,b2);for(i=0;i<=7;i++){i3=i2+c[b2[i]][0]; j3=j2+c[b2[i]][1];if (map[i3][j3]==0){ map[i3][j3]=kp; search(i3,j3); map[i3][j3]=0; }}kp--;}main(){init1();map[5][2]=1; kp=1;search(5,2);}运行结果:2 3 4 4 4 4 3 23 4 6 6 6 6 4 34 6 8 8 8 8 6 44 6 8 8 8 8 6 44 6 8 8 8 8 6 44 6 8 8 8 8 6 43 4 6 6 6 6 4 32 3 4 4 4 4 3 232 17 42 3 34 19 44 541 2 33 18 43 4 35 2016 31 64 53 38 59 6 451 40 61 58 63 52 21 3630 15 54 39 60 37 46 755 12 57 62 51 48 25 2214 29 10 49 24 27 8 4711 56 13 28 9 50 23 2617. ( ex 6_32 p.201 选择排序,利用递归实现 ) void select(int a[],int begin,int n){int i,t,min;min=begin;for (i=begin+1;i<n;i++)if(a[i]<a[min]) min=i;t=a[begin]; a[begin]=a[min]; a[min]=t;if (begin<n-1)select(a,begin+1,n);}main(){int a[10]={5,6,7,99,1,2,0,45,21,-97};int i,n=10;for(i=0;i<=n-1;i++) printf("%5d ",a[i]);printf("\n");select(a,0,n);for(i=0;i<=n-1;i++)printf("%5d ",a[i]);printf("\n");}18.( ex 6_25 p.202 二分查找,递归方法 )void binsearch(int b[],int x,int low,int high){int mid;if (low>high){printf("\n%d dosn't exists in the array!\n",x);exit(0);}mid=(low+high)/2;if(x==b[mid]){printf("OK! b[%d]=%d\n",mid,x);exit(0);}if(x>b[mid])binsearch(b,x,mid+1,high);elsebinsearch(b,x,mid,high-1);}main(){int a[10]={2,3,4,5,7,10,20,40,50,100};int key,n=10;;printf("input a number for search:\n");scanf("%d",&key);binsearch(a,key,0,n-1);}信息学 (计算机) 奥林匹克训练题 (中级部分)天津师范大学李学武编 1997.7.1. 给定等式 A B C D E 其中每个字母代表一个数字,且不同数字对应不D F G 同字母。
算法设计与分析习题答案

算法设计与分析习题答案算法设计与分析是计算机科学中一个重要的领域,它涉及到算法的创建、优化以及评估。
以下是一些典型的算法设计与分析习题及其答案。
习题1:二分查找算法问题描述:给定一个已排序的整数数组,编写一个函数来查找一个目标值是否存在于数组中。
答案:二分查找算法的基本思想是将数组分成两半,比较中间元素与目标值的大小,如果目标值等于中间元素,则查找成功;如果目标值小于中间元素,则在左半部分继续查找;如果目标值大于中间元素,则在右半部分继续查找。
这个过程会不断重复,直到找到目标值或搜索范围为空。
```pythondef binary_search(arr, target):low, high = 0, len(arr) - 1while low <= high:mid = (low + high) // 2if arr[mid] == target:return Trueelif arr[mid] < target:low = mid + 1else:high = mid - 1return False```习题2:归并排序算法问题描述:给定一个无序数组,使用归并排序算法对其进行排序。
答案:归并排序是一种分治算法,它将数组分成两半,分别对这两半进行排序,然后将排序好的两半合并成一个有序数组。
```pythondef merge_sort(arr):if len(arr) > 1:mid = len(arr) // 2left_half = arr[:mid]right_half = arr[mid:]merge_sort(left_half)merge_sort(right_half)i = j = k = 0while i < len(left_half) and j < len(right_half): if left_half[i] < right_half[j]:arr[k] = left_half[i]i += 1else:arr[k] = right_half[j]j += 1k += 1while i < len(left_half):arr[k] = left_half[i]i += 1k += 1while j < len(right_half):arr[k] = right_half[j]j += 1k += 1arr = [38, 27, 43, 3, 9, 82, 10]merge_sort(arr)print("Sorted array is:", arr)```习题3:动态规划求解最长公共子序列问题问题描述:给定两个序列,找到它们的最长公共子序列。
四个经典的算法案例
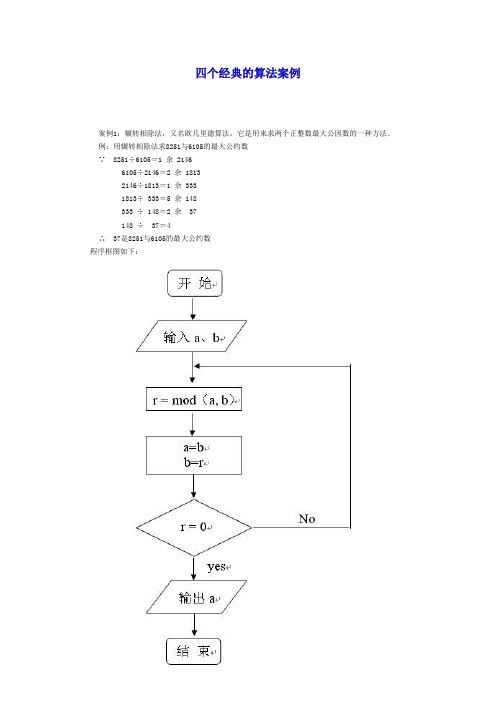
四个经典的算法案例案例1:辗转相除法,又名欧几里德算法,它是用来求两个正整数最大公因数的一种方法。
例:用辗转相除法求8251与6105的最大公约数∵ 8251÷6105=1 余 21466105÷2146=2 余 18132146÷1813=1 余 3331813÷ 333=5 余 148333 ÷ 148=2 余 37148 ÷ 37=4∴ 37是8251与6105的最大公约数程序框图如下:其中 r = mod(a, b) r表示a÷b的余数案例2:秦九韶算法,它是中国南宋时期数学家秦九韶提出的,用来解决多项式的求值问题,在西方被称作霍纳算法。
首先看一道例题:求多项式f(x)=2x5―5x4―4x3+3x2―6x+7当x=5时的值。
根据秦九韶算法:f(x)可表示为f(x)=({[(2x―5)x―4]x+3}x―6)x+7于是令 V0=5则 V1=2V0―5=2×5―5=5V2=V1X―4=5×5―4=21V3=V2X+3=21×5+3=108V4=V3X―6=108×5―6=534V5=V4X+7=534×5+7=2677∴ f(5) = 2677秦九韶算法只用到乘法、加法两个简单运算,不需要乘方运算,它是多项式求值的简化算法。
下面看程序框图,其中a0、a1、a2、a3、a4、a5是f (x) 从右向左的系数。
案例3:排序:是一种基本并且常用的算法,排序的算法很多,可以参阅课本,这里不再叙述。
案例4:进位制例:画程序框图,表示把k进制数a(共有n位),转化为十进制数b的过程框图如下:其中:t = GET a│i│ t表示a右数第i位利用上面的算法,把2进制数110011化为十进制的数即:1×20+1×21+0×22+0×23+1×24+1×25= 51以上是四个经典算法,大家可以从中体会算法的基本思想和算法的基本结构,并尝试用算法的基本语句描述它。
经典算法题解

经典算法题解经典算法题解涵盖了各种计算机科学和编程领域的经典问题。
这些题目不仅具有代表性,而且在算法设计和分析方面具有较高的价值。
以下是一些经典算法题解的例子:1. 动态规划:动态规划是一种解决复杂问题的方法,通过将问题分解成子问题,并求解子问题的最优解,从而找到原问题的最优解。
经典动态规划问题包括背包问题、最长公共子序列(LCS)问题、最长递增子序列(LIS)问题等。
2. 贪心算法:贪心算法是一种解决复杂问题的方法,它总是选择局部最优解,以期望达到全局最优解。
经典贪心算法问题包括哈夫曼编码问题、最小生成树(Kruskal算法、Prim算法等)、最短路径(Dijkstra算法等)等。
3. 分治算法:分治算法是一种解决复杂问题的方法,它将原问题分解成规模较小的子问题,并在子问题上求解,最后合并子问题的解得到原问题的解。
经典分治算法问题包括归并排序、快速排序、归并查找等。
4. 回溯算法:回溯算法是一种解决复杂问题的方法,它通过递归的方式,从一条路线上不断地尝试,直到找到一条可行的路径。
经典回溯算法问题包括八皇后问题、数独问题、背包问题等。
5. 深度优先搜索(DFS)和广度优先搜索(BFS):DFS和BFS 是解决复杂问题的搜索算法,它们通过搜索树或图的方式,寻找问题的解。
经典DFS和BFS问题包括无序集合问题、图的遍历、最短路径等。
6. 字符串匹配算法:字符串匹配算法是解决在文本中查找某个子串的问题。
经典字符串匹配算法包括朴素匹配算法、KMP算法、Boyer-Moore算法等。
7. 数据结构:数据结构是解决计算机科学问题的重要工具。
经典数据结构问题包括链表、栈、队列、树、图等数据结构的操作和应用。
8. 算法复杂度分析:算法复杂度分析是研究算法时间复杂度和空间复杂度的问题。
经典算法复杂度分析问题包括大O标记、大Ω标记、大Ω标记、大Ω标记等。
这些经典算法题解对于提高编程能力和解决实际问题具有很大的帮助。
算法设计与分析常见习题及详解

算法设计与分析常见习题及详解⽆论在以后找⼯作还是⾯试中,都离不开算法设计与分析。
本博⽂总结了相关算法设计的题⽬,旨在帮助加深对贪⼼算法、动态规划、回溯等算法的理解。
1、计算下述算法执⾏的加法次数:输⼊:n =2^t //t 为整数输出:加法次数 k K =0while n >=1 do for j =1 to n do k := k +1 n = n /2return k解析:第⼀次循环执⾏n次加法,第⼆次循环执⾏1/2次加法,第三次循环执⾏1/次加法…因此,上述算法执⾏加法的次数为==2n-12、考虑下⾯每对函数 f(n) 和 g(n) ,如果它们的阶相等则使⽤Θ记号,否则使⽤ O 记号表⽰它们的关系解析:前导知识:,因为解析:,因为解析:,因为解析:解析:3、在表1.1中填⼊ true 或 false解析:利⽤上题的前导知识就可以得出。
2=21/4n +n +21n +41...+1n +n −n +21n −21n +41....−1f (n )=(n −2n )/2,g (n )=6n1<logn <n <nlogn <n <2n <32<n n !<n ng (n )=O (f (n ))f (n )=Θ(n ),g (n )=2Θ(n )f (n )=n +2,g (n )=n n 2f (n )=O (g (n ))f (n )=Θ(n ),g (n )=Θ(n )2f (n )=n +nlogn ,g (n )=n nf (n )=O (g (n ))f (n )=Θ(nlogn ),g (n )=Θ(n )23f (n )=2(log ),g (n )=n 2logn +1g (n )=O (f (n ))f (n )=log (n !),g (n )=n 1.05f (n )=O (g (n ))4、对于下⾯每个函数 f(n),⽤f(n) =Θ(g(n))的形式,其中g(n)要尽可能简洁,然后按阶递增序排列它们(最后⼀列)解析:最后⼀个⽤到了调和公式:按阶递增的顺序排列:、、、、、、、、、(n −2)!=Θ((n −2)!)5log (n +100)=10Θ(logn )2=2n Θ(4)n 0.001n +43n +31=Θ(n )4(lnn )=2Θ(ln n )2+3n logn =Θ()3n 3=n Θ(3)n log (n !)=Θ(nlogn )log (n )=n +1Θ(nlogn )1++21....+=n1Θ(logn )=∑k =1nk 1logn +O (1)1++21....+n 15log (n +100)10(lnn )2+3n logn log (n !)log (n )n +10.001n +43n +313n 22n (n −2)!5、求解递推⽅程前导知识:主定理前导知识:递归树:例⼦:递归树是⼀棵节点带权的⼆叉树,初始递归树只有⼀个结点,标记为权重W(n),然后不断进⾏迭代,最后直到树种不再含有权为函数的结点为⽌,然后将树根结点到树叶节点的全部权值加起来,即为算法的复杂度。
贪心算法经典例题

贪心算法经典例题引言贪心算法是一种常见的算法策略,它在求解问题时每一步都选择当前状态下的最优解,从而最终得到全局最优解。
本文将介绍一些经典的贪心算法例题,帮助读者更好地理解贪心算法的思想和应用。
背景知识在讨论贪心算法之前,我们先了解一些背景知识。
1. 贪心算法的特点贪心算法具有以下特点: - 每一步都选择当前状态下的最优解; - 不进行回溯;- 不保证能得到全局最优解,但通常能得到较优解; - 算法运行效率高。
2. 贪心算法的适用情况贪心算法适用于满足以下条件的问题: - 具有最优子结构性质:问题的最优解包含子问题的最优解; - 贪心选择性质:局部最优解能导致全局最优解; - 没有后效性:当前的选择不会影响后续的选择。
经典例题1:找零钱问题问题描述假设有1元、5元、10元、20元、50元、100元面值的纸币,如何用最少的纸币数量找零给顾客?对于找零问题,贪心算法可以得到最优解。
具体步骤如下: 1. 首先,我们选择最大面额的纸币进行找零。
2. 然后,将选择的纸币数量减去顾客需找的金额,得到剩余金额。
3. 重复步骤1和步骤2,直到剩余金额为0。
实现代码int[] denominations = {100, 50, 20, 10, 5, 1};int[] counts = new int[denominations.length];int amount = 168;for (int i = 0; i < denominations.length; i++) {counts[i] = amount / denominations[i];amount %= denominations[i];}System.out.println("找零纸币面额及数量:");for (int i = 0; i < denominations.length; i++) {if (counts[i] > 0) {System.out.println(denominations[i] + "元:" + counts[i] + "张");}}分析与总结通过贪心算法,我们可以得到找零纸币的最优解。
c++贪心算法经典例题

c++贪心算法经典例题和详解贪心算法(Greedy Algorithm)是一种优化问题解决方法,其基本思想是每一步都选择当前状态下的最优解,以期望达到全局最优解。
贪心算法的特点是每一步都要做出一个局部最优的选择,而这些局部最优选择最终构成了全局最优解。
下面是一个经典的贪心算法例题以及详解:例题:活动选择问题(Activity Selection Problem)假设有一个需要在同一时段使用同一个资源的活动集合,每个活动都有一个开始时间和结束时间。
设计一个算法,使得能够安排最多数量的互不相交的活动。
# 输入:-活动的开始时间数组`start[]`。
-活动的结束时间数组`end[]`。
# 输出:-选择的互不相交的活动的最大数量。
# 算法详解:1. 首先,将活动按照结束时间从小到大排序。
2. 选择第一个活动,并将其加入最终选择的集合中。
3. 对于剩下的活动,选择下一个结束时间最早且与前一个活动不冲突的活动。
4. 重复步骤3,直到所有活动都被选择。
```cpp#include <iostream>#include <algorithm>#include <vector>using namespace std;// 定义活动结构体struct Activity {int start, end;};// 比较函数,用于排序bool compareActivities(Activity a, Activity b) {return a.end < b.end;}// 贪心算法解决活动选择问题void activitySelection(vector<Activity>& activities) {// 按照结束时间排序sort(activities.begin(), activities.end(), compareActivities);// 第一个活动总是被选中cout << "Selected activity: (" << activities[0].start << ", " << activities[0].end << ")" << endl;// 选择其余活动int lastSelected = 0;for (int i = 1; i < activities.size(); i++) {// 如果当前活动的开始时间大于等于上一个选择的活动的结束时间,则选择该活动if (activities[i].start >= activities[lastSelected].end) {cout << "Selected activity: (" << activities[i].start << ", " << activities[i].end << ")" << endl;lastSelected = i;}}}int main() {vector<Activity> activities = {{1, 2}, {3, 4}, {0, 6}, {5, 7}, {8, 9}, {5, 9}};cout << "Activities before sorting:" << endl;for (const Activity& activity : activities) {cout << "(" << activity.start << ", " << activity.end << ") ";}cout << endl;activitySelection(activities);return 0;}```在这个例子中,我们首先定义了一个活动的结构体`Activity`,然后编写了一个比较函数`compareActivities` 用于排序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在前面的章节中大家对C语言有了大概的了解,本 章将重点讲解几个常用到的经典例题,帮助大家加 深对C语言的掌握。
现有8×8的棋盘,要求在其中放入8个皇后,可以 使任意两个皇后不能吃掉对方。如果两个皇后在同 一行、同一列或者同一对角线,则其中的一个皇后 会吃掉另外一个皇后。试求出其所有可能的解,并 输出到屏幕。
开始
现有9件商品,从中选出3件使得其重量之和与600 克之间差值最小,其中每件商品的重量由键盘输入。
假设9件商品的重量分别为88、90、40、100、60、 50、55、99、66,我们对这些商品进行分析,如图 16.11所示。我们可以选择其中重量最重的三件商品, 看一看重量是否超过600克,如果超过选择次其中 的商品。
否 否 单元格是否以满
是
结束
假设有一条绳子,上面有红、白、蓝3中颜色的多 面旗子,这些旗子的排列是没有顺序的,要求用最 少的步骤将绳子上的旗子按蓝、白、红3种颜色排 列。要求只能在绳子上进行旗子的移动,并且每次 只能调换两个旗子。
假设从绳子的一端开始进行,遇到蓝色的旗子向前 移,遇到白色的旗子就留在中间,遇到红色的旗子 就往后移,根据题意,看一下此题的分析图,如图 所示。
1 1 3 2 2 1
1 3 4 2 3 4
1 5 2 3 4
1 5
6
2
1 3 4 5
6 7 2
8 3 4
1 5
6 7 2
8 3 4
1 5 9
6 7 2
根据分析图,可以推到出魔术方正的流程图,如图 所示。
开始 将1放到一行的中间
下一个数填入右1、 上1的单元格 重新填写上一个数 填数单元格是否有数 是
红 白 蓝
R
W
B
W
W
B
R
B
W
R
B
W
W
W
W
B
R
B
R
R
B
B
W
W
W
W
R
B
R
R
BBBFra bibliotekWW
W
W
R
R
R
B
B
B
W
W
W
W
R
R
R
根据分析图,可以推到出三色旗的流程图,如图所 示。
开始 创建一维数组有n个 元素 移动旗子
判断旗子的颜色
红旗子
蓝旗子
白旗子
向后移
向前移
留在中间
是否移完旗子
否
是
结束
人类建造迷宫已有5000年的历史。在世界的不同文 化发展时期,这些奇特的建筑物始终吸引人们沿着 弯弯曲曲、困难重重的小路吃力地行走,寻找真相。 现在给定一迷宫,编写一程序实现从入口走出迷宫。
下一只猴子数数下一 个数
否 判断猴子是不是数到三
是
判断是不是最后一只猴子
否 去掉数三的猴子,下 一只从一开始数
是
结束
最小公倍数(Least Common Multiple,缩写 L.C.M.),如果有一个自然数a能被自然数b整除, 则称a为b的倍数,b为a的约数,对于两个整数来说, 指该两数共有倍数中最小的一个。
3 2 1 3 3 3 3 3 3 4 1 6 6 6 3 7 6 2 7 7 7 7 9 10 12 13 15 16 3 9 10 12 13 15 16 1 2 3 10 12 13 15 16 1 2 10 12 15 16 3 2 4 4 4 4 4 4 3 5 1 6 6 6 6 6 2 7 7 7 7 7 3 8 1 9 10 11 12 13 14 15 16 2 3 1 2 3 8 9 10 11 12 13 14 15 16 5 6 7 8 9 10 11 12 13 14 15 16
7 8 5 6 3 4 1 2
8 7 6 5 4 3 2 1
根据分析图,可以推到出循环赛问题的流程分析图, 如图所示。
开始 创建一个二维数组
将选手两两进行比赛
判断该选手是否以比赛过 否 否
是
另一个选手
人数是否超出 是 比赛结束
现有n´m个格子的棋盘,马在棋盘上行走,只能走 日字。编写程序,求出马从任意位置出发,将所有 格子走完并且只能走过一次的所有路径。
在遇到循环赛问题时,我们可以将队员的人数分成 两半,即8个选手的比赛日程由4个选手的比赛日程 决定。用这种一分为二的方法对选手进行划分直至 只剩下两个对手为止,单独设置其比赛日程,然后 将这些单独的块最后合并起来即为最终的解。根据 题意,看一下此题的分析图。如图所示。
1
2
3
4
5
6
7
8
先将8个人两组,进行比赛
9 10 11 12 13 14 15 16 9 10 12 13 14 15 16 1 2 9 10 12 13 15 16
1 2 3 10 12 15 16
6 10 12 16 10 15
根据问题分析,可以推导出猴子选王算法设计流程 图,如图16.6所示。
开始 将猴子编号,放入一个数组中 第一只猴子数开始从1 数
500 600 70 100 80 25 55 40 90
500 600 100 500+600+100=1200
500 100 90 500+100+90=690
500 90 80 500+90+80=670
500 90 55 500+90+55=645
500 80 25 500+80+25=605
是 结束
魔术方正又称幻方阵、魔方阵,是一种已流传千年 的数字排列,不管是中西方对这奇妙的阵列都有所 理解。所谓魔术方阵,就是将连续的整数1、2、 3、…、n,按某种特别的顺序排在方阵里,方阵中 的每一行每一列或对角线位置的数各自相加的和均 相等。用简捷连续填数法创建魔术方正。
下面以填充一个3阶魔术方正为例,根据题意,看 一下此题的分析图,如图16.20所示
求出的最小公倍数看是否能整除这三个数。若能整 除这三个数,则输出其中的最小的数,就是公倍数。 根据题意,看一下此问题的具体分析,如图16.8所 示
求3 6 9的最小给倍数: 选出3个数中的最大数:9 用选出的最大数乘以1:9×1=9 用乘得的数除以这三个数:9÷3=3 9÷6有余数,所以不是最小公倍数 用选出的最大数乘以2:9×1=18
…
500 70 25 600-500-70-25=5
将这些差值进行比较,最小的就是要选的三件物品
根据问题分析,可以推导出背包问题的流程图,如 图6.12所示。
开始 创建一个数组,存放九件 商品的重量
选出三件商品,将总重量 的值减去600
否
是否超出商品个数
是
将商品的差值做比较
结束
循环赛是大家经常见到的,现在设有n个选手要进 行乒乓球选拔赛,编写一个程序设计其比赛日程安 排表,具有以下要求: (1)每名选手都必须与其他选手比赛一次。 (2)每名选手一天之内只能进行一次比赛。 (3)所有选手的比赛在n-1天内比完。
是
否
走下一个格子
否
是否以走到最后
是
结束
在本章中重点讲解了经典的C语言例题,其中包括 八皇后、汉诺塔、马遍历、循环赛等问题。这些都 对以后学习C语言有很大的帮助。大家应该熟练掌 握其中的解题方法。
1 2 3 4
2 1 4 3
3 4 1 2
4 3 2 1
5 6 7 8
6 5 8 7
7 8 5 6
8 7 6 5
每组和另一组比赛
1 2 3 4 5 6 7 8
2 1 4 3 6 5 8 7
3 4 1 2 7 8 5 6
4 3 2 1 8 7 6 5
5 6 7 8 1 2 3 4
6 5 8 7 2 1 4 3
假设迷宫是由许多格子组成的矩形,其中用1表示 有墙,0表示有路。走迷宫即为沿上、下、左、右 方向走,直到最后走出迷宫。根据题意,看一下此 问题的分析图,如图所示。
根据分析图,可以推到出迷宫的流程图,如图16.26 所示。
开始 创建一个数组
开始走第一个格子
返回上一个格子,从 新走出口
是否有障碍
棋盘总共有n行和m列,马的位置是任意的,马从某 点走日字走完所有格子并且只能走的一次,根据题 意,看一下此题的分析图所示
马行走的方式
根据分析图,可以推到出马遍历的流程图所示。
开始
创建一个一维数组
以某一点为出发点, 走日字
走下一个日子 重新选择上一步的走 法 否 判断是否重复 否 是
判断是否走完所有格子
设A柱上有从小到大的3个盘子,因为大盘不能在小 盘之上,因此将A柱中最大的盘子移动到C柱之前, C柱必须为空。可以先将A柱中的2个盘子先移动到 B柱上,然后将第3个盘子移动到C柱上。当C柱上 已放有最大的盘子时,A柱为空,B柱上有2个盘子。 这时可将B柱上的1个盘子移动到A柱上,再将B柱 上的剩下的1个盘子移动到C柱上,如此循环直到最 后盘子的个数为1为止,直接将盘子移动到C盘上, 循环结束。根据题意,来看一下此问题的具体分析, 如图16.4所示。
用乘得的数除以这三个数:18÷3=6 18÷6=3,18÷9=2,所以18是最 小公倍数
根据问题分析,可以推导出三个数的最小公倍数的 流程图,如图16.9所示。
开始 找出三个数的最大值
最大值乘以1 最大值一次乘以下一 个自然数 用乘得的数取出这 三个数
否 这三个数是否被整除
