西北工业大学信号与系统期末试题及答案
[工学]信号与系统答案西北工业大学段哲民信号与系统1-3章答案
![[工学]信号与系统答案西北工业大学段哲民信号与系统1-3章答案](https://img.taocdn.com/s3/m/822cee280812a21614791711cc7931b765ce7b0f.png)
[⼯学]信号与系统答案西北⼯业⼤学段哲民信号与系统1-3章答案[⼯学]信号与系统答案西北⼯业⼤学段哲民信号与系统1-3章答案第⼀章习题-t1-1 画出下列各信号的波形:(1) f(t)=(2-e)U(t); (2) 1-tf(t)=ecos10πt×[U(t-1)-U(t-2)]。
2答案f(t)1 (1)的波形如图1.1(a)所⽰.,2T,,0.2sf(t)cos10,t,102(2) 因的周期,故的波形如图题1.1(b)所⽰.1-2 已知各信号的波形如图题1-2所⽰,试写出它们各⾃的函数式。
答案f(t),t[u(t),u(t,1)],u(t,1)1f(t),,(t,1)[u(t),u(t,1)]2f(t),(t,2)[u(t,2),u(t,3)]31-3 写出图题1-3所⽰各信号的函数表达式。
答案11,(t,2),t,1,2,t,0,22f(t),,1110,t,2,(,t,2),,t,122,f(t),u(t),u(t,1)u(t,2)2,f(t),,sint[u(t,2),u(t,2)]32f(t),u(t,2),2u(t,1),3u(t,1),4u(t,2),2u(t,3)421-4 画出下列各信号的波形:(1) f(t)=U(t-1); (2) f(t)=(t-1)U(t-1); 1222(3) f(t)=U(t-5t+6); (4)f(t)=U(sinπt)。
34答案f(t),u(t,1),u(,t,1)1 (1) ,其波形如图题1.4(a)所⽰.f(t),(t,1)[u(t,1),u(,t,1)],(t,1)u(t,1),(t,1)u(,t,1)2(2)其波形如图题1.4(b)所⽰.f(t),u(,t,2),u(t,3)3(3) ,其波形如图1.4(c)所⽰.f(t),u(sin,t)4(4) 的波形如图题1.4(d)所⽰.1-5 判断下列各信号是否为周期信号,若是周期信号,求其周期T。
西北工业大学《827信号与系统》习题解析讲义

西北工业大学《827 信号与系统》习题解析 第 1 讲第 一 章信号与系统的基本概念1 -1 画出下列各信号的波形: (1)f 1 ( t ) = (2 -e -t )U ( t );(2)f 2 ( t ) =e -t cos10πt ×[U ( t -1) -U ( t -2) ] 。
1 -2 已知各信号的波形如图题 1 -2 所示,试写出它们各自的函数式。
1 -3 写出图题 1 -3 所示各信号的函数表达式。
(图见视频)1 -4 画出下列各信号的波形:(1) f 1 ( t ) =U ( t 2 -1); (2) f 2 ( t ) = ( t -1)U ( t 2 -1); (3) f 3 ( t ) =U ( t 2 -5t +6); (4)f 4 ( t ) =U ( sin πt ) 。
1 -5 判断下列各信号是否为周期信号,若是周期信号,求其周期 T 。
1) f 1 ( t ) = 2 cos (2t -) 2) f 2 ( t ) = [ sin ( t -) ]3) f 3 ( t ) = 3 cos2πtU ( t ) 1 -6 化简下列各式: (1)jt -wδ(2τ-1)d τ1; (2)[ cos ( t +)( δ(t ))]; (3)jw -w[ cost δ(t ) ] sintdt 。
1 -7 求下列积分: (1)jw cos [ ω( t -3) δ(t -2)] dt ;(2)jδ(t +3)dt ;(3) jwe -2t δ(t 0 -t )dt 。
— 1 —21-8试求图题1-8中各信号一阶导数的波形,并写出其函数表达式,其中f3( t) =cos t[ U( t) -U( t-5) ] 。
1-9已知信号f() 的波形如图题1-9所示,试画出y( t) =f(t+1)U( -t)的波形。
1-10已知信号f( t)的波形如图题1-10所示,试画出信号与信号的波形。
西北工业大学信号与系统真题

题号:827《信号与系统》考试大纲一、考试内容:根据我校教学及该试题涵盖专业多的特点,对考试范围作以下要求:1、信号与系统的基本概念:信号的变换与运算;线性时不变系统基本性质。
2、连续系统时域分析:系统模型和自然频率;系统零输入响应、冲激响应、阶跃响应求解;系统零状态响应的卷积积分求解;全响应的求解。
3、连续信号频域分析:付立叶变换及其性质与应用;常用信号付立叶变换;周期信号、抽样信号付立叶变换;抽样定理及其应用。
4、连续系统频域分析:频域系统函数H(jω)及其求法;系统频率特性;系统零状态响应的频域求解;理想低通滤波器及其特性;信号不失真传输条件。
5、连续系统复频域分析:拉氏变换及其基本性质;拉氏反变换求解;s域的电路模型和电路定理;线性时不变系统的复频域分析。
6、复频域系统函数H(s):H(s)定义、分类、求法和零、极点图;系统模拟框图与信号流图;系统频率特性、正弦稳态响应求解以及系统稳定性判定;梅森公式及其应用。
7、离散信号与系统时域分析:离散信号时域变换、运算以及卷积求和;离散系统数学模型;线性时不变离散系统的性质、零输入响应、单位序列响应、阶跃响应、零状态响应的求解。
8、离散系统Z域分析:Z变换及其基本性质;Z反变换;系统Z域分析;系统函数H(z)及求法;H(z)零、极点图;离散系统模拟框图与信号流图;离散系统频率特性、正弦稳态响应求解以及稳定性判定;梅森公式及其应用。
9、系统状态变量分析:连续、离散系统状态方程与输出方程列写与求解;系统函数矩阵与单位冲激响应的求解;根据状态方程判断系统的稳定性;状态方程与输出方程的模拟与信号流图。
二、参考书目:[1] 段哲民等编,《信号与系统》,西北工业出版社,1997年[2] 吴大正主编,《信号与线性系统分析》(第3版),高等教育出版社,1998.10[3] 范世贵等编《信号与系统常见题型解析及模拟题》(第2版),西北工业出版社,2001.5注:以上[1]、[2]和[3]各任选之一即可。
《信号与系统》期末测验试题及答案

5.下列信号中为周期信号的是 D
。
f1 (t) sin 3t sin 5t
f 2 (t) cos 2t cost
f3
(k)
sin
6
k
sin
2
k
f
4
(k
)
1 2
k
(k
)
A f1 (t) 和 f2 (t)
c f1 (t), f 2 (t) 和 f3 (k)
所以:
(+2 分)
f (k) 10 [0.5k (k 1) 0.2k (k)] 3
(+2 分)
7.已知 f1 (t) 和 f2 (t) 的波形如下图所示,画出 f (t) f1 (t) f 2 (t) 的的波形图 解: 8.已知 f (t) 的波形如下图所示。请画出 f(-2t+1)的图形
(t
1)
d r(t) dt
de(t) dt
e(t)
描述的系统是:
A
。
(A)线性时变系统; (B)线性时不变系统;
(C)非线性时变系统;(D)非线性时不变系统
13.如图所示周期为 8 的信号 f (t) 中,下列对其含有的谐波分量的描述中最准确的是
D。 A 只有直流、正弦项 C 只有奇次余弦项
(z 0.5)(z 2)
B。
(A)|z|<0.5 (B)|z|>2 (C)0.5<|z|<2 (D)以上答案都不对
4. 下面关于离散信号的描述正确的是 B
。
(A) 有限个点上有非零值,其他点为零值的信号。
(B) 仅在离散时刻上有定义的信号。 (C) 在时间 t 为整数的点上有非零值的信号。
信号与系统l试题

四、系统分析题(共 30 分) 系统分析题(
1、如下图所示系统:其中激励为 e(t),响应为 i(t); 如下图所示系统: e(t), i(t);
i(t) +
R1=1 e(t)
L=0.1H C=0.5F R2=2
(1)求系统函数 H(s)? h(t)? (2)冲激响应 h(t)? 下系统的零输入响应? (3)求初始状态为 i (0 - ) = 2, i ′(0 - ) = −11 下系统的零输入响应? 求初始状态为 作用下系统的零状态响应? (4)求在 e( t ) = e − t ε ( t ) 作用下系统的零状态响应?
∑
D
-a
D
图3
b
∑
y (k )
Im[z]
8、已知某序列的 Z 变换为 F (z ) = 、
z ,其收敛区 z − 2z + 1
2
Re[z] 图4
所示, 域如图 4 所示,则对应的原序列为 ⑩
教务处印制
。
共 7 页
第 2 页
西北工业大学命题专用纸
⑩
A. kε (k ) .
B . kε ( k - 1)
诚信保证
本人知晓我校考场规则和违纪处分条例的有关规定,保证遵守考场 规则,诚实做人。 本人签字: 编号:
西北工业大学考试试题( 西北工业大学考试试题(卷)
2007 - 2008
开课学院 计算机学院 课程 考试时间
学 号
学年第 2 学期
信号与系统 2 小时 学时
成 绩
考试日期 2008 年 5 月 29 日
4、零输入响应是 、 ⑤ 。 A.部分自然响应 ⑤ .部分自然 C.部分零状态响应 .
信号与系统期末考试A试卷及答案

《信号与系统》考核试卷
专业班级:电子、通信工程考核方式:闭卷考试时量:120 分钟试卷类型: A
第2页共 8 页第1页共 8 页
图:
域模型图:
)的表达式:
第3页共 8 页第4页共 8 页
(a)
(b) (c) (d)
A 、
B 、
C 、
D 、
Y(w):
5、已知离散系统的差分方程为)(2)2(2)1(3)(n f n y n y n y =-+-+,求该
系统的系统函数)(z H 、单位响应)(n h 以及当激励信号)(2)(n n f n ε=时,
系统的零状态响应)(n y 。
(13分)
利用z 变换的移位特性,将差分方程变换为零状态下的z 域方程:
)(2)(2)(3)(21z F z Y z z Y z z Y =++--
2
322312)()()
(2221++=
++==--z z z z z z F z Y z H
2
412232)(22+++-=++=z z
z z z z z z H )(])2(4)1(2{)(n n h n n ε+--=∴
当激励信号)(2)(n n f n ε=时,2
)(-=
z z
z F 22)()()(3
2==z z z z H z F z Y 2
2
-
z
z 第5页 共 8 页
④由于该系统函数的所有极点均在
所以该系统是稳定系统。
第7页共页第8页共页第9页共页第10页共页
第7页共 8 页第8页共 8 页。
西工大信号与系统大纲以及范世贵等编《信号与系统常见题型解析及模拟题》答案

题号:827《信号与系统》考试大纲一、考试内容:根据我校教学及该试题涵盖专业多的特点,对考试范围作以下要求:1、信号与系统的基本概念:信号的变换与运算;线性时不变系统基本性质。
2、连续系统时域分析:系统模型和自然频率;系统零输入响应、冲激响应、阶跃响应求解;系统零状态响应的卷积积分求解;全响应的求解。
3、连续信号频域分析:付立叶变换及其性质与应用;常用信号付立叶变换;周期信号、抽样信号付立叶变换;抽样定理及其应用。
4、连续系统频域分析:频域系统函数H(jω)及其求法;系统频率特性;系统零状态响应的频域求解;理想低通滤波器及其特性;信号不失真传输条件。
5、连续系统复频域分析:拉氏变换及其基本性质;拉氏反变换求解;s域的电路模型和电路定理;线性时不变系统的复频域分析。
6、复频域系统函数H(s):H(s)定义、分类、求法和零、极点图;系统模拟框图与信号流图;系统频率特性、正弦稳态响应求解以及系统稳定性判定;梅森公式及其应用。
7、离散信号与系统时域分析:离散信号时域变换、运算以及卷积求和;离散系统数学模型;线性时不变离散系统的性质、零输入响应、单位序列响应、阶跃响应、零状态响应的求解。
8、离散系统Z域分析:Z变换及其基本性质;Z反变换;系统Z域分析;系统函数H(z)及求法;H(z)零、极点图;离散系统模拟框图与信号流图;离散系统频率特性、正弦稳态响应求解以及稳定性判定;梅森公式及其应用。
9、系统状态变量分析:连续、离散系统状态方程与输出方程列写与求解;系统函数矩阵与单位冲激响应的求解;根据状态方程判断系统的稳定性;状态方程与输出方程的模拟与信号流图。
二、参考书目:[1] 段哲民等编,《信号与系统》,西北工业出版社,1997年[2] 吴大正主编,《信号与线性系统分析》(第3版),高等教育出版社,1998.10[3] 范世贵等编《信号与系统常见题型解析及模拟题》(第2版),西北工业出版社,2001.5本人强烈推荐这本,一定要至少看两遍,每道题都不能落下。
信号与系统答案 西北工业大学 段哲民 第四章
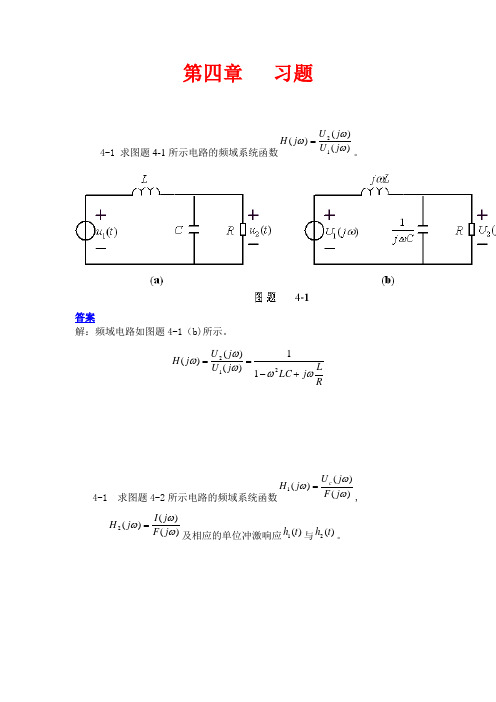
第四章 习题4-1 求图题4-1所示电路的频域系统函数)()()(12ωωωj U j U j H =。
答案解:频域电路如图题4-1(b)所示。
RL j LC j U j U j H ωωωωω+-==21211)()()(4-1 求图题4-2所示电路的频域系统函数)()()(1ωωωj F j U j H c =,)()()(2ωωωj F j I j H =及相应的单位冲激响应)(1t h 与)(2t h 。
答案解: 频域电路如图题4-2(b)所示。
RCj RCj F j U j H c 111)()()(1+⨯==ωωωω)111(1)()()(2RCj RC R j F j I j H +-⨯==ωωωω)(1)]([)(1111t U e RCj H F t h tRC--==ω)(1)(1)]([)(12212t U e CR t Rj HFt h tRC---==δω4-3 图题4-3所示电路,Vt U t U e t f t)](2)(10[)(+=-。
求关于)(t i 的单位冲激响应)(t h 和零状态响应)(t i 。
答案解: 频域电路如图题4-3(b)所示。
2121)()()(+⨯==ωωωωj j F j I j H所以At U et h t)(21)(2-=]1)([211525.5)()()(ωωπδωωωωωj j j j F j H j I +++++-==所以 At U t U eet i tt)(21)()55.5()(2++-=--4-4 已知频域系统函数235)(22++-++-=ωωωωωj j j H ,激励)()(3t U et f t-=。
求零状态响应)(t y 。
答案解:31)(+=ωωj j F)2)(1(31)(++++=ωωωωj j j j H211131)()()(+-+++==ωωωωωωj j j j F j H j Y所以 )()()(23t U eeet y ttt----+=4-5 已知频域系统函数65)(2++-=ωωωωj j j H ,系统的初始状态,2)0(=y 1)0(='y ,激励)()(t U e t f t-=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西北工业大学信号与系统期末试题及答案————————————————————————————————作者:————————————————————————————————日期:23 / 20诚信保证本人知晓我校考场规则和违纪处分条例的有关规定,保证遵守考场规则,诚实做人。
本人签字: 编号:西北工业大学考试试题(卷)2010 - 2011 学年第 2 学期开课学院 计算机学院 课程 信号与系统 学时 48考试日期 2011年6月3日 考试时间 2 小时 考试形式(闭开)(B A)卷考生班级学 号姓 名★注:请将各题答案做在答题纸上,答在试题纸上无效。
一、单项选择题(每题有且仅有一个答案是正确的,共20分)1、已知某系统方程为)(10)()()(d 22t e dt t dr t r dt t r =-,则该系统是 ① 。
① A .线性时不变系统 B .非线性时变系统C .线性时变系统D .非线性时不变系统2、已知某连续线性时不变系统的初始状态不为零,设当激励为e(t)时,全响应为r(t),则当激励增大一倍为2e(t)时,其全响应为 ② 。
② A .也增大一倍为2r(t) B .也增大但比2r(t)小C .保持不变仍为r(t)D .发生变化,但以上答案均不正确 3、积分式dt t t t t )]2(2)()[23(442-+++⎰-δδ的积分结果是 ③ 。
③ A .14 B .24 C .26 D .28注:1. 命题纸上一般不留答题位置,试题请用小四、宋体打印且不出框。
成绩2. 命题教师和审题教师姓名应在试卷存档时填写。
共7 页第1 页4 / 205 / 20T/2T-T/2图2t-Tf(t)4、已知)F(j )(ω↔t f ,对应的频谱带宽为10B ,则要使得频谱带宽变为20B ,需要时间信号变为 ④ 。
④ A .)20(t f B .)t f 201(C .)2(t fD .)21(t f 5、已知信号)(t f 的波形如图1所示,其表达式=)(t f ⑤ 。
⑤ A .)3()2()1()(---+-+=t t t t εεεε)(t fB .)3(3)2()1()(+-++++=t t t t εεεε)(t fC . )3(3)2()1()(---+-+=t t t t εεεε)(t fD .)2()1()1(2---++=t t t εεε)(t f 6、周期矩形脉冲的谱线间隔 ⑥ 。
⑥ A .只与脉冲幅度有关 B .只与脉冲宽度有关C .只与脉冲周期有关D .与周期和脉冲宽度都有关7、一函数如图2所示, 此函数为 ⑦ 函数,其傅立叶级数只包含 ⑧ 分量。
⑦ A .奇谐函数 B .奇函数 C .奇函数和奇谐函数 D .偶谐函数 ⑧ A .正弦分量的奇次谐波B .正弦分量的偶次谐波C .奇次谐波D .偶次谐波8、)3(*)5(21-+t f t f = ⑨ 。
⑨ A .)3(*)5(21+-t f t f B .)8(*)(21-t f t fC .)(*)8(21t f t f +D .)1(*)3(21-+t f t f9、设)()(k k f ε的Z 变换为F(z),R z >,则)()(k k f --ε的Z 变换为 ⑩ 。
⑩ A . )(z F B . )(z F - C . )1(zF - D . )1(z F教务处印制 共 7 页 第 2 页图32 1f(t)t1 2 36 / 20二、填空题(共20分) 1、积分[]=--⎰+∞∞--dt t t t e j )()(0δδω ① 。
2、已知)()(ωj F t f ↔,求)()(a t t f -δ的傅立叶变换,即:↔-)()(a t t f δ ② 。
3、若一离散时间序列为左边序列且其Z 变换存在,则其收敛域在 ③ (圆内,圆外),若其为双边序列且其Z 变换存在,则收敛域在 ④ 。
4、一连续周期矩形信号的波形如图3所示,τ=2s,A=1V,T=10s,则其频谱带宽(从零频率到第一个过零点的频率)ωm = ⑤ ,每个过零周期内的谱线条数为 ⑥ 。
现对该信号进行均匀离散化,至少应以ωs = ⑦ 的频率采样,才能保证由离散信号可重建原连续信号。
(已知该周期信号的幅值谱为:)(2n ΩSa T 2A τA n τ=)。
5、图4所示系统的差分方程为⑧ 。
6、)()1(k k k ε-的Z 变换为 ⑨ 。
7、z 平面中特征根为0.5所对应的自然响应项为 __⑩ 。
三、简单计算题(共35分)1、判断系统稳定性并说明原因。
(12分) ①特征方程322)(234++++=s s s s s D ②系统函数()10s 25134++++=s s s s H③系统方程)()(20)(4)(5)()3(t e t r t r t r t r =+'+''+ ④特征方程)25.0)(1(3)(2+---=z z z z z H-T tf(t)-τ/2 τ/2TA图)(k y ∑-aDc)(k e 图3Db∑图acb教务处印制共7 页第3 页7 / 20西北工业大学命题专用纸2、求信号)1()1(---tet atε的拉普拉斯变换。
(5分)3、已知积分()⎰+∞---=)()(ttedxxfe txtε,求f(t)。
(5分)(已知存在拉普拉斯变换()11)(11)(2+↔+↔--stestte ttεε、。
)4、已知f(k),h(k)如图5、图6所示,求f(k)*h(k)。
(7分)图5 图62、已知系统极零图如图7所示, 该系统的单位阶跃响应终值为23,求系统函数)(sH。
(6分)四、系统分析题(共25分)1、(15分)一连续线性时不变系统具有一定初始条件,其单位阶跃响应为())(1te tε--,初始条件不变时,若其对)(3te tε-的全响应为())(5.05.13tee ttε---,求此时的:①写出系统微分方程②零输入响应)(trzi③零状态响应)(trzs④初始条件)0(-r⑤自由响应和受迫响应-1-2-jj0s-3图8jω图78 / 20教务处印制共7 页第4 页西北工业大学命题专用纸9 / 2010 / 202、(10分)已知系统差分方程)1()()2(2)1(3)(++=+++-k e k e k y k y k y ;2)0(=y ;0)1(=y 。
(1)求系统零输入响应、单位函数响应; (2)若)(2)(k k e k ε=,求零状态响应。
***********************************************************************常用公式***********************************************************************表1:常用傅立叶变换、拉普拉斯变换和Z 变换时域函数 傅立叶变换拉普拉斯变换 )(t δ 1 1)(t ε ωωπδj 1)(+ s1)(t e at ε-ωj a +1 a s +1表2:常用傅立叶变换、拉普拉斯变换和Z 变换时域函数 Z 变换 )(k δ 1)(k ε 1-z z)(k v k εvz z - 教务处印制 共 7 页 第 5 页西北工业大学命题专用纸表3:变换性质(0,0>≥n t )性质 傅立叶变换拉普拉斯变换Z 变换线性 )()()()(22112211ωωj F a j F a t f a t f a +↔+)()()()(22112211s F a s F a t f a t f a +↔+)()()()(22112211z F a z F a k f a k f a +↔+延时 0)()(0t j e j F t t f ωω-↔- 0)()(0st es F t t f -↔-⎥⎦⎤⎢⎣⎡-↔+∑-=-10)()()(n i i nz i f z F z n k f移频 )()(c tj j j F e t f c ωωω-↔)()(00s s F e t f t s -↔尺度变换 )(1)(a j F a at f ω↔)(1)(asF a at f ↔)()(azF k f a k ↔时域微分 )()(ωωj F j dtt df ↔ )0()()(--↔f s sF dtt df时域积分 )(1)(ωωττj F j d f t↔⎰∞- sd f ss F d f t⎰⎰∞-∞-+↔0)()()(ττττ频域微分 )()(ωωj F d dt jtf ↔-ds s dF t tf )()(↔-dzz dF z k kf )()()(-↔ 频域积分⎰∞↔s dx x F t f t)()(1初值定理)(lim )0(s sF f s ∞→+=终值定理)(lim )(0s sF f s →=∞卷积)()()(*)(2121ωωj F j F t f t f ↔)()()(*)(2121s F s F t f t f ↔)()()(*)(2121z F z F k f k f ↔教务处印制 共 7 页 第 6 页西北工业大学考试试题(答题纸)2010 -2011 学年第 2 学期开课学院 计算机学院 课程 信号与系统 学时 48考试日期 2011年06月3日 考试时间 2 小时 考试形式(闭开)(B A)卷考生班级学 号姓 名★注:请将各题答案做在答题纸上。
一、单项选择题(共20分)二、填空题(共20分) 1. ① 2. ②3. ③ ④4. ⑤ ⑥ ⑦5. ⑧6. ⑨7. ⑩(★注:三、四题答在后面答题纸上,请将大小题号写清楚。
)题号 ①②③④⑤⑥⑦⑧⑨⑩选择教务处印制 共 7 页 第 7 页西北工业大学考试试题(答案)2010 -2011 学年第 2 学期开课学院 计算机学院 课程 信号与系统 学时 48考试日期 2011年06月3日 考试时间 2 小时 考试形式(闭开)(B A)卷一、单项选择题(共20分)(每空2份)二、填空题(共20分)(每空2份) 1. ① 0 2. ② f(a)3. ③ 圆外 ④ 环内4. ⑤ π ⑥ 5 ⑦ 2π5. ⑧ 2)-ce(k 1)-be(k 1)-ay(k -y(k) +=6. ⑨ 1,)1(2>+-z z z7. ⑩ )(21 kk ε⎪⎭⎫⎝⎛题号 ①②③④⑤⑥⑦⑧⑨⑩选择BDBCCCACDD三、简答题(共35分)1、解:(共12分) ①s s s ss 12343 2 12 1 3 ε(1分)03-2<εε3(1分)有变号,所以不稳定 ……)(1分② ∵特征方程10s 25)(34+++=s s s D 有缺项 ……)(1分 ∴系统不稳定 ……(1分)③2045)(23+++=s s s s D方法一:2045)(23+++=s s s s D 有3个极点,s 1=-5,s 2=2j,s 3=-2j ……(2分)∵极点在左半平面,虚轴上的极点是单极点 ……(1分) ∴系统稳定(临界稳定) ……(1分)方法二:4 120 5(2分)s s D s s D 10)(205)(121='+='1020(1分)s s s123s,j 2s ,0205s 2系统临界稳定。
