2019年高考数学一轮复习课时分层训练2命题及其关系充分条件与必要条件理北师大版
高考大一轮总复习1.2命题及其关系、充分条件与必要条件

§1.2命题及其关系、充分条件与必要条件考纲展示► 1.理解命题的概念.2.了解“若p,则q”形式的命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系.3.理解充分条件、必要条件与充要条件的含义.考点1命题及其相互关系1.命题2.四种命题及其相互关系(1)四种命题间的相互关系:(2)四种命题中真假性的等价关系:原命题等价于________,原命题的否命题等价于________.在四种形式的命题中真命题的个数只能是________.答案:(1)若q,则p若綈p,则綈q若綈q,则綈p(2)逆否命题逆命题0,2,4(1)[教材习题改编]命题“若m<0,则方程x2+x-2m=0有实根”的否命题是_______________________________________________.答案:若m≥0,则方程x2+x-2m=0无实根(2)[教材习题改编]“若a,b都是偶数,则ab必是偶数”的逆否命题为___________________________________________________.答案:若ab不是偶数,则a,b不都是偶数命题中的易错点:对条件、结论的否定不当.“单调函数不是周期函数”的逆否命题是___________________________________________________________________________.答案:周期函数不是单调函数解析:原命题可改写为“若函数是单调函数,则函数不是周期函数”,故其逆否命题是“若函数是周期函数,则函数不是单调函数”,简化为“周期函数不是单调函数”.[典题1](1)命题“若a>b,则a-1>b-1”的否命题是()A.若a>b,则a-1≤b-1B.若a>b,则a-1<b-1C.若a≤b,则a-1≤b-1D.若a<b,则a-1<b-1[答案] C[解析]根据否命题的定义可知,命题“若a>b,则a-1>b-1”的否命题应为“若a≤b,则a-1≤b-1”.(2)[2017·宁夏银川模拟]命题“若x2+y2=0,x,y∈R,则x=y=0”的逆否命题是()A.若x≠y≠0,x,y∈R,则x2+y2=0B.若x=y≠0,x,y∈R,则x2+y2≠0C.若x≠0且y≠0,x,y∈R,则x2+y2≠0D.若x≠0或y≠0,x,y∈R,则x2+y2≠0[答案] D[解析]将原命题的条件和结论否定,并互换位置即可.由x=y=0知x=0且y=0,其否定是x≠0或y≠0.(3)已知:命题“若函数f(x)=e x-mx在(0,+∞)上是增函数,则m≤1”,则下列结论正确的是()A.否命题是“若函数f(x)=e x-mx在(0,+∞)上是减函数,则m>1”,是真命题B.逆命题是“若m≤1,则函数f(x)=e x-mx在(0,+∞)上是增函数”,是假命题C.逆否命题是“若m>1,则函数f(x)=e x-mx在(0,+∞)上是减函数”,是真命题D.逆否命题是“若m>1,则函数f(x)=e x-mx在(0,+∞)上不是增函数”,是真命题[答案] D[解析]由f(x)=e x-mx在(0,+∞)上是增函数,则f′(x)=e x-m≥0恒成立,∴m≤1.∴命题“若函数f(x)=e x-mx在(0,+∞)上是增函数,则m≤1”是真命题,∴其逆否命题“若m>1,则函数f(x)=e x-mx在(0,+∞)上不是增函数”是真命题.[点石成金] 1.写一个命题的其他三种命题时,需注意:(1)对于不是“若p,则q”形式的命题,需先改写;(2)若命题有大前提,写其他三种命题时需保留大前提.2.判断一个命题为真命题,要给出推理证明;判断一个命题是假命题,只需举出反例即可.3.根据“原命题与逆否命题同真同假,逆命题与否命题同真同假”这一性质,当一个命题直接判断不易进行时,可转化为判断其等价命题的真假.考点2充分条件、必要条件的判定充要条件答案:充分必要充分不必要真子集必要不充分真子集充要A=B既不充分也不必要包含1.充要条件的易混点:混淆条件的充分性和必要性.“x(x-1)=0”是“x=1”的________条件.答案:必要不充分解析:x(x-1)=0⇒x=0或x=1;反之,由x=1可得x(x-1)=0.故“x(x-1)=0”是“x=1”的必要不充分条件.2.充要条件的易错点:否定形式下充分条件、必要条件判断错误.“a≠b”是“a2≠b2”的________条件.答案:必要不充分解析:由a≠b不能得到a2≠b2,但由a2≠b2一定得出a≠b,故为必要不充分条件.1.充分、必要条件的判断方法:定义判断法;集合判断法.(1)[2014·浙江卷改编]设四边形ABCD的两条对角线分别为AC,BD,则“四边形ABCD为菱形”是“AC⊥BD”的________条件.答案:充分不必要解析:若四边形ABCD为菱形,则AC⊥BD;反之,若AC⊥BD,则四边形ABCD不一定为菱形.故“四边形ABCD为菱形”是“AC⊥BD”的充分不必要条件.(2)[2015·安徽卷改编]设p:x<3,q:-1<x<3,则p是q成立的________条件.答案:必要不充分解析:因为p:x<3,q:-1<x<3,所以q⇒p,但p⇒/q,所以p是q成立的必要不充分条件.2.充要条件的两个结论:传递性;等价性.(1)若p是q的充分不必要条件,q是r的充分不必要条件,则p是r的________条件.答案:充分不必要解析:根据充分条件的概念可知,p⇒q,q⇒r,则p⇒r.又因为q⇒/p,r⇒/q,则r⇒/p,所以p是r的充分不必要条件.(2)若p是q的充分不必要条件,则綈q是綈p的________条件答案:充分不必要解析:因为原命题和它的逆否命题是等价命题,所以綈q是綈p的充分不必要条件.[典题2](1)设x∈R,则“|x-2|<1”是“x2+x-2>0”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件[答案] A[解析]|x-2|<1⇔1<x<3,x2+x-2>0⇔x>1或x<-2.由于{x|1<x<3}是{x|x>1或x<-2}的真子集,所以“|x-2|<1”是“x2+x-2>0”的充分不必要条件.(2)若p是綈q的充分不必要条件,则綈p是q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件[答案] B[解析]∵p是綈q的充分不必要条件,∴綈q是p的必要不充分条件.∴綈p是q的必要不充分条件,故选B.(3)已知a,b∈R,下列四个条件中,使a>b成立的必要不充分的条件是()A.a>b-1 B.a>b+1C.|a|>|b| D.2a>2b[答案] A[解析]因为a>b⇒a>b-1,但a>b-1⇒/ a>b,故A是a>b的必要不充分条件;B是a>b 的充分不必要条件;C是a>b的既不充分也不必要条件;D是a>b的充要条件.[点石成金]充要条件的三种判断方法(1)定义法:根据p⇒q,q⇒p进行判断.(2)集合法:根据p,q成立的对象的集合之间的包含关系进行判断.(3)等价转化法:根据一个命题与其逆否命题的等价性,把判断的命题转化为其逆否命题进行判断.这个方法特别适合以否定形式给出的问题,常用的是逆否等价法.如“xy≠1”是“x≠1或y≠1”的某种条件,即可转化为判断“x=1且y=1”是“xy=1”的某种条件.①綈q是綈p的充分不必要条件⇔p是q的充分不必要条件;②綈q是綈p的必要不充分条件⇔p是q的必要不充分条件;③綈q是綈p的充要条件⇔p是q的充要条件.1.[2017·山东淄博模拟]“a=2”是“函数f(x)=x2-2ax-3在区间[2,+∞)上为增函数”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案:A解析:“a=2”⇒“函数f(x)=x2-2ax-3在区间[2,+∞)上为增函数”,但反之不成立.2.[2017·河北武邑中学高三上期中]设a,b∈R,则“(a-b)a2≥0”是“a≥b”的() A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案:B解析:若“(a -b )a 2≥0”,则“a ≥b ”不成立,故“(a -b )a 2≥0”不是“a ≥b ”的充分条件;若“a ≥b ”,则“(a -b )a 2≥0”成立,故“(a -b )a 2≥0”是“a ≥b ”的必要条件,故选B.考点3 充分条件、必要条件的应用[典题3] (1)[2017·江西南昌模拟]已知条件p :|x -4|≤6;条件q :(x -1)2-m 2≤0(m >0),若p 是q 的充分不必要条件,则m 的取值范围是( )A .[21,+∞)B .[9,+∞)C .[19,+∞)D .(0,+∞)[答案] B[解析] 条件p :-2≤x ≤10,条件q :1-m ≤x ≤m +1, 又因为p 是q 的充分不必要条件,所以有⎩⎪⎨⎪⎧1-m ≤-2,1+m ≥10,解得m ≥9.(2)已知P ={x |x 2-8x -20≤0},非空集合S ={x |1-m ≤x ≤1+m }.若x ∈P 是x ∈S 的必要条件,则m 的取值范围为________.[答案] [0,3][解析] 由x 2-8x -20≤0得-2≤x ≤10, ∴P ={x |-2≤x ≤10},由x ∈P 是x ∈S 的必要条件,知S ⊆P .则⎩⎪⎨⎪⎧1-m ≤1+m ,1-m ≥-2,1+m ≤10,∴0≤m ≤3.所以当0≤m ≤3时,x ∈P 是x ∈S 的必要条件,即所求m 的取值范围是[0,3]. [题点发散1] 本例(2)条件不变,问是否存在实数m ,使x ∈P 是x ∈S 的充要条件. 解:若x ∈P 是x ∈S 的充要条件,则P =S ,∴⎩⎪⎨⎪⎧ 1-m =-2,1+m =10,∴⎩⎪⎨⎪⎧m =3,m =9,即不存在实数m ,使x ∈P 是x ∈S 的充要条件.[题点发散2] 本例(2)条件不变,若綈P 是綈S 的必要不充分条件,求实数m 的取值范围. 解:由例题知P ={x |-2≤x ≤10}, ∵綈P 是綈S 的必要不充分条件, ∴P ⇒S 且S ⇒/ P .∴[-2,10][1-m,1+m ],∴⎩⎪⎨⎪⎧ 1-m ≤-2,1+m >10或⎩⎪⎨⎪⎧1-m <-2,1+m ≥10,∴m ≥9,即m 的取值范围是[9,+∞).[点石成金] 充分条件、必要条件的应用,一般表现在参数问题的求解上.解题时需注意:(1)把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式(或不等式组)求解.(2)要注意区间端点值的检验.1.已知p :x >1或x <-3,q :x >a ,若q 是p 的充分不必要条件,则a 的取值范围是( ) A .[1,+∞) B .(-∞,1] C .[-3,+∞)D .(-∞,-3)答案:A解析:解法一:设P ={x |x >1或x <-3},Q ={x |x >a },因为q 是p 的充分不必要条件,所以Q P ,因此a ≥1.解法二:令a =-3,则q :x >-3,则由命题q 推不出命题p ,此时q 不是p 的充分条件,排除B ,C ;同理,取a =-4,排除D.故选A.2.已知不等式|x -m |<1成立的充分不必要条件是13<x <12,则m 的取值范围是( )A.⎝⎛⎦⎤-∞,-12 B .⎣⎡⎭⎫43,+∞ C.⎣⎡⎦⎤-43,12 D .⎣⎡⎦⎤-12,43 答案:D解析:由|x -m |<1得m -1<x <1+m ,又因为|x -m |<1的充分不必要条件是13<x <12,借助数轴,所以⎩⎨⎧m -1≤13,m +1≥12,解得-12≤m ≤43.[方法技巧] 1.判断四种命题间关系的方法写出一个命题的逆命题、否命题及逆否命题的关键是分清原命题的条件和结论,然后按定义来写;在判断原命题、逆命题、否命题以及逆否命题的真假时,要借助原命题与其逆否命题同真或同假,逆命题与否命题同真或同假来判定.2.充分、必要条件的判断方法(1)定义法:直接判断“若p ,则q ”“若q ,则p ”的真假即可.(2)利用集合间的包含关系判断:设A ={x |p (x )},B ={x |q (x )},若A ⊆B ,则p 是q 的充分条件或q 是p 的必要条件;若A B ,则p 是q 的充分不必要条件;若A =B ,则p 是q 的充要条件.[易错防范] 1.当一个命题有大前提而要写出其他三种命题时,必须保留大前提. 2.判断命题的真假及写四种命题时,一定要明确命题的结构,可以先把命题改写成“若p ,则q ”的形式.3.判断条件之间的关系要注意条件之间关系的方向,要注意“A 是B 的充分不必要条件”与“A 的充分不必要条件是B ”的区别,要正确理解“p 的一个充分不必要条件是q ”的语言.真题演练集训1.[2015·山东卷]设m ∈R ,命题“若m >0,则方程x 2+x -m =0有实根”的逆否命题是( )A .若方程x 2+x -m =0有实根,则m >0B .若方程x 2+x -m =0有实根,则m ≤0C .若方程x 2+x -m =0没有实根,则m >0D .若方程x 2+x -m =0没有实根,则m ≤0答案:D解析:根据逆否命题的定义,命题“若m >0,则方程x 2+x -m =0有实根”的逆否命题是“若方程x 2+x -m =0没有实根,则m ≤0”.故选D.2.[2015·北京卷]设α,β是两个不同的平面,m 是直线且m ⊂α,“m ∥β”是“α∥β”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件 答案:B解析:当m ∥β时,过m 的平面α与β可能平行也可能相交,因而m ∥β D ⇒/ α∥β;当α∥β时,α内任一直线与β平行,因为m ⊂α,所以m ∥β.综上知,“m ∥β”是“α∥β”的必要而不充分条件.3.[2015·重庆卷]“x >1”是“log 12 (x +2)<0”的( )A .充要条件B .充分而不必要条件C .必要而不充分条件D .既不充分也不必要条件 答案:B解析:∵ x >1⇒log 12 (x +2)<0,log 12 (x +2)<0⇒x +2>1⇒x >-1,∴ x >1是log 12 (x +2)<0的充分而不必要条件.4.[2016·四川卷]设p :实数x ,y 满足(x -1)2+(y -1)2≤2,q :实数x ,y 满足⎩⎪⎨⎪⎧y ≥x -1,y ≥1-x ,y ≤1,则p 是q 的( )A .必要不充分条件B .充分不必要条件C .充要条件D .既不充分也不必要条件 答案:A解析:取x =y =0满足条件p ,但不满足条件q ,反之,对于任意的x ,y 满足条件q ,显然必满足条件p ,所以p 是q 的必要不充分条件,故选A.课外拓展阅读根据充要条件求参数取值范围的方法1.解决根据充要条件求参数取值范围的问题一般是把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的包含、相等关系列出关于参数的不等式(组)求解;有时也采用等价转化思想把复杂、疑难问题转化为简单、熟悉的问题来解决.2.在解求参数的取值范围的题目时,一定要注意区间端点值的检验,在利用集合关系列不等式时,不等式是否能取到等号直接决定着端点值的取舍,在这里容易增解或漏解.[典例] 已知p :⎪⎪⎪⎪1-x -13≤2,q :x 2-2x +1-m 2≤0(m >0),且綈p 是綈q 的必要不充分条件,则实数m 的取值范围为________.[答案] [9,+∞)[解析] 解法一:由⎪⎪⎪⎪⎪⎪1-x -13≤2,得-2≤x ≤10,∴綈p 对应的集合为{x |x >10或x <-2}, 设A ={x |x >10或x <-2}. 由x 2-2x +1-m 2≤0(m >0), 得1-m ≤x ≤1+m (m >0),∴綈q 对应的集合为{x |x >m +1或x <1-m ,m >0}, 设B ={x |x >m +1或x <1-m ,m >0}.∵綈p 是綈q 的必要而不充分的条件,∴B A ,∴⎩⎪⎨⎪⎧m >0,1-m ≤-2,1+m ≥10,且不能同时取得等号,解得m ≥9,∴实数m 的取值范围为[9,+∞). 解法二:∵綈p 是綈q 的必要而不充分条件, ∴q 是p 的必要而不充分条件,即p 是q 的充分而不必要条件. 由x 2-2x +1-m 2≤0(m >0),得 1-m ≤x ≤1+m (m >0).∴q 对应的集合为{x |1-m ≤x ≤1+m ,m >0}, 设M ={x |1-m ≤x ≤1+m ,m >0},又由⎪⎪⎪⎪⎪⎪1-x -13≤2,得-2≤x ≤10,∴p 对应的集合为{x |-2≤x ≤10}, 设N ={x |-2≤x ≤10}.由p 是q 的充分而不必要条件知N M , ∴⎩⎪⎨⎪⎧m >0,1-m ≤-2,1+m ≥10,且不能同时取等号,解得m ≥9.∴实数m 的取值范围为[9,+∞).本例涉及参数问题,直接解决较为困难,先用等价转化思想,将复杂、生疏的问题转化为简单、熟悉的问题来解决.一般地,在涉及字母参数的取值范围的充要关系问题中,常常要利用集合的包含、相等关系来考虑,这是破解此类问题的关键.课时跟踪检测(二) [高考基础题型得分练]1.命题“若一个数是负数,则它的平方是正数”的逆命题是( ) A .“若一个数是负数,则它的平方不是正数” B .“若一个数的平方是正数,则它是负数” C .“若一个数不是负数,则它的平方不是正数”D .“若一个数的平方不是正数,则它不是负数” 答案:B解析:依题意,得原命题的逆命题为:若一个数的平方是正数,则它是负数.2.[2017·山东荣成六中高三月考]已知复数z =(a 2-4)+(a +2)i(a ∈R ),则“a =2”是“z 为纯虚数”的( )A .充分不必要条件B .必要不充分条件C .既不充分也不必要条件D .充要条件 答案:D解析:当a =2时,z =4i 为纯虚数;当z 为纯虚数时,a 2-4=0,a +2≠0⇒a =2,所以“a =2”是“z 为纯虚数”的充要条件,故选D.3.给出命题:“若函数y =f (x )是幂函数,则函数y =f (x )的图象不过第四象限”.在它的逆命题、否命题、逆否命题3个命题中,真命题的个数是( )A .3B .2C .1D .0答案:C解析:原命题是真命题,故它的逆否命题是真命题;它的逆命题为“若函数y =f (x )的图象不过第四象限,则函数y =f (x )是幂函数”,显然逆命题为假命题,故原命题的否命题也为假命题.因此在它的逆命题、否命题、逆否命题3个命题中真命题只有1个. 4.下列结论错误的是( )A .命题“若x 2-3x -4=0,则x =4”的逆否命题为“若x ≠4,则x 2-3x -4≠0”B .“x =4”是“x 2-3x -4=0”的充分条件C .命题“若m >0,则方程x 2+x -m =0有实根”的逆命题为真命题D.命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0”答案:C解析:C项命题的逆命题为“若方程x2+x-m=0有实根,则m>0”.若方程有实根,则Δ=1+4m≥0,即m≥-14,不能推出m>0,所以不是真命题,故选C.5.命题“∀x∈[1,2],x2-a≤0”为真命题的一个充分不必要条件是()A.a≥4 B.a≤4C.a≥5 D.a≤5答案:C解析:命题“∀x∈[1,2],x2-a≤0”为真命题的充要条件是a≥4,故其充分不必要条件是集合[4,+∞)的真子集.故选C.6.设U为全集,A,B是集合,则“存在集合C使得A⊆C,B⊆∁U C”是“A∩B=∅”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案:C解析:由Venn图易知充分性成立.反之,A∩B=∅时,由Venn图(如图)可知,存在A=C,同时满足A⊆C,B⊆∁U C.故“存在集合C使得A⊆C,B⊆∁U C”是“A∩B=∅”的充要条件.7.[2017·湖南长沙模拟]已知函数f(x)=x2-2ax+b,则“1<a<2”是“f(1)<f(3)”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案:A解析:函数f(x)=x2-2ax+b,所以f(1)=1-2a+b,f(3)=9-6a+b,1<a<2,所以1-2a<9-6a,即f(1)<f(3);反过来,当f(1)<f(3)时,得1-2a+b<9-6a+b,解得a<2,不能得到1<a<2,所以“1<a<2”是“f(1)<f(3)”的充分不必要条件.故选A.8.函数f(x)=⎩⎪⎨⎪⎧log2x,x>0,-2x+a,x≤0有且只有一个零点的充分不必要条件是() A.a<0 B.0<a<12C.12<a<1 D.a≤0或a>1答案:A解析:因为函数f(x)过点(1,0),所以函数f(x)有且只有一个零点⇔函数y=-2x+a(x≤0)没有零点⇔函数y=2x(x≤0)与直线y=a无公共点.由数形结合,可得a≤0或a>1.观察选项,根据集合间的关系得{a|a<0}为{a|a≤0或a>1}的真子集,故选A.9.命题“若a≤b,则ac2≤bc2”,则命题的原命题、逆命题、否命题和逆否命题中,真命题的个数是________.答案:2解析:其中原命题和逆否命题为真命题,逆命题和否命题为假命题.10.给定两个命题p,q,若綈p是q的必要不充分条件,则p是綈q的________条件.答案:充分不必要解析:若綈p是q的必要不充分条件,则q⇒綈p但綈p⇒/q,其逆否命题为p⇒綈q但綈q ⇒/ p ,所以p 是綈q 的充分不必要条件.11.若x <m -1或x >m +1是x 2-2x -3>0的必要不充分条件,则实数m 的取值范围是________.答案:[0,2]解析:由已知易得{x |x 2-2x -3>0}为{x |x <m -1或x >m +1}的真子集, 又{x |x 2-2x -3>0}={x |x <-1或x >3},∴⎩⎪⎨⎪⎧ -1≤m -1,m +1<3或⎩⎪⎨⎪⎧-1<m -1,m +1≤3,∴0≤m ≤2. 12.下列命题: ①若ac 2>bc 2,则a >b ; ②若sin α=sin β,则α=β;③“实数a =0”是“直线x -2ay =1和直线2x -2ay =1平行”的充要条件; ④若f (x )=log 2x ,则f (|x |)是偶函数. 其中正确命题的序号是________. 答案:①③④解析:对于①,ac 2>bc 2,c 2>0,∴a >b 正确; 对于②,sin 30°=sin 150°⇒/ 30°=150°,∴②错误;对于③,l 1∥l 2⇔A 1B 2=A 2B 1,即-2a =-4a ⇒a =0且A 1C 2≠A 2C 1,所以③正确;④显然正确.[冲刺名校能力提升练]1.已知a ,b ,c ∈R ,命题“如果a +b +c =3,则a 2+b 2+c 2≥3”的否命题是( ) A .如果a +b +c ≠3,则a 2+b 2+c 2<3 B .如果a +b +c =3,则a 2+b 2+c 2<3 C .如果a +b +c ≠3,则a 2+b 2+c 2≥3 D .如果a 2+b 2+c 2≥3,则a +b +c =3答案:A解析:“a +b +c =3”的否定是“a +b +c ≠3”,“a 2+b 2+c 2≥3”的否定是“a 2+b 2+c 2<3”,故根据否命题的定义知选A.2.给定下列四个命题:①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行; ②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直; ③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直. 其中,为真命题的是( ) A .①和② B .②和③ C .③和④ D .②和④答案:D解析:只有一个平面内的两条相交直线与另一个平面都平行时,这两个平面才相互平行,所以①为假命题;②符合两个平面相互垂直的判定定理,所以②为真命题;垂直于同一直线的两条直线可能平行,也可能相交或异面,所以③为假命题;根据两个平面垂直的性质定理易知④为真命题.3.在斜三角形ABC 中,命题甲:A =π6,命题乙:cos B ≠12,则甲是乙的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 答案:A解析:因为△ABC 为斜三角形,所以若A =π6,则B ≠π3且B ≠π2,所以cos B ≠12且cos B ≠0;反之,若cos B ≠12,则B ≠π3,不妨取B =π6,A =π4,C =7π12,满足△ABC 为斜三角形,故选A.。
高考数学一轮复习课时分层训练2命题及其关系充分条件与必要条件文北师大版

课时分层训练(二)命题及其关系、充分条件与必要条件A组基础达标(建议用时:30分钟)一、选择题1.命题“若a2+b2=0,则a=0且b=0”的逆否命题是()A.若a2+b2≠0,则a≠0且b≠0B.若a2+b2≠0,则a≠0或b≠0C.若a=0且b=0,则a2+b2≠0D.若a≠0或b≠0,则a2+b2≠0D[“若a2+b2=0,则a=0且b=0”的逆否命题是“若a≠0或b≠0,则a2+b2≠0”,故选D.]2.设α,β是两个不同的平面,m是直线且mα.则“m∥β”是“α∥β”的() A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件B[mα,m∥βDα∥β,但mα,α∥β⇒m∥β,∴“m∥β”是“α∥β”的必要不充分条件.]3.已知x∈R,则“x>2”是“x2-3x+2>0”成立的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件A[由x2-3x+2>0得x<1或x>2,所以“x>2”是“x2-3x+2>0”的充分不必要条件,故选A.]4.有下列四个命题:①若“xy=1,则x,y互为倒数”的逆命题;②“面积相等的三角形是全等三角形”的否命题;③“若m≤1,则x2-2x+m=0有实数解”的逆否命题;④“若A∩B=B,则A⊆B”的逆否命题.其中真命题为()【导学号:00090006】A.①②B.②③C.①④D.①②③D[①的逆命题:“若x,y互为倒数,则xy=1”是真命题;②的否命题:“面积不相等的三角形不是全等三角形”是真命题;③的逆否命题:“若x 2-2x +m =0没有实数解,则m >1”,由Δ=4-4m <0得m >1,故③是真命题;命题④是假命题,所以它的逆否命题也是假命题.故选D.]5.m =-1是直线mx +(2m -1)y +1=0和直线3x +my +9=0垂直的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 A [由直线mx +(2m -1)y +1=0与3x +my +9=0垂直可知3m +m (2m -1)=0,∴m =0或m =-1,∴m =-1是两直线垂直的充分不必要条件.]6.设p :1<x <2,q :2x >1,则p 是q 成立的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 A [由2x >1,得x >0,所以p ⇒q ,但qp ,所以p 是q 的充分不必要条件.] 7.若x >2m 2-3是-1<x <4的必要不充分条件,则实数m 的取值范围是()A .[-3,3]B .(-∞,-3]∪[3,+∞)C .(-∞,-1]∪[1,+∞)D .[-1,1]D [由题意知{}x |-1<x <4x |x >2m 2-3} 所以2m 2-3≤-1,解得-1≤m ≤1,故选D.]二、填空题8.已知a ,b ,c 都是实数,则在命题“若a >b ,则ac 2>bc 2”与它的逆命题、否命题、逆否命题这四个命题中,真命题的个数是________.2[由a >bD ac 2>bc 2,但ac 2>bc 2⇒a >b .所以原命题是假命题,它的逆命题是真命题.从而否命题是真命题,逆否命题是假命题.]9.“m <14”是“一元二次方程x 2+x +m =0有实数解”的________条件. 充分不必要[x 2+x +m =0有实数解等价于Δ=1-4m ≥0,即m ≤14,因为m <14⇒m ≤14,反之不成立. 故“m <14”是“一元二次方程x 2+x +m =0有实数解”的充分不必要条件.] 10.已知集合A ={x |y =lg(4-x )},集合B ={x |x <a },若“x ∈A ”是“x ∈B ”的充分不必要条件,则实数a 的取值范围是________.(4,+∞)[A ={x |x <4},由题意知A B ,所以a >4.]B 组能力提升(建议用时:15分钟)1.已知α,β均为第一象限的角,那么α>β是sin α>sin β的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件D [如α=13π6,β=π3都是第一象限角,且α>β,但sin α=12<sin β=32,所以α>β不是sin α>sin β的充分条件;反之,若sin α>sin β,也得不出α>β,如sin π3>sin 13π6,但π3<13π6,所以α>β是sin α>sin β的既不充分也不必要条件,故选D.]2.已知条件p :x 2-2ax +a 2-1>0,条件q :x >2,且q 是p 的充分不必要条件,则a 的取值范围是()【导学号:00090007】A .a ≥1B .a ≤1C .a ≥-3D .a ≤-3 B [条件p :x >a +1或x <a -1,条件q :x >2,又q 是p 的充分不必要条件,故q ⇒p ,pDq ,所以a +1≤2,即a ≤1.]3.有下列几个命题:①“若a >b ,则a 2>b 2”的否命题;②“若x +y =0,则x ,y 互为相反数”的逆命题;③“若x 2<4,则-2<x <2”的逆否命题.其中真命题的序号是________.②③[①原命题的否命题为“若a ≤b ,则a 2≤b 2”错误.②原命题的逆命题为:“若x ,y 互为相反数,则x +y =0”正确.③原命题的逆否命题为“若x ≥2或x ≤-2,则x 2≥4”正确.]4.已知不等式|x -m |<1成立的充分不必要条件是13<x <12,则实数m 的取值范围是________. ⎣⎢⎡⎦⎥⎤-12,43[由|x -m |<1得-1+m <x <1+m , 由题意知⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ 13<x <12x |-1+m <x <1+m },所以⎩⎪⎨⎪⎧ -1+m ≤13,1+m ≥12,解得-12≤m ≤43, 所以实数m 的取值范围是⎣⎢⎡⎦⎥⎤-12,43.]。
2019高三数学文北师大版一轮教师用书:第1章 第2节 命

第二节命题及其关系、充分条件与必要条件[考纲传真] 1.理解命题的概念;了解“若p,则q”形式的命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系.2.理解必要条件、充分条件与充要条件的意义.(对应学生用书第3页)[基础知识填充]1.命题可以判断真假,用文字或符号表述的语句叫做命题,其中判断为真的叫做真命题,判断为假的叫做假命题.2.四种命题及其相互关系(1)四种命题间的相互关系图1-2-1(2)四种命题的真假关系①两个命题互为逆否命题,它们有相同的真假性;②两个命题互为逆命题或互为否命题,它们的真假性没有关系.3.充分条件与必要条件(1)如果p⇒q,则p是q的充分条件,q是p的必要条件.(2)如果p⇔q,那么p与q互为充要条件.(3)如果pD q,且qD p,则p是q的既不充分也不必要条件.[知识拓展]1.充分条件、必要条件的两个结论(1)若p是q的充分不必要条件,q是r的充分不必要条件,则p是r的充分不必要条件;(2)若p是q的充分不必要条件,则綈q是綈p的充分不必要条件.2.充分条件、必要条件与集合的关系A BB A1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)“x2+2x-3<0”是命题.()(2)命题“若p,则q”的否命题是“若p,则綈q”.()(3)当q是p的必要条件时,p是q的充分条件.()(4)“若p不成立,则q不成立”等价于“若q成立,则p成立”.()[解析](1)错误.该语句不能判断真假,故该说法是错误的.(2)错误.否命题既否定条件,又否定结论.(3)正确.q是p的必要条件说明p⇒q,所以p是q的充分条件.(4)正确.原命题与逆否命题是等价命题.[答案](1)×(2)×(3)√(4)√2.(教材改编)命题“若α=π4,则tan α=1”的逆否命题是()A.若α≠π4,则tan α≠1B.若α=π4,则tan α≠1C.若tan α≠1,则α≠π4D.若tan α≠1,则α=π4C[“若p,则q”的逆否命题是“若綈q,则綈p”,显然綈q:tan α≠1,綈p:α≠π4,所以该命题的逆否命题是“若tan α≠1,则α≠π4”.]3.已知集合A={1,a},B={1,2,3},则“a=3”是“A⊆B”的() A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件A[a=3时,A={1,3},显然A⊆B.但A⊆B时,a=2或3.∴“a=3”是“A⊆B”的充分不必要条件.]4.命题“若a>-3,则a>-6”以及它的逆命题、否命题、逆否命题中假命题的个数为() 【导学号:00090004】A.1B.2C.3D.4B[原命题正确,从而其逆否命题也正确;其逆命题为“若a>-6,则a>-3”是假命题,从而其否命题也是假命题.因此4个命题中有2个假命题.]5.(2017·天津高考)设x∈R,则“2-x≥0”是“|x-1|≤1”的() A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件B[∵2-x≥0,∴x≤2.∵|x-1|≤1,∴0≤x≤2.∵当x≤2时不一定有x≥0,当0≤x≤2时一定有x≤2,∴“2-x≥0”是“|x-1|≤1”的必要而不充分条件.故选B.](对应学生用书第3页)(1)()A.“若x=4,则x2-3x-4=0”为真命题B.“若x≠4,则x2-3x-4≠0”为真命题C.“若x≠4,则x2-3x-4≠0”为假命题D.“若x=4,则x2-3x-4=0”为假命题(2)原命题为“若z1,z2互为共轭复数,则|z1|=|z2|”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是()A.真,假,真B.假,假,真C.真,真,假D.假,假,假(1)C(2)B[(1)根据逆否命题的定义可以排除A,D,由x2-3x-4=0,得x=4或-1,所以原命题为假命题,所以其逆否命题也是假命题.(2)由共轭复数的性质,原命题为真命题,因此其逆否命题也为真命题.当z1=1+2i,z2=2+i时,显然|z1|=|z2|,但z1与z2不共轭,所以逆命题为假命题,从而它的否命题亦为假命题.][规律方法] 1.已知原命题写出该命题的其他命题时,先要分清命题的条件与结论.特别注意的是,如果命题不是“若p,则q”形式的命题,需先改写为“若p,则q”的形式.2.给出一个命题,要判断它是真命题,需经过严格的推理证明;而要说明它是假命题,只需举一反例即可.3.由于原命题与其逆否命题的真假性相同,所以有时可以利用这种等价性间接地证明命题的真假.[变式训练1](1)某食品的广告词为“幸福的人们都拥有”,这句话的等价命题是()A.不拥有的人们会幸福B.幸福的人们不都拥有C.拥有的人们不幸福D.不拥有的人们不幸福(2)原命题为“若a n+a n+12<a n,n∈N*,则{an}为递减数列”,关于其逆命题、否命题、逆否命题真假性的判断依次如下,正确的是() A.真,真,真B.假,假,真C.真,真,假D.假,假,假(1)D(2)A[(1)等价命题即为逆否命题,故选D.(2)由a n+a n+12<a n,得a n+a n+1<2a n,即a n+1<a n.所以当a n+a n+12<a n时,必有a n+1<a n,则{a n}是递减数列.反之,若{a n}是递减数列,必有a n+1<a n,从而有a n+a n+12<a n.所以原命题及其逆命题均为真命题,从而其否命题及其逆否命题也均是真命题.]m=λn”是“m·n<0”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件(2)设x∈R,则“1<x<2”是“|x-2|<1”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件(1)A(2)A[(1)法一:由题意知|m|≠0,|n|≠0.设m与n的夹角为θ.若存在负数λ,使得m=λn,则m与n反向共线,θ=180°,∴m·n=|m||n|cos θ=-|m||n|<0.当90°<θ<180°时,m·n<0,此时不存在负数λ,使得m=λn.故“存在负数λ,使得m=λn”是“m·n<0”的充分而不必要条件.故选A.法二:∵m =λn ,∴m ·n =λn ·n =λ|n |2.∴当λ<0,n ≠0时,m ·n <0. 反之,由m ·n =|m ||n |cos 〈m ,n 〉<0⇔cos 〈m ,n 〉<0⇔〈m ,n 〉∈⎝ ⎛⎦⎥⎤π2,π,当〈m ,n 〉∈⎝ ⎛⎭⎪⎫π2,π时,m ,n 不共线.故“存在负数λ,使得m =λn ”是“m ·n <0”的充分而不必要条件. 故选A .(2)|x -2|<1⇔1<x <3.由于{x |1<x <2}是{x |1<x <3}的真子集,所以“1<x <2”是“|x -2|<1”的充分不必要条件.] [规律方法] 充分条件、必要条件的三种判断方法(1)定义法:根据p ⇒q ,q ⇒p 进行判断,适用于定义、定理判断性问题.(2)集合法:根据p ,q 成立的对象的集合之间的包含关系进行判断,多适用于命题中涉及字母的范围的推断问题.(3)等价转化法:根据一个命题与其逆否命题的等价性,把判断的命题转化为其逆否命题进行判断,适用于条件和结论带有否定性词语的命题.[变式训练2] (1)(2018·九江十校联考)已知函数f (x )=⎩⎨⎧e x,x ≥-1,ln (-x ),x <-1,则“x=0”是“f (x )=1”的( )【导学号:00090005】A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件(2)(2018·东北三省四市联考)设a ,b 均为实数,则“a >|b |”是“a 3>b 3”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件(1)B (2)A [(1)若x =0,则f (x )=1,若f (x )=1,则e x =1或ln(-x )=1,解得x =0或x =-e. 故“x =0”是“f (x )=1”的充分不必要条件,故选B .(2)a >|b |能推出a >b ,进而得a 3>b 3;当a 3>b 3时,有a >b ,但若b <a <0,则a >|b |不成立,所以“a >|b |”是“a 3>b 3”的充分不必要条件,故选A .]已知}.若x ∈P是x ∈S 的必要条件,求m 的取值范围.[解] 由x 2-8x -20≤0得-2≤x ≤10,∴P ={x |-2≤x ≤10}.∵x ∈P 是x ∈S 的必要条件,则S ⊆P ,∴⎩⎨⎧1-m ≥-2,1+m ≤10,1-m ≤1+m ,∴0≤m ≤3.综上,可知0≤m ≤3时,x ∈P 是x ∈S 的必要条件.[母题探究1] 本例条件不变,问是否存在实数m ,使x ∈P 是x ∈S 的充要条件. [解] 由例题知P ={x |-2≤x ≤10}.若x ∈P 是x ∈S 的充要条件,则P =S ,∴⎩⎨⎧1-m =-2,1+m =10,∴⎩⎨⎧m =3,m =9,这样的m 不存在.[母题探究2] 本例条件不变,若綈P 是綈S 的必要不充分条件,求实数m 的取值范围.[解] 由例题知P ={x |-2≤x ≤10}.∵綈P 是綈S 的必要不充分条件, ∴P 是S 的充分不必要条件, ∴P ⇒S 且SDP ,∴[-2,10][1-m,1+m ],∴⎩⎨⎧ 1-m ≤-2,1+m >10或⎩⎨⎧1-m <-2,1+m ≥10,∴m ≥9,即m 的取值范围是[9,+∞).[规律方法] 充分条件、必要条件的应用,一般表现在参数问题的求解上.解题时需注意:(1)把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式(组)求解.(2)要注意区间端点值的检验.[变式训练3] (1)(2017·长沙模拟)已知命题p :a ≤x ≤a +1,命题q :x 2-4x <0,若p 是q 的充分不必要条件,则a 的取值范围是________.(2)方程ax 2+2x +1=0(a ∈R ,a 为常数)的解集只有一个负实根的充要条件是________.(1)(0,3) (2)a ≤0或a =1 [(1)令M ={x |a ≤x ≤a +1},N ={x |x 2-4x <0}={x |0<x <4}.∵p 是q 的充分不必要条件,∴M N , ∴⎩⎨⎧a >0,a +1<4,解得0<a <3.(2)当a =0时,原方程为2x +1=0,∴原方程有一个负实根x =-12.当a ≠0时,ax 2+2x +1=0只有一个负实根.∴方程有一个正根和一个负根或方程有两个相等的负根.当方程有一正一负根时,则x 1x 2<0,∴1a <0,且Δ=4-4a >0,解得a <0;当方程有两个相等的负根时,Δ=4-4a =0,a =1,此时方程的根为-1,符合题意. 综上,方程的解集只有一个负实根的充要条件是a ≤0或a =1.]。
2019年高考数学一轮复习课时分层训练平行关系理北师大版

课时分层训练(四十二) 平行关系A 组 基础达标一、选择题1.(2017·合肥模拟)在空间四边形ABCD 中,E ,F 分别是AB 和BC 上的点,若AE ∶EB =CF ∶FB =1∶2,则对角线AC 和平面DEF 的位置关系是( ) A .平行 B .相交 C .在平面内D .不能确定A [如图,由AE EB =CFFB 得AC ∥EF .又因为EF 平面DEF ,AC ⊆/平面DEF ,所以AC ∥平面DEF .]2.(2017·湖南长沙二模)已知m ,n 是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中正确的是( ) A .m ∥α,n ∥α,则m ∥n B .m ∥n ,m ∥α,则n ∥α C .m ⊥α,m ⊥β,则α∥βD .α⊥γ,β⊥γ,则α∥βC [对于A ,平行于同一平面的两条直线可能相交,可能平行,也可能异面,故A 不正确;对于B ,m ∥n ,m ∥α,则n ∥α或n α,故B 不正确; 对于C ,利用垂直于同一直线的两个平面平行,可知C 正确;对于D ,因为垂直于同一平面的两个平面的位置关系是相交或平行,故D 不正确.故选C.]3.(2017·豫西五校4月联考)已知m ,n ,l 1,l 2表示不同直线,α、β表示不同平面,若m α,n α,l 1β,l 2β,l 1∩l 2=M ,则α∥β的一个充分条件是( )A .m ∥β且l 1∥αB .m ∥β且n ∥βC .m ∥β且n ∥l 2D .m ∥l 1且n ∥l 2D [对于选项A ,当m ∥β且l 1∥α时,α,β可能平行也可能相交,故A 不是α∥β的充分条件;对于选项B ,当m ∥β且n ∥β时,若m ∥n ,则α,β可能平行也可能相交,故B 不是α∥β的充分条件;对于选项C ,当m ∥β且n ∥l 2时,α,β可能平行也可能相交,故C 不是α∥β的充分条件;对于选项D ,当m ∥l 1,n ∥l 2时,由线面平行的判定定理可得l 1∥α,l 2∥α,又l 1∩l 2=M ,由面面平行的判定定理可以得到α∥β,但α∥β时,m ∥l 1且n ∥l 2不一定成立,故D 是α∥β的一个充分条件.故选D.]4.(2017·山东济南模拟)如图735所示的三棱柱ABC A 1B 1C 1中,过A 1B 1的平面与平面ABC交于DE,则DE与AB的位置关系是( )【导学号:79140231】图735A.异面B.平行C.相交D.以上均有可能B[在三棱柱ABCA1B1C1中,AB∥A1B1.∵AB平面ABC,A1B1⊆/平面ABC,∴A1B1∥平面ABC.∵过A1B1的平面与平面ABC交于DE,∴DE∥A1B1,∴DE∥AB.]5.(2018·合肥二检)若平面α截三棱锥所得截面为平行四边形,则该三棱锥与平面α平行的棱有( )A.0条B.1条C.2条D.0条或2条C[如图设平面α截三棱锥所得的四边形EFGH是平行四边形,则EF∥GH,EF⊆/平面BCD,GH 平面BCD,所以EF∥平面BCD,又EF平面ACD,平面ACD∩平面BCD=CD,则EF∥CD,EF 平面EFGH,CD⊆/平面EFGH,则CD∥平面EFGH,同理AB∥平面EFGH,所以该三棱锥与平面α平行的棱有2条,故选C.]二、填空题6.如图736,α∥β,△PAB所在的平面与α,β分别交于CD,AB,若PC=2,CA=3,CD=1,则AB=________.图73652[∵α∥β,∴CD ∥AB , 则PC PA =CD AB ,∴AB =PA ×CD PC =5×12=52.] 7.如图737所示,正方体ABCD A 1B 1C 1D 1中,AB =2,点E 为AD 的中点,点F 在CD 上.若EF ∥平面AB 1C ,则线段EF 的长度等于________.图7372 [在正方体ABCD A 1B 1C 1D 1中,AB =2, ∴AC =2 2.又E 为AD 中点,EF ∥平面AB 1C ,EF 平面ADC , 平面ADC ∩平面AB 1C =AC , ∴EF ∥AC ,∴F 为DC 中点, ∴EF =12AC = 2.]8.如图738,在四面体ABCD 中,M ,N 分别是△ACD ,△BCD 的重心,则四面体的四个面中与MN 平行的是________.图738平面ABC ,平面ABD [连接AM 并延长交CD 于E ,则E 为CD 的中点.由于N 为△BCD 的重心, 所以B ,N ,E 三点共线,且EM MA =EN NB =12,所以MN ∥AB . 于是MN ∥平面ABD 且MN ∥平面ABC .] 三、解答题9.一个正方体的平面展开图及该正方体的直观图的示意图如图739所示.(1)请将字母F ,G ,H 标记在正方体相应的顶点处(不需说明理由); (2)判断平面BEG 与平面ACH 的位置关系,并证明你的结论.【导学号:79140232】图739[解] (1)点F ,G ,H 的位置如图所示.(2)平面BEG ∥平面ACH ,证明如下: 因为ABCD EFGH 为正方体, 所以BC ∥FG ,BC =FG .又FG ∥EH ,FG =EH ,所以BC ∥EH ,BC =EH , 于是四边形BCHE 为平行四边形,所以BE ∥CH . 又CH 平面ACH ,BE ⊆/平面ACH , 所以BE ∥平面ACH . 同理BG ∥平面ACH .又BE ∩BG =B ,所以平面BEG ∥平面ACH .10.(2017·石家庄质检(一))如图7310,四棱锥P ABCD 中,PA ⊥底面ABCD ,底面ABCD 为梯形,AD ∥BC ,CD ⊥BC ,AD =2,AB =BC =3,PA =4,M 为AD 的中点,N 为PC 上一点,且PC =3PN .图7310(1)求证:MN ∥平面PAB ; (2)求点M 到平面PAN 的距离.[解] (1)在平面PBC 内作NH ∥BC 交PB 于点H ,连接AH (图略),在△PBC 中,NH ∥BC ,且NH =13BC =1,AM =12AD =1.又AD ∥BC ,∴NH ∥AM 且NH =AM ,∴四边形AMNH 为平行四边形, ∴MN ∥AH ,又AH 平面PAB ,MN ⊆/平面PAB , ∴MN ∥平面PAB .(2)连接AC ,MC ,PM (图略),平面PAN 即为平面PAC ,设点M 到平面PAC 的距离为h .由题意可得CD =22,AC =23,∴S △PAC =12PA ·AC =43,S △AMC =12AM ·CD =2,由V M PAC =V P AMC ,得13S △PAC ·h =13S △AMC ·PA , 即43h =2×4,∴h =63, ∴点M 到平面PAN 的距离为63.] B 组 能力提升11.如图7311,在四面体ABCD中,截面PQMN是正方形,则在下列结论中,错误的是( )图7311A.AC⊥BDB.AC∥截面PQMNC.AC=BDD.异面直线PM与BD所成的角为45°C[因为截面PQMN是正方形,所以MN∥PQ,则MN∥平面ABC,由线面平行的性质知MN∥AC,则AC∥截面PQMN,同理可得MQ∥BD,又MN⊥QM,则AC⊥BD,故A,B正确.又因为BD∥MQ,所以异面直线PM与BD所成的角等于PM与QM所成的角,即为45°,故D正确.]12.如图7312所示,棱柱ABCA1B1C1的侧面BCC1B1是菱形,设D是A1C1上的点且A1B∥平面B1CD,则A1D∶DC1的值为________.【导学号:79140233】图73121 [设BC1∩B1C=O,连接OD.∵A1B∥平面B1CD且平面A1BC1∩平面B1CD=OD,∴A1B∥OD.∵四边形BCC1B1是菱形,∴O 为BC 1的中点, ∴D 为A 1C 1的中点, 则A 1D ∶DC 1=1.]13.如图7313,四棱锥P ABCD 中,AB ∥CD ,AB =2CD ,E 为PB 的中点.图7313(1)求证:CE ∥平面PAD ;(2)在线段AB 上是否存在一点F ,使得平面PAD ∥平面CEF ?若存在,证明你的结论,若不存在,请说明理由.[解] (1)证明:取PA 的中点H ,连接EH ,DH ,因为E 为PB 的中点,所以EH ∥AB ,EH =12AB ,又AB ∥CD ,CD =12AB ,所以EH ∥CD ,EH =CD ,因此四边形DCEH 是平行四边形, 所以CE ∥DH , 又DH平面PAD ,CE ⊆/平面PAD ,因此CE ∥平面PAD .(2)存在点F 为AB 的中点,使平面PAD ∥平面CEF , 证明如下:取AB 的中点F ,连接CF ,EF , 所以AF =12AB ,又CD =12AB ,所以AF =CD ,又AF ∥CD ,所以四边形AECD 为平行四边形,因此CF ∥AD , 又CF ⊆/平面PAD ,所以CF ∥平面PAD , 由(1)可知CE ∥平面PAD ,又CE ∩CF =C ,故平面CEF ∥平面PAD ,故存在AB 的中点F 满足要求.。
2019年高考数学一轮复习学案北师大版文科课时分层训练2命题及其关系、充分条件与必要条件 文

课时分层训练(二) 命题及其关系、充分条件与必要条件A组基础达标(建议用时:30分钟)一、选择题1.(2018·聊城模拟)命题“若a2+b2=0,则a=0且b=0”的逆否命题是( ) A.若a2+b2≠0,则a≠0且b≠0B.若a2+b2≠0,则a≠0或b≠0C.若a=0且b=0,则a2+b2≠0D.若a≠0或b≠0,则a2+b2≠0D[“若a2+b2=0,则a=0且b=0”的逆否命题是“若a≠0或b≠0,则a2+b2≠0”,故选D.]2.(2017·杭州调研)设α,β是两个不同的平面,m是直线且mα.则“m∥β”是“α∥β”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件B[mα,m∥βDα∥β,但mα,α∥β⇒m∥β,∴“m∥β”是“α∥β”的必要不充分条件.]3.(2018·济南模拟)已知x∈R,则“x>2”是“x2-3x+2>0”成立的( ) A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件A[由x2-3x+2>0得x<1或x>2,所以“x>2”是“x2-3x+2>0”的充分不必要条件,故选A.]4.有下列四个命题:①若“xy=1,则x,y互为倒数”的逆命题;②“面积相等的三角形是全等三角形”的否命题;③“若m≤1,则x2-2x+m=0有实数解”的逆否命题;④“若A∩B=B,则A⊆B”的逆否命题.其中真命题为( ) 【导学号:00090006】A.①②B.②③C.①④D.①②③D [①的逆命题:“若x ,y 互为倒数,则xy =1”是真命题;②的否命题:“面积不相等的三角形不是全等三角形”是真命题;③的逆否命题:“若x 2-2x +m =0没有实数解,则m >1”,由Δ=4-4m <0得m >1,故③是真命题;命题④是假命题,所以它的逆否命题也是假命题.故选D.]5.(2017·南昌调研)m =-1是直线mx +(2m -1)y +1=0和直线3x +my +9=0垂直的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 A [由直线mx +(2m -1)y +1=0与3x +my +9=0垂直可知3m +m (2m -1)=0,∴m =0或m =-1,∴m =-1是两直线垂直的充分不必要条件.]6.设p :1<x <2,q :2x >1,则p 是q 成立的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 A [由2x >1,得x >0,所以p ⇒q ,但qp ,所以p 是q 的充分不必要条件.] 7.(2018·武汉模拟)若x >2m 2-3是-1<x <4的必要不充分条件,则实数m 的取值范围是( )A .[-3,3]B .(-∞,-3]∪[3,+∞)C .(-∞,-1]∪[1,+∞)D .[-1,1]D [由题意知{}x |-1<x <4x |x >2m 2-3} 所以2m 2-3≤-1,解得-1≤m ≤1,故选D.]二、填空题8.(2018·肇庆模拟)已知a ,b ,c 都是实数,则在命题“若a >b ,则ac 2>bc 2”与它的逆命题、否命题、逆否命题这四个命题中,真命题的个数是________.2 [由a >bD ac 2>bc 2,但ac 2>bc 2⇒a >b .所以原命题是假命题,它的逆命题是真命题.从而否命题是真命题,逆否命题是假命题.]9.“m <14”是“一元二次方程x 2+x +m =0有实数解”的________条件. 充分不必要 [x 2+x +m =0有实数解等价于Δ=1-4m ≥0,即m ≤14,因为m <14⇒m ≤14,反之不成立. 故“m <14”是“一元二次方程x 2+x +m =0有实数解”的充分不必要条件.]10.已知集合A ={x |y =lg(4-x )},集合B ={x |x <a },若“x ∈A ”是“x ∈B ”的充分不必要条件,则实数a 的取值范围是________.(4,+∞) [A ={x |x <4},由题意知A B ,所以a >4.]B 组 能力提升(建议用时:15分钟)1.(2018·南昌模拟)已知α,β均为第一象限的角,那么α>β是sin α>sin β的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件D [如α=13π6,β=π3都是第一象限角,且α>β,但sin α=12<sin β=32,所以α>β不是sin α>sin β的充分条件;反之,若sin α>sin β,也得不出α>β,如sin π3>sin 13π6,但π3<13π6,所以α>β是sin α>sin β的既不充分也不必要条件,故选D.]2.已知条件p :x 2-2ax +a 2-1>0,条件q :x >2,且q 是p 的充分不必要条件,则a 的取值范围是( )【导学号:00090007】A .a ≥1B .a ≤1C .a ≥-3D .a ≤-3 B [条件p :x >a +1或x <a -1,条件q :x >2,又q 是p 的充分不必要条件,故q ⇒p ,pDq ,所以a +1≤2,即a ≤1.]3.有下列几个命题:①“若a >b ,则a 2>b 2”的否命题;②“若x +y =0,则x ,y 互为相反数”的逆命题;③“若x 2<4,则-2<x <2”的逆否命题.其中真命题的序号是________.②③ [①原命题的否命题为“若a ≤b ,则a 2≤b 2”错误.②原命题的逆命题为:“若x ,y 互为相反数,则x +y =0”正确.③原命题的逆否命题为“若x ≥2或x ≤-2,则x 2≥4”正确.]4.已知不等式|x -m |<1成立的充分不必要条件是13<x <12,则实数m 的取值范围是________.⎣⎢⎡⎦⎥⎤-12,43 [由|x -m |<1得-1+m <x <1+m , 由题意知⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ 13<x <12x |-1+m <x <1+m },所以⎩⎪⎨⎪⎧ -1+m ≤13,1+m ≥12,解得-12≤m ≤43, 所以实数m 的取值范围是⎣⎢⎡⎦⎥⎤-12,43.]。
高考第一轮复习第二讲命题及其关系、充分条件与必要条件

第二节 命题及其关系、充分条件与必要条件
第一章 集合与常用逻辑用语
1.命题
用 语言、符号 、式子 叫做命题,其中判断为真 的语句叫做假命题.
表达的,可以判断语真句假的 的陈述句叫判做断真为命假题,
第一章 集合与常用逻辑用语
2.四种命题及其关系 (1)四种命题
命题 原命题 逆命题 否命题 逆否命题
第一章 集合与常用逻辑用语
1.下列语句是命题的是( )
①求证x是无理数;
②x2+4x+4≥0;
③你是高一的学生吗?
④一个正数不是素数就是合数;
⑤若x∈R,则x2+4x+7>0.
A.①②③
B.②③④
C.②④⑤
D.③④⑤
【答案】 C
第一章 集合与常用逻辑用语
2.命题“若x2≥1,则x≥1或x≤-1”的逆否命题是( ) A.若x2<1,则-1<x<1 B.若x≥1或x≤-1,则x2≥1 C.若-1≤x≤1,则x2≤1 D.若-1<x<1则x2<1 【答案】 D
表述形式 若p则q 若q则p
若綈p则綈q 若綈q则綈p
第一章 集合与常用逻辑用语 (2)四种命题间的相互关系
(3)四种命题的真假关系 ①两个命题互为逆否命题,它们有相同 的真假性; ②两个命题互为逆命题或互为否命题,它们的真假 性 不确定 .
第一章 集合与常用逻辑用语
3.充分条件与必要条件 (1)“若p,则q”为真命题,记p⇒q,则 p是q成立的充分 条件, q是p成立 的必要条件. (2)如果既有p⇒q,又有q⇒p,记作:p⇔q, 则 p是q成立 的充要条件,q也是p成立的 充要条件 .
第一章 集合与常用逻辑用语
(2)逆命题:若两个三角形全等,则这两个三角形等底等 高.真命题.
高考一轮复习第1章集合与常用逻辑用语第2讲命题及其关系充分条件与必要条件
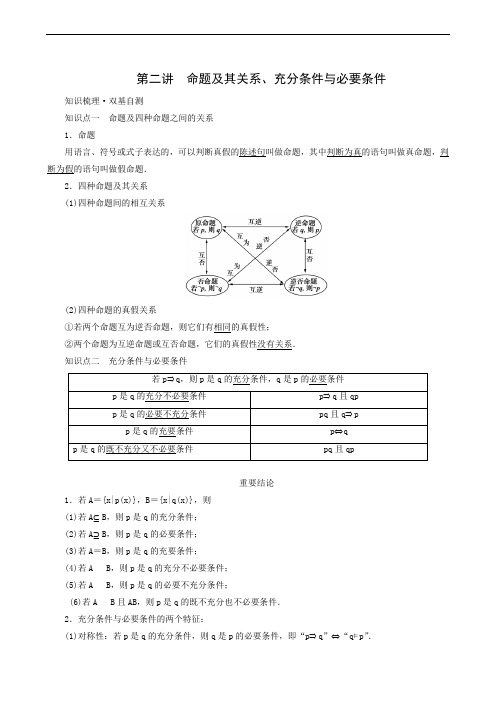
第二讲命题及其关系、充分条件与必要条件知识梳理·双基自测知识点一命题及四种命题之间的关系1.命题用语言、符号或式子表达的,可以判断真假的陈述句叫做命题,其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.2.四种命题及其关系(1)四种命题间的相互关系(2)四种命题的真假关系①若两个命题互为逆否命题,则它们有相同的真假性;②两个命题为互逆命题或互否命题,它们的真假性没有关系.知识点二充分条件与必要条件若p⇒q,则p是q的充分条件,q是p的必要条件p是q的充分不必要条件p⇒q且qpp是q的必要不充分条件pq且q⇒pp是q的充要条件p⇔qp是q的既不充分又不必要条件pq且qp重要结论1.若A={x|p(x)},B={x|q(x)},则(1)若A⊆B,则p是q的充分条件;(2)若A⊇B,则p是q的必要条件;(3)若A=B,则p是q的充要条件;(4)若A B,则p是q的充分不必要条件;(5)若A B,则p是q的必要不充分条件;(6)若A B且AB,则p是q的既不充分也不必要条件.2.充分条件与必要条件的两个特征:(1)对称性:若p是q的充分条件,则q是p的必要条件,即“p⇒q”⇔“q⇐p”.(2)传递性:若p 是q 的充分(必要)条件,q 是r 的充分(必要)条件,则p 是r 的充分(必要)条件,即“p ⇒q 且q ⇒r ”⇒“p ⇒r ”(“p ⇐q 且q ⇐r ”⇒“p ⇐r ”).注意:不能将“若p ,则q”与“p ⇒q ”混为一谈,只有“若p ,则q”为真命题时,才有“p ⇒q ”,即“p ⇒q ”⇔“若p ,则q”为真命题.双基自测题组一 走出误区1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)语句x 2-3x +2=0是命题.( × )(2)命题“三角形的内角和是180°”的否命题是“三角形的内角和不是180°”.( × ) (3)已知集合A ,B ,则A∪B=A∩B 的充要条件是A =B .( √ ) (4)“α=β”是“tan α=tan β”的充分不必要条件.( × ) (5)“若p 不成立,则q 不成立”等价于“若q 成立,则p 成立”.( √ )[解析] (4)当α=β=π2时,tan α、tan β都无意义.因此不能推出tan α=tan β,当tan α=tan β时,α=β+k π,k∈Z,不一定α=β,因此是既不充分也不必要条件.题组二 走进教材2.(选修2-1P 8T3改编)下列命题是真命题的是( A ) A .矩形的对角线相等 B .若a>b ,c>d ,则ac>bd C .若整数a 是素数,则a 是奇数 D .命题“若x 2>0,则x>1”的逆否命题3.(选修2-1P 10T4改编)x 2-3x +2≠0是x≠1的充分不必要条件. [解析] x =1是x 2-3x +2=0的充分不必要条件. 题组三 走向高考4.(2020·天津,2,5分)设a∈R,则“a>1”是“a 2>a ”的( A ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件[解析] 易知a>1⇒a 2>a ,而a 2>a ⇒a<0或a>1,所以“a>1”是“a 2>a ”的充分不必要条件. 5.(2015·山东,5分)设m∈R,命题“若m>0,则方程x 2+x -m =0有实根”的逆否命题是( D ) A .若方程x 2+x -m =0有实根,则m>0 B .若方程x 2+x -m =0有实根,则m≤0 C .若方程x 2+x -m =0没有实根,则m>0 D .若方程x 2+x -m =0没有实根,则m≤0 [解析] 由原命题和逆否命题的关系可知D 正确.6.(2018·北京,5分)能说明“若f(x)>f(0)对任意的x∈(0,2]都成立,则f(x)在[0,2]上是增函数”为假命题的一个函数是f(x)=sin_x(答案不唯一).[解析]这是一道开放性试题,答案不唯一,只要满足f(x)>f(0)对任意的x∈(0,2]都成立,且函数f(x)在[0,2]上不是增函数即可.如f(x)=sin x,答案不唯一.考点突破·互动探究KAO DIAN TU PO HU DONG TAN JIU考点一命题及其关系——自主练透例1 (1)(2021·新高考八省联考)关于x的方程x2+ax+b=0,有下列四个命题:甲:x=1是该方程的根;乙:x=3是该方程的根;丙:该方程两根之和为2;丁:该方程两根异号.如果只有一个假命题,则该命题是( A )A.甲B.乙C.丙D.丁(2)(2021·长春模拟)已知命题α:如果x<3,那么x<5,命题β:如果x≥3,那么x≥5,则命题α是命题β的( A )A.否命题B.逆命题C.逆否命题D.否定形式(3)(多选题)下列命题为真命题的是( CD )A.“若a2<b2,则a<b”的否命题B.“全等三角形面积相等”的逆命题C.“若a>1,则ax2-2ax+a+3>0的解集为R”的逆否命题D.“若3x(x≠0)为有理数,则x为无理数”的逆否命题(4)命题“若a+b=0,则a,b中最多有一个大于零”的否定形式为若a+b=0,则a,b都大于零,否命题为若a+b≠0,则a,b都大于零.[解析](1)若乙、丙、丁正确,显然x1=-1,x2=3,两根异号,x1+x2=2,故甲错,因此选A.(2)命题α:如果x<3,那么x<5,命题β:如果x≥3,那么x≥5,则命题α是命题β的否命题.(3)对于A ,否命题为“若a 2≥b 2,则a≥b”,为假命题;对于B ,逆命题为“面积相等的三角形是全等三角形”,是假命题;对于C ,当a>1时,Δ=-12a<0,原命题正确,从而其逆否命题正确,故C 正确;对于D ,原命题正确,因此该命题的逆否命题也正确,D 正确.故选C 、D .(4)否定形式:若a +b =0,则a ,b 都大于零.否命题:若a +b ≠0,则a ,b 都大于零. 名师点拨 MING SHI DIAN BO(1)由原命题写出其他三种命题,关键要分清原命题的条件和结论,如果命题不是“若p ,则q”的形式,应先改写成“若p ,则q”的形式;如果命题有大前提,写其他三种命题时需保留大前提不变.(2)判断一个命题为真命题,要给出严格的推理证明;判断一个命题为假命题,只需举出反例. (3)根据“原命题与逆否命题同真同假,逆命题与否命题同真同假”这一性质,当一个命题直接判断不易进行时,可转化为判断其等价命题的真假.考点二 充分必要条件考向1 充分条件与必要条件的判断——师生共研 方法1:定义法判断例2 ( 2020·北京,9,4分)已知α,β∈R,则“存在k∈Z 使得α=k π+(-1)kβ”是“sinα=sin β”的( C )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件[解析] (1)充分性:已知存在k∈Z 使得α=k π+(-1)kβ,(ⅰ)若k 为奇数,则k =2n +1,n∈Z,此时α=(2n +1)π-β,n∈Z,sin α=sin(2n π+π-β)=sin(π-β)=sin β;(ⅱ)若k 为偶数,则k =2n ,n∈Z,此时α=2n π+β,n∈Z,sin α=sin(2n π+β)=sin β. 由(ⅰ)(ⅱ)知,充分性成立.(2)必要性:若sin α=sin β成立,则角α与β的终边重合或角α与β的终边关于y 轴对称,即α=β+2m π或α+β=2m π+π,m∈Z,即存在k∈Z 使得α=k π+(-1)kβ,必要性也成立,故选C . 方法2:集合法判断例3 (2020·天津一中高三月考)设x∈R,则“|x-1|<4”是“x -52-x >0”的( B )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件[解析] 解绝对值不等式可得-4<x -1<4,即-3<x<5, 将分式不等式变形可得x -5x -2<0,解得2<x<5,因为(2,5)(-3,5),所以“|x-1|<4”是“x -52-x >0”的必要而不充分条件.方法3 等价转化法判断例4 (1)给定两个条件p ,q ,若¬ p 是q 的必要不充分条件,则p 是¬q 的( A ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件(2)“已知命题p :cos α≠12,命题q :α≠π3”,则命题p 是命题q 的( A )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件[解析] (1)因为¬ p 是q 的必要不充分条件,则q ⇒¬ p ,但¬pq ,其逆否命题为p ⇒¬q ,但¬qp ,所以p 是¬q 的充分不必要条件.(2) ¬p :cos α=12,¬q :α=π3,显然¬q ⇒¬p ,¬p ¬q ,∴¬q 是¬p 的充分不必要条件,从而p 是q 的充分不必要条件,故选A .另解:若cos α≠12,则α≠2kπ±π3(k∈Z),则α也必然不等于π3,故p ⇒q ;若α≠π3,但α=-π3时,依然有cos α=12,故q p.所以p 是q 的充分不必要条件.故选A . 名师点拨 MING SHI DIAN BO有关充要条件的判断常用的方法(1)根据定义判断:①弄清条件p 和结论q 分别是什么;②尝试p ⇒q ,q ⇒p.若p ⇒q ,则p 是q 的充分条件;若q ⇒p ,则p 是q 的必要条件;若p ⇒q ,qp ,则p 是q 的充分不必要条件;若pq ,q ⇒p ,则p 是q 的必要不充分条件;若p ⇒q ,q ⇒p ,则p 是q 的充要条件.(2)利用集合判断 记法 A ={x|p(x)},B ={x|q(x)} 关系 ABBAA =BAB 且BA结论p 是q 的充分不必要条件p 是q 的必要不充分条件p 是q 的充要条件p 是q 的既不充分也不必要条件断¬q 是¬p 的什么条件.〔变式训练1〕(1)指出下列各组中,p 是q 的什么条件(在“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中选出一种作答).①非空集合A ,B 中,p :x∈(A∪B),q :x∈B;②已知x ,y∈R,p :(x -1)2+(y -2)2=0,q :(x -1)(y -2)=0; ③在△ABC 中,p :A =B ,q :sin A =sin B ; ④对于实数x ,y ,p :x +y≠8,q :x≠2或y≠6.(2)(2020·天津部分区期末)设x∈R,则“x 2-2x<0”是“|x-1|<2”的( A ) A .充分不必要条件 B .充要条件C .必要不充分条件D .既不充分也不必要条件[解析] (1)①显然x∈(A∪B)不一定有x∈B,但x∈B 一定有x∈(A∪B),所以p 是q 的必要不充分条件.②条件p :x =1且y =2,条件q :x =1或y =2,所以p ⇒q 但qp ,故p 是q 的充分不必要条件. ③在△ABC 中,A =B ⇒sin A =sin B ;反之,若sin A =sin B ,因为A 与B 不可能互补(三角形三个内角之和为180°),所以只有A =B ,故p 是q 的充要条件.④易知¬p :x +y =8,¬q :x =2且y =6,显然¬q ⇒¬p ,但¬p ¬q ,所以¬q 是¬p 的充分不必要条件,根据原命题和逆否命题的等价性知,p 是q 的充分不必要条件.(2)解不等式x 2-2x<0得0<x<2,解不等式|x -1|<2得-1<x<3,所以“x 2-2x<0”是“|x-1|<2”的充分不必要条件.故选A .考向2 充要条件的应用——多维探究 角度1 充要条件的探究例 5 (多选题)下列函数中,满足“x 1+x 2=0”是“f(x 1)+f(x 2)=0”的充要条件的是( BC )A .f(x)=tan xB .f(x)=3x -3-xC .f(x)=x 3D .f(x)=log 3|x|[解析] 因为f(x)=tan x 是奇函数,所以x 1+x 2=0⇒f(x 1)+f(x 2)=0,但f ⎝ ⎛⎭⎪⎫π4+f ⎝ ⎛⎭⎪⎫3π4=0时,π4+3π4≠0,不符合要求,所以A 不符合题意;因为f(x)=3x -3-x 和f(x)=x 3均为单调递增的奇函数,所以满足“x 1+x 2=0”是“f(x 1)+f(x 2)=0”的充要条件,符合题意;对于选项D ,由f(x)=log 3|x|的图象易知不符合题意,故选BC .注:满足条件的函数是奇函数且单调. 角度2 利用充要条件求参数的值或取值范围例6 已知P ={x|x 2-8x -20≤0},非空集合S ={x|1-m ≤x ≤1+m}.若x ∈P 是x∈S 的必要条件,则m 的取值范围是[0,3].[解析] 由x 2-8x -20≤0,得-2≤x≤10, 所以P ={x|-2≤x≤10},由x∈P 是x∈S 的必要条件,知S ⊆P.则⎩⎪⎨⎪⎧1-m≤1+m ,1-m≥-2,1+m≤10,所以0≤m≤3. 所以当0≤m≤3时,x∈P 是x∈S 的必要条件,即所求m 的取值范围是[0,3].[引申1]若本例将条件“若x∈P 是x∈S 的必要条件”改为“若x∈P 是x∈S 的必要不充分条件”,则m 的取值范围是[0,3].[解析] 解法一:由(1)若x∈P 是x∈S 的必要条件,则0≤m ≤3,当m =0时,S ={1},不充分;当m =3时,S ={x|-2≤x≤4}也不充分,故m 的取值范围为[0,3].解法二:若x∈P 是x∈S 的必要且充分条件,则P =S ,即⎩⎪⎨⎪⎧1-m =-2,1+m =10⇒m 无解,∴m 的取值范围是[0,3].[引申2]若本例将条件“若x∈P 是x∈S 的必要条件”变为“若非P 是非S 的必要不充分条件”,其他条件不变,则m 的取值范围是[9,+∞).[解析] 由(1)知P ={x|-2≤x≤10), ∵非P 是非S 的必要不充分条件, ∴S 是P 的必要不充分条件,∴P ⇒S 且SP. ∴[-2,10] [1-m ,1+m].∴⎩⎪⎨⎪⎧1-m≤-2,1+m>10或⎩⎪⎨⎪⎧1-m<-2,1+m≥10. ∴m ≥9,即m 的取值范围是[9,+∞). 名师点拨 MING SHI DIAN BO充分条件、必要条件的应用,一般表现在参数问题的求解上.解题时需注意:(1)把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式(或不等式组)求解.(2)一定要注意端点值的取舍,处理不当容易出现漏解或增解的现象.(3)注意区别以下两种不同说法:①p 是q 的充分不必要条件,是指p ⇒q 但qp ;②p 的充分不必要条件是q ,是指q ⇒p 但pq.(4)注意下列条件的等价转化:①p 是q 的什么条件等价于¬q 是¬p 的什么条件,②p 是¬q 的什么条件等价于q 是¬ p 的什么条件.〔变式训练2〕(1)(角度1)(多选题)(2020·江西赣州十四县市高三上期中改编)角A ,B 是△ABC 的两个内角.下列四个条件下,“A>B”的充要条件是( ABD )A .sin A>sinB B .cos A<cos BC .tan A>tan BD .cos 2A<cos 2B(2)(角度2)(2021·山东省实验中学高三诊断)已知p :x≥k,q :(x +1)(2-x)<0.如果p 是q 的充分不必要条件,那么实数k 的取值范围是( B )A .[2,+∞)B .(2,+∞)C .[1,+∞)D .(-∞,-1][解析] (1)当A>B 时,根据“大边对大角”可知,a>b ,由于a sin A =bsin B ,所以sin A>sin B ,则A 是“A>B”的充要条件;由于0<B<A<π,余弦函数y =cos x 在区间(0,π)内单调递减,所以cos A<cosB ,则B 是“A>B”的充要条件;当A>B 时,若A 为钝角,B 为锐角,则tan A<0<tan B ,则C 不是“A>B”的充要条件;当cos 2A<cos 2B ,即1-sin 2A<1-sin 2B ,所以sin 2A>sin 2B ,所以D 是“A>B”的充要条件;故选A 、B 、D .(2)由q :(x +1)(2-x)<0,可知q :x<-1或x>2.因为p 是q 的充分不必要条件,所以x≥k ⇒x<-1或x>2,即[k ,+∞)是(-∞,-1)∪(2,+∞)的真子集,故k>2.故选B .名师讲坛·素养提升MING SHI JIANG TAN SU YANG TI SHENG抽象命题间充要条件的判定例7 已知p 是r 的充分不必要条件,q 是r 的充分条件,s 是r 的必要条件,q 是s 的必要条件,现有下列命题:①r 是q 的充要条件;②p 是q 的充分不必要条件;③r 是q 的必要不充分条件;④¬p 是¬s 的必要不充分条件;⑤r 是s 的充分不必要条件,则正确命题的序号是( B )A .①④⑤B .①②④C .②③⑤D .②④⑤[分析] 本题涉及命题较多,关系复杂,因此采用“图解法”.[解析] 由题意得p,显然q ⇒r 且r ⇒s ⇒q ,即q ⇔r ,①正确;p ⇒r ⇒s ⇒q 且qp ,②正确;r⇔q ,③错误;由p ⇒s 知¬ s ⇒¬ p ,但sp ,∴¬ p ¬ s ,④正确;r ⇔s ,⑤错误.故选B .名师点拨 MING SHI DIAN BO命题较多、关系复杂时,画出各命题间关系图求解,简洁直观,一目了然. 〔变式训练3〕若p 是r 的必要不充分条件,q 是r 的充分条件,则p 是q 的必要不充分条件. [解析] 由题意可知q ⇒rp ,∴p 是q 的必要不充分条件.。
2019年高考数学一轮复习 命题及其关系、充分条件与必要条件

解:原命题:若 x=-1,向量 a=(1,-1),b=(1,-1),
a 与 b 共线,所以原命题为真,故逆否命题也为真. 逆命题为:若向量 a=(1,x)与 b=(x+2,x)共线,则 x= -1.当 a 与 b 共线时,x(x+2)=x,解得 x=0 或-1.所以逆命题 为假命题,从而否命题也为假命题. 故真命题的个数为 2.
真假 语言、符号或式子 表达的,
的
陈述句 叫作命题.
(2)真命题:判断为真的语句叫作 真命题 . (3)假命题:判断为假的语句叫作 假命题 .
复习目标
课前预习
高频考点
课时小结
课后练习
2.四种命题的形式 (1)原命题:“若 p,则 q”,其中 p 为命题的条件,q 为命题的结论. (2)逆命题:“若 q,则 p”,即交换原命题的条件和 结论. (3)否命题:“若﹁p,则﹁q”,即同时否定原命题的条 件和结论. (4)逆否命题:“若﹁q,则﹁p”,即交换原命题的条件 和结论后,再同时加以否定.
复习目标
课前预习
高频考点
课时小结
课后练习
3.四种命题的关系
4.四种命题的真假关系 (1)互为逆否的两个命题的真假性
相同 ;
(2)互逆或互否的两个命题的真假性 没有关系 . (3)四种命题的真假成对出现,即原命题与逆否命题的真 假性
相同 ,逆命题与否命题的真假性 相同 .
复习目标
课前预习
高频考点
课时小结
(5)如果 p q, 且 q p, 则 p 是 q 的既不充分也不必要 条件.
复习目标 课前预习 高频考点 课时小结
课后练习
1. 若 p 是 q 的充分不必要条件,则﹁p 是﹁q 的 必要不充分 条件. 2.若 p,q 以集合的形式出现,记条件 p、q 对应的集合分别 为 P,Q,一般地有: 若 P⊆Q,则 p 是 q 的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时分层训练(二) 命题及其关系、充分条件与必要条件
A 组 基础达标
一、选择题
1.命题“若a >b ,则a -1>b -1”的否命题是( )
A .若a >b ,则a -1≤b -1
B .若a >b ,则a -1<b -1
C .若a ≤b ,则a -1≤b -1
D .若a <b ,则a -1<b -1
C [根据否命题的定义可知:命题“若a >b ,则a -1>b -1”的否命题应为“若a ≤b ,则a -1≤b -1”.故选C.] 2.下列命题是真命题的是( )
【导学号:79140009】
A .若1x =1
y
,则x =y
B .若x 2
=1,则x =1 C .若x =y ,则x =y
D .若x <y ,则x 2
<y 2
A [由1x =1y
得x =y ,A 正确;由x 2
=1得x =±1,B 错误;由x =y ,x ,y 不一定
有意义,C 错误;由x <y 不一定能得到x 2<y 2
,如x =-2,y =-1,D 错误,故选A.] 3.设M ={1,2},N ={a 2
},则“a =1”是“N ⊆M ”的( )
A .充分不必要条件
B .必要不充分条件
C .充要条件
D .既不充分也不必要条件 A [若N ⊆M ,则a 2
=1或a 2
=2, 解得a =±1或a =±2,
所以“a =1”是“N ⊆M ”的充分不必要条件,故选A.]
4.已知m ∈R ,“函数y =2x +m -1有零点”是“函数y =log m x 在(0,+∞)上为减函数”的( )
A .充分不必要条件
B .必要不充分条件
C .充要条件
D .既不充分也不必要条件
B [若函数y =2x +m -1有零点,则m -1<0,得m <1;若函数y =log m x 在(0,+∞)上为减函数,则0<m <1,由于(0,1)
(-∞,1),所以“函数y =2x +m -1有零点”
是“函数y =log m x 在(0,+∞)上为减函数”的必要不充分条件.] 5.若x >5是x >a 的充分条件,则实数a 的取值范围为( )
A.a>5 B.a≥5
C.a<5 D.a≤5
D[由x>5是x>a的充分条件知,{x|x>5}⊆{x|x>a}.∴a≤5,故选D.] 6.(2018·青岛质检)已知λ∈R,向量a=(3,λ),b=(λ-1,2),则“λ=3”是“a∥b”
的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
A[由题意得a∥b⇔3×2-λ(λ-1)=0,解得λ=-2或λ=3,所以“λ=3”
是“a∥b”的充分不必要条件,故选A.]
7.(2017·浙江高考)已知等差数列{a n}的公差为d,前n项和为S n,则“d>0”是“S4+S6>2S5”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
C[法一:∵数列{a n}是公差为d的等差数列,
∴S4=4a1+6d,S5=5a1+10d,S6=6a1+15d,
∴S4+S6=10a1+21d,2S5=10a1+20d.
若d>0,则21d>20d,10a1+21d>10a1+20d,
即S4+S6>2S5.
若S4+S6>2S5,则10a1+21d>10a1+20d,即21d>20d,
∴d>0.∴“d>0”是“S4+S6>2S5”的充分必要条件.
故选C.
法二:∵S4+S6>2S5⇔S4+S4+a5+a6>2(S4+a5)⇔a6>a5⇔a5+d>a5⇔d>0,∴“d>0”是“S4+S6>2S5”的充分必要条件.
故选C.]
二、填空题
8.(2017·北京高考)能够说明“设a,b,c是任意实数.若a>b>c,则a+b>c”是假命题的一组整数a,b,c的值依次为________.
-1,-2,-3(答案不唯一) [只要取一组满足条件的整数即可.如-1,-2,-3;
-3,-4,-6;-4,-7,-10等.]
9.函数f(x)=x2+mx+1的图像关于直线x=1对称的充要条件是________.
m =-2 [∵f (x )=x 2+mx +1图像的对称轴为直线x =-m
2
,∴f (x )的图像关于直线x
=1对称⇔-m
2
=1⇔m =-2.]
10.已知集合A ={x |y =lg(4-x )},集合B ={x |x <a },若“x ∈A ”是“x ∈B ”的充分不必要条件,则实数a 的取值范围是________.
【导学号:79140010】
(4,+∞) [A ={x |x <4},由题意知A B ,所以a >4.]
B 组 能力提升
11.“a =1”是“函数f (x )=x 2
-4ax +3在区间[2,+∞)上为增函数”的( )
A .必要不充分条件
B .充分不必要条件
C .充要条件
D .既不充分又不必要条件
B [函数f (x )=x 2
-4ax +3在区间[2,+∞)上为增函数等价于--4a 2
=2a ≤2,即
a ≤1,所以“a =1”是“函数f (x )=x 2-4ax +3在区间[2,+∞)上为增函数”的充
分不必要条件,故选B.]
12.(2018·石家庄质检(二))在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,则“sin A >sin B ”是“a >b ”的( )
【导学号:79140011】
A .充分不必要条件
B .必要不充分条件
C .充要条件
D .既不充分也不必要条件
C [由正弦定理a sin A =b
sin B
=2R (R 为三角形外接圆半径)得,a =2R sin A ,b =2R sin
B ,故sin A >sin B ⇔2R sin A >2R sin B ⇔a >b .]
13.已知命题p :x 2
+2x -3>0;命题q :x >a ,且﹁
q 的一个充分不必要条件是﹁
p ,则a 的取值范围是( ) A .(-∞,1] B .[1,+∞) C .[-1,+∞)
D .(-∞,-3]
B [解x 2
+2x -3>0,得x <-3或x >1,故﹁
p :-3≤x ≤1,又﹁
q :x ≤a ,由﹁
q 的一个充分不必要条件是﹁
p ,可知﹁
p 是﹁
q 的充分不必要条件,故a ≥1.]
14.(2016·四川高考)设p :实数x ,y 满足(x -1)2
+(y -1)2
≤2,q :实数x ,y 满足
⎩⎪⎨⎪
⎧
y ≥x -1,y ≥1-x ,y ≤1,
则p 是q 的( )
A .必要不充分条件
B .充分不必要条件
C .充要条件
D .既不充分也不必要条件
A [p 表示以点(1,1)为圆心,2为半径的圆面(含边界),如图所示.q 表示的平面区域为图中阴影部分(含边界). 由图可知,p 是q 的必要不充分条件.] 15.有下列几个命题:
①“若a >b ,则a 2
>b 2
”的否命题;
②“若x +y =0,则x ,y 互为相反数”的逆命题; ③“若x 2
<4,则-2<x <2”的逆否命题. 其中真命题的序号是________.
【导学号:79140012】
②③ [①原命题的否命题为“若a ≤b ,则a 2
≤b 2
”错误. ②原命题的逆命题为:“若x ,y 互为相反数,则x +y =0”正确. ③原命题的逆否命题为“若x ≥2或x ≤-2,则x 2≥4”正确.]
16.已知集合A =⎩⎪⎨⎪⎧⎭
⎪⎬⎪
⎫x ⎪⎪
⎪
12
<2x
<8,x ∈R ,B ={x |-1<x <m +1,x ∈R },若x ∈B 成立的一
个充分不必要的条件是x ∈A ,则实数m 的取值范围是________.
(2,+∞) [A =⎩⎪⎨⎪⎧⎭
⎪⎬⎪
⎫x ⎪⎪
⎪
1
2
<2x
<8,x ∈R ={x |-1<x <3},
∵x ∈B 成立的一个充分不必要条件是x ∈A , ∴A B ,∴m +1>3,即m >2.]。
