各类平均数的简单定义
平均数的概念

平均数的概念平均数是一种用于描述一组数据中集中趋势的统计量。
它能够帮助我们了解数据的中心位置,是常用的数据摘要方法之一。
在统计学和数学中,平均数有多种计算方法和应用场景。
本文将以清晰的语句和整洁美观的排版来论述平均数的概念及其相关内容。
一、算术平均数算术平均数是最基本的平均数概念,也是我们最常见的平均数计算方法。
它是一组数据中所有数据值的总和除以数据的个数。
以一组数据x1、x2、x3、...、xn为例,其算术平均数的计算公式为:平均数 = (x1 + x2 + x3 + ... + xn) / n算术平均数常被用于描述事物或现象的一般水平,如某班级学生的平均成绩、某公司员工的平均工资等。
通过求取平均数,我们可以得到一个数据集的总体趋势,较好地代表了所有数据的特征。
二、加权平均数加权平均数是在计算平均数时给不同数据赋予不同的权重,以反映出数据的重要性差异。
若一组数据的权重为w1、w2、w3、...、wn,对应的数值为x1、x2、x3、...、xn,则加权平均数的计算公式为:加权平均数 = (w1*x1 + w2*x2 + w3*x3 + ... + wn*xn) / (w1 + w2 + w3 + ... + wn)加权平均数常用于处理带有不同权重的数据集,如考试成绩中不同科目的权重不同、某产品销售额中不同渠道的权重不同等。
通过给予不同数据以适当的权重,加权平均数更准确地反映了数据集的整体情况。
三、几何平均数几何平均数是一组数据值的连乘积开n次方根的结果,用于计算一组数据的平均程度。
对于一组数据x1、x2、x3、...、xn,其几何平均数的计算公式为:几何平均数 = (x1 * x2 * x3 * ... * xn) ^ (1/n)几何平均数常用于处理涉及比例和增长率的数据集,如计算平均增长率、计算指数平均数等。
几何平均数能够有效地描述数据的相对变化程度,常用于金融和经济领域。
四、调和平均数调和平均数是一组数据数值的倒数的平均数的倒数,用于描述集合中多个值的平均倒数。
平均数知识点总结

平均数知识点总结一、平均数的定义平均数是一组数据的集中趋势的代表值,用来表示数据的中间位置。
它是所有数据之和除以数据的个数。
平均数的计算公式如下:平均数 = 总和 / 数据个数例如,如果有一组数据{3, 5, 7, 9},那么它们的平均数为(3+5+7+9)/4 = 6。
二、计算平均数的方法1.简单平均数简单平均数是最基本的平均数计算方法,也是我们日常生活中常用的方法。
它是将所有数据的和除以数据的个数。
2.加权平均数加权平均数是在计算平均数时,对不同数据的权重进行调整,以反映它们在整体中的重要程度。
例如,计算某班学生的平均成绩时,可以根据学生人数给每个学生的成绩乘以权重。
3.几何平均数几何平均数一般用于一组相对变化的数据的平均值计算,它是将所有数据的乘积的n次方根。
例如,计算一组相对增长率的平均值时,就可以使用几何平均数。
三、平均数的应用场景1.描述数据的集中趋势平均数可以直观地反映一组数据的集中程度,帮助我们了解数据的分布情况。
2.比较不同组数据通过比较不同组数据的平均数,可以直观地了解它们的差异和异同,帮助我们做出合理的决策。
3.预测未来趋势利用历史数据的平均数,可以对未来的趋势进行预测,为个人和企业的决策提供参考依据。
四、注意事项和常见误区1.极值的影响在计算平均数时,极大值和极小值往往会对平均数造成较大的影响。
因此,需要谨慎处理极值数据,避免对平均数的准确性造成干扰。
2.数据的分布情况平均数只能反映数据的中心位置,不能完全代表数据的分布情况。
因此,在对数据进行分析时,需要综合考虑数据的分布情况,避免过分依赖平均数造成误解。
3.样本大小的影响样本大小越大,平均数的可靠性就越高。
因此,在比较不同数据的平均数时,要考虑样本的大小对结果的影响。
4.加权平均数的权重选择在计算加权平均数时,需要合理选择权重,以反映不同数据在整体中的重要程度。
五、实际案例分析1.个人理财在个人理财中,平均数可以帮助我们了解自己的收入和支出状况,帮助我们合理规划支出和储蓄。
八年级平均数知识点

八年级平均数知识点平均数是一个常见的数学概念,它在我们的日常生活和各个领域中都有广泛的应用。
在八年级数学中,平均数也是一个非常重要的知识点,掌握平均数的相关概念和计算方法,对于学生的数学学习和今后生活中的各种实际问题都有很大的帮助。
一、平均数的概念平均数是一组数据的总和与数量的比值。
当我们需要对一组数据进行综合性的描述时,通常会考虑使用平均数。
平均数有三种常见的形式:算术平均数、几何平均数和调和平均数。
二、算术平均数算术平均数是指一组数据所有数值之和与数据个数之比。
算术平均数的计算方法如下:设一组数据为:a1,a2,a3,……,an则这组数据的算术平均数为:平均数= (a1 + a2 + a3 + … + an) ÷ n例如:对于数据4,2,6,8,5,其算术平均数为:平均数 = (4 + 2 + 6 + 8 + 5) ÷ 5 = 25 ÷ 5 = 5三、几何平均数几何平均数是多组数据相乘的积的n次方根,其中n为数据的数量。
几何平均数的计算方法如下:设一组数据为:a1,a2,a3,……,an则这组数据的几何平均数为:平均数= (a1 × a2 × a3 × … × an) 的 1/n 次方例如:对于数据4,2,6,8,5,其几何平均数为:平均数 = (4 × 2 × 6 × 8 × 5) 的 1/5 次方≈ 5.091四、调和平均数调和平均数是指一组数据的倒数的平均值的倒数。
调和平均数的计算方法如下:设一组数据为:a1,a2,a3,……,an则这组数据的调和平均数为:平均数= n ÷ ((1/a1) + (1/a2) + (1/a3) + … + (1/an))例如:对于数据4,2,6,8,5,其调和平均数为:平均数= 5 ÷ ((1/4) + (1/2) + (1/6) + (1/8) + (1/5)) ≈ 3.91五、如何选择平均数对于多组数据,可以采用不同的平均数来描述其特征。
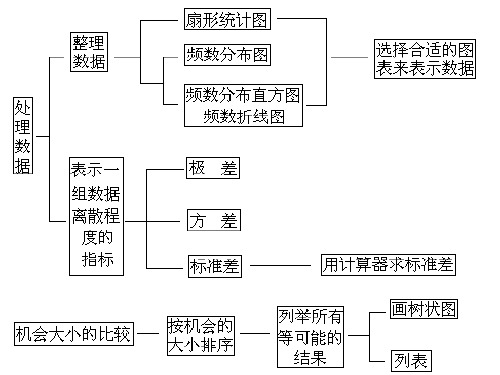
极差、方差、平均数
4、众数的概念:一组数据中出现次数最多的数据叫做这组数据的众数。 注意:1.众数一定在所给数据中。 2.众数可能不唯一。 1、如何理解“中位数”? 中位数与数据排列有关,且一组数据的中位数是唯一的,它可以是该组数据中的某个数, 也可能不是这组数据的数,中位数和平均数一样也反映了一组数据的“平均水平”,不过 考虑角度不同。 2、如何理解“众数”? 众数是指一组数据中出现次数最多的那个数据,它的大小只与一组一组数据中的部分数据 有关,一组数据的众数可能有一个或几个,也可能没有。 3、如何合理地选用平均数、中位数和众数? 平均数、中位数和众数都是一组数据的代表,分别代表这组数据的“一般水平”、“中等 水平”和“多数水平”,平均数涉及所有的数据,中位数和众数只涉及部分数据,它们表 示的意义各不相同。 平均数、中位数与众数都有哪些自己的特点? 平均数:充分利用数据所提供的信息,应用最为广泛,但„„ 中位数:计算简单,受极端值影响较小,但„„ 众数:当一组数据中有些数据多次重复出现时,众数往往是人们尤为关心的一个量
从方差的计算过程,可以看出S 2 的数量单位与原数据的不一致,因此在实际应 用时常常将求出的方差再开平方,这就是标准差。 用符号表示为 标准差=
S2 方差 ,方差=标准差
2
极差、方差和标准差的区别与联系: 联系:极差、方差和标准差都是用来衡量(或描述)一组数据偏离平均数的大小(即波 动大小)的指标,常用来比较两组数 据的波动情况。 区别:极差是用一组数据中的最大值与最小值的差来反映数据的变化范围,主要反映 一组数据中两个极端值之间的差异情况,对其他的数据的波动不敏感。 方差是用“先平均,再求差,然后平方,最后再平均”的方法得到的结果, 主要反映整组数据的波动情况,是反映一组数据与其平均值离散程度的一个重要 指标,每个数年据的变化都将影响方差的结果,是一个对整组数据波动情况更敏 感的指标。在实际使用时,往往计算一组数据的方差,来衡量一组数据的波动大 小。 标准差实际是方差的一个变形,只是方差的单位是原数据单位的平方,而标准差 的单位与原数据单位相同。
平均数再认识知识点

平均数再认识知识点一、平均数的基本概念。
1. 定义。
- 平均数是指在一组数据中所有数据之和再除以这组数据的个数。
例如,有一组数据2、4、6,它们的和是2 + 4+6=12,数据个数是3,那么这组数据的平均数就是12÷3 = 4。
2. 计算方法。
- 公式:平均数¯x=frac{x_1+x_2+·s+x_n}{n},其中x_1,x_2,·s,x_n是数据中的各个数值,n是数据的个数。
例如,对于数据3、5、7、9,n = 4,x_1=3,x_2=5,x_3=7,x_4=9,则平均数¯x=(3 + 5+7+9)/(4)=(24)/(4)=6。
二、平均数的意义。
1. 代表一组数据的平均水平。
- 它可以反映一组数据的总体情况。
比如在统计一个班级学生的考试成绩时,平均数可以让我们大致了解这个班级学生成绩的平均状况。
如果一个班级数学考试成绩的平均数是80分,那么我们可以知道这个班级整体的数学学习水平大概处于80分左右的程度。
2. 用于比较不同组数据。
- 当我们要比较两个班级的学习成绩、两个工厂的生产效率等情况时,平均数是一个很有用的指标。
例如,甲班数学平均成绩是85分,乙班数学平均成绩是80分,我们可以初步判断甲班整体数学成绩比乙班好。
三、加权平均数。
1. 概念。
- 在实际生活中,有些数据的重要性或者出现的频率是不一样的,这时候就需要用到加权平均数。
加权平均数是不同比重数据的平均数,加权平均数就是把原始数据按照合理的比例来计算。
2. 计算方法。
- 公式:若n个数x_1,x_2,·s,x_n的权数分别是w_1,w_2,·s,w_n,那么加权平均数¯x=frac{w_1x_1+w_2x_2+·s+w_nx_n}{w_1+w_2+·s+w_n}。
例如,某学生的平时成绩为80分,权数为30%,期末考试成绩为90分,权数为70%,那么加权平均成绩¯x=(80×0.3 + 90×0.7)/(0.3+0.7)=(24 + 63)/(1)=87分。
小学数学平均数知识点总结

小学数学平均数知识点总结平均数是数学中的一个重要概念,它是一组数据的中心趋势的度量之一。
在小学阶段,学生开始接触平均数的概念,并学习如何计算平均数。
本文将总结小学数学中与平均数相关的知识点,帮助学生更好地理解和掌握这一概念。
1. 平均数的定义平均数是一组数据相加后再除以数据个数所得的值。
它代表了整个数据集的中心位置。
2. 平均数的计算计算平均数的方法是将数据相加,然后除以数据个数。
设有n个数据x₁, x₂, x₃,..., xn,它们的平均数记作x,可以表示为:x = (x₁ + x₂ + x₃ + ... + xn) / n3. 平均数的应用场景平均数在日常生活中有广泛的应用。
例如,平均成绩可以用来评价一个班级的学生平均水平;平均年龄可以衡量一个人群的年龄分布等。
4. 平均数与数据的关系平均数可以用来表示整个数据集的中心位置。
当数据集中的数据值变化较小或相差不大时,平均数比较能够代表整体情况;但当数据集中的数据值相差较大时,平均数可能会被极端值所影响,此时需谨慎使用平均数。
5. 算术平均数与加权平均数在计算平均数时,有两种常见的方法:算术平均数和加权平均数。
- 算术平均数:对于一组等权重的数据,算术平均数即为每个数据值的总和除以数据个数。
- 加权平均数:对于一组具有不同权重的数据,加权平均数的计算要考虑到每个数据的权重。
加权平均数可以更准确地反映数据间的关系。
6. 类型数据的平均数计算在小学数学中,学生还需要了解如何计算不同类型数据的平均数。
- 自然数的平均数:自然数的平均数是整数,可以直接通过算术平均数的方法计算。
- 分数的平均数:分数的平均数是通过将分数相加,再除以数据个数来计算的。
确保分数在计算过程中保持通分,最后可以化简为最简形式。
- 带小数的平均数:带小数的平均数可以通过将小数相加,再除以数据个数来计算。
7. 求未知数的平均数有时候,题目会给出平均数和一部分数据,要求计算剩余数据的平均数。
初中数学知识点精讲精析 算术平均数与加权平均数

第1节 算术平均数与加权平均数
要点精讲
1.简单平均数定义:如果有n 个数 x 1,x 2,…,x n ,那么121(...)n x x x x n
=
++ 叫做这n 个数的平均数,读作“x 拔”。
*上述平均数是较简单的平均数,只与每个数据的大小有关。
2.加权平均数定义:若n 个数x 1,x 2,…,x n 的权分别是12,...n w w w ,则
叫做这n 个数的加权平均数。
*数据的权能够反映数据的相对“重要程度”,某数的权数越大,对平均数的影响越大。
典型例题
【例1】
某校高一年级的甲、乙两个班级(均为50人)的语文测试成绩如下(总分:150),试确定这次考试中,哪个班的语文成绩更好一些。
甲班
乙班 x n n
n w w w w x w x w x ++++++ 21221
1
【答案】
用科学计算器分别求得甲班的平均分为101.1,乙班的平均分为105.4 ,故这次考试乙班成绩要好于甲班
【解析】
我们可用一组数据的平均数衡量这组数据的水平,因此,分别求得甲、乙两个班级的平均分即可
【例2】
下面是某校学生日睡眠时间的抽样频率分布表(单位:h ),试估计该学生的日平均睡眠时间。
【答案】
总睡眠时间约为
故平均睡眠时间约为7.39h
【解析】
要确定这100名学生的平均睡眠时间,就必须计算其总睡眠时间,由于每组中的个体睡眠时间只是一个范围,可以用各组区间的组中值近似地表示。
3775.73325.71775.6525.6⨯+⨯+⨯+⨯)(739275.8625.8h =⨯+⨯+。
平均数的概念

平均数的概念平均数在数学中是一个重要的概念,用于描述一组数据的集中趋势。
平均数常被用于衡量数据的中心位置,是统计学中常见的方法之一。
本文将介绍平均数的概念与计算方法,并讨论其在实际应用中的意义。
一、平均数的定义与形式平均数是一组数据的总和除以数据的个数得到的结果。
在统计学中,常见的平均数有算术平均数、加权平均数和几何平均数等。
1.1 算术平均数算术平均数,也叫简称平均数,是最常见的一种平均数形式。
计算算术平均数的方法是将一组数据的总和除以数据的个数。
例如,给定一组数据:2, 4, 6, 8, 10,计算它们的算术平均数:(2 + 4 + 6 + 8 + 10) / 5 = 30 / 5 = 6因此,该组数据的算术平均数为6。
1.2 加权平均数加权平均数是根据数据的重要程度不同,给予不同的权重进行计算的平均数形式。
在计算加权平均数时,需要将每个数据乘以相应的权重,然后将加权后的数据总和除以权重的总和。
例如,考虑一个班级的成绩情况,数学占比为40%,英语占比为30%,语文占比为30%。
学生A的数学成绩为90分,英语成绩为80分,语文成绩为70分。
计算学生A的加权平均分:(90 × 0.4 + 80 × 0.3 + 70 × 0.3) / (0.4 + 0.3 + 0.3) = 84因此,学生A的加权平均分为84分。
1.3 几何平均数几何平均数是一组数据乘积的n次方根,其中n为数据的个数。
几何平均数常用于描述多个数据的综合指标。
例如,考虑一组数据:2, 4, 8。
计算它们的几何平均数:(2 × 4 × 8)^(1/3) = 4因此,该组数据的几何平均数为4。
二、平均数的应用意义平均数在实际应用中具有广泛的意义,下面将介绍几个常见的应用场景。
2.1 统计数据的中心趋势平均数是衡量一组数据的中心趋势的重要指标之一,可以用来描述数据的集中程度。
在描述一组数据时,通过计算平均数可以得到一个总体的概貌。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
各类平均数的简单定义
一、算术平均数
1.简单算术平均数
简单算术平均数主要用于未分组的原始数据。
设一组数据为X1,
X2,...,Xn,简单的算术平均数的计算公式为:
M=(X1+X2+...+Xn)/n
例如,某销售小组有5名销售员,元旦一天的销售额分别为520元、600元、480元、750元和500元,求该日平均销售额。
平均销售额=(520+600+480+750+500)/5=570(元)
计算结果表明,元旦一天5名销售员的平均营业额为570元。
拓展:一组数据X1,x2...Xn在数a上下波动,则,原数据分别减掉a,得到一组新数据
X1'=X1-a X2'=X2-a .......Xn'=Xn-a
所以X1=X1'+a X2=X2'+a........Xn=Xn'+a
所以:平均数=(X1+X2+....+Xn)/n
将上面的 X1'=X1-a X2'=X2-a .......Xn'=Xn-a 代入
得到了:(X1'+X2'+....+Xn')/n+a
即=x'拔+a
所以:x拔=x'拔+a
2.加权算术平均数
加权算术平均数主要用于处理经分组整理的数据。
设原始数据为被分成K组,各组的组中的值为X1,X2,...,Xk,各组的频数分别为f1,f2,...,fk,加权算术平均数的计算公式为:
M=(X1f1+X2f2+...+Xkfk)/(f1+f2+...+fk)
二、调和平均数
调和平均数又称倒数平均数,是变量倒数的算术平均数的倒数。
(数值倒数的平均数的倒数。
)
调和平均数是给定数据的倒数之算术平均数的倒数。
(简单平均式)
(加权平均式)
三、几何平均数
是指n个观察值连乘积的n次方根。
根据资料的条件不同,几何平均数有加权和不加权之分。
设一组数据为X1,X2,...,Xn,且均大于0,则几何平均数Xg为:[1]
四、位置平均数
位置平均数:是指按数据的大小顺序或出现频数的多少,确定的集中趋势的代表值,主要有众数、中位数等。
1、算术平均值:有样本标志值的总和除以样本数据个数得出。
它是描述样本集中区是最常用的统计量。
它的指标仅适用于定比数据和定距数据。
2、中位数:一组数据按从小到大的顺序依次排列,处在中间位置的一个数(或最中间两个数据的平均数,注意:和众数不同,中位数不一定在这组数据中)。
中位数是样本数据所占频率的等分线,它不受少数几个极端值
得影响,有时也会成为优点。
在奇偶数中:第、项分别是中位数。
3、众数:是一组数据中出现次数最多的数值,叫众数,有时众数在一组数中有好几个。
用M表示。
理性理解:简单的说,就是一组数据中占比例最多的那个数。
用众数代表一组数据,可靠性较差,不过,众数不受极端数据的影响,并且求法简便。
在一组数据中,如果个别数据有很大的变动,选择中位数表示这组数据的“集中趋势”就比较适合。
