8位二进制地址码与编码位置对照表
关于云台地址码的介绍及地址码编码参照表
*232—485转换器的选择,100米以内可采用无源转换器,大于100米建议用有源转换器。
*本解码板采用AC24V供电,请选择正确的供电电压。
技术指标
电气指标
供电电源:24V±10% AC? 50/60HZ? 35W(1.5A)。
关于云台地址码的介绍及地址码编码参照表
云台的协议就是云台和操作系统进行交流的一种方式或者说是一种机器的语言,操作系统通过这一种语言位方法的图表,给大家参考。
8位拨码开关的1-6位用于云台的地址码设置,共可接63个不同的云台,每个云台地址码的编号应与硬盘录像机、对云台进行控制,
波特率即调制速率,指的是信号被调制以后在单位时间内的波特数,即单位时间内载波参数变化的次数。它是对信号传输速率的一种度量,通常以“波特每秒”(Bps)为单位。
1 1 0 0
PELCON
5
0 0 1 0
KALATEL-312
6
1 0 1 0
CCR-20G
7
0 1 1 0
ADR-8060
8
1 1 1 0
HY
9
0 0 0 1
M800-CIA
10
1 0 0 1
PANASONIC
11
0 1 0 1
LILIN
12
1 1 0 1
KRE-301
13
0 0 1 1
WISDOM
2
010000
6
011000
10
000010
14
001010
3
110000
7
111000
11
100010
8位二进制地址码与编码位置对照表

1268
179
12568
195
1278
132
38
148
358
164
368
180
3568
196
378
133
138
149
1358
165
1368
181
13568
197
1378
134
238
150
2358
166
2368
182
23568
198
2378
135
1238
151
12358
167
12368
183
123568
119
123567
对应数字拨到NO方向,其它数字不动
地址
编码
地址
编码
地址
编码
地址
编码
地址
编码
地址
编码
地址
编码
128
8
144
58
160
68
176
568
192
78
129
18
145
158
161
168
177
1568
193
178
130
28
146
258
162
268
178
2568
194
278
131
128
147
1258
141
1348
157
13458
173
13468
189
134568
142
2348
158
23458
174
各种编码码制知识
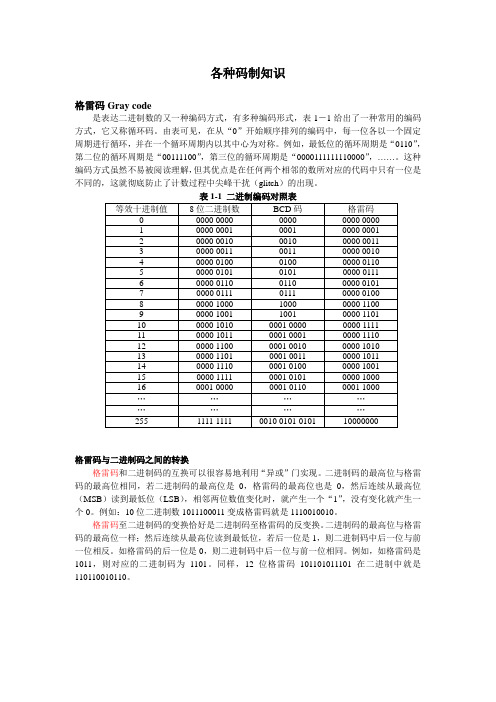
各种码制知识格雷码Gray code是表达二进制数的又一种编码方式,有多种编码形式,表1-1给出了一种常用的编码方式,它又称循环码。
由表可见,在从“0”开始顺序排列的编码中,每一位各以一个固定周期进行循环,并在一个循环周期内以其中心为对称。
例如,最低位的循环周期是“0110”,第二位的循环周期是“00111100”,第三位的循环周期是“0000111111110000”,……。
这种编码方式虽然不易被阅读理解,但其优点是在任何两个相邻的数所对应的代码中只有一位是不同的,这就彻底防止了计数过程中尖峰干扰(glitch)的出现。
格雷码与二进制码之间的转换格雷码和二进制码的互换可以很容易地利用“异或”门实现。
二进制码的最高位与格雷码的最高位相同,若二进制码的最高位是0,格雷码的最高位也是0,然后连续从最高位(MSB)读到最低位(LSB),相邻两位数值变化时,就产生一个“1”,没有变化就产生一个0。
例如:10位二进制数1011100011变成格雷码就是1110010010。
格雷码至二进制码的变换恰好是二进制码至格雷码的反变换。
二进制码的最高位与格雷码的最高位一样;然后连续从最高位读到最低位,若后一位是1,则二进制码中后一位与前一位相反。
如格雷码的后一位是0,则二进制码中后一位与前一位相同。
例如,如格雷码是1011,则对应的二进制码为1101。
同样,12位格雷码101101011101在二进制中就是110110010110。
111二进制格雷码111二进制格雷码常用双极性代码符号位不变,其余取反对负数:加一无论正负数,最高位取反各种双极性代码的相互关系。
标准ascii用8位二进制对128种符号进行编码

标准ascii用8位二进制对128种符号进行编码ASCII是一种基于8位二进制编码的字符集,其中包含128种不同的字符。
ASCII的全称是美国信息交换标准代码(American Standard Code for Information Interchange),它在20世纪60年代被制定出来,并成为了标准化的字符编码方式。
在计算机科学的发展史上,ASCII扮演了非常重要的角色,它为后来的编码方式奠定了基础。
在ASCII编码中,每一个字符都对应着一个唯一的8位二进制数字,也就是8个0或1组成的序列。
因为8个二进制数字总共有256种不同的组合方式,而ASCII只使用了其中的128种组合。
其中包括数字、字母、标点符号和一些控制字符等等。
让我们来看一下具体的ASCII编码规则。
1. 数字:ASCII编码中包含了0-9的十个数字,分别对应了0x30-0x39这十个16进制数字。
例如,字符“1”的ASCII码为0x31,字符“9”的ASCII码为0x39。
2. 字母:ASCII编码中包含了大小写26个英文字母,分别从0x41-0x5A为大写字母A到Z,0x61-0x7A为小写字母a到z。
例如,字符“A”的ASCII码为0x41,字符“a”的ASCII码为0x61。
3. 标点符号:ASCII编码中包含了常用的标点符号,例如句号、逗号、感叹号、分号等等,这些字符分别对应了0x20-0x2F和0x3A-0x3F这两个区间。
例如,字符“!”的ASCII码为0x21,字符“.”的ASCII码为0x2E。
4. 控制字符:ASCII编码中还包含了一些不可打印的控制字符,这些字符用于控制计算机的硬件以及通信协议等方面。
例如,回车键的ASCII码为0x0D,换行键的ASCII码为0x0A,空格键的ASCII码为0x20。
总的来说,ASCII编码是一种非常基础的字符编码方式,它使用8位二进制数来对128种字符进行编码,广泛应用于计算机科学的各个领域。
8位二进制地址码与编码位置对照表.doc

9 14 28
345 48
56 68
37 88
457 108 3457
10 24 29 1345 49
156 69
137 89 1457 109 13467
11 124 30 2345 50
256 70
237 90 2457 110 23467
12 34 31 12345 51 1256 71 1237 91 12457 111 123467
235 42
246 62 23456 82
257 102 23467 122 24567
4
3 23 1235 43 1246 63 123456 83 1257 103 12367 123 124567
5 13 24
45 44
346 64
7 84
357 104 467 124 34567
6 23 25
135 1238 151 12358 167 12368 183 123568 199 12378
136 48 152
458 168
468 184 4568 200
478
137 148 153 1458 169 1468 185 14568
138 248 154 2458 170 2468 186 24568
139 1248 155 12458 171 12468 187 124568
140 348 156 3458 172 3468 188 34568
141 1348 157 13458 173 13468 189 134568
142 2348 158 23458 174 23468 190 234568
278
131 128 147 1258 163 1268 179 12568 195 1278
8_位二进制数(1_位符号位,7_位数值位),其原码所能表示的十进制数范围_解释说明

8 位二进制数(1 位符号位,7 位数值位),其原码所能表示的十进制数范围解释说明1. 引言1.1 概述本文将介绍8位二进制数的表示方法及其所能表示的十进制数范围。
二进制数是计算机系统中最基本的数字表示方式之一,它由0和1两个数字组成,并且能够通过不同的编码方式来表示正负数。
了解二进制数的表示方法对于理解计算机内部运算和数据储存有着重要意义。
1.2 文章结构文章将按照以下结构进行介绍:首先,我们会从二进制数的概念入手,解释什么是二进制数以及它如何在计算机中表示。
随后,我们会详细讨论8位二进制数的结构和表示范围,分别涵盖正数和负数。
接着,我们会给出从十进制到八位二进制数以及从八位二进制数到十进制的转换示例。
最后,我们会总结文章内容,并探讨原码在计算机中应用场景和限制。
1.3 目的本文旨在提供读者关于8位二进制数和其原码表示法所能表示的十进制范围的全面理解。
通过阅读本文,读者将了解到不同编码方式对于数字范围和精度带来的影响,并且可以更好地理解计算机内部的数值运算和数据表示。
对于学习计算机科学和数字电路等领域的读者来说,本文将为他们打下坚实的基础。
2. 二进制数的表示方法2.1 二进制数的概念二进制数是一种数字系统,只包含两个数字,0和1。
在计算机中,信息以二进制形式存储和处理。
2.2 二进制数的符号位和数值位在一个n 位的二进制数中,第一位为符号位(最高位),用来表示正负。
剩余的n-1 位为数值位,用来表示具体的值。
2.3 原码表示法原码表示法是一种最简单直观的表示方式,即用二进制表示一个数,将符号位与数值位组合起来。
其中最高位为符号位(0代表正数,1代表负数),其余各个位置代表对应的权重。
例如,在8位二进制中,00011001 表示十进制数+25, 而10011001 则表示-25。
原码表示法的优点是简单易理解,在加法运算时也比较简单、直观。
但是也存在一些缺点。
首先,任何一个非零整数都有两个零对应:+0 和-0 ,造成了冗余;其次,在进行减法时需要自行判断两个操作数之间大小关系,并注意借位的处理。
8位原码反码补码表

***************************************************************************** 对于8位带符号的二进制数:原码:范围-127~-0,+0~+127??????二进制正数00000000-01111111?,??十进制+0~+127,共128种状态??????二进制负数10000000-11111111?,??十进制-0~-127,共128种状态??反码:范围-127~-0,+0~+127??????二进制正数00000000-0?1111111?,??十进制+0~+127,共128种状态??????二进制负数11111111-10000000?,??十进制-127~-0,共128种状态??补码:范围-128~0~+127??????二进制正数?00000000-0?1111111?,??十进制+0~+127,共128种状态??????二进制负数10000000-10000001?,??十进制-128~-1,共128种状态??注:[-0]补码=[-0]反码+1=100000000=[+0]补码,即[-0]补码=[+0]补码[-1]补码=[10000001]补码=11111110+1=11111111,即[-1]补码是-127[-127]补码=[11111111]补码=10000000+1=10000001,即[-127]补码是-1[-128]补码=[-127]补码+[-1]补码=10000001+11111111=10000000结论:原码范围:-127~-0,+0~+127,256种状态反码范围:-127~-0,+0~+127,256种状态补码范围:-128~-1,+0~+127,256种状态,因为[-0]补码和[+0]补码相同,在补码中-128代替了-0。
也可认为是一种规定,这样可都是256种状态。
要注意:(-128)没有相对应的原码和反码,(-128)=*****************************************************************************。
二、八、十、十六进制对照表

二、八、十、十六进制对照表进制转换是计算机科学中的一个重要课题,并且在数字逻辑和计算中发挥着重要作用。
在一种进制转换成另一种进制时,我们常常需要借助“进制表”来辅助计算。
在本文中,我们将对比分析二进制、八进制、十进制和十六进制之间的关系,并用表格的形式来展现它们的对照表。
下面就来一起认识一下吧!首先,让我们来了解一下什么是进制。
所谓进制,就是指一个计数系统里使用的基数或底数。
当我们把一个数表示成几个数之和的形式时,每一个数就叫做一个进制。
常见的进制有二进制、八进制、十进制和十六进制,分别使用0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F这15个数来表示。
其次,让我们看一下它们之间的转换。
要从十进制转换成其它进制,我们可以采用除法取余法,先除以2,然后除以8,再除以16,我们就可以得到每一位的余数,然后以进制表中对应的数字来表示。
同样的,我们可以用乘法取商法来从其它进制转换成十进制,先把每一位的数字乘以2,8,16,再把它们相加,就可以得到转换的结果。
最后,让我们来看看它们之间的对照表:二进制|八进制|十进制|十六进制------|------|------|------0|0|0|01|1|1|110|2|2|211|3|3|3100|4|4|4101|5|5|5110|6|6|6111|7|7|71000|10|8|81001|11|9|91010|12|10|A1011|13|11|B1100|14|12|C1101|15|13|D1110|16|14|E1111|17|15|F从上面的表格中,我们可以发现它们之间的关系,当我们从十进制转换成其它进制时,我们只需要从左到右逐位除以进制的底数,然后取余数;当我们从其它进制转换成十进制时,我们只需要从右到左把每一位乘以底数的幂,然后把它们相加即可。
以上就是二、八、十、十六进制之间的对照表,希望本文能够帮助大家熟悉这几种有关进制转换的知识。
