二进制和十进制常用表
进制知识点总结

进制知识点总结一、基本概念1. 十进制十进制是我们最熟悉的进制,也叫做“常用数字系统”。
它由数字0到9组成,每个位置上的数字代表不同的权值。
比如1234表示的是1*1000+2*100+3*10+4*1。
十进制是我们日常生活中最常用的进制,因为我们通常使用的数字系统都是十进制的。
2. 二进制二进制是计算机领域中最常用的进制,它只由0和1组成。
它的表示方式与十进制类似,每个位置上的数字代表的是2的幂次。
比如1011表示的是1*2^3+0*2^2+1*2^1+1*2^0。
在计算机中,所有的数据都是以二进制的形式存储的。
3. 八进制八进制是一种较少使用的进制,它由数字0到7组成。
每个位置上的数字代表的是8的幂次。
比如543表示的是5*8^2+4*8^1+3*8^0。
在计算机领域中,八进制用的较少,主要是因为它不够直观,而且没有特别的优势。
4. 十六进制十六进制是一种常用的进制,在计算机领域中也经常使用。
它由数字0到9以及字母A到F组成,每个位置上的数字代表的是16的幂次。
比如1A3表示的是1*16^2+10*16^1+3*16^0。
在计算机领域中,经常使用十六进制来表示颜色、地址、编码等信息。
5. 进制的转换规则在不同的进制之间进行转换,通常有两种方式:逐位转换和除法转换。
逐位转换是指将原始数的每一位数字转换成目标进制对应的数,然后相加得到最终结果。
而除法转换是指不断地进行除法运算,得到目标进制对应的余数,然后按照一定顺序进行排列,得到最终结果。
二、进制之间的转换1. 二进制与十进制的转换二进制转换成十进制,可以按照逐位转换的方式,将每一位数字乘以对应的权值,然后相加即可得到结果。
比如1011转换成十进制,则是1*2^3+0*2^2+1*2^1+1*2^0=11。
而十进制转换成二进制,则可以采用除法转换的方式,不断地进行除以2操作,得到余数,然后按照逆序排列得到结果。
2. 八进制与十进制的转换八进制转换成十进制和二进制类似,也是采用逐位转换或者除法转换的方式。
常用的进位计数制
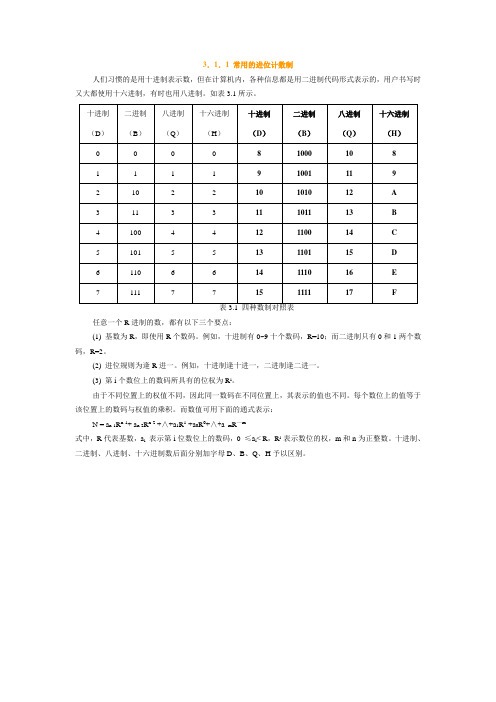
3.1.1 常用的进位计数制
人们习惯的是用十进制表示数,但在计算机内,各种信息都是用二进制代码形式表示的,用户书写时又大都使用十六进制,有时也用八进制。
如表3.1所示。
任意一个R进制的数,都有以下三个要点:
(1) 基数为R,即使用R个数码。
例如,十进制有0~9十个数码,R=10;而二进制只有0和1两个数码,R=2。
(2) 进位规则为逢R进一。
例如,十进制逢十进一,二进制逢二进一。
(3) 第i个数位上的数码所具有的位权为R i。
由于不同位置上的权值不同,因此同一数码在不同位置上,其表示的值也不同。
每个数位上的值等于该位置上的数码与权值的乘积。
而数值可用下面的通式表示:
N = a n-1R n-1+ a n-2R n-2 +∧+a1R1 +a0R0+∧+a--m R—m
式中,R代表基数,a i表示第i位数位上的数码,0 ≤a i< R,R i 表示数位的权,m和n为正整数。
十进制、二进制、八进制、十六进制数后面分别加字母D、B、Q、H予以区别。
二进制和十进制之间的转换

NEXT
即156D =10011100B (156)10=(10011100)2
2.小数部分
法则:乘2取整数,直到小数部分为零,正 序排列 例2:将十进制小数0.625转换成二进制 数。 练习: 1.将十进制小数0.2转换成二进制数。 2.将十进制数225.15转换成二进制数。
进制之间的转换
授课教师:郭秀平 指导教师:张文菊
要 点
1.二进制和十进制的数值特点
2.二进制和十进制的转换
•十进制转换二进制 • 二进制转换十进制
小结
3.八进制和十六进制的数值特点
二进制和十进制的数值特点
1. 基数(基本符号的个数)
2. 进位规则
3. 对照表
4. 权 5. 形式表示
十进制转化为二进制
二进制转化为十进制
法则:按权展开求和(即将R进制按位权 形式展开多项式和的形式,求和 ) 例1: 把 (1001.01)2转换为十进制。
(1 2 0 2 0 2 1 2 0 2 1 2 )10
3 2 1 0
1
2
=(9.25)10
练习: 1. 11111111B=( 2. 10101011.1100B=(
Hale Waihona Puke )D )D八进制和十六进制的数值特点
1. 基数(基本符号的个数)
2. 进位规则
3. 对照表
4. 权 5. 符号表示
小结
乘2取整正序排列 除2取余反序排列 十进制 按权值展开求和 二进制
作
1. 192.15D=()B
二进制到十进制代码

二进制到十进制代码二进制到十进制是计算机科学中一个基本的转换问题。
在计算机中,二进制是最基本的数制,由0和1两个数字组成。
而十进制是我们日常生活中最常用的数制,由0到9这10个数字组成。
将一个二进制数转换为十进制数,可以帮助我们更好地理解计算机内部的运算和表示方式。
我们需要了解二进制数的表示方法。
在二进制中,每一位上的数字表示的是2的幂次方。
最右边的一位是2的0次方,第二位是2的1次方,以此类推。
例如,二进制数1011表示的是:1*(2^3) + 0*(2^2) + 1*(2^1) + 1*(2^0) = 8 + 0 + 2 + 1 = 11。
接下来,我们可以使用编程语言来实现二进制到十进制的转换。
下面是一个示例的Python代码:```pythondef binary_to_decimal(binary):decimal = 0power = 0while binary > 0:decimal += (binary % 10) * (2 ** power)binary //= 10power += 1return decimalbinary_number = 1011decimal_number = binary_to_decimal(binary_number)print(decimal_number)```在这段代码中,我们定义了一个函数`binary_to_decimal`来完成二进制到十进制的转换。
首先,我们初始化`decimal`和`power`两个变量为0,`decimal`用来保存最终的十进制数,`power`用来表示当前位数的幂次方。
然后,我们使用一个循环来遍历二进制数的每一位。
通过取余运算`binary % 10`来获取当前位上的数字,然后乘以2的`power`次方,加到`decimal`上。
接着,我们将二进制数除以10(即去掉最右边的一位),并将`power`加1,继续下一位的转换。
计算机各进制换算

计算机各进制换算⼀:⼗进制数转换成⼆进制数。
随便拿出⼀个⼗进制数“39”,(假如你今天买书⽤了39元)先来把这个39转换成2进制数。
商余数步数39/2= 19 1第⼀步19/2= 9 1 (这⾥的19是第⼀步运算结果的商)第⼆步9/2= 4 1 (这⾥的9是第⼆步运算结果的商)第三步4/2= 2 0 (这⾥的4是第三步运算结果的商)第四步2/2= 1 0 (这⾥的2是第四步运算结果的商)第五步1/2= 0 1 (这⾥的1是第五步运算结果的商)第六步那么⼗进制数39转换成2进制数就是100111. 既39(10)=100111(2)解析⼀:1. 当要求把⼀个10进制数转换成2进制数的时候,就⽤那个数⼀直除以2得到商和余数。
2. ⽤上⼀步运算结果的商在来除以2,再来得到商和余数。
3. 就这样,⼀直⽤上⼀步的商来除以2,得到商和余数!那么什么时候停⽌呢?4. 请看上述运算图,第六步的运算过程是⽤1除以2.得到的商是0,余数是1. 那么请你记住,记好了啊共2点。
A: 当运算到商为“0”的时候,就不⽤运算了。
B:1/2的商为“0”余数为“1”。
这个你要死记住,答案并不是0.5!答案就是商为“0”余数为“1”。
你不⽤去思考为什么,记好了就⾏了!5. 在上述图中你会清晰的看到每⼀步运算结果的余数,你倒着把它们写下来就是“100111”了。
那么这个就是结果了。
6. 在上述图中符号“/”代表“除以”。
⼆:⼗进制数转换成⼋进制数。
随便拿出⼀个⼗进制数“358”,(假如你今天买彩票中了358元)。
358是我们现实⽣活中所⽤10进制表达出来的⼀个数值,转换成⼋进制数⼗多少?商余数步数358/8= 44 6第⼀步44/8= 5 4 (这⾥的44是第⼀步运算结果的商)第⼆步5/8= 0 5 (这⾥的5是第⼆步运算结果的商)第三步那么⼗进制数358转换成8进制数就是546。
既358(10)=546(8)解析⼆: 1.没什么好说的啦,10进制数转换成2进制数和10进制数转换成8进制数的唯⼀不⼀样的地⽅就是除数变了,除数由“2” 变成了“8”。
进制之间的转换

计算机中常用的数制一、几种常用的进位计数制1.十进制 (10个基本数码:0、1、2、3、4、5、6、7、8、9)2.二进制(2个基本数码:0、1)3.八进制(8个基本数码:0、1、2、3、4、5、6、7)4.十六进制(16个基本数码:0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F)二、计算机常用的各种进制数的特点三、不同进位计数制间数据的转化1.二进制数转换成十进制数方法:把二进制各数位的权和该位上的数码相乘,乘积逐项相加。
注意:整数部分权由0,1,2依次展开,小数部分权由-1,-2依次展开。
遇0时可以省略,因为0乘以任何数都为0。
例题:把二进制111010和101.101转换成十进制数。
(111010)2=1ⅹ25+1ⅹ24+1ⅹ23+1ⅹ21=(58)10(101.101)2=1ⅹ22+1ⅹ20+1ⅹ2-1+1ⅹ2-3=(5.625)102.十进制数转换成二进制数方法:整数部分“除2取余法”,小数部分“乘2取整法”注意:整数部分在取余数时,从后向前取,小数部分从前向后取。
例题:把十进制205.8125转换成二进制数。
整数部分205转换过程如下:小数部分0.8125转换过程如下:(205.8125)10=(11001101.1101)23.十进制数转换成八进制数方法:整数部分“除8取余法”,小数部分“乘8取整法”注意:整数部分在取余数时,从后向前取,小数部分从前向后取。
例题:把十进制1645.6875转换成八进制数。
(1645.6875)10=(3155.54)84.十进制数转换成十六进制数方法:整数部分“除16取余法”,小数部分“乘16取整法”注意:整数部分在取余数时,从后向前取,小数部分从前向后取。
例题:把十进制205.21875转换成十六进制数。
(205.21875)10=(CD.38)165.十六进制数和八进制数转换成二进制数方法:十六进制和八进制到二进制分别为24和23,因此,把十六进制和八进制数的每一个数码转成3位和4位的二进制即可.注意:整数前的高位O和小数后的低位O可以去掉。
计算机常用进制

计算机常用进制计算机常用进制计算机是一种基于二进制的数字系统,即所有的数据都是以0和1的形式表示。
然而,在计算机中,除了二进制进制之外,还涉及到其他几种常用的进制。
本文将介绍常见的几种计算机进制,并对其进行详细的讲解。
一、二进制进制(Binary)二进制进制是计算机使用最广泛的进制形式。
在二进制中,每个位代表一种状态,0表示关,1表示开。
因此,二进制数只有两个数字0和1。
二进制数一般用前缀0b表示,例如0b10表示二进制的数字2。
计算机内部所有的数据都是以二进制的形式存储和处理的。
二进制数可以通过“位运算”(Bitwise operation)进行逻辑运算,例如与(AND)、或(OR)和非(NOT)。
这些运算在计算机科学中经常被使用。
二、十进制进制(Decimal)十进制是我们日常生活中最常用的进制。
它由10个数字0-9组成。
例如,10表示数字十,100表示数字一百。
在计算机中,我们通常使用十进制来表示整数和实数,因为这种进制更加直观,易于理解。
三、八进制进制(Octal)八进制是一种以8为基数的进制。
它由8个数字0-7组成。
例如,八进制数10表示十进制的数字8,八进制数100表示十进制的数字64。
在计算机中,八进制数一般用前缀0o表示。
八进制数在计算机中的应用相对较少,但在一些特定的场景下,如Unix文件权限的表示中,还是会使用到八进制。
四、十六进制进制(Hexadecimal)十六进制是一种以16为基数的进制。
它由16个数字0-9和字母A-F组成。
字母A表示十进制的数字10,字母B表示十进制的数字11,以此类推。
所以,十六进制的数字范围是0-9和A-F。
在计算机中,十六进制数一般用前缀0x表示。
例如,0x10表示十进制的数字16,0xFF表示十进制的数字255。
十六进制有较强的可读性,同时也有利于压缩和表示二进制数据。
因此,在底层编程、硬件调试和图形领域中,经常会使用十六进制。
五、常见进制之间的转换在计算机中,常常需要对不同进制进行转换。
进制数知识点

进制数知识点进制数是数学中的一个重要概念,用于表示数值的计数系统。
常见的进制包括十进制、二进制、八进制和十六进制。
本文将逐步介绍这些进制数的概念和转换方法。
1.十进制(Decimal)十进制是我们最常用的计数系统,它使用10个不同的数字来表示所有的数值,从0到9。
每一位数字的位置代表了10的幂次,例如:125 = 1 * 10^2 + 2 * 10^1 + 5 * 10^0。
2.二进制(Binary)二进制是计算机中最基础的进制系统,它只使用两个数字0和1来表示数值。
每一位数字的位置代表了2的幂次,例如:101 = 1 * 2^2 + 0 * 2^1 + 1 * 2^0。
3.八进制(Octal)八进制使用八个数字0到7来表示数值。
每一位数字的位置代表了8的幂次,例如:17 = 1 * 8^1 + 7 * 8^0。
4.十六进制(Hexadecimal)十六进制使用16个数字0到9和字母A到F来表示数值。
每一位数字的位置代表了16的幂次,字母A到F分别表示数值10到15。
例如:1A = 1 * 16^1 + 10 * 16^0。
在实际应用中,我们经常需要在不同进制之间进行转换。
下面是一些常用的转换方法:1.二进制转十进制将二进制数每一位与对应的2的幂次相乘,并相加得到十进制数。
例如:1011 = 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 = 11。
2.十进制转二进制将十进制数不断除以2,直到商为0为止。
将每一步的余数倒序排列即可得到二进制数。
例如:23 / 2 = 11余1,11 / 2 = 5余1,5 / 2 = 2余1,2 / 2 = 1余0,1 / 2 = 0余1,倒序排列得到二进制数10111。
3.十进制转八进制和十六进制类似于二进制转换,将十进制数不断除以8或16,直到商为0为止。
将每一步的余数倒序排列即可得到八进制或十六进制数。
4.八进制和十六进制转十进制将八进制或十六进制数每一位与对应的8或16的幂次相乘,并相加得到十进制数。
