第一章水静力学.doc
水力学基本概念

目录绪论:1第一章:水静力学1第二章:液体运动的流束理论3第三章:液流形态及水头损失3第四章:有压管中的恒定流5第五章:明渠恒定均匀流5第六章:明渠恒定非均匀流6第七章:水跃7第八章:堰流及闸空出流8第九章:泄水建筑物下游的水流衔接与消能9第十一章:明渠非恒定流10第十二章:液体运动的流场理论10第十三章:边界层理论11第十四章:恒定平面势流11第十五章:渗流12第十六章:河渠挟沙水流理论基础12第十七章:高速水流12绪论:1 水力学定义:水力学是研究液体处于平衡状态和机械运动状态下的力学规律,并探讨利用这些规律解决工程实际问题的一门学科。
b5E2RGbCAP2 理想液体:易流动的,绝对不可压缩,不能膨胀,没有粘滞性,也没有表面张力特性的连续介质。
3 粘滞性:当液体处在运动状态时,若液体质点之间存在着相对运动,则质点见要产生内摩擦力抵抗其相对运动,这种性质称为液体的粘滞性。
可视为液体抗剪切变形的特性。
<没有考虑粘滞性是理想液体和实际液体的最主要差别)p1EanqFDPw4 动力粘度:简称粘度,面积为1m2并相距1m的两层流体,以1m/s做相对运动所产生的内摩擦力。
5 连续介质:假设液体是一种连续充满其所占空间毫无空隙的连续体。
6 研究水力学的三种基本方法:理论分析,科学实验,数值计算。
第一章:水静力学要点:<1)静水压强、压强的量测及表示方法;<2)等压面的应用;<3)压力体及曲面上静水总压力的计算方法。
DXDiTa9E3d7 静水压强的两个特性:1)静水压强的方向与受压面垂直并指向受压面2)任一点静水压强的大小和受压面方向无关,或者说作用于同一点上各方向的静水压强大小相等。
RTCrpUDGiT8 等压面:1)在平衡液体中等压面即是等势面2)等压面与质量力正交3)等压面不能相交4)绝对静止等压面是水平面5)两种互不相混的静止液体的分界面必为等压面6)不同液体的交界面也是等压面5PCzVD7HxA9 静水压强的计算公式:p=p0+10 绕中心轴作等角速度旋转的液体:11 绝对压强:以设想没有大气存在的绝对真空状态作为零点计量的压强,称为绝对压强。
1 水静力学

△
作用在ABD上 的静水压力 △ FPy 图 微元四面体受力分析
• ①表面力:
(只有各面上的垂直压力即周围液体的静水压力)
dPx dPy dPz dPn
1 px dAx px dydz 2 1 p y dAy p y dxdz 2 1 pz dAz pz dxdy 2 pn dAn
dU fxdx fydy fzdz dp ( fxdx fydy fzdz )
故,dp dU 积分得,p U C 若已知平衡液体边界压强为p0 , 力势函数为U 0,则积分常数为 C p0 U 0 则p (U U 0) p0
巴斯加原理:平衡液体中,边界上的压强
②.自由液面
2 C gz0 1 2 2 r g ( z z0 ) 2 1 2 2 r g ( zs z0 ) 2
式中, (x,y,z) 为液面任意点坐标
为使 z 坐标与液体内部点(x,y,z)区分,用
zs 表示自由液面的铅垂坐标
③.静水压强的分布规律
p p0 g ( zs z) p0 gh
液体的平衡状态
1 静止状态:相对于地球没有相对运动,处于相对静止状态;
2 相对平衡状态:整个液体对于地球而言具有相对运动,但是
液体对于容器或者液体内部质点之间没有相对运动,处于相对
平衡。
dv 0 da 0
水静力学中,无需区分理想液体与实际液体。
1-1 静水压强及其特性
一、静水压强
静水压力:是指液体内部相邻两部分之间相互作用的力或指液体对固
(3)在静止液体中,位于同一深度(h=常数)的各点的静压 强相等,即任一水平面都是等压面。
水力学

M ρ= V
流体质量( ) 流体质量(kg) 流体体积( 流体体积(m3)
非均质: 非均质:
牛顿内摩擦定律的内容: 牛顿内摩擦定律的内容: 的内容 流体相对运动时,层间内摩擦力 的大小与接触面积 的大小与接触面积、 流体相对运动时,层间内摩擦力T的大小与接触面积、 速度梯度成正比,与流体种类及温度有关, 速度梯度成正比,与流体种类及温度有关,即:
内摩擦力 动力粘性系数 (与流体性质、 与流体性质、 温度有关) 温度有关)
授课计划
绪论(4学时) 第一章 绪论 水静力学(10学时 学时) 第二章 水静力学 学时 水动力学基础(16学时) 第三章 水动力学基础 第四章 流动型态与水头损失 流动型态与水头损失(10学时) 孔口、管嘴出流和有压管流(14学时) 第五章 孔口、管嘴出流和有压管流 明渠恒定均匀流(6学时) 第六章 明渠恒定均匀流 第七章明渠恒定非均匀流
水力学的研究对象: 包括液体和气体,统称为流体 ① 、流体的概念 流体是一种受任何微小剪切力 剪切力都能 发生连续变形的物质。 流体是一种受任何微小剪切力都能 发生连续变形的物质。 它是气体和液体的通称。 它是气体和液体的通称。 ② 、流体的特点 液体 共同点 气体
不同点
易流动,只受压力, 切力, 易流动,只受压力,不受拉力和 切力, 没有固定形状,受到微小的剪切力就产生 没有固定形状 受到微小的剪切力就产生 变形或流动 有固定的体积,不易压 没有固定的体积, 有固定的体积 不易压 没有固定的体积 表面, 易压缩, 缩,有自由 表面,存 易压缩,没有 在表面张力 自由表面
1.水静力学
第一章水静力学一、判断题1、相对压强必为正值。
( )2、图示为一盛水容器。
当不计瓶重时, 作用于地面上的力等于水作用于瓶底的总压力。
( )3、静水总压力的压力中心就是受力面面积的形心. ( )4、二向曲面上的静水总压力的作用点就是静水总压力的水平分力与铅直分力的交点。
( ) 5、一个任意形状的倾斜平面与水面的夹角为α。
则该平面上的静水总压力P=ρgy D A sinα。
(y D为压力中心D的坐标,ρ为水的密度,A 为斜面面积) ()6、图示为二块置于不同液体中的矩形平板,它们的宽度b,长度L及倾角α均相等,则二板上的静水总压力作用点在水面以下的深度是相等的。
( )7、作用于两种不同液体接触面上的压力是质量力。
( )8、静水压强仅是由质量力引起的。
( )9、在一盛水容器的侧壁上开有两个小孔A、B,并安装一U 形水银压差计,如图所示。
由于A、B两点静水压强不等,水银液面一定会显示出∆h 的差值。
( )10、物体在水中受到的浮力等于作用于物体表面的静水总压力。
( )二、选择题1、选择下列正确的等压面: ( )(1) A − A (2) B − B (3) C − C (4) D − D2、压力中心是( )(1) 淹没面积的中心;(2) 压力体的中心;(3) 总压力的作用点;(4) 受压面的形心。
3、平衡液体中的等压面必为( )(1) 水平面;(2) 斜平面;(3) 旋转抛物面;(4) 与质量力相正交的面。
4、图示四个容器内的水深均为H,则容器底面静水压强最大的是( )(1) a ; (2) b ; (3) c ; (4) d 。
5、欧拉液体平衡微分方程( )(1) 只适用于静止液体;(2) 只适用于相对平衡液体;(3) 不适用于理想液体;(4) 理想液体和实际液体均适用。
6、容器中盛有两种不同重度的静止液体,如图所示,作用在容器A B 壁面上的静水压强分布图应为( )(1) a (2) b (3) c (4) d7、液体某点的绝对压强为58 kP a,则该点的相对压强为( ) (1) 159.3 kP a;(2) 43.3 kP a;(3) -58 kP a(4) -43.3 kP a。
水静力学

第一章 水静力学水静力学的任务是研究液体的平衡规律及其工程应用。
液体的平衡状态有两种:一种是静止状态,即液体相对与地球没有运动,处于静止状态。
另一种是相对平衡,即所研究的整个液体相对于地球在运动,但液体相对于容器或液体质点之间没有相对运动,即处于相对平衡状态。
例如,等速直线行驶或等加速直线行驶小车中所盛的液体,等角速度旋转容器中所盛的液体。
本章的核心问题是根据平衡条件来求解静水压强的分布规律,并根据静水压强的分布规律来确定各种情况下的静水总压力。
即先从点、再到面,最后对整个物体确定静水总压力的大小、方向、作用点。
水静力学是解决水利工程中水力荷载问题的基础,同时也是今后学习水动力学的必要知识。
从后面章节的学习中可以知道,即使水流处于运动状态,在有些情况下,动水压强的分布规律也可认为与静水压强的分布规律相同。
第一节 静止压强及其特性一.静水压强的概念.在静水中有一受压面,其面积为ΔA ,作用其上的压力为ΔP ,则该微小面积上的平均静水压强为A P p ∆∆=,当ΔA →0时,平均压强的极限就是点压强,),,(0lim z y x A P A p p ==∆∆→∆,这也说明了静水压强是关于空间位置坐标的函数。
静水压强的单位有三种表示方法:(1)用应力的单位表示,即N/m 2或kN/m 2;(2)用大气压强的倍数表示;(3)用液柱高度表示。
静水压力并非集中作用于某一点,而是连续地分布在整个受压面上,它是静水压强这一分布荷载的合力。
静水压强反映的是荷载集度。
今后的学习中将重点掌握如何根据静水压强的分布规律推求静水总压力。
由于水利工程中有时习惯将压强称为压力,故水力学中就将静水压力称为静水总压力,以示区别。
游泳胸闷,木桶箍都说明静水压力的存在。
二.静水压强的特性1>方向 垂直指向受压面,用反证法说明。
2>大小 静水中任何一点各个方向的静水压强大小都相等。
n z y x p p p p === 而),,(z y x p p =三.绝对压强 相对压强1> 绝对压强以设想的没有大气压存在的绝对真空状态为零点计量得到的压强称为绝对压强,以p ab 或p '来表示。
水力学部分章节知识点

绪论1、密度是指单位体积液体所含有的质量 量纲为[M/L3],单位为kg/m32、容重是指单位体积液体所含有的重量 量纲为[F/L3],单位为N/m3一般取ρ水=1000 kg/m3,γ水=9800N/m3=9.8kN/m3第一章 水静力学1、静水压强的特性:①静水压强垂直指向受压面②作用于同一点上各方向的 静水压强的大小相等2、3、绝对压强——以设想没有大气存在的绝对真空状态作为零点计量的压强,用p ′表示(绝对压强恒为正值)相对压强——以当地大气压作为零点计量的压强,用p 表示。
(相对压强可正可负) 4、真空——当液体中某点的绝对压强小于当地大气压强pa , 即其相对压强为负值时,称为水力意义上的“真空”真空值(或真空压强)——指绝对压强小于大气压强的数值,用pk 来表示 5、压强的单位:1个工程大气压=98kN/㎡ =10m 水柱压=735mm 水银柱压6、压强的测量①测压管②U 形水银测压计③差压计7、静水压强分布图的绘制规则:1.按一定比例,用线段长度代表该点静水压强的大小 2.用箭头表示静水压强的方向,并与作用面垂直 8、平面的静水总压力的计算 ①图解法②解析法9、作用于曲面上的静水总压力(投影) 第二章 液体运动的流束理论1、迹线——某液体质点在运动过程中,不同时刻所流经的空间点所连成的线。
流线——是指某一瞬时,在流场中绘出的一条光滑曲线,其上所有各点的速度向量都与该曲线相切。
/流管——由流线构成的一个封闭的管状曲面 微小流束——充满以流管为边界的一束液流总流——在一定边界内具有一定大小尺寸的实际流动的水流,它是由无数多个微小流束组成2、水流的分类(1)按运动要素是否随时间变化①恒定流——运动要素不随时间变化②非恒定流——运动要素随时间变化(2)按同一流线上各质点的流速矢是否沿流程变化①均匀流——同一流线上流速矢沿流程不发生变化②非均匀流 a 、渐变流b 、急变流 3、均匀流的重要特性(1)过水断面为平面,且过水断面的形状和尺寸沿程不变(2) 同一流线上不同点的流速应相等,从而各过水断面上的流速分布相同,断面平均流速相等(3) 均匀流(包括非均匀的渐变流)过水断面上的动水压强分布规律与静水压强分布规律p z C gρ+=0p p ghρ=+相同,即在同一过水断面上各点的测压管水头为一常数推论:均匀流(包括非均匀的渐变流)过水断面上动水总压力的计算方法与静水总压力的计算方法相同。
《水力学》第一章 水静力学
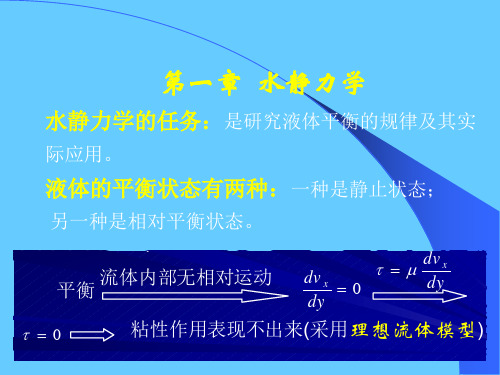
理论证明静水压力具有各项同性
四面体体积:V 1 xyz
6
总质量力在三个坐标
方向的投影为:
Fpx
1 6
xyzf x
Fpy
1 6
xyzf y
按照平衡条件,所有
Fpz
1 6
xyzf z
作用于微小四面体上
的外力在各坐标轴上
投影的代数和应分别 为零。
即在绕中心轴作等角速旋转的液体中有:只有r值相同的 那些点,即位于同心圆柱面上的各点 z p 才保持不变。
g
29
例1-1 有一圆柱形容器,内径为R,原
盛水深度为H,将容器以等角速度
绕中心轴oz旋转,试求运动稳定后容器 中心及边壁处的水深。
30
解 : 在 容 器 边 壁 处 r = R , Zs=Zw ,
1-3 等压面
等压面:静水压强值相等的点连接成的面(可
能是平面也可能是曲面)。
等压面性质:
1.在平衡液体中等压面即是等势面。 2.等压面与质量力正交。
15
1-3 等压面
等压面性质: dp ( U dx U dy U dz) dU
x
y
dz
1.在平衡液体中等压面即是等势面。
17
等压面性质2:等压面与质量力正交。
力 F 沿 ds 移动所做的功可写作矢量F与ds的数性积:
W F ds ( fxdx f ydy fzdz)dm W dUdm
因等压面上 dU=0 ,所以W=F*ds=0。也即质量力必 须与等压面正交。
注意: (1) 静止液体质量力仅为重力时,等压面必定 是水平面;
以 p' 表示绝对压强,p表示相对压强,pa 则表示当地
水力学课件 第一章 水静力学

§1.1 静水压强及其特征
联立上面各式代入后得:
1 2
pxyz
1 2
pnyz
1 6
xyzf x
0
1 2
p y xz
1 2
pnxz
1 6
xyzf y
0
1 2
pz xy
1 2
pnxy
1 6
xyzf z
0
联立上面各式代入后得:
1 2
pxyz
1 2
pnyz
1 6
xyzf x
0
1 2
p y xz
1 2
pnxz
§1.4 等压面
一、等压面(Isobaric Surface):在平衡的液体中, 由压强相等的各点所组成的面叫做等压面。 等压面的重要特性是: 1.在静止的或相对平衡的液体中,等压面同时也是
等势面(Isopotential Surface)。 dp dU
2.在相对平衡的液体中,等压面与质量力正交。
条件:只适用于静止、同种、连续液体
三、气体压强计算
p p0
§ 1.5几种质量力同时作用下的液体平衡
z
gm h z
zs
o
x
以z轴为对称轴的旋转抛物面方程:
R
o
r
x
m
F
y 1 2rBiblioteka gz C 2§ 1.5几种质量力同时作用下的液体平衡 平衡微分方程: dp ( fxdx f ydy fzdz) 质量力:离心惯性力和重力 F m 2r, mg 单位质量力: fx 2 x, f y 2 y, fz g 自由面上压强不变为大气压: dp 0
§ 1.5几种质量力同时作用下的液体平衡
2、圆筒中液体内任一点静水压强分布规律:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实用标准文案第一章水静力学一、填空1.等压面与质量力(正交)。
2.以设想没有大气存在的绝对真空状态作为零点计算的压强称为(绝对压强)。
3.以当地大气压为零点计量的压强称为(相对压强)。
4.相对压强为负值时的绝对值称为(真空值)。
5.由静水压强的基本公式p p0h 可知,静水压强呈(线性)分布。
6.某点的压强水头和该点的位置水头之和叫该点的(测压管水头)。
7.作用在单位宽度上的静水压力,应等于静水压强分布图的(面积)。
8.任一点静水压强的大小和受压面方向(无关)二、判断1.在重力作用下,同一连续液体的水平面就是一个等压面。
(对)2.任一点静水压强的大小和受压面方向相关。
(错)3.静水压强的方向只能是垂直指向受压面。
(对)4.在只有重力的同一种连续液体中,淹没深度相等的水平面是等压面。
(对)5.在同一种连续液体中,淹没深度相等的水平面是等压面。
(错)6.在只有重力的连续液体中,淹没深度相等的水平面是等压面。
(错)7.在只有重力的同一种液体中,淹没深度相等的水平面是等压面。
(错)8.不同流体的交界面是等压面。
(对)9.若平衡液体具有与大气相接触的自由表面,则自由表面必为等压面(对)10.作用于任意平面上的静水压力,等于平面形心点上的静水压强与平面面积的乘积。
(对)三、简答1.何为等压面?等压面的性质是什么?答:等压面是在静止液体中,压强相等的各点连接成的面。
等压面的性质是:(1)在平衡液体中等压面即是等势面。
(2)等压面与质量力正交。
2.静水压强有那些特性?静水压强的分布规律是什么?答:静水压强的特性是:(1)静水压强的方向是垂直指向受压面;(2)任一点静水压强的大小和受压面方向无关,即同一点静水压强的大小相等。
由静水压强的基本公式p p0h 可知,静水压强呈线性分布。
3.何谓绝对压强,相对压强和真空值?它们的表示方法有哪三种?它们之间有什么关系?答:绝对压强:以设想没有大气存在的绝对真空状态作为零点计算的压强 p 。
相对压强:以当地大气压为零点计量的压强p。
真空值:指相对压强为负值时绝对值p k。
压强的三种表示方法是:单位面积上所受的压力,液柱高度和工程大气压(或标准大气压)。
三种压强之间的关系为:p p p a p k(式中 p a为大气压)。
单位之间关系为:21 工程大气压= 98000N/m=10m水柱高= 0.736 米汞柱高。
4.什么叫测压管水头?测压管高度?在静止液体中各点的F“ Z常数”表示什么意思?r答:某点的压强水头和该点的位置水头之和叫该点的测压管水头。
以某点到大气压作用的液面的竖直距离叫测压管高度。
在静止液体中,F“ Z常数”表明其液体内任意两点的测压管水头相等。
r5.什么叫压力体?答:由静水中曲线上每一点引垂直于自由面的垂直形成的柱面和自由面组成的封闭柱体叫压力体。
四、画图1.试画出下列图中各曲面上的压力体图,并指出垂直压力的方向。
2.画出下列图中各标有文字的受压面上的静水压强分布图。
3.画出图中指定曲面的水平方向的压强分布图及铅垂方向压力体图,并指明方向。
五、计算1.图示为一密闭容器,两侧各装一测压管,右管上端封闭,其中水面高出容器水面3m,管内液面压强p0为 78000Pa;左管与大气相通。
求:(1)容器内液面压强p c;(2)左侧管内水面距容器液面高度 h?解:(1)通过容器自由表面的水平面位等压面故 P c P0gh=107.4Ka(2)P c P a ghP c P a0.959m得 hg32.盛有同种介质(容重γA=γB=11.lkN /m)的两容器,其中心点A、B位于同一高程,今用U形差压计测定 A、B 点之压差(差压计内盛3油,容重γ 0=8.5kN/m),A点还装有一水银测压计。
其它有关数据如图题 1-2 所示。
问:1.A 、 B两点之压差为多少?2.A 、 B两点中有无真空存在,其值为多少?解:(1)由图知道 A 点喝 B 点得压差是由 h1 高度得两种密度不同引起的,即密度差引起的。
所以P P (0A )ghB A 10.52kPa(2)存在真空由 A点在的等压面知 P AA gs m gh5.89P AK5.89KN / m 2P BK P AK 0.52 5.37KPa33.图示一圆柱形油桶,内装轻油及重油。
轻油容重γ1为 6.5kN / m ,3重油容重γ 2 为 8.7kN /m ,当两种油重量相等时,求:( 1)两种油的深度 h 1 及 h 2 为多少?( 2)两测压管内油面将上升至什么高度?解:( 1)由两种油的重量相同有1gS 1h12gS 2h2即 1h 1= 2h 2再由 h 1h 2=5m解得 h 1=2.86m h 2= 2.14 m( 2)左侧测压管内油面与将上升至与油桶内轻油油面等高,即油面与桶底的垂距为 5m设右侧测压管内油面与桶底的垂距为h ,则1 gh 12 gh 2=ghh = 1gh 12gh 2=4.28mg4.在盛满水的容器盖上,加上6154N的荷载 G(包括盖重),若盖与容器侧壁完全密合,试求 A、B、C、D各点的相对静水压强(尺寸见图)。
解:荷载 G作用在 AB液面上得P A P B F G=7.8355KPaS SC点和 D点的压强相等由巴斯加原理有:P C P DP A gh27.439KN / m25.今采用三组串联的U形水银测压计测量高压水管中压强,测压计顶端盛水。
当 M点压强等于大气压强时,各支水银面均位于0-0 水平面上。
今从最末一组测压计右支测得水银面在0-0 平面以上的读数为h。
试求 M点的压强?解:P M 6 m gh 5 gh26.一 U形差压计如图题 1-6 所示,下端为横截面积等于 a 的玻璃管,顶端为横截面积 A=50a 的圆筒,左支内盛水 ( γw=9800N/m3),右支3内盛油(γ 0 =9310N/m),左右支顶端与欲测压差处相接。
当p1=p2 时,右支管内的油水交界面在x-x 水平面处,试计算右支管内油水交界面下降 25cm时,( p2-p 1)为若干?解:设当 P1=P2时左边液面到交界面的垂距为h1,右边液面到交界面的垂距为h2得水 gh1油gh2当交界面下降 25cm后因为粗细管面积比为50:1,当细管下降 25cm时左边粗管上升0.5cm,右边粗管下降0.5cm得水(g h10.255)P油(g h20.245)P=水 g 0.255-油 g0.245=218.05 Pa7.圆柱形容器静止时盛水深度H=0.225m,筒深为 0.3m,内径 D=0.1m,若把该圆筒绕中心轴作等角速度旋转,问:(1)不使水溢出容器,最大角速度为多少?(2)为不使容器中心露底,最大角速度为多少?22解:(1)当容器旋转时,边壁最高点水深比静止液面高1R;2 2g中心最低点比静止液面低 1 2R 2 ,所以有:2 2g0.3 0.2251 2R2 2D 22 2g 16g116 0.075g 34.3 rad/ sD(2)当34.3 rad/ s 时, Z 0 12R 21 24.32 0.0520.15 0H2g0.2252 9.82 2所以,当容器底部恰好露出水面,即 Z0 0,则容器已经溢出了一些水了。
显然,这时圆筒静止时的水深H' H,又由旋转抛物面的特点可知: 1Z H'2令 Z 0 12R 2 2R 22H 'ZH '2g 0 2g2即:2gZ 2 9.8 0.348.5 rad / sR0.058.有一小车,内盛液体,车内纵横剖面均为矩形,试证明当小车以等加速度 a 直线行驶后,液面将成为与水平面相交成α角的倾斜面,导出α的表达式以及静水压强的计算公式。
若静止时原水深为h ,水箱高为 H ,长为 L ,问要使水不溢出水箱,小车最大的加速度 a 为若干?解:作用在液体质点上的单位质量力有重力和惯性力,其合力为f , 且液面为等压面,所以 f必与倾斜的液面垂直,因此有:tg a H h g 1 L2a 2g(H h)L根据液体平衡微分方程dpr( Xdx Ydy Zdz) ( adx gdz) (adx gdz)g积分得 p p x0z zc p rzp g r(ax gz) p rz p r ( z z a g x)故静水压强 p p rh9.图示一混凝土重力坝,为了校核坝的稳定性,试分别计算当下游有水和下游无水两种情况下,作用于一米长坝体上水平方向的水压力及垂直水压力。
解: 当下游无水时 :水平分力Px rhC1Ax19.8 13 26 1 3312.4KN (水平向右)垂直分力Pz rV19.8 梯形 abcd 19.8 0.5 (26 18) 4 186204KN (竖直向下)当下游有水时水平分力P x rhC 1Ax1rhc 2Ax 23312.4 9.8 3 6 1 3316KN (水平向右 z z)垂直分力P z rV1 rV2 862.4 9.8 三角形 efg 1862.4 9.8 0.5 3 6 1950.6KN (竖直向下)10.水电站前池进入压力管道的进口处装有一矩形平板闸门,长L为1.8m,宽 b 为 2.5m,闸门重 1860N,倾角α为 75°,闸门与门槽之间摩擦系数 f 为 0.35 ,求启动闸门所需的拉力?解:设水体作用在闸门上的静水压力为F PF P= bh1 10 L sin 8.2613mh2 10mF P= b 402.662 KN设闸门重力分为对斜面的压力F1和沿斜面向下的力F2F1cos G 0.4814KNF2sin G 1.7966KNF拉F2( F P F1 ) f 142.897KN11.一矩形平板闸门 AB,门的转轴位于 A 端,已知门宽 3m,门重 9800N (门厚均匀),闸门与水平面夹角a 为60°,h l为1.0m,h2为1.73m,若不计门轴摩擦,在门的 B 端用铅垂方向钢索起吊。
试求:(1)当下游无水,即 h 3 为 0 时启动闸门所需的拉力T ;(2)当下游有水,h 3 为 h 2 时启动所需的拉力 T 。
h 3 0P9.8 [1 (1 1.73)]1.73 3 109.66 KN 2sin 60e11.73 2 1.0( 1.01.73)0.845m3 sin 60o1.0 (1.0 1.73)T ctg 60o1.73 G 1ctg60o 1.73 P( 1.73e)2sin 60oT 9.8 1 (2 0.845) .662 131.56KN2h 3 h 2 1.73mP9.8 1 1.7358.8KN1sin 60oT ? ctg60o1.739.8 1ctg60o1.73 58.8 1 1.732 2 sin 60oT9.8 1 58.5 63.7KN212.有—直立的矩形自动翻板闸门,门高 H 为 3m ,如果要求水面超过门顶 h 为 lm 时,翻板闸门即可自动打开, 若忽略门轴摩擦的影响,问该门转动轴 0-0 应放在什么位置?解:作用在闸门上的总压力 P 若作用在转动轴 0-0 上,闸门不会翻转,若水位增高,总压力增大,作用点将提高,这样翻转门就会自动打开,所以求出作用点距闸底的距离,即为0-0 转轴应放的位置 :L(2h1 h2 )e 1.2m3(h1 h2 )13. 侧壁上,开有圆形放水孔,放水孔直径 d 为 0.5m,孔顶至水面的深度 h 为 2m,试求放水孔闸门上的水压力及作用点位置。
