2020年中考数学压轴题真题汇编(含答案)
2020年初三数学中考压轴题综合训练:《二次函数》含答案

2020年初三数学中考压轴题综合训练:《二次函数》1.已知抛物线的顶点A(﹣1,4),且经过点B(﹣2,3),与x轴分别交于C,D两点.(1)求直线OB和该抛物线的解析式;(2)如图1,点M是抛物线上的一个动点,且在直线OB的上方,过点M作x轴的平行线与直线OB交于点N,求MN的最大值;(3)如图2,AE∥x轴交x轴于点E,点P是抛物线上A、D之间的一个动点,直线PC、PD与AE分别交于F、G,当点P运动时,求tan∠PCD+tan∠PDC的值.解:(1)设直线OB的解析式为y=kx,∵B(﹣2,3),∴﹣2k=3,∴k=﹣,∴直线OB的解析式为y=﹣x,∵抛物线的顶点为A(﹣1,4),∴设抛物线对应的函数表达式为y=a(x+1)2+4.将B(﹣2,3)代入y=a(x+1)2+4,得:3=a+4,解得:a=﹣1,∴抛物线对应的函数表达式为y=﹣(x+1)2+4,即y=﹣x2﹣2x+3.(2)设M(t,﹣t2﹣2t+3),MN=s,则N的横坐标为t﹣s,纵坐标为﹣(t﹣s),∵,∴x1=﹣2,x2=,∵点M是直线OB的上方抛物线上的点,∴﹣2<t<,∵MN∥x轴,∴﹣t2﹣2t+3=﹣(t﹣s),∴s=﹣t+2=﹣,∵﹣2<t<,∴当t=﹣时,MN的最大值为;(3)解:过点P作PQ∥y轴交x轴于Q,设P(t,﹣t2﹣2t+3),则PQ=﹣t2﹣2t+3,CQ=t+3,DQ=1﹣t,∴tan∠PCD+tan∠PDC=,=,=,=1﹣t+t+3,=4.2.如图,在平面直角坐标系中,直线y=﹣x+2与x轴交于点B,与y轴交点C,抛物线y=﹣x2+bx+c经过B,C两点,与x轴交于另一点A.如图1,点P为抛物线上任意一点.过点P作PM⊥x轴交BC于M.(1)求抛物线的解析式;(2)当△PCM是直角三角形时,求P点坐标;(3)如图2,作P点关于直线BC的对称点P′,作直线P′M与抛物线交于EF,设抛物线对称轴与x轴交点为Q,当直线P′M经过点Q时,请你直接写出EF的长.解:(1)∵直线y=﹣x+2与x轴交于点B,与y轴交点C,∴B(4,0),C(0,2),∴把B(4,0),C(0,2)代入y=﹣x2+bx+c得,,解得,,∴抛物线的解析式为:y=﹣+2;(2)∵PM⊥x轴交BC于M.BC不平行x轴,∴∠PMC≠90°,当∠CPM=90°时,PC∥x轴,则P点的纵坐标为2,∵y=﹣+2的对称轴为x=1,∴P点的横坐标为:2,此时P(2,2);当∠PCM=90°时,设P(m,),则M(m,﹣m+2),由PC2+CM2=PM2得,=,解得,m=0(与C的横坐标相同,舍去),或m=﹣6,此时P(﹣6,﹣10);综上,P点的坐标为(2,2)或(﹣6,﹣10);(3)作Q点关于直线BC的对称点K,QK与BC相交于点N,再过K作KL⊥x轴于点L,如图所示,则根据题意可知,KL与BC的交点为M,P点在KM上,P'在QM上,∵y=﹣+2,∴抛物线的对称轴为x=1,∴Q(1,0),∴BQ=4﹣1=3,∵∠QBN=∠CBO,∠QNB=∠COB=90°,∴△BQN∽△BCO,∴,即,∴QN=,∴QK=2QN=,∠BQN=∠KQL,∠BNQ=∠KLQ=90°,∴△BQN∽△KQL,∴,即,∴QL=,∴OL=1+,∴M(,),设QM的解析式为:y=kx+b(k≠0),则,∴,∴直线QM的解析式为:y=,联立方程组,解得,,或,∴E(,),F(,),∴EF=.3.如图,抛物线y=ax2+bx﹣2与x轴交于A、B两点,与y轴交于点C,已知A(﹣1,0),且直线BC的解析式为y=x﹣2,作垂直于x轴的直线x=m,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).(1)求抛物线的解析式;(2)若△CEF是以CE为腰的等腰三角形,求m的值;(3)点P为y轴左侧抛物线上的一点,过点P作PM⊥BC交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.解:(1)∵直线BC的解析式为y=x﹣2,∴C(0,﹣2),B(4,0),将A(﹣1,0),B(4,0)代入y=ax2+bx﹣2,得,解得,,∴y=x﹣2;(2)∵∴,=,,若以C为顶点,则CE2=CF2,∴,解得:m1=2,m2=4(舍去),若以E为顶点,则EC2=EF2,∴=,解得:m3=4﹣,m4=4+(舍去),综合以上得m=2或m=4﹣.(3)①∵AC=,BC=2,∴AC2+BC2=25=AB2,∴当点P与点A重合时,点M与点C重合,此时P1(﹣1,0),②如图,当△BPM∽△ABC时,过点M作HR∥x轴,作PH⊥HR于点H,BR⊥HR于点R,∵∠PMB=∠PHM=∠BRM=90°,∴∠BMR=∠MPH,∴△PHM∽△MRB,∴又∵AB∥HR,∴∠ABC=∠BMR,∴tan∠BMR=tan∠ABC=,令BR=a,MR=2a,又∵∠ABC=∠BMR,∴tan∠BMR=tan∠ABC=,∴,∴PH=4a,HM=2a,PQ=3a,∴HR=4a,∴P(4﹣4a,3a),又∵点P在抛物线上,将P(4﹣4a,3a)代入y=x﹣2得:(4﹣4a)﹣2=3a,∴a(8a﹣13)=0,a 1=0(舍),a2=.∴.∴符合条件的点P为P1(﹣1,0)或.4.如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.(1)求b,c的值:(2)如图1,点P是第一象限抛物线上一动点,过点P作x轴的垂线1,交BC于点H.当△PHC为等腰三角形时,求点P的坐标;(3)如图2,抛物线顶点为E.已知直线y=kx﹣k+3与二次函数图象相交于M、N两点,求证:无论k为何值,△EMN恒为直角三角形.解:(1)∵抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),∴,解得:,∴b=2,c=3;(2)∵抛物线的函数表达式为:y=﹣x2+2x+3,∴C(0,3),设直线BC的解析式为y=kx+3,将点B(3,0)代入y=kx+3,解得:k=﹣1,∴直线BC的解析式为y=﹣x+3,设点P(x,﹣x2+2x+3),则点H(x,﹣x+3),①如图1,过点C作CM⊥PH于点M,则CM=x,PH=﹣x2+3x,当CP=CH时,PM=MH,∠MCH=∠MCP,∵OB=OC,∴∠OBC=45°,∵CM∥OB,∴∠MCH=∠OBC=45°,∴∠PCH=90°,∴MC=PH=(﹣x2+3x),即x=(﹣x2+3x),解得:x1=0(舍去),x2=1,∴P(1,4);②如图2,当PC=PH时,∵PH∥OC,∴∠PHC=∠OCB=45°,∴∠CPH=90°,∴点P的纵坐标为3,∴﹣x2+2x+3=3,解得:x=2或x=0(舍去),∴P(2,3);③当CH=PH时,如图3,∵B(3,0),C(0,3),∴BC==3.∵HF∥OC,∴,∴,解得:x=3﹣,∴P(3﹣,4﹣2).综合以上可得,点P的坐标为(1,4)或(2,3)或(3﹣,4﹣2).(3)∵函数表达式为:y =﹣x 2+2x +3=﹣(x ﹣1)2+4, ∴点E (1,4);设点M 、N 的坐标为(x 1,y 1),(x 2,y 2),∴MN 2=(x 1﹣x 2)2+(y 1﹣y 2)2,ME 2=(x 1﹣1)2+(y 1﹣4)2,NE 2=(x 2﹣1)2+(y 2﹣4)2,∵ME 2+NE 2=(x 1﹣1)2+(y 1﹣4)2+(x 2﹣1)2+(y 2﹣4)2=x 12+x 22﹣2(x 1+x 2)+2+y 12+y 22﹣8(y 1+y 2)+32=x 12+x 22﹣2x 1x 2+2﹣4+y 12+y 22﹣2y 1•y 2+18﹣48+32 ═(x 1﹣x 2)2+(y 1﹣y 2)2, ∴MN 2=ME 2+NE 2, ∴∠MEN =90°, 故EM ⊥EN ,即:△EMN 恒为直角三角形.5.如图1所示,已知直线y =kx +m 与抛物线y =ax 2+bx +c 分别交于x 轴和y 轴上同一点,交点分别是点B (6,0)和点C (0,6),且抛物线的对称轴为直线x =4; (1)试确定抛物线的解析式;(2)在抛物线的对称轴上是否存在点P ,使△PBC 是直角三角形?若存在请直接写出P 点坐标,不存在请说明理由;(3)如图2,点Q 是线段BC 上一点,且CQ =,点M 是y 轴上一个动点,求△AQM的最小周长.解:(1)∵抛物线y=ax2+bx+c与x轴交于点A、B两点,对称轴为直线x=4,∴点A的坐标为(2,0).∵抛物线y=ax2+bx+c过点A(2,0),B(6,0),C(0,6),∴,解得a=,b=﹣4,c=6.∴抛物线的解析式为:y=;(2)设P(4,y),∵B(6,0),C(0,6),∴BC2=62+62=72,PB2=22+y2,PC2=42+(y﹣6)2,当∠PBC=90°时,BC2+PB2=PC2,∴72+22+y2=42+(y﹣6)2,解得:y=﹣2,∴P(4,﹣2);当∠PCB=90°时,PC2+BC2=PB2,∴42+(y﹣6)2+72=22+y2,解得:y=10,∴P(4,10);当∠BPC=90°时,PC2+PB2=BC2.∴42+(y﹣6)2+22+y2=72,解得:y=3.∴P(4,3+)或P(4,3﹣).综合以上可得点P的坐标为(4,﹣2)或(4,10)或(4,3+)或P(4,3﹣).(3)过点Q作QH⊥y轴于点H,∵B(6,0),C(0,6),∴OB=6,OC=6,∴∠OCB=45°,∴∠CQH=∠HCQ=45°,∵CQ=,∴CH=QH=,∴OH=6﹣,∴点Q的坐标为(,),在x轴上取点G(﹣2,0),连接QG交y轴于点M,则此时△AQM的周长最小,∴AQ==,QG==,∴AQ+QG=,∴△AQM的最小周长为4.6.如图,三角形ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=﹣x+3的图象与y轴、x轴的交点,点B在二次函数y=x2+bx+c的图象上,且该二次函数图象上存在一点D,使四边形ABCD能构成平行四边形.(1)试求b、c的值,并写出该二次函数表达式;(2)动点P沿线段AD从A到D,同时动点Q沿线段CA从C到A都以每秒1个单位的速度运动,问:①当P运动过程中能否存在PQ⊥AC?如果不存在请说明理由;如果存在请说明点的位置?②当P运动到何处时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?解:(1)由y=﹣x+3,令x=0,得y=3,所以点A(0,3);令y=0,得x=4,所以点C(4,0),∵△ABC是以BC为底边的等腰三角形,∴B点坐标为(﹣4,0),又∵四边形ABCD是平行四边形,∴D点坐标为(8,3),将点B(﹣4,0)、点D(8,3)代入二次函数y=x2+bx+c,∴,解得:,故该二次函数解析式为:y=x2﹣x﹣3.(2)∵OA=3,OB=4,∴AC=5.①设点P运动了t秒时,PQ⊥AC,此时AP=t,CQ=t,AQ=5﹣t,∵PQ⊥AC,∴∠AQP=∠AOC=90°,∠PAQ=∠ACO,∴△APQ∽△CAO,∴,即,解得:t=.即当点P运动到距离A点个单位长度处,有PQ⊥AC.②∵S四边形PDCQ +S△APQ=S△ACD,且S△ACD=×8×3=12,∴当△APQ的面积最大时,四边形PDCQ的面积最小,当动点P运动t秒时,AP=t,CQ=t,AQ=5﹣t,设△APQ底边AP上的高为h,作QH⊥AD于点H,由△AQH∽△CAO可得:,解得:h=(5﹣t),∴S△APQ=t×(5﹣t)=(﹣t2+5t)=﹣(t﹣)2+,∴当t=时,S△APQ 达到最大值,此时S四边形PDCQ=12﹣=,故当点P运动到距离点A个单位处时,四边形PDCQ面积最小,最小值为.7.如图,抛物线y=﹣x2+bx+c过点x轴上的A(﹣1,0)和B点,交y轴于点C,点P是该抛物线上第一象限内的一动点,且CO=3AO.(1)抛物线的解析式为:y=﹣x2+2x+3 ;(2)过点P作PD∥y轴交直线BC于点D,求点P在运动的过程中线段PD长度的最大值;(3)若sin∠BCP=,在对称轴左侧的抛物线上是否存在点Q,使∠QBC=∠PBC?若存在,请求出点Q的坐标,若不存在,请说明理由.解:(1)∵A(﹣1,0),∴OA=1,又∵CO=3AO,∴OC=3,∴C(0,3),把A,C两点的坐标代入y=﹣x2+bx+c得,,解得:,∴抛物线的解析式为y=﹣x2+2x+3,故答案为:y=﹣x2+2x+3.(2)由﹣x2+2x+3=0,得B(3,0),设直线BC的解析式为y=kx+b,将点B(3,0),C(0,3)代入得,,解得:,∴直线BC的解析式为y=﹣x+3,设点P(x,﹣x2+2x+3),则D(x,﹣x+3)(0<x<3),∴PD=(﹣x2+2x+3)﹣(﹣x+3)=﹣x2+3x=.∴当时,PD有最大值.(3)存在.∵,点P在第一象限,∴∠BCP=45°,∵B(3,0),C(0,3),∴OC=OB,∴△BOC是等腰直角三角形,∴∠OBC=∠OCB=45°,∴∠BCP=∠OCB=45°,∴CP∥OB,∴P(2,3),设BQ与y轴交于点G,在△CPB和△CGB中:2,∴△CPB≌△CGB(ASA),∴CG=CP=2,∴OG=1,∴点G(0,1),设直线BQ:y=kx+1,将点B(3,0)代入y=kx+1,∴,∴直线BQ:,联立直线BQ和二次函数解析式,解得:或(舍去),∴Q(,).8.如图,以D为顶点的抛物线y=ax2+2x+c交x轴于点A,B(6,0),交y轴于点C(0,6).(1)求抛物线的解析式;(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;(3)在x轴上是否存在一点Q,使得以A,C,Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.解:(1)将B(6,0),C(0,6)代入y=ax2+2x+c,得:,解得:,∴抛物线的解析式为y=﹣x2+2x+6.(2)当y=0时,﹣x2+2x+6=0,解得:x1=﹣2,x2=6,∴点A的坐标为(﹣2,0).∵点B的坐标为(6,0),点C的坐标为(0,6),∴直线BC的解析式为y=﹣x+6.如图1,作O关于BC的对称点O′,则点O′的坐标为(6,6).∵O与O′关于直线BC对称,∴PO=PO′,∴PO+PA的最小值=PO′+PA=AO′═=10.设直线AO′的解析式为y=kx+m,将A(﹣2,0),Q′(6,6)代入y=kx+m,得:,解得:,∴直线AO′的解析式为y=x+.联立直线AO′和直线BC的解析式成方程组,得:,解得:,∴点P的坐标为(,).(3)∵y=﹣x2+2x+6=﹣(x﹣2)2+8,∴点D的坐标为(2,8).又∵点C的坐标为(0,6),点B的坐标为(6,0),∴CD=2,BC═=6,BD═=4,∴CD2+BC2=BD2,∴∠BCD=90°.∵点A的坐标(﹣2,0),点C的坐标为(0,6),∴OA=2,OC=6,∴==2,.又∵∠AOC=∠DCB=90°,∴△AOC∽△DCB,∴当Q的坐标为(0,0)时,△AQC∽△DCB.如图2,连接AC,过点C作CQ⊥AC,交x轴与点Q.∵△ACQ为直角三角形,CO⊥AQ,∴△ACQ∽△AOC.又∵△AOC∽△DCB,∴△ACQ∽DCB,∴,即,∴AQ=20,∴点Q的坐标为(18,0).综上所述:当Q的坐标为(0,0)或(18,0)时,以A,C,Q为顶点的三角形与△BCD 相似.9.如图,抛物线L:y=ax2﹣2ax+a+k(a,k为常数且a>0)经过点C(﹣1,0),顶点为M,经过点P(0,a+4)的直线m与x轴平行,且m与L交于点A,B(B在A的右侧),与L的对称轴交于点F,直线n:y=ax+c经过点C.(1)用a表示k及点M的坐标;(2)BP﹣AP的值是否是定值?若是,请求出这个定值;若不是,请说明理由;(3)当直线n经过点B时,求a的值及点A,B的坐标;(4)当a=1时,设△ABC的外心为点N,则:①求点N的坐标;②若点Q在L的对称轴上,其纵坐标为b,且满足∠AQB<∠ACB,直接写出b的取值范围.解:(1)把点C(﹣1,0)代入L,得0=a×(1﹣)2﹣2a×(﹣1)+a+k,∴k=﹣4a.又L:y=ax2﹣2ax+a+k=a(x﹣1)2﹣4a,∴顶点M(1,﹣4a).(2)是定值.根据图象,由抛物线的轴对称性,可知BF=AF,又QL的对称轴为x=1,故PF=1,∴由图象可得,BP﹣AP=(BF+PF)﹣(AF﹣PF),=BF+PF﹣AF+PF=2PF=2.(3)当直线n经过点B时,有ax+a=a(x﹣1)2﹣4a,化简得,ax2﹣3ax﹣4a=0,∵a>0,∴x2﹣3x﹣4=0,解得:x1=﹣1,x2=4,∵B在A的右侧,对称轴为x=1,∴B(4,a+4),A(﹣2,a+4),把点B代入直线n,得a+4=4a+a,解得a=1,∴A(﹣2,5),B(4,5).(4)①根据抛物线的轴对称性可知,L的对称轴x=1就是AB的垂直平分线,故△ABC的外心N就在直线x=1上,则有AN=CN.∴设N(1,c),由(3)可知A(﹣2,5),及C(﹣1,0),∴(﹣2﹣1)2+(5﹣c)2=(﹣1﹣1)2+(0﹣c)2,即32+(5﹣c)2=22+c2,解得c=3.∴N(1,3).②或b.如图,对于点Q(1,b),若∠AQB=∠ACB,根据同弧所对的圆周角相等,可得点Q为x=1与⊙N的交点,由(4)①得,⊙N的半径为r=NC=(﹣1﹣1)2+(0﹣3)2=,则b=﹣(r﹣c)=﹣(﹣3)=3﹣;设点Q关于直线AB的对称点为Q'(1,d),若∠AQ'B=∠ACB,则d=FQ'+5=FQ+5=(5+|3﹣|)+5=+7.综上,若点Q满足∠AQB<∠ACB,则有b或b.10.如图1,抛物线y=﹣x2+bx+c与x轴交于点A(4,0),与y轴交于点B(0,4),在x轴上有一动点D(m,0)(0<m<4),过点D作x轴的垂线交直线AB于点C,交抛物线于点E,(1)直接写出抛物线和直线AB的函数表达式.(2)当点C是DE的中点时,求出m的值,并判定四边形ODEB的形状(不要求证明).(3)在(2)的条件下,将线段OD绕点O逆时针旋转得到OD′,旋转角为α(0°<a <90°),连接D′A、D′B,求D′A+D′B的最小值.解:(1)将点B、A的坐标代入抛物线y=﹣x2+bx+c得,,解得:,∴抛物线的函数表达式为y=﹣.设直线AB的解析式为y=kx+b,∴,解得:,∴直线AB的解析式为y=﹣x+4;(2)∵过点D(m,0)(0<m<4)作x轴的垂线交直线AB于点C,交抛物线于点E,∴E(m,),C(m,﹣m+4).∴EC==.∵点C是DE的中点,∴.解得:m=2,m=4(舍去).∴ED=OB=4,∴四边形ODEB为矩形.(3)如图,由(2)可知D(2,0),在y轴上取一点M′使得OM′=1,连接AM′,在AM′上取一点D′使得OD′=OD.∵OD′=2,OM′•OB=1×4=4,∴OD′2=OM′•OB,∴,∵∠BOD′=∠M′OD′,∴△M′OD′∽△D′OB,∴.∴.∴D′A+D′B=D′A+M′D′=AM′,此时D′A+D′B最小(两点间线段最短,A、M′、D′共线时),∴D′A+D′B的最小值=AM′==.11.如图,抛物线y=ax2+bx+c与x轴交于点A和点B,与y轴交于点C,且OA=2,OB=OC =6,点D是抛物线的顶点,过点D作x轴的垂线,垂足为E.(1)求抛物线的解析式及点D的坐标;(2)连接BD,若点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标:(3)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,请求出点Q的坐标.解:(1)∵OA=2,OB=OC=6,∴A(﹣2,0),B(6,0),C(0,6),∴可设抛物线解析式为y=a(x+2)(x﹣6),把C点的坐标代入可得6=﹣12a,解得a=.∴抛物线解析式为y=(x+2)(x﹣6)=﹣x2+2x+6;∴D(2,8);(2)如图1,过F作FG⊥x轴于点G,设F(x,﹣x2+2x+6),则FG=|﹣x2+2x+6|,∵∠FBA=∠BDE,∠FGB=∠BED=90°,∴△FBG∽△BDE,∴.∵B(6,0),D(2,8),∴E(2,0),BE=4,DE=8,OB=6,∴BG=6﹣x,∴,当点F在x轴上方时,有,解得x=﹣1或x=6(舍去),此时F点的坐标为(﹣1,),当点F在x轴下方时,有,解得x=﹣3或x=6(舍去),此时F点的坐标为(﹣3,),综上可知F点的坐标为(﹣1,)或(﹣3,);(3)如图2,设对角线MN、PQ交于点O′,∵点M、N关于抛物线对称轴对称,且四边形MPNQ为正方形,∴点P为抛物线对称轴与x轴的交点,点Q在抛物线的对称轴上,QO′=MO′=PO′=NO′,PQ⊥MN,设Q(2,2n),则M坐标为(2﹣n,n),∵点M在抛物线y=﹣x2+2x+6的图象上.∴n=﹣(2﹣n)2+2(2﹣n)+6,解得n=﹣1+或n=﹣1﹣,∴满足条件的点Q有两个,其坐标分别为(2,﹣2+2)或(2,﹣2﹣2).12.如图,直线y=x﹣4与x轴,y轴交于点B,C,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,抛物线经过B,C,与x轴交于另一点A.(1)求抛物线的解析式;(2)点E从A点出发,在线段AB上以每秒3个单位的速度向B点运动,同时点F从B 点出发,在线段BC上以每秒1个单位的速度向C点运动,当其中一个点到达终点时,另一个点将停止运动.设△EBF的面积为S,点E运动的时间为t.①求S与t的函数关系式,并求出S有最大值时点F的坐标;②点E,F在运动过程中,若△EBF为直角三角形,求t的值.解:(1)∵直线y=x﹣4与x轴,y轴交于点B,C,∴x=0时,y=﹣4,y=0时,x=4,∴B(4,0),C(0,﹣4).∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,∴A点坐标为(﹣2,0),∴,解得:.∴抛物线的解析式为.(2)由题意得,BF=t,BE=6﹣3t,①作FH⊥x轴,如图,∵B(4,0),C(0,﹣4).∴OB=OC=4,∴,∵FH∥BC,∴△BHF∽△BOC,∴,∴.解得:HF=.∴=.当S有最大值时,t=1,此时点F的坐标为().②∵OB=OC,∴∠OBC=45°,若∠BEF=90°,则cos∠EBF=,解得:t=.若∠EFB=90°,则cos∠EFB=.解得:t=.综合以上可得,若△EBF 为直角三角形,t 的值为或.13.如图,在直角坐标系中,y =ax 2﹣4ax +3a 与x 轴交于A 、B 两点(A 点在B 点左),与y 轴交于C 点.(1)若△ABC 的面积为,求抛物线的解析式;(2)已知点P 为B 点右侧抛物线上一点,连PC ,PB 交y 轴于D 点,若∠BCP =2∠ABC ,求的值;(3)若P 为对称轴右侧抛物线上的动点,PA 交y 轴于E 点,判断的值是否为定值,说明理由.解:(1)∵y =ax 2﹣4ax +3a 与x 轴交于A 、B 两点,∴ax 2+4 ax +3a =0,解得x 1=1,x 2=3,∴A (1,0),B (3,0),当x =0,y =3a ,∴OC =﹣3a ,∵S △ABC =, ∴, 解得a =﹣,∴抛物线的解析式为y =﹣;(2)如图,过B 点作BM ⊥x 轴交CP 于M ,过点C 作CF ⊥BM 于点F ,∵AB∥CF,∴∠ABC=∠BCF,∵∠BCP=2∠ABC,∴∠ABC=∠BCF=∠FCM,∵CF=CF,∴△CBF≌△CMF(ASA),∴BF=FM,∴M(3,6a),又∵C(0,3a),设CP解析式y=mx﹣3m,∴8a=m×2,∴m=4a,∴y=4ax﹣12a,∴,解得:x1=3,x2=5,∴P(5,8a),∴直线BP的解析式为y=4ax﹣12a,∴D(0,﹣12a),∵OC=|3a|,OD=|﹣12a|,∴;(3)∵A(1,0),∴设PA的解析式y=k1x﹣k1,∴∴ax2﹣(4a+k1)x+3a+k1=0,∴(ax﹣3a﹣k1)(x﹣1)=0,解得,x=1或x=,∴x p=3+,∵B(3,0),∴设PB的解析式y=k2x﹣3k2,∴,∴ax2﹣(4a+k2)x+3a+3k2=0,∴(ax﹣a﹣k2)(x﹣3)=0,∴x p=1+.又∵EC=﹣k1﹣3 a,DE=﹣3k2﹣3 a,∴==.14.如图,已知抛物线y=ax2﹣2x+c经过△ABC的三个顶点,其中点点A(0,1)、点B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP面积最大时,求点P的坐标;(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.解:(1)将A (0,1),B (9,10)代入函数解析式,得, 解得,∴抛物线的解析式y =x 2﹣2x +1;(2)∵AC ∥x 轴,A (0,1), ∴x 2﹣2x +1=1,解得x 1=6,x 2=0(舍),即C 点坐标为(6,1),∵点A (0,1),点B (9,10),∴直线AB 的解析式为y =x +1,设P (m ,m 2﹣2m +1),∴E (m ,m +1),∴PE =m +1﹣(m 2﹣2m +1)=﹣m 2+3m .∵AC ⊥PE ,AC =6,∴S 四边形AECP =S △AEC +S △APC =AC •EF +AC •PF =AC •(EF +PF )=AC •EP =×6×(﹣m 2+3m )=﹣m 2+9m =﹣(m ﹣)2+,∵0<m <6,∴当m =时,四边形AECP 的面积最大,此时P (,﹣);(3)∵y =x 2﹣2x +1=(x ﹣3)2﹣2,∴P (3,﹣2).∴PF=y F﹣y p=3,CF=x F﹣x C=3,∴PF=CF,∴∠PCF=45°,同理可得∠EAF=45°,∴∠PCF=∠EAF,∴在直线AC上存在满足条件得点Q,设Q(t,1)且AB=9,AC=6,CP=3,∵以C,P,Q为顶点的三角形与△ABC相似,①当△CPQ∽△ABC时,,即,解得t=4,∴Q(4,1);②当△CQP∽△ABC时,,即,解得t=﹣3,∴Q(﹣3,1).综上所述:当点P为抛物线的顶点时,在直线AC上存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,Q点的坐标为(4,1)或(﹣3,1).15.已知抛物线y=ax2+bx+3与x轴交于点A(3,0),B(1,0),与y轴交于点C.(1)求抛物线的解析式;(2)如图1,若点P为抛物线的对称轴上一点,连接BP,CP,当四边形BOCP的周长最小时,求点P的坐标;(3)如图2,点D为抛物线的顶点,在线段CD上是否存在点M(不与点C重合),使得△AMO与△ABC相似?若存在,请求出点M的坐标;若不存在,请说明理由.解:(1)∵抛物线y=ax2+bx+3与x轴交于点A(3,0),B(1,0),∴,解得:,∴抛物线的解析式为y=x2﹣4x+3;(2)∵抛物线的解析式为y=x2﹣4x+3,∴令x=0,y=3,∴C(0,3).∴OC+OB=3+1=4,∴当四边形BOCP的周长最小时,则CP+BP最小,如图1,连接AC,与对称轴的交点即为所求的点P,设直线AC的解析式为y=kx+b,∴,解得:.∴直线AC的解析式为y=﹣x+3,∵抛物线的对称轴为x==2,∴x=2时,y=﹣2+3=1,∴P(2,1).(3)∵抛物线的解析式为y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的顶点D的坐标为(2,﹣1),又∵C(0,3),∴直线CD为y=﹣2x+3,OC=3,∵A(3,0),∴AB=2,∠BAC=∠OCA=45°,∴AC=3,∴.∵∠ABC=90°+∠OCB,∴∠ABC为钝角,若△AMO与△ABC相似,显然∠ABC=∠OMA,则在线段CD上存在点M使得以M,A,O为顶点的三角形与△ABC相似,则有两种情况,①若点M在x轴上方时,如图2,当∠AOM=∠CAB=45°时,△ABC∽△OMA,设M(a,﹣2a+3),∴a=﹣2a+3,解得a=1,∴M(1,1).此时OM=,OA=3,∴,∴.则△ABC∽△OMA.②若点M在x轴下方,如图3,∵M在线段CD上,∴∠AOM≠45°,∴∠OAM=∠BAC=45°,∴M(2,﹣1),此时点M与点D重合,AM=,OA=3,∴.则△ABC∽△AMO.综合以上可得,在线段CD上存在点M(不与点C重合),使得△AMO与△ABC相似,此时点M的坐标为(1,1)或(2,﹣1).16.如图,一次函数y=﹣x+2的图象与坐标轴交于A、B两点,点C的坐标为(﹣1,0),二次函数y=ax2+bx+c的图象经过A、B、C三点.(1)求二次函数的解析式;(2)如图1,已知点D(1,n)在抛物线上,作射线BD,点Q为线段AB上一点,过点Q 作QM⊥y轴于点M,作QN⊥BD于点M,过Q作QP∥y轴交抛物线于点P,当QM与QN的积最大时,求线段PG的长;(3)在(2)的条件下,连接AP,若点E为抛物线上一点,且满足∠APE=∠ABO,求S.△OBE解:(1)一次函数y=﹣x+2的图象与坐标轴交于A、B两点,则点A、B的坐标分别为:(0,2)、(4,0),则抛物线的表达式为:y=a(x﹣4)(x+1)=a(x2﹣3x﹣4),即﹣4a=2,解得:a=﹣,则抛物线的表达式为:y=﹣x2+x+2;(2)点D(1,3),点B(4,0),则BD所在的函数表达式为:y=﹣x+4;即直线BD的倾斜角为45°,则∠QGN=45°,QN=QG,设点Q(m,﹣m+2),则点G(m,﹣m+4),QM•QN=m×(﹣m+4+m﹣2)=(﹣m2+2m),当m=2时,QM与QN的积最大,则点P(2,3);(3)设:∠APE=∠ABO=∠α,则tan;①当PE在AP下方时,如图1,由点A(0,2)、P(2,3)知,AP=,设AP与y轴的夹角为β,则tanβ=2,过点H作MH⊥PA交PA的延长线于点M,设:MA=x,则MH=2x,tan∠APH===tanα=,解得:x=,则AH=x=,则点H(0,),设直线PH的表达式为:y=kx+b,∴,解得:,∴直线PH的解析式为y=x+,联立抛物线的解析式和直线的解析式:,解得:x=2(舍去)或﹣,∴点E(﹣,﹣),∴==.②当PE在AP上方时,如图2,过点P作PM⊥y轴交于点M,交抛物线于点E,∵tan∠APM=.tan∠ABO=,∴∠APM=∠ABO,∵PE∥x轴,∴E点的纵坐标为3,将y=3代入抛物线解析式求得x=1,∴E(1,3),∴=6.综上可得△OBE的面积为或6.17.如图,抛物线y=﹣x2+bx+c与x轴分别交于点A(﹣1,0)、B(3,0),与y轴交于点C,顶点为D,对称轴交x轴于点Q.(1)求抛物线对应的二次函数的表达式;(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;(3)在抛物线的对称轴上是否存在一点M,使得△DCM与△BQC相似?如果存在,求出点M的坐标;如果不存在,请说明理由.解:(1)∵A(﹣1,0),B(3,0).代入y=﹣x2+bx+c,得,解得b=2,c=3.∴抛物线对应二次函数的表达式为:y=﹣x2+2x+3;(2)如图1,设直线CD切⊙P于点E.连结PE、PA,作CF⊥DQ于点F.∴PE⊥CD,PE=PA.由y=﹣x2+2x+3,得对称轴为直线x=1,C(0,3)、D(1,4).∴DF=4﹣3=1,CF=1,∴DF=CF,∴△DCF为等腰直角三角形.∴∠CDF=45°,∴∠EDP=∠EPD=45°,∴DE=EP,∴△DEP为等腰三角形.设P(1,m),∴EP2=(4﹣m)2.在△APQ中,∠PQA=90°,∴AP2=AQ2+PQ2=[1﹣(﹣1)]2+m2∴(4﹣m)2=[1﹣(﹣1)]2+m2.整理,得m2+8m﹣8=0解得,m=﹣4±2.∴点P的坐标为(1,﹣4+2)或(1,﹣4﹣2).(3)存在点M,使得△DCM∽△BQC.如图2,连结CQ、CB、CM,∵C(0,3),OB=3,∠COB=90°,∴△COB为等腰直角三角形,∴∠CBQ=45°,BC=3.由(2)可知,∠CDM=45°,CD=,∴∠CBQ=∠CDM.∴△DCM与△BQC相似有两种情况.当时,∴,解得DM=.∴QM=DQ﹣DM=4﹣=.∴M(1,).1当时,∴,解得DM=3,∴QM=DQ﹣DM=4﹣3=1.∴M(1,1).2综上,点M的坐标为或(1,1).18.如图,抛物线y=﹣x2+bx+c与x轴交于点A(1,0)、B(3,0)(点A在点B的左边),与y轴交于点C,过点C作CD∥x轴,交抛物线于点D,过点D作DE∥y轴,交直线BC 于点E,点P在抛物线上,过点P作PQ∥y轴交直线CE于点Q,连结PB,设点P的横坐标为m,PQ的长为d.(1)求抛物线对应的函数表达式;(2)求直线BC的函数表达式;(3)当0<m<4时,求d关于m的函数关系式;(4)当△PQB是等腰三角形时,直接写出m的值.解:(1)∵抛物线y=﹣x2+bx+c与x轴交于点A(1,0)、B(3,0),∴解得:∴抛物线解析式为:y=﹣x2+4x﹣3;(2)∵抛物线y=﹣x2+4x﹣3与y轴交于点C,∴点C(0,﹣3)设直线BC解析式为:y=kx﹣3,∴0=3k﹣3∴k=1,∴直线BC解析式为:y=x﹣3;(3)∵设点P的横坐标为m,PQ∥y轴,∴点P(m,﹣m2+4m﹣3),点Q(m,m﹣3),当0<m<3时,PQ=d=﹣m2+4m﹣3﹣(m﹣3)=﹣m2+3m,当3≤m<4时,PQ=d=(m﹣3)﹣(﹣m2+4m﹣3)=m2﹣3m;(4)B(3,0),点C(0,﹣3),∴OB=OC=3,∴∠OCB=∠OBC=45°,∵PQ∥OC,∴∠PQB=45°,若BP=PQ,∴∠PQB=∠PBQ=45°,∴∠BPQ=90°,即点P与点A重合,∴m=1,若BP=QB,∴∠BQP=∠BPQ=45°,∴∠QBP=90°,∴BP解析式为:y=﹣x+3,∴解得:,∴点P(2,1)∴m=2;若PQ=QB,∴(3﹣m)2+(m﹣3﹣0)2=(﹣m2+3m)2,或(3﹣m)2+(m﹣3﹣0)2=(m2﹣3m)2,∴m=±,综上所述:m=1或2或±.19.如图1,抛物线y=ax2+bx+c(a≠0)的顶点为C(1,4),交x轴于A、B两点,交y 轴于点D,其中点B的坐标为(3,0).(1)求抛物线的解析式;(2)如图2,点P为直线BD上方抛物线上一点,若S=3,请求出点P的坐标.△PBD(3)如图3,M为线段AB上的一点,过点M作MN∥BD,交线段AD于点N,连接MD,若△DNM∽△BMD,请求出点M的坐标.解:(1)设抛物线的解析式为y=a(x﹣1)2+4,将点B(3,0)代入得,(3﹣1)2×a+4=0.解得:a=﹣1.∴抛物线的解析式为:y=﹣(x﹣1)2+4=﹣x2+2x+3.(2)过点P作PQ∥y轴交DB于点Q,∵抛物线的解析式为y=﹣x2+2x+3∴D(0,3).设直线BD的解析式为y=kx+n,∴,解得:,∴直线BD的解析式为y=﹣x+3.设P(m,﹣m2+2m+3),则Q(m,﹣m+3),∴PQ=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m.∵S△PBD =S△PQD+S△PQB,∴S△PBD=×PQ×(3﹣m)=PQ=﹣m,∵S△PBD=3,∴﹣m=3.解得:m1=1,m2=2.∴点P的坐标为(1,4)或(2,3).(3)∵B(3,0),D(0,3),∴BD==3,设M(a,0),∵MN∥BD,∴△AMN∽△ABD,∴,即.∴MN=(1+a),DM==,∵△DNM∽△BMD,∴,∴DM2=BD•MN.∴9+a2=3(1+a).解得:a=或a=3(舍去).∴点M的坐标为(,0).20.如图,直线y=﹣x+3与x轴、y轴分别交于B、C两点,抛物线y=﹣x2+bx+c经过B、C两点,与x轴另一交点为A,顶点为D.(1)求抛物线的解析式;(2)在x轴上找一点E,使△EDC的周长最小,求符合条件的E点坐标;(3)在抛物线的对称轴上是否存在一点P,使得∠APB=∠OCB?若存在,求出PB2的值;若不存在,请说明理由.解:(1)直线y=﹣x+3与x轴、y轴分别交于B、C两点,则点B、C的坐标分别为(3,0)、(0,3),将点B、C的坐标代入二次函数表达式得:,解得:,故函数的表达式为:y=﹣x2+2x+3,(2)如图1,作点C关于x轴的对称点C′,连接CD′交x轴于点E,此时EC+ED为最小,则△EDC的周长最小,抛物线的顶点D坐标为(1,4),点C′(0,﹣3),将C′、D的坐标代入一次函数表达式并解得:∴直线C′D的表达式为:y=7x﹣3,当y=0时,x=,故点E(,0),(3)①当点P在x轴上方时,如图2,∵OB=OC=3,则∠OCB=45°=∠APB,过点B作BH⊥AP于点H,设PH=BH=a,则PB=PA=a,由勾股定理得:AB2=AH2+BH2,16=a2+(a﹣a)2,解得:a2=8+4,则PB2=2a2=16+8.②当点P在x轴下方时,同理可得.综合以上可得,PB2的值为16+8.。
2020年中考数学压轴题(含答案)
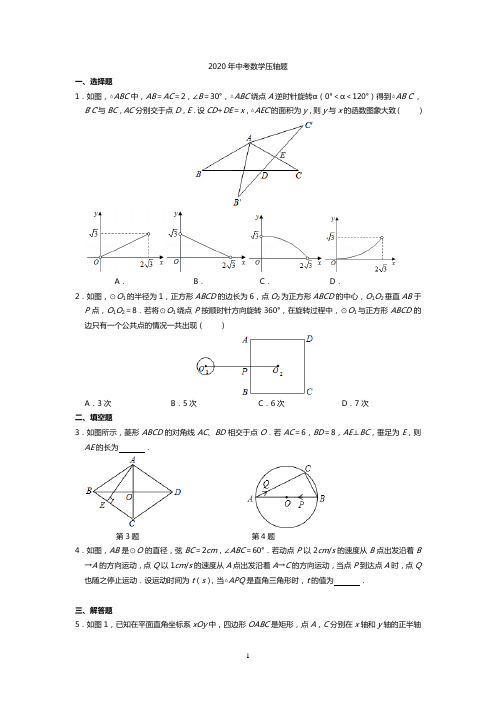
2020年中考数学压轴题一、选择题1.如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0°<α<120°)得到△AB′C′,B′C′与BC,AC分别交于点D,E.设CD+DE=x,△AEC′的面积为y,则y与x的函数图象大致()A.B.C.D.2.如图,⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,O1O2=8.若将⊙O1绕点P按顺时针方向旋转360°,在旋转过程中,⊙O1与正方形ABCD的边只有一个公共点的情况一共出现()A.3次B.5次C.6次D.7次二、填空题3.如图所示,菱形ABCD的对角线AC、BD相交于点O.若AC=6,BD=8,AE⊥BC,垂足为E,则AE的长为.第3题第4题4.如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60°.若动点P以2cm/s的速度从B点出发沿着B →A的方向运动,点Q以1cm/s的速度从A点出发沿着A→C的方向运动,当点P到达点A时,点Q 也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t的值为.三、解答题5.如图1,已知在平面直角坐标系xOy中,四边形OABC是矩形,点A,C分别在x轴和y轴的正半轴上,连结AC,OA=3,∠OAC=30°,点D是BC的中点,(1)OC=:点D的坐标为(2)若点E在线段0A上,直线DE把矩形OABC面积分成为2:1,求点E坐标;(3)如图2,点P为线段AB上一动点(与A、B重合),连接DP;①将△DBP沿DP所在的直线翻折,若点B恰好落在AC上,求此时BP的长;②以线段DP为边,在DP所在直线的右上方作等边△DPQ,当动点P从点B运动到点A时,点Q也随之运动,请直接写出点Q运动路径的长.6.如图,抛物线y=ax2+bx+4交x轴于A(﹣1,0)、B(3,0)两点,交y轴于点C,连接BC.(1)求抛物线的解析式;(2)点P是抛物线上一点,设P点的横坐标为m.①当点P在第一象限时,过点P作PD⊥x轴,交BC于点D,过点D作DE⊥y轴,垂足为E,连接PE,当△PDE和△BOC相似时,求点P的坐标;②请直接写出使∠PBA=∠ABC的点P的坐标.【答案与解析】一、选择题1.【分析】可证△ABF≌△AC′E(AAS)、△CDE≌△B′DF(AAS),则B′D+DE=CD+ED=x,y=EC′×△AEC′的EC′边上的高,即可求解.【解答】解:∵△ABC绕点A逆时针旋转α,设AB′与BC交于点F,则∠BAB′=∠CAC′=α,∠B=∠C′=30°,AB=AC=AC′,∴△ABF≌△AC′E(AAS),∴BF=C′E,AE=AF,同理△CDE≌△B′DF(AAS),∴B′D=CD,∴B′D+DE=CD+ED=x,AB=AC=2,∠B=30°,则△ABC的高为1,等于△AEC′的高,BC=2=B′C′,y=EC′×△AEC′的EC′边上的高=(2)=﹣x+,故选:B.2.【分析】根据⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,设O1O2交圆O于M,求出PM=4,得出圆O1与以P为圆心,以4为半径的圆相外切,即可得到答案.【解答】解:∵⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,设O1O2交圆O于M,∴PM=8﹣3﹣1=4,圆O1与以P为圆心,以4为半径的圆相外切,∴根据图形得出有5次.故选:B.二、填空题3.【分析】利用菱形的面积公式:•AC•BD=BC•AE,即可解决问题;【解答】解:∵四边形ABCD是菱形,∴AC⊥BD,OA=OC=3,OB=OD=4,∴AB=BC=5,∵•AC•BD=BC•AE,∴AE=,故答案为:,4.【分析】应分两种情况进行讨论:①当PQ⊥AC时,△APQ为直角三角形,根据△APQ∽△ABC,可将时间t求出;②当PQ⊥AB时,△APQ为直角三角形,根据△APQ∽△ACB,可将时间t求出.【解答】解:∵AB是直径,∴∠C=90°,又∵BC=2cm,∠ABC=60°,∴AB=2BC=4,AC=2,则AP=(4﹣2t)cm,AQ=t,∵当点P到达点A时,点Q也随之停止运动,∴0<t≤2,①如图1,当PQ⊥AC时,PQ∥BC,则△APQ∽△ABC,∴,∴,解得t=3﹣,②如图2,当PQ⊥AB时,△APQ∽△ACB,则,故,解得t=,故答案为:3﹣,.三、解答题5.【分析】(1)在Rt△AOC中,解直角三角形求出OC即可解决问题.(2)设E(m,0).由题意,分两种情形:S四边形OEDC=•(CD+OE)•OC=•S矩形OABC或S四边形OEDC=•(CD+OE)•OC=•S矩形OABC,分别构建方程即可解决问题.(3)①如图1﹣1中,在Rt△DPB中,解直角三角形求出PB即可.②如图2中,以BD为边向上作等边三角形DBQ′,连接QQ′.证明△Q′DQ≌△BDP(SAS),推出QQ′=PB,∠DQ′Q=∠DBP=90°,推出点Q的运动轨迹是线段QQ′,即可解决问题.【解答】解:(1)如图1中,∵四边形OABC是矩形,∴∠AOC=90°,∵OA=3,∠OAC=30°,∴OC=OA•tan30°=,故答案为,(,).(2)设E(m,0).由题意,S四边形OEDC=•(CD+OE)•OC=•S矩形OABC或S四边形OEDC=•(CD+OE)•OC=•S矩形OABC,∴•(CD+OE)•OC=×3×或•(CD+OE)•OC=×3×,∴•(+m)•=×3×或•(+m)•OC=×3×,解得,m=4﹣或2﹣.(3)①如图1﹣1中,∵tan∠OAC=,∴∠OAC=30°,∴∠ACB=∠OAC=30°,设将△DBP沿DP所在的直线翻折后,点B恰好落在AC上的B'处,则DB'=DB=DC,∠BDF=∠B'DF,∴∠DB'C=∠ACB=30°∴∠BDB'=60°,∴∠BDP=∠B'DF=30°,∴BP=BD•tan30°=,②如图2中,以BD为边向上作等边三角形DBQ′,连接QQ′.∵∠Q′DB=∠QDP=60°,∴∠Q′DQ=∠BDP,∵Q′D=BD,QD=PD,∴△Q′DQ≌△BDP(SAS),∴QQ′=PB,∠DQ′Q=∠DBP=90°,∴点Q的运动轨迹是线段QQ′,当动点P从点B运动到点A时,QQ′=AB=,∴点Q运动路径的长为.6.【分析】(1)用待定系数法进行解答便可;(2)①设出P点的横坐标为m,用m的代数式表示PD和DE,根据相似三角形的两种情况,由两直角边对应成比例,列出m的方程便可;②过B作BP平分∠ABC,交抛物线于点P,交OC于点M,过M作MN⊥BC于点N,设OM=x,根据勾股定理求出x值,求得M点坐标,进而求出直线BM与抛物线的交点坐标便可得出其中一个满足条件的P点坐标;再取M关于x轴的对称点K的坐标,进而求得BK与抛物线的交点坐标,便可得另一个满足条件的P点坐标.【解答】解:(1)∵抛物线y=ax2+bx+4交x轴于A(﹣1,0)、B(3,0)两点,∴,解得,,∴抛物线的解析式为:;(2)令x=0,得=4,∴C(0,4),∴OC=4,∵B(3,0),设直线BC的解析式为y=kx+n(k≠0),则,解得,∴直线BC的解析式为:y=,设P(m,),则D(m,),∴DP=,DE=m,∴,∵∠BOC=∠PDE=90°,∴当△PDE和△BOC相似时,有两种情况:当△PDE∽△BOC时,则,即=,解得,m=,∴P(,);当△PDE∽△COB时,则,即=,解得,m=2,∴P(2,4).综上,当△PDE和△BOC相似时,点P的坐标(,)或(2,4);②过B作BP平分∠ABC,交抛物线于点P,交OC于点M,过M作MN⊥BC于点N,如图1,则∠PBA=∠ABC,OM=MN,在Rt△BOM和Rt△BNM中,,∴Rt△BOM≌Rt△BNM(HL),∴BN=BO=3,设OM=t,则MN=MO=t,CM=4﹣t,CN=BC﹣BN=﹣3=2,∵MN2+CN2=MC2,∴t2+22=(4﹣t)2,∴t=,∴M(0,),设BM的解析式为:y=mx+(m≠0),代入B(3,0)得,m=,∴直线BM的解析式为:y=﹣,解方程组得,,,∴p(,),取M(0,)关于x轴的对称点,K(0,﹣),连接BK,延长BK,交抛物线于点P',如图2所示,则∠ABP=∠ABC,设直线BK的解析式为y=px(p≠0),代入B(3,0)得,p=,∴直线BK的解析式为:y﹣,解方程组得,,∴P'(,),综上,使∠PBA=∠ABC的点P的坐标为(,)或(,).2020年中考数学压轴题每日一练(5.4)一、选择题1.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是()A.5 B.6 C.7 D.82.如图,在Rt△ABC中,∠C=90°,AC=BC,AB=8,点D为AB的中点,若直角EDF绕点D旋转,分别交AC于点E,交BC于点F,则下列说法正确的个数有()①AE=CF;②EC+CF=AD;③DE=DF;④若△ECF的面积为一个定值,则EF的长也是一个定值.A.1个B.2个C.3个D.4个二、填空题3.如图,在矩形ABCD中,AB=2AD=6,点P为AB边上一点,且AP≤3,连接DP,将△ADP沿DP 折叠,点A落在点M处,连接CM,BM,当△BCM为等腰三角形时,BP的长为.第3题第4题4.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是.三、解答题5.如图,已知△ABC和△ADE均为等腰三角形,AC=BC,DE=AE,将这两个三角形放置在一起.(1)问题发现如图①,当∠ACB=∠AED=60°时,点B、D、E在同一直线上,连接CE,则∠CEB的度数为,线段AE、BE、CE之间的数量关系是;(2)拓展探究如图②,当∠ACB=∠AED=90°时,点B、D、E在同一直线上,连接CE.请判断∠CEB的度数及线段AE、BE、CE之间的数量关系,并说明理由;(3)解决问题如图③,∠ACB=∠AED=90°,AC=2,AE=2,连接CE、BD,在△AED绕点A旋转的过程中,当DE⊥BD时,请直接写出EC的长.6.如图,点A与点B的坐标分别是(1,0),(5,0),点P是该直角坐标系内的一个动点.(1)使∠APB=30°的点P有个;(2)若点P在y轴上,且∠APB=30°,求满足条件的点P的坐标;(3)当点P在y轴上移动时,∠APB是否有最大值?若有,求点P的坐标,并说明此时∠APB最大的理由;若没有,也请说明理由.【答案与解析】一、选择题1.【分析】设⊙O与AC相切于点D,连接OD,作OP⊥BC垂足为P交⊙O于F,此时垂线段OP最短,MN最小值为OP﹣OF=,当N在AB边上时,M与B重合时,MN最大值=+1=,由此不难解决问题.【解答】解:如图,设⊙O与AC相切于点D,连接OD,作OP⊥BC垂足为P交⊙O于F,此时垂线段OP最短,PF最小值为OP﹣OF,∵AC=4,BC=3,∴AB=5∵∠OPB=90°,∴OP∥AC∵点O是AB的三等分点,∴OB=×5=,==,∴OP=,∵⊙O与AC相切于点D,∴OD⊥AC,∴OD∥BC,∴==,∴OD=1,∴MN最小值为OP﹣OF=﹣1=,如图,当N在AB边上时,M与B重合时,MN经过圆心,经过圆心的弦最长,MN最大值=+1=,∴MN长的最大值与最小值的和是6.故选:B.2.【分析】①如果连接CD,可证△ADE≌△CDF,得出AE=CF;②由①知,EC+CF=EC+AE=AC,而AC为等腰直角△ABC的直角边,由于斜边AB=8,由勾股定理可求出AC=BC=4;③由①知DE=DF;④△ECF的面积=×CE×CF,如果这是一个定值,则CE•CF是一个定值,又EC+CF=4,从而可唯一确定EC与EF的值,由勾股定理知EF的长也是一个定值.【解答】解:①连接CD.∵在Rt△ABC中,∠ACB=90°,AC=BC,点D为AB的中点,∴CD⊥AB,CD=AD=DB,在△ADE与△CDF中,∠A=∠DCF=45°,AD=CD,∠ADE=∠CDF,∴△ADE≌△CDF,∴AE=CF.说法正确;②∵在Rt△ABC中,∠ACB=90°,AC=BC,AB=8,∴AC=BC=4.由①知AE=CF,∴EC+CF=EC+AE=AC=4.说法正确;③由①知△ADE≌△CDF,∴DE=DF.说法正确;④∵△ECF的面积=×CE×CF,如果这是一个定值,则CE•CF是一个定值,又∵EC+CF=4,∴可唯一确定EC与EF的值,再由勾股定理知EF的长也是一个定值,说法正确.故选:D.二、填空题3.【分析】①当BC=CM时,△BCM为等腰三角形,当BM=CM时,当△BCM为等腰三角形时,③当BC=BM=3时,由折叠的性质得,根据等腰三角形的性质和勾股定理即可得到结论.【解答】解:①如图1,当BC=CM时,△BCM为等腰三角形,∴点M落在CD边上,如图1,DN=AD=3,∴四边形APMD是正方形,∴AP=3,∵AB=CD=6,∴BP=3;②如图2,当BM=CM时,当△BCM为等腰三角形时,∴点M落在BC的垂直平分线上,如图2,过M作BC的垂直平分线交AD于H交BC于G,∴AH=DH=AD,∵将△ADP沿DP折叠,点A落在点M处,∴AD=DM,∴DH=DM,∴∠ADM=60°,∴∠ADP=∠PDM=30°,∴AP=AD=,∴PB=6﹣;③当BC=BM=3时,由折叠的性质得,DM=AD=3,∴DM+BM=6,而BD==3,∴DM+BM<BD,故这种情况不存在,综上所述,BP的长为3或6﹣,故答案为:3或6﹣.4.【分析】设QP的中点为F,圆F与AB的切点为D,连接FD,连接CF,CD,则有FD⊥AB;由勾股定理的逆定理知,△ABC是直角三角形FC+FD=PQ,由三角形的三边关系知,CF+FD>CD;只有当点F在CD上时,FC+FD=PQ有最小值为CD的长,即当点F在直角三角形ABC的斜边AB的高上CD时,PQ=CD有最小值,由直角三角形的面积公式知,此时CD=BC•AC÷AB=4.8.【解答】解:如图,∵AB=10,AC=8,BC=6,∴AB2=AC2+BC2,∴∠ACB=90°,∴PQ是⊙F的直径,设QP的中点为F,圆F与AB的切点为D,连接FD,连接CF,CD,则FD⊥AB.∴FC+FD=PQ,∴CF+FD>CD,∵当点F在直角三角形ABC的斜边AB的高上CD时,PQ=CD有最小值∴CD=BC•AC÷AB=4.8.故答案为4.8.三、解答题5.【分析】(1)证明△ACE≌△ABD,得出CE=AD,∠AEC=∠ADB,即可得出结论;(2)证明△ACE∽△ABD,得出∠AEC=∠ADB,BD=CE,即可得出结论;(3)先判断出BD=CE,再求出AB=2,①当点E在点D上方时,先判断出四边形APDE是矩形,求出AP=DP=AE=2,再根据勾股定理求出,BP=6,得出BD=4;②当点E在点D下方时,同①的方法得,AP=DP=AE=1,BP=4,进而得出BD=BP+DP=8,即可得出结论.【解答】解:(1)在△ABC为等腰三角形,AC=BC,∠ACB=60°,∴△ABC是等边三角形,∴AC=AB,∠CAB=60°,同理:AE=AD,∠AED=∠ADE=∠EAD=60°,∴∠EAD=∠CAB,∴∠EAC=∠DAB,∴△ACE≌△ABD(SAS),∴CE=AD,∠AEC=∠ADB,∵点B、D、E在同一直线上,∴∠ADB=180°﹣∠ADE=120°,∴∠AEC=120°,∴∠CEB=∠AEC﹣∠AEB=60°,∵DE=AE,∴BE=DE+BD=AE+CE,故答案为60°,BE=AE+CE;(2)在等腰三角形ABC中,AC=BC,∠ACB=90°,∴AB=AC,∠CAB=45°,同理,AD=AE,∠AED=90°,∠ADE=∠DAE=45°,∴,∠DAE=∠CAB,∴∠EAC=∠DAB,∴△ACE∽△ABD,∴,∴∠AEC=∠ADB,BD=CE,∵点B、D、E在同一条直线上,∴∠ADB=180°﹣∠ADE=135°,∴∠AEC=135°,∴∠EBC=∠AEC﹣∠AED=45°,∵DE=AE,∴BE=DE+BD=AE+CE;(3)由(2)知,△ACE∽△ABD,∴BD=CE,在Rt△ABC中,AC=2,∴AB=AC=2,①当点E在点D上方时,如图③,过点A作AP⊥BD交BD的延长线于P,∵DE⊥BD,∴∠PDE=∠AED=∠APD,∴四边形APDE是矩形,∵AE=DE,∴矩形APDE是正方形,∴AP=DP=AE=2,在Rt△APB中,根据勾股定理得,BP==6,∴BD=BP﹣AP=4,∴CE=BD=2;②当点E在点D下方时,如图④同①的方法得,AP=DP=AE=2,BP=4,∴BD=BP+DP=8,∴CE=BD=4,即:CE的长为2或4.6.【分析】(1)已知点A、点B是定点,要使∠APB=30°,只需点P在过点A、点B的圆上,且弧AB所对的圆心角为60°即可,显然符合条件的点P有无数个.(2)结合(1)中的分析可知:当点P在y轴的正半轴上时,点P是(1)中的圆与y轴的交点,借助于垂径定理、等边三角形的性质、勾股定理等知识即可求出符合条件的点P的坐标;当点P在y轴的负半轴上时,同理可求出符合条件的点P的坐标.(3)由三角形外角的性质可证得:在同圆或等圆中,同弧所对的圆周角大于同弧所对的圆外角.要∠APB最大,只需构造过点A、点B且与y轴相切的圆,切点就是使得∠APB最大的点P,然后结合切线的性质、三角形外角的性质、矩形的判定与性质、勾股定理等知识即可解决问题.【解答】解:(1)以AB为边,在第一象限内作等边三角形ABC,以点C为圆心,AC为半径作⊙C,交y轴于点P1、P2.在优弧AP1B上任取一点P,如图1,则∠APB=∠ACB=×60°=30°.∴使∠APB=30°的点P有无数个.故答案为:无数.(2)①当点P在y轴的正半轴上时,过点C作CG⊥AB,垂足为G,如图1.∵点A(1,0),点B(5,0),∴OA=1,OB=5.∴AB=4.∵点C为圆心,CG⊥AB,∴AG=BG=AB=2.∴OG=OA+AG=3.∵△ABC是等边三角形,∴AC=BC=AB=4.∴CG===2.∴点C的坐标为(3,2).过点C作CD⊥y轴,垂足为D,连接CP2,如图1,∵点C的坐标为(3,2),∴CD=3,OD=2.∵P1、P2是⊙C与y轴的交点,∴∠AP1B=∠AP2B=30°.∵CP2=CA=4,CD=3,∴DP2==.∵点C为圆心,CD⊥P1P2,∴P1D=P2D=.∴P2(0,2﹣).P1(0,2+).②当点P在y轴的负半轴上时,同理可得:P3(0,﹣2﹣).P4(0,﹣2+).综上所述:满足条件的点P的坐标有:(0,2﹣)、(0,2+)、(0,﹣2﹣)、(0,﹣2+).(3)当过点A、B的⊙E与y轴相切于点P时,∠APB最大.理由:可证:∠APB=∠AEH,当∠APB最大时,∠AEH最大.由sin∠AEH=得:当AE最小即PE最小时,∠AEH最大.所以当圆与y轴相切时,∠APB最大.①当点P在y轴的正半轴上时,连接EA,作EH⊥x轴,垂足为H,如图2.∵⊙E与y轴相切于点P,∴PE⊥OP.∵EH⊥AB,OP⊥OH,∴∠EPO=∠POH=∠EHO=90°.∴四边形OPEH是矩形.∴OP=EH,PE=OH=3.∴EA=3.∵∠EHA=90°,AH=2,EA=3,∴EH===∴OP=∴P(0,).②当点P在y轴的负半轴上时,同理可得:P(0,﹣).理由:①若点P在y轴的正半轴上,在y轴的正半轴上任取一点M(不与点P重合),连接MA,MB,交⊙E于点N,连接NA,如图2所示.∵∠ANB是△AMN的外角,∴∠ANB>∠AMB.∵∠APB=∠ANB,∴∠APB>∠AMB.②若点P在y轴的负半轴上,同理可证得:∠APB>∠AMB.综上所述:当点P在y轴上移动时,∠APB有最大值,此时点P的坐标为(0,)和(0,﹣).2020年中考数学压轴题每日一练(5.9)一、选择题1.在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为()A.(,0)B.(2,0)C.(,0)D.(3,0)2.如图,在等腰直角三角形ABC中,∠ACB=90°,BC=2,D是BC边上一动点,将AD绕点A逆时针旋转45°得AE,连接CE,则线段CE长的最小值为()A.B.C.﹣1 D.2﹣二、填空题3.如图,在矩形ABCD中,AB=5,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点F,则CF的长为.第3题第4题4.问题背景:如图1,将△ABC绕点A逆时针旋转60°得到△ADE,DE与BC交于点P,可推出结论:PA+PC =PE.问题解决:如图2,在△MNG中,MN=6,∠M=75°,MG=.点O是△MNG内一点,则点O 到△MNG三个顶点的距离和的最小值是.三、解答题5.如图(1),在△ABC中,∠C=90°,AB=5cm,BC=3cm,动点P在线段AC上以5cm/s的速度从点A运动到点C,过点P作PD⊥AB于点D,将△APD绕PD的中点旋转180°得到△A′DP,设点P的运动时间为x(s).(1)当点A′落在边BC上时,求x的值;(2)在动点P从点A运动到点C过程中,当x为何值时,△A′BC是以A′B为腰的等腰三角形;(3)如图(2),另有一动点Q与点P同时出发,在线段BC上以5cm/s的速度从点B运动到点C,过点Q作QE⊥AB于点E,将△BQE绕QE的中点旋转180°得到△B′EQ,连结A′B′,当直线A′B′与△ABC的一边垂直时,求线段A′B′的长.6.在△AOB中,∠ABO=90°,AB=3,BO=4,点C在OB上,且BC=1,(1)如图1,以O为圆心,OC长为半径作半圆,点P为半圆上的动点,连接PB,作DB⊥PB,使点D落在直线OB的上方,且满足DB:PB=3:4,连接AD①请说明△ADB∽△OPB;②如图2,当点P所在的位置使得AD∥OB时,连接OD,求OD的长;③点P在运动过程中,OD的长是否有最大值?若有,求出OD长的最大值:若没有,请说明理由.(2)如图3,若点P在以O为圆心,OC长为半径的圆上运动.连接PA,点P在运动过程中,PA﹣是否有最大值?若有,直接写出最大值;若没有,请说明理由.【答案与解析】一、选择题1.【分析】过点B作BD⊥x轴于点D,易证△ACO≌△BCD(AAS),从而可求出B的坐标,进而可求出反比例函数的解析式,根据解析式与A的坐标即可得知平移的单位长度,从而求出C的对应点.【解答】解:过点B作BD⊥x轴于点D,∵∠ACO+∠BCD=90°,∠OAC+∠ACO=90°,∴∠OAC=∠BCD,在△ACO与△BCD中,∴△ACO≌△BCD(AAS)∴OC=BD,OA=CD,∵A(0,2),C(1,0)∴OD=3,BD=1,∴B(3,1),∴设反比例函数的解析式为y=,将B(3,1)代入y=,∴k=3,∴y=,∴把y=2代入,∴x=,当顶点A恰好落在该双曲线上时,此时点A移动了个单位长度,∴C也移动了个单位长度,此时点C的对应点C′的坐标为(,0)故选:A.2.【分析】在AB上截取AF=AC=2,由旋转的性质可得AD=AE,由勾股定理可求AB=2,可得BF =2﹣2,由“SAS”可证△ACE≌△AFD,可得CE=DF,则当DF⊥BC时,DF值最小,即CE的值最小,由直角三角形的性质可求线段CE长的最小值.【解答】解:如图,在AB上截取AF=AC=2,∵旋转∴AD=AE∵AC=BC=2,∠ACB=90°∴AB=2,∠B=∠BAC=45°,∴BF=2﹣2∵∠DAE=45°=∠BAC∴∠DAF=∠CAE,且AD=AE,AC=AF∴△ACE≌△AFD(SAS)∴CE=DF,当DF⊥BC时,DF值最小,即CE的值最小,∴DF最小值为=2﹣故选:D.二、填空题3.【分析】连接OE,延长EO交CD于点G,作OH⊥B′C,由旋转性质知∠B′=∠B′CD′=90°、AB=CD =5、BC=B′C=4,从而得出四边形OEB′H和四边形EB′CG都是矩形且OE=OD=OC=2.5,继而求得CG=B′E=OH===2,根据垂径定理可得CF的长.【解答】解:连接OE,延长EO交CD于点G,作OH⊥B′C于点H,则∠OEB′=∠OHB′=90°,∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′,∴∠B′=∠B′CD′=90°,AB=CD=5、BC=B′C=4,∴四边形OEB′H和四边形EB′CG都是矩形,OE=OD=OC=2.5,∴B′H=OE=2.5,∴CH=B′C﹣B′H=1.5,∴CG=B′E=OH===2,∵四边形EB′CG是矩形,∴∠OGC=90°,即OG⊥CD′,∴CF=2CG=4,故答案为:4.4.【分析】(1)在BC上截取BG=PD,通过三角形全等证得AG=AP,BG=DP,得出△AGP是等边三角形,得出AP=GP,则PA+PC=GP+PC=GC=PE,即可证得结论;(2)以MG为边作等边三角形△MGD,以OM为边作等边△OME.连接ND,可证△GMO≌△DME,可得GO=DE,则MO+NO+GO=NO+OE+DE,即当D、E、O、N四点共线时,MO+NO+GO值最小,最小值为ND的长度,根据勾股定理先求得MF、DF,然后求ND的长度,即可求MO+NO+GO 的最小值.【解答】(1)证明:如图1,在BC上截取BG=PD,在△ABG和△ADP中,∴△ABG≌△ADP(SAS),∴AG=AP,BG=DP,∴GC=PE,∵∠GAP=∠BAD=60°,∴△AGP是等边三角形,∴AP=GP,∴PA+PC=GP+PC=GC=PE∴PA+PC=PE;(2)解:如图2:以MG为边作等边三角形△MGD,以OM为边作等边△OME.连接ND,作DF⊥NM,交NM的延长线于F.∵△MGD和△OME是等边三角形∴OE=OM=ME,∠DMG=∠OME=60°,MG=MD,∴∠GMO=∠DME在△GMO和△DME中∴△GMO≌△DME(SAS),∴OG=DE∴NO+GO+MO=DE+OE+NO∴当D、E、O、M四点共线时,NO+GO+MO值最小,∵∠NMG=75°,∠GMD=60°,∴∠NMD=135°,∴∠DMF=45°,∵MG=.∴MF=DF=4,∴NF=MN+MF=6+4=10,∴ND===2,∴MO+NO+GO最小值为2,故答案为2,三、解答题5.【分析】(1)根据勾股定理求出AC,证明△APD∽△ABC,△A′PC∽△ABC,根据相似三角形的性质计算;(2)分A′B=BC、A′B=A′C两种情况,根据等腰三角形的性质解答;(3)根据题意画出图形,根据锐角三角函数的概念计算.【解答】解:(1)如图1,∵在△ABC中,∠C=90°,AB=5cm,BC=3cm,∴AC==4cm,当点A′落在边BC上时,由题意得,四边形APA′D为平行四边形,∵PD⊥AB,∴∠ADP=∠C=90°,∵∠A=∠A,∴△APD∽△ABC,∵AP=5x,∴A′P=AD=4x,PC=4﹣5x,∵∠A′PD=∠ADP,∴A′P∥AB,∴△A′PC∽△ABC,∴,即=,解得:x=,∴当点A′落在边BC上时,x=;(2)当A′B=BC时,(5﹣8x)2+(3x)2=32,解得:.∵x≤,∴;当A′B=A′C时,x=.(3)Ⅰ、当A′B′⊥AB时,如图6,∴DH=PA'=AD,HE=B′Q=EB,∵AB=2AD+2EB=2×4x+2×3x=5,∴x=,∴A′B′=QE﹣PD=x=;Ⅱ、当A′B′⊥BC时,如图7,∴B′E=5x,DE=5﹣7x,∴cos B=,∴x=,∴A′B′=B′D﹣A′D=;Ⅲ、当A′B′⊥AC时,如图8,由(1)有,x=,∴A′B′=PA′sin A=;当A′B′⊥AB时,x=,A′B′=;当A′B′⊥BC时,x=,A′B′=;当A′B′⊥AC时,x=,A′B′=.6.【分析】(1)①由∠ABO=90°和DB⊥PB可得∠DBA=∠PBO,结合边长关系由两边对应成比例及其夹角相等的三角形相似即可证明结论.②过D点作DH⊥BO交OB延长线于H点,由AD∥OB平行可得∠DAB=90°,而△ADB∽△OPB可知∠POB=90°,由已知可求出AD.由Rt△DHO即可计算OD的长,③由△ADB∽△OPB可知,可求AD=,由此可知D在以A为圆心AD为半径的圆上运动,所以OD的最大值为OD过A点时最大.求出OA即可得到答案.(2)在OC上取点B′,使OB′=OP=,构造△BOP~△POB′,可得=PA﹣PB′≤AB',求出AB’即可求出最大值.【解答】解:(1)①∵DB⊥PB,∠ABO=90°,∴∠ADB=∠CDP,又∵AB=3,BO=4,DB:PB=3:4,即:,∴△ADB∽△OPB;②如解图(2),过D点作DH⊥BO交OB延长线于H点,∵AD∥OB,∠ABD=90°,∴∠DAB=90°,又∵△ADB∽△OPB,∴,∴AD=,∵四边形ADHB为矩形,∴HD=AB=3,HB=AD=,∴OH=OB+HB=在Rt△DHO中,OD===.③在△AOB中,∠ABO=90°,AB=3,BO=4,∴OA=5.由②得AD=,∴D在以A为圆心AD为半径的圆上运动,∴OD的最大值为OD过A点时最大,即OD的最大值为=OA+AD=5+=.(2)如解图(4),在OC上取点B′,使OB′=OP=,∵∠BOP=∠POB′,=,∴△BOP~△POB′,∴,∴=PA﹣PB′≤AB',∴∴有最大值为AB′,在Rt△ABB′中,AB=3,BB′==,∴AB′===,即:点P在运动过程中,PA﹣有最大值为,2020年中考数学压轴题每日一练(5.8)一、选择题1.如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在BC、DE上分别找一点M、N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为()A.90°B.100°C.110°D.120°2.如图,P是半圆O上一点,Q是半径OA延长线上一点,AQ=OA=1,以PQ为斜边作等腰直角三角形PQR,连接OR.则线段OR的最大值为()A.B.3 C.D.1二、填空题3.如图,E、F,G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,连接AC、HE、EC,GA,GF.已知AG⊥GF,AC=,则AB的长为.第3题第4题4.如图,AB为半圆O的直径,点C在半圆O上,AB=8,∠CAB=60°,P是弧上的一个点,连接AP,过点C作CD⊥AP于点D,连接BD,在点P移动过程中,BD长的最小值为.三、解答题5.如图,⊙O是四边形ABCD的外接圆.AC、BD是四边形ABCD的对角线,BD经过圆心O,点E在BD的延长线上,BA与CD的延长线交于点F,DF平分∠ADE.(1)求证:AC=BC;(2)若AB=AF,求∠F的度数;(3)若,⊙O半径为5,求DF的长.6.如图,△ABC是边长为2的等边三角形,点D与点B分别位于直线AC的两侧,且AD=AC,联结BD、CD,BD交直线AC于点E.(1)当∠CAD=90°时,求线段AE的长.(2)过点A作AH⊥CD,垂足为点H,直线AH交BD于点F,①当∠CAD<120°时,设AE=x,y=(其中S△BCE表示△BCE的面积,S△AEF表示△AEF的面积),求y关于x的函数关系式,并写出x的取值范围;②当=7时,请直接写出线段AE的长.【答案与解析】一、选择题1.【分析】根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和ED的对称点A′,A″,即可得出∠AA′M+∠A″=∠HAA′=60°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″)即可得出答案.【解答】解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交ED于N,则A′A″即为△AMN的周长最小值.作EA延长线AH,∵∠BAE=120°,∴∠HAA′=60°,∴∠A′+∠A″=∠HAA′=60°,∵∠A′=∠MAA′,∠NAE=∠A″,且∠A′+∠MAA′=∠AMN,∠NAE+∠A″=∠ANM,∴∠AMN+∠ANM=∠A′+∠MAA′+∠NAE+∠A″=2(∠A′+∠A″)=2×60°=120°,故选:D.2.【分析】将△RQO绕点R顺时针旋转90°,可得△RPE,可得ER=RO,∠ERO=90°,PE=OQ=2,由直角三角形的性质可得EO=RO,由三角形三边关系可得EO≤PO+EP=3,即可求解.【解答】解:将△RQO绕点R顺时针旋转90°,可得△RPE,∴ER=RO,∠ERO=90°,PE=OQ=2∴EO=RO,∵EO≤PO+EP=3∴RO≤3∴OR的最大值=故选:A.二、填空题3.【分析】如图,连接BD.由△ADG∽△GCF,设CF=BF=a,CG=DG=b,可得=,推出=,可得b=a,在Rt△GCF中,利用勾股定理求出b,即可解决问题;【解答】解:如图,连接BD.∵四边形ABCD是矩形,∴∠ADC=∠DCB=90°,AC=BD=,∵CG=DG,CF=FB,∴GF=BD=,∵AG⊥FG,∴∠AGF=90°,∴∠DAG+∠AGD=90°,∠AGD+∠CGF=90°,∴∠DAG=∠CGF,∴△ADG∽△GCF,设CF=BF=a,CG=DG=b,∴=,∴=,∴b2=2a2,∵a>0.b>0,∴b=a,在Rt△GCF中,3a2=,∴a=,∴AB=2b=2.故答案为2.4.【分析】以AC为直径作圆O′,连接BO′、BC.在点P移动的过程中,点D在以AC为直径的圆上运动,当O′、D、B共线时,BD的值最小,最小值为O′B﹣O′D,利用勾股定理求出BO′即可解决问题.【解答】解:如图,以AC为直径作圆O′,连接BO′、BC,O'D,∵CD⊥AP,∴∠ADC=90°,∴在点P移动的过程中,点D在以AC为直径的圆上运动,∵AB是直径,∴∠ACB=90°,在Rt△ABC中,∵AB=8,∠CAB=60°,∴BC=AB•sin60°=4,AC=AB•cos60°=4,∴AO'=CO'=2,∴BO'===2,∵O′D+BD≥O′B,∴当O′、D、B共线时,BD的值最小,最小值为O′B﹣O′D=2﹣2,故答案为2﹣2.三、解答题5.【分析】(1)根据角平分线的定义得到∠EDF=∠ADF,根据圆内接四边形的性质和圆周角定理结论得到结论;(2)根据圆周角定理得到AD⊥BF,推出△ACB是等边三角形,得到∠ADB=∠ACB=60°,根据等腰三角形的性质得到结论;(3)设CD=k,BC=2k,根据勾股定理得到BD==k=10,求得=2,BC=AC=4,根据相似三角形的性质即可得到结论【解答】(1)证明:∵DF平分∠ADE,∴∠EDF=∠ADF,∵∠EDF=∠ABC,∠BAC∠BDC,∠EDF=∠BDC,∴∠BAC=∠ABC,∴AC=BC;(2)解:∵BD是⊙O的直径,∴AD⊥BF,∵AF=AB,∴DF=DB,∴∠FDA=∠BDA,∴∠ADB=∠CAB=∠ACB,∴△ACB是等边三角形,∴∠ADB=∠ACB=60°,∴∠ABD=90°﹣60°=30°,∴∠F=∠ABD=30°;(3)解:∵,∴=,设CD=k,BC=2k,∴BD==k=10,∴k=2,∴CD=2,BC=AC=4,∵∠ADF=∠BAC,∴∠FAC=∠ADC,∵∠ACF=∠DCA,∴△ACF∽△DCA,∴=,∴CF=8,∴DF=CF﹣CD=6.6.【分析】(1)过点E作EG⊥BC,垂足为点G.AE=x,则EC=2﹣x.根据BG=EG构建方程求出x 即可解决问题.(2)①证明△AEF∽△BEC,可得,由此构建关系式即可解决问题.②分两种情形:当∠CAD<120°时,当120°<∠CAD<180°时,分别求解即可解决问题.【解答】解:(1)∵△ABC是等边三角形,∴AB=BC﹣AC=2,∠BAC=∠ABC=∠ACB=60°.∵AD=AC,∴AD=AB,∴∠ABD=∠ADB,∵∠ABD+∠ADB+∠BAC+∠CAD=180°,∠CAD=90°,∠ABD=15°,∴∠EBC=45°.过点E作EG⊥BC,垂足为点G.设AE=x,则EC=2﹣x.在Rt△CGE中,∠ACB=60°,∴,,∴BG=2﹣CG=1+x,在Rt△BGE中,∠EBC=45°,∴,解得.所以线段AE的长是.(2)①设∠ABD=α,则∠BDA=α,∠DAC=∠BAD﹣∠BAC=120°﹣2α.∵AD=AC,AH⊥CD,∴,又∵∠AEF=60°+α,∴∠AFE=60°,∴∠AFE=∠ACB,又∵∠AEF=∠BEC,∴△AEF∽△BEC,∴,由(1)得在Rt△CGE中,,,∴BE2=BG2+EG2=x2﹣2x+4,∴(0<x<2).②当∠CAD<120°时,y=7,则有7=,整理得3x2+x﹣2=0,解得x=或﹣1(舍弃),.当120°<∠CAD<180°时,同法可得y=当y=7时,7=,整理得3x2﹣x﹣2=0,解得x=﹣(舍弃)或1,∴AE=1.2020年中考数学压轴题每日一练(5.7)一、选择题1.已知函数y =ax 2+bx +c 的图象的一部分如图所示,则a +b +c 取值范围是( )A .﹣2<a +b +c <0B .﹣2<a +b +c <2C .0<a +b +c <2D .a +b +c <22.如图所示,矩形OABC 中,OA =2OC ,D 是对角线OB 上的一点,OD =OB ,E 是边AB 上的一点.AE =AB ,反比例函数y =(x >0)的图象经过D ,E 两点,交BC 于点F ,AC 与OB 交于点M .EF与OB 交于点G ,且四边形BFDE 的面积为.下列结论:①EF ∥AC ;②k =2;③矩形OABC 的面积为;④点F 的坐标为(,)正确结论的个数为( )A .1个B .2个C .3个D .4个 二、填空题 3.如图,二次函数y =(x +2)2+m 的图象与y 轴交于点C ,与x 轴的一个交点为A (﹣1,0),点B 在抛物线上,且与点C 关于抛物线的对称轴对称.已知一次函数y =kx +b 的图象经过A ,B 两点,根据图象,则满足不等式(x +2)2+m ≤kx +b 的x 的取值范围是 .4.如图,AE=4,以AE 为直径作⊙O ,点B 是直径AE 上的一动点,以AB 为边在AE 的上方作正方形ABCD ,取CD 的中点M ,将△ADM 沿直线AM 对折,当点D 的对应点D ´落在⊙O 上时,BE 的长为 .三、解答题5.在平面直角坐标系xOy 中,有不重合的两个点Q (x 1,y 1)与P (x 2,y 2).若Q ,P 为某个直角三角形的两个锐角顶点,且该直角三角形的直角边均与x 轴或y 轴平行(或重合),则我们将该直角三角形的两条直角边的边长之和称为点Q 与点P 之间的“折距”,记做D PQ .特别地,当PQ 与某条坐标轴平EA OB D CM D´行(或重合)时,线段PQ的长即点Q与点P之间的“折距”.例如,在图1中,点P(1,﹣1),点Q(3,﹣2),此时点Q与点P之间的“折距”D PQ=3.(1)①已知O为坐标原点,点A(3,﹣2),B(﹣1,0),则D AO=,D BO=.②点C在直线y=﹣x+4上,请你求出D CO的最小值.(2)点E是以原点O为圆心,1为半径的圆上的一个动点,点F是直线y=3x+6上以动点.请你直接写出点E与点F之间“折距”D EF的最小值.6.如图1,在矩形ABCD中,AB=4,BC=5,点E在AD上,ED=3.动点P从点B出发沿BC方向以每秒3个单位的速度向点C运动,过点P作PF∥CE,与边BA交于点F,过点F作FG∥BC,与CE交于点G,当点F与点A重合时,点P停止运动,设点P运动的时间为t秒.(1)用含t的代数式分别表示线段BF和PF的长度,则有BF=,PF=.(2)如图2,作点D关于CE的对称点D′,当FG恰好过点D′时,求t的值.(3)如图3,作△FGP的外接圆⊙O,当点P在运动过程中.①当外接圆⊙O与四边形ABCE的边BC或CE相切时,请求出符合要求的t的值;②当外接圆⊙O的圆心O落在△FGP的内部(不包括边上)时,直接写出t的取值范围.【答案与解析】一、选择题1.【分析】函数y=ax2+bx+c的图象开口向下可知a小于0,由于抛物线顶点在第一象限即抛物线对称轴在y轴右侧,当x=1时,抛物线的值必大于0由此可求出a的取值范围,将a+b+c用a表示出即可得出答案.【解答】解:由图象可知:a<0,图象过点(0,1),所以c=1,图象过点(﹣1,0),则a﹣b+1=0,当x=1时,应有y>0,则a+b+1>0,将a﹣b+1=0代入,可得a+(a+1)+1>0,解得a>﹣1,所以,实数a的取值范围为﹣1<a<0.又a+b+c=2a+2,∴0<a+b+c<2.故选:C.2.【分析】设E(a,b),F(m,n),则a=OA=BC,b=AE,CF=m,n=CO=AB,证明=即可判断①;表示出D和E的坐标,根据系数k的几何意义求得k的值即可判断②;求得B的坐标,求得矩形OABC的面积即可判断③;求得F的坐标即可判断④.【解答】解:设E(a,b),F(m,n),则a=OA=BC,b=AE,CF=m,n=CO=AB,∴B(a,n),∵E,F在反比例函数y=上,∴ab=mn,∴BC•AE=CF•AB,∴=,∴EF∥AC,故①正确;∵OD=OB,AE=AB,∴D(a,n),E(a,n),∵OA=2OC,∴a=2n,∴B(2n,n),D(n,n),E(2n,n),∵反比例函数y=经过点F,E,∴k=mn=2n•n,∴m=n,∴F(n,n),∴BF=2n﹣n=n,BE=n,∵四边形BFDE的面积=S△BDF+S△BDE=,。
2020年中考数学压轴题(含答案)
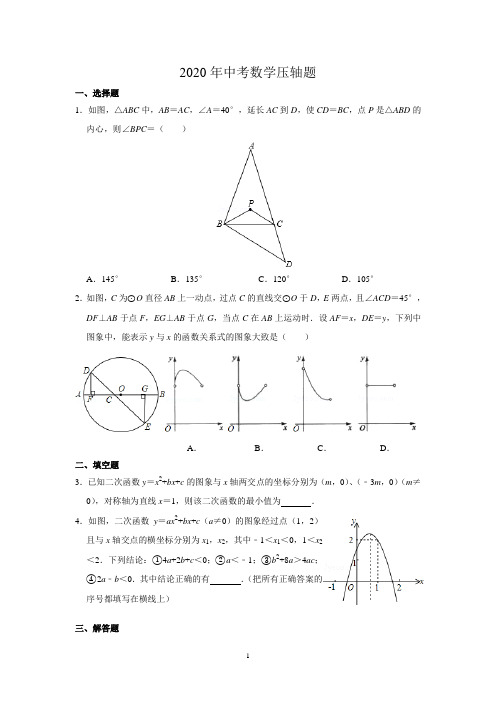
2020年中考数学压轴题一、选择题1.如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是△ABD的内心,则∠BPC=()A.145°B.135°C.120°D.105°2.如图,C为⊙O直径AB上一动点,过点C的直线交⊙O于D,E两点,且∠ACD=45°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时.设AF=x,DE=y,下列中图象中,能表示y与x的函数关系式的图象大致是()A.B.C.D.二、填空题3.已知二次函数y=x2+bx+c的图象与x轴两交点的坐标分别为(m,0)、(﹣3m,0)(m≠0),对称轴为直线x=1,则该二次函数的最小值为.4.如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣1<x1<0,1<x2<2.下列结论:①4a+2b+c<0;②a<﹣1;③b2+8a>4ac;④2a﹣b<0.其中结论正确的有.(把所有正确答案的序号都填写在横线上)三、解答题5.如图,在四边形ABCD中,AB∥DC,CB⊥AB.AB=16cm,BC=6cm,CD=8cm,动点P从点D开始沿DA边匀速运动,动点Q从点A开始沿AB边匀速运动,它们的运动速度均为2cm/s.点P和点Q同时出发,设运动的时间为t(s),0<t<5.(1)用含t的代数式表示AP;(2)当以点A.P,Q为顶点的三角形与△ABD相似时,求t的值;(3)当QP⊥BD时,求t的值.6.如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(﹣4,0),B(0,3),动点P从点O出发,沿x轴负方向以每秒1个单位的速度运动,同时动点Q从点B出发,沿射线BO方向以每秒2个单位的速度运动,过点P作PC⊥AB于点C,连接PQ,CQ,以PQ,CQ为邻边构造平行四边形PQCD,设点P运动的时间为t秒.(1)当点Q在线段OB上时,用含t的代数式表示PC,AC的长;(2)在运动过程中.①当点D落在x轴上时,求出满足条件的t的值;②若点D落在△ABO内部(不包括边界)时,直接写出t的取值范围;(3)作点Q关于x轴的对称点Q′,连接CQ′,在运动过程中,是否存在某时刻使过A,P,C三点的圆与△CQQ′三边中的一条边相切?若存在,请求出t的值;若不存在,请说明理由.【答案与解析】一、选择题1.【分析】已知P为△ABD的内心,则P点必在∠BAC的角平分线上,由于AB=AC,根据等腰三角形的性质可知:P点必在BC的垂直平分线上,即BP=PC,△BPC也是等腰三角形,欲求∠BPC,必先求出∠PBC的度数.等腰△ABC中,已知了顶角∠A的度数,可求得∠ABC、∠ACB的度数;由于CB=CD,∠ACB是△ABC的外角,由此可求出∠D和∠CBD的度数;由于P是△ABD的内心,则PB平分∠ABD,由此可求得∠PBD的度数,根据∠PBC=∠PBD﹣∠CBD可求出∠PBC的度数,由此得解.【解答】解:△ABC中,AB=AC,∠A=40°;∴∠ABC=∠ACB=70°;∵P是△ABD的内心,∴P点必在等腰△ABC底边BC的垂直平分线上,∴PB=PC,∠BPC=180°﹣2∠PBC;在△CBD中,CB=CD,∴∠CBD=∠D=∠ACB=35°;∵P是△ABD的内心,∴PB平分∠ABD,∴∠PBD=∠ABD=(∠ABC+∠CBD)=52.5°,∴∠PBC=∠PBD﹣∠CBD=52.5°﹣35°=17.5°;∴∠BPC=180°﹣2∠PBC=145°.故选:A.2.【分析】本题考查动点函数图象的问题.【解答】解:点C从点A运动到点B的过程中,x的值逐渐增大,DE的长度随x值的变化先变大再变小,当C与O重合时,y有最大值,∵x=0,y=ABx=AB﹣AB时,DE过点O,此时:DE=ABx=AB,y=AB所以,随着x的增大,y先增后降,类抛物线故选:A.二、填空题3.【分析】根据抛物线与x轴的交点坐标和抛物线的对称性得到x=﹣m=1,解得m=﹣1,则抛物线与x轴两交点的坐标分别为(﹣1,0)、(3,0),根据抛物线的交点式得到y=(x+1)(x﹣3)=x2﹣2x﹣3=(x﹣1)2﹣4,然后根据抛物线的最值问题求解.【解答】解:∵二次函数y=x2+bx+c的图象与x轴两交点的坐标分别为(m,0)、(﹣3m,0)(m≠0),∴抛物线的对称轴为直线x=﹣m=1,解得m=﹣1,∴抛物线与x轴两交点的坐标分别为(﹣1,0)、(3,0),∴y=(x+1)(x﹣3)=x2﹣2x﹣3=(x﹣1)2﹣4,∴x=1时,y的最小值为﹣4.故答案为﹣4.4.【分析】由抛物线可知当x=2时y<0,x=﹣1时y<0,则有4a+2b+c<0,a﹣b+c<0;由抛物线过(1,2)可得a+b+c=2;由抛物线的开口方向可得a<0;由抛物线的顶点位置和对称轴位置可得,>0;然后进行推理,即可对各个结论作出判断.【解答】解:由二次函数的图象可得:当x=2时y<0,则有4a+2b+c<0(1),故①正确;∵二次函数的图象经过点(1,2),∴a+b+c=2(2),由二次函数的图象可得:当x=﹣1时,y<0,则有a﹣b+c<0(3),把(2)代入(1)得到2+3a+b<0,则有a<,把(2)代入(3)得到2﹣2b<0,则有b>1,则a<﹣1,故②正确;由二次函数的图象中顶点的位置,可得:>2(4),由抛物线开口向下,可得:a<0,则由(4)可得4ac﹣b2<8a,即b2+8a>4ac,故③正确;由抛物线的对称轴的位置,可得>0,则b>0,又由a<0,则有2a﹣b<0,故④正确;故答案为:①②③④.三、解答题5.【分析】(1)如图作DH⊥AB于H则四边形DHBC是矩形,利用勾股定理求出AD的长即可解决问题;(2)根据相似三角形的性质列方程即可得到结论;(3)当PQ⊥BD时,∠PQN+∠DBA=90°,∠QPN+∠PQN=90°,推出∠QPN=∠DBA,推出tan∠QPN==,由此构建方程即可解决问题.【解答】解:(1)如图作DH⊥AB于H,则四边形DHBC是矩形,∴CD=BH=8,DH=BC=6,∴AH=AB﹣BH=8,AD==10,BD==10,由题意AP=AD﹣DP=10﹣2t.(2)当以点A.P,Q为顶点的三角形与△ABD相似时,∴或,∴=或,解得:t=或t=,∴当t=或t=时,当以点A,P,Q为顶点的三角形与△ABD相似;(3)过P作PN⊥AB于N,当PQ⊥BD时,∠PQN+∠DBA=90°,∵∠QPN+∠PQN=90°,∴∠QPN=∠DBA,∴tan∠QPN==,∴=,解得t=,经检验:t=是分式方程的解,∴当t=s时,PQ⊥BD.6.【分析】(1)利用三角函数sin∠OAB==,cos∠OAB==,列出关系式即可解决问题.(2)①当D在x轴上时,如图2中,由QC∥OA,得=,由此即可解决问题.②当点D在AB上时,如图3中,由PQ∥AB,得=,求出时间t,求出①②两种情形时的△POQ的面积即可解决问题.(3)如图4中,当QC与⊙M相切时,则QC⊥CM,首先证明QB=QC,作QN∠BC 于N,根据cos∠ABO==,列出方程即可解决问题,当CQ′是⊙M切线时,方法类似,t=0时,也符合题意;【解答】解:(1)如图1中,∵OA=3,OB=4,∴AB===5,在Rt△ACP中,P A=4﹣t,∵sin∠OAB==,∴PC=(4﹣t),∵cos∠OAB==,∴AC=(4﹣t).(2)①当D在x轴上时,如图2中,∵QC∥OA,∴=,∴=,解得t=.∴t=s时,点D在x轴上,②如图3中,∵PQ∥AB,∴=,∴=,∴t=,综上所述,当<t<时,点D落在△ABO内部(不包括边界).(3)如图4中,作QN⊥BC于N,∵Q(0,3﹣2t),Q′(0,2t﹣3),当QC与⊙M相切时,则QC⊥CM,∴∠QCM=90°,∴∠QCP+∠PCM=90°,∵∠QCP+∠QCB=90°,∴∠BCQ=∠PCM=∠CPM,∵∠CPM+∠P AC=90°,∠OBA+∠OAB=90°,∴∠APC=∠OBA,∴∠QBC=∠QCB,∴BQ=CQ,∵cos∠ABO==,∴=,解得t=,当CQ′是⊙M切线时,同法可得=,解得t=,t=0时,⊙M与QQ′相切∴t=0s或s或时,过A,P,C三点的圆与△CQQ′三边中的一条边相切.2020年中考数学压轴题一、选择题1.如图,菱形AOBC的顶点A在x轴上,反比例函数kyx=(0,0k x>>)的图像经过顶点B,和边AC的中点D.若6OA=,则k的值为A. 5B. 25C. 45D.852.已知⊙O的半径为2,A为圆内一定点,AO=1.P为圆上一动点,以AP为边作等腰△APG,AP=PG,∠APG=120°,OG的最大值为()A.1+B.1+2C.2+D.2﹣1二、填空题3.如图,矩形ABCD中,E为BC的中点,将△ABE沿直线AE折叠,使点B落在点F处,连接FC,若∠DAF=18°,则∠DCF=度.第3题第4题4.如图,抛物线y=x2﹣4与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段P A的中点,连结OQ.则线段OQ的最大值是.三、解答题5.如图,平面直角坐标系中,O为原点,点A、B分别在y轴、x轴的正半轴上.△AOB 的两条外角平分线交于点P,P在反比例函数y=的图象上.P A的延长线交x轴于点C,PB的延长线交y轴于点D,连接CD.(1)求∠P的度数及点P的坐标;(2)求△OCD的面积;(3)△AOB的面积是否存在最大值?若存在,求出最大面积;若不存在,请说明理由.6.已知:如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O.点P 从点A出发,沿AD方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6),解答下列问题:(1)当t为何值时,△AOP是等腰三角形?(2)设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式;(3)在运动过程中,是否存在某一时刻t,使S五边形OECQF:S△ACD=9:16?若存在,求出t的值;若不存在,请说明理由;(4)在运动过程中,是否存在某一时刻t,使OD平分∠COP?若存在,求出t的值;若不存在,请说明理由.【答案与解析】一、选择题 1.【分析】如图,延长CB 交y 轴于点E ,设出D 点坐标,表示出C ,B 的坐标,因为B ,D 在反比例函数图像上,利用反比例函数积为定值,从而构造出方程,进而解决问题. 【解答】延长CB 交y 轴于点E ,设D (a ,k a ),所以C (2a -6, 2k a ),B (2a -12, 2ka )因为,B (2a -12,2k a )在反比例函数y=kx上, 所以,(2a -12)·2ka =k ,解得a =8 所以B (4, k4)所以BE =4,因为BO =6,在直角三角形BEO 中,由勾股定理得EO =2 5 所以k =4×2 5 =8 5 故选D2.【分析】如图,将线段OA 绕点O 顺时针旋转120°得到线段OT ,连接AT ,GT ,OP .则AO =OT =1,AT =,利用相似三角形的性质求出GT ,再根据三角形的三边关系解决问题即可,【解答】解:如图,将线段OA 绕点O 顺时针旋转120°得到线段OT ,连接AT ,GT ,OP .则AO =OT =1,AT =,∵△AOT ,△APG 都是顶角为120°的等腰三角形, ∴∠OAT =∠P AG =30°,E∴∠OAP=∠TAG,==∴=,∴△OAP∽△TAG,∴==,∵OP=2,∴TG=2,∵OG≤OT+GT,∴OG≤1+2,∴OG的最大值为1+2,故选:B.二、填空题3.【分析】由折叠的性质得:FE=BE,∠F AE=∠BAE,∠AEB=∠AEF,求出∠BAE=∠F AE=36°,由直角三角形的性质得出∠AEF=∠AEB=54°,求出∠CEF=72°,求出FE=CE,由等腰三角形的性质求出∠ECF=54°,即可得出∠DCF的度数.【解答】解:∵四边形ABCD是矩形,∴∠BAD=∠B=∠BCD=90°,由折叠的性质得:FE=BE,∠F AE=∠BAE,∠AEB=∠AEF,∵∠DAF=18°,∴∠BAE=∠F AE=(90°﹣18°)=36°,∴∠AEF=∠AEB=90°﹣36°=54°,∴∠CEF=180°﹣2×54°=72°,∵E为BC的中点,∴BE=CE,∴FE=CE,∴∠ECF=(180°﹣72°)=54°,∴∠DCF=90°﹣∠ECF=36°;故答案为:36.4.【分析】连接BP,如图,先解方程x2﹣4=0得A(﹣4,0),B(4,0),再判断OQ为△ABP的中位线得到OQ=BP,利用点与圆的位置关系,BP过圆心C时,PB最大,如图,点P运动到P′位置时,BP最大,然后计算出BP′即可得到线段OQ的最大值.【解答】解:连接BP,如图,当y=0时,x2﹣4=0,解得x1=4,x2=﹣4,则A(﹣4,0),B(4,0),∵Q是线段P A的中点,∴OQ为△ABP的中位线,∴OQ=BP,当BP最大时,OQ最大,而BP过圆心C时,PB最大,如图,点P运动到P′位置时,BP最大,∵BC==5,∴BP′=5+2=7,∴线段OQ的最大值是.三、解答题5.【分析】(1)如图,作PM⊥OAYM,PN⊥OB于N,PH⊥AB于H.利用全等三角形的性质解决问题即可.(2)设OA=a,OB=b,则AM=AH=3﹣a,BN=BH=3﹣b,利用勾股定理求出a,b 之间的关系,求出OC,OD即可解决问题.(3)设OA=a,OB=b,则AM=AH=3﹣a,BN=BH=3﹣b,可得AB=6﹣a﹣b,推出OA+OB+AB=6,可得a+b+=6,利用基本不等式即可解决问题.【解答】解:(1)如图,作PM⊥OAYM,PN⊥OB于N,PH⊥AB于H.∴∠PMA=∠PHA=90°,∵∠P AM=∠P AH,P A=P A,∴△P AM≌△P AH(AAS),∴PM=PH,∠APM=∠APH,同理可证:△BPN≌△BPH,∴PH=PN,∠BPN=∠BPH,∴PM=PN,∵∠PMO=∠MON=∠PNO=90°,∴四边形PMON是矩形,∴∠MPN=90°,∴∠APB=∠APH+∠BPH=(∠MPH+∠NPH)=45°,∵PM=PN,∴可以假设P(m,m),∵P(m,m)在y=上,∴m2=9,∵m>0,∴m=3,∴P(3,3).(2)设OA=a,OB=b,则AM=AH=3﹣a,BN=BH=3﹣b,∴AB=6﹣a﹣b,∵AB2=OA2+OB2,∴a2+b2=(6﹣a﹣b)2,可得ab=18﹣6a﹣6b,∴9﹣3a﹣3b=ab,∵PM∥OC,∴=,∴=,∴OC=,同法可得OD=,∴S△COD=•OC•DO====6.(3)设OA=a,OB=b,则AM=AH=3﹣a,BN=BH=3﹣b,∴AB=6﹣a﹣b,∴OA+OB+AB=6,∴a+b+=6,∴2+≤6,∴(2+)≤6,∴≤3(2﹣),∴ab≤54﹣36,∴S△AOB=ab≤27﹣18,∴△AOB的面积的最大值为27﹣18.6.【分析】(1)根据矩形的性质和勾股定理得到AC=10,①当AP=PO=t,如图1,过P 作PM⊥AO,根据相似三角形的性质得到AP=t=,②当AP=AO=t=5,于是得到结论;(2)过点O作OH⊥BC交BC于点H,已知BE=PD,则可求△BOE的面积;可证得△DFQ∽△DOC,由相似三角形的面积比可求得△DFQ的面积,从而可求五边形OECQF 的面积.(3)根据题意列方程得到t=,t=0,(不合题意,舍去),于是得到结论;(4)由角平分线的性质得到DM=DN=,根据勾股定理得到ON=OM==,由三角形的面积公式得到OP=5﹣t,根据勾股定理列方程即可得到结论.【解答】解:(1)∵在矩形ABCD中,AB=6cm,BC=8cm,∴AC=10,①当AP=PO=t,如图1,过P作PM⊥AO,∴AM=AO=,∵∠PMA=∠ADC=90°,∠P AM=∠CAD,∴△APM∽△ACD,∴,∴AP=t=,②当AP=AO=t=5,∴当t为或5时,△AOP是等腰三角形;(2)过点O作OH⊥BC交BC于点H,则OH=CD=AB=3cm.由矩形的性质可知∠PDO=∠EBO,DO=BO,又得∠DOP=∠BOE,∴△DOP≌BOE,∴BE=PD=8﹣t,则S△BOE=BE•OH=×3(8﹣t)=12﹣t.∵FQ∥AC,∴△DFQ∽△DOC,相似比为=,∴=∵S△DOC=S矩形ABCD=×6×8=12cm2,∴S△DFQ=12×=∴S五边形OECQF=S△DBC﹣S△BOE﹣S△DFQ=×6×8﹣(12﹣t)﹣=﹣t2+t+12;∴S与t的函数关系式为S=﹣t2+t+12;(3)存在,∵S△ACD=×6×8=24,∴S五边形OECQF:S△ACD=(﹣t2+t+12):24=9:16,解得t=3,或t=,∴t=3或时,S五边形S五边形OECQF:S△ACD=9:16;(4)如图3,过D作DM⊥PE于M,DN⊥AC于N,∵∠POD=∠COD,∴DM=DN=,∴ON=OM==,∵OP•DM=3PD,∴OP=5﹣t,∴PM=﹣t,∵PD2=PM2+DM2,∴(8﹣t)2=(﹣t)2+()2,解得:t=16(不合题意,舍去),t=,∴当t=时,OD平分∠COP.2020年中考数学压轴题一、选择题1.若整数a使关于x的不等式组无解,且使关于x的分式方程﹣=﹣3有正整数解,则满足条件的a的值之积为()A.28 B.﹣4 C.4 D.﹣22.如图,等边三角形ABC的边长为4,点O是△ABC的中心,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB、BC于D、E两点,连接DE,给出下列四个结论:①OD=OE;②S△ODE=S△BDE;③四边形ODBE的面积始终等于;④△BDE周长的最小值为6.上述结论中正确的个数是()A.1 B.2 C.3 D.4二、填空题3.如图,点P是⊙O的直径AB的延长线上一点,过点P作直线交⊙O于C、D两点.若AB=6,BP=2,则tan∠P AC•tan∠P AD=.第3题第4题4.如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E,F分别在AC,BC边上运动(点E不与点A,C重合),且保持ED⊥FD,连接DE,DF,EF,在此运动变化的过程中,有下列结论:①AE=CF;②EF最大值为2;③四边形CEDF的面积不随点E位置的改变而发生变化;④点C到线段EF的最大距离为.其中结论正确的有(把所有正确答案的序号都填写在横线上)三、解答题5.阅读下列材料,解答下列问题材料一:一个三位以上的自然数,如果该自然数的末三位表示的数与末三位之前的数字表示的数之差是11的倍数,我们称满足此特征的数叫“网红数”,如:65362,362﹣65=297=11×27,称65362是“网红数”.材料二:对任的自然数p均可分解为P=100x+10y+z(x≥0,0≤y≤9,0≤z≤9且x、y,z均为整数)如:5278=52×100+10×7+8,规定:G(P)=.(1)求证:任两个“网红数”之和一定能被11整除;(2)已知:S=300+10b+a,t=1000b+100a+1142(1≤a≤7,0≤b≤5,其a、b均为整数),当s+t为“网红数”时,求G(t)的最大值.6.如图已知:直线y=﹣x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.(1)求抛物线的解析式;(2)若点D的坐标为(﹣1,0),在直线y=﹣x+3上有一点P,使△ABO与△ADP相似,求出点P的坐标;(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使△ADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由.【答案与解析】一、选择题1.【分析】表示出不等式组的解集,由不等式组无解确定出a的范围,分式方程去分母转化为整式方程,表示出分式方程的解,由分式方程有正整数解确定出a的值,即可求出所求.【解答】解:不等式组整理得:,由不等式组无解,得到3a﹣2≤a+2,解得:a≤2,分式方程去分母得:ax+5=﹣3x+15,即(a+3)x=10,由分式方程有正整数解,得到x=,即a+3=1,2,10,解得:a=﹣2,2,7,综上,满足条件a的为﹣2,2,之积为﹣4,故选:B.2.【分析】连接OB、OC,如图,利用等边三角形的性质得∠ABO=∠OBC=∠OCB=30°,再证明∠BOD=∠COE,于是可判断△BOD≌△COE,所以BD=CE,OD=OE,则可对①进行判断;利用S△BOD=S△COE得到四边形ODBE的面积=S△ABC=,则可对③进行判断;作OH⊥DE,如图,则DH=EH,计算出S△ODE=OE2,利用S△ODE随OE的变化而变化和四边形ODBE的面积为定值可对②进行判断;由于△BDE的周长=BC+DE=4+DE=4+OE,根据垂线段最短,当OE⊥BC时,OE最小,△BDE的周长最小,计算出此时OE的长则可对④进行判断.【解答】解:连接OB、OC,如图,∵△ABC为等边三角形,∴∠ABC=∠ACB=60°,∵点O是△ABC的中心,∴OB=OC,OB、OC分别平分∠ABC和∠ACB,∴∠ABO=∠OBC=∠OCB=30°∴∠BOC=120°,即∠BOE+∠COE=120°,而∠DOE=120°,即∠BOE+∠BOD=120°,∴∠BOD=∠COE,在△BOD和△COE中,∴△BOD≌△COE,∴BD=CE,OD=OE,所以①正确;∴S△BOD=S△COE,∴四边形ODBE的面积=S△OBC=S△ABC=××42=,所以③正确;作OH⊥DE,如图,则DH=EH,∵∠DOE=120°,∴∠ODE=∠OEH=30°,∴OH=OE,HE=OH=OE,∴DE=OE,∴S△ODE=•OE•OE=OE2,即S△ODE随OE的变化而变化,而四边形ODBE的面积为定值,∴S△ODE≠S△BDE;所以②错误;∵BD=CE,∴△BDE的周长=BD+BE+DE=CE+BE+DE=BC+DE=4+DE=4+OE,当OE⊥BC时,OE最小,△BDE的周长最小,此时OE=,∴△BDE周长的最小值=4+2=6,所以④正确.故选:C.二、填空题3.【分析】连接BC、BD.因为AB是直径,推出∠ACB=∠ADB=90°,可得tan∠P AC•tan ∠P AD=•=•,利用相似三角形的性质转化即可解决问题;【解答】解:连接BC、BD.∵AB是直径,∴∠ACB=∠ADB=90°,∴tan∠P AC•tan∠P AD=•=•,∵△PCB∽△P AD,∴=,∵△PBD∽△PCA,∴=,∴tan∠P AC•tan∠P AD=•==,故答案为.4.【分析】①作常规辅助线连接CD,由SAS定理可证△CDF和△ADE全等,即可证得AE =CF;②根据AE=CF,设CE=x,用含x的式子表示出CF的长,根据勾股定理,即可表示出EF的长,根据二次函数的增减性,表示出EF的最小值;③由割补法可知四边形CEDF的面积保持不变;④由①可知,DE=EF,可得△DEF是等腰直角三角形,当DF与BC垂直,即DF最小时,FE取最小值2,此时点C到线段EF的最大距离.【解答】解:如图,连接CD.∵在△ABC中,AC=BC,∠ACB=90°,∴∠A=∠B=45°,∵D是AB的中点,∴CD=AD=BD,∠ADC=90°,∠ACD=∠BCD=45°,∴∠1+∠2=90°,∵ED⊥FD,∴∠2+∠3=90°,∴∠1=∠3,在△ADE和△CDF中,,∴△ADE≌△CDF(ASA),∴AE=CF;故①正确;(2)设CE=x,则CF=AE=4﹣x,在Rt△CEF中,,∵2(x﹣2)2+8有最小值,最小值为8,∴EF有最小值,最小值为.故②错误;③由①知,△ADE≌△CDF,∴S四边形EDFC=S△EDC+S△FDC=S△EDC+S△ADE=S△ADC,∴四边形CEDF的面积不随点E位置的改变而发生变化.故③正确;④由①可知,△ADE≌△CDF,∴DE=DF,∴△DEF是等腰直角三角形,∴,当EF∥AB时,∵AE=CF,∴E,F分别是AC,BC的中点,故EF是△ABC的中位线,∴EF取最小值=,∵CE=CF=2,∴此时点C到线段EF的最大距离为.故④正确.故答案为:①③④.三、解答题5.【分析】(1)设两个“网红数”为,,(n、b表示末三位表示的数,m、a表示末三位之前的数字),则n﹣m=11k,b﹣a=11h,所以+=1001m+1001a+11(k+h)=11(91m+91n+h+k),即可证明;(2)s=3×100+10b+a,t=1000(b+1)+100(a+1)+4×10+2,所以s+t=1000(b+1)+100(a+4)+10(b+4)+a+2;①当1≤a≤5时,s+t=,则﹣(b+1)能被11整除,即101a+9b+441=11×9a+2a+11b﹣2b+40×11+1能被11整除,由已知可得﹣7≤2a﹣2b+1≤11,求出a=5,b=0;②当6≤a≤7时,s+t=,则﹣(b+2)能被11整除,所以101a+9b﹣560=11×9a+2a+11b﹣2b﹣51×11+1能被11整除,可得3≤2a﹣2b+1≤15,求出a=6,b=1或a=7,b=2,分别求出相应的G(t)值即可.【解答】解:(1)设两个“网红数”为,,(n、b表示末三位表示的数,m、a表示末三位之前的数字),∴n﹣m=11k,b﹣a=11h,∵+=1001m+1001a+11(k+h)=11(91m+91n+h+k),∴m、a、k、h都是整数,∴91m+91n+h+k为整数,∴任两个“网红数”之和一定能被11整除;(2)s=3×100+10b+a,t=1000(b+1)+100(a+1)+4×10+2,∴s+t=1000(b+1)+100(a+4)+10(b+4)+a+2,①当1≤a≤5时,s+t=,则﹣(b+1)能被11整除,∴101a+9b+441=11×9a+2a+11b﹣2b+40×11+1能被11整除,∴2a﹣2b+1能被11整除,∵1≤a≤5,0≤b≤5,∴﹣7≤2a﹣2b+1≤11,∴2a﹣2b+1=0或11,∴a=5,b=0,∴t=1642,G(1642)=17.25;②当6≤a≤7时,s+t=,则﹣(b+2)能被11整除,∴101a+9b﹣560=11×9a+2a+11b﹣2b﹣51×11+1能被11整除,∴2a﹣2b+1能被11整除,∵6≤a≤7,0≤b≤5,∴3≤2a﹣2b+1≤15,∴2a﹣2b+1=11,∴a=6,b=1或a=7,b=2,∴t=2742或3842,∴G(2742)=28或G(3842)=39,∴G(t)的最大值39.6.【分析】(1)首先确定A、B、C三点的坐标,然后利用待定系数法求抛物线的解析式;(2)△ABO为等腰直角三角形,若△ADP与之相似,则有两种情形,如答图1所示.利用相似三角形的性质分别求解,避免遗漏;(3)如答图2所示,分别计算△ADE的面积与四边形APCE的面积,得到面积的表达式.利用面积的相等关系得到一元二次方程,将点E是否存在的问题转化为一元二次方程是否有实数根的问题,从而解决问题.需要注意根据(2)中P点的不同位置分别进行计算,在这两种情况下,一元二次方程的判别式均小于0,即所求的E点均不存在.【解答】解:(1)由题意得,A(3,0),B(0,3)∵抛物线经过A、B、C三点,∴把A(3,0),B(0,3),C(1,0)三点分别代入y=ax2+bx+c,得方程组解得:∴抛物线的解析式为y=x2﹣4x+3(2)由题意可得:△ABO为等腰三角形,如答图1所示,若△ABO∽△AP1D,则∴DP1=AD=4,∴P1(﹣1,4)若△ABO∽△ADP2 ,过点P2作P2 M⊥x轴于M,AD=4,∵△ABO为等腰三角形,∴△ADP2是等腰三角形,由三线合一可得:DM=AM=2=P2M,即点M与点C重合,∴P2(1,2)综上所述,点P的坐标为P1(﹣1,4),P2(1,2);(3)不存在.理由:如答图2,设点E(x,y),则S△ADE=①当P1(﹣1,4)时,S四边形AP1CE=S△ACP1+S△ACE==4+|y| ∴2|y|=4+|y|,∴|y|=4∵点E在x轴下方,∴y=﹣4,代入得:x2﹣4x+3=﹣4,即x2﹣4x+7=0,∵△=(﹣4)2﹣4×7=﹣12<0∴此方程无解②当P2(1,2)时,S四边形AP2CE=S△ACP2+S△ACE==2+|y|,∴2|y|=2+|y|,∴|y|=2∵点E在x轴下方,∴y=﹣2,代入得:x2﹣4x+3=﹣2,即x2﹣4x+5=0,∵△=(﹣4)2﹣4×5=﹣4<0∴此方程无解综上所述,在x轴下方的抛物线上不存在这样的点E.2020年中考数学压轴题一、选择题1.如图,小桥用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成,按照这样的规律排列下去,则第9个图案中共有()和黑子.A.37 B.42 C.73 D.1212.如图,已知A,B是反比例函数y=(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于t的函数图象大致为()A.B.C.D.二、填空题3.如图,长方形纸片ABCD中,AB=4,将纸片折叠,折痕的一个端点F在边AD上,另一个端点G在边BC上,若顶点B的对应点E落在长方形内部,E到AD的距离为1,BG=5,则AF的长为.第3题第4题4.如图,射线OP过Rt△ABC的边AC、AB的中点M、N,AC=4cm,BC=4cm,OM =3cm.射线OP上有一动点Q从点O出发,沿射线OP以每秒1cm的速度向右移动,以Q为圆心,QM为半径的圆,经过t秒与BC、AB中的一边所在的直线相切,请写出t的所有可能值(单位:秒)三、解答题5.△ABC内接⊙O,AD⊥BC与D,连接OA.(1)如图1,求证:∠BAO=∠CAD;(2)如图2,作BE⊥AC交CA延长线于E交⊙O于F,延长AD交⊙O于G,连接AF,求证:AD+AF=DG;(3)在第(2)问的条件下,如图3,OA交BC于点T,CA=CT,AD=2AF,AB=4,求DT长.6.如图1,在平面直角坐标系xOy中,三角形ABC如图放置,点C(0,4),点A,B 在x轴上,且OB=4OA,tan∠CBO=.(1)求过点A、C直线解析式;(2)如图2,点M为线段BC上任意一点,点D在OC上,且CD=DM,设M的横坐标为t,△CDM的面积为S,求S与t之间的函数关系式,直接写出t的取值范围;(3)在(2)的条件下,如图3,在OB上取点N,过N作NF⊥DM,垂足为点F,连接CF,AF,∠DCF+∠AFN=60°,NF=BO时,求点D的坐标.【答案与解析】一、选择题1.【分析】观察图象得到第1、2图案中黑子有1个,第3、4图案中黑子有1+2×6=13个,第5、6图案中黑子有1+2×6+4×6=37个,…,据此规律可得.【解答】解:第1、2图案中黑子有1个,第3、4图案中黑子有1+2×6=13个,第5、6图案中黑子有1+2×6+4×6=37个,第7、8图案中黑子有1+2×6+4×6+6×6=73个,第9、10图案中黑子有1+2×6+4×6+6×6+8×6=121个,故选:D.2.【分析】结合点P的运动,将点P的运动路线分成O→A、A→B、B→C三段位置来进行分析三角形OMP面积的计算方式,通过图形的特点分析出面积变化的趋势,从而得到答案.【解答】解:设∠AOM=α,点P运动的速度为a,当点P从点O运动到点A的过程中,S==a2•cosα•sinα•t2,由于α及a均为常量,从而可知图象本段应为抛物线,且S随着t的增大而增大;当点P从A运动到B时,由反比例函数性质可知△OPM的面积为k,保持不变,故本段图象应为与横轴平行的线段;当点P从B运动到C过程中,OM的长在减少,△OPM的高与在B点时相同,故本段图象应该为一段下降的线段;故选:A.二、填空题3.【分析】设EH与AD相交于点K,过点E作MN∥CD分别交AD、BC于M、N,然后求出EM、EN,在Rt△ENG中,利用勾股定理列式求出GN,再根据△GEN和△EKM相似,利用相似三角形对应边成比例列式求出EK、KM,再求出KH,然后根据△FKH和△EKM 相似,利用相似三角形对应边成比例列式求解即可.【解答】解:设EH与AD相交于点K,过点E作MN∥CD分别交AD、BC于M、N,∵E到AD的距离为1,∴EM=1,EN=4﹣1=3,在Rt△ENG中,GN===4,∵∠GEN+∠KEM=180°﹣∠GEH=180°﹣90°=90°,∠GEN+∠NGE=180°﹣90°=90°,∴∠KEM=∠NGE,又∵∠ENG=∠KME=90°,∴△GEN∽△EKM,∴==,即==,解得EK=,KM=,∴KH=EH﹣EK=4﹣=,∵∠FKH=∠EKM,∠H=∠EMK=90°,∴△FKH∽△EKM,∴=,即=,解得FH=,∴AF=FH=.故答案为.4.【分析】如图,作OG⊥AB于G,由题意OG=ON=>3,所以⊙Q在AC的左边不可能与AB相切.接下来分三种情形讨论求解即可.【解答】解:如图,作OG⊥AB于G,由题意OG=ON=>3,所以⊙Q在AC的左边不可能与AB相切.相切有三种可能:当⊙Q与BC相切时,MQ=2,∴|t﹣3|=2,∴t=1或5.当⊙Q与AB相切时,设切点为H,连接QH.易知QN=2QH,∴2﹣(t﹣3)=2(t﹣3),解得t=,综上所述,t=1s或5s或()s时,⊙Q与BC/AB相切.故答案为1s或5s或()s三、解答题5.△ABC内接⊙O,AD⊥BC与D,连接OA.(1)如图1,求证:∠BAO=∠CAD;(2)如图2,作BE⊥AC交CA延长线于E交⊙O于F,延长AD交⊙O于G,连接AF,求证:AD+AF=DG;(3)在第(2)问的条件下,如图3,OA交BC于点T,CA=CT,AD=2AF,AB=4,求DT长.【分析】(1)延长AO交圆于点M,连结BM,由∠M+∠BAM=90°,∠C+∠CAD=90°,结论可得证;(2)分别延长DA、BE交于点H,连结BG,可证得△AFM和△BGM是等腰三角形,由等腰三角形的性质可证出结论;(3)连GO并延长GO交AB于点N,连BG,由CA=CT可得∠TAC=∠ATC,证得AG =BG,得出AN长,证出△BAD∽△GAN,由比例线段可求出AD长,BD长,再证明△ADT∽△BDA,得AD2=DT•BD,则DT长可求.【解答】(1)证明:如图1,延长AO交圆于点M,连结BM,∵AM是圆的直径,∴∠ABM=90°,∴∠M+∠BAM=90°,∵AD⊥BC,∴∠C+∠CAD=90°,∵∠M=∠C,∴∠BAO=∠CAD;(2)证明:如图2,分别延长DA、BE交于点H,连结BG,∵AE⊥BE,AD⊥DC,∴∠EAH+∠H=90°,∠DAC+∠C=90°,∵∠DAC=∠EAH,∴∠H=∠C,∵四边形AFBC是圆内接四边形,∴∠EF A=∠C,∴∠EF A=∠H,∴AF=AH,又∵∠C=∠BGH,∴∠H=∠BGH,∵BD⊥GH,∴DG=DM=AD+AH=AD+AF;(3)解:如图3,连GO并延长GO交AB于点N,连BG,∵CT=AC,∴∠TAC=∠ATC,∵∠TAC=∠TAD+∠DAC,∠ATC=∠TBA+∠BAT,∠DAC=∠BAT,∴∠TAD=∠TBA,又∵∠GBC=∠DAC=∠BAO,∴AG=BG,由轴对称性质可知NG⊥AB,∴∠GNA=∠BDA=90°,AN=BN=2,∵∠NAG=∠BAD∴△BAD∽△GAN,∴,∵AD+AF=DG,AD=2AF,∴,∴,设AD=x,则AG=,∴,解得:x=4,即AD=4,∴==8,在△ADT和△BDA中,∠TAD=∠DBA,∠TDA=∠BDA=90°,∴△ADT∽△BDA,∴,∴,∴DT=2.6.【分析】(1)由锐角三角函数可求点A坐标,由待定系数法可求解析式;(2)过点M作MH⊥OC于H,由锐角三角函数可求∴∠BCO=30°,由直角三角形的性质可求CD的长,由三角形面积公式可求解;(3)作FE⊥OB于E,CP⊥EF于P,FK⊥OC于K.则四边形CPEO是矩形,设PC=OE=m.只要证明△PCF∽△EF A,可得,由此构建方程求出m即可解决问题.【解答】解:(1)∵点C(0,4),∴OC=4,∵tan∠CBO==,∴OB=4,∵OB=4OA,∴OA=1,∴点A(﹣1,0)设过点A、C直线解析式为:y=kx+4,∴0=﹣k+4,∴k=4,∴过点A、C直线解析式为:y=4x+4;(2)如图2,过点M作MH⊥OC于H,∵M的横坐标为t,∴MH=t,∵tan∠BCO===,∴∠BCO=30°,∵CD=DM,∴∠DCM=∠CMD=30°,∴∠MDH=60°,且MH⊥OC,∴DH=t,DM=2DH=t=CD,∴△CDM的面积为S=×t×t=t2,(0<t≤4)(3)作FE⊥OB于E,CP⊥EF于P,FK⊥OC于K.则四边形CPEO是矩形,∴CP=OE,CO=PE=4,设PC=OE=m.∵∠DON+∠DFN+∠ODF+∠ONF=360°,∴∠FNO=120°,∴∠FNE=60°,且EF⊥BO,FN=OB=4,∴EF=2,∴PF=2∵∠DCF+∠AFN=60°,∠DCF+∠DFC=60°,∴∠DFC=∠AFN,∴∠CF A=∠DFN=90°,∴∠FCP+∠PFC=90°,∠PFC+∠AFE=90°,∴∠PCF=∠AFE,且∠P=∠AEF=90°,∴△PCF∽△EF A,∴,∴∴m=3或﹣4(舍弃),∴F(3,2),在Rt△DEK中,∵∠DFK=30°,FK=3,∴DK=,∴OD=3,∴D(0,3).2020年中考数学压轴题一、选择题1.如图,是半径为1的圆弧,△AOC为等边三角形,D是上的一动点,则四边形AODC 的面积s的取值范围是()A.≤s≤B.<s≤C.≤s≤D.<s<2.如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和等边△ACE,F 为AB的中点,DE,AB相交于点G,若∠BAC=30,下列结论:①EF⊥AC;②AD=AE;③AD=4AG;④记△ABC的面积为S1,四边形FBCE的面积为S2,则S1:S2=2:3.其中正确的结论的序号是()A.①③B.②④C.①③④D.①②③④二、填空题3.如图,⊙O是△ABC的外接圆,其中AB是⊙O的直径,将△ABC沿AB翻折后得到△ABD,点E在AD延长线上,BE与⊙O相切于点B,分别延长线段AE、CB相交于点F,若BD=3,AE=10,则线段EF的长为.4.已知关于x的方程x2﹣4x+t﹣2=0(t为实数)两非负实数根a,b,则(a2﹣1)(b2﹣1)的最小值是.三、解答题5.如图,已知AC为正方形ABCD的对角线,点P是平面内不与点A,B重合的任意一点,连接AP,将线段AP绕点P顺时针旋转90°得到线段PE,连接AE,BP,CE.(1)求证:△APE∽△ABC;(2)当线段BP与CE相交时,设交点为M,求的值以及∠BMC的度数;(3)若正方形ABCD的边长为3,AP=1,当点P,C,E在同一直线上时,求线段BP 的长.6.如图,在平面直角坐标系xOy中,抛物线y=ax2+x+c与x轴交于A,B两点(点A 在点B的左侧),交y轴于点C,经过B,C两点的直线为y=.(1)求抛物线的函数表达式;(2)点P为抛物线上的动点,过点P作x轴的垂线,交直线BC于点M,连接PC,若△PCM为直角三角形,求点P的坐标;(3)当P满足(2)的条件,且点P在直线BC上方的抛物线上时,如图2,将抛物线沿射线BC方向平移,平移后B,P两点的对应点分别为B′,P′,取AB的中点E,连接EB′,EP′,试探究EB'+EP'是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.【答案与解析】一、选择题1.【分析】根据题意,得四边形AODC的最小面积即是三角形AOC的面积,最大面积即是当OD⊥OC时四边形的面积.要求三角形AOC的面积,作CD⊥AO于D.根据等边三角形的性质以及直角三角形的性质,求得CD=,得其面积是;要求最大面积,只需再进一步求得三角形DOC的面积,即是,则最大面积是.【解答】解:根据题意,得四边形AODC的面积最小即是三角形AOC的面积,最大面积即是当OD⊥OC时四边形的面积.作CH⊥AO于H,∵△AOC为等边三角形∴CH=∴S△AOC=;当OD⊥OC时面积最大,∴S△OCD=,则最大面积是+=∴四边形AODC的面积s的取值范围是<s≤.故选:B.2.【分析】根据直角三角形的性质和线段垂直平分线的性质,可得①正确;根据等边三角形的性质和直角三角形的斜边与直角边不相等,可得②不正确;根据等边三角形的性质、全等三角形的判定和性质、平行四边形的判定和性质,可得③正确;根据直角三角形的性质、三角形面积、梯形面积公式,可得④正确.【解答】证明:如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD 和等边△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30,下列结论:①EF。
2020年中考数学10道压轴题(附答案)(4)

2020年中考数学10道压轴题(附答案)1.已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A (-1,0)、B (0,3)两点,其顶点为D. (1) 求该抛物线的解析式;(2) 若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积;(3) △AOB 与△BDE 是否相似?如果相似,请予以证明;如果不相似,请说明理由. (注:抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫⎝⎛--a b ac a b 44,22)2. 如图,在Rt ABC △中,90A ∠=o ,6AB =,8AC =,D E ,分别是边AB AC ,的中点,点P 从点D 出发沿DE 方向运动,过点P 作PQ BC ⊥于Q ,过点Q 作QR BA ∥交AC 于R ,当点Q 与点C 重合时,点P 停止运动.设BQ x =,QR y =.(1)求点D 到BC 的距离DH 的长;(2)求y 关于x 的函数关系式(不要求写出自变量的取值范围); (3)是否存在点P ,使PQR△为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在,请说明理由.3在△ABC 中,∠A =90°,AB =4,AC =3,M 是AB 上的动点(不与A ,B 重合),过M 点作MN ∥BC 交AC 于点N .以MN 为直径作⊙O ,并在⊙O 内作内接矩形AMPN .令AM =x .(1)用含x 的代数式表示△MNP 的面积S ; (2)当x 为何值时,⊙O 与直线BC 相切? (3)在动点M 的运动过程中,记△MNP 与梯形BCNM 重合的面积为y ,试求y 关于x 的函数表达式,并求x 为何值时,y 的值最大,最大值是多少?4.如图1,在平面直角坐标系中,己知ΔAOB 是等边三角形,点A 的坐标是(0,4),点B 在第一象限,点P 是x 轴上的一个动点,连结AP ,并把ΔAOP 绕着点A 按逆时针方向A BCD ERP H QA BCM N P图 3OABC MND图 2OACMNP图 1O旋转.使边AO与AB重合.得到ΔABD.(1)求直线AB的解析式;(2)当点P运动到点(3,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使ΔOPD的面积等于3,若存在,请求出符合条件的点P的坐标;若不存在,4请说明理由.5如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.(1)求证:△BDE≌△BCF;(2)判断△BEF的形状,并说明理由;(3)设△BEF的面积为S,求S的取值范围.6如图,抛物线21:23L y x x =--+交x 轴于A 、B 两点,交y 轴于M 点.抛物线1L 向右平移2个单位后得到抛物线2L ,2L 交x 轴于C 、D 两点.(1)求抛物线2L 对应的函数表达式;(2)抛物线1L 或2L 在x 轴上方的部分是否存在点N ,使以A ,C ,M ,N 为顶点的四边形是平行四边形.若存在,求出点N 的坐标;若不存在,请说明理由;(3)若点P 是抛物线1L 上的一个动点(P 不与点A 、B 重合),那么点P 关于原点的对称点Q 是否在抛物线2L 上,请说明理由.7.如图,在梯形ABCD 中,AB ∥CD ,AB =7,CD =1,AD =BC =5.点M ,N 分别在边AD ,BC 上运动,并保持MN ∥AB ,ME ⊥AB ,NF ⊥AB ,垂足分别为E ,F .(1)求梯形ABCD 的面积; (2)求四边形MEFN 面积的最大值.(3)试判断四边形MEFN 能否为正方形,若能, 求出正方形MEFN 的面积;若不能,请说明理由.8.如图,点A (m ,m +1),B (m +3,m -1)都在反比例函数xk y 的图象上.(1)求m ,k 的值;(2)如果M 为x 轴上一点,N 为y 轴上一点,以点A ,B ,M ,N 为顶点的四边形是平行四边形,试求直线MN 的函数表达式.(3)选做题:在平面直角坐标系中,点P 的坐标为(5,0),点Q 的坐标为(0,3),把线段PQ 向右平 移4个单位,然后再向上平移2个单位,得到线段P 1Q 1, 则点P 1的坐标为 ,点Q 1的坐标为 .C D A BE F NMxO yAB 友情提示:本大题第(1)小题4分,第(2)小题7分.对完成第(2)小题有困难的同学可以做下面的(3)选做题.选做题2分,所得分数计入总分.但第(2)、(3)小题都做的,第(3)小题的得分不重复计入总分.x O y 123 1 QP 2 P 1Q 19.如图16,在平面直角坐标系中,直线33y x =--与x 轴交于点A ,与y 轴交于点C ,抛物线223(0)3y ax x c a =-+≠经过A B C ,,三点. (1)求过A B C ,,三点抛物线的解析式并求出顶点F 的坐标; (2)在抛物线上是否存在点P ,使ABP △为直角三角形,若存在,直接写出P 点坐标;若不存在,请说明理由;(3)试探究在直线AC 上是否存在一点M ,使得MBF △的周长最小,若存在,求出M 点的坐标;若不存在,请说明理由.10.如图所示,在平面直角坐标系中,矩形ABOC 的边BO 在x 轴的负半轴上,边OC 在y 轴的正半轴上,且1AB =,3OB =,矩形ABOC绕点O 按顺时针方向旋转60o 后得到矩形EFOD .点A 的对应点为点E ,点B 的对应点为点F ,点C 的对应点为点D ,抛物线2y ax bx c =++过点A E D ,,.(1)判断点E 是否在y 轴上,并说明理由; (2)求抛物线的函数表达式;A OxyBFC(3)在x 轴的上方是否存在点P ,点Q ,使以点O B P Q ,,,为顶点的平行四边形的面积是矩形ABOC 面积的2倍,且点P 在抛物线上,若存在,请求出点P ,点Q 的坐标;若不存在,请说明理由.11.已知:如图14,抛物线2334y x =-+与x 轴交于点A ,点B ,与直线34y x b =-+相交于点B ,点C ,直线34y x b =-+与y 轴交于点E . (1)写出直线BC 的解析式. (2)求ABC △的面积.(3)若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动(不与A B ,重合),同时,点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动.设运动时间为t 秒,请写出MNB △的面积S 与t 的函数关系式,并求出点M 运动多少时间时,MNB △的面积最大,最大面积是多少?y xOD EC FA B12.在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆过点C若C的坐标为(0,2),AB=5, A,B两点的横坐标X A,X B是关于X的方程2(2)10-++-=的两根:x m x n(1)求m,n的值(2)若∠ACB的平分线所在的直线l交x轴于点D,试求直线l对应的一次函数的解析式(3)过点D任作一直线`l分别交射线CA,CB(点C除外)于点M,N,则11+的值是否为定值,若是,求出定值,若不CM CN是,请说明理由13.已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A (-1,0)、B (0,3)两点,其顶点为D. (1)求该抛物线的解析式;(2)若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积;(3)△AOB 与△BDE 是否相似?如果相似,请予以证明;如果不相似,请说明理由. (注:抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛--a bac a b 44,22)14.已知抛物线c bx ax y ++=232,ACO BNDML`(Ⅰ)若1==b a ,1-=c ,求该抛物线与x 轴公共点的坐标;(Ⅱ)若1==b a ,且当11<<-x 时,抛物线与x 轴有且只有一个公共点,求c 的取值范围;(Ⅲ)若0=++c b a ,且01=x 时,对应的01>y ;12=x 时,对应的02>y ,试判断当10<<x 时,抛物线与x 轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.15.已知:如图①,在Rt △ACB 中,∠C =90°,AC =4cm ,BC =3cm ,点P 由B 出发沿BA 方向向点A 匀速运动,速度为1cm/s ;点Q 由A 出发沿AC 方向向点C 匀速运动,速度为2cm/s ;连接PQ .若设运动的时间为t (s )(0<t <2),解答下列问题:(1)当t 为何值时,PQ ∥BC ?(2)设△AQP 的面积为y (2cm ),求y 与t 之间的函数关系式; (3)是否存在某一时刻t ,使线段PQ 恰好把Rt △ACB 的周长和面积同时平分?若存在,求出此时t 的值;若不存在,说明理由;(4)如图②,连接PC ,并把△PQC 沿QC 翻折,得到四边形PQP ′C ,那么是否存在某一时刻t ,使四边形PQP ′C 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.图②A Q CPB图①QP16.已知双曲线k y x =与直线14y x =相交于A 、B 两点.第一象限上的点M (m ,n )(在A 点左侧)是双曲线k y x=上的动点.过点B 作BD ∥y 轴于点D.过N (0,-n )作NC ∥x 轴交双曲线k y x=于点E ,交BD 于点C.(1)若点D 坐标是(-8,0),求A 、B 两点坐标及k 的值. (2)若B 是CD 的中点,四边形OBCE 的面积为4,求直线CM 的解析式.(3)设直线AM 、BM 分别与y 轴相交于P 、Q 两点,且MA =pMP ,MB =qMQ ,求p -q 的值.压轴题答案1. 解:( 1)由已知得:310c b c =⎧⎨--+=⎩解得c=3,b=2∴抛物线的线的解析式为2y x =-+(2)4)所以对称轴为x=1,A,E 关于称,所以E(3,0)D BCE NO A Myx设对称轴与x 轴的交点为F所以四边形ABDE 的面积=ABO DFE BOFD S S S ∆∆++梯形=111()222AO BO BO DF OF EF DF ⋅++⋅+⋅=11113(34)124222⨯⨯++⨯+⨯⨯ =9 (3)相似如图,2222112BG DG +=+=22223332BO OE +=+= 22222425DF EF ++=所以2220BD BE +=, 220DE =即: 222BD BE DE +=,所以BDE ∆是直角三角形所以90AOB DBE ∠=∠=︒,且2AO BO BD BE ==所以AOB DBE ∆∆:.2 解:(1)Q Rt A ∠=∠,6AB =,8AC =,10BC ∴=.Q 点D 为AB 中点,132BD AB ∴==. 90DHB A ∠=∠=o Q ,B B ∠=∠.BHD BAC ∴△∽△, DH BD AC BC ∴=,3128105BD DH AC BC ∴==⨯=g . (2)QR AB Q ∥,90QRC A ∴∠=∠=o .C C ∠=∠Q ,RQC ABC ∴△∽△, RQ QCAB BC∴=,10610y x-∴=,即y 关于x 的函数关系式为:365y x =-+. (3)存在,分三种情况:①当PQ PR =时,过点P 作PM QR ⊥于M ,则QM RM =.1290∠+∠=o Q ,290C ∠+∠=o ,1C ∴∠=∠.84cos 1cos 105C ∴∠===,45QM QP ∴=, 1364251255x ⎛⎫-+ ⎪⎝⎭∴=,185x ∴=. ②当PQ RQ =时,312655x -+=, 6x ∴=.③当PR QR =时,则R 为PQ 中垂线上的点, 于是点R 为EC 的中点,11224CR CE AC ∴===.tan QR BAC CR CA ==Q , 366528x -+∴=,152x ∴=.综上所述,当x 为185或6或152时,PQR △为等腰三角形. 3解:(1)∵MN ∥BC ,∴∠AMN =∠B ,∠ANM =∠C . ∴ △AMN ∽ △ABC .∴AM AN AB AC=,即43x AN =. ∴ AN =43x . (2)分ABCD ERP H QM 21 A BCD E RP HQA BCD E R PHQACM NP 图 1O∴ S =2133248MNP AMN S S x x x ∆∆==⋅⋅=.(0<x <4) ……………3分(2)如图2,设直线BC 与⊙O 相切于点D ,连结AO ,OD ,则AO =OD =21MN .在Rt △ABC 中,BC =22AB AC +=5.由(1)知 △AMN ∽ △ABC .∴AM MN AB BC=,即45x MN=.∴ 54MN x =, ∴58OD x =. (5)分过M 点作MQ ⊥BC 于Q ,则58MQ OD x ==. 在Rt △BMQ 与Rt △BCA 中,∠B 是公共角, ∴ △BMQ ∽△BCA . ∴ BM QMBC AC=.∴55258324xBM x ⨯==,25424AB BM MA x x =+=+=. ∴ x =4996. ∴ 当x =4996时,⊙O 与直线B C 相切. (7)分(3)随点M 的运动,当P 点落在直线BC 上时,连结AP ,则O 点为AP 的中点.∵ MN ∥BC ,∴ ∠AMN =∠B ,∠AOM =∠APC . ∴ △AMO ∽ △ABP . ∴12AM AO AB AP ==. AM =MB =2. ABCMND图 2O QAC MNP图 3O故以下分两种情况讨论: ① 当0<x ≤2时,2Δ83x S y PMN ==.∴ 当x=2时,2332.82y =⨯=最大 (8)分② 当2<x <4时,设PM ,PN 分别交BC 于E ,F .∵ 四边形AMPN 是矩形, ∴ PN ∥AM ,PN =AM =x . 又∵ MN ∥BC ,∴ 四边形MBFN 是平行四边形. ∴ FN =BM =4-x . ∴ ()424PF x x x =--=-. 又△PEF ∽ △ACB . ∴2PEF ABC S PF AB S ∆∆⎛⎫= ⎪⎝⎭.∴ ()2322PEF S x ∆=-. (9)分MNP PEF y S S ∆∆=-=()222339266828x x x x --=-+-.……………………1分当2<x <4时,29668y x x =-+-298283x ⎛⎫=--+ ⎪⎝⎭. ∴当83x =时,满足2<x<4,2y =最大. (11)分综上所述,当83x =时,y 值最大,最大值是ABCMN图 4OEF2. …………………………12分4 解:(1)作BE ⊥OA ,∴ΔAOB 是等边三角形∴BE=OB ·sin60o =23B(3∵A(0,4),设AB 的解析式为4y kx =+,所以2342k +=,解得33k =-,以直线AB 的解析式为343y x =-+ (2)由旋转知,AP=AD, ∠PAD=60o , ∴ΔAPD 是等边三角形,PD=PA=2219AO OP +如图,作BE ⊥AO,DH ⊥OA,GB ⊥DH,显然ΔGBD 中∠GBD=30° ∴GD=12BD=33+3=53,∴GB=32BD=32,OH=OE+HE=OE+BG=37222+= ∴D(532,72) (3)设OP=x,则由(2)可得D(323,22x x +)若ΔOPD 的面积为:133(2)2x x +=g 解得:2321x -±=所以2321-±,0) yxH G E DBA OP567解:(1)分别过D ,C 两点作DG ⊥AB 于点G ,CH ⊥AB 于点H . ……………1分 ∵ AB ∥CD ,∴ DG =CH ,DG ∥CH .∴ 四边形DGHC 为矩形,GH =CD =1.∵ DG =CH ,AD =BC ,∠AGD =∠BHC =90°, ∴ △AGD ≌△BHC (HL ).∴ AG =BH =2172-=-GH AB =3. ………2分 ∵ 在Rt △AGD 中,AG =3,AD =5, ∴ DG =4.C D ABE F NMG H∴()174162ABCD S +⨯==梯形. ………………………………………………3分(2)∵ MN ∥AB ,ME ⊥AB ,NF ⊥AB , ∴ ME =NF ,ME ∥NF . ∴ 四边形MEFN 为矩形. ∵ AB ∥CD ,AD =BC , ∴ ∠A =∠B .∵ ME =NF ,∠MEA =∠NFB =90°, ∴ △MEA ≌△NFB (AAS ).∴ AE =BF . ……………………4分 设AE =x ,则EF =7-2x . ……………5分 ∵ ∠A =∠A ,∠MEA =∠DGA =90°, ∴ △MEA ∽△DGA . ∴ DGMEAG AE =.∴ME =x 34. …………………………………………………………6分 ∴ 6494738)2(7342+⎪⎭⎫ ⎝⎛--=-=⋅=x x x EF ME S MEFN矩形. (8)分当x =47时,ME =37<4,∴四边形MEFN 面积的最大值为649.……………9分(3)C D E FNMG H能. ……………………………………………………………………10分由(2)可知,设AE =x ,则EF =7-2x ,ME =x 34.若四边形MEFN 为正方形,则ME =EF . 即=34x 7-2x .解,得1021=x . ……………………………………………11分∴ EF =21147272105x -=-⨯=<4.∴ 四边形MEFN 能为正方形,其面积为251965142=⎪⎭⎫⎝⎛=MEFNS 正方形.8解:(1)由题意可知,()()()131-+=+m m m m .解,得 m =3. ………………………………3分∴ A (3,4),B (6,2);∴ k =4×3=12. ……………………………4分 (2)存在两种情况,如图:①当M 点在x 轴的正半轴上,N 点在y 轴的正半轴 上时,设M 1点坐标为(x 1,0),N 1点坐标为(0,y 1).∵ 四边形AN 1M 1B 为平行四边形,∴ 线段N 1M 1可看作由线段AB 向左平移3个单位, 再向下平移2个单位得到的(也可看作向下平移2个单位,再向左平移3个单位得到的).由(1)知A 点坐标为(3,4),B 点坐标为(6,2), ∴ N 1点坐标为(0,4-2),即N 1(0,2); ………………………………5分xO yAB M 1N 1M 2 N 2M 1点坐标为(6-3,0),即M 1(3,0). ………………………………6分设直线M 1N 1的函数表达式为21+=x k y ,把x =3,y =0代入,解得321-=k .∴ 直线M 1N 1的函数表达式为232+-=x y . (8)分②当M 点在x 轴的负半轴上,N 点在y 轴的负半轴上时,设M 2点坐标为(x 2,0),N 2点坐标为(0,y 2).∵ AB ∥N 1M 1,AB ∥M 2N 2,AB =N 1M 1,AB =M 2N 2, ∴ N 1M 1∥M 2N 2,N 1M 1=M 2N 2.∴ 线段M 2N 2与线段N 1M 1关于原点O 成中心对称. ∴ M 2点坐标为(-3,0),N 2点坐标为(0,-2). ………………………9分设直线M 2N 2的函数表达式为22-=x k y ,把x =-3,y =0代入,解得322-=k ,∴ 直线M 2N 2的函数表达式为232--=x y .所以,直线MN 的函数表达式为232+-=x y 或232--=x y . (11)分(3)选做题:(9,2),(4,5). ………………………………………………2分 9解:(1)Q 直线33y x =-x 轴交于点A ,与y 轴交于点C .(10)A ∴-,,(03)C -, ········································· 1分Q 点A C ,都在抛物线上,23033a c c ⎧=++⎪∴⎨⎪-=⎩ 333a c ⎧=⎪∴⎨⎪=-⎩ ∴抛物线的解析式为2323333y x x =-- ····················· 3分 ∴顶点4313F ⎛⎫- ⎪ ⎪⎝⎭, ··········································· 4分(2)存在 ················································ 5分 1(03)P -, ··················································· 7分 2(23)P -, ··················································9分(3)存在 ·············································· 10分 理由: 解法一:延长BC 到点B ',使B C BC '=,连接B F '交直线AC 于点M ,则点M 就是所求的点.······························· 11分 过点B '作B H AB '⊥于点H .B Q 点在抛物线2323333y x x =--上,(30)B ∴, 在Rt BOC △中,3tan 3OBC ∠=,30OBC ∴∠=o ,23BC =,在Rt BB H '△中,1232B H BB ''==,36BH B H '==,3OH ∴=,(323)B '∴--, (12)分设直线B F '的解析式为y kx b =+A O xyBFC HBM233433k b k b ⎧-=-+⎪∴⎨-=+⎪⎩ 解得36332k b ⎧=⎪⎪⎨⎪=-⎪⎩33362y x ∴=- ············································ 13分3333362y x y x ⎧=--⎪∴⎨=-⎪⎩ 解得371037x y ⎧=⎪⎪⎨⎪=-⎪⎩,310377M ⎛⎫∴- ⎪ ⎪⎝⎭, ∴在直线AC上存在点M ,使得MBF △的周长最小,此时310377M ⎛⎫- ⎪ ⎪⎝⎭,. ··········································· 14分解法二:过点F 作AC 的垂线交y 轴于点H ,则点H 为点F 关于直线AC 的对称点.连接BH 交AC 于点M ,则点M 即为所求. 11分过点F 作FG y ⊥轴于点G ,则OB FG ∥,BC FH ∥.90BOC FGH ∴∠=∠=o ,BCO FHG ∠=∠HFG CBO ∴∠=∠同方法一可求得(30)B ,. 在Rt BOC △中,3tan 3OBC ∠=,30OBC ∴∠=o ,可求得33GH GC ==,GF ∴为线段CH 的垂直平分线,可证得CFH △为等边三角形, AC ∴垂直平分FH .即点H 为点F 关于AC 的对称点.5303H ⎛⎫∴- ⎪ ⎪⎝⎭, ············· 12分设直线BH 的解析式为y kx b =+,由题意得A OxyBF C HM G03533k b b =+⎧⎪⎨=⎪⎩ 解得539533k b ⎧=⎪⎪⎨⎪=⎪⎩553393y ∴=··········································· 13分55339333y x y x ⎧=⎪∴⎨⎪=⎩ 解得37103x y ⎧=⎪⎪⎨⎪=⎪⎩310377M ⎛∴- ⎝⎭, ∴在直线AC上存在点M ,使得MBF △的周长最小,此时31037M ⎛ ⎝⎭. 110解:(1)点E 在y 轴上 ·································· 1分 理由如下:连接AO ,如图所示,在Rt ABO △中,1AB =Q ,3BO =,2AO ∴=1sin 2AOB ∴∠=,30AOB ∴∠=o 由题意可知:60AOE ∠=o306090BOE AOB AOE ∴∠=∠+∠=+=o o oQ 点B 在x 轴上,∴点E 在y 轴上. (3)分(2)过点D 作DM x ⊥轴于点M1OD =Q ,30DOM ∠=o∴在Rt DOM △中,12DM =,32OM =Q 点D 在第一象限,∴点D 的坐标为3122⎛⎫⎪ ⎪⎝⎭, ····································· 5分由(1)知2EO AO ==,点E 在y 轴的正半轴上∴点E 的坐标为(02),∴点A 的坐标为(31), ······································ 6分Q 抛物线2y ax bx c =++经过点E ,2c ∴=由题意,将(31)A ,,312D ⎫⎪⎪⎝⎭,代入22y ax bx =++中得 3321331242a b a ⎧+=⎪⎨+=⎪⎩ 解得8953a b ⎧=-⎪⎪⎨⎪=⎪⎩∴所求抛物线表达式为:285329y x x =-+ (9)分(3)存在符合条件的点P ,点Q . ······················ 10分 理由如下:Q 矩形ABOC 的面积3AB BO ==g ∴以O B P Q ,,,为顶点的平行四边形面积为3由题意可知OB 为此平行四边形一边, 又3OB =QOB ∴边上的高为2 ······································· 11分依题意设点P 的坐标为(2)m ,Q 点P 在抛物线285329y x x =-+上 2853229m ∴-+= 解得,10m =,2538m =-1(02)P ∴,,25328P ⎛⎫- ⎪ ⎪⎝⎭,Q 以O B P Q ,,,为顶点的四边形是平行四边形,PQ OB ∴∥,3PQ OB ==, ∴当点1P 的坐标为(02),时,点Q 的坐标分别为1(32)Q -,,2(32)Q ,;当点2P 的坐标为5328⎛⎫- ⎪ ⎪⎝⎭,时,点Q 的坐标分别为313328Q ⎛⎫-⎪ ⎪⎝⎭,,43328Q ⎛⎫⎪ ⎪⎝⎭,. ·············· 14分(以上答案仅供参考,如有其它做法,可参照给分) 11解:(1)在2334y x =-+中,令0y =23304x ∴-+= 12x ∴=,22x =-(20)A ∴-,,(20)B , ······················ 1分又Q 点B 在34y x b =-+上 302b ∴=-+ 32b = BC ∴的解析式为3342y x =-+ ·································2分 (2)由23343342y x y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩,得11194x y =-⎧⎪⎨=⎪⎩ 2220x y =⎧⎨=⎩ ···················· 4分914C ⎛⎫∴- ⎪⎝⎭,,(20)B ,y xO D EC FA B Mx yA B CE M D P N O4AB ∴=,94CD = ··········································· 5分 1994242ABCS ∴=⨯⨯=△ ·········································6分(3)过点N 作NP MB ⊥于点PEO MB ⊥Q NP EO ∴∥BNP BEO ∴△∽△ ············································7分 BN NPBE EO∴=················································· 8分由直线3342y x =-+可得:302E ⎛⎫ ⎪⎝⎭, ∴在BEO △中,2BO =,32EO =,则52BE = 25322t NP∴=,65NP t ∴= ········································ 9分 16(4)25S t t ∴=-g g2312(04)55S t t t =-+<< ······································ 10分2312(2)55S t =--+ ·········································· 11分Q 此抛物线开口向下,∴当2t =时,125S =最大∴当点M 运动2秒时,MNB △的面积达到最大,最大为125.12解: (1)m=-5,n=-3 (2)y=43x+2(3)是定值.因为点D 为∠ACB 的平分线,所以可设点D 到边AC,BC 的距离均为h ,设△ABC AB 边上的高为H, 则利用面积法可得:222CM h CN h MN H⋅⋅⋅+=(CM+CN )h=MN ﹒HCM CN MNH h+=又 H=CM CNMN⋅化简可得 (CM+CN)﹒1MN CM CN h=⋅故 111CM CN h+=13解:( 1)由已知得:310c b c =⎧⎨--+=⎩解得 c=3,b=2∴抛物线的线的解析式为223y x x =-++ (2)由顶点坐标公式得顶点坐标为(1,4)所以对称轴为x=1,A,E 关于x=1设对称轴与x 轴的交点为F所以四边形ABDE 的面积=ABO DFE BOFD S S S ∆∆++梯形=111()222AO BO BO DF OF EF DF ⋅++⋅+⋅=11113(34)124222⨯⨯++⨯+⨯⨯ =9 (3)相似如图,2222112BG DG +=+=yxDEA BFOG22223332BO OE +=+= 22222425DF EF ++=所以2220BD BE +=, 220DE =即: 222BD BE DE +=,所以BDE ∆是直角三角形所以90AOB DBE ∠=∠=︒,且22AO BO BD BE ==所以AOB DBE ∆∆:.14解(Ⅰ)当1==b a ,1-=c 时,抛物线为1232-+=x x y , 方程01232=-+x x 的两个根为11-=x ,312=x .∴该抛物线与x 轴公共点的坐标是()10-,和103⎛⎫⎪⎝⎭,. ········· 2分(Ⅱ)当1==b a 时,抛物线为c x x y ++=232,且与x 轴有公共点. 对于方程0232=++c x x ,判别式c 124-=∆≥0,有c ≤31. ······ 3分①当31=c 时,由方程031232=++x x ,解得3121-==x x .此时抛物线为31232++=x x y 与x 轴只有一个公共点103⎛⎫-⎪⎝⎭,. · 4分②当31<c 时,11-=x 时,c c y +=+-=1231, 12=x 时,c c y +=++=5232.由已知11<<-x 时,该抛物线与x 轴有且只有一个公共点,考虑其对称轴为31-=x ,应有1200.y y ⎧⎨>⎩≤, 即1050.c c +⎧⎨+>⎩≤,解得51c -<-≤.综上,31=c 或51c -<-≤. ······························ 6分(Ⅲ)对于二次函数c bx ax y ++=232,由已知01=x 时,01>=c y ;12=x 时,0232>++=c b a y , 又0=++c b a ,∴b a b a c b a c b a +=++++=++22)(23. 于是02>+b a .而c a b --=,∴02>--c a a ,即0>-c a .∴0>>c a . ············································· 7分 ∵关于x 的一元二次方程0232=++c bx ax 的判别式0])[(412)(4124222>+-=-+=-=∆ac c a ac c a ac b ,∴抛物线c bx ax y ++=232与x 轴有两个公共点,顶点在x 轴下方.8分 又该抛物线的对称轴abx 3-=,由0=++c b a ,0>c ,02>+b a , 得a b a -<<-2, ∴32331<-<a b . 又由已知01=x 时,01>y ;12=x 时,02>y ,观察图象,可知在10<<x 范围内,该抛物线与x 轴有两个公共点. ··· 10分15 解:(1)由题意:BP =tcm ,AQ =2tcm ,则CQ =(4-2t)cm , ∵∠C =90°,AC =4cm ,BC =3cm ,∴AB =5cm ∴AP =(5-t )cm ,x∵PQ ∥BC ,∴△APQ ∽△ABC ,∴AP ∶AB =AQ ∶AC ,即(5-t )∶5=2t ∶4,解得:t =107∴当t 为107秒时,PQ ∥BC ………………2分(2)过点Q 作QD ⊥AB 于点D ,则易证△AQD ∽△ABC ∴AQ ∶QD =AB ∶BC ∴2t ∶DQ =5∶3,∴DQ =65t∴△APQ 的面积:12×AP ×QD =12(5-t )×65t ∴y 与t 之间的函数关系式为:y =2335t t -………………5分(3)由题意:当面积被平分时有:2335t t -=12×12×3×4,解得:t 55± 当周长被平分时:(5-t )+2t =t +(4-2t )+3,解得:t =1∴不存在这样t 的值………………8分(4)过点P 作PE ⊥BC 于E易证:△PAE ∽△ABC ,当PE =12QC 时,△PQC 为等腰三角形,此时△QCP ′为菱形∵△PAE ∽△ABC ,∴PE ∶PB =AC ∶AB ,∴PE ∶t =4∶5,解得:PE =45t∵QC =4-2t ,∴2×45t =4-2t,解得:t =109∴当t =109时,四边形PQP ′C 为菱形 此时,PE =89,BE =23,∴CE =73………………10分在Rt △CPE 中,根据勾股定理可知:PC 22PE CE +2287()()93+=5059505cm ………………12分16 解:(1)∵D (-8,0),∴B 点的横坐标为-8,代入14y x =中,得y =-2.∴B 点坐标为(-8,-2).而A 、B 两点关于原点对称,∴A (8,2)从而k =8×2=16(2)∵N (0,-n ),B 是CD 的中点,A ,B ,M ,E 四点均在双曲线上,∴mn =k ,B (-2m ,-2n),C (-2m ,-n ),E (-m ,-n )DCNO S 矩形=2mn =2k ,DBO S △=12mn =12k ,OEN S △=12mn =12k.∴OBCE S 矩形=DCNO S 矩形―DBO S △―OEN S △=k.∴k =4.由直线14y x =及双曲线4y x=,得A (4,1),B (-4,-1) ∴C (-4,-2),M (2,2)设直线CM 的解析式是y ax b =+,由C 、M 两点在这条直线上,得4222a b a b -+=-⎧⎨+=⎩,解得a =b =23∴直线CM 的解析式是y =23x +23.(3)如图,分别作AA 1⊥x 轴,MM 1⊥x 轴,垂足分别为A 1,M设A 点的横坐标为a ,则B 点的横坐标为-a.于是111A M MA a mp MP M O m-===, 同理MB m aq MQ m+== ∴p -q =a m m --m am+=-2D B CE N O A My xQ A 1M 1。
2020年九年级中考数学压轴题专项训练:圆的综合卷(附答案)

2020年九年级中考数学压轴题专项训练:圆的综合卷(含答案)1.如图,点O为Rt△ABC斜边AB上的一点,∠C=90°,以OA为半径的⊙O与BC交于点D,与AC交于点E,连接AD且AD平分∠BAC.(1)求证:BC是⊙O的切线;(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π)(1)证明:连接OD,∵AD平分∠BAC,∴∠BAD=∠DAC,∵AO=DO,∴∠BAD=∠ADO,∴∠CAD=∠ADO,∴AC∥OD,∵∠ACD=90°,∴OD⊥BC,∴BC与⊙O相切;(2)解:连接OE,ED,∵∠BAC=60°,OE=OA,∴△OAE为等边三角形,∴∠AOE=60°,∴∠ADE=30°,又∵∠OAD=∠BAC=30°,∴∠ADE=∠OAD,∴ED∥AO,∴四边形OAED是菱形,∴OE⊥AD,且AM=DM,EM=OM,∴S△AED =S△AOD,∴阴影部分的面积=S扇形ODE==π.2.如图,已知AB是⊙O的直径,AC是⊙O的弦,点E在⊙O外,连接CE,∠ACB的平分线交⊙O于点D.(1)若∠BCE=∠BAC,求证:CE是⊙O的切线;(2)若AD=4,BC=3,求弦AC的长.(1)证明:连接OC,∵AB是⊙O的直径,∴∠ACB=90°,∴∠ACO+∠BCO=90°,∵OA=OC,∴∠OAC=∠OCA,∵∠BAC=∠BCE,∴∠ACO=∠BCE,∴∠BCE+∠BCO=90°,∴∠OCE=90°,∴CE是⊙O的切线;(2)解:连接BD,∵∠ACB的平分线交⊙O于点D,∴∠ACD=∠BCD,∴=,∴AD=BD,∵AB是⊙O的直径,∴∠ADB=90°,∴△ADB是等腰直角三角形,∴AB=AD=4,∵BC=3,∴AC===.3.如图,AB是⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.(1)求证:CD是⊙O的切线;(2)∠C=45°,⊙O的半径为2,求阴影部分面积.(1)证明:连接OE .∵OA =OE ,∴∠OAE =∠OEA ,又∵∠DAE =∠OAE ,∴∠OEA =∠DAE ,∴OE ∥AD ,∴∠ADC =∠OEC ,∵AD ⊥CD ,∴∠ADC =90°,故∠OEC =90°.∴OE ⊥CD ,∴CD 是⊙O 的切线;(2)解:∵∠C =45°,∴△OCE 是等腰直角三角形,∴CE =OE =2,∠COE =45°,∴阴影部分面积=S △OCE ﹣S 扇形OBE =2×2﹣=2﹣.4.如图①,BC 是⊙O 的直径,点A 在⊙O 上,AD ⊥BC 垂足为D ,弧AE =弧AB ,BE 分别交AD 、AC 于点F 、G .(1)判断△FAG的形状,并说明理由;(2)如图②若点E与点A在直径BC的两侧,BE、AC的延长线交于点G,AD的延长线交BE于点F,其余条件不变(1)中的结论还成立吗?请说明理由.(3)在(2)的条件下,若BG=26,DF=5,求⊙O的直径BC.解:(1)△FAG等腰三角形;理由:∵BC为直径,∴∠BAC=90°,∴∠ABE+∠AGB=90°,∵AD⊥BC,∴∠ADC=90°,∴∠ACD+∠DAC=90°,∵弧AE=弧AB,∴∠ABE=∠ACD,∴∠DAC=∠AGB,∴FA=FG,∴△FAG是等腰三角形;(2)成立;∵BC为直径,∴∠BAC=90°∴∠ABE+∠AGB=90°∵AD⊥BC,∴∠ADC=90°,∴∠ACD+∠DAC=90°,∵弧AE=弧AB,∴∠ABE=∠ACD,∴∠DAC=∠AGB,∴FA=FG,∴△FAG是等腰三角形;(3)由(2)知∠DAC=∠AGB,且∠BAD+∠DAC=90°,∠ABG+∠AGB=90°,∴∠BAD=∠ABG,∴AF=BF,又∵AF=FG,∴F为BG的中点∵△BAG为直角三角形,∴AF=BF=BG=13,∵DF=5,∴AD=AF﹣DF=13﹣5=8,∴在Rt△BDF中,BD==12,∴在Rt△BDA中,AB==4,∵∠ABC=∠DBA,∠BAC=∠ADB=90°∴△ABC∽△DBA,∴=,∴=,∴BC=,∴⊙O的直径BC=.5.如图,已知矩形ABCD的边AB=6,BC=4,点P、Q分别是AB、BC边上的动点.(1)连接AQ、PQ,以PQ为直径的⊙O交AQ于点E.①若点E恰好是AQ的中点,则∠QPB与∠AQP的数量关系是∠QPB=2∠AQP;②若BE=BQ=3,求BP的长;(2)已知AP=3,BQ=1,⊙O是以PQ为弦的圆.①若圆心O恰好在CB边的延长线上,求⊙O的半径;②若⊙O与矩形ABCD的一边相切,求⊙O的半径.解:(1)①∵点E恰好是AQ的中点,∠ABQ=90°,∴BE=AE=EQ,∴∠EAB=∠EBA,∴∠QEB=2∠EBP,∵以PQ为直径的⊙O交AQ于点E,∴∠QPB=∠QEB,∠PBE=∠PQA,∴∠QPB=2∠AQP,故答案为:∠QPB=2∠AQP;②∵BE=BQ,∴∠BEQ=∠BQE,且∠BPQ=∠BEQ,∴∠BPQ=∠BQE,∴tan∠BPQ=tan∠BPQ,∴,∴,∴BP=(2)①如图1,过点O作OE⊥PQ,∵AP=3,AB=6,∴BP=3,∴PQ===,∵OE⊥PQ,∴QE=PE=,∵cos∠PQB==,∴=∴OQ=5,∴⊙O的半径为5;②如图2,若⊙O与BC相切于点Q,连接OQ,过点O作OE⊥PQ于E,∴EQ=PE=,∵BC是⊙O切线,∴OQ⊥BC,且AB⊥BC,∴OQ∥AB,∴∠OQP=∠BPQ,∴cos∠OQP=cos∠BPQ,∴,∴∴OQ=;如图3,若⊙O与AB相切于点P,连接OP,过点O作OE⊥PQ于E,∴EQ=PE=,∵AB是⊙O切线,∴OP⊥AB,且AB⊥BC,∴OP∥BC,∴∠OPQ=∠PQB,∴cos∠OPQ=cos∠PQB,∴∴,∴OP=5;如图4,若⊙O与AD相切于点M,连接OM,OQ,OP,延长MO交BC于F,作OH⊥AB于H 点,∴OM⊥AD,且BC∥AD,∴OF⊥BC,∵∠A=∠B=∠AMO=∠OFB=∠OHB=90°,∴四边形AHOM,OHBF是矩形,∴OM=AH,OH=BF,∵OQ2=OF2+FQ2,OP2=OH2+PH2,∴OQ2=(6﹣OQ)2+(BF﹣1)2,OQ2=BF2+(OQ﹣3)2,∴OQ=5﹣若图5,若⊙O与CD相切于点N,连接ON,OQ,OP,延长NO交BC于E,作OH⊥BC于H 点,同理可得:OP2=PE2+OE2,OQ2=OH2+QH2,∴OQ2=(3﹣OH)2+(4﹣OQ)2,OQ2=OH2+(4﹣OQ﹣1)2,∴OQ=35﹣6.6.如图,在矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取一点O,以点O为圆心,OF为半径作⊙O与AD相切于点P.AB =6,BC=,(1)求证:F是DC的中点.(2)求证:AE=4CE.(3)求图中阴影部分的面积.(1)证明:由折叠的性质可知,AF=AB=6,在Rt△ADF中,DF===3,∴CF=DC﹣DF=3,∴DF=FC,即F是CD的中点;(2)证明:在Rt△ADF中,DF=3,AF=6,∴∠DAF=30◦,∴∠BAF=60◦,由折叠的性质可知,∠EAF=∠EAB,∠AFE=∠B=90°,∴∠EAF=∠EAB=30°,∴AE=2EF,∠EFC=180°﹣∠AFD﹣∠AFE=30◦,∴EF=2CE,∴AE=4CE;(3)解:连接OP、OH、PH,∵⊙O与AD相切于点P,∴OP⊥AD,∴OP∥DF,∵∠DAF=30°,∴∠AOP=90°﹣∠DAF=60°,OF=OP=OA,∴∠OFH=∠AOP=60°,OP=OF=2,∴AP==2,∴DP=AD﹣AP=,∵∠OFH=60°,OH=OF,∴△OHF为等边三角形,∴∠FOH=∠OHF=60°,HF=OF=2,∴DH=DF﹣HF=1,∵OP∥DF,∴∠POH=∠OHF=60°,∴∠POH=∠HOF,∴=,∴阴影部分的面积=△PDH的面积=×DH×DP=.7.如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,连接BD.(1)求证:∠A=∠CBD.(2)若AB=10,AD=6,M为线段BC上一点,请写出一个BM的值,使得直线DM与⊙O 相切,并说明理由.(1)证明:∵AB为⊙O直径,∴∠ADB=90°,∴∠A+∠ABD=90°.∵∠ABC=90°,∴∠CBD+∠ABD=90°,∴∠A=∠CBD;(2)BM=.理由如下:如图,连接OD,DM,∵∠ADB=90°,AB=10,AD=6,∴BD==8,OA=5,∵∠A=∠CBD,∵Rt△CBD∽Rt△BAD,∴=,即=,解得BC=取BC的中点M,连接DM、OD,如图,∵DM为Rt△BCD斜边BC的中线,∴DM=BM,∵∠2=∠4,∵OB=OD,∴∠1=∠3,∴∠1+∠2=∠3+∠4=90°,即∠ODM=90°,∴OD⊥DM,∴DM为⊙O的切线,此时BM=BC=.8.如图,AB是⊙O的直径,直线MC与⊙O相切于点C.过点A作MC的垂线,垂足为D,线段AD与⊙O相交于点E.(1)求证:AC是∠DAB的平分线;(2)若AB=10,AC=4,求AE的长.(1)证明:连接OC,∵直线MC与⊙O相切于点C,∴∠OCM=90°,∵AD⊥CD,∴∠ADM=90°,∴∠OCM=∠ADM,∴OC∥AD,∴∠DAC=∠ACO,∵OA=OC,∴∠ACO=∠CAO,∴∠DAC=∠CAB,即AC是∠DAB的平分线;(2)解:连接BC,连接BE交OC于点F,∵AB是⊙O的直径,∴∠ACB=∠AEB=90°,∵AB=10,AC=4,∴BC===2,∵OC∥AD,∴∠BFO=∠AEB=90°,∴∠CFB=90°,F为线段BE中点,∵∠CBE=∠EAC=∠CAB,∠CFB=∠ACB,∴△CFB∽△BCA.∴=,即=,解得,CF=2,∴OF=OC﹣CF=3.∵O为直径AB中点,F为线段BE中点,∴AE=2OF=6.9.如图,AB是⊙O的直径,点C是圆上一点,点D是半圆的中点,连接CD交OB于点E,点F是AB延长线上一点,CF=EF.(1)求证:FC是⊙O的切线;(2)若CF=5,tan A=,求⊙O半径的长.(1)证明:如图,连接OD.∵点D是半圆的中点,∴∠AOD=∠BOD=90°,∴∠ODC+∠OED=90°,∵OD=OC,∴∠ODC=∠OCD.又∵CF=EF,∴∠FCE=∠FEC.∵∠FEC=∠OED,∴∠FCE=∠OED.∴∠FCE+∠OCD=∠OED+∠ODC=90°,即FC⊥OC,∴FC是⊙O的切线;(2)解:∵tan A=,∴在Rt△ABC中,=,∵∠ACB=∠OCF=90°,∴∠ACO=∠BCF=∠A,∵△ACF∽△CBF,∴===.∴AF=10,∴CF2=BF•AF.∴BF=.∴AO==.10.如图,AB是⊙O的直径,弦DE垂直半径OA,C为垂足,DE=6,连接DB,∠B=30°,过点E作EM∥BD,交BA的延长线于点M.(1)求的半径;(2)求证:EM是⊙O的切线;(3)若弦DF与直径AB相交于点P,当∠APD=45°时,求图中阴影部分的面积.解:(1)连结OE,∵DE垂直OA,∠B=30°,∴CE=DE=3,,∴∠AOE=2∠B=60°,∴∠CEO=30°,OC=OE,由勾股定理得OE=2;(2)∵EM∥BD,∴∠M=∠B=30°,∠M+∠AOE=90°,∴∠OEM=90°,即OE⊥ME,∴EM是⊙O的切线;(3)再连结OF,当∠APD=45°时,∠EDF=45°,∴∠EOF=90°,S=π(2)2﹣(2)2=3π﹣6.阴影11.如图,Rt△ABC中,∠C=90°.BE平分∠ABC交AC于点D,交△ABC的外接圆于点E,过点E作EF⊥BC交BC的延长线于点F.请补全图形后完成下面的问题:(1)求证:EF是△ABC外接圆的切线;(2)若BC=5,sin∠ABC=,求EF的长.(1)证明:补全图形如图所示,∵△ABC是直角三角形,∴△ABC的外接圆圆心O是斜边AB的中点.连接OE,∴OE=OB.∴∠2=∠3,∵BE平分∠ABC,∴∠1=∠2,∴∠1=∠3.∴OE∥BF.∵EF⊥BF,∴EF⊥OE,∴EF是△ABC外接圆的切线;(2)解:在Rt△ABC中,BC=5,sin∠ABC=,∴=.∵AC2+BC2=AB2,∴AC=12.∵∠ACF=∠CFE=∠FEH=90°,∴四边形C FEH是矩形.∴EF=HC,∠EHC=90°.∴EF=HC=AC=6.12.我们定义:如果圆的两条弦互相垂直,那么这两条弦互为“十字弦”,也把其中的一条弦叫做另一条弦的“十字弦”.如:如图,已知⊙O的两条弦AB⊥CD,则AB、CD互为“十字弦”,AB是CD的“十字弦”,CD也是AB的“十字弦”.(1)若⊙O的半径为5,一条弦AB=8,则弦AB的“十字弦”CD的最大值为10 ,最小值为 6 .(2)如图1,若⊙O的弦CD恰好是⊙O的直径,弦AB与CD相交于H,连接AC,若AC=12,DH=7,CH=9,求证:AB、CD互为“十字弦”;(3)如图2,若⊙O的半径为5,一条弦AB=8,弦CD是AB的“十字弦”,连接AD,若∠ADC=60°,求弦CD的长.解:(1)如图a,当CD是直径时,CD的长最大,则CD的最大值为10;如图b,当点D与点A重合时,CD有最小值,过点O作OE⊥CD于E,OF⊥AB于F,∴AF=BF=4,DE=CE,∴OF===3,∵OE⊥CD,OF⊥AB,∠CDB=90°,∴四边形CEOF是矩形,∴CE=OF=3,∴CD=6,∴CD最小值为6,故答案为:10,6;(2)如图1,连接AD,∵DH=7,CH=9,∴CD=16,∵CD是直径,∴∠CAD=90°,∴AD===4,∵,=,∴,∠ADH=∠ADC,∴△ADH∽△CDA,∴∠AHD=∠CAD=90°,∴AB⊥CD,∴AB、CD互为“十字弦”;(3)如图2,过点O作OE⊥CD于E,过点O作OF⊥AB于点F,连接AO,CO,过点O作ON⊥AC于N,∵∠ADC=60°,AB⊥CD,∴AF=DF,∵OE⊥CD,OF⊥AB,AB⊥CD,∴四边形OEHF是矩形,AF=BF=4,CE=ED,∴OF=EH,∵OF===3,∴EH=3,∴ED=CE=3+DH,∴CF=3+2DH,∵∠AOC=2∠ADC=120°,且AO=CO=5,ON⊥AC,∴∠CAO=30°,AN=CN,∴NO=,AN=,∴AC=5,∵AH2+CH2=AC2,∴75=3DH2+(3+2DH)2,∴DH=2﹣,∴CD=2CE=2(3+2﹣)=.13.如图,AB是⊙O的弦,AB=4,点P在上运动(点P不与点A、B重合),且∠APB =30°,设图中阴影部分的面积为y.(1)⊙O的半径为 4 ;(2)若点P到直线AB的距离为x,求y关于x的函数表达式,并直接写出自变量x的取值范围.解:(1)∵∠AOB=2∠APB=2×30°=60°,而OA=OB,∴△OAB为等边三角形,∴OA=AB=4,即⊙O的半径为4;故答案为4;(2)过点O作OH⊥AB,垂足为H,如图,则∠OHA=∠OHB=90°∵∠APB=30°∴∠AOB=2∠APB=60°,∵OA=OB,OH⊥AB,∴AH=BH=AB=2,在Rt△AHO中,∠AHO=90°,AO=4,AH=2,∴OH==2,∴y=﹣×4×2+×4×x=2x+π﹣4(0<x≤2+4).14.如图,四边形ABCD内接于⊙O,AC为⊙O的直径,D为的中点,过点D作DE∥AC,交BC的延长线于点E.(1)判断DE与⊙O的位置关系,并说明理由;(2)若CE=,AB=6,求⊙O的半径.(1)解:结论:DE与⊙O相切证:连接OD在⊙O中,∵D为的中点,∴=,∴AD=DC,∵AD=DC,点O是AC的中点,∴OD⊥AC,∴∠DOA=∠DOC=90°,∵DE∥AC,∴∠DOA=∠ODE=90°,∵∠ODE=90°,∴OD⊥DE,∵OD⊥DE,DE经过半径OD的外端点D,∴DE与⊙O相切.(2)解:连接BD.∵四边形ABCD是⊙O的内接四边形,∴∠DAB+∠DCB=180°,又∵∠DCE+∠DCB=180°,∴∠DAB=∠DCE,∵AC为⊙O的直径,点D、B在⊙O上,∴∠ADC=∠ABC=90°,∵=,∴∠ABD=∠CBD=45°,∵AD=DC,∠ADC=90°,∴∠DAC=∠DCA=45°,∵DE∥AC,∴∠DCA=∠CDE=45°,在△ABD和△CDE中,∵∠DAB=∠DCE,∠ABD=∠CDE=45°,∴△ABD∽△CDE,∴=,∴=,∴AD=DC=4,在Rt△ADC中,∠ADC=90°,AD=DC=4,∴AC===8,∴⊙O的半径为4.15.(1)如图①,点A,B,C在⊙O上,点D在⊙O外,比较∠A与∠BDC的大小,并说明理由;(2)如图②,点A,B,C在⊙O上,点D在⊙O内,比较∠A与∠BDC的大小,并说明理由;(3)利用上述两题解答获得的经验,解决如下问题:在平面直角坐标系中,如图③,已知点M(1,0),N(4,0),点P在y轴上,试求当∠MPN度数最大时点P的坐标.解:(1)∠A>∠BDC,理由如下:设CD交⊙O于E,连接BE,如图1所示:∠BEC=∠BDC+∠DBE,∴∠BEC>∠BDC,∵∠A=∠BEC,∴∠A>∠BDC;(2)∠A<∠BDC,理由如下:延长CD交⊙O于点F,连接BF,如图2所示:∵∠BDC=∠BFC+∠FBD,∴∠BDC>∠BFC,又∵∠A=∠BFC,∴∠A<∠BDC;(3)由(1)、(2)可得:当点P是经过M、N两点的圆和y轴相切的切点时,∠MPN度数最大,①当点P在y轴的正半轴上时,如图3所示:设⊙O′为点P是经过M、N两点的圆和y轴相切的切点的圆,连接O′P、O′M、O′N,作O′H⊥MN于H,则四边形OPO′H是矩形,MH=HN,∴OP=O′H,O′P=OH=O′M,∵M(1,0),N(4,0),∴OM=1,MN=3,∴MH=HN=MN=,设O′P=OH=O′M=x,MH=OH﹣OM=x﹣1,∴x﹣1=,∴x=,∴O′H===2,∴OP=2,∴点P的坐标为(0,2);②当点P在y轴的负半轴上时,如图4所示:同理可得O′H=OP=2,∴点P的坐标为(0,﹣2);综上所述,当∠MPN度数最大时点P的坐标为(0,2)或(0,﹣2).。
2020年九年级数学典型中考压轴题专练:圆有关题型(含答案)

2020年九年级数学典型中考压轴题专练:圆有关题型1、如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC 交AC的延长线于点E.(1)求证:DE是⊙O的切线.(2)求DE的长.2、如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD的延长线交于点F,且∠AFB=∠ABC.(1)求证:直线BF是⊙O的切线.(2)若CD=2,OP=1,求线段BF的长.3、如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.(1)求证:∠1=∠CAD;(2)若AE=EC=2,求⊙O的半径.4、如图,在四边形ABCD 中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD 为直径作圆O ,过点D 作DE ∥AB 交圆O 于点E(1)证明点C 在圆O 上;(2)求tan ∠CDE 的值;(3)求圆心O 到弦ED 的距离.5、如图,AB 是半圆O 的直径,点P 是BA 延长线上一点,PC 是⊙O 的切线,切点为C. 过点B 作BD ⊥PC 交PC 的延长线于点D ,连接BC. 求证:(1)∠PBC =∠CBD;(2)BC 2=AB ·BD6、如图,AB 是⊙O 的直径,点P 是弦AC 上一动点(不与A 、C 重合),过点P 作PE ⊥AB,垂足为E ,弧AC 射线EP 交于点F ,交过点C 的切线于点D.(1)求证DC=DP(2)若∠CAB=30°,当F 是 的中点时,判断以A 、O 、C 、F 为顶点的四边形是什么特殊四边形?说明理由;7、如图,在△ABC 中,∠C=90°,D 是BC 边上一点,以DB 为直径的⊙O 经过AB 的中点E ,交AD 的延长线于点F ,连结EF .AC(1)求证:∠1=∠F.(2)若sinB=,EF=2,求CD的长.8、如图,已知四边形ABCD内接于⊙O,A是的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且.(1)求证:△ADC∽△EBA;(2)如果AB=8,CD=5,求tan∠CAD的值.9、如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.(1)求证:∠ACD=∠B;(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;①求tan∠CFE的值;②若AC=3,BC=4,求CE的长.10、如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD 到E,且有∠EBD=∠CAB.(1)求证:BE是⊙O的切线;(2)若BC=,AC=5,求圆的直径AD及切线BE的长.11、已知:如图,⊙O是△ABC的外接圆, =,点D在边BC上,AE∥BC,AE=BD.(1)求证:AD=CE;(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.12、如图,△ABC中,∠BAC=120°,AB=AC=6.P是底边BC上的一个动点(P与B、C不重合),以P为圆心,PB为半径的⊙P与射线BA交于点D,射线PD交射线CA于点E.(1)若点E在线段CA的延长线上,设BP=x,AE=y,求y关于x的函数关系式,并写出x 的取值范围.(2)当BP=2时,试说明射线CA与⊙P是否相切.(3)连接PA,若S△APE=S△ABC,求BP的长.13、如图,AB是⊙O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.(1)判断BD与⊙O的位置关系,并说明理由;(2)若CD=15,BE=10,tanA=,求⊙O的直径.14、如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6.(1)求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;(2)求CD的长.15、如图1是一个用铁丝围成的篮框,我们来仿制一个类似的柱体形篮框.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2,矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、A n B n C n D n,OEFG围成,其中A1、G、B1在上,A2、A3…、A n与B2、B3、…B n分别在半径OA2和OB2上,C2、C3、…、C n和D2、D3…D n分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、C n D n依次等距离平行排放(最后一个矩形状框的边C n D n与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥A n C n(1)求d的值;(2)问:C n D n与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?16、在平面直角坐标中,△ABC三个顶点坐标为A(﹣,0)、B(,0)、C(0,3).(1)求△ABC内切圆⊙D的半径.(2)过点E(0,﹣1)的直线与⊙D相切于点F(点F在第一象限),求直线EF的解析式.(3)以(2)为条件,P为直线EF上一点,以P为圆心,以2为半径作⊙P.若⊙P上存在一点到△ABC三个顶点的距离相等,求此时圆心P的坐标.答案:1、【解答】证明:(1)连接OD,∵AD平分∠BAC,∴∠DAE=∠DAB,∵OA=OD,∴∠ODA=∠DAO,∴∠ODA=∠DAE,∴OD∥AE,∵DE⊥AC,∴OD⊥DE,∴DE是⊙O切线.(2)过点O作OF⊥AC于点F,∴AF=CF=3,∴OF===4.∵∠OFE=∠DEF=∠ODE=90°,∴四边形OFED是矩形,∴DE=OF=4.2、【解答】(1)证明:∵∠AFB=∠ABC,∠ABC=∠ADC,∴∠AFB=∠ADC,∴CD∥BF,∴∠AFD=∠ABF,∵CD⊥AB,∴AB⊥BF,∴直线BF是⊙O的切线.(2)解:连接OD,∵CD⊥AB,∴PD=CD=,∵OP=1,∴OD=2,∵∠PAD=∠BAF,∠APO=∠ABF,∴△APD∽△ABF,∴=,∴=,∴BF=.3、【解答】(1)证明:∵AB为⊙O的直径,∴∠ADB=90°,∴∠ADO+∠BDO=90°,∵AC为⊙O的切线,∴OA⊥AC,∴∠OAD+∠CAD=90°,∵OA=OD,∴∠OAD=∠ODA,∵∠1=∠BDO,∴∠1=∠CAD;(2)解:∵∠1=∠CAD,∠C=∠C,∴△CAD∽△CDE,∴CD:CA=CE:CD,∴CD2=CA•CE,∵AE=EC=2,∴AC=AE+EC=4,∴CD=2,设⊙O的半径为x,则OA=OD=x,则Rt△AOC中,OA2+AC2=OC2,∴x2+42=(2+x)2,解得:x=.∴⊙O的半径为.4、【解答】(1)证明:如图1,连结CO.∵AB=6,BC=8,∠B=90°,∴AC=10.又∵CD=24,AD=26,102+242=262,∴△ACD是直角三角形,∠C=90°.∵AD为⊙O的直径,∴AO=OD,OC为Rt△ACD斜边上的中线,∴OC=AD=r,∴点C在圆O上;(2)解:如图2,延长BC、DE交于点F,∠BFD=90°.∵∠BFD=90°,∴∠CDE+∠FCD=90°,又∵∠ACD=90°,∴∠ACB+∠FCD=90°,∴∠CDE=∠ACB.在Rt△ABC中,tan∠ACB==,∴tan∠CDE=tan∠ACB=;(3)解:如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=AE.易证△ABC∽△CFD,∴=,即=,∴CF=,∴BF=BC+CF=8+=.∵∠B=∠F=∠AE D=90°,∴四边形ABFE是矩形,∴AE=BF=,∴OG=AE=,即圆心O到弦ED的距离为.5、【解答】证明:(1)连接OC,∵PC是⊙O的切线,∴∠OCD=90°.又∵BD⊥PC∴∠BDP=90°∴OC∥BD.∴∠CBD=∠OCB.∴OB=OC .∴∠OCB=∠PBC.∴∠PBC=∠CBD.(2)连接AC∵AB 是直径,∴∠BDP=90°.又∵∠BDC=90°,∴∠ACB=∠BDC.∵∠PBC=∠CBD,∴△ABC ∽△CBD. ∴BC AB =BD BC .∴BC 2=AB ·BD6、【解析】 (1) 如图连接OC, ∵CD 是⊙O 的切线,∴ OC ⊥CD ∴∠OCD=90º,∴∠DCA= 90º-∠OCA .又PE⊥AB ,点D在EP的延长线上,∴∠DEA=90º,∴∠DPC=∠APE=90º-∠OAC.∵OA=OC , ∴∠OCA=∠OAC.∴∠DCA=∠DPC ,∴DC=DP.(2) 如图四边形AOCF是菱形.连接CF、AF,∵F是弧AC的中点,∴弧AF=弧CF ∴ AF=FC .∵∠BAC=30º,∴弧BC =60º,又AB是⊙O的直径,∴弧ACB =120º,∴弧AF=弧CF= 60º,∴∠ACF=∠FAC =30º .∵OA=OC, ∴∠OCA=∠BAC=30º,∴⊿OAC≌⊿FAC (ASA) , ∴AF=OA ,∴AF=FC=OC=OA , ∴四边形AOCF是菱形.7、【解答】解:(1)证明:连接DE,∵BD是⊙O的直径,∴∠DEB=90°,∵E是AB的中点,∴DA=DB,∴∠1=∠B,∵∠B=∠F,∴∠1=∠F;(2)∵∠1=∠F,∴AE=EF=2,∴AB=2AE=4,在Rt△ABC中,AC=AB•sinB=4,∴BC==8,设CD=x,则AD=BD=8﹣x,∵AC2+CD2=AD2,即42+x2=(8﹣x)2,∴x=3,即CD=3.8、【解答】(1)证明:∵四边形ABCD内接于⊙O,∴∠CDA=∠ABE.∵,∴∠DCA=∠BAE.∴△ADC∽△EBA;(2)解:∵A是的中点,∴∴AB=AC=8,∵△ADC∽△EBA,∴∠CAD=∠AEC,,即,∴AE=,∴tan∠CAD=tan∠AEC===.9、【解答】(1)证明:如图1中,连接OC.∵OA=OC,∴∠1=∠2,∵CD是⊙O切线,∴OC⊥CD,∴∠DCO=90°,∴∠3+∠2=90°,∵AB是直径,∴∠1+∠B=90°,∴∠3=∠B.(2)解:①∵∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,∵∠CDE=∠FDB,∠ECD=∠B,∴∠CEF=∠CFE,∵∠ECF=90°,∴∠CEF=∠CFE=45°,∴tan∠CFE=tan45°=1.②在RT△ABC中,∵AC=3,BC=4,∴AB==5,∵∠CDA=∠BDC,∠DCA=∠B,∴△DCA∽△DBC,∴===,设DC=3k,DB=4k,∵CD2=DA•DB,∴9k2=(4k﹣5)•4k,∴k=,∴CD=,DB=,∵∠CDE=∠BDF,∠DCE=∠B,∴△DCE∽△DBF,∴=,设EC=CF=x,∴=,∴x=.∴CE=.10、【解答】解:如图,连接OB,∵BD=BC,∴∠CAB=∠BAD,∵∠EBD=∠CAB,∴∠BAD=∠EBD,∵AD是⊙O的直径,∴∠ABD=90°,OA=BO,∴∠BAD=∠ABO,[来源:学科网]∴∠EBD=∠ABO,∴∠OBE=∠EBD+∠OBD=∠ABD+∠OBD=∠ABD=90°,∵点B在⊙O上,∴BE是⊙O的切线,(2)如图2,设圆的半径为R,连接CD,∵AD为⊙O的直径,∴∠ACCD=90°,∵BC=BD,∴OB⊥CD,∴OB∥AC,∵OA=OD,∴OF=AC=,∵四边形ACBD是圆内接四边形,∴∠BDE=∠ACB,∵∠DBE=∠ACB,∴△DBE∽△CAB,∴,∴,∴DE=,∵∠OBE=∠OFD=90°,∴DF∥BE,∴,∴,∵R>0,∴R=3,∵BE是⊙O的切线,∴BE===.11、【解答】证明:(1)在⊙O中,∵=,∴AB=AC,∴∠B=∠ACB,∵AE∥BC,∴∠EAC=∠ACB,∴∠B=∠EAC,在△ABD和△CAE中,,∴△ABD≌△CAE(SAS),∴AD=CE;(2)连接AO并延长,交边BC于点H,∵=,OA为半径,∴AH⊥BC,∴BH=CH,∵AD=AG,∴DH=HG,∴BH﹣DH=CH﹣GH,即BD=CG,∵BD=AE,∴CG=AE,∵CG∥AE,∴四边形AGCE是平行四边形.12、【解答】解:(1)过A作AF⊥BC于F,过P作PH⊥AB于H,∵∠BAC=120°,AB=AC=6,∴∠B=∠C=30°,∵PB=PD,∴∠PDB=∠B=30°,CF=AC•cos30°=6×=3,∴∠ADE=30°,∴∠DAE=∠CPE=60°,∴∠CEP=90°,∴CE=AC+AE=6+y,∴PC==,∵BC=6,∴PB+CP=x+=6,∴y=﹣x+3,∵BD=2BH=x<6,∴x<2,∴x的取值范围是0<x<2;(2)∵BP=2,∴CP=4,∴PE=PC=2=PB,∴射线CA与⊙P相切;(3)当D点在线段BA上时,连接AP,∵S△ABC=BC•AF=××3=9,∵S△APE=AE•PE=y•×(6+y)=S△ABC=,解得:y=,代入y=﹣x+3得x=4﹣.当D点BA延长线上时,PC=EC=(6﹣y),∴PB+CP=x+(6﹣y)=6,∴y=x﹣3,∵∠PEC=90°,∴PE===(6﹣y),∴S△APE=AE•PE=x•=y•(6﹣y)=S△ABC=,解得y=或,代入y=x﹣3得x=3或5.综上可得,BP的长为4﹣或3或5.13、【解答】(1)证明:连接OB,∵OB=OA,DE=DB,∴∠A=∠OBA,∠DEB=∠ABD,又∵CD⊥OA,∴∠A+∠AEC=∠A+∠DEB=90°,∴∠OBA+∠ABD=90°,∴OB⊥BD,∴BD是⊙O的切线;(2)如图,过点D作DG⊥BE于G,∵DE=DB,∴EG=BE=5,∵∠ACE=∠DGE=90°,∠AEC=∠GED,∴∠GDE=∠A,∴△ACE∽△DGE,∴sin∠EDG=sinA==,即CE=13,在Rt△ECG中,∵DG==12,∵CD=15,DE=13,∴DE=2,∵△ACE∽△DGE,∴=,∴AC=•DG=,∴⊙O的直径2OA=4AD=.4、【解答】(1)①证明:连接OC.∵OA=OB,AC=CB,∴OC⊥AB,∵点C在⊙O上,∴AB是⊙O切线.②证明:∵OA=OB,AC=CB,∴∠AOC=∠BOC,∵OD=OF,∴∠ODF=∠OFD,∵∠AOB=∠ODF+∠OFD=∠AOC+∠BOC,∴∠BOC=∠OFD,∴OC∥DF,∴∠CDF=∠OCD,∵OD=OC,∴∠ODC=∠OCD,∴∠ADC=∠CDF.(2)作ON⊥DF于N,延长DF交AB于M.∵ON⊥DF,∴DN=NF=3,在RT△ODN中,∵∠OND=90°,OD=5,DN=3,∴ON==4,∵∠OCM+∠CMN=180°,∠OCM=90°,∴∠OCM=∠CMN=∠MNO=90°,∴四边形OCMN是矩形,∴ON=CM=4,MN=OC=5,在RT△CDM中,∵∠DMC=90°,CM=4,DM=DN+MN=8,∴CD===4.15、【解答】解:(1)在RT△D2EC2中,∵∠D2EC2=90°,EC2=ED2=r,EF⊥C2D2,∴EH1=r,FH1=r﹣r,∴d=(r﹣r)=r,(2)假设C n D n与点E间的距离能等于d,由题意•r=r,这个方程n没有整数解,所以假设不成立.∵r÷r=2+2≈4.8,∴n=6,此时C n D n与点E间的距离=r﹣4×r=r.16、【解答】解:(1)连接BD,∵B(,0),C(0,3),∴OB=,OC=3,∴tan∠CBO==,∴∠CBO=60°∵点D是△ABC的内心,∴BD平分∠CBO,∴∠DBO=30°,∴tan∠DBO=,∴OD=1,∴△ABC内切圆⊙D的半径为1;(2)连接DF,过点F作FG⊥y轴于点G,∵E(0,﹣1)∴OE=1,DE=2,∵直线EF与⊙D相切,∴∠DFE=90°,DF=1,∴sin∠DEF=,∴∠DEF=30°,∴∠GDF=60°,∴在Rt△DGF中,∠DFG=30°,∴DG=,由勾股定理可求得:GF=,∴F(,),设直线EF的解析式为:y=kx+b,∴,∴直线EF的解析式为:y=x﹣1;(3)∵⊙P上存在一点到△ABC三个顶点的距离相等,∴该点必为△ABC外接圆的圆心,由(1)可知:△ABC是等边三角形,∴△ABC外接圆的圆心为点D∴DP=2,设直线EF与x轴交于点H,∴令y=0代入y=x﹣1,∴x=,∴H(,0),∴FH=,当P在x轴上方时,过点P1作P1M⊥x轴于M,由勾股定理可求得:P1F=3,∴P1H=P1F+FH=,∵∠DEF=∠HP1M=30°,∴HM=P1H=,P1M=5,∴OM=2,∴P1(2,5),当P在x轴下方时,过点P2作P2N⊥x轴于点N,由勾股定理可求得:P2F=3,∴P2H=P2F﹣FH=,∴∠DEF=30°∴∠OHE=60°∴sin∠OHE=,∴P2N=4,令y=﹣4代入y=x﹣1,∴x=﹣,∴P2(﹣,﹣4),综上所述,若⊙P上存在一点到△ABC三个顶点的距离相等,此时圆心P的坐标为(2,5)或(﹣,﹣4).。
教育部2020年中考数学必考压轴题及答案

教育部2020年中考数学必考压轴题及答案教育部2020年中考数学必考压轴题及答案一、函数与几何综合的压轴题1.如图①,在平面直角坐标系中,AB、CD都垂直于x轴,垂足分别为B、D且AD与B相交于E点.已知:A(-2,-6),C(1,-3)求证:E点在y轴上;如果有一抛物线经过A,E,C三点,求此抛物线方程.如果AB位置不变,再将DC水平向右移动k(k>0)个单位,此时AD与BC相交于E′点,如图②,求△AE′C的面积S关于k的函数解析式.[解](1)(本小题介绍二种方法,供参考)方法一:过E作EO′⊥x轴,垂足O′∴AB∥EO′∥DC∴又∵DO′+BO′=DB∴∵AB=6,DC=3,∴EO′=2又∵,∴∴DO′=DO,即O′与O重合,E在y轴上方法二:由D(1,0),A(-2,-6),得DA直线方程:y=2x-2①再由B(-2,0),C(1,-3),得BC直线方程:y=-x-2②联立①②得∴E点坐标(0,-2),即E点在y轴上(2)设抛物线的方程y=ax2+bx+c(a≠0)过A(-2,-6),C(1,-3)E(0,-2)三点,得方程组解得a=-1,b=0,c=-2∴抛物线方程y=-x2-2(3)(本小题给出三种方法,供参考)由(1)当DC水平向右平移k后,过AD与BC的交点E′作E′F⊥x 轴垂足为F。
同(1)可得:得:E′F=2方法一:又∵E′F∥AB,∴S△AE′C=S△ADC-S△E′DC===DB=3+kS=3+k为所求函数解析式方法二:∵BA∥DC,∴S△BCA=S△BDA∴S△AE′C=S△BDE′∴S=3+k为所求函数解析式.证法三:S△DE′C∶S△AE′C=DE′∶AE′=DC∶AB=1∶2同理:S△DE′C∶S△DE′B=1∶2,又∵S△DE′C∶S△ABE′=DC2∶AB2=1∶4∴∴S=3+k为所求函数解析式.2.已知:如图,在直线坐标系中,以点M(1,0)为圆心、直径AC为的圆与y轴交于A、D两点.求点A的坐标;设过点A的直线y=x+b与x轴交于点B.探究:直线AB是否⊙M 的切线?并对你的结论加以证明;连接BC,记△ABC的外接圆面积为S1、⊙M面积为S2,若,抛物线y=ax2+bx+c经过B、M两点,且它的顶点到轴的距离为.求这条抛物线的解析式.解:由已知AM=,OM=1,在Rt△AOM中,AO=,∴点A的坐标为A(0,1)证:∵直线y=x+b过点A(0,1)∴1=0+b即b=1∴y=x+1令y=0则x=-1∴B(—1,0),AB=在△ABM中,AB=,AM=,BM=2∴△ABM是直角三角形,∠BAM=90°∴直线AB是⊙M的切线解法一:由⑵得∠BAC=90°,AB=,AC =2,∴BC=∵∠BAC=90°∴△ABC的外接圆的直径为BC,∴而,设经过点B(—1,0)、M(1,0)的抛物线的解析式为:y=a(+1)(x-1),(a≠0)即y=ax2-a,∴-a=±5,∴a =±5∴抛物线的解析式为y=5x2-5或y=-5x2+5解法二:(接上)求得∴h=5由已知所求抛物线经过点B(—1,0)、M(1、0),则抛物线的对称轴是y轴,由题意得抛物线的顶点坐标为(0,±5)∴抛物线的解析式为y=a(x-0)2±5又B(-1,0)、M(1,0)在抛物线上,∴a±5=0,a=±5∴抛物线的解析式为y=5x2-5或y=-5x2+5解法三:(接上)求得∴h=5因为抛物线的方程为y=ax2+bx+c(a≠0)由已知得∴抛物线的解析式为y=5x2-5或y=-5x2+5.3.如图,在直角坐标系中,以点P(1,-1)为圆心,2为半径作圆,交x轴于A、B两点,抛物线过点A、B,且顶点C在⊙P上.(1)求⊙P上劣弧的长;(2)求抛物线的解析式;(3)在抛物线上是否存在一点D,使线段OC与PD互相平分?若存在,求出点D的坐标;若不存在,请说明理由如图,连结PB,过P 作PM⊥x轴,垂足为M.在Rt△PMB中,PB=2,PM=1,∴∠MPB=60°,∴∠APB=120°的长=(2)在Rt△PMB中,PB=2,PM=1,则MB=MA=.又OM=1,∴A(1-,0),B(1+,0),由抛物线及圆的对称性得知点C在直线PM上,则C(1,-3).点A、B、C在抛物线上,则解之得抛物线解析式为(3)假设存在点D,使OC与PD互相平分,则四边形OPCD为平行四边形,且PC∥OD.又PC∥y轴,∴点D在y轴上,∴OD=2,即D(0,-2).又点D(0,-2)在抛物线上,故存在点D(0,-2),使线段OC与PD互相平分.如图,在平面直角坐标系内,Rt△ABC的直角顶点C(0,)在轴的正半轴上,A、B是轴上是两点,且OA∶OB=3∶1,以OA、OB为直径的圆分别交AC于点E,交BC于点F.直线EF交OC于点Q.求过A、B、C三点的抛物线的解析式;请猜想:直线EF与两圆有怎样的位置关系?并证明你的猜想.在△AOC中,设点M是AC边上的一个动点,过M作MN∥AB交OC于点N.试问:在轴上是否存在点P,使得△PMN是一个以MN为一直角边的等腰直角三角形?若存在,求出P点坐标;若.[解](1)在Rt△AB C中,OC⊥AB,∴△AOC≌△COB.∴OC2=OA·OB.∵OA∶OB=3∶1,C(0,),∴∴OB=1.∴OA=3.∴A(-3,0),B(1,0).设抛物线的解析式为则解之,得∴经过A、B、C三点的抛物线的解析式为(2)EF与⊙O1、⊙O2都相切.证明:连结O1E、OE、OF.∵∠ECF=∠AEO=∠BFO=90°,∴四边形EOFC为矩形.∴QE=QO.∴∠1=∠2.∵∠3=∠4,∠2+∠4=90°,∴EF与⊙O1相切.同理:EF理⊙O2相切.(3)作MP⊥OA于P,设MN=a,由题意可得MP=MN=a.∵MN∥OA,∴△CMN∽△CAO.∴∴解之,得此时,四边形OPMN是正方形.∴∴考虑到四边形PMNO此时为正方形,∴点P在原点时仍可满足△PNN是以MN为一直角边的等腰直角三角形.故轴上存在点P使得△PMN是一个以MN为一直角边的等腰直角三角形且或5.如图,已知点A(0,1)、C(4,3)、E(,),P是以AC为对角线的矩形ABCD内部(不在各边上)的—个动点,点D在y轴,抛物线y =ax2+bx+1以P为顶点.(1)说明点A、C、E在一条条直线上;(2)能否判断抛物线y=ax2+bx+1的开口方向?请说明理由;(3)设抛物线y=ax2+bx+1与x轴有交点F、G(F在G的左侧),△GAO与△FAO的面积差为3,且这条抛物线与线段AE有两个不同的交点.这时能确定a、b的值吗?若能,请求出a、b的值;若不能,请确定a、b的取值范围.(本题图形仅供分析参考用)x+1.将点E的坐标E(,)代入y=x+1中,左边=,右边=×+1=,∵左边=右边,∴点E在直线y=x+1上,即点A、C、E在一条直线上.(2)解法一:由于动点P在矩形ABCD内部,∴点P的纵坐标大于点A的纵坐标,而点A与点P都在抛物线上,且P为顶点,∴这条抛物线有最高点,抛物线的开口向下解法二:∵抛物线y=ax2+bx+c的顶点P的纵坐标为,且P在矩形ABCD内部,∴1<<3,由1<1—得—>0,∴a<0,∴抛物线的开口向下.(3)连接GA、FA,∵S△GAO—S△FAO=3∴GO·AO—FO·AO=3∵OA=1,∴GO—FO=6.设F(x1,0)、G(x2,0),则x1、x2为方程ax2+bx+c=0的两个根,且x1<x2,又∵a<0,∴x1·x2=<0,∴x1<0<x2,∴GO=x2,FO=—x1,∴x2—(—x1)=6,即x2+x1=6,∵x2+x1=—∴—=6,∴b=—6a,∴抛物线解析式为:y=ax2—6ax+1,其顶点P的坐标为(3,1—9a),∵顶点P在矩形ABCD内部,∴1<1—9a<3,∴—<a<0.∴x=0或x==6+.当x=0时,即抛物线与线段AE交于点A,而这条抛物线与线段AE有两个不同的交点,则有:0<6+≤,解得:—≤a<—综合得:—<a<—∵b=—6a,∴<b<6.已知两点O(0,0)、B(0,2),⊙A过点B且与x轴分别相交于点O、C,⊙A被y轴分成段两圆弧,其弧长之比为3∶1,直线l与⊙A切于点O,抛物线的顶点在直线l上运动.求⊙A的半径;若抛物线经过O、C两点,求抛物线的解析式;过l上一点P的直线与⊙A交于C、E两点,且PC=CE,求点E的坐标;若抛物线与x轴分别相交于C、F两点,其顶点P的横坐标为m,求△PEC的面积关于m的函数解析式.(1)由弧长之比为3∶1,可得∠BAO=90o再由AB=AO=r,且OB=2,得r=(2)⊙A的切线l过原点,可设l为y=kx任取l上一点(b,kb),由l与y轴夹角为45o可得:b=-kb或b=kb,得k=-1或k=1,∴直线l的解析式为y=-x或y=x又由r=,易得C(2,0)或C(-2,0)由此可设抛物线解析式为y=ax(x-2)或y=ax(x+2)再把顶点坐标代入l的解析式中得a=1∴抛物线为y=x2-2x或y=x2+2x ……6分(3)当l的解析式为y=-x时,由P在l上,可设P(m,-m)(m >0)过P作PP′⊥x轴于P′,∴OP′=|m|,PP′=|-m|,∴OP=2m2,又由切割线定理可得:OP2=PC.PE,且PC=CE,得PC=PE=m=PP′7分∴C与P′为同一点,即PE⊥x轴于C,∴m=-2,E(-2,2) (8)分同理,当l的解析式为y=x时,m=-2,E(-2,2)(4)若C(2,0),此时l为y=-x,∵P与点O、点C不重合,∴m≠0且m≠2,当m<0时,FC=2(2-m),高为|yp|即为-m,∴S =同理当0<m<2时,S=-m2+2m;当m>2时,S=m2-2m;∴S=又若C(-2,0),此时l为y=x,同理可得;S=.如图,直线与函数的交于A、B两点,且与x、y轴分别交于C、D两点.(1)若的面积的倍,求与之间的函数关系式;(2)在(1)的条件下,是否存在和,使得以为直径的圆经过点.若存在,求出和的值;若不存在,请说明理由.[解](1)设,(其中),由,得∴··(····),,又,∴,即,由可得,代入可得①∴,,∴,即.又方程①的判别式,∴所求的函数关系式为.(2)假设存在,,使得以为直径的圆经过点.则,过、分别作轴的垂线,垂足分别为、.∵与都与互余,∴.∴Rt∽Rt,∴.∴,∴,∴,即②由(1)知,,代入②得,∴或,又,∴或,∴存在,,使得以为直径的圆经过点,且或.8.已知抛物线与x轴交于两点、,与y轴交于点C,且AB=6.(1)求抛物线和直线BC的解析式.(2)在给定的直角坐标系中,画抛物线和直线BC.(3)若过A、B、C三点,求的半径.(4)抛物线上是否存在点M,过点M作轴于点N,使被直线BC 分成面积比为1)由题意得:解得经检验m=1,∴抛物线的解析式为:或:由得,或抛物线的解析式为由得∴A(-50),B(1,0),C(0,-5.设直线BC的解析式为则∴直线BC的解析式为(2)图象略.(3)法一:在中,.又∴的半径法二:由题意,圆心P在AB的中垂线上,即在抛物线的对称轴直线上,设P(-2-hh>0),连结PB、PC,则,由,即,解得h=2.的半径.法三:延长CP交于点F.为的直径,又又的半径为(4)设MN交直线BC于点E,点M的坐标为则点E的坐标为若则解得(不合题意舍去),若则解得(不合题意舍去),存在点M,点M的坐标为或(15,280).9.如图,⊙M与x轴交于A、B两点,其坐标分别为、,直径CD⊥x轴于N,直线CE切⊙M于点C,直线FG切⊙M于点F,交CE于G,已知点G的横坐标为3.若抛物线经过A、B、D三点,求m的值及点D的坐标.求直线DF的解析式.是否存在过点G的直线,使它与(1)中抛物线的两个交点的横坐标之和等于4?若存在,请求出满足条件的直线的解析式;若不存在,请说明理由.[解](1)∵抛物线过A、B两点,∴,m=3.∴抛物线为.又抛物线过点D,由圆的对称性知点D为抛物线的顶点. ∴D点坐标为.(2)由题意知:AB=4.∵CD⊥x轴,∴NA=NB=2.∴ON=1.由相交弦定理得:NA·NB=ND·NC,∴NC×4=2×2.∴NC=1.∴C点坐标为.设直线DF交CE于P,连结CF,则∠CFP=90°.∴∠2+∠3=∠1+∠4=90°.∵GC、GF是切线,∴GC=GF.∴∠3=∠4.∴∠1=∠2.∴GF=GP.∴GC=GP.可得CP=8.∴P点坐标为设直线DF的解析式为则解得∴直线DF的解析式为:(3)假设存在过点G的直线为,则,∴.由方程组得由题意得,∴.当时,,∴方程无实数根,方程组无实数解.∴满足条件的直线不存在.10.已知二次函数的图象经过点A(-3,6),并与x轴交于点B (-1,0)和点C,顶点为P.求这个二次函数的解析式,并在下面的坐标系中画出该二次函数的图象;设D为线段OC上的一点,满足∠DPC=∠BAC,求点D的坐标;在x轴上是否存在一点M,使以M为圆心的圆与AC、PC所在的直线及y轴都相切?如果存在,请求出点M的坐标;若不存在,请说明理由.(1)解:∵二次函数的图象过点A(-3,6),B(-1,0)得解得∴这个二次函数的解析式为:由解析式可求P(1,-2),C(3,0)画出二次函数的(2)解法一:易证:∠ACB=∠PCD=45°又已知:∠DPC=∠BAC∴△DPC∽△BAC∴易求∴∴∴解法二:过A作AE⊥x轴,垂足为E.设抛物线的对称轴交x轴于F.亦可证△AEB∽△PFD、∴.易求:AE=6,EB=2,PF=2∴∴∴(3)存在.(1°)过M作MH⊥AC,MG⊥PC垂足分别为H、G,设AC交y轴于S,CP的延长线交y轴于T∵△SCT是等腰直角三角形,M是△SCT的内切圆圆心,∴MG=MH=OM又∵且OM+MC=OC∴∴(2°)在x轴的负半轴上,存在一点M′同理OM′+OC=M′C,得∴M′即在x轴上存在满足条件的两个点.在平面直角坐标系中,A(-1,0),B(3,0).(1)若抛物线过A,B两点,且与y轴交于点(0,-3),求此抛物线的顶点坐标;(2)如图,小敏发现所有过A,B两点的抛物线如果与y轴负半轴交于点C,M为抛物线的顶点,那么△ACM与△ACB的面积比不变,请你求出这个比值;(3)若对称轴是AB的中垂线l的抛物线与x轴交于点E,F,与y轴交于点C,过C作CP∥x轴交l于点P,M为此抛物线的顶点.若四边形PEMF是有一个内角为60°的菱形,求次抛物线的解析式.(1),顶点坐标为(1,-4).(2)由题意,设y=a(x+1)(x-3),即y=ax2-2ax-3a,∴A(-1,0),B(3,0),C(0,-3a),M(1,-4a),∴S△ACB=×4×=6,而a>0,∴S△ACB=6A、作MD⊥x轴于D,又S△ACM=S△ACO+SOCMD-S△AMD=·1·3a+(3a+4a)-·2·4a=a,∴S△ACM:S△ACB=1:6.(3)①当抛物线开口向上时,设y=a(x-1)2+k,即y=ax2-2ax+a+k,有菱形可知=,a+k>0,k<0,∴k=,∴y=ax2-2ax+,∴.记l与x轴交点为D,若∠PEM=60°,则∠FEM=30°,MD=DE·tan30°=,∴k=-,a=,∴抛物线的解析式为.若∠PEM=120°,则∠FEM=60°,MD=DE·tan60°=,∴k=-,a=,∴抛物线的解析式为.②当抛物线开口向下时,同理可得,.已知:在平面直角坐标系xOy中,一次函数的图象与x轴交于点A,抛物线经过O、A两点。
2020年中考数学压轴题(含答案)
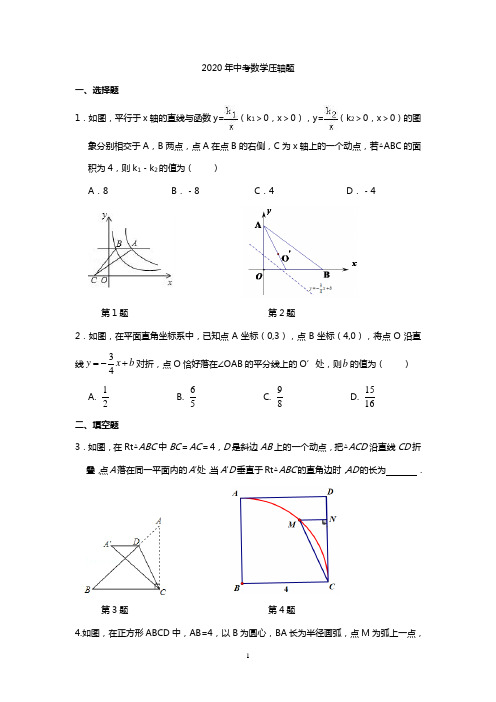
2020年中考数学压轴题一、选择题1.如图,平行于x轴的直线与函数y=(k1>0,x>0),y=(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为4,则k1﹣k2的值为()A.8 B.﹣8 C.4 D.﹣4第1题第2题2.如图,在平面直角坐标系中,已知点A坐标(0,3),点B坐标(4,0),将点O沿直线34y x b=-+对折,点O恰好落在∠OAB的平分线上的O’处,则b的值为()A.12B.65C.98D.1516二、填空题3.如图,在Rt△ABC中BC=AC=4,D是斜边AB上的一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D垂直于Rt△ABC的直角边时,AD的长为.第3题第4题4.如图,在正方形ABCD中,AB=4,以B为圆心,BA长为半径画弧,点M为弧上一点,MN ⊥CD 于N ,连接CM ,则CM -MN 的最大值为 . 三、解答题5.如图,四边形ABCD 是⊙O 的内接四边形,AC 为直径, ⌒ BD = ⌒AD ,DE ⊥BC ,垂足为E . (1)求证:CD 平分∠ACE ;(2)判断直线ED 与⊙O 的位置关系,并说明理由; (3)若CE =2,AC =8,阴影部分的面积为 .6.如图,抛物线y =ax 2+bx +c (a <0,a 、b 、c 为常数)与x 轴交于A 、C 两点,与y 轴交于B 点,A (﹣6,0),C (1,0),B (0,).(1)求该抛物线的函数关系式与直线AB 的函数关系式;(2)已知点M (m ,0)是线段OA 上的一个动点,过点M 作x 轴的垂线l ,分别与直线AB 和抛物线交于D 、E 两点,当m 为何值时,△BDE 恰好是以DE 为底边的等腰三角形?(3)在(2)问条件下,当△BDE 恰妤是以DE 为底边的等腰三角形时,动点M 相应位置记为点M ′,将OM ′绕原点O 顺时针旋转得到ON (旋转角在0°到90°之间);i :探究:线段OB 上是否存在定点P (P 不与O 、B 重合),无论ON 如何旋转,始终保持不变,若存在,试求出P 点坐标:若不存在,请说明理由;ii :试求出此旋转过程中,(NA +NB )的最小值.EO CBA【答案与解析】一、选择题1.A2.D二、填空题3.【分析】由等腰直角三角形的性质和勾股定理得出AB=4,∠B=∠A′CB=45°,①如图1,当A′D∥BC,设AD=x,根据折叠的性质得到∠A′=∠A=∠A′CB=45°,A′D=AD =x,推出A′C⊥AB,求得BH=BC=2,DH=A′D=x,然后列方程即可得到结果,②如图2,当A′D∥AC,根据折叠的性质得到AD=A′D,AC=A′C,∠ACD =∠A′CD,根据平行线的性质得到∠A′DC=∠ACD,于是得到∠A′DC=∠A′CD,推出A′D=A′C,于是得到AD=AC=2.【解答】解:Rt△ABC中,BC=AC=4,∴AB=4,∠B=∠A′CB=45°,①如图1,当A′D∥BC,设AD=x,∵把△ACD沿直线CD折叠,点A落在同一平面内的A′处,∴∠A′=∠A=∠A′CB=45°,A′D=AD=x,∵∠B =45°, ∴A ′C ⊥AB , ∴BH =BC =2,DH =A ′D =x ,∴x +x +2=4,∴x =4﹣4, ∴AD =4﹣4;②如图2,当A ′D ∥AC ,∵把△ACD 沿直线CD 折叠,点A 落在同一平面内的A ′处, ∴AD =A ′D ,AC =A ′C ,∠ACD =∠A ′CD , ∵∠A ′DC =∠ACD , ∴∠A ′DC =∠A ′CD , ∴A ′D =A ′C , ∴AD =AC =4, 综上所述:AD 的长为:4﹣4或4.4. 2 三、解答题 5、(1),BD AD BAD ACD =∴=∠∠°+180ABCD O BAD BCD ∴=四边形内接于圆,∠∠°+180BCD DCE =又∠∠,DCE BAD ∴=∠∠ACD DCE ∴=∠∠即CD 平分∠ACE(2)直线ED 与⊙O 相切。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年中考数学压轴题真题汇编(真题试卷+详细解析答案,值得下载)1.(2019年四川省攀枝花市)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=的图象在第二象限交于点B,与x轴交于点C,点A在y轴上,满足条件:CA⊥CB,且CA=CB,点C的坐标为(﹣3,0),cos∠ACO=.(1)求反比例函数的表达式;(2)直接写出当x<0时,kx+b<的解集.【分析】(1)过点B作BD⊥x轴于点D,证明△AOC≌△CDB得到BD与CD的长度,便可求得B点的坐标,进而求得反比例函数解析式;(2)观察函数图象,当一次函数图象在反比例函数图象下方时的自变量x的取值范围便是结果.【解答】解:(1)过点B作BD⊥x轴于点D,∵CA⊥CB,∴∠BCD+∠ACO=∠BCD+CBD=90°,∴∠ACO=∠CBD,∵∠BDC=∠AOC=90°,AC=BC,∴△AOC≌△CDB(AAS),∴OC=DB=3,CD=AO,∵cos∠ACO=.∴AC=,∴CD=AO=,∴OD=OC+CD=3+6=9,∴B(﹣9,3),把B(﹣9,3)代入反比例函数y=中,得m=﹣27,∴反比例函数为;(2)当x<0时,由图象可知一次函数y=kx+b的图象在反比例函数y=图象的下方时,自变量x的取值范围是﹣9<x<0,∴当x<0时,kx+b<的解集为﹣9<x<0.【点评】本题考查了反比例函数和一次函数的交点问题,熟练掌握函数解析式的求法以及利用数形结合根据函数图象的上下位置关系得出不等式的解集是重点.2.(2019年四川省成都市)如图,在平面直角坐标系xOy中,一次函数y=x+5和y=﹣2x的图象相交于点A,反比例函数y=的图象经过点A.(1)求反比例函数的表达式;(2)设一次函数y=x+5的图象与反比例函数y=的图象的另一个交点为B,连接OB,求△ABO的面积.【分析】(1)联立方程求得A的坐标,然后根据待定系数法即可求得;(2)联立方程求得交点B的坐标,进而求得直线与x轴的交点,然后利用三角形面积公式求得即可.【解答】解:(1)由得,∴A(﹣2,4),∵反比例函数y=的图象经过点A,∴k=﹣2×4=﹣8,∴反比例函数的表达式是y=﹣;(2)解得或,∴B(﹣8,1),由直线AB的解析式为y=x+5得到直线与x轴的交点为(﹣10,0),∴S△AOB=×10×4﹣×10×1=15.【点评】本题考查了一次函数和反比例函数的交点问题,通过方程组求得交点坐标是解题的关键.3.(2019年四川省资阳市)如图,直线y=x与双曲线y=(x>0)相交于点A,且OA=,将直线向左平移一个单位后与双曲线相交于点B,与x轴、y轴分别交于C、D两点.(1)求直线BC的解析式及k的值;(2)连结OB、AB,求△OAB的面积.【分析】(1)根据平移的性质即可求得直线BC的解析式,由直线y=x和OA=即可求得A的坐标,然后代入双曲线y=(x>0)求得k的值;(2)作AE⊥x轴于E,BF⊥x轴于F,联立方程求得B点的坐标,然后根据S△AOB=S梯+S△BOF﹣S△AOE=S梯形AEFB,求得即可.形AEFB【解答】解:(1)根据平移的性质,将直线y=x向左平移一个单位后得到y=x+1,∴直线BC的解析式为y=x+1,∵直线y=x与双曲线y=(x>0)相交于点A,∴A点的横坐标和纵坐标相等,∵OA=,∴A(1,1),k=1×1=1;(2)作AE⊥x轴于E,BF⊥x轴于F,解得或∴B(,),∵S△AOB=S梯形AEFB+S△BOF﹣S△AOE=S梯形AEFB,∴S△AOB=S梯形AEFB=(1+)(1﹣)=2.【点评】本题考查反比例函数与一次函数的交点问题,解题的关键是熟练掌握待定系数法,学会构建方程组确定交点坐标,属于中考常考题型.4.(2019年甘肃省天水市)如图,一次函数y=kx+b与反比例函数y=的图象交于A(m,4)、B(2,n)两点,与坐标轴分别交于M、N两点.(1)求一次函数的解析式;(2)根据图象直接写出kx+b﹣>0中x的取值范围;(3)求△AOB的面积.【分析】(1)将点A、点B的坐标分别代入解析式即可求出m、n的值,从而求出两点坐标;(2)根据题意,结合图象确定出x的范围即可;(3)将△AOB的面积转化为S△AON﹣S△BON的面积即可.【解答】解:(1)∵点A在反比例函数y=上,∴=4,解得m=1,∴点A的坐标为(1,4),又∵点B也在反比例函数y=上,∴=n,解得n=2,∴点B的坐标为(2,2),又∵点A、B在y=kx+b的图象上,∴,解得,∴一次函数的解析式为y=﹣2x+6.(2)根据图象得:kx+b﹣>0时,x的取值范围为x<0或1<x<2;(3)∵直线y=﹣2x+6与x轴的交点为N,∴点N的坐标为(3,0),S△AOB=S△AON﹣S△BON=×3×4﹣×3×2=3.【点评】此题考查了反比例函数与一次函数的交点问题,利用了数形结合的思想,熟练掌握待定系数法是解本题的关键.5.(2019年四川省宜宾市)如图,已知反比例函数y=(k>0)的图象和一次函数y=﹣x+b的图象都过点P(1,m),过点P作y轴的垂线,垂足为A,O为坐标原点,△OAP 的面积为1.(1)求反比例函数和一次函数的解析式;(2)设反比例函数图象与一次函数图象的另一交点为M,过M作x轴的垂线,垂足为B,求五边形OAPMB的面积.【分析】(1)根据系数k的几何意义即可求得k,进而求得P(1,2),然后利用待定系数法即可求得一次函数的解析式;(2)设直线y=﹣x+3交x轴、y轴于C、D两点,求出点C、D的坐标,然后联立方程求得P、M的坐标,最后根据S五边形=S△COD﹣S△APD﹣S△BCM,根据三角形的面积公式列式计算即可得解;【解答】解:(1)∵过点P作y轴的垂线,垂足为A,O为坐标原点,△OAP的面积为1.∴S△OP A=|k|=1,∴|k|=2,∵在第一象限,∴k=2,∴反比例函数的解析式为y=;∵反比例函数y=(k>0)的图象过点P(1,m),∴m==2,∴P(1,2),∵次函数y=﹣x+b的图象过点P(1,2),∴2=﹣1+b,解得b=3,∴一次函数的解析式为y=﹣x+3;(2)设直线y=﹣x+3交x轴、y轴于C、D两点,∴C(3,0),D(0,3),解得或,∴P(1,2),M(2,1),∴P A=1,AD=3﹣2=1,BM=1,BC=3﹣2=1,∴五边形OAPMB的面积为:S△COD﹣S△BCM﹣S△ADP=×3×3﹣×1×1﹣×1×1=.【点评】本题考查了反比例函数与一次函数的交点问题,三角形的面积以及反比例函数系数k的几何意义,求得交点坐标是解题的关键.6.(2019年四川省巴中市)如图,一次函数y1=k1x+b(k1、b为常数,k1≠0)的图象与反比例函数y2=(k2≠0,x>0)的图象交于点A(m,8)与点B(4,2).①求一次函数与反比例函数的解析式.②根据图象说明,当x为何值时,k1x+b﹣<0.【分析】①把B点坐标代入反比例函数解析式可求得k2的值,把点A(m,8)代入求得的反比例函数的解析式求得m,然后利用待定系数法即可求得一次函数的解析式;②直接由A、B的坐标可求得答案.【解答】解:①把点B(4,2)代入反比例函数y2=(k2≠0,x>0)得,k2=4×2=8,∴反比例函数的解析式为y2=,将点A(m,8)代入y2得,8=,解得m=1,∴A(1,8),将A、B的坐标代入y1=k1x+b(k1、b为常数,k1≠0)得,解得,∴一次函数的解析式为y1=﹣2x+10;②由图象可知:当0<x<1或x>4时,y1<y2,即k1x+b﹣<0.【点评】本题考查了一次函数和反比例函数的交点,待定系数法求一次函数和反比例函数的解析式,熟练掌握待定系数法是解题的关键.7.(2019年江苏省宿迁市)如图,一次函数y=kx+b的图象与反比例函数y=﹣的图象相交于点A(﹣1,m)、B(n,﹣1)两点.(1)求一次函数表达式;(2)求△AOB的面积.【分析】(1)先利用反比例函数解析式确定A点和B点坐标,然后利用待定系数法求一次函数解析式;(2)先求OD的长,根据面积和可得结论.【解答】解:(1)把A(﹣1.m),B(n,﹣1)代入y=﹣,得m=5,n=5,∴A(﹣1,5),B(5,﹣1),把A(﹣1,5),B(5,﹣1)代入y=kx+b得,解得,∴一次函数解析式为y=﹣x+4;(2)x=0时,y=4,∴OD=4,∴△AOB的面积=S△AOD+S△BOD=×4×1+=12.【点评】本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,也考查了待定系数法求函数解析式.8.(2019年浙江省丽水市)如图,在平面直角坐标系中,正六边形ABCDEF的对称中心P在反比例函数y=(k>0,x>0)的图象上,边CD在x轴上,点B在y轴上,已知CD=2.(1)点A是否在该反比例函数的图象上?请说明理由;(2)若该反比例函数图象与DE交于点Q,求点Q的横坐标;(3)平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.【分析】(1过点P作x轴垂线PG,连接BP,可得BP=2,G是CD的中点,所以P(2,);(2)易求D(3,0),E(4,),待定系数法求出DE的解析式为x﹣3,联立反比例函数与一次函数即可求点Q;(3)E(4,),F(3,2),将正六边形向左平移两个单位后,E(2,),F(1,2),则点E与F都在反比例函数图象上;【解答】解:(1)过点P作x轴垂线PG,连接BP,∵P是正六边形ABCDEF的对称中心,CD=2,∴BP=2,G是CD的中点,∴PG=,∴P(2,),∵P在反比例函数y=上,∴k=2,∴y=,由正六边形的性质,A(1,2),∴点A在反比例函数图象上;(2)D(3,0),E(4,),设DE的解析式为y=mx+b,∴,∴,∴y=x﹣3,联立方程解得x=,∴Q点横坐标为;(3)E(4,),F(3,2),将正六边形向左平移两个单位后,E(2,),F(1,2),则点E与F都在反比例函数图象上;【点评】本题考查反比例函数的图象及性质,正六边形的性质;将正六边形的边角关系与反比例函数上点的坐标将结合是解题的关系.9.(2019年四川省南充市)双曲线y=(k为常数,且k≠0)与直线y=﹣2x+b,交于A(﹣m,m﹣2),B(1,n)两点.(1)求k与b的值;(2)如图,直线AB交x轴于点C,交y轴于点D,若点E为CD的中点,求△BOE的面积.【分析】(1)将A、B两点的坐标代入一次函数解析式可得b和n的值,则求出点B(1,﹣2),代入反比例函数解析式可求出k的值.(2)先求出点C、D两点的坐标,再求出E点坐标,则S△BOE=S△ODE+S△ODB=,可求出△BOE的面积.【解答】解:(1)∵点A(﹣m,m﹣2),B(1,n)在直线y=﹣2x+b上,∴,解得:,∴B(1,﹣2),代入反比例函数解析式,∴,∴k=﹣2.(2)∵直线AB的解析式为y=﹣2x﹣2,令x=0,解得y=﹣2,令y=0,解得x=﹣1,∴C(﹣1,0),D(0,﹣2),∵点E为CD的中点,∴E(),∴S△BOE=S△ODE+S△ODB===.【点评】本题考查了反比例函数与一次函数的交点问题,三角形的面积,熟练掌握待定系数法是解题的关键.10.(2019年四川省绵阳市)如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=(m≠0且m≠3)的图象在第一象限交于点A、B,且该一次函数的图象与y轴正半轴交于点C,过A、B分别作y轴的垂线,垂足分别为E、D.已知A(4,1),CE=4CD.(1)求m的值和反比例函数的解析式;(2)若点M为一次函数图象上的动点,求OM长度的最小值.【分析】(1)将点A(4,1)代入y=,即可求出m的值,进一步可求出反比例函数解析式;(2)先证△CDB∽△CEA,由CE=4CD可求出BD的长度,可进一步求出点B的坐标,以及直线AC的解析式,直线AC与坐标轴交点的坐标,可证直线AC与坐标轴所围成和三角形为等腰直角三角形,利用垂线段最短可求出OM长度的最小值.【解答】解:(1)将点A(4,1)代入y=,得,m2﹣3m=4,解得,m1=4,m2=﹣1,∴m的值为4或﹣1;反比例函数解析式为:y=;(2)∵BD⊥y轴,AE⊥y轴,∴∠CDB=∠CEA=90°,∴△CDB∽△CEA,∴,∵CE=4CD,∴AE=4BD,∵A(4,1),∴AE=4,∴BD=1,∴x B=1,∴y B==4,∴B(1,4),将A(4,1),B(1,4)代入y=kx+b,得,,解得,k=﹣1,b=5,∴y AB=﹣x+5,设直线AB与x轴交点为F,当x=0时,y=5;当y=0时x=5,∴C(0,5),F(5,0),则OC=OF=5,∴△OCF为等腰直角三角形,∴CF=OC=5,则当OM垂直CF于M时,由垂线段最知可知,OM有最小值,即OM=CF=.【点评】本题考查了反比例函数的性质,相似三角形的性质,垂线段最短等定理,解题关键是能够熟练运用反比例函数的性质及相似三角形的性质.11.(2019年甘肃省)如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(﹣1,n)、B(2,﹣1)两点,与y轴相交于点C.(1)求一次函数与反比例函数的解析式;(2)若点D与点C关于x轴对称,求△ABD的面积;(3)若M(x1,y1)、N(x2,y2)是反比例函数y=上的两点,当x1<x2<0时,比较y2与y1的大小关系.【分析】(1)利用待定系数法即可解决求问题.(2)根据对称性求出点D坐标,发现BD∥x轴,利用三角形的面积公式计算即可.(3)利用反比例函数的增减性解决问题即可.【解答】解:(1)∵反比例函数y=经过点B(2,﹣1),∴m=﹣2,∵点A(﹣1,n)在y=上,∴n=2,∴A(﹣1,2),把A,B坐标代入y=kx+b,则有,解得,∴一次函数的解析式为y=﹣x+1,反比例函数的解析式为y=﹣.(2)∵直线y=﹣x+1交y轴于C,∴C(0,1),∵D,C关于x轴对称,∴D(0,﹣1),∵B(2,﹣1)∴BD∥x轴,∴S△ABD=×2×3=3.(3)∵M(x1,y1)、N(x2,y2)是反比例函数y=﹣上的两点,且x1<x2<0,∴y1<y2.【点评】本题考查反比例函数与一次函数的交点问题,解题的关键是熟练掌握待定系数法解决问题,学会利用函数的增减性,比较函数值的大小.12.(2019年江苏省盐城市)如图,一次函数y=x+1的图象交y轴于点A,与反比例函数y=(x>0)的图象交于点B(m,2).(1)求反比例函数的表达式;(2)求△AOB的面积.【分析】(1)根据一次函数y=x+1的图象交y轴于点A,与反比例函数y=(x>0)的图象交于点B(m,2),可以求得点B的坐标,进而求得反比例函数的解析式;(2)根据题目中一次函数的解析式可以求得点A的坐标,再根据(1)中求得的点B的坐标,即可求得△AOB的面积.【解答】解:(1)∵点B(m,2)在直线y=x+1上,∴2=m+1,得m=1,∴点B的坐标为(1,2),∵点B(1,2)在反比例函数y=(x>0)的图象上,∴2=,得k=2,即反比例函数的表达式是y=;(2)将x=0代入y=x+1,得y=1,则点A的坐标为(0,1),∵点B的坐标为(1,2),∴△AOB的面积是;.【点评】本题考查反比例函数与一次函数的交点问题,解答本题的关键是明确题意,利用数形结合的思想解答.13.(2019年江苏省连云港市)如图,在平面直角坐标系xOy中,函数y=﹣x+b的图象与函数y=(x<0)的图象相交于点A(﹣1,6),并与x轴交于点C.点D是线段AC上一点,△ODC与△OAC的面积比为2:3.(1)k=﹣6,b=5;(2)求点D的坐标;(3)若将△ODC绕点O逆时针旋转,得到△OD'C',其中点D'落在x轴负半轴上,判断点C'是否落在函数y=(x<0)的图象上,并说明理由.【分析】(1)将A(﹣1,6)代入y=﹣x+b可求出b的值;将A(﹣1,6)代入y=可求出k的值;(2)过点D作DM⊥x轴,垂足为M,过点A作AN⊥x轴,垂足为N,由△ODC与△OAC的面积比为2:3,可推出,由点A的坐标可知AN=6,进一步求出DM=4,即为点D的纵坐标,把y=4代入y=﹣x+5中,可求出点D坐标;(3)过点C'作C'G⊥x轴,垂足为G,由题意可知,OD'=OD==,由旋转可知S△ODC=S△OD'C',可求出C'G=,在Rt△OC'G中,通过勾股定理求出OG的长度,即可写出点C'的坐标,将其坐标代入y=﹣可知没有落在函数y=(x<0)的图象上.【解答】解:(1)将A(﹣1,6)代入y=﹣x+b,得,6=1+b,∴b=5,将A(﹣1,6)代入y=,得,6=,∴k=﹣6,故答案为:﹣6,5;(2)如图1,过点D作DM⊥x轴,垂足为M,过点A作AN⊥x轴,垂足为N,∵,∴,又∵点A的坐标为(﹣1,6),∴AN=6,∴DM=4,即点D的纵坐标为4,把y=4代入y=﹣x+5中,得,x=1,∴D(1,4);(3)由题意可知,OD'=OD==,如图2,过点C'作C'G⊥x轴,垂足为G,∵S△ODC=S△OD'C',∴OC•DM=OD'•C'G,即5×4=C'G,∴C'G=,在Rt△OC'G中,∵OG===,∴C'的坐标为(﹣,),∵(﹣)×≠﹣6,∴点C'不在函数y=﹣的图象上.【点评】本题考查了待定系数法求解析式,三角形的面积,反比例函数的性质,勾股定理等,解题关键是能够熟练运用反比例函数的性质.14.(2019年浙江省嘉兴市)如图,在直角坐标系中,已知点B(4,0),等边三角形OAB的顶点A在反比例函数y=的图象上.(1)求反比例函数的表达式.(2)把△OAB向右平移a个单位长度,对应得到△O'A'B'当这个函数图象经过△O'A'B'一边的中点时,求a的值.【分析】(1)过点A作AC⊥OB于点C,根据等边三角形的性质得出点A坐标,用待定系数法求得反比例函数的解析式即可;(2)分两种情况讨论:①反比例函数图象过AB的中点;②反比例函数图象过AO的中点.分别过中点作x轴的垂线,再根据30°角所对的直角边是斜边的一半得出中点的纵坐标,代入反比例函数的解析式得出中点坐标,再根据平移的法则得出a的值即可.【解答】解:(1)过点A作AC⊥OB于点C,∵△OAB是等边三角形,∴∠AOB=60°,OC=OB,∵B(4,0),∴OB=OA=4,∴OC=2,AC=2.把点A(2,2)代入y=,得k=4.∴反比例函数的解析式为y=;(2)分两种情况讨论:①点D是A′B′的中点,过点D作DE⊥x轴于点E.由题意得A′B′=4,∠A′B′E=60°,在Rt△DEB′中,B′D=2,DE=,B′E=1.∴O′E=3,把y=代入y=,得x=4,∴OE=4,∴a=OO′=1;②如图3,点F是A′O′的中点,过点F作FH⊥x轴于点H.由题意得A′O′=4,∠A′O′B′=60°,在Rt△FO′H中,FH=,O′H=1.把y=代入y=,得x=4,∴OH=4,∴a=OO′=3,综上所述,a的值为1或3.。
