05化工分离工程-泡露点计算
合集下载
泡点和露点计算
正丁烷 (1)
2.1
0.315
正戊烷 (2) 0.71
0.284
正己烷 (3) 0.25
0.1125
∑ 0.7115
传质分离过程
设温度为60℃,查P-T-K 图得K,将K值列于下表
组分 正丁烷 正戊烷 正己烷
∑
Ki
2.8
0.93
0.36
Kixi
0.42
0.372 0.162 0.954
yi
0.42
Ki f T, P, xi , yi
计算步骤:
L i
Pi S
iS
ˆ Vi P
exp ViL
P PiS RT
已知p,假设T 求出(或查出)各组分的相应参数
由已知的 x按i 理想状态求出Ki,初步算出 yi
求出 Ki,由已知的xi yi Ki xi
Ki xi 1 (通常取为0.005) 泡点T
如果 Ki xi 1 ; 升高T,重新计算。 Ki xi 1 ; 降低T,重新计算。
传质分离过程
开始 Y
输入P、y及有关参数
设T并令 1 作第一次迭代
计算PiS ,ViL ,iS ,ˆiV
调整T
计算 K i和xi 计算 xi
是否第一次迭代
圆整 xi
计算 i
Y
N
xi有无变化
N
xi 1 N
第二章 传质分离过程的热力学基础
2.2 多组分物系的泡点和露点的计算
1、定义:泡点Tb、泡点压力P、露点Td、露点压力P 2、泡、露点计算方法:根据相律 f=c-π+2=c。
类型 泡点温度
泡点压力 露点温度 露点压力
规定变量
P, x1 , x2 L L xc
化工分离过程第二章

18
yi yj
2.1.2 相平衡常数的计算
ˆ 计算K——状态方程法 一、根据逸度系数
ˆ V V y P 汽相: f i i i
ˆ L L x P 液相: f i i i
yi iL 相平衡常数: Ki V xi i
(2-14)
关键: 选择一 个既适用于汽 相、又适用于 液相的状态方 程。
式中:fi0V 在系统温度和压力下纯组分i的气相逸度 γiV 组分i的气相活度系数 φi0V在系统温度和压力下,纯组分i的气相逸度系数 φiV 在系统温度和压力下,组分i的气相分逸度系数且
V 0V V ˆ i i i
9
同样,液相逸度与液相组成的关系为:
ˆ L f 0L L x P 0L L x P ˆL x f i i i i i i i i i
式中的逸度系数可从该物质的p-V-T(状态方程)关系或 实测数据计算。逸度系数通过状态方程计算: 此法适用于中压下,液相非理想性不是很强的烃类系统。
19
由热力学原理可以推导出以下表达式:
以V为自变量பைடு நூலகம்
RT 1 P ˆ lni dVt lnZ m v RT ni T ,V ,n Vt j
应用:已知 T,P,xi , yi ( i 1, 2, 求
V i
c)
26
L i
步骤:
输入:T、P、Tc、i、Pc、i,xi、yi
i=1
i) (1)式求V( t (i) (2)式求Z M ˆ(i) (3)式求 i
i=i+1
i=1
Yes No
V L ˆ ˆ 输出 i 或 i
注意:
● i=1时求汽相逸度系数;i=2时求液相逸度系数。
yi yj
2.1.2 相平衡常数的计算
ˆ 计算K——状态方程法 一、根据逸度系数
ˆ V V y P 汽相: f i i i
ˆ L L x P 液相: f i i i
yi iL 相平衡常数: Ki V xi i
(2-14)
关键: 选择一 个既适用于汽 相、又适用于 液相的状态方 程。
式中:fi0V 在系统温度和压力下纯组分i的气相逸度 γiV 组分i的气相活度系数 φi0V在系统温度和压力下,纯组分i的气相逸度系数 φiV 在系统温度和压力下,组分i的气相分逸度系数且
V 0V V ˆ i i i
9
同样,液相逸度与液相组成的关系为:
ˆ L f 0L L x P 0L L x P ˆL x f i i i i i i i i i
式中的逸度系数可从该物质的p-V-T(状态方程)关系或 实测数据计算。逸度系数通过状态方程计算: 此法适用于中压下,液相非理想性不是很强的烃类系统。
19
由热力学原理可以推导出以下表达式:
以V为自变量பைடு நூலகம்
RT 1 P ˆ lni dVt lnZ m v RT ni T ,V ,n Vt j
应用:已知 T,P,xi , yi ( i 1, 2, 求
V i
c)
26
L i
步骤:
输入:T、P、Tc、i、Pc、i,xi、yi
i=1
i) (1)式求V( t (i) (2)式求Z M ˆ(i) (3)式求 i
i=i+1
i=1
Yes No
V L ˆ ˆ 输出 i 或 i
注意:
● i=1时求汽相逸度系数;i=2时求液相逸度系数。
《化工分离工程》PPT课件-第4讲分离过程
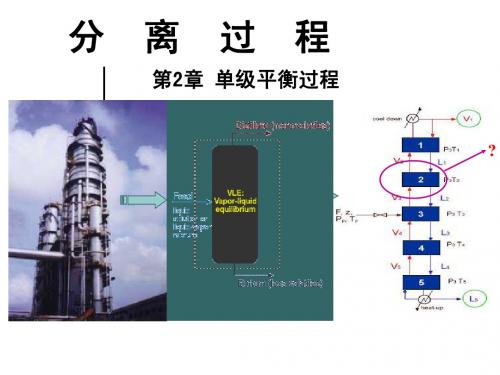
y i = K i xi
C
i = 1,2,..., C
C
(2)摩尔分率加和方程: 2个 摩尔分率加和方程:
∑x
i =1
i
= 1 .0
∑y
i =1
i
= 1.0
2C+ 2C+2 C个
(3)汽液平衡常数关联式: 汽液平衡常数关联式:
Ki = f (T , P, x, y)
i = 1,2,...,C
变量数: 变量数:
泡点和露点计算在设计计算中应用
精馏塔各级温度确定
泡点和露点计算在设计计算中应用
精馏塔操作压力的选择
① 塔顶蒸汽的冷凝温度和釜液的 沸腾温度 ② 对组分相对挥发度的影响 ③塔的造价和操作费用 ④对传质效率的影响
计算出发点: 计算出发点:
单级汽液平衡系统, 单级汽液平衡系统,汽液相具有相同的温度T和压力p, 组分的液相组成与汽相组成成平衡关系。 组分的液相组成与汽相组成成平衡关系。 (1)相平衡方程: 相平衡方程: 计 算 方 程: C个
( new )
yi
yi(old ) = (old ) ∑ yi
(3)判断收敛的准则或者是温度的调节方案直接 ) 关系到收敛速度和稳定性。 关系到收敛速度和稳定性。
二、泡点压力的计算
仍然依据的是泡点方程: 仍然依据的是泡点方程:
f ( p ) = ∑ K i xi − 1 = 0
i =1 C
当汽相为理想气体,液相为理想溶液时: 当汽相为理想气体,液相为理想溶液时:
f (T ) = ∑ K i xi − 1 = 0
i =1 C
泡点温度计算
泡点压力计算
一、泡点温度的计算
1. Ki与组成无关: 与组成无关: 泡点方程: 泡点方程: 假定T 假定
05化工分离工程-泡露点计算

i 1
C
计算方法: 设T 由P T K图查K i yi K i x i YES T T设 f(T) 结束 yi K i xi NO
给定P
计算中:若 K i x i 1, 说明T偏高; 若 K i x i 1, 说明T偏低。
2.平衡常数与组成有关的情况
计算框图: 开始
输入P、y及有关参数 设T并令 1 作第一次迭代
S L S ˆV 计算Pi ,Vi ,f i ,f i
Y
N xi有无变化
xi 1
Y 输出T、y
结束
N
N
计算 K i 和xi 调整T 计算 xi 是否第一次迭代
圆整 x i 计算 i Y
∴采用试差法
s s i Pi f i Ki V ˆi P f
L
S
计算框图: 开始
输入P、x及有关参数
V ˆ 设T并令f i
N Y
yi有无变化
1作第一次迭代
S
ln yi
Y 输出T、y 结束
N
N
计算 Pi
,Vi L ,f iS , i
圆整 y i ˆiV 计算 f Y
计算 K i 和y i 调整T
解法3:电算(Newtow迭代法)
t
( k 1)
t
(k )
f (t k ) ; K F (t )
t
( k 1)
t
(k )
0.001
Pi S f (t ) K i xi 1 xi 1 P ( k 1) K i xi 1 (k ) t — 迭代式 t Bi K i xi [ ] 2 (t Ci ) Bi 1 K i exp[ Ai ( k ) ] — 子程序 P t Ci 设T=70℃(初值), 5次完成及:可用ln yi 判别
C
计算方法: 设T 由P T K图查K i yi K i x i YES T T设 f(T) 结束 yi K i xi NO
给定P
计算中:若 K i x i 1, 说明T偏高; 若 K i x i 1, 说明T偏低。
2.平衡常数与组成有关的情况
计算框图: 开始
输入P、y及有关参数 设T并令 1 作第一次迭代
S L S ˆV 计算Pi ,Vi ,f i ,f i
Y
N xi有无变化
xi 1
Y 输出T、y
结束
N
N
计算 K i 和xi 调整T 计算 xi 是否第一次迭代
圆整 x i 计算 i Y
∴采用试差法
s s i Pi f i Ki V ˆi P f
L
S
计算框图: 开始
输入P、x及有关参数
V ˆ 设T并令f i
N Y
yi有无变化
1作第一次迭代
S
ln yi
Y 输出T、y 结束
N
N
计算 Pi
,Vi L ,f iS , i
圆整 y i ˆiV 计算 f Y
计算 K i 和y i 调整T
解法3:电算(Newtow迭代法)
t
( k 1)
t
(k )
f (t k ) ; K F (t )
t
( k 1)
t
(k )
0.001
Pi S f (t ) K i xi 1 xi 1 P ( k 1) K i xi 1 (k ) t — 迭代式 t Bi K i xi [ ] 2 (t Ci ) Bi 1 K i exp[ Ai ( k ) ] — 子程序 P t Ci 设T=70℃(初值), 5次完成及:可用ln yi 判别
泡点和露点的计算
0.7115
传质分离过程
设温度为60℃,查P-T-K 图得K,将K值列于下表
组分 Ki
K i xi yi 组分 Ki K i xi yi
正丁烷 2.8
0.42 0.42
正戊烷 0.93
0.372 0.372
正己烷 0.36
0.162 0温度为62℃,查P-T-K 图得K,将K 值列于下表 正丁烷 2.9 0.435 0.435 正戊烷 0.98 0.392 0.392
已知p, 假设T 求出(或查出)各组分的相应参数
由已知的 x 按理想状态求出 Ki,初步算出 i 求出 K i,由已知的xi yi Kixi
yi
Ki xi 1 ( 通常取为0. 005) 泡点T
如果
Ki xi 1 ;
降低T,重新计算。
Ki xi 1 ; 升高T,重新计算。
第二章 传质分离过程的热力学基础
2.2 多组分物系的泡点和露点的计算
1、定义:泡点Tb、泡点压力P、露点Td、露点压力P 2、泡、露点计算方法:根据相律 f=c-π+2=c。
类型
泡点温度
规定变量
P, x1 , x2 T , x1 , x2
P, y1 , y2
求解变量
xc xc
yc
T , y1 , y2 yc
N
Y
yi 有无变化
ln yi
Y 输出P、y 结束
N
N
计算 Pi
S
,Vi L , iS , i
圆整 y i ˆiV 计算 Y
计算 K i 和yi
调整P 计算 yi 是否第一次迭代
传质分离过程
4、露点温度和压力的计算
3.泡、露点计算

露点温度(压力)
根据相律:
f = c −π + 2 = c
在以上每一类计算中,规定C个参数,必定可求取C个未知数。
2
精馏
2.2.15 多组分系统的泡点计算
1、泡点计算基本方程 相平衡关系 归一方程 相平衡常数式 方程数 变量
∑y =1 ∑x =1
i i i i
yi = Ki xi
(i =1, , c) 2 (i =1, , c)
F(T)=1-∑ Kixi=0
泡点方程 新值Tb
参照 Sy =∑ Kixi 之值调整。
当P一定,T↑,K↑;T↓,K↓ Sy =∑Kixi > 1,原设 T 过高; Sy =∑Kixi < 1,原设 T 过低。
5
精馏
(2)当 Ki=f(T,P,x,y)机算 如系统压力P<1.5Mpa
ˆ f i 0γ i ϕ iL Ki = V = V ˆ ˆ ϕi P ϕi
精馏
x 输入T,
泡点压力计算框图
估计初值Pb和 y
0 ˆV 计算 K i = γ i f i / ϕ i P
ˆ ϕ iL Ki = V ˆ ϕi
计算 yi = K i xi 及 y i = K i xi / ∑ K i xi Pb=Pb(1-F) 否
F =1 − ∑ Ki xi
F ≤ ε ( 如 .0 0 1) ?
F (T ) = 1− ∑ yi Ki = 0
i
F (P) = 1− ∑ yi Ki = 0
i
10
精馏
2.露点计算
给定:P(或T)和汽相组成
ቤተ መጻሕፍቲ ባይዱ
y1 , y2 ,
, yC −1
计算:此P下,凝结出第一滴露珠时的TD及此露珠的组成 xi 此T下,凝结出第一滴露珠时的PD及此露珠的组成 露点压力:计算的迭代式为: 露点压力:
泡点和露点计算

本节内容
气液平衡系统的设计变量 泡露点计算的重点、难点 泡点温度计算 露点温度计算
2.2 多组分物系的泡点和露点计算 Bubble-point and Dew-point Calculation for Multicomponent Systems
分离过程设计中最基本的气液平衡计算。 例如:
练习1
求含乙烷(1)0.15、丙烯(2)0.4、丙烷(3)0.35、 异丁烷(4)0.1(摩尔百分比)的烃类混合物在 300kPa时的泡点温度
问题:
什么样的情况下可认为K与组成无关?
答:1)汽相为理想气体,液相为理想溶液。
Ki pis / p
2)汽相为理想溶液,液相为理想溶液
Ki fiL /fivபைடு நூலகம்
精馏计算: 各塔板温度---泡点计算 操作压力---泡露点压力计算
等温闪蒸计算: 估计闪蒸过程是否可行---泡露点温度计算
一、气液平衡系统设计变量
气相
液相
气液平衡系统
请分析一下上图气液平衡系统的总变量、独立约束方程和 设计变量(10min)
气相 液相 气液平衡系统
?定义哪些变量 称为设计变量
一、气液平衡系统设 计变量
Ki
ˆiL ˆiV
(2-12)
Ki
yi xi
i
Pi
s s i
ˆiV P
exp
viL
(P RT
Pi
s
)
(2-30)
If :
Ki f p,T , c
开始
输入p,x及有关参数
设T并令iV=1,作第一次迭代
计算pis、ViL、is、i
调整T
N
计算Ki和yi
计算yi
泡点和露点计算课件

1. Ki与组成无关:if Ki f(T,P)
泡点方程:
C
fTKixi 10
i1
计算过程:
已知p 设T
计算或查图 得Ki
计算
C
f (T ) Ki xi 1 i 1
调整T
f (T )
是
结束 输出T,y
否
例题2-3
• 例2-3
• 三种组分含量 相差不大,取 分子量居中的 正戊烷在该压 力下的沸点为 初值
?定义哪些变量
称为设计变量
一、气液平衡系统设计 变量
多组分泡点、露点 计算的类型
二、泡露点计算重点、难点
相平衡常数Ki
• 与系统T、p有关
• 对非理想体系,还与气液相组成x,y
有关
• 计算的重点、难点:Ki的计算
(1)列线图 法求K值
p12
部分轻烃 忽略组成变化 对K值的影响
T升高,K如何变化? P增加,K如何变化?
计算中,如何适当的调整试差的温度(或压力)?
本节内容
• 气液平衡系统的设计变量 • 泡露点计算的重点、难点 • 泡点温度计算 • 露点温度计算
2.2 多组分物系的泡点和露点计算 Bubble-point and Dew-point Calculation for Multicomponent Systems
Kx yii iˆpV iis pisexV piL(R pT pis)
(2)活度系数、逸度系数法计算K值
Liquid
Gas
Ideal solution Real solution
Ideal gas
Ki
Pi s P
Ki
i Pi s
P
Ideal solution Real gas
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
与T有关的变量: ˆiV , i,Pi s,f is,Vi L f
ˆiV 与yi 有关的变量:f
与P有关的变量: ˆiL,P f
相同
框图
泡点方程比较:
求泡点温度
C
求泡点压力
C
i 1 常用的简化形式: C PS i
f (T ) K i x i 1 0 ( 2 15) f ( p) K i xi 1 0 ( 2 56) f(T) xi 1 0
Ki 1 K x 1有: ( )x i iK x i i i KK KK
iK 随T变化不大,取某温度范围内的均值
计算方法:
iK
设T=98 ℃ (离泡点不远) S
Pi S PK T泡
KK
1
Pi
S
iK x i ∴T=99.7 ℃
S PK
KK P
2.平衡常数与组成有关的情况
Vi ( P Pi ) exp[ ] 与T、P、x i、yi 有关 RT yi K i xi — 泡点方程 y 1 i 已知条件:P、x i, 求:T、yi 计算分析: V S S L ˆ 与T有关的参数:f i 、 i、Pi 、f i 、Vi V ˆ 与yi 有关的参数:f i
计算 y i 是否第一次迭代
判别收敛条件:
用于低压时近似看成:
Ki
i Pi S
Bi ; ln Pi Ai P Ci t
S S
Bi 1 ln K i ln Pi ln A f( ) P Ci t t 1 ln K i x i G ( ) T i 1
1.2.2.1 泡点温度的计算 1.2.2.2泡点压力的计算
1.2.2 多组分物系的露点计算
1.2.2.1 露点温度的计算 1.2.2.2露点压力的计算
汽液平衡时:
F C 2 C 2 2 C — 与组分数相当
计算类型 泡点温度 规定量(C个) 求解量
P , x1 x2 xc1 T , x1 x2 xc1
2.平衡常数与组成有关的情况
计算框图: 开始
输入P、y及有关参数 设T并令 1 作第一次迭代
S L S ˆV 计算Pi ,Vi ,f i ,f i
Y
N xi有无变化
xi 1
Y 输出T、y
结束
N
N
计算 K i 和xi 调整T 计算 xi 是否第一次迭代
圆整 x i 计算 i Y
例1—2:计算50℃时蒸汽混合物露点压力
S T , P i ; 12 , 21 , 13 , 31 , 23 , 32 已知:1.
2. 汽相组成 解:汽相假定为理想气体,液相为非理想溶液 计算式:
ViL ( P PiS ) Ki exp[ ] P RT L S Vi ( P Pi ) S p i Pi x i exp[ ] RT P K i xi
解法3:电算(Newtow迭代法)
t
( k 1)
t
(k )
f (t k ) ; K F (t )
t
( k 1)
t
(k )
0.001
Pi S f (t ) K i xi 1 xi 1 P ( k 1) K i xi 1 (k ) t — 迭代式 t Bi K i xi [ ] 2 (t Ci ) Bi 1 K i exp[ Ai ( k ) ] — 子程序 P t Ci 设T=70℃(初值), 5次完成。T=99.812
0
计算框图:
开始 输入T、x及有关参数
N
Y
yi有无变化
ˆi 估计P并令f
V
1作第一次迭代
ln yi
Y 输出P、y 结束
N
N
计算 Pi
S
,Vi L ,f iS , i
圆整 y i ˆiV 计算f Y
计算 K i 和y i
调整P 计算 y i 是否第一次迭代
1.2.2.2 露点温度和压力的计算
C
i
某一函数式
及:可用ln yi 判别
二、泡点压力的计算 与泡点温度相同,比较与分析如下:
项目 求泡点温度
(已知P,x) 计算 变量 与函 数关 系
s s i Pi f i Ki V ˆi P f
求泡点压力
(已知T,x)
S
Ki
Vi ( P Pi ) exp[ ] RT
L
相同
i 1Leabharlann C计算方法: 设T 由P T K图查K i yi K i x i YES T T设 f(T) 结束 yi K i xi NO
给定P
计算中:若 K i x i 1, 说明T偏高; 若 K i x i 1, 说明T偏低。
化工分离工程-多组分物系的 气液平衡
多组分物系的泡露点计算
化工与药学院 祝 阳 2015.03
内容:
多组分物系单级平衡过程 的计算1
第一章 多组分精馏过程
1.2 多组分物系的气液平衡
1.3 闪蒸过程的计算
1.4 塔顶、塔底产品数量与组成 1.5 多元精馏的简捷计算
1.7 多元精馏的计算机模型
1.2.2 多组分物系的泡点计算
i 1 常用的简化形式: C S P泡 Pi xi 0 (2 57) i 1 — 完全理想系,不用试差 C P泡 Pi S i xi 0 ( 2 58) i 1 — 理汽、非理液,不试差
i 1 P — 完全理想系,试差计算 C P S i i f(T) xi 1 i 1 P — 理汽、非理液,试差
解法1:用试差法计算
Pi Ki P
T(设)
S
K i xi 1
110 ℃ 98 ℃ 100℃
1.00
70 ℃
0.379
K i xi
1.344 0.951 3 ∴ T=100℃
解法2:用 iK计算(不试差,实用于完全理想系) iK x i K i Pi S yi x 而: iK K S PK iK i K
已知:P(或T) T(或P) 1.平衡常数与组成无关的情况 露点方程: C
C
yi f (T ) 1.0 0 (1 11) i 1 K i yi f ( P) 1.0 0 (1 12) i 1 K i
计算方法同于泡点计算: 1.试差;2.用 iK 计算;3.电算;4.查K图
i PiS
结果:P=85.101kPa
计算过程:
开始
输入T、y及有关参数 估计P,X值 计算 i 计算 K i 调整P 圆整 x i Y
( yi K i ) 1
Y 输出P、x 结束 例题图
N
xi有无变化
N
作 业
• 见word
∴采用试差法
s s i Pi f i Ki V ˆi P f
L
S
计算框图: 开始
输入P、x及有关参数
V ˆ 设T并令f i
N Y
yi有无变化
1作第一次迭代
S
ln yi
Y 输出T、y 结束
N
N
计算 Pi
,Vi L ,f iS , i
圆整 y i ˆiV 计算 f Y
计算 K i 和y i 调整T
P , y1 y2 yc1 T , y1 y2 yc1
T , y1 y2 yc P , y1 y2 yc
泡点压力
露点温度 露点压力
T , x1 x2 xc P , x1 x2 xc
1.2.2.1 泡点温度和压力的计算
• 变量分析:
变量数:T
方程: yi K i xi
P
xi C
yi C
1 1
2C 2
数目: C
1 xi 1 1 yi 1 C2 (2C 2) (C 2) C 指定:T(或P)、x ( , 2, c 1) i i 1 — C个变量
一、泡点温度的计算 1.平衡常数与组成无关的情况 K i f ( P ,T ) * P T K 查图得 K i * 计算
S 1 . K i Pi P (汽相为理想气体,液相为理想溶液) 2 . K i T 数据回归
3
Ki
2 3 T b1 i b 2 i T b 3i T b4 i T
V fi
L 3 . Ki fi
f iL f iV (气液相均为理想溶液)
采用泡点方程:
f (T ) K i x i 1 0 (1-10) ( 2 51)
例1—1:计算烃类混合物的泡点
已知:1. xi
2. 压力
解:用P—T—K图计算方法:
K图查 计算
设T(已知P)
重新设T
K
No
K x
Yes
i i
K i xi 1
T T设
例1—2:计算塔釜温度(完全理想系)
已知:1. x i, w
2. ln Pi Ai 3. 常压操作
S
Bi ( t C i )
