实验一达西定律验证实验
液体流动实验报告

一、实验目的1. 理解和掌握液体流动的基本原理;2. 观察液体在不同条件下的流动现象;3. 分析液体流动速度与液体性质、管道结构等因素的关系。
二、实验原理液体流动是指液体在重力、压力、粘度等作用下,在管道内流动的过程。
液体流动的基本原理包括:1. 牛顿粘性定律:液体的流动速度与剪切应力成正比,与剪切率成反比;2. 达西定律:液体在管道内流动时,其流量与管道长度、管道截面积、液体粘度和压力差成正比;3. 伯努利方程:在液体流动过程中,流速增加,压力降低。
三、实验材料与仪器1. 实验材料:水、酒精、肥皂水、色拉油等;2. 实验仪器:管道、阀门、流量计、计时器、压力计、温度计等。
四、实验步骤1. 实验一:观察液体在管道中的流动现象(1)将管道安装好,连接好阀门和流量计;(2)打开阀门,观察水在管道中的流动现象,记录流量计的读数;(3)分别将肥皂水、酒精、色拉油等液体加入管道中,观察其流动现象,记录流量计的读数;(4)分析不同液体在管道中的流动速度、压力、粘度等参数。
2. 实验二:观察液体流动速度与管道结构的关系(1)将管道连接好,安装好阀门和流量计;(2)调整管道的弯曲程度、管道直径、管道长度等参数;(3)观察液体在管道中的流动现象,记录流量计的读数;(4)分析不同管道结构对液体流动速度的影响。
3. 实验三:观察液体流动速度与液体性质的关系(1)将管道连接好,安装好阀门和流量计;(2)调整液体的粘度、密度等参数;(3)观察液体在管道中的流动现象,记录流量计的读数;(4)分析不同液体性质对流动速度的影响。
五、实验结果与分析1. 实验一:观察液体在管道中的流动现象实验结果显示,不同液体在管道中的流动速度、压力、粘度等参数存在差异。
肥皂水在管道中的流动速度较快,压力较低;酒精的流动速度较慢,压力较高;色拉油的流动速度最慢,压力最高。
2. 实验二:观察液体流动速度与管道结构的关系实验结果显示,管道的弯曲程度、管道直径、管道长度等参数对液体流动速度有显著影响。
达西定律实验

达西定律实验引言:达西定律是描述流体流动的经验定律之一,由法国科学家达西于1799年提出。
该定律表明,当流体通过管道流动时,流速增大、压力降低。
为了验证达西定律的准确性,并进一步了解流体在管道中的流动规律,科学家们进行了一系列的实验。
实验一:流体通过水平管道实验目的:通过实验验证达西定律在水平管道中的适用性,并观察不同流速下的压力变化。
实验装置和步骤:1. 准备一根水平透明管道,长度为1米,管径为2厘米,并在管道两端安装好压力计和流量计。
2. 将流体(如水)注入管道中,并控制不同的流速。
3. 测量不同流速下管道入口和出口处的压力,并记录数据。
实验结果和讨论:经过实验观察和数据分析,我们发现达西定律在水平管道中得到了有效验证。
随着流速的增大,管道入口处的压力降低,出口处的压力也较低。
这与达西定律的预期结果相符。
实验二:流体通过斜管道实验目的:通过实验验证达西定律在斜管道中的适用性,并研究不同斜度对流体流动的影响。
实验装置和步骤:1. 准备一根倾斜的透明管道,长度为1米,管径为2厘米,并在管道两端安装好压力计。
2. 将流体注入管道中,并控制不同斜度下的流速。
3. 测量不同斜度下管道入口和出口处的压力,并记录数据。
实验结果和讨论:根据实验结果和数据分析,我们可以得出结论:在斜管道中,流体流动时同样符合达西定律。
不同斜度下流速的增大,导致入口处和出口处的压力下降情况类似于水平管道中的观察结果。
实验三:流体通过不同直径的管道实验目的:通过实验验证达西定律在不同直径管道中的适用性,并研究不同管道直径对流体流动的影响。
实验装置和步骤:1. 准备两根透明管道,长度均为1米,其中一根管径为2厘米,另一根管径为4厘米。
2. 将流体注入这两根管道中,并控制相同的流速。
3. 测量两根管道入口和出口处的压力,并记录数据。
实验结果和讨论:实验结果表明,不同直径的管道中达西定律同样成立。
尽管管径变大,但流速增加,从而导致管道入口和出口处的压力均有所降低。
渗透定律试验实验报告

一、实验目的1. 理解渗透定律试验的基本原理。
2. 掌握渗透定律试验的操作方法。
3. 学习如何通过实验数据计算渗透系数。
4. 分析不同条件下渗透系数的变化规律。
二、实验原理渗透定律,又称达西定律,描述了在层流条件下,土体中水渗流速度与水力梯度之间的关系。
其表达式为:\[ V = k \cdot i \]其中,\( V \) 为水渗流速度,\( k \) 为渗透系数,\( i \) 为水力梯度。
渗透系数 \( k \) 是土体渗透性能的重要指标,其数值的大小取决于土体的颗粒组成、孔隙结构、孔隙水性质等因素。
三、实验仪器与材料1. 达西实验装置:包括直立圆筒、滤板、土样、测压管等。
2. 天然土样:采集不同类型的土样,如砂土、粘土等。
3. 量筒、天平、计时器等。
四、实验步骤1. 准备实验装置,包括直立圆筒、滤板、土样等。
2. 将土样放入圆筒中,使其密实。
3. 在土样上下两端分别安装测压管,并用橡皮塞封闭。
4. 向圆筒中加入水,使水位高于土样顶部。
5. 记录初始水头差 \( h_1 \)。
6. 打开橡皮塞,让水自由渗流,同时开始计时。
7. 每隔一定时间 \( t \) 记录测压管中的水头差 \( h_2 \)。
8. 当水头差基本稳定时,记录最终水头差 \( h_3 \)。
9. 重复上述步骤,进行多次实验。
五、实验数据与结果处理1. 计算水力梯度 \( i \):\[ i = \frac{h_2 - h_1}{L} \]其中,\( L \) 为土样长度。
2. 计算渗透速度 \( V \):\[ V = \frac{h_2 - h_1}{t} \]3. 计算渗透系数 \( k \):\[ k = \frac{V}{i} \]六、实验结果与分析1. 通过实验数据计算不同土样的渗透系数 \( k \)。
2. 分析不同压实方式和配合比对渗透系数的影响。
3. 比较不同土样的渗透系数,探讨其渗透性能差异。
七、实验结论1. 渗透定律适用于层流条件下土体中水的渗流。
不同填料的渗透系数测定实验——达西定律
不同填料的渗透系数测定实验——达西定律一、实验意义通过描绘流速与水头差的函数关系图,来确定渗透流量与水头损失的关系,从而来验证达西定律。
以及通过平行实验和对比实验,对数据进行比较处理,从而可知那些数据受到粒径的影响。
二、实验目的1.了解达西实验装置,通过稳定流条件下的渗流实验,测定不同粒径填料的渗透系数k 值。
2.加深理解渗流速度、水力梯度、渗透系数之间的关系,并验证达西定律。
二、实验仪器1.达西实验装置(自行设计),分别装有不同粒径的均质试样:①砂体(粒径<0.5mm ,0.7~1mm );②煤块(粒径5~10mm );③砖块(粒径5~10mm )。
2.秒表、量筒、直尺、温度计、电子称等。
三、实验原理室内渗透系数测定是根据达西关于多孔介质中地下水的线性渗透定律而设计的。
由达西定律,在常水头条件下,水流在单位时间内透过岩石空隙的流量(Q )与岩石的断面面积(ω)、水力坡度(I )成正比:测定不同试样的渗透系数。
H Q K K I Lωω∆==式中:Q ——渗透流量(cm 3); ω——过水断面面积(cm 2);∆H ——上下游过水断面的水头差(cm );L ——渗透途径(cm );I ——水力梯度。
由上式可推知,QV KIIω==,亦即,渗透系数在数值上等于水力坡度为1时,透过某单位过水断面的渗流量(亦即渗流速度)。
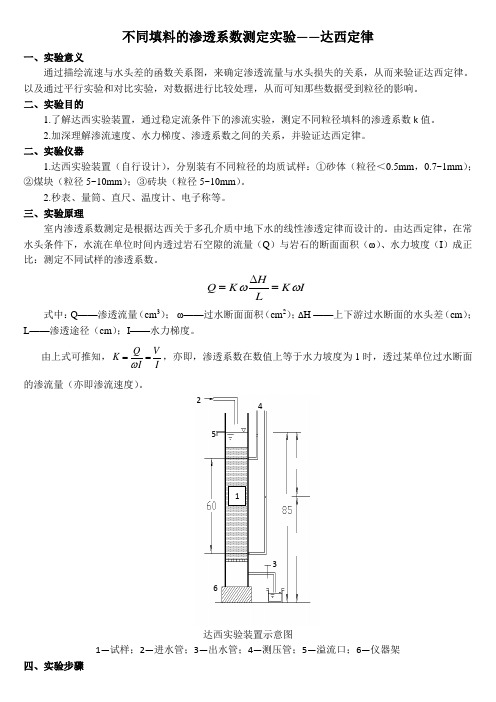
达西实验装置示意图1—试样;2—进水管;3—出水管;4—测压管;5—溢流口;6—仪器架四、实验步骤1234651.测量仪器的几何参数。
分别测量过水断面面积( ω )、测压管a 、b 的间距或渗透途径(L );记入(表1)。
2.调试仪器。
打开进水管,将水引入实验筒内,底部控制阀T 打开,此时要保持溢水管有少量水溢出,这时可以进行第一次实验。
3.测定水头待a 、b 两个测压管的水位稳定后,读出各测压管的水头值,记入(表1)中。
4.测定流量在进行步骤3的同时,利用秒表和量筒测量t 时间内水管流出的水体积,及时计算流量Q 。
渗流的基本定律(达西定律)

根据实验需求,设计并建立渗流装置,包括渗流管、压力源、流量 计等。
设定实验条件
设定恒定的水头压力、流量等实验条件,确保实验数据的准确性和 可靠性。
实验结果分析
01
02
03
数据记录
详细记录实验过程中的水 头压力、流量等数据,并 确保数据的准确性和完整 性。
数据处理
对实验数据进行整理、分 析和处理,绘制水头压力 与流量之间的关系曲线。
达西定律的发现可以追溯到19世纪初,由法国工程师达西通 过实验观察到流体在砂质土壤中的流动规律,并提出了该定 律。
达西定律的概述
达西定律描述了流体在多孔介质中的流动速度与压力梯度 之间的关系。具体来说,当流体在多孔介质中流动时,流 速与作用在流体上的压力梯度成正比,同时与介质的渗透 系数有关。
达西定律的数学表达式为:v = -K * grad(p),其中v是流速, K是介质的渗透系数,grad(p)是压力梯度。该公式表明流速 与压力梯度成正比,与渗透系数成反比。
达西定律与实际渗流过程的联系
01
达西定律是描述均匀、定常、不可压缩流体在多孔介质中稳态 流动的基本定律。
02
它指出,在一定条件下,流体的流量与压力梯度成正比,与介
质孔隙的阻力成反比。
达西定律适用于小孔径、低流速、高孔隙度、均质的多孔介质。
03
达西定律的局限性
1
达西定律不适用于非均匀、非定常、非线性流动, 以及大孔径、高流速、低孔隙度、非均质的多孔 介质。
渗流的基本定律(达西定律)
目录
• 引言 • 达西定律的数学表达 • 达西定律的物理意义 • 达西定律的实验验证 • 达西定律的应用实例 • 达西定律的发展与展望
01 引言
达西实验报告

达西实验报告
《达西实验报告》
在科学研究领域,达西实验是一种经典的实验方法,它被广泛应用于物理学、
化学、生物学等领域。
达西实验的原理是通过控制变量的方法,观察不同条件
下的实验结果,从而得出科学结论。
本文将介绍达西实验的基本原理和应用。
首先,达西实验的基本原理是设计实验条件,控制变量,观察实验结果,从而
得出科学结论。
在达西实验中,研究者需要设计实验条件,例如温度、压力、
光照等,然后控制其他变量不变,观察实验结果的变化。
通过比较不同条件下
的实验结果,研究者可以得出科学结论,指导后续的科学研究和实践应用。
其次,达西实验在物理学、化学、生物学等领域都有广泛的应用。
在物理学中,达西实验可以用于研究光学、热力学等问题;在化学中,可以用于研究化学反应、物质变化等问题;在生物学中,可以用于研究生物体对环境因素的适应能
力等问题。
通过达西实验,科学家们可以深入研究各种自然现象,为人类社会
的发展提供科学依据。
最后,达西实验的结果对科学研究和实践应用都具有重要意义。
通过达西实验,科学家们可以得出结论,指导后续的科学研究和实践应用。
例如,在医学领域,通过达西实验可以研究药物的疗效和副作用,为临床治疗提供科学依据;在环
境保护领域,通过达西实验可以研究污染物的分布和迁移规律,为环境保护提
供科学依据。
总之,达西实验是一种重要的科学研究方法,它通过控制变量的方法,观察实
验结果,得出科学结论,指导后续的科学研究和实践应用。
在未来的科学研究中,达西实验将继续发挥重要作用,为人类社会的发展做出更大的贡献。
达西定律实验

达西定律实验水力学及流体力学实验仪系列产品DXY型达西定律实验仪仪器编号:北京新华教仪科贸有限公司华同丰(北京)科技有限公司达西定律实验一、实验目的1.测定渗透砂体的渗透量与水头损失的关系,验证渗流的达西定律。
2.测定均质砂的渗透系数K值;二、实验设备设备由水泵、供水箱、存水箱及升降装置构成供水系统。
实验箱内装均质砂,底部及砂体的上表面各装一块滤板,中部设二个多孔测压管测定渗流水头损失。
用体积法测流量。
1—水泵2—升降定位手柄3—供水箱4—供水箱溢流槽5—供水调节阀6—排气软管7—测压管8—实验箱溢流槽9—实验箱10—多孔测压管11—转向阀12—计量箱13—存水箱14—泄流槽15—泄水阀16—供水阀*实验前请用地脚螺丝调平实验台三、实验原理及计算式液体在孔隙介质中流动时,由于粘滞性作用将会产生能量损失。
达西(Henri Darcy)在1852-1855年间通过实验,总结出渗流能量损失与渗流速度成一次方的线性规律,后人称为达西定律。
由于渗流速度很小,故速度水头可以忽略不计。
因此总水头H可用测管水头h来表示,水头损失h w可用测管水头差来表示,即于是,水力坡度J可用测管水头坡度来表示:式中,L为两个测压管孔之间的距离,h1与h2为两个测压孔的测管水头。
达西通过实验,得到实验圆筒内渗流量Q与圆筒断面积A和水力坡度J成正比,并和土壤的透水性有关,所建立基本关系式如下:Q=KAJ v=Q/A=KJ式中,v为渗流简化模型的断面平均流速,系数K为反映孔隙介质透水性能的综合系数,称为参透系数。
实验中的渗流区为一圆柱形的均质砂体,属于均匀渗流,可以认为各点的流动状态是相同的,任意点的渗流流速u等于断面平均渗流流速,因此达西定律也可以表示为:u= v= KJ上式表明,渗流的水力坡度,即单位距离上的水头损失与渗流流速的一次方成正比,因此称为渗流线性定律。
Darcy’s Law 是描述以粘滞力为主、雷诺数Re< 1~10的层流状态下的地下水渗流基本定律,指出渗流速度V与水力坡度J成线性关系,V=KJ,或Q=KAJ,又称线性渗透定律。
地下水水文学实验

系数有关,因此在计算温热矿水或预测不同水温的渗透系数时,应考虑水
温的影响,现以校正成水温为10℃时为例对渗透系数校正计算,其计算公
式为:
;
K10
KT
10 T
K10
KT
mT m1
T
m0 mT
式中: K0,K10, KT―分别为水温在10℃;T℃的渗透系数。
t0,t10, tT ―分别为水温在10℃;T℃的温度校正系数。
渗 透
速 度
V= Q/F (cm 3/s)
测 压 管 水 位 (cm )
h1 h2 h3 h1-h2
水 位 差 (cm )
h2-h3 平 均 h
水 渗 透 力 系 数 坡 度 Kt I (cm /s)
水 温 t oC
平 均 渗 透 系 数Kcp
(cm /s)
I II III
实验一 达西定律--4.作业要求
表1-1 普阿杰里表
m
T℃
m
0.0139
16 0.0111
0.0135 17
0.0108
0.0131 18
0.0105
0.0127 19
0.0103
0.0124 20
0.0101
0.0120 21
0.0117
22
0.0114
23
0.0099 0.0097 0.0095
T℃ m
24 0.0093 25 0.0091 26 0.0089 27 0.0087 28 0.0085 29 0.0083 30 0.0081
(1) 掌握实验室测定岩石渗透系数的方法,加深对岩石渗透系数 的认识。 (2) 验证达西定律,从而提高对直线渗透定律的理解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一 达西定律验证实验
1 实验目的和要求
(1)测定均质沙柱的渗透系数K 值;
(2)测定通过沙柱的渗流量与水头损失的关系,验证渗流的达西定律。
2 实验原理
液体在孔隙介质中流动时,由于粘滞性作用将会产生能量损失。
达西(Henry Darcy )在1852-1855年间通过实验,总结得出渗流能 量损失与渗流速度成一次方的线性规律,后人称为达西定律。
由于渗流速度很小,故速度水头可以忽略不计。
因此总水头H 可用测压水头h 来表示,水头损失w h 可用测压水头差来表示,即
,
于是,水力坡度J 可用测管水头坡度来表示:
12w h h h h
J L L L
-∆=
==
式中:L 为两个测压管孔之间距离;1h 与2h 为两个测压孔的测压水头。
达西通过大量实验,得到砂柱内渗流量Q 与过水断面面积A 和水力坡度J 成正比,并和砂的透水性能有关,所建立基本关系式如下:
12
h h Q KA
KAJ L
-==或者
式中v 为渗流简化模型的断面平均流速,即渗流速度;系数K 为反映孔隙介质透水性能的综合系数,即渗透系数。
实验中的渗流区为一圆柱形的均质砂体,属于均匀渗流,可以认为各点的流动状态是相同的,任意点的渗流流速v 等于断面平均渗流流速,因此达西定律也可以表示为:v KJ =。
渗流雷诺数用下列经验公式求:1
0.750.23
e
e vd R n υ
=
⋅
+
式中e d 为砂样有效粒径、v 为渗流速度、υ为流体的运动粘滞系数、n 为孔隙率。
3 实验仪器或设备
直立圆筒沙柱;供水箱;量筒;测压管;秒表等。
4 实验步骤
(1)记录基本常数,包括实验圆筒内径D 、测孔间距L及砂样有效粒径d e、孔隙率n 与水温T。
(2)开启供水管注水,让水浸透圆筒内全部砂体并使圆筒充满水;一般按流量从大到小顺
h),通过调节出水口位置高度(即序进行实验。
本次实验采用固定供水箱以及该测压水头(
1
h)来改变测压水头差。
待水流稳定后,即可用体积法测定渗流量。
2
(3)依次调整水头,待水流稳定后进行上述测量,共测10次。
5 实验数据记录
(1)相关常数:
圆筒内径D=cm;
渗透路径L=cm;
d= cm;
沙粒有效粒径
e
孔隙率n=;
渗透水温T=℃;
运动粘滞系数υ=cm2/s
(2)实验记录表格
6 实验结果与数据处理
h,渗流量Q,水利坡度J,渗流速度v,渗透系数K,(1)计算出各测次的渗流水头损失
w
并填如下表;
h的关系曲线;
(2)给出流量Q与水头损失
w
(3)给出渗流速度v与水力坡度J的关系曲线;
R。
(4)计算出相应的临界雷诺数
e
7 分析思考问题
d不变时,流量Q为多少即为渗流实验上限?反过来当流量Q不变(1)当砂样有效粒径
e
d等于多大时为实验上限?若要确定达西定律的适用范围,实验应如何进行?
时,
e
(2)盛砂样的圆筒垂直放置、倾斜放置或水平放置,对实验测得的Q、v、J与渗透系数K 值有无影响?如将圆筒倒置,上述各值是否改变?。
