第六章 树和二叉树(2)
数据结构-6 树和二叉树

第六章树和二叉树一.选择题1. 以下说法错误的是。
A.树形结构的特点是一个结点可以有多个直接前趋B.线性结构中的一个结点至多只有一个直接后继C.树形结构可以表达(组织)更复杂的数据D.树(及一切树形结构)是一种"分支层次"结构2. 如图6-2所示的4 棵二叉树中,不是完全二叉树。
图6-2 4 棵二叉树3. 在线索化二叉树中,t 所指结点没有左子树的充要条件是。
A. t->left == NULLB. t->ltag==1C. t->ltag==1 且t->left==NULL D .以上都不对4. 以下说法错误的是。
A.二叉树可以是空集B.二叉树的任一结点最多有两棵子树C.二叉树不是一种树D.二叉树中任一结点的两棵子树有次序之分5. 以下说法错误的是。
A.完全二叉树上结点之间的父子关系可由它们编号之间的关系来表达B.在三叉链表上,二叉树的求双亲运算很容易实现C.在二叉链表上,求根,求左、右孩子等很容易实现D.在二叉链表上,求双亲运算的时间性能很好6. 如图6-3所示的4 棵二叉树,是平衡二叉树。
图6-3 4 棵二叉树7. 如图6-4所示二叉树的中序遍历序列是。
A. abcdgefB. dfebagcC. dbaefcgD. defbagc图6-4 1 棵二叉树8. 已知某二叉树的后序遍历序列是dabec,中序遍历序列是debac,它的前序遍历序列是。
A. acbedB. decabC. deabcD. cedba9. 如果T2 是由有序树T 转换而来的二叉树,那么T 中结点的前序就是T2 中结点的。
A. 前序B.中序C. 后序D. 层次序10. 某二叉树的前序遍历结点访问顺序是abdgcefh,中序遍历的结点访问顺序是dgbaechf,则其后序遍历的结点访问顺序是。
A. bdgcefhaB. gdbecfhaC. bdgaechfD. gdbehfca11. 将含有83个结点的完全二叉树从根结点开始编号,根为1号,后面按从上到下、从左到右的顺序对结点编号,那么编号为41的双亲结点编号为。
一棵度为2的有序属于一棵二叉树有何区别?

第六章 树和二叉树第一次作业6.1试分别画出具有3个结点的树和3个结点的二叉树的所有不同形态。
分析:一棵度为2的有序树与一棵二叉树的区别是:度为2的树有二个分支,没有左右之分;一棵二叉树也有两个分支,但有左右之分,且左右不能交换.33个结点的二叉树:6.4一个深度为H 的满k 叉树有如下性质:第H 层上的结点都是叶子结点,其余各层上每个结点都有k 棵非空子树。
如果按层次顺序(同层自左至右)从未有过开始对全部结点编号,问:(1) 各层的结点数目是多少?(2) 编号为i 的结点的双亲结点(若存在)的编号是多少?(3)编号为i 的结点的第j 个孩子结点(若存在)的编号是多少?(4) 编号为i 的结点有右兄弟的条件是什么?其右兄弟的编号是多少? 解:(1) K i -1(2) i =1时,该节点为根,无父节点;否则其父节点编号为(2)i k k +-⎢⎥⎢⎥⎣⎦(k ≥2) 分析:编号为p 的孩子结点的范围[(p -1)*k +2, p *k +1] 得出(i -1)/k ≤p ≤(i -2)/k +1(3) K *i +j +1-k(4)(i -1)MOD K <>0,该结点有右兄弟,其右兄弟的编号是i +16.5 已知一棵度为k 的树中有1n 个度为1的结点,2n 个度为2的结点,…,k n 个度为k 的结点,问该树中有多少个叶子结点?解: ∑=-+=k 1i i 0n )1i (1n分析:结点总数:n=n 0+n 1+n 2+……+n k ,n=1+n 1+2n 2+……+kn k所以得n 0 = n 2 + 2n 3 + …… + (k -1)n k + 1 6.6 已知在一棵含有n 个结点的树中,只有度为k 的分支结点和度为0的叶子结点,试求该树的叶子结点数目解:度:一个结点含有的子树的个数称为该节点的度;设有n k 个度为k 的分支结点,n 0个度为0的分支结点各点度数总和为:n=k*n k +1,最后计算得到叶节点个数为n-(n-1)/k 。
第6章_数据结构习题题目及答案_树和二叉树_参考答案

一、基础知识题6.1设树T的度为4,其中度为1,2,3和4的结点个数分别为4,2,1,1,求树T中的叶子数。
【解答】设度为m的树中度为0,1,2,…,m的结点数分别为n0, n1, n2,…, nm,结点总数为n,分枝数为B,则下面二式成立n= n0+n1+n2+…+nm (1)n=B+1= n1+2n2 +…+mnm+1 (2)由(1)和(2)得叶子结点数n0=1+即: n0=1+(1-1)*4+(2-1)*2+(3-1)*1+(4-1)*1=86.2一棵完全二叉树上有1001个结点,求叶子结点的个数。
【解答】因为在任意二叉树中度为2 的结点数n2和叶子结点数n0有如下关系:n2=n0-1,所以设二叉树的结点数为n, 度为1的结点数为n1,则n= n0+ n1+ n2n=2n0+n1-11002=2n0+n1由于在完全二叉树中,度为1的结点数n1至多为1,叶子数n0是整数。
本题中度为1的结点数n1只能是0,故叶子结点的个数n0为501.注:解本题时要使用以上公式,不要先判断完全二叉树高10,前9层是满二叉树,第10层都是叶子,……。
虽然解法也对,但步骤多且复杂,极易出错。
6.3 一棵124个叶结点的完全二叉树,最多有多少个结点。
【解答】由公式n=2n0+n1-1,当n1为1时,结点数达到最多248个。
6.4.一棵完全二叉树有500个结点,请问该完全二叉树有多少个叶子结点?有多少个度为1的结点?有多少个度为2的结点?如果完全二叉树有501个结点,结果如何?请写出推导过程。
【解答】由公式n=2n0+n1-1,带入具体数得,500=2n0+n1-1,叶子数是整数,度为1的结点数只能为1,故叶子数为250,度为2的结点数是249。
若完全二叉树有501个结点,则叶子数251,度为2的结点数是250,度为1的结点数为0。
6.5 某二叉树有20个叶子结点,有30个结点仅有一个孩子,则该二叉树的总结点数是多少。
第6章树和二叉树

9
6.1.4 树的存储结构
3.孩子兄弟表示法 孩子兄弟表示法 在结点中设置两个指针域, 在结点中设置两个指针域,一个指针域指向该结 点的第一个孩子,另一个指针域指向其右兄弟。 点的第一个孩子,另一个指针域指向其右兄弟。
2
6.1.1树的定义 树的定义
结点的度:结点所拥有子树的个数称为结点的度。 结点的度:结点所拥有子树的个数称为结点的度。 子树 称为结点的度 树的度:树中所有结点的度的最大值称为树的度。 最大值称为树的度 树的度:树中所有结点的度的最大值称为树的度。 叶结点:度为零的结点称为叶结点。也称终端结点 终端结点或 叶结点:度为零的结点称为叶结点。也称终端结点或叶 子 分支结点:度不为零的结点称为分支结点。也称非终端 分支结点:度不为零的结点称为分支结点。也称非终端 结点。除根结点以外,分支结点也称为内部结点。 结点。除根结点以外,分支结点也称为内部结点。 孩子结点和双亲结点: 孩子结点和双亲结点:树中一个结点的子树的根结点称 为孩子结点。该结点就称为孩子结点的双亲结点。 为孩子结点。该结点就称为孩子结点的双亲结点。 兄弟结点:具有同一双亲的孩子结点互为兄弟结点。 兄弟结点:具有同一双亲的孩子结点互为兄弟结点。 结点的祖先:从根到该结点所经分支上的所有结点, 结点的祖先:从根到该结点所经分支上的所有结点,称 为结点的祖先。 为结点的祖先。
17
6.2.2 二叉树的性质
性质4 具有n( 性质 具有 (n>0)个结点的完全二叉树的深度 )个结点的完全二叉树的深度h= log 2 n + 1 证明: 证明: 根据完全二叉树的定义可知深度为h-1层及以上的结点构成 根据完全二叉树的定义可知深度为 层及以上的结点构成 满二叉树,因此由性质2得深度为 得深度为h的完全二叉树满足 满二叉树,因此由性质 得深度为 的完全二叉树满足 n>2h-1-1和n≤2h-1 和 整理后得到 2h-1≤n<2h 不等式两边取对数, 不等式两边取对数,得 h-1≤log2n<h 由于h为正整数 为正整数, 由于 为正整数,因此 h= log 2 n + 1
第6章树和二叉树(2)培训讲学

第6章树和二叉树(2)第六章树和二叉树一、选择题1.算术表达式a+b*(c+d/e)转为后缀表达式后为()A.ab+cde/* B.abcde/+*+ C.abcde/*++ D.abcde*/++2. 设森林F对应的二叉树为B,它有m个结点,B的根为p,p的右子树结点个数为n,森林F中第一棵树的结点个数是()A.m-n B.m-n-1 C.n+1 D.条件不足,无法确定3.若度为m的哈夫曼树中,其叶结点个数为n,则非叶结点的个数为()。
A.n-1 B.⎣n/m⎦-1 C.⎡(n-1)/(m-1)⎤ D.⎡n/(m-1)⎤-1E.⎡(n+1)/(m+1)⎤-14.深度为h的满m叉树的第k层有()个结点。
(1=<k=<h)A.m k-1 B.m k-1 C.m h-1 D.m h-15. 若X是二叉中序线索树中一个有左孩子的结点,且X不为根,则x的前驱为( )A.X的双亲B.X的右子树中最左的结点C.X的左子树中最右结点D.X的左子树中最右叶结点6. 引入二叉线索树的目的是()A.加快查找结点的前驱或后继的速度 B.为了能在二叉树中方便的进行插入与删除C.为了能方便的找到双亲 D.使二叉树的遍历结果唯一7.由3 个结点可以构造出多少种不同的二叉树?()A.2 B.3 C.4 D.58.下述编码中哪一个不是前缀码()。
A.(00,01,10,11) B.(0,1,00,11) C.(0,10,110,111)D.(1,01,000,001)二、判断题1. 给定一棵树,可以找到唯一的一棵二叉树与之对应。
2.将一棵树转成二叉树,根结点没有左子树;3. 在中序线索二叉树中,每一非空的线索均指向其祖先结点。
4. 一棵哈夫曼树的带权路径长度等于其中所有分支结点的权值之和。
5.当一棵具有n个叶子结点的二叉树的WPL值为最小时,称其树为Huffman树,且其二叉树的形状必是唯一的。
三、填空题1.一棵树T中,包括一个度为1的结点,两个度为2的结点,三个度为3的结点,四个度为4的结点和若干叶子结点,则T的叶结点数为___ ___。
数据结构考试题库含答案

数据构造习题集含答案目录目录1选择题2第一章绪论2第二章线性表4第三章栈和队列6第四章串7第五章数组和广义表8第六章树和二叉树8第七章图11第八章查找13第九章排序14简答题19第一章绪论19第二章线性表22第三章栈和队列24第四章串26第五章数组和广义表27第六章树和二叉树28第七章图31第八章查找31第九章排序32编程题34第一章绪论34第二章线性表34第三章栈和队列45第四章串45第五章数组和广义表45第六章树和二叉树45第七章图45第八章查找45第九章排序50选择题第一章绪论1.数据构造这门学科是针对什么问题而产生的?〔A 〕A、针对非数值计算的程序设计问题B、针对数值计算的程序设计问题C、数值计算与非数值计算的问题都针对D、两者都不针对2.数据构造这门学科的研究容下面选项最准确的是〔D 〕A、研究数据对象和数据之间的关系B、研究数据对象C、研究数据对象和数据的操作D、研究数据对象、数据之间的关系和操作3.*班级的学生成绩表中查得三同学的各科成绩记录,其中数据构造考了90分,则下面关于数据对象、数据元素、数据项描述正确的选项是〔C 〕A、*班级的学生成绩表是数据元素,90分是数据项B、*班级的学生成绩表是数据对象,90分是数据元素C、*班级的学生成绩表是数据对象,90分是数据项D、*班级的学生成绩表是数据元素,90分是数据元素4.*数据构造是指〔A 〕。
A、数据元素的组织形式B、数据类型C、数据存储构造D、数据定义5.数据在计算机存储器表示时,物理地址与逻辑地址不一样,称之为〔C 〕。
A、存储构造B、逻辑构造C、链式存储构造D、顺序存储构造6.算法分析的目的是〔C 〕A、找出数据的合理性B、研究算法中的输入和输出关系C、分析算法效率以求改良D、分析算法的易懂性和文档型性7.算法分析的主要方法〔A 〕。
A、空间复杂度和时间复杂度B、正确性和简明性C、可读性和文档性D、数据复杂性和程序复杂性8.计算机部处理的根本单元是〔B 〕A、数据B、数据元素C、数据项D、数据库9.数据在计算机有链式和顺序两种存储方式,在存储空间使用的灵活性上,链式存储比顺序存储要〔B 〕。
第六章-树和二叉树

之
树 和 二 叉 树 13
1 2 3 A B C
4 5 6 7 0 D E F
8 0
9 10 0 G
¾ 二叉树顺序存储的算法描述
数 据 结 构
¾ 初始化二叉树
之
树 和 二 叉 树 14
#define Max_Size 100 typedef int TElemType; typedef TElemType SqBT[Max_Size+1]; void InitBT(SqBT bt){//设置空树 int i; for(i=1;i<=Max_Size;i++) bt[i]=0; }
数 据 结 构
之
树 和 二 叉 树 19
¾ 后序遍历顺序二叉树算法 void PostBT(SqBT bt,int i){ if(i>Max_Size||!bt[i]) return; PostBT(bt,2*i); PostBT(bt,2*i+1); printf("%3d ",bt[i]); }
数 据 结 构
之
树 和 二 叉 树 4
5. 孩子结点、双亲结点、兄弟结点、堂兄弟 结点、祖先结点、子孙结点…… 6. 结点的层次从根开始,根为第一层,根的 孩子为第二层;若某结点在第L层,则其 子树的根就在第L+1层。 7. 树的深度或高度:树中结点的最大层次。 8. 有序树:如果将树中结点的各子树看成是 从左至右有次序的;反之,则是无序树。 9. 森林:是m棵互不相交的树的集合。
数 据 结 构
之
树 和 二 叉 树 25
¾ 打印一维数组 void printSq(SqBT bt){ int i; printf("\nSeqArray:"); for(i=1;i<=Max_Size;i++) printf("%3d ",bt[i]); }
第6章树和二叉树2
深度遍历策略
二叉树由根、左子树、右子树三部分组成
二叉树的遍历可以分解为: 访问根(D) 遍历左子树(L) 遍历右子树(R) 有六种遍历方法: D L R,L D R,L R D, D R L,R D L,R L D
A B C
D G
E
F
约定先左后右,有三种遍历方法: 分别称为先序遍历、中序遍历、后序遍历
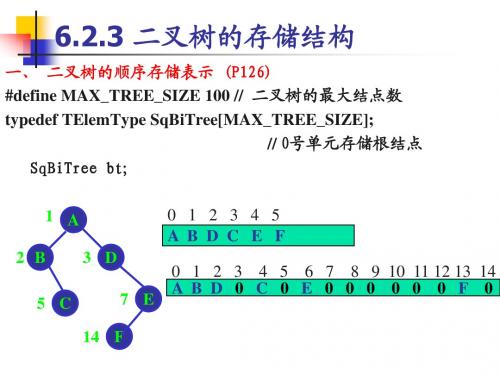
6.2.3 二叉树的存储结构
二、二叉树的链式存储表示 1、二叉链表(P126) typedef struct BiTNode { lchild data rchild TElemType data; struct BiTNode *lchild, *rchild; // 左右孩子指针 } BiTNode, *BiTree; A B D
B D G E
C F
后序遍历(LRD)
后序遍历动态演示
A B D G
D, G, E, B, F, C, A
C
E F
2007-1 试题
对下图所示的二叉树进行后序遍历(左子树、 右子树、根结点)的结果是 (42) 。
5 2 4 6 3 1
(42)A. 5 2 3 4 6 1 C. 2 6 4 1 3 5
if (!StackEmpty(s)) { p=pop(s); visite(p->data); //访问根结点 p=p->rchild; //通过下一次循环实现右子树遍历 }//endif }//endwhile }//InOrderUnrec
6.3.1 遍历二叉树
后序遍历的非递归算法描述
后序遍历时,每遇到一个结点,先把它推入栈中,让PopTim=0。在遍历其 左子树前,改结点的PopTim=1,将其左孩子推入栈中。在遍历完左子树后,还 不能访问该结点,必须继续遍历右子树,此时改结点的PopTim=2,并把其右孩 子推入栈中。在遍历完右子树后,结点才退栈访问。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结束
第 2 页
60 30 15 30 15 60 30 15 5 10 30 15 5 15 10 15 30
结束
5 10
WPL=5*1+10*2+15*3+30*3=160
30 15
WPL=5*3+10*3+15*2+30*1=105
WPL=5*2+10*2+15*2+30*2=120
第 3 页
weight parent lchild rchild
HTNode类型的结构变量
结束
第 18 页
w 100 42 23 11 5 19 8 3 29 14 7 58 29 15 8 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
p 5 29 7 8 14 23 3 11 8 15 19 29 42 58 100
100 60 30 15 5 10
结束
40 30
15
第 5 页
3 哈夫曼树的构造 构造哈夫曼树的步骤: 1.根据给定的n个权值 ,构造n棵只有一个根结点的二叉树, n个权值分 别是这些二叉树根结点的权。设F是由这n棵二叉树构成的集合 2.在F中选取两棵根结点权值最小的树作为左、右子树,构造一颗新的 二叉树,置新二叉树根的权值=左、右子树根结点权值之和; 3.从F中删除这两棵树,并将新树加入F; 4.重复 2、3,直到F中只含一棵树为止;
b: c: d: e: f: g: h: 10 1110 1111 110 00 0111 010
结束
第 17 页
3.哈夫曼编码算法 设用一维数组W存储n个权值, 用静态三叉链表HT存储哈夫曼树
存储哈夫曼树的静态三叉链表类型定义 typedef struct { unsigned int weight; unsigned int parent, lchild, rchild; }HTNode, *HuffmanTree; //动态分配数组存储哈夫曼树
100 42 23 11 5 19 8 3 29 14 7 58 29 15 8 a: b: c: d: e: f: g: h: 0110 10 1110 1111 110 00 0111 010
结束
第 15 页
*哈夫曼树的应用 哈夫曼树的应用 1)报文到电文的译码 a) 从根出发 b) 取一位报文,若取完,译码结束。 c) 若报文=1,向右分支行进一个结点 若报文=0,向左分支行进一个结点 d) 若所得结点不是叶结点,转b) e) 若所得结点是叶结点,则字符即为译码结果,得到一个 字符,转a) 例:报文:111010001100100111 c b f e h g
哈夫曼树
哈夫曼树对应的静态三叉链表
结束
第 19 页
哈夫曼算法 void HuffmanTree(HuffmanTree &HT, int * w, int n){ //w 存放n 个字符的权值(均>0),构造赫夫曼树HT if (n<=1) return; m=2* n-1; HT=(HuffmanTree)malloc(m+1) * sizeof(HTNode); //为哈夫曼树分配存储 //空间 for (p=HT, i=1; i<=n; ++i, ++p, ++w) * p={ * w, 0, 0, 0}; //用给定的n个权// 值 ,构造n棵只有一个根结点的二叉树 for (; i<m; ++i; ++p) { //按构造哈夫曼树的步骤2、3、4,建哈夫曼树 //在HT[1..i-1] 选择parent为0且weight最小的两个结点,其序号分别为s1和 s2。 Select(HT, i-1, s1, s2); HT[s1]. parent =i; HT[s2].parent=i; //HT[i]存放新子树的根结点, HT[i].lchild=s1; HT[i].rchild=s2; HT[i].weight=HT[s1].weight+HT[s2].weight;
结束
第 9 页
采用不等长的编码,并且让字符串中出现频率大的字符的编码尽可 能的短,则电文的(字符串的编码)总长度即可减少,但这时会出现 编码的唯一性问题。 如果:A,B,C,D的编码分别为:0,00,1,01 则:上述电文:000011010 共9位,长度减少。但是译文困难。前面的 连续四个0,可以译成AAAA,BB,ABA。不唯一。 3).前缀 前缀编码 3).前缀编码 任一字符的编码都不是另一个字符编码的前缀。如果我们的不等长 编码是前缀编码,则问题就解决了。 前缀编码可以用二叉树来设计。方法: 1)字符放在叶结点上。 2)树中度为1的结点个数为0。 3)左右分支的编码分别为0,1。 4)从根结点到叶结点的路径上各分支的字符组成的二进制串作为 叶结点的编码。
第 22 页
HT
w
p
lch rch
0 5 0 0 0 1 2 29 0 0 0 5 7 0 0 0 3 8 0 0 0 4 5 14 0 0 0 6 23 0 0 0 3 0 0 0 7 8 11 0 0 0 9 10 11 12 13 14 15 8 棵只有一个结点的二叉树
结束
第 6 页
例:构造以W=(5,15,40,30,10)为权的哈夫曼树。
100 5 15 40 30 10 30 15 5 10 15 40 30 5 15 10 15 60 30 40
60 30 15 5 10 15 40 30 5 15 10 30 15 40
结束
30
第 7 页
6.6.2 哈夫曼编码 1.哈夫曼编码 哈夫曼编码 哈夫曼树除了能求解最优判定问题解,还用于其他一些最优问题的求 解。这里介绍用哈夫曼树求解数据的二进制编码。 在进行数据通讯时,涉及数据编码问题。所谓数据编码就是数据与 二进制字符串的转换。例如:数据压缩、邮局发电报,发送方将原文转 换成二进制字符串,接收方将二进制字符串还原成原文。 原文 ---电文(二进制字符串) ----原文 例 要传输的原文为ABACCDA 设ABCD的编码为 A;00 B;01 C:10 D:11 发送方:将ABACCDA 转换成 00010010101100 接收方:将 00010010101100 还原为 ABACCDA
分数 0-59 60-69 70-79 80-89 90-100 0.15 0.40 0.30 0.10 比例数 0.05
结束
第 4 页
按图的判定过程,转换一个分数所需的比较次数=从根到对应结点的路径 长度。转换10000个分数所需的总比较次数= 10000(0.05 × 1+0.15 × 2+0.4 × 3+0.3 × 4+0.1 × 4) 若将学生成绩在5个等级以上的分布比例看作描述判定过程二叉树叶子结 点权值,(0.05 × 1+0.15 × 2 +0.4 × 3+0.3 × 4+0.1 × 4)正是该二叉树的带 权路径长度。可见要想获得效率较高的转换程序,可构造以分数的分布 比例为权值的哈夫曼树。
结束
第 8 页
1).等长编码 1).等长编码 等长 每个字符都有相同长度的二进制编码。 我们上面的例子是一个等长编码的例子。 *优点:译文容易。 *缺点:报文长。 若某种文字有n个字符,每个字符的编码为k位,则: K=log2(n+1) 例如:英文字母26个,若要等长的给每个字母一个编码,则需要5 位二 进制。 2).不等长编码 2).不等长编码 不等长 每个字符具有长度不同的二进制编码。 在电报通讯的例子中,我们总希望电文长度尽可能的短。在数据 压缩时总希望压缩比尽可能的大。
结束
第 10 页
A :0
A B C
B: 10 C:11 用这种方式得到的编码是前缀编码。
结束
第 11 页
例 某通讯系统只使用8种字符a、b、c、d、e、f、g、h,其使用频率分 别为0.05,0.29,0.07,0.08, 0.14,0.23, 0.03,0.11,利用二叉树设计一种不等长 编码: 1)构造以 a、b、c、d、e、f、g、h为叶子结点的二叉树; 2)将该二叉树所有左分枝标记0,所有右分枝标记1; 3)从根到叶子结点路径上标记作为叶子结点所对应字符的编码;
结束
第 1 页
6.6 哈夫曼树及其应用
6.6.1 哈夫曼树及构造 1 哈夫曼树的概念 哈夫曼树的概念 路径:从一个祖先结点到子孙结点之间的分支构成这两个结点间的路径; 路径长度:路径上的分支数目称为路径长度; 结点的权:根据应用的需要可以给树的结点赋权值; 结点的带权路径长度:从根到该结点的路径长度与该结点权的乘积; 树的带权路径长度=树中所有叶子结点的带权路径之和; 通常记作 WPL= ∑ wi × Li 哈夫曼树:假设有n个权值(w1 , w2 , … , wn ),构造有n个叶子结点的二叉 树,每个叶子结点有一个 wi 作为它的权值。则带权路径长度最小的二叉 树称为哈夫曼树。 哈夫曼树。 哈夫曼树
a: b: c: d: e: f: g: h: 0000 0001 0010 0011 010 011 10 11
结束
g e a b c d f
h
第 12 页
如何得到使二进制 串总长最短编码
应用中每个字符的使用频率是不一样的。显然,为使传输的二进制 串尽可能的短,使用频率高的字符用较短编码,使用频率低的字符用较 长的编码。如何使得电文最短呢?这就希望常用的字符编码尽可能的短。 统计语言各个字符的使用频度Wi,利用哈夫曼树就可以对这种语言 定义出一种最优的编码,使∑WiLi最小(电文最短)。
结束
第 13 页
2.哈夫曼编码 目的:得到使报文最短的前缀码表 途径:构造哈夫曼树 依据:字符的使用频度
