五点法画正弦交流电波形图
正弦交流电相关数学知识讲解浅析
Science &Technology Vision科技视界0引言正弦交流电是电工基础课程中的一个重要的章节,涉及三角函数、复数等大量数学知识。
技工院校的学生大多数学基础薄弱,而电工老师不可能拿出大量时间讲授相关数学知识,导致学生无法真正掌握其中原理。
作为电工相关专业的数学老师,有必要将数学的有关知识和原理渗透于正弦交流电的学习中,在数学和正弦交流电之间搭起一座桥梁。
这需要数学老师掌握相关的电工知识,科学系统地设计出一套行之有效的教学方案。
只要在三角函数和复数的教学中把握以下三条主线,就能为正弦交流电铺平道路。
本文浅析正弦交流电相关数学知识的讲解。
1在线段“旋转”中阐释两个“为什么”“为什么线圈切割磁感线形成的交流电可以用一个正弦型函数来表示?”“为什么正弦量可以用复数来表示?”很多学生被这两个问题困扰着。
要从本质上认识正弦交流电及掌握有关计算,就绕不开这两个核心问题。
从数学的角度来看,问题的本质都是研究线段“旋转”过程中在垂直方向或水平方向产生的投影值的变化规律。
1.1在“旋转”中阐释“为什么正弦量可以用复数来表示?”正弦量用复数表示的推理过程与正弦函数图像的形成过程是相通的,运用相似的“旋转”原理。
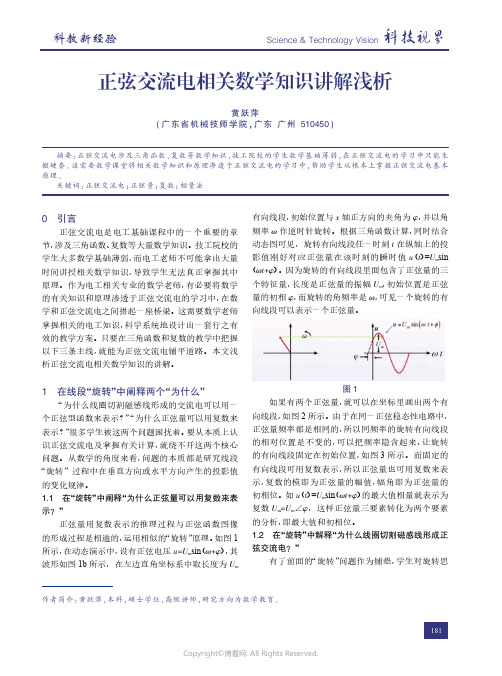
如图1所示,在动态演示中,设有正弦电压u=U m sin (ω+φ),其波形如图1b 所示,在左边直角坐标系中取长度为U m有向线段,初始位置与x 轴正方向的夹角为φ,并以角频率ω作逆时针旋转。
根据三角函数计算,同时结合动态图可见,旋转有向线段任一时刻t 在纵轴上的投影值刚好对应正弦量在该时刻的瞬时值u (t )=U m sin(ωt+φ)。
因为旋转的有向线段里面包含了正弦量的三个特征量,长度是正弦量的振幅U m ,初始位置是正弦量的初相φ,而旋转的角频率是ω,可见一个旋转的有向线段可以表示一个正弦量。
图1如果有两个正弦量,就可以在坐标里画出两个有向线段,如图2所示。
由于在同一正弦稳态性电路中,正弦量频率都是相同的,所以同频率的旋转有向线段的相对位置是不变的,可以把频率隐含起来,让旋转的有向线段固定在初始位置,如图3所示。
第5章 正弦交流电路

j I2 I
I1 +1
O
例2 相量图(三角形) 相量图(三角形)
j I I2
I1 +1
O
§5 – 3 单一参数的正弦交流电路
一、电阻元件 1. u – i 关系 R u i ωt u
i
相量表示
U=RI
I
U
2. 功率关系 p
P i ωt
p 始终 ,R——耗能元件 始终>0, 耗能元件 P = UI = RI2 = U2/R
导纳角 φY = tg-1 (BC –XL )/G ——阻抗角 阻抗角 当 BC >BL 时,φY > 0 ,i 超前于 u ——容性 容性 当 BC <BL 时, φY < 0 ,u 超前于 i ——感性 感性 当 BC= BL 时, φY = 0 ,u 、i 同相 ——纯电导 纯电导
二、相量图——两个三角形 相量图 两个三角形 I= IG + IL + IC I U IG G IL L IC C
G
பைடு நூலகம்
φY
U IG IB I IL IC
φY
y
B
例题
R=30
XL=40
U=120V
求各电流及Y 求各电流及 设U = 120
I
0o V
U
R
IR
IL
L
IR = U/R= 4 A IL = U/jXL = – j3A I = IR+ IL =4 – j3A=5 – 37oA Y=1/R – j/XL=1/30 – j1/40(S) I IR IL U
2. 频率特性 XL=ωL ω U 相量表示 U = j(ωL) I I
3. 功率关系 p ωt
《电工基础》第5章 正弦交流电路ppt课件

最新课件
11
三、正弦交流电的变化范围
1. 最大值 :正弦交流电在一个周期所能达到的 最大瞬时值,又称峰值、幅值。
用大写字母加下标m表示,如Em、Um、 Im。
2.有效值 :加在同样阻值的电阻上,在相同的 时间内产生与交流电作用下相等的热量的直 流电的大小。
用大写字母表示,如E、U、I。
最新课件
12
最新课件
14
• 用数字万用表测量正弦交流电压时要选择交流
挡,测量的结果是电压有效值;若不慎错用直 流挡,则显示为零。
用直流挡测量市电显示为零
最新课件
15
• 用数字万用表测量直流电压时要选择直流挡, 测量的结果是电压平均值;若不慎错用交流挡, 则显示为零 。
用交流挡测量最叠新层课电件池显示为零
16
(1)同一相量图中,相同单位的相量应按相 同比例画出。
(2)一般取直角坐标轴的水平正方向为参考 方向,逆时针转动的角度为正,反之为负。
(3)用相量图表示正弦交流电后,它们的加、 减运算可按平行四边形法则或三角形法则进行。
最新课件
27
§5-3 单一参数的交流电路
最新课件
28
一、纯电阻电路
• 只含有电阻元件的交流电路称为纯电 阻交流电路。
QCUCICIC 2XCU XC C 2
最新课件
50
§5-4 LC谐振电路
最新课件
51
一、RLC串联电路
• 1.电压三角形 如图所示为RLC串
联电路,为正弦交流 电压,这三个元件流 过同一电流,电流与 各元件电压参考方向 如图所示。
最新课件
52
• 设电流的解析式为
iImsint
• 电阻、电感和电容两端的电压分别为
正弦交流电路(1)

U 4
U 2 U1 U 2 U 3 U 4 U 5 U 6 0 U1
U 5
U 6
例: i1 6 2 sin(t 30)
i2 8 2 sin(t 60)
求i=i1+i2
i
解: I1 630 5.196 j3
i1 i2
I2 8 60 4 j6.928
I I1 I2 (5.196 j3) (4 j6.928) 9.296 j3.928 10 23.1A
2、旋转矢量 Aej ωt
设A=ρej θ 则: Aej ωt= ρej θej ωt=ρej(θ+ ωt)
二、正弦量的几种表示方法
• 正弦量具有幅值、频率及初相位三个基 本特征量,表示一个正弦量就要将这三 要素表示出来。
• 表示一个正弦量可以多种方式,这也正 是分析和计算交流电路的工具。
u 1、三角函数表示法:
一、电压电流关系
1 、L中的瞬时电流与电压
基本关系式: u L di dt
i uL
设 i 2 I sin t
则 u L di 2 I L cos t
dt
2 U sin( t 90 )
结论(a) 电感电压、电流有效值的关系为:
UL =ωLIL (b) 电感电压超前电流90°即Ψu =Ψi+90°
反映交变快慢的量
角频率
反映大小的量 X m 正弦量的幅值
反映初始值的量
0 初相位
四、正弦量的三要素
1、周期 T (s) 正弦量完整变化一周所需要的时间
频率 f (Hz) 正弦量在单位时间内变化的周数
角频率 (Rad s ) 正弦量单位时间内变化的弧度数
周期与频率的关系: f 1
T
正弦交流电的三种表示法
u1 U m sin(t ) 250sin (100 t )
3
)V
小结:
i I m sin
最大值
t 0
初相位
角频率
周期
i
最大值
Im
T
t
初相位 0
I m 最大值
0
初相位
作业:
0
。
例
已知:某正弦交流电流的振幅为2A,频率为50Hz,
初相角为
解:已知
6
, 请写出瞬时值表达式。
i
6
I m 2A
f 50Hz
2f 2 50 100 rad / s
i I m sin t 0 2sin (100
6
习题册:P80
u Um
u Um sin( t -/2)
t
-/2 /2 3/2 2 5/2
小规律: 若起点在坐标原点(或纵轴)的左侧, 0 >0; 若起点在坐标原点(或纵轴)的右侧, 0 <0。
几种不同起点的正弦电流波的初相位:
i
Im
i1
i
i
Im
0
i2
Im
t
0
i3
0
t
3
3
小技巧: i I m sin t 0 sin前面的值为最大值;
)
t前面的值为角频率ω ;
t后面的值为初相位
。
找到问题了吗?
I 5 sin100t A 6
11 12正弦交流电基本概念与表示方法

ω = 2π f π
二、有效值
在电工技术中,有时并不需要知道交流电的瞬时值, 在电工技术中,有时并不需要知道交流电的瞬时值,而 规定一个能够表征其大小的特定值——有效值,其依据是交 有效值, 规定一个能够表征其大小的特定值 有效值 流电流和直流电流通过电阻时,电阻都要消耗电能(热效应) 流电流和直流电流通过电阻时,电阻都要消耗电能(热效应)。
2.有效值相量表示法 .
有效值相量表示法是用正弦量的有效值做为相量的模( 有效值相量表示法是用正弦量的有效值做为相量的模(长 是用正弦量的有效值做为相量的模 度大小) 仍用初相角做为相量的幅角, 度大小)、仍用初相角做为相量的幅角,例如
u = 220 2 sin(ωt + 53°) V,i = 0.41 2 sin ωt A
二、交流电的表示法
1.解析式表示法 . 2.波形图表示法 .
i(t) = Imsin(ωt + ϕi0) () ( u(t) = Umsin ( ωt + ϕu0 ) () e (t) = Emsin ( ωt + ϕe0 ) ) 波形图表示法即用正弦量解析 式的函数图形表示正弦量的方法。 式的函数图形表示正弦量的方法。
时间内, 设正弦交流电流 i( t ) 在一个周期 T 时间内,使一电 ( 阻R 消耗的电能为 QR ,另有一相应的直流电流 I 在时间 T 消耗相同的电能, 内也使该电阻 R 消耗相同的电能,即 QR = I2RT 。
就平均对电阻作功的能力来说,这两个电流( 就平均对电阻作功的能力来说,这两个电流(i 与 I)是等效 ) 的,则该直流电流 I 的数值可以表示交流电流 i(t) 的大小,于 ( ) 的大小, 称为交流电流的有效值。 是把这一特定的数值 I 称为交流电流的有效值。理论与实验均 可证明,正弦交流电流 i 的有效值 I 等于其振幅(最大值)Im 的 可证明, 等于其振幅(最大值) 0.707 倍,即
正弦交流电路的相量表示法

解析式 波形图
1、相量图
相
量
法
2、相量式
(复数
符号法)
正弦交流电的3大类表示方法
iImsi nt
i
Im
t
T
U
.
I a jb
I (cos j sin )
I
具体见下页内容:
1.复数的实部、虚部和模
1
叫虚单位,数学上用 i 来代表它,因为在电工中i代表电流,所以改用 j 代表虚单位,即 j =
3. 复数的运算 1)复数的加减
实部与实部加减,作为结果的实部 虚部与虚部加减,作为结果的虚部
用有向线段加减时,符合平行四边形法则
例:A1=2+j3 A2=4+j4
则 A1+A2=(2+j3)+(4+j4)=6+j7 A1-A2=(2+j3)-(4+j4)=-2-j
正弦量的相量表示法
2) 复数的乘除
u(t)200sint V
解:
I1= 1 0- 60 (A)
I2= 1 514(7 V)
U=100 20(V )
3.3 正弦量的相量表示法
【例题讲解】
对应
u(t)2Usin(tθ)
•
U U θ
例1. 已知
i 141.4sin(314t 30o)A u311.1sin(314t60o)V
试用相量表示i, u .
u22 si(0 ω nt4)5 I 4ej30 复数
• 220
?
U 45
42si(n ωt30 ) ?
2
有效值
j45
瞬时值
U m22e0 45 ?
第2章 正流交流电路

正弦量的波形图表示:求和: i i1 i2
三者间的关系示为:
f =1/ T ω =2 /T=2 f 我国和大多数国家采用50Hz作为电力工业标 准频率(简称工频),少数国家采用60Hz。
2.1.2
振幅和有效值
i
描述正弦量数值大小的参数: 瞬时值:正弦量任意瞬间的值 0 称为瞬时值,用小字母表示: i、u、e 振幅:正弦量在一个周期内的 最大值,用带有下标m的大写字母表示: Im、Um、Em
振幅 Im
T
t
有效值:一个交流电流的做功能力相当于某一数值的 直流电流的做功能力,这个直流电流的数值就叫该交 流电流的有效值。用大写字母表示: I、U、E
有效值与幅值的关系推导如下: 以电流为例:设同一个负载电阻R,分别通入 周期电流 i 和直流电流 I 。
i
I
R
T
0
pdt=
T
同一时间T 内消耗的 能量
2
0
-1
. π . . . . 2π x . 0 -1 .
1
2
3 2
y
五点法
i
2.1.1 频率与周期
描述正弦量变化快慢的参数:
0
T T/2 2
t
t
T
周期(T): 变化一个循环所需要 的时间,单位(s)。
频率( f ): 单位时间内的周期数 单位(Hz)。
角频率(ω ): 每秒钟变化的弧度数,单位(rad/s)。
i i 1
i2
t
O
② 不同频率的正弦量比较无意义。
例:已知: i 幅度:
sin1000 t 30A
I 1 0.707 A 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五点法画正弦交流电波
形图
Document number:NOCG-YUNOO-BUYTT-UU986-1986UT
“五点法”画正弦交流电波形图
叶和人(辽宁丹东市技师学院辽宁丹东118002)
摘要:已知解析式画波形图一般有两种,一是u-ωt波形图,二是u-t波形图。
“五点法”画波形图的方法:一、由u=Umsinωt左右平移角得出波形图;二、由u=Umsinωt确定t值得出波形图。
无论哪种方法,都要记住正弦曲线的基本形状,知道“五点”是哪五点,纵坐标总是0、Um、0、-Um、0不变。
关键词:正弦交流电“五点”坐标平移波形图
“五点法”画正弦曲线,学生在数学课中学习过,对其波形图形状已熟知。
《电工基础》课教学中,要求学生掌握正弦交流电的三种表示法:解析式、波形图、相量图。
教材中没有介绍具体画法,本文将介绍用“五点法”画正弦交流电波形图的方法。
会画波形图将对学生在正弦交流电路的相关计算和今后正弦交流电路分析时有所帮助。
正弦交流电解析式的一般表达式为:
i=Ims in(ωt+i)
u=Umsin(ωt+u)
e=Emsin(ωt+e)
在已知解析式的条件下,画波形图一般有两种,一是u-ωt波形图,二是u-t波形图,下面以正弦交流电压波形图为例讲解“五点法”画波形图的方法。
一、由u=Umsinωt左右平移角得出波形图
1、u-ωt波形图?
(1)u=Umsinωt的波形图(初相位0)
①波形图的五点坐标为:(0、0)、(、Um)、(π、0)、(、-Um)、(2π、0)。
②由五点画出波形图为:
?
上述五点坐标和波形图在数学课中已为学生所熟知。
(2)初相大于0,即u=Umsin(ωt+)的波形图
①由u=Umsinωt波形图向左平移角,五点横坐标变为-、-、π-、-、2π-,即初相为0时横坐标均减去;纵坐标不变。
②画出五点,描绘出波形图为:
?
(3)初相小于0,u=Umsin(ωt-)的波形图
①由u=Umsinωt波形图向右平移角,五点横坐标为、+、π+、+、2π+,即五点坐标均加上;纵坐标不变。
②画出五点,描绘出波形图。
?
例
一,画出正弦电压为u=2202sin(100πt+60°)的波形图。
解:=60°,Um=2202v,五点横坐标为-60°、90°-60°=30°、180°-
60°=120°、270°-60°=210°、360°-60°=300°;纵坐标为0、2202、0、-220 2、0。
在直角坐标系下画出五点,绘出波形图:
?
2、u-t波形
图
(1)u=Umsinωt的波形图
①由解析式求出T=。
②五点坐标为:(0、0)、(、Um)、(、0)、(T、-Um)、(T、0)。
③画出五点,绘出波形图。
?
(2)u=Umsin(ωt+)的波形图(初相大于0)。
①由u=Umsinωt波形图向左平移t0,t0=。
②五点横坐标为-t0、-t0、-t0、T-t0、T-t0;纵坐标不变。
(T=)
③画出五点,绘出波形图
?
(3)u=Umsin(ωt+)的波形图(初相小于0)
同理可得波形图为:
?
小结:以u=Umsinωt的波形图为参考,1、五点横坐标,初相大于0,向左平移(或t0=);初相小于0,向右平移(或t0=)。
2、纵坐标任何情况下都是0、Um、0、-Um、0。
二、由u=Umsinωt确定值得出波形图
设u=Umsin(ωt+),(包括大于0、小于0、等于0三种情况)。
1、求五点坐标,按下列表格进行:
?
画u-t波形图,求五对u、t值,画u-ωt波形图求五对u、ωt值,本身带符号。
2、在直角坐标系下画出五点,描绘出波形图。
例二,画出u=3802sin(100πt-60°)v的波形图。
解:(1)求五点坐标,ω=100π,=60°=-,Um=3802v
?
(2)画出五点,描绘出波形图。
①u-ωt波形图
?
②u-t波形图
?
小结:无论哪种方法,都要记住正弦曲线的基本形状,知道“五点”是哪五点,纵坐标总是0、Um、0、-Um、0不变。
